Похожие презентации:
Повышение качества обучения математики с учетом результатов ГИА (ЕГЭ) в 2021 году
1. Повышение качества обучения математики с учетом результатов ГИА в 2021 году
ПОВЫШЕНИЕ КАЧЕСТВАОБУЧЕНИЯ МАТЕМАТИКИ
С УЧЕТОМ РЕЗУЛЬТАТОВ
ГИА В 2021 ГОДУ
СП «Ресурсно-методический центр» МАУ ДО
«Центр творчества»
2. ГИА 9 в форме ОГЭ
3. Содержание КИМ
МАТЕМАТИКАНе геометрия
Геометрия
1 часть:
15 заданий
1 часть:
4 задания
2 часть: 3
задания
2 часть: 3
задания
25 заданий:
19 – базовый уровень
4 – повышенный уровень
2 – высокий уровень
Шкала пересчета балла в отметку
(с учётом корректировки)
«2»
0-6
«5»
22 - 31
«3»
7 – 14, 1 балл
за задания по
геометрии
«4»
15 – 21, , 1
балл за
задания по
геометрии
минимальный критерий: 7 баллов,
набранные по всей работе, , 1 балл за
задания по геометрии
Всего за работу – 31 балл
Из них
10 баллов – за задания по геометрии
4.
Порядок проведения государственной итоговой аттестации пообразовательным
программам
основного
общего
образования с изменениями
П.13 Органы исполнительной власти субъектов Российской
Федерации, осуществляющие государственное управление в
сфере образования, обеспечивают проведение ГИА :
определяют минимальное количество баллов;
обеспечивают перевод суммы первичных баллов за
экзаменационные работы ОГЭ и ГВЭ в пятибалльную систему
оценивания
Минимальное
количество
баллов
по
математике,
свидетельствующее об освоении образовательных программ
основного
общего
образования
обучающимися
образовательных организаций ВО в 2021 году при проведении
ГИА-9 в форме ОГЭ – 7 баллов, без учёта количества баллов,
набранных за задания по геометрии определено на заседании
государственной экзаменационной комиссии 7 июня
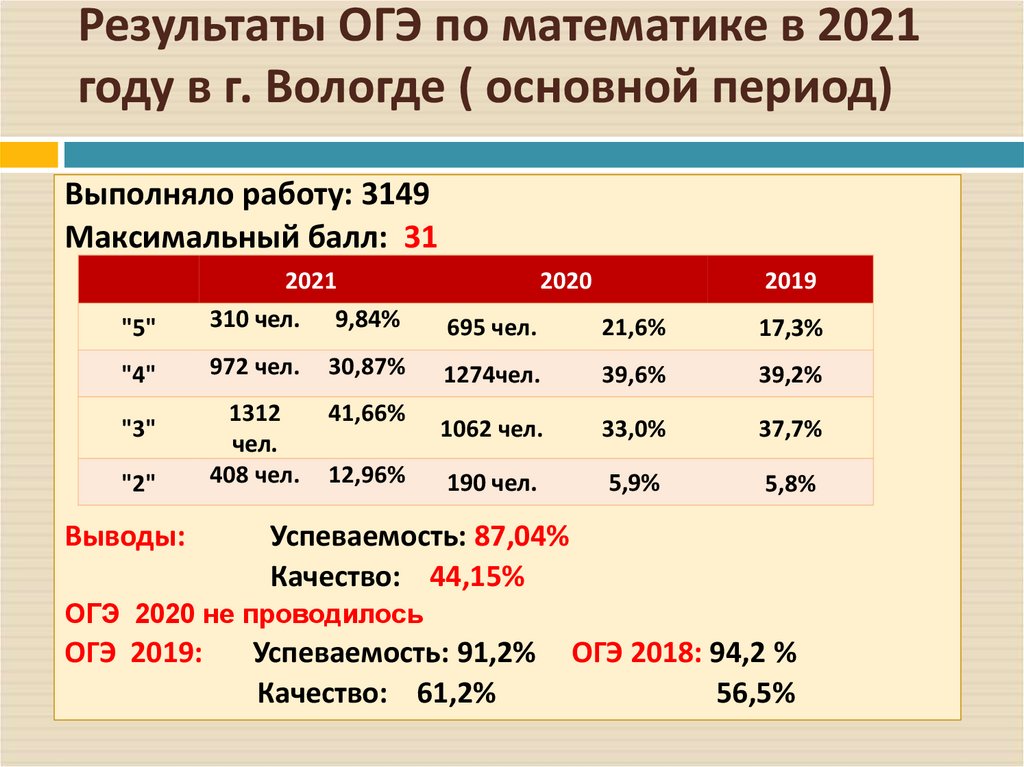
5. Результаты ОГЭ по математике в 2021 году в г. Вологде ( основной период)
Выполняло работу: 3149Максимальный балл: 31
2021
2020
2019
"5"
310 чел.
9,84%
695 чел.
21,6%
17,3%
"4"
972 чел.
30,87%
1274чел.
39,6%
39,2%
1312
чел.
408 чел.
41,66%
1062 чел.
33,0%
37,7%
190 чел.
5,9%
5,8%
"3"
"2"
Выводы:
12,96%
Успеваемость: 87,04%
Качество: 44,15%
ОГЭ 2020 не проводилось
ОГЭ 2019:
Успеваемость: 91,2%
Качество: 61,2%
ОГЭ 2018: 94,2 %
56,5%
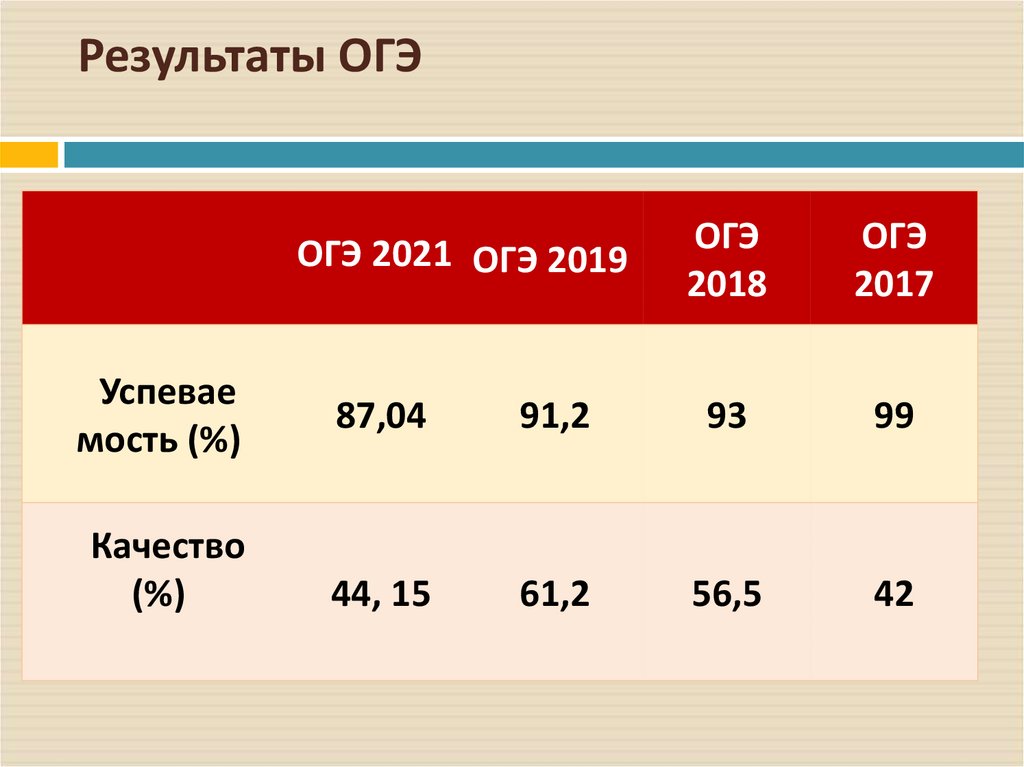
6. Результаты ОГЭ
ОГЭ 2021 ОГЭ 2019Успевае
мость (%)
Качество
(%)
ОГЭ
2018
ОГЭ
2017
87,04
91,2
93
99
44, 15
61,2
56,5
42
7. Диаграмма распределения первичных баллов участников ОГЭ по предмету в 2021 г.
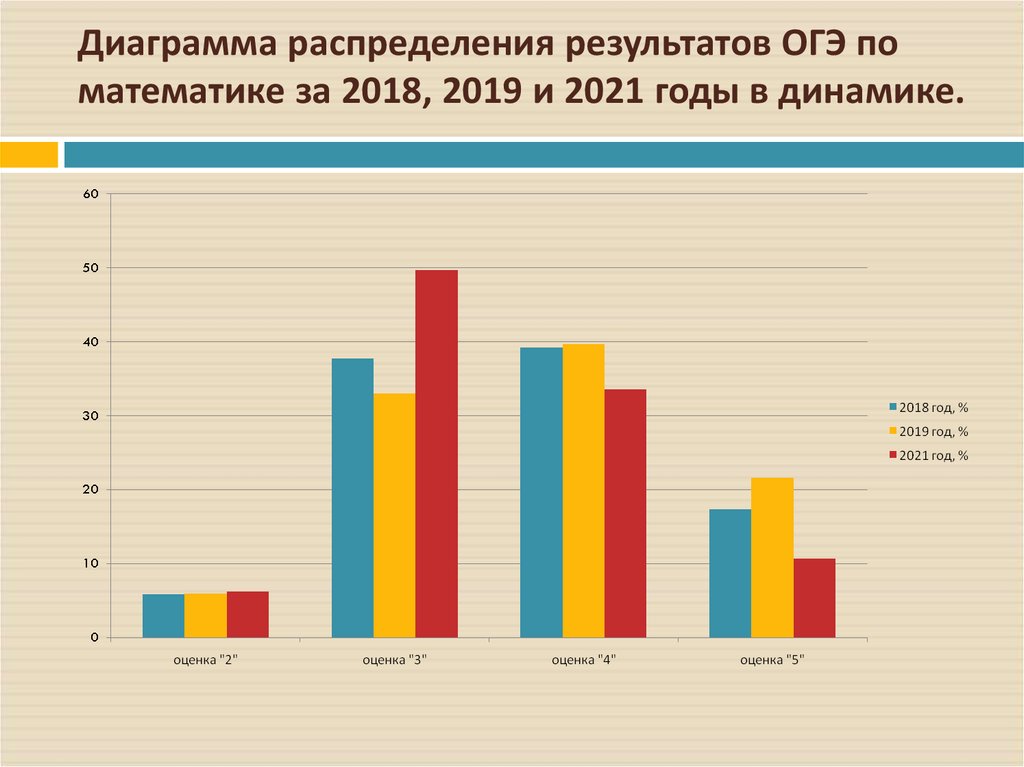
8. Диаграмма распределения результатов ОГЭ по математике за 2018, 2019 и 2021 годы в динамике.
9. Выделение перечня ОО, продемонстрировавших наиболее высокие результаты ОГЭ по предмету:
№п
/
п
2
доля участников ОГЭ, получивших отметки «4» и «5», имеет максимальные
значения (по сравнению с другими ОО г. Вологда);
доля участников ОГЭ, получивших неудовлетворительную отметку, имеет
минимальные значения (по сравнению с другими ОО г. Вологда).
Название
ОО
1
. Лицей №32
Школа №1
3
Средний балл
23,2
18,2
17,2
Школа №8
4
5
6
16,6
Школа №18
Гимназия
№2
Школа №9
16,4
16,0
Доля
участников
,
получивши
х отметку
«2»
Доля участников,
получивших
отметки «4» и «5»
(качество
обучения)
Доля участников,
получивших
отметки
«3», «4» и «5»
(уровень
обученности)
1%
93%
99%
0%
77%
100%
6%
66%
94%
2%
64%
98%
0%
67%
100%
2%
69%
98%
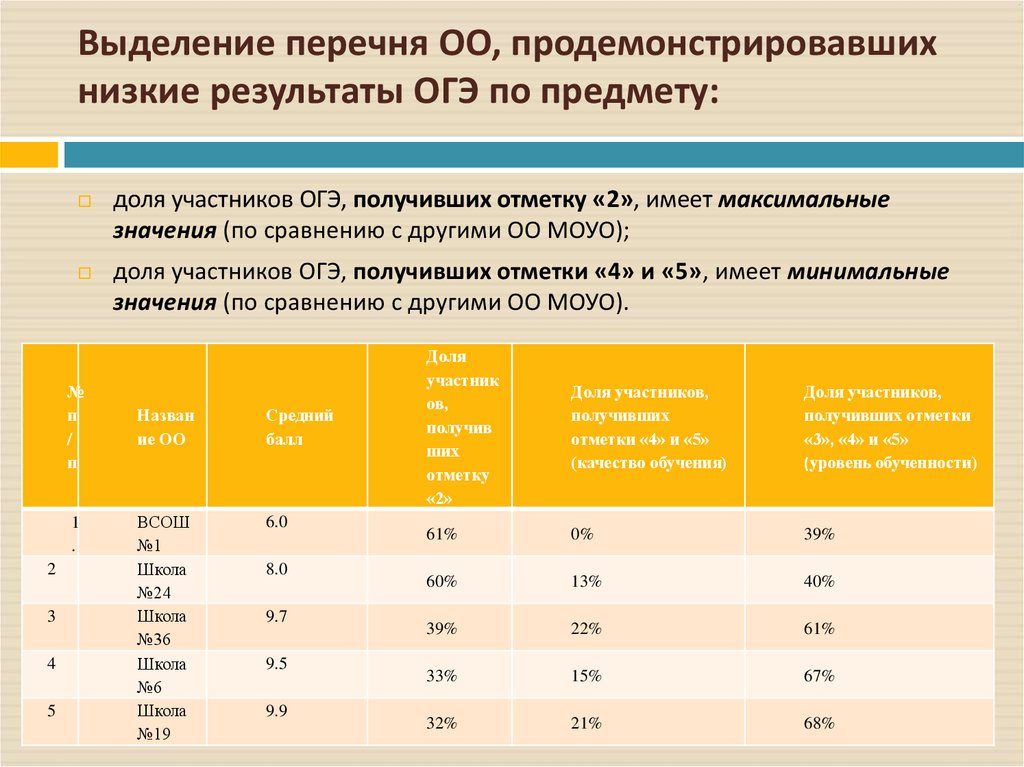
10. Выделение перечня ОО, продемонстрировавших низкие результаты ОГЭ по предмету:
доля участников ОГЭ, получивших отметку «2», имеет максимальныезначения (по сравнению с другими ОО МОУО);
доля участников ОГЭ, получивших отметки «4» и «5», имеет минимальные
значения (по сравнению с другими ОО МОУО).
№
п
/
п
1
.
2
3
4
5
Назван
ие ОО
Средний
балл
ВСОШ
№1
Школа
№24
Школа
№36
Школа
№6
Школа
№19
6.0
8.0
9.7
9.5
9.9
Доля
участник
ов,
получив
ших
отметку
«2»
Доля участников,
получивших
отметки «4» и «5»
(качество обучения)
Доля участников,
получивших отметки
«3», «4» и «5»
(уровень обученности)
61%
0%
39%
60%
13%
40%
39%
22%
61%
33%
15%
67%
32%
21%
68%
11. Средний балл ОГЭ
Средний баллОГЭ 2021
ОГЭ
2019
ОГЭ 2018
ОГЭ
2017
средний по
городу
13,8
16,5
15,6
13,4
Только 26,7% девятиклассников сможет изучать
математику на профильном уровне в старших
классах (первичный балл не ниже 18)
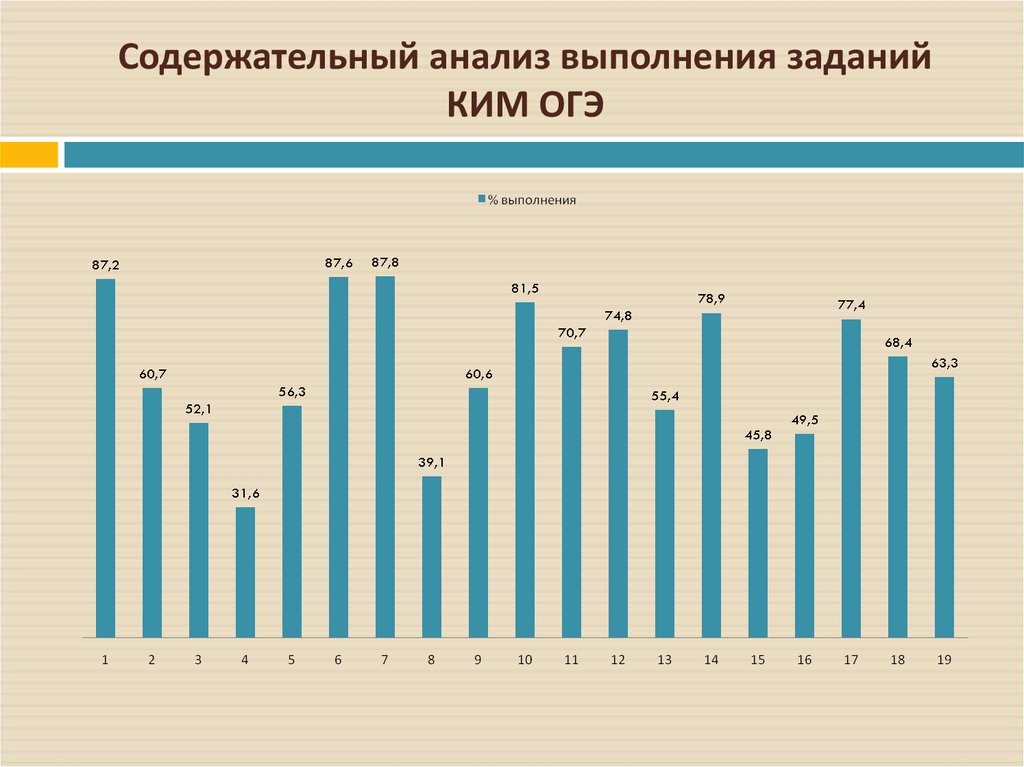
12. Результаты выполнения заданий (% верно выполнивших)
№задания
1
2
3
4
5
6
7
8
9
10
%
87,2
60,7
52,1
31,6
56,3
87,6
87,8
39,1
60,6
81,5
№
задания
11
12
13
14
15
16
17
18
19
%
70,7
74,8
55,4
78,9
45,8
49,5
77,4
68,4
63,3
13. Выводы:
по всем содержательным блокам курса математики есть проблемыв подготовке учащихся, только три задания части 1 попали в разряд
«легких» (задания №1, 7, 18). Особенную тревогу вызывает
выполнение
заданий
по
геометрии
и
задание
на
последовательности чисел №14. По сравнению с прошлым годом,
лучше выполнены задания №1-5, 18.
Получили 0 баллов за задания 1 части – 54 человек из 16 школ (2020
- 56 человек)
Выполнили все задания 1 части – 62 человека из 11 школ (2020 - 63
человека), что соответствует отметке «4».
Получили 0 баллов за задания второй части 2016 человек или 66,1%.
Максимальный балл (31) набрали 2 человек из лицея. №32
14. Содержательный анализ выполнения заданий КИМ ОГЭ
15. Из диаграммы видно, что учащиеся испытывают трудности по заданиям:
- № 4 и 8 (Умение выполнять вычисления ипреобразования),
- №11 (Уметь строить и читать графики
функций),
- № 12 (Осуществлять практические расчёты по
формулам),
- № 14 (Умение строить и читать графики
функций),
- № 15, 16 (Умение выполнять действия с
геометрическими фигурами, координатами и
векторами).
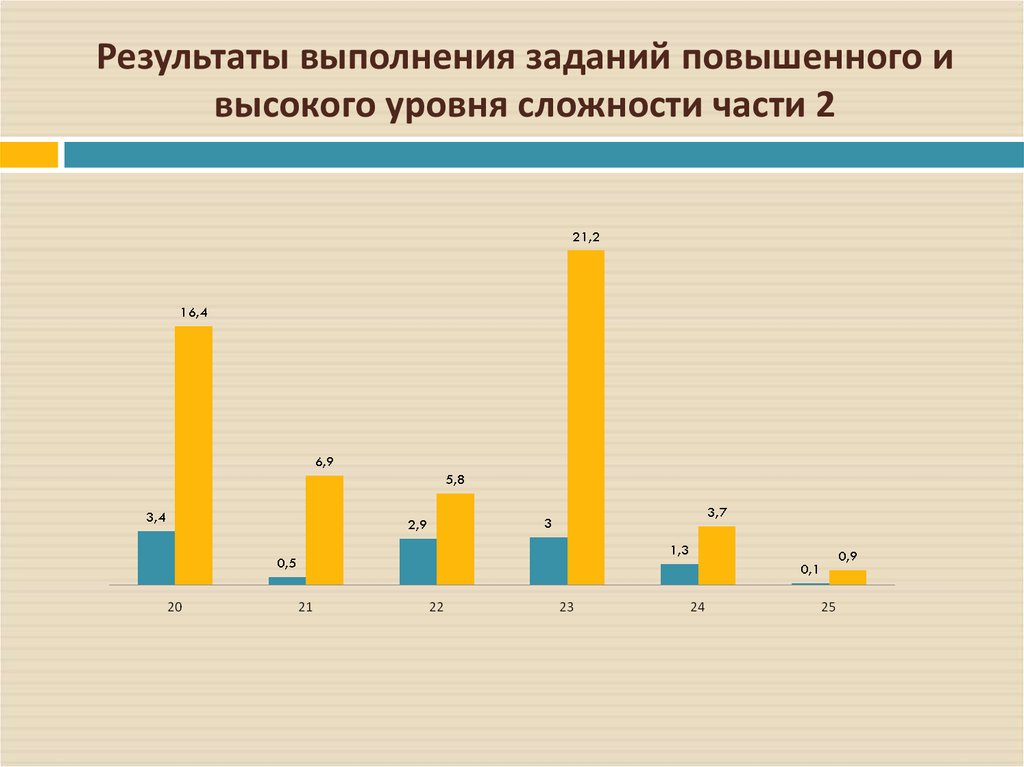
16. Результаты выполнения заданий повышенного и высокого уровня сложности части 2
17. Основные проблемы, возникающие при написании выпускниками экзаменационной работы
неумение понять суть вопроса, содержание задания, приводящее кпостроению неверного хода решения
- недостаточно развитые умения смыслового чтения, не
позволяющие построить адекватную математическую модель по
условию задания
- несформированность вычислительных навыков
- неспособность грамотно сформулировать решение в письменном
виде, небрежное оформлении письменного решения задачи
- недостаточные геометрические знания, слабая графическая
культура
- недостаточное усвоение алгоритмов решения неравенств
- недостаточно развитая культура построения геометрического
чертежа к задаче, трудности при обосновании решения
18. Пересдача ОГЭ по математике 8 сентября
В сентябре ОГЭ пересдавали те школьники,которые:
получили один или два «неуда», но решили не
торопиться с пересдачей, а собрались
тщательно подготовиться к ней в течение двух
месяцев;
по состоянию здоровья и другим уважительным
причинам не смогли использовать второй шанс
в июне;
Снова получили «2» в резервные дни летом.
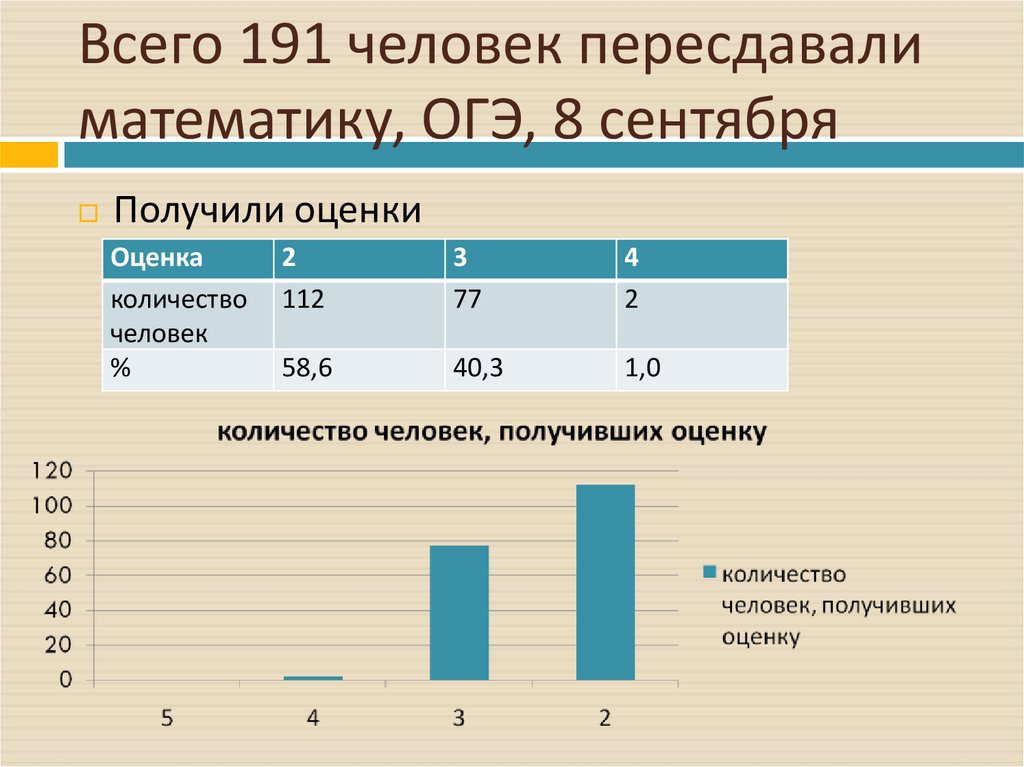
19. Всего 191 человек пересдавали математику, ОГЭ, 8 сентября
Получили оценкиОценка
количество
человек
%
2
112
3
77
4
2
58,6
40,3
1,0
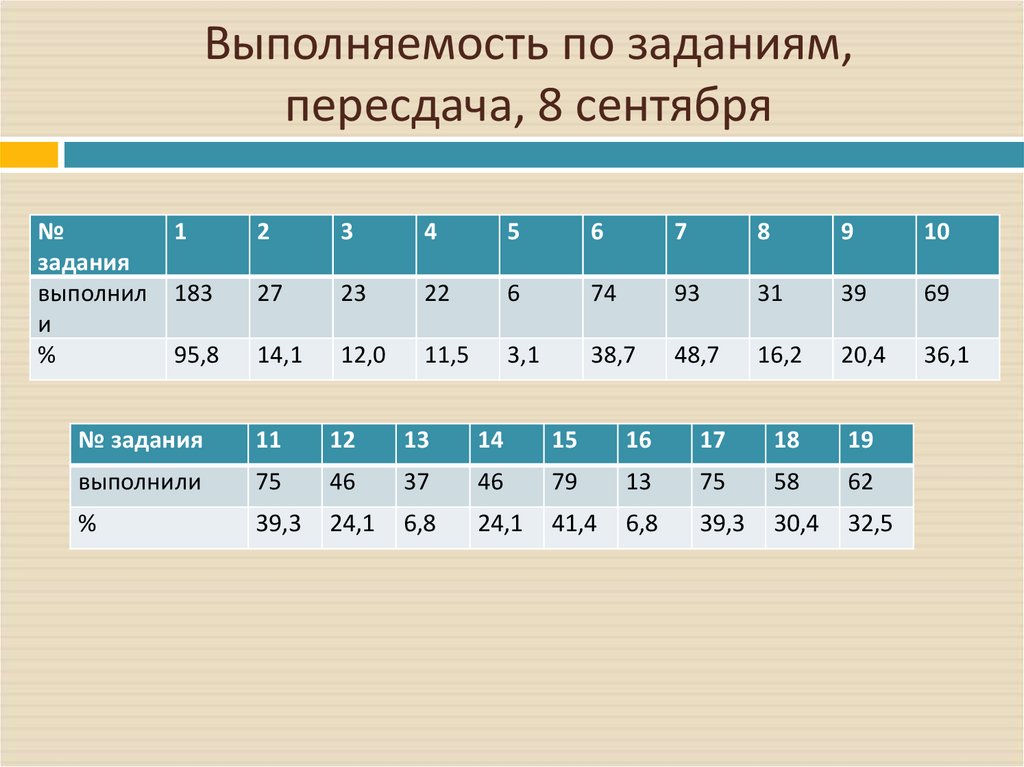
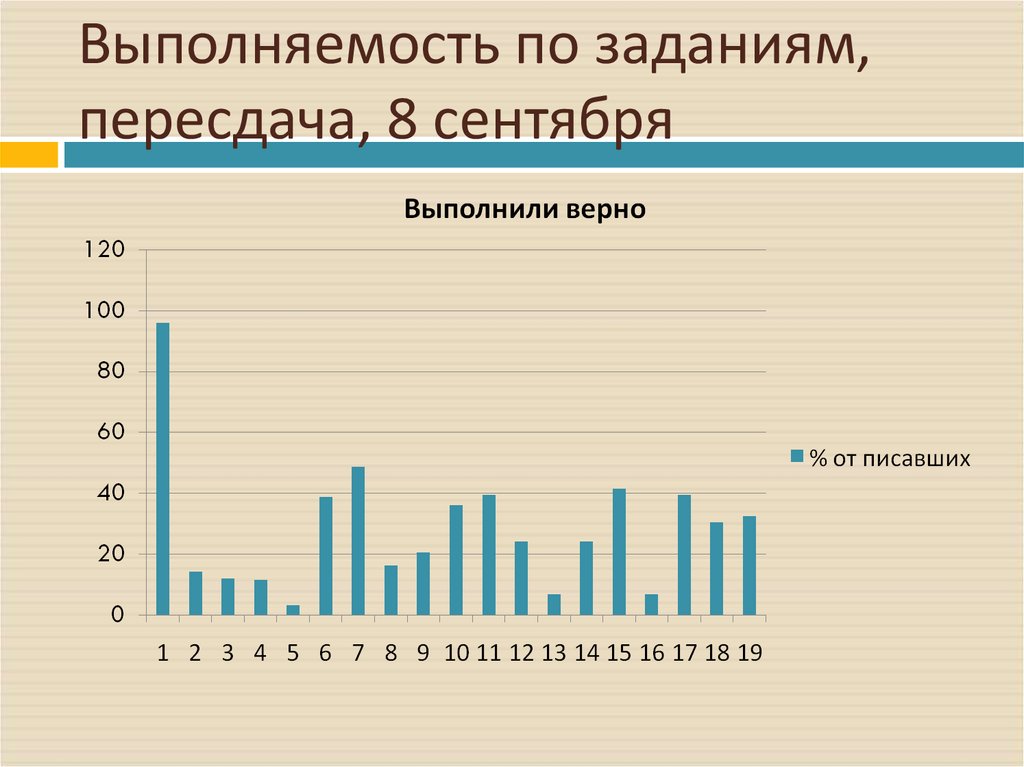
20. Выполняемость по заданиям, пересдача, 8 сентября
№задания
выполнил
и
%
1
2
3
4
5
6
7
8
9
10
183
27
23
22
6
74
93
31
39
69
95,8
14,1
12,0
11,5
3,1
38,7
48,7
16,2
20,4
36,1
№ задания
11
12
13
14
15
16
17
18
19
выполнили
75
46
37
46
79
13
75
58
62
%
39,3
24,1
6,8
24,1
41,4
6,8
39,3
30,4
32,5
21. Выполняемость по заданиям, пересдача, 8 сентября
22. Баллы по геометрии
Количеств 0о баллов
1
2
3
4
5
количеств
о человек
%
24
66
52
35
12
2
12,6
34,6
27,2
18,3
6,2
1,0
Набрали баллы по алгебре, но не набрали по геометрии – таких нет.
Не набрали бы баллы по геометрии по критериям ФИПИ 90 человек (0 или 1
балл).
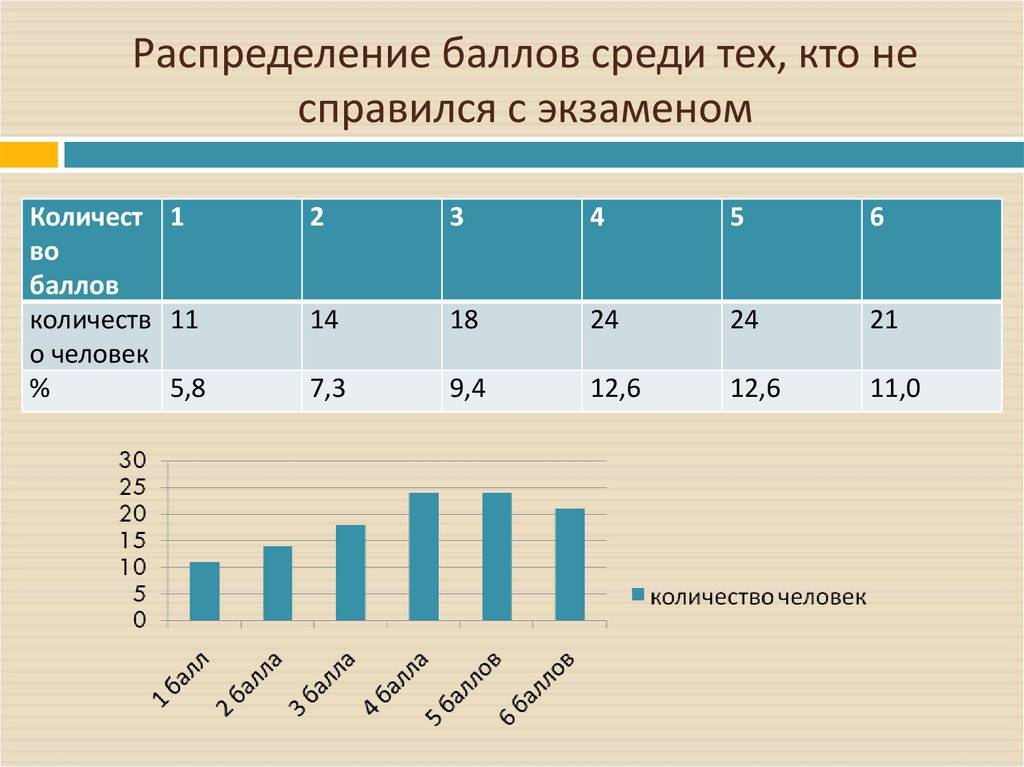
23. Распределение баллов среди тех, кто не справился с экзаменом
Количест 1во
баллов
количеств 11
о человек
%
5,8
2
3
4
5
6
14
18
24
24
21
7,3
9,4
12,6
12,6
11,0
24. Задания, наиболее вероятно решаемые школьниками «зоны риска»
№1 Уметь выполнять вычисления и преобразования,уметь использовать приобретённые знания и умения в
практической деятельности и повседневной жизни, уметь
строить и исследовать простейшие математические
модели
№6, №7 Уметь выполнять вычисления и преобразования
№9 Уметь решать уравнения, неравенства и их системы
25. Задания, наиболее вероятно решаемые школьниками «зоны риска»
№10 Уметь работать со статистической информацией,находить частоту и вероятность случайного события
№15, №17, №18 Уметь выполнять действия с
геометрическими фигурами, координатами и векторами
№19 Проводить доказательные рассуждения при
решении задач, оценивать логическую правильность
рассуждений, распознавать ошибочные заключения
Количество неудовлетворительных результатов за ОГЭ по
математике
снизилось от 408 (12,96%) до 198 (6,27%)
26. Задания, которые необходимо максимально приблизить к вероятно решаемым заданиям школьниками «зоны риска»
№12 Осуществлять практические расчёты поформулам; составлять несложные формулы,
выражающие зависимости между величинами
№14 Уметь строить и читать графики функций,
уметь использовать приобретённые знания и
умения в практической деятельности и
повседневной жизни, уметь строить и
исследовать простейшие математические
модели
27. Система работы учителя с детьми, испытывающими стойкие затруднения в процессе изучения математики
Система работы учителя с детьми,испытывающими стойкие
затруднения в процессе изучения
математики
28. Понятие школьной неуспеваемости
• Отклонения всостоянии
здоровья
1
2
3
• Нарушения
социальнопсихологической
адаптации
• Субъективная
позиция учителя
к ребёнку
29. Трудности в процессе обучения и адаптации
Школьная неуспеваемость детейОтсутствие интереса к
учению, труду, организованному досугу
Невыполнение общественных норм поведения
Конфликтность, высокая тревожность; наличие
нежелательных качеств личности (лени, лживости,
эгоистичности, грубости)
30. Как помочь отстающему ребенку по математике
Ученик с низкой интенсивностью учебнойдеятельности в области математики
Учащиеся с низкой эффективностью учебной
деятельности
Ученик сочетает в себе признаки с низкой
интенсивностью и низкой эффективностью
учебной деятельности
31. Для того, чтобы добиться успеха в обучении необходимо
1. Жесткий контроль над выполнением всехзаданий, особенно у слабоуспевающих
учащихся
2. Следить за тем, чтобы каждый учащийся
положительно сдал каждую тему (обязательные
результаты обучения)
3. Осуществлять дифференцированный подход
к учащимся при опросе
4. Домашнее задание должно содержать
дополнительную часть и необязательную
32. Для того, чтобы добиться успеха в обучении необходимо
5.Дифференцированные задания должны бытьи на самостоятельных и на контрольных работах
6. Не допускать отставания учащихся, для этого
систематически проводить консультации и
дополнительные занятия
7.Не каждый раз ставить «двойку», а уметь
терпеливо ждать учащиеся с замедленным
восприятием
8. Не унижать ученика и постараться самим
найти к нему подход
33. Кого учить?
Особенности неуспевающих учащихся:- низкий уровень знаний, как следствие этого
низкий уровень интеллектуального развития
- отсутствие познавательного интереса
- не сформированы элементарные
организационные навыки
- учащиеся требуют индивидуального подхода с
психологической и педагогической (в плане
обучения) точки зрения
34. Кого учить?
- нет опоры на родителей как союзниковучителя - предметника
- дети, в основном, из асоциальных семей
- отсутствие адекватной самооценки со стороны
учащихся
- частые пропуски уроков без уважительной
причины, что приводит к отсутствию системы в
знаниях и как следствие этого - низкий уровень
интеллекта
35. Признаки отставания ученика
Низкий уровень умственного развития.Несформированность учебных навыков.
Дефицит внимания с гиперактивностью
Отсутствие познавательного интереса.
Несформированность произвольной сферы
Конфликтные отношения
Низкий познавательный интерес
Низкий уровень развития словесно-логического
мышления
Низкая работоспособность
36. Чему учить?
выяснить причину отставания,определить действительный уровень его
знаний,
“возвратить его” на ту ступень обучения, где он
будет соответствовать требованиям программы,
Государственным Образовательным
Стандартам.
37. Как учить?
Продумать и осуществить индивидуальный планобучения.
Своевременно выявлять образовавшиеся пробелы в
знаниях, умениях и навыках учащихся и организовать
своевременную ликвидацию этих пробелов.
Установить правильность и разумность способов учебной
работы, применяемых учащимися, и при необходимости
корректировать эти способы.
Нужно систематически обучать учащихся общеучебным
умениям и навыкам.
Учитель для себя и для ученика должен сформулировать
минимум знаний и навыков, который должен усвоить
ученик.
38. Как повысить работоспособность:
Разнообразить виды деятельности.- Проветривать кабинет.
- Проводить физминутки.
Всегда надо помнить о соблюдении принципа
необходимости и достаточности
39. Виды работ со слабоуспевающими учениками
Карточки для индивидуальной работыЗадания с выбором ответа
“Разрезные” теоремы
Карточки - тренажеры.
“Карточки-информаторы”,
“Карточки-с образцами решения”,
Задания «заполни пропуски»
40. Рекомендации по совершенствованию преподавания учебного предмета для всех обучающихся
Учителям необходимо реализовывать методикуработы с алгоритмами
Начало решения любой задачи (текстовой,
планиметрической) – это анализ текста условия,
визуализация связей между компонентами
задачи (схема, граф, чертеж, таблица).
Решение проблемы оформления выполнения
заданий следует начать с запрета
использования "собственных" аббревиатуры и
обозначений.
41. Рекомендации по совершенствованию преподавания учебного предмета для всех обучающихся
Подготовку к ОГЭ по математике спланироватьне как процесс прорешивания вариантов, а как
процесс обобщения и систематизации знаний
за курс основной школы.
При изучении нового материала и его отработке
необходимо сочетать различные методы
обучения
Особое внимание следует уделять
формированию навыков самоконтроля и
самопроверки выполненных заданий.
42. Рекомендации по совершенствованию преподавания учебного предмета для всех обучающихся
Необходимо повышать уровеньвычислительных навыков, развивать умение
пользоваться справочными материалами
Систематически учимся читать условие и вопрос
задачи, выделять главное в условии,
преобразовывать данные задачи в удобную для
восприятия форму, записывать математически
верно решение задачи, применять знания в
нестандартных ситуациях.
43. Рекомендации по совершенствованию преподавания учебного предмета для всех обучающихся
Для сильных учеников требуется созданиеусловия для продвижения:
дифференцированные по уровню сложности
задания, возможность саморазвития, помощь в
решении и оформлении заданий второй части.
44. Рекомендации по совершенствованию преподавания учебного предмета для всех обучающихся
Со слабо успевающими обучающимися необходимовыделить круг доступных ему заданий, помочь освоить
основные математические факты, позволяющие их
решать и сформировать уверенные навыки их решения.
Для «средних» учеников необходимо использовать
методику, при которой они смогут перейти от
теоретических знаний к практическим навыкам, от
решения стандартных алгоритмических задач к решению
задач похожего содержания, но иной формулировки и
применению уже отработанных навыков в новой
ситуации.
45. Решение заданий Открытого банка ОГЭ
Систематически включать задания Открытогобанка ОГЭ в тематический и промежуточный
контроль, домашние задания, индивидуальные
задания.
В течение всего периода обучения знакомить
учеников с критериями оценивания открытых
заданий ОГЭ.
Демонстрировать школьникам образцы
правильного оформления трудных заданий,
особенно по геометрии.
46. Пример включения заданий из банка ФИПИ в тематический контроль.
Контрольная работа по теме «Правильные многоугольники. Длина окружности, дугиокружности. Площадь круга. Площадь кругового сектора, площадь кругового
сегмента».
1.
Периметр треугольника равен 140, одна из сторон равна 56, а радиус вписанной в него
окружности равен 9. Найдите площадь этого треугольника.
2.
Сторона квадрата равна 18√2. Найдите радиус окружности, описанной около этого
квадрата.
3.
Радиус вписанной в квадрат окружности равен 18√2. Найдите диагональ этого
квадрата.
4.
Радиус окружности, описанной около квадрата, равен 22√2. Найдите длину стороны
этого квадрата.
5.
Радиус окружности, вписанной в трапецию, равен 38. Найдите высоту этой трапеции.
6.
Радиус окружности, вписанной в прямоугольную трапецию, равен 28. Найдите высоту
этой трапеции.
7.
Сторона равностороннего треугольника равна 16√3. Найдите радиус окружности,
описанной около этого треугольника.
47. Пример включения заданий из банка ФИПИ в тематический контроль.
1.Радиус окружности, вписанной в равносторонний треугольник, равен 11. Найдите высоту этого треугольника.
2.
Радиус окружности, вписанной в равносторонний треугольник, равен 9√3. Найдите длину стороны этого
треугольника.
3.
В треугольнике ABC угол C равен 60°, AB=10√3. Найдите радиус окружности, описанной около этого треугольника.
4.
Найдите площадь квадрата, описанного около окружности радиуса 14.
5.
Найдите угол, который образуют минутная и часовая стрелки часов в 15:00. Ответ дайте в градусах.
1.
Найдите площадь заштрихованной на рисунке фигуры, если диаметр большого круга равен 5 м, а
внутренние круги равны.
Найдите площадь заштрихованной на рисунке фигуры, если радиус большого полукруга равен 12см, а <ВАС
2.
= 300.
Задания 1-12 оцениваются в 1 балл. Задания 13-15 соответственно в 2 балла. 3 балла и 3 балла. Максимальное количество баллов – 20 баллов.
Нормы оценок: «5»- 14- 20 баллов, «4»- 10- 13 баллов, «3»- 8- 11 баллов, «2»- 1- 7 баллов, «1»- 0 баллов.
Решение заданий 1- 12 оформляйте кратко, заданий 13-15 – более подробно. За аккуратное оформление работы 1 «бонусный балл».
48. Пример включения заданий из банка ФИПИ в тематический контроль.
1.2.
3.
4.
5.
6.
7.
8.
9.
10.
Уравнения и их системы, вместе
Решите уравнение 7x2=42x.Если уравнение имеет более одного корня, в ответ запишите меньший
из корней.
Решите уравнение x2 −18=7x. Если уравнение имеет более одного корня, в ответ запишите больший
из корней.
Решите уравнение x2 +10=7x.Если уравнение имеет более одного корня, в ответ запишите больший
из корней.
Найдите корень уравнения (x−5)2 =(x−8)2.
Решите уравнение (− 5x−3)(2x−1)=0.Если уравнение имеет более одного корня, в ответ запишите меньший
из корней.
Решите уравнение 3x2 +18x=0.Если уравнение имеет более одного корня, в ответ запишите меньший
из корней.
Решите уравнение 5x2 −9x+4=0.Если уравнение имеет более одного корня, в ответ запишите меньший
из корней.
Решите уравнение x2 −10x+21=0.Если уравнение имеет более одного корня, в ответ запишите больший
из корней.
Решите уравнение x2 −10x+24=0.Если уравнение имеет более одного корня, в ответ запишите меньший
из корней.
Решите уравнение x2 −4=0.Если уравнение имеет более одного корня, в ответ запишите меньший
из корней.
49. Пример включения заданий из банка ФИПИ в тематический контроль.
1.Решите систему уравнений {5x2 +y=12,9x2 −y=2.
2.
Решите систему уравнений {6x2 +y=14,12x2 −y=4.
3.
Решите систему уравнений {3x2 −2x=y,3x−2=y.
4.
Решите систему уравнений {3x2 −4x=y,3x−4=y.
5.
Решите систему уравнений {5x2 +y2 =61,15x2 +3y2 =61x.
6.
Решите систему уравнений {3x2 +2y2 =50,12x2 +8y2 =50x.
7.
Решите уравнение 1/x2−1/x−6=0.
8.
Решите уравнение 1/(x−2)2−1/(x−2)−6=0.







































 Математика
Математика








