Похожие презентации:
Случайные величины (Лекция 8)
1.
Лекция 82. Случайные величины
Виды случайных величин.Задание дискретной
случайной величины
3. Определение. Пусть дано вероятностное пространство
, S , pТогда случайная величина Xчисловая функция
X : R
4. ОБОЗНАЧЕНИЯ
Будем обозначать случайныевеличины буквами X, Y, Z, а их
значения – x, y, z.
5.
Примерслучайная величина X имеет
три возможных значения
x1 , x 2 , x 3
6. Пусть X-случайная величина.
Рассмотрим событияA : X x
B : X x
C : X x
7. Следовательно,
P A P X xP B P X x
P C P X x
8. Классификация случайных величин
Два основных класса:Дискретные
1.
2.
Конечные
Бесконечные
Непрерывные
9.
Дискретной(прерывной) называют
случайную величину с
дискретным
множеством значений.
10.
Дискретные и непрерывныеслучайные величины
П1. Бросание монеты. X=1, если
выпал герб, иначе X=0.
П2. Стрельба по мишени. Значение
случайной величины – количество
выбитых очков.
П3. Измерение роста человека.
Случайная величина – рост случайно
выбранного человека.
11. Закон распределения вероятностей ДСВ(дискретной случайной величины)
12.
Закон распределения ДСВ соответствие между значениями иих вероятностями;
основные способы задания:
таблично, аналитически (в виде
формулы) и графически.
13.
Табличный способ задании законараспределения ДСВ
Х
р
x1
x2
…
p1
p2
…
xn
pn
14.
СобытияX x1 , X x 2 , ..., X x n
образуют полную группу;
следовательно,
p1 p 2 ... p n 1.
15.
Если множество возможныхзначений X бесконечно , то ряд
p1 p2 ...
сходится и его сумма равна
единице.
Данную таблицу при
возрастании xi называют рядом
распределения дискретной
случайной величины.
16.
ПримерВ денежной лотерее выпущено
100 билетов. Разыгрывается один
выигрыш в 50 рублей и десять
выигрышей по 1 рублю.
Найти ряд распределения
случайной величины X – стоимости
возможного выигрыша для
владельца одного лотерейного
билета.
17.
Решениеx3 50, x2 1, x1 0.
p3 0,01, p2 0,1, p1 0,89.
X
P
0
0.89
1
0.1
50
0.01
18.
ПримерВ денежной лотерее выпущено
100 билетов по цене 10 рублей.
Разыгрывается один выигрыш в 100
рублей и десять выигрышей по 20
рублей.
Найти закон распределения
случайной величины X – прибыль
владельца одного лотерейного
билета.
19.
Решениеx3 90, x2 10, x1 10.
p3 0, 01, p2 0,1, p1 0,89.
X
P
-10
0.89
10
0.1
90
0.01
20. Равномерное дискретное распределение
XP
x1
x2
1/n
1/n
…
…
xn
1/n
21.
Биномиальное распределениеПусть производится n испытаний по
схеме Бернулли с параметрами р и
q=1– p.
ДСВ X ─ число успехов в этих
испытаниях.
22.
Значения X :x1 0, x 2 1, x 3 2,...., x n 1 n.
По формуле Бернулли:
Pn ( X k ) C p q
k
n
k
n k
,
где k = 0, 1, 2, …, n.
Формула является аналитическим
выражением искомого закона
распределения.
23.
Такая ДСВ называетсябиномиальной (имеет
биномиальный закон
распределения)
n 1
n
n 1
( p q) C p C p q ...
n
k
n
n
... C p q
k
n
k
n k
... C q .
0 n
n
24.
РЯД РАСПРЕДЕЛЕНИЯX
P
0
q
1
n
npq
…
n 1
…
n
p
n
25. Пример
Монета брошена 2 раза.Написать ряд распределения
случайной величины X – числа
выпадений «герба».
26. Решение
1p
2
1 1
q 1 .
2 2
1 2
P2 (0) C q ( ) 0,25.
2
0
2
2
1 1
P2 (1) C pq 2 0,5,
2 2
1
2
1 2
P2 (2) C p ( ) 0,25,
2
2
2
2
27. Искомый ряд распределения
X0
1
2
P
0.25
0.5
0.25
28. Распределение Пуассона
Пусть производятся испытанияпо схеме Пуассона с параметром
.
X – случайная величина,
показывающая число успехов.
29. Тогда
eP( X k )
.
k!
k
30.
Эта формула выражает законраспределения Пуассона вероятностей
массовых (n велико) и редких (р мало )
событий.
31. ГЕОМЕТРИЧЕСКОЕ РАСПРЕДЕЛЕНИЕ
Обозначим через Х дискретнуюслучайную величину – число
испытаний, которые нужно провести до
первого появления события А.
P( X k ) q
k 1
p.
32.
Полагая k = 1, 2, …, получимгеометрическую прогрессию с первым
членом р и знаменателем q (0<q<1):
2
p, qp , q p, ..., q
k 1
p,...
По этой причине распределение
называют геометрическим.
Сумма ряда
p
p
1.
1 q p
33. Пример
Охотник стреляет по зайцу,пока не попадет.
Составить ряд распределения
случайной величины X – количество
сделанных выстрелов,
если вероятность попадания при
одном выстреле равна 0,6.
34.
p=0,6 и q=0,4.P( X k ) q
X
1
P
0,6 0,24
2
…
k 1
p.
n
0,4 0,6
n 1
…
…
35. Ограниченное ГЕОМЕТРИЧЕСКОЕ РАСПРЕДЕЛЕНИЕ
Охотник, имея 4 патрона, стреляет позайцу, пока не попадет или не
закончатся патроны.
36.
Составить ряд распределенияслучайной величины X – количество
сделанных выстрелов,
если вероятность попадания при
одном выстреле равна 0,6.
37. Решение
p=0,6; q=0,4.P(X=1)=0,6 будет один выстрел с
попаданием;
P(X=2)=0,4 0,6=0,24 первый выстрел
промах, второй попадание;
P(X=3)=0,4 0,4 0,6=0,096 два промаха,
третий попадание;
P(X=4)=0,4 0,4 0,4 0,6+0,4 0,4 0,4 0,4=
=0,064
38.
P( X k ) q p, k nk 1
P( X k ) q , k n
k 1
X
1
P
0,6 0,24 0,096 0,064
2
3
4
39. Гипергеометрическое распределение
P ( X m)m
n m
C M C N M
n
CN
.
40.
Гипергеометрическоераспределение определяется тремя
параметрами: N, M, n. Или
M
N, n и p =
,
N
где р – вероятность того, что первое
извлечённое изделие стандартное.
41.
ПримерСреди 50 изделий 20 окрашенных.
Составить ряд распределения
случайной величины X – количества
окрашенных изделий среди 3
отобранных изделий.
42. Решение
По условию, N = 50,M = 20, n =3, а m принимает значения
от 0 до 3.
m
M
n m
N M
n
N
C C
P ( X m)
C
43.
0C20
C503 020 1 C303
29
P( X 0)
3
3
C50
C50
140
1
C20
C503 120 20 C302
87
P( X 1)
3
3
C50
C50
196
2
3 2
2
1
C20
C50
C
C
57
20
20
30
P( X 2)
3
3
C50
C50
196
3
3
C20
C503 320 C20
C300
57
P( X 3)
3
3
C50
C50
980
44.
XP
0
1
2
3
29/140 87/196 57/196 57/980
45.
ФУНКЦИИ СЛУЧАЙНЫХВЕЛИЧИН
46.
Пусть C – некоторая константа, неравная нулю. Определим новую
дискретную случайную величину
Y=СХ.
X
x1
…
p
p1
…
Y
Cx1
…
Cxn
p
p1
…
p1
xn
pn
47. Пример. Y=2X
XP
-1
0,2
0
0,5
2
0,3
Y
P
-2
0,2
0
0,5
4
0,3
48. Независимые СВ
Определение.Две случайные величины называются
независимыми, если закон
распределения одной из них не зависит
от того, какие возможные значения
приняла другая величина.
49. Строгое определение
ДСВ X и Y называются независимыми,если для всех возможных их значений
P X x Y y P X x P Y y
50. Сумма ДСВ
Z X Y;z
k
xi y j ;
P zk
P X x Y y
zk xi y j
i
j
51. Замечание
Для независимых СВP X x Y y P X x P Y y
Для зависимых СВ
P X x Y y P X x PX x Y y
52. Пример Z=X+Y, где X,Y-независимые СВ.
XP
-1
0,3
0
0,3
1
0,4
Y
P
-1
0,1
0
0,5
1
0,4
Z=X+Y
-2
P
0,03
-1
0
1
2
0,18 0,31 0,32 0,16
53.
P Z 2 P X 1 Y 1P Z 1 P X 1 Y 0 P X 0 Y 1
P Z 0 P X 1 Y 1 P X 0 Y 0 P X 1 Y 1
P Z 1 P X 0 Y 1 P X 1 Y 0
P Z 2 P X 1 Y 1
54. Произведение ДСВ
Z XY ;z
k
xi y j ;
P zk
P X x Y y
zk xi y j
i
j
55. Пример Z=XY, где X,Y-независимые.
XP
-1
0,3
0
0,3
1
0,4
Y
P
-1
0,1
0
0,5
1
0,4
Z=XY
-1
0
1
P
0,16
0,65
0,19
56. ЧИСЛОВЫЕ ХАРАКТЕРИСТИКИ СЛУЧАЙНЫХ ВЕЛИЧИН
57. Математическое ожидание дискретной случайной величины
Обозначение:MX или M(X)
58. Математическое ожидание М(Х) конечной случайной величины Х определяется равенством:
M ( X ) x1 p1 x 2 p 2 ... x n p n .M ( X ) xi pi
i 1
(математическое ожидание существует,
если ряд сходится абсолютно.)
59.
ПримерНайти математическое ожидание
случайной величины Х
Х
р
3
0,1
5
0,6
2
0,3
60. Решение
M ( X ) 3 0,1 5 0,6 2 0,3 3,9.61.
ПримерНайти математическое ожидание числа
появлений события А в одном
испытании, если вероятность события А
равна p.
62. Решение
X0
1
P
q
P
M ( X ) 1 p 0 q p.
63. Вероятностный смысл математического ожидания
Пусть произведено n испытаний, вкоторых случайная величина Х приняла
m1 раз значение x1 , m 2 раз значение
x2 ,..., mk раз значение x k , причём
m1 m 2 ... m k n.
Х=
x1 m1 x 2 m 2 ... x k m k .
64.
Среднее арифметическоеx1 m1 x 2 m 2 ... x k m k
X
,
n
или
mk
m1
m2
X x1 x 2
... x k
n
n
n
65.
m1n
m2
n
- относительная частота
значения x1 ,
- относительная частота
значения x 2 и т.д.,
W1
W2
X x1W1 x2W2 ... xk Wk .
66.
Допустим, что число испытанийдостаточно велико. Тогда :
W1 p1 , W2 p 2 , ...,Wk p k
или
X x1 p1 x2 p2 ... xk pk
67.
Итак,X M (X )
Вероятностный смысл
полученного результата таков:
Математическое ожидание
приближённо равно (тем точнее, чем
больше число испытаний) среднему
арифметическому значений
случайной величины.
68. Свойства математического ожидания
69. Свойство 1
Математическое ожиданиепостоянной величины равно
самой постоянной:
М (С) = С.
M (C ) C 1 C.
70. Свойство 2
Постоянный множитель можновыносить за знак математического
ожидания:
М (cХ) = cМ (Х).
71.
Доказательство:X
x1
x2
…
xn
P
p1
p2
…
pn
Закон распределения СВ cХ:
cX
cx1
cx2
…
cxn
P
p1
p2
…
pn
72.
M (cX ) cx1 p1 cx2 p2 ... cxn pnc( x1 p1 x2 p2 ... xn pn ) cM ( X ).
Итак, М (cХ) = cМ (Х).
73. Пример Y=2X
Y=2XПример
X
P
-1
0,2
0
0,5
2
0,3
Y
P
-2
0,2
0
0,5
4
0,3
MX=(-1) 0,2+0 0,5+2 0,3=0,4
MY=(-2) 0,2+0 0,5+4 0,3=0,8=2 MX
74. Свойство 3
Математическое ожидание суммыдвух случайных величин равно сумме
математических ожиданий слагаемых:
M (X+Y) = M (X) + M (Y).
75. Следствие
Математическое ожидание суммынескольких случайных величин равно
сумме математических ожиданий
слагаемых.
76.
ПримерПроизводятся 3 выстрела с
вероятностями попадания в цель,
равными:
p1 0,4, p 2 0,3, p 3 0,6.
Найти математическое ожидание
общего числа попаданий.
77.
РешениеX 1 ={число попаданий при первом
выстреле}
M ( X 1 ) 0,4.
M ( X 2 ) 0,3, M ( X 3 ) 0,6.
X X1 X 2 X 3.
78.
M ( X ) M ( X1 X 2 X 3 )M ( X1 ) M ( X 2 ) M ( X 3 )
0, 4 0,3 0, 6 1,3
79.
ПримерНайти математическое ожидание
суммы числа очков, которые могут
выпасть при бросании двух
игральных костей.
80.
РешениеХ ={число очков на первой кости},
Y ={число очков на второй кости}.
Возможные значения этих величин
одинаковы и равны 1, 2, 3, 4, 5, и 6,
причём вероятность каждого из этих
1
значений равна
.
6
81.
11
1
1
1
1 7
M (X ) 1 2 3 4 5 6 .
6
6
6
6
6
6 2
7
.
Очевидно, что и M (Y) = 2
7 7
M ( X Y ) M ( X ) M (Y ) 7.
2 2
82. Свойство 4
Математическое ожиданиепроизведения двух независимых
случайных величин равно
произведению их математических
ожиданий:
M (XY) = M (X) M (Y).
83. Следствие
Математическое ожиданиепроизведения нескольких взаимно
независимых случайных величин равно
произведению их математических
ожиданий.
M ( XYZ ) M ( XY Z ) M ( XY ) M ( Z )
M ( X ) M (Y ) M ( Z ).
84. Пример
Независимые случайные величины Xи Y заданы следующими законами
распределения:
X
P
5
2
4
0,6 0,1 0,3
Y
7
9
P
0,8
0,2
Найти математическое ожидание
случайной величины XY.
85.
РешениеM ( X ) 5 0, 6 2 0,1 4 0,3 4, 4;
M (Y ) 7 0,8 9 0, 2 7, 4.
M ( XY ) M ( X )M (Y ) 4,4 7,4 32,56.
86. Математическое ожидание биномиальной случайной величины
87.
Теорема.Если X-биномиальная СВ с
параметрами n и p, то
М X = np
88. Пример
Вероятность попадания в цель пристрельбе из орудия р = 0,6. Найти
математическое ожидание общего
числа попаданий, если будет
произведено 10 выстрелов.
89. Решение
M ( X ) np 10 0,6 690. Математическое ожидание СВ, имеющей распределение Пуассона
91. По определению математического ожидания
eMX kP k k
k!
k 0
k 1
k
e
e
k 1 !
k 1
m 0 m !
k
e
e
m
92.
Теорема.Математическое ожидание
случайной величины , имеющей
распределение Пуассона с
параметром
, равно .
93. Математическое ожидание СВ, имеющей геометрическое распределение
94.
ТеоремаМатематическое ожидание
случайной величины ,
имеющей геометрическое
распределение с параметром
p, равно 1/p.
95.
Задачи96. Задача 1
Дискретная случайная величина Xимеет закон распределения
X
p
-6
0,6
4
0,1
0
-1
0,1
0,2
Найти математическое ожидание с.в. X
97. Решение
MX x1 p1 x2 p2 ... xk pkMX=(-6) 0,6+4 0,1+0 0,1+(-1) 0,2=-3,4
98. Задача 2
Случайная величина Х имеет законраспределения
X
0
p
1/2
1
1/4
2
1/8
3
4
1/16 1/32
Найти математическое ожидание с.в. X
99. Решение
MX x1 p1 x2 p2 ... xk pkMX=0 1/2+1 1/4+2 1/8+3 1/16+4 1/32=
=13/16
100. Задача 3
Известно, что MX=2; MY=6. Найти MZ,если Z=3 X+4 Y.
101. Решение
Так как Z=3 X+4 Y, тоMZ=M(3 X+4 Y)=M(3 X)+M(4 Y)=3 MX+
+4 MY=3 2+4 6=6+24=30
102. Задача 4
Независимы дискретные случайные величиныХ и Y заданы следующими законами
распределения
X
0
p
0,3
3
5
Y
0
2
0,5
0,2
p
0,2
0,8
Найти закон распределения с.в. Z=X+Y
103. Решение
Случайная величина Z принимаетследующие значения
0; 2; 3; 5; 7.
Найдем вероятности для каждого из
значений
P(Z=0)=P(X=0) P(Y=0)=0,3 0,2=0,06
P(Z=2)=P(X=0) P(Y=2)=0,3 0,8=0,25
104.
P(Z=3)=P(X=3) P(Y=0)=0,5 0,2=0,1P(Z=5)=P(X=3) P(Y=2)+P(X=5) P(Y=0)=
=0,5 0,8+0,2 0,2=0,4+0,04=0,44
P(Z=7)=P(X=5) P(Y=2)=0,2 0,8=0,16
Z
p
0
2
0,06 0,25
3
0,1
5
0,44
7
0,16
105. Задача 5
Вероятность попадания в цель пристрельбе из орудия равна 0,5. Найти
математическое ожидание общего
числа попаданий, если будет
произведено 24 выстрела.
106. Решение
Имеем дело с биномиальнымраспределением
MX=n p, где X ─ общее число попаданий
MX=24 0,5=12
107. Задача 6
Вероятность отказа прибора равна 0,1.Опыт проводится до тех пор, пока
прибор не откажет. Построить закон
распределения и найти математическое
ожидание c.в. X ─ числа опытов.
108. Решение
Случайная величина Х принимаетзначения 1; 2; 3; …; k; …
Используя геометрическое
распределение найдем вероятности
P(X=1)=0,1
P(X=2)=0,9 0,1
P(X=3)=0,9 0,9 0,1
109.
…P(X=k)=
0,9
k 1
0,1
Закон распределения с.в. X
X
1
p
0,1
2
0,09
…
…
k
0,9k 1 0,1
110.
k 10,9
0,1 =
MX=1 0,1+2 0,9 0,1+…k
=0,1 (1+2 0,9+…+ k
=
0,1
10
2
(1 0,9)
0,9k 1 0,1
)=
111.
Задачи112. Задача 1
Две кости бросили два раза. Построитьзакон распределения Случайной
величины Х ─ четное число очков на обеих
костях.
113. Решение
Кости бросают два раза, то есть n=2.Четное число очков может быть, если
(2,2); (2,4); (4,2); (4,4); (4,6); (6,4);
(6,6); (2,6); (6,2).
p=9/36
Воспользуемся гипергеометрической
схемой:
114.
9P2 (0) C
36
0
0
2
1
2
9
27
36 16
1
9
P2 (1) C
36
27 3
36 8
9
P2 (2) C
36
2
1
2
2
2
0
1
27
36 16
115.
Закон распределения случайнойвеличины X
X
0
1
p
9/16
3/8
2
1/16
116. Задача 2
Построить ряд распределенияслучайной величины X ─ количество
пятерок при трех бросках игральной кости.
117. Решение
Пятерка может выпасть 0,1,2 или 3раза.
Вероятность выпадения пятерки в
одном броске равна p=1/6.
Вероятность, что в трех бросках
пятерка ни разу не выпадет равна
p=5/6 5/6 5/6=125/216.
118.
Вероятность, что в трех бросках пятеркавыпадет три раза равна
p=1/6 1/6 1/6=1/216.
Вероятность, что в трех бросках пятерка
выпадет один раз равна
p=1/6 5/6 5/6+5/6 1/6 5/6+5/6 5/6 1/6=
=75/216
Вероятность, что в трех бросках пятерка
выпадет два раза
p=1/6 1/6 5/6+1/6 5/6 1/6+5/6 1/6 1/6=
=15/216
119.
Ряд распределения случайнойвеличины X
X
P
0
1
125/216 75/216
2
3
15/216
1/216
120. Задача 3
В денежной лотерее 500 билетов.Разыгрываются 2 по 100 рублей; 2 по
500 рублей; 10 по 50 рублей. Найти
закон распределения случайной
величины X ─ стоимость возможного
выигрыша для владельца одного билета.
121. Решение
Случайная величина X принимаетзначения возможного выигрыша, то
есть 0, 50, 100 и 500.
Вероятность выигрыша 500 рублей
равна p= 2/500;
Вероятность выигрыша 100 рублей
равна p=2/500;
Вероятность выигрыша 50 рублей равна
p=10/500.
122.
Всего выигрышных билетов 14, значитневыигрышных билетов 500-14=486.
Вероятность, что выигрыша не будет равна
p=486/500.
Закон распределения случайной величины Х
X
p
0
50
486/500 10/500
100
500
2/500
2/500
123. Задача 4
В партии из 10 деталей 3нестандартных. Наудачу отобраны 2
детали. Построить закон распределения
случайной величины Х ─ числа
нестандартных деталей.
124. Решение
Воспользуемся гипергеометрическойсхемой: N=10; n=2; M=3; m=0,1,2.
Случайная величина Х принимает
значения 0,1,2.
125.
C C7
P2 (0)
2
C10
15
0
3
2
7
C C
7
P2 (1)
2
C10
15
1
3
1
7
C C
1
P2 (2)
2
C10
15
2
3
0
7
126.
Закон распределения случайнойвеличины Х
X
0
p
7/15
1
7/15
2
1/15
127. Вопросы к лекции 8
Перечислите виды случайных величин.Какая случайная величина называется
дискретной? Примеры.
Что называют законом распределения
случайной величины?
Биномиальное распределение.
Распределение Пуассона.
Геометрическое распределение.
Гипергеометрическое распределение.




















































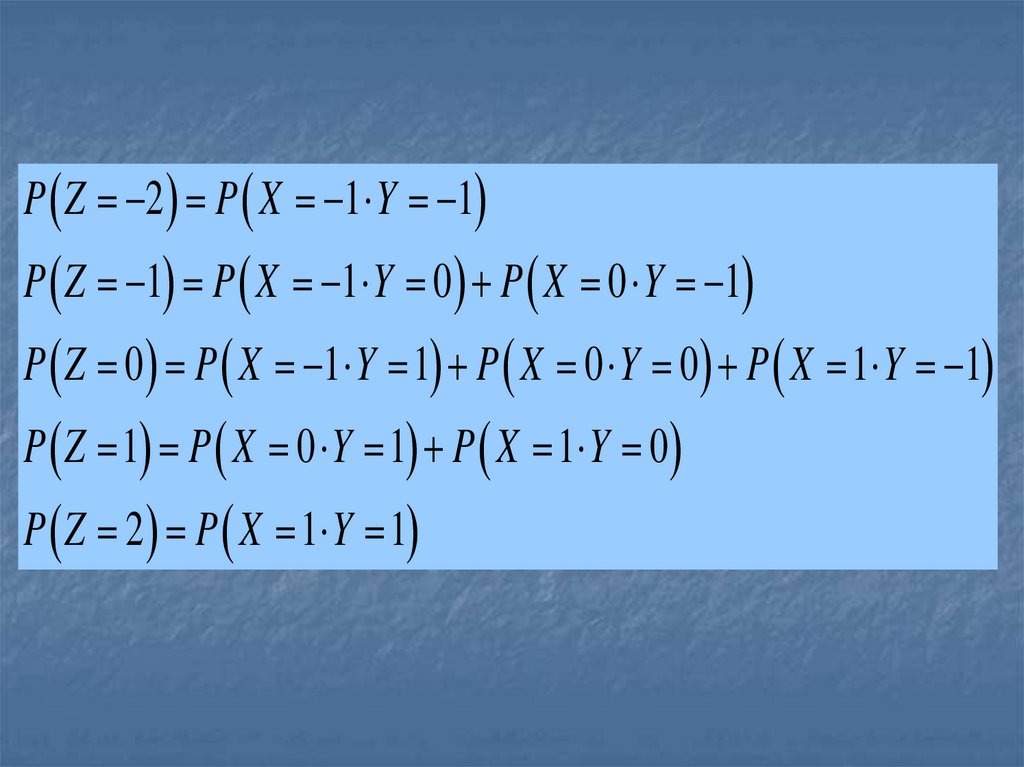
























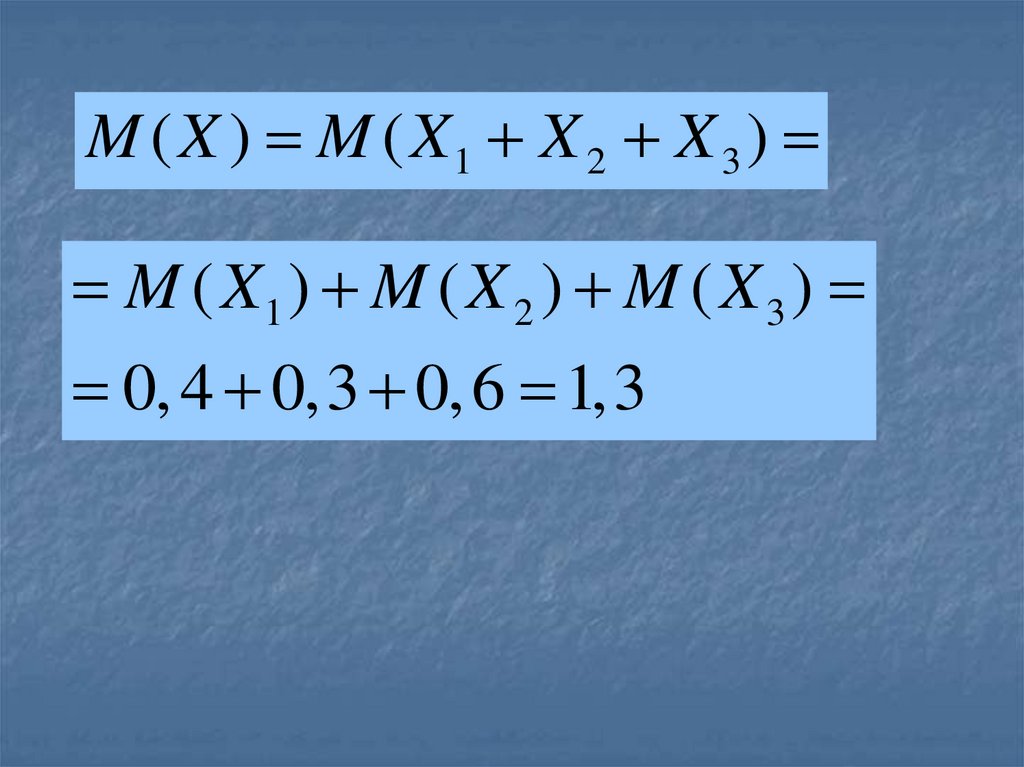


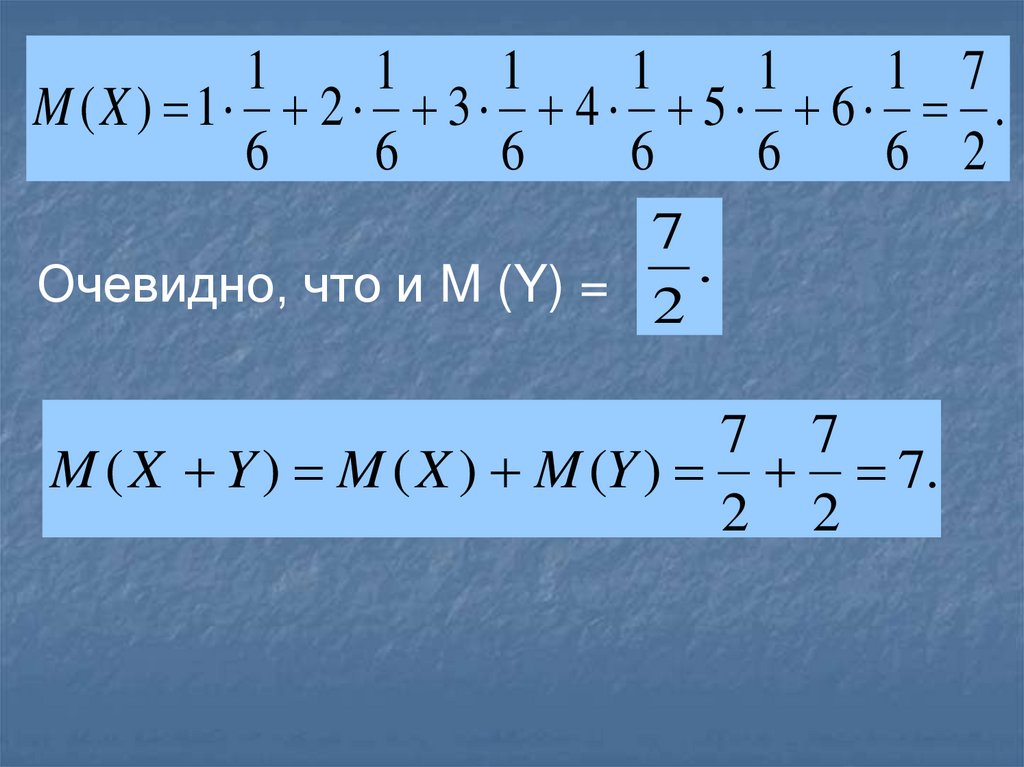

















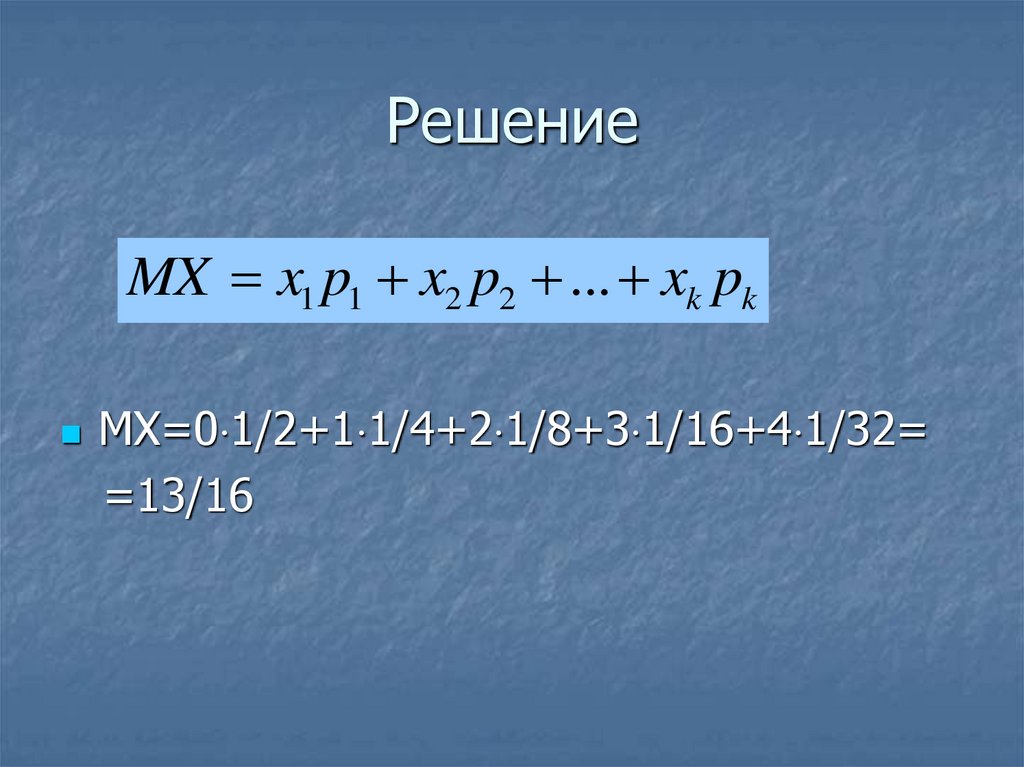










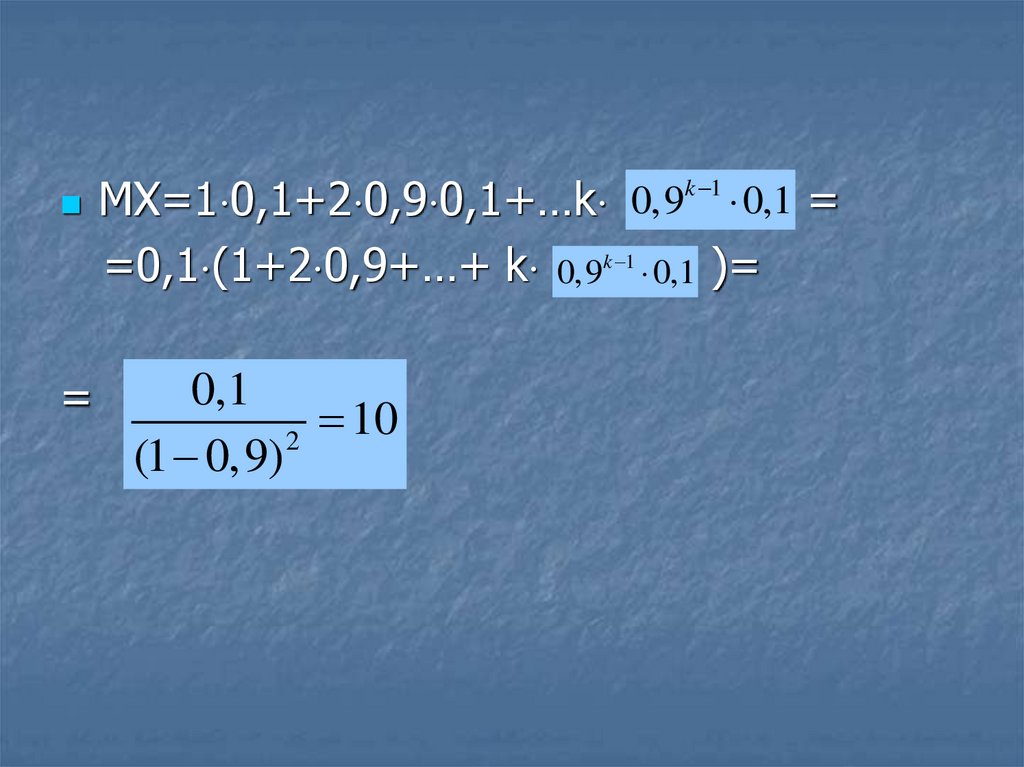


















 Математика
Математика








