Элементы комбинаторики и теории вероятностей

1.

НОВОАЗОВСКИЙ ИНДУСТРИАЛЬНЫЙ
ТЕХНИКУМ
Элементы
комбинаторики
и теории
вероятностей.

2.

«Крупное научное открытие даёт
решение крупной проблемы, но и в
решении любой задачи
присутствует крупица
открытия».
Д.Пойа:

3.

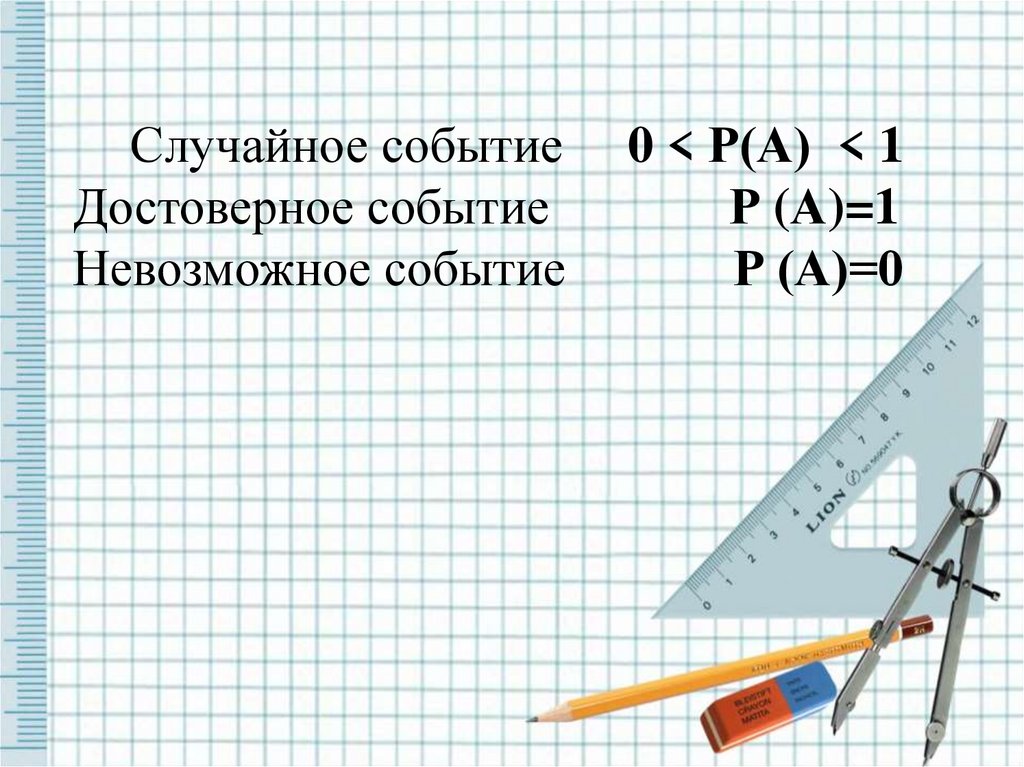
Случайное событие
Достоверное событие
Невозможное событие
0 < Р(А) < 1
Р (А)=1
Р (А)=0

4.

«Устный счёт»:
1. Из слова «математика» выбирается наугад одна буква.
а) Какова вероятность, что эта буква будет гласной?
б) Какова вероятность, что эта буква будет буквой «у»?
2. Выбирается наугад одно из чисел 4, 5, 6, 7, 8, 9, 10, 11, 12.
а) Какова вероятность, что это число будет чётным? б) Какова
вероятность, что оно будет чётным, и будет делиться на 3?
3. Лотерея состоит из 10000 билетов, среди них 1250
выигрышных. Какова вероятность, что наудачу купленный билет
окажется выигрышным?
4. Из колоды в 36 карт выбирается наугад одна карта. Какова
вероятность, что это будет карта: а) черной масти; б) картинка; в)
картинка червонной масти?
5. На рисунке изображена квадратная мишень ABCD, М середина стороны ВС. Стрелок, не целясь, стреляет в мишень и
попадает. Какова вероятность того, что он попадает: а) в
треугольник AMD; б) в треугольник MCD?
B M C
A
D

5.

1а) 0,5
1б) 0
2а) 5/9
2б) 2/9
3) 0,125
4а) 0,5
4б) 4/9
4в) 1/9
5а) 0,5
5б) 0,25

6.

Задача 1.
Двое приятелей договорились
встретиться между 12 и 13 часами и
ждать друг друга не более 15 минут.
Какова вероятность того, что
встреча состоится?

7.

Задача 1.
Двое приятелей договорились
встретиться между 12 и 13 часами и
ждать друг друга не более 15 минут.
Какова вероятность того, что
встреча состоится?

8.

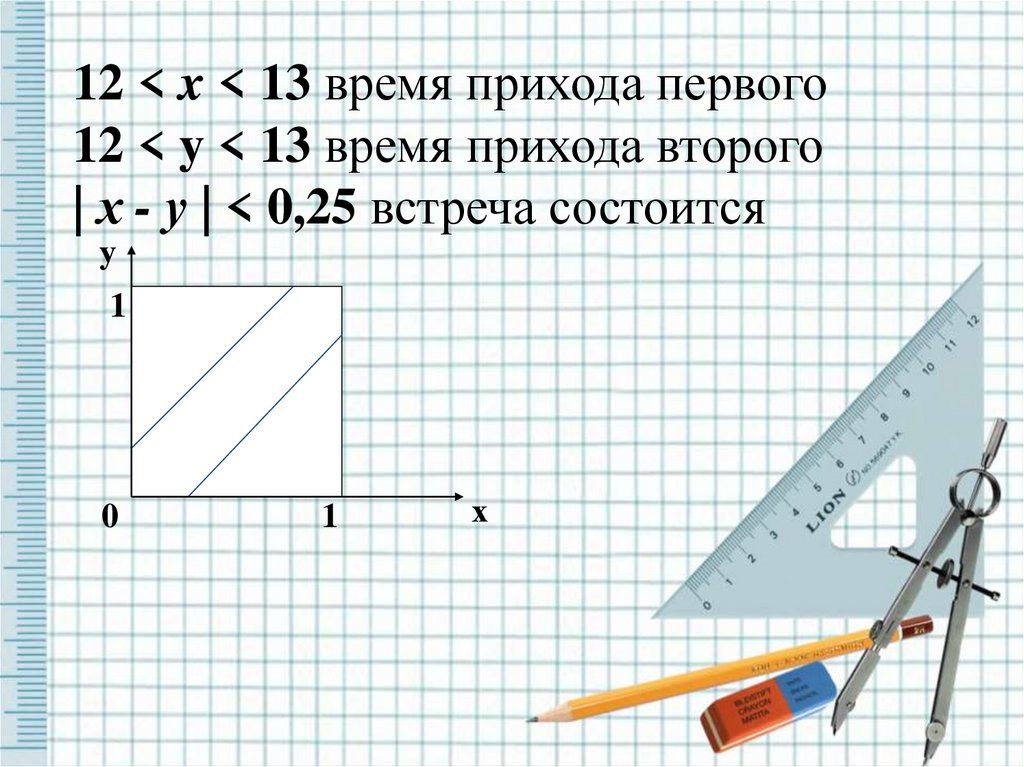
12 < x < 13 время прихода первого
12 < y < 13 время прихода второго
| х - у | < 0,25 встреча состоится

9.

12 < x < 13 время прихода первого
12 < y < 13 время прихода второго
| х - у | < 0,25 встреча состоится
у
1
0
1
х

10.

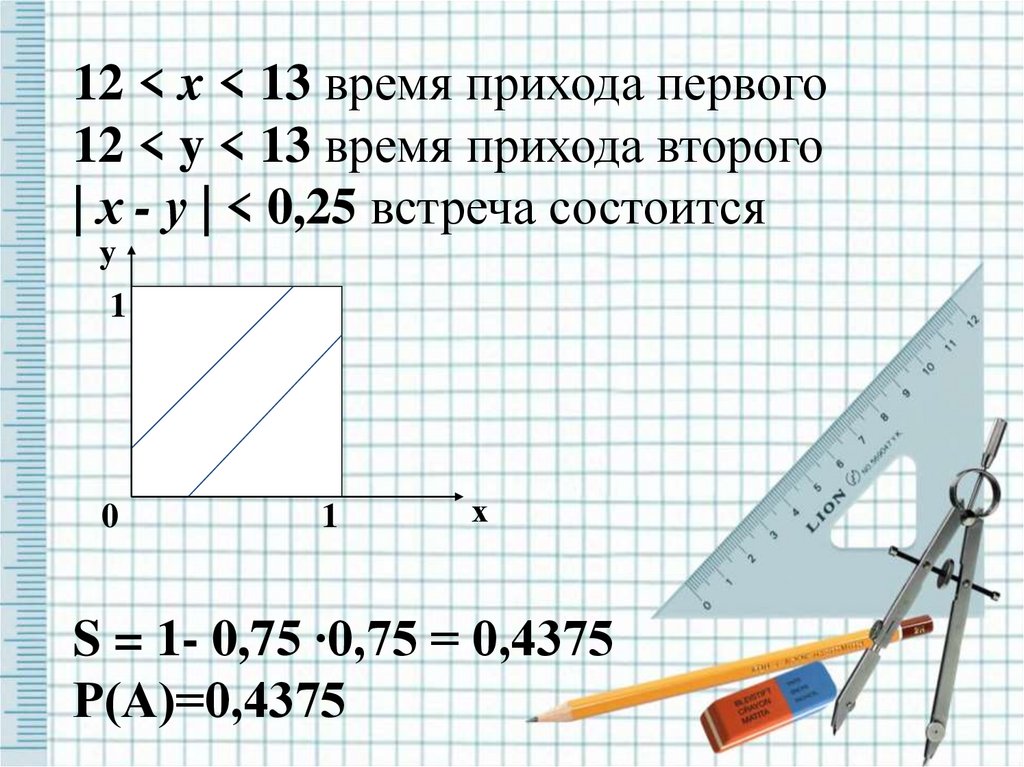
12 < x < 13 время прихода первого
12 < y < 13 время прихода второго
| х - у | < 0,25 встреча состоится
у
1
0
1
х
S = 1- 0,75 ∙0,75 = 0,4375
Р(А)=0,4375

11.

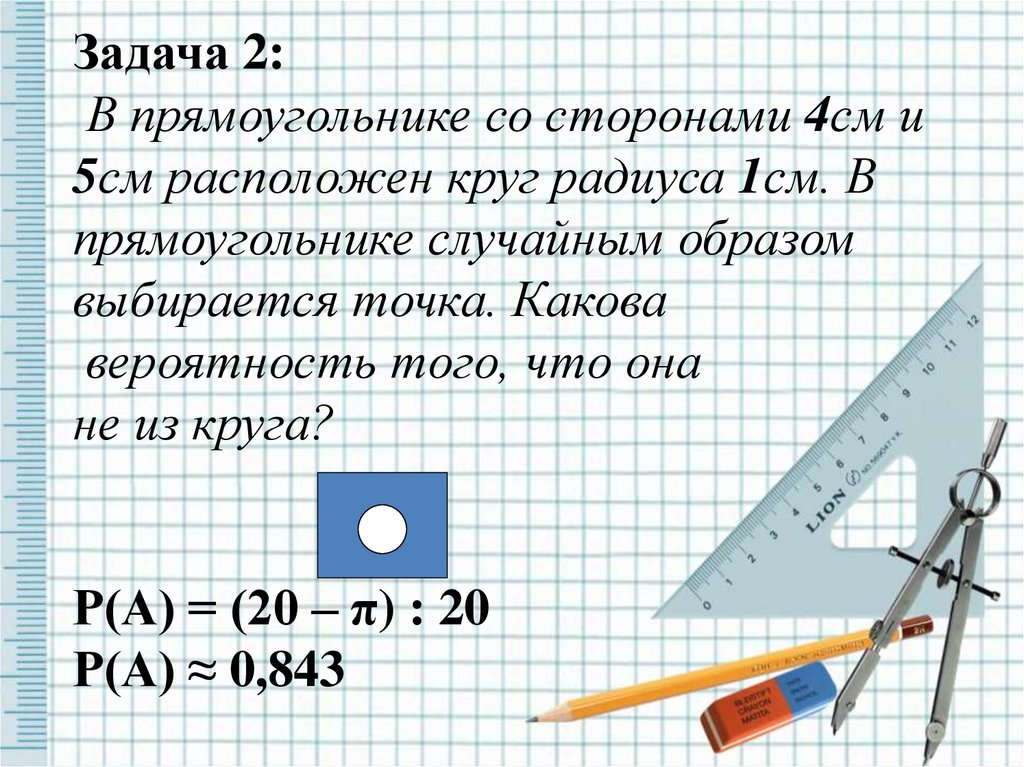
Задача 2:
В прямоугольнике со сторонами 4см и
5см расположен круг радиуса 1см. В
прямоугольнике случайным образом
выбирается точка. Какова
вероятность того, что она
не из круга?

12.

Задача 1:
Из урны, содержащей 4 белых. 3 черных и 7
красных шаров, вынимают один шар.
Какова вероятность того, что он будет
белым или черным?
РЕШЕНИЕ
Пусть А – событие, состоящее в появлении белого
или черного шара.
Всего случаев (шаров) - n =14, а событий,
благоприятствующих событию А, m = 7.
Итак P (А) = 7/14 = 1/2

13.

Задача 2:
В прямоугольнике со сторонами 4см и
5см расположен круг радиуса 1см. В
прямоугольнике случайным образом
выбирается точка. Какова
вероятность того, что она
не из круга?
Р(А) = (20 – π) : 20
Р(А) ≈ 0,843

14.

1) В мешке находятся жетоны с номерами от 1 до 15. Из
мешка наугад вынимают один жетон. Какова
вероятность того, что номер вынутого жетона не
делится ни на 2, ни на 3?
2) За круглым столом 8 посадочных мест, на которые
среди прочих претендуют Олег и Максим. Какова
вероятность, что при случайном распределении мест
ребята не будут сидеть рядом?
3) В случайном эксперименте монету бросают 3 раза.
Найдите вероятность того, что «орёл» не выпал ни разу.
4) Стрелок стреляет по круглой мишени радиуса 10 см.
Какова вероятность того, что, не целясь, он попадёт в
яблочко радиуса 2 см?
5) Мишень представляет собой три круга (один внутри
другого), радиусы которых равны 4, 5 и 9 см. Стрелок
выстрелил, не целясь, и попал в мишень. Найдите
вероятность того, что он попал в средний круг, но не
попал в маленький круг.

15.

Ответы:
1)
5 : 15 = 1/3
2) 5/7
3) 0,5 ∙ 0,5 ∙ 0,5 = 0,125
4) 4π : (100π) = 0,04
5) (25π-16π) : 81π = 1/9

16.

Спасибо за внимание