Коды Рида - Маллера

1. Коды Рида - Маллера

2. Коды Рида - Маллера над GF(2)

• Коды
Рида
–
Маллера
(РМ)
представляют собой класс линейных
кодов над GF(2) с простым описанием и
декодированием.
• Для любых целых m и l, l < m существует
код РМ длиной 2m, который называется
кодом РМ l–го порядка.

3. Порождающая матрица

• Порождающая матрица кода РМ l-го
порядка длиной 2m определяется как
совокупность блоков
G G0
G1
T
Gl

4. Порождающая матрица (Булевы функции)

• где G0 – вектор размерностью n = 2m ,
состоящий из одних единиц;
• G1- матрица размером (m 2m ),
содержащая в качестве столбцов все
двоичные коды из m бит;
• строки матрицы Gl получаются как все
возможные произведения l строк
матрицы G1

5. Порождающая матрица

• Для определенности будем считать, что
первый столбец в G1 состоит из одних
нулей, последний из одних единиц, а
остальные – коды чисел 1,2,…,
упорядоченных по возрастанию, считая,
что младший бит расположен в нижней
строке.

6. Порождающая матрица

• Поскольку существует всего
m
j
• способов выбора j строк, входящих в
произведение, то матрица Gj имеет
размер
m
2 m
j

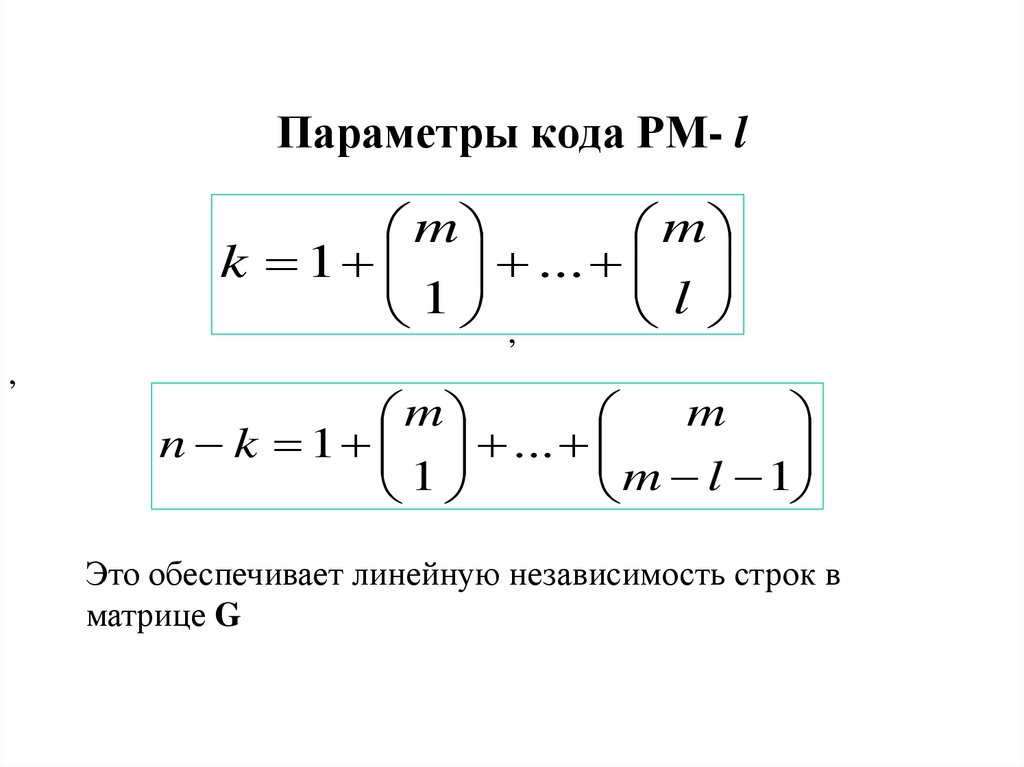
7. Параметры кода РМ- l

m
m
k 1 ...
1 ,
l
,
m
m
n k 1 ...
1
m l 1
Это обеспечивает линейную независимость строк в
матрице G

8. Параметры кода РМ- l

• Код Рида – Маллера l-го порядка длиной
n = 2m представляет собой бинарный код
с параметрами
l
i
(n, k ) (2 , Cm )
i 0
m

9. Кодовые расстояния

• Код РМ-1 является двойственным
расширенному коду Хемминга, для него
d min 2 m 1
• Код РМ-2 имеет
1 h m / 2
d min 2
m 1
2
m 1 h

10.

11.

12. РМ

13. Формирование через булевы переменные

1
2
Кодовых слов

14. Обобщенный GRM (n,k)

• Кодовых слов
h=2

15. Не-бинарный код

• На основе системе счисления по
смешанному основанию

16. Система счисления по смешанному основанию

• Пусть рассматривается множество целых чисел
• {0,1, …, N –1}.
• Если N = N1 N2 …Nm
• то любое число
a
• из этого множества можно представить в виде
a am am 1N m am 2 N m N m 1 ... a1N m N m 1...N 2
a1 {0,1,..., N1 1}
a2 {0,1,..., N 2 1}
am {0,1,..., N m 1}
• Числу a можно поставить в соответствие код
(«m – ка»
a (a1, a2 ,...,am )

17. Матрица Паскаля

18. На основе матрицы Паскаля

19. Алгоритм мажоритарного декодирование кода РМ

• Рассмотрим
метод
мажоритарного
декодирования кода РМ по большинству
голосов на конкретном примере.
l 1
k 4 n 23 8
m 3

20. Кодирование

• Информационная вектор-строка
• код
a a0 , a1,..., ak 1
C a G PM a0 v 0 a1v1 ... ak 1v m

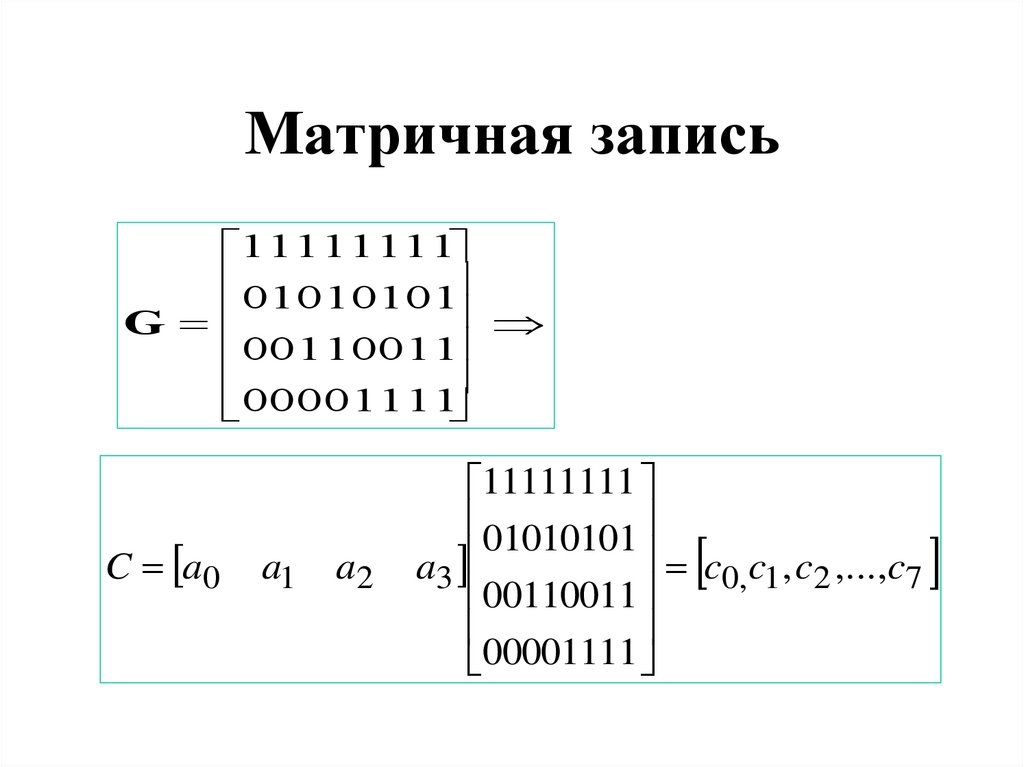
21. Матричная запись

11111111
01010101
G
00110011
00001111
C a0
a1
a2
11111111
01010101
c0, c1 , c2 ,...,c7
a3
00110011
00001111

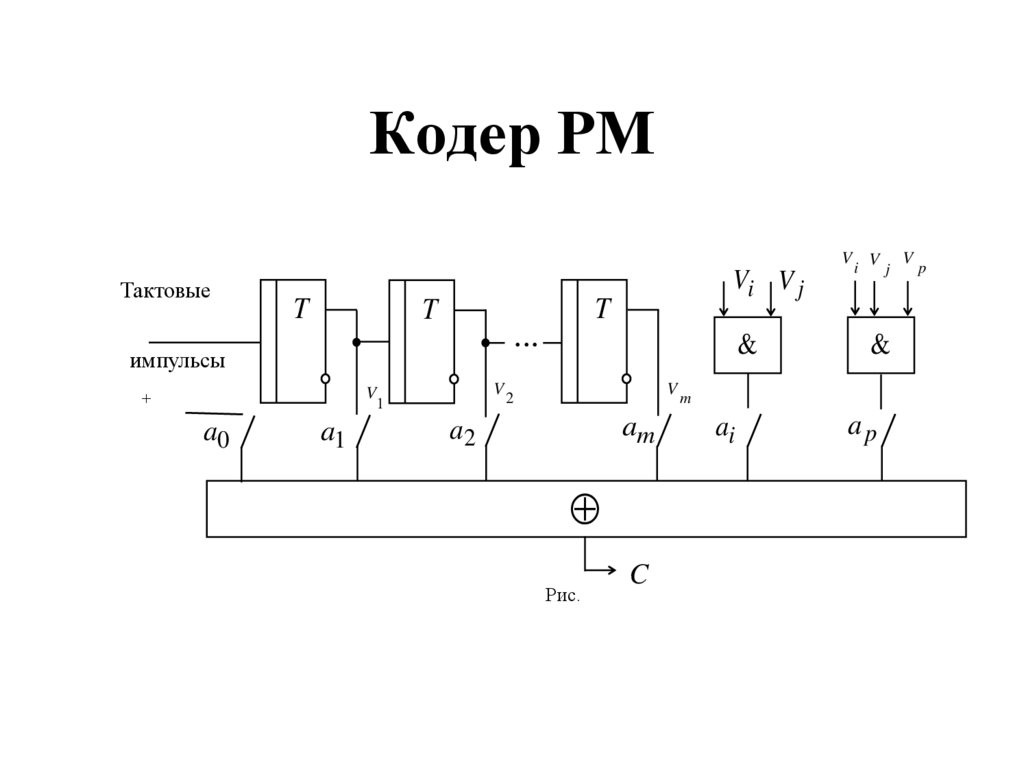
22. Кодер РМ

Тактовые
T
T
V
V
1
a0
a1
T
...
импульсы
Vi V j
&
V
2
am
a2
Рис.
C
V V
i
&
m
ai
j
ap
V
p

23. Проверочные соотношения

• Можно построить проверочные
соотношения, связывающие
информационный символ с символами
кодового слова.
• Эти соотношения имеют вид:

24. Проверочные соотношения Ортогональная система проверок

c0 a 0
c1 a0 a1
a1 c0 c1 l11 a3 c0 c4 l31
a1 c2 c3 l12 a3 c1 c5 l 32
c 2 a0 a 2
c3 a0 a1 a2
a1 c4 c5 l13 a3 c2 c6 l33
a1 c6 c7 l14 a3 c3 c7 l34
a2 c0 c2 l21
c 4 a0 a3
c5 a0 a1 a3
c6 a0 a2 a3
a2 c1 c3 l22
a2 c4 c6 l23
c7 a0 a1 a2 a3 a2 c5 c7 l34

25. Правило принятия решений

n
Если
2
d min
0 lij
2
j 1
n
Если
2
d min
lij d min
2
j 1
ai 0
ai 1

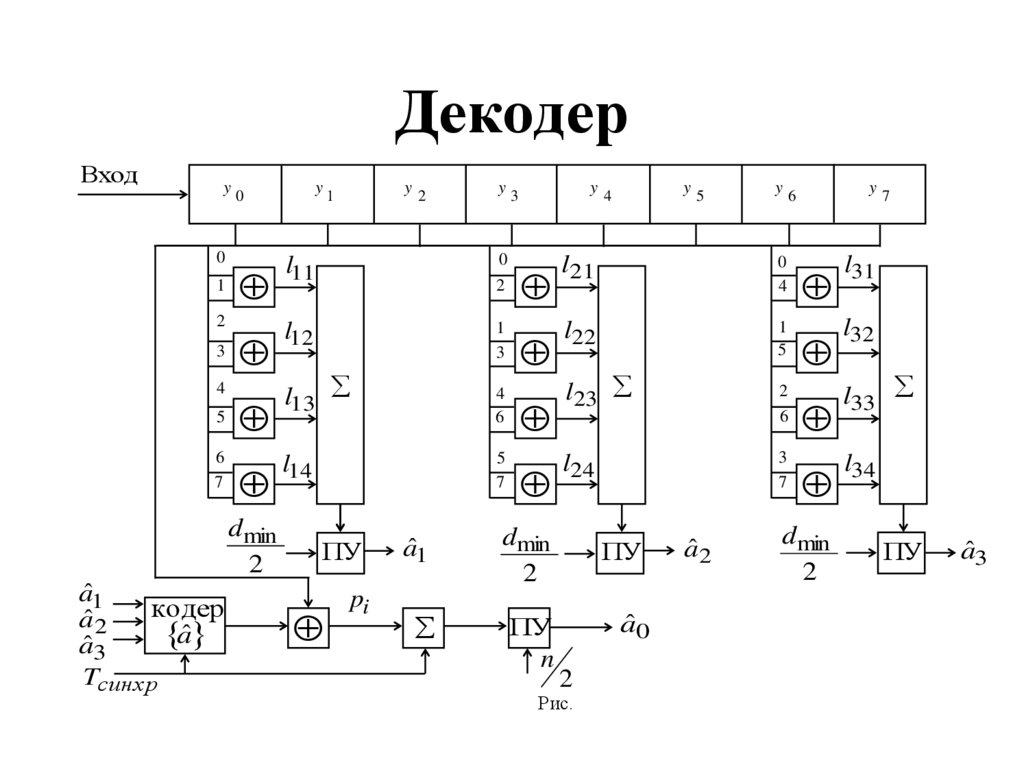
26. Декодер

Вход
y0
0
1
2
3
4
5
6
7
l11
l12
dmin
2
â1
кодер
â2
â
â3
Tсинхр
y1
y2
y3
0
2
1
3
l13
4
6
5
7
l14
ПУ
pi
â1
y4
y5
y6
l21
0
4
l22
1
5
l23
2
l24
3
7
dmin
2
ПУ
ПУ
n
â0
2
Рис.
6
â2
y7
l31
l32
dmin
2
l33
l34
ПУ
â3

27. Вероятность ошибки на бит

d
i i
d i
C
p
(
1
p
)
для ДСК при нечетном d
d
i ( d 1) / 2
d
i i
d i
1 C d / 2 p d / 2 (1 p) d / 2
C
p
(
1
p
)
для ДСК при четном d
d
d
Pc ( j ) 2
i ( d / 2) 1
Q 2dEs / N 0 для канала с АБГШ

28. Здесь

• d – кодовое расстояние, p – вероятность
ошибки на входе декодера, Es/N0 –
отношение сигнал-шум в канале, Q(x) –
функция Маркума.

29. Вопросы

•?