Похожие презентации:
Помехоустойчивое кодирование. Циклические коды – подкласс линейных кодов
1. Помехоустойчивое кодирование
Циклические коды – подкласслинейных кодов
2. Примеры использования линейных кодов
• Пример 1. Протокол передачи данных потелефонному каналу ISDN-D, в котором
используется формат передачи данных
LAPD.
1
2 1(2)
F
A
C
max 260
I
2
1
FCS
F
3. Примеры использования линейных кодов
• F=01111110 (flag)• А – поле адреса (address)
• С поле команд (control)
• I –информационное поле (information)
• FCS – проверочные разряды (frame check sequence)
• Общая длина 266х8=21128 бит, проверочных – 16 бит
F
1
A
C
2 1(2)
I
max 260
FCS F
2
1
4. Примеры использования линейных кодов
• Пример 2. Протокол передачи данных в 802.3CSMA/CD для передачи данных в локальных сетях
связи (LAN)
Преамбула
7
Разделитель
Адрес получателя
Адрес источника
Данные
Контроль четности
1
2(6)
2(6)
65-1518
4
5. Линейные циклические коды
Циклические коды интенсивно изучаются, так как:Циклические коды обладают богатой алгебраической
структурой, что используется в различных
приложениях.
• Для циклических кодов чрезвычайно кратко
формулируются технические требования
(спецификации).
Циклические коды легко реализуются с помощью
сдвиговых регистров.
• Многие практически важные коды являются
циклическими.
6. Линейные циклические коды
Линейный (n,k)-код С называется циклическим, еслициклический сдвиг любого кодового слова из С также
принадлежит С:
x0
x
1
...
xn 2
xn 1
(1)
xn 1
x
0
...
xn 3
xn 2
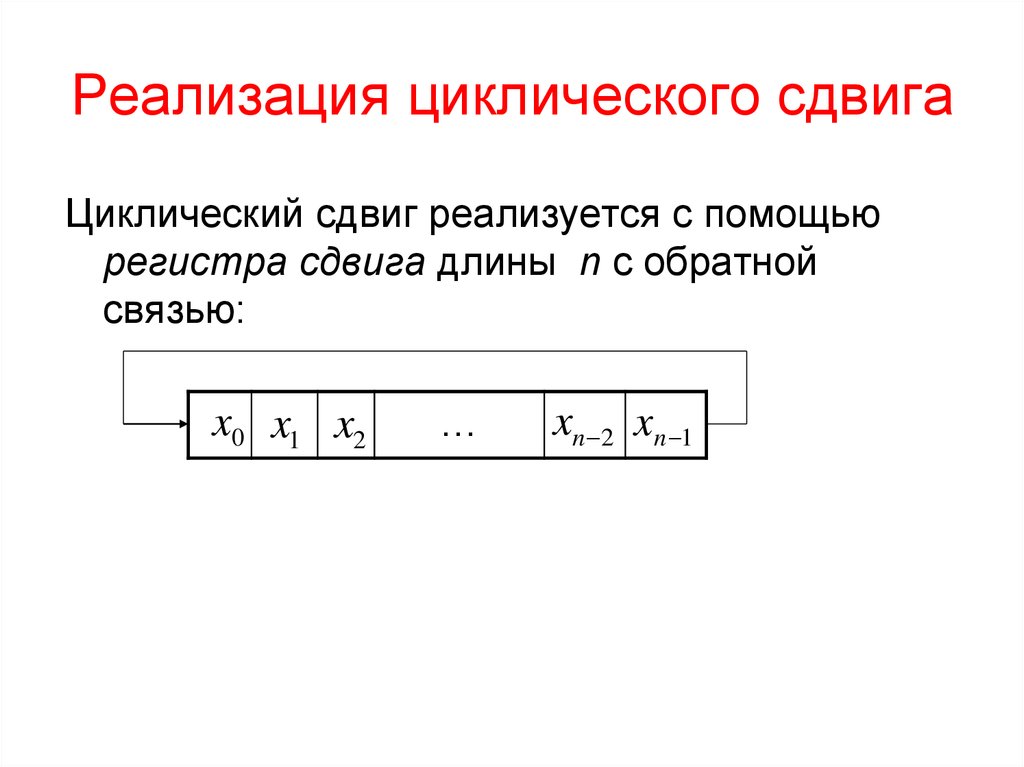
7. Реализация циклического сдвига
Циклический сдвиг реализуется с помощьюрегистра сдвига длины n с обратной
связью:
x0 x1 x2
…
xn 2 xn 1
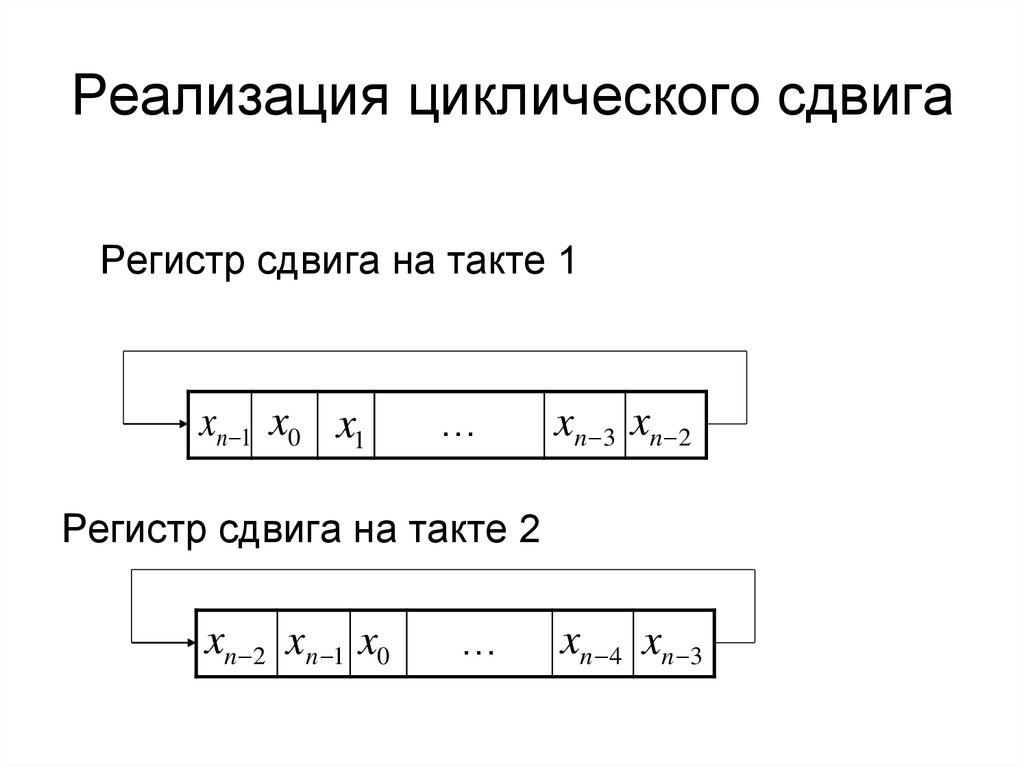
8. Реализация циклического сдвига
Регистр сдвига на такте 1xn 1 x0 x1
…
xn 3 xn 2
Регистр сдвига на такте 2
xn 2 xn 1 x0
…
xn 4 xn 3
9. Замечания
• Для задания произвольного кода из 2kслов длины n необходимо выписать
все 2k кодовых слов длины n.
• Для задания линейного кода из 2k слов
длины n достаточно выписать k
базисных слов длины n (порождающая
матрица).
• Для задания линейного циклического
кода из 2k слов длины n достаточно
выписать одно кодовое слово.
10. Представление кодовых слов в виде кодовых многочленов
a0a
1
n 1
... a ( x) a0 a1 x ... an 1 x
a
n 2
an 1
11. Представление кодовых слов в виде многочленов
Кодовое словоМногочлен
0000
1010
0101
1111
0
1+x2
x+x3
1+x+x2+x3
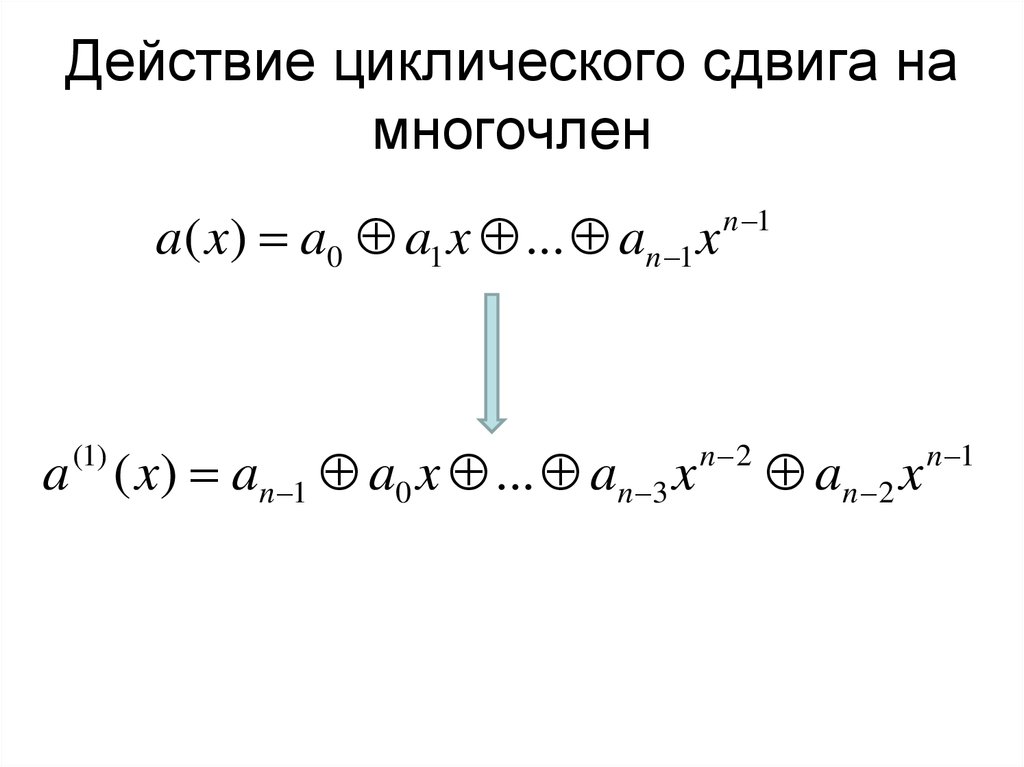
12. Действие циклического сдвига на многочлен
a( x) a0 a1 x ... an 1 xa ( x) an 1 a0 x ... an 3 x
(1)
n 1
n 2
an 2 x
n 1
13. Сложение и умножение многочленов по модулю
1 x (mod x 1)n
n
14. Пример
a( x) 1 x x , n 73
1101000
15. Пример
(1 x x )a( x) (1 x x )(1 x x )4
4
3
1 x x 4 x x 2 x5 x3 x 4 x7
1 x 2 x 3 x 5 x 7 1 x 2 x 3 x5 1 (mod x 7 1)
x x x mod( x 1)
2
3
5
7
16. Пример
(1 x x )a ( x) (1 x x )(1 x x )4
4
1101000
0110100
1000110
0011010 x x x
2
3
5
3
17. Действие циклического сдвига на многочлен
n 1a( x) a0 a1 x ... an 1 x
a (1) ( x) an 1 a0 x ... an 3 x n 2 an 2 x n 1
a0 x ... an 3 x
n 2
an 2 x
n 1
an 1 x (mod x 1)
n
x a( x)(mod x 1)
n
n
18. Циклический сдвиг многочлена на i позиций
(i )an i
a
n i 1
i
n
... x a ( x)(mod x 1)
an i 2
an i 1
19.
• Пространство слов длины n –множество многочленов степени n
• Циклический код длины n –
подмножество многочленов степени n 1
20. Важные теоремы
• Теорема 1. Циклический код содержитединственный кодовый многочлен
минимальной степени.
• Теорема 2.Если g (x ) – кодовый многочлен
минимальной степени, то его младший
коэффициент g 0 1.
• Теорема 3.Пусть g (x )-кодовый многочлен
минимальной степени. Многочлен a(x)
является кодовым многочленом тогда и
g (x).
только тогда, когда он кратен
21. Порождающий многочлен
Пусть g (x ) -кодовый многочлен минимальной степени,этот многочлен называется порождающим
многочленом.
Базис (n,k)- кода: к базисных многочлена
g ( x), x g ( x), x
2
g ( x) ,..., x k 1 g ( x)
Степень порождающего многочлена
deg g ( x) n k
22. Теоремы о порождающем многочлене
• Теорема1. Порождающий многочленциклического кода g (x ) делит без остатка
n
x
многочлен 1. .
• Теорема 2. Если некоторый многочлен g (x ) степени n-k делит многочлен x n 1 без
остатка, то g (x ) порождает циклический
(n,k)-код.
23. Пример
Разложениеx 1 ( x 1)(1 x x )(1 x x )
7
3
2
3
24. Различные циклические коды
g ( x) 1g ( x) 1 x
g ( x) 1 x x
3
g ( x) 1 x 2 x 3
g ( x) (1 x)(1 x x 3 )
g ( x) (1 x)(1 x 2 x 3 )
g ( x) (1 x x )(1 x x )
3
2
3
g ( x) (1 x)(1 x x )(1 x x )
3
2
3
25. Кодирование
• Кодирование циклического кода –умножение информационного
многочлена на порождающий
многочлен
26. Циклический (7,4)-код Хэмминга
g ( x) 1 x x
3
27.
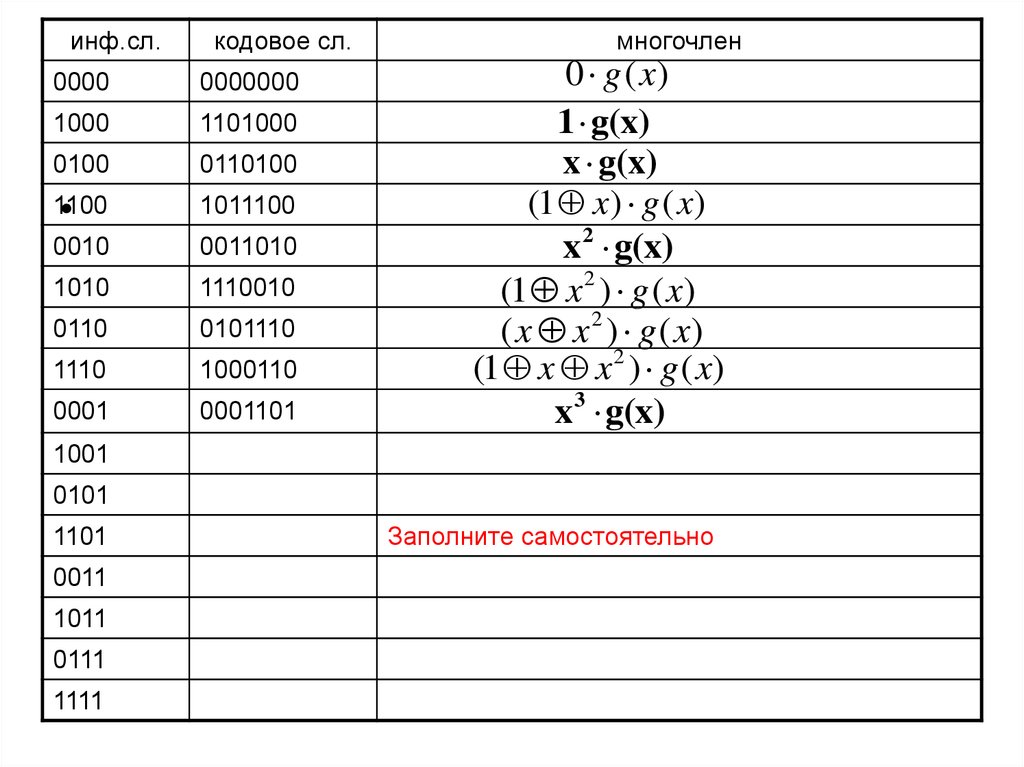
инф.сл.кодовое сл.
0000
0000000
1000
1101000
0100
0110100
1100
1011100
0010
0011010
1010
1110010
0110
0101110
1110
1000110
0001
0001101
многочлен
0 g ( x)
1 g(x)
x g(x)
(1 x) g ( x)
x 2 g(x)
(1 x 2 ) g ( x)
( x x 2 ) g ( x)
(1 x x 2 ) g ( x)
x 3 g(x)
1001
0101
1101
0011
1011
0111
1111
Заполните самостоятельно
28. Циклический (7,4)-код
• Минимальный вес (7,4)-кода равен 3,код исправляет 1 ошибку
29. Замечания (1)
•По сравнению с линейными,циклические коды редки. Например,
существует порядка 300000
линейных двоичных (7,3)-кодов, но
только два из них являются
циклическими.
30. Замечания (2)
•Тривиальные двоичные циклические коды.•Код без информации – код из нулевого слова.
•Код с повторением – код состоящий из двух
слов: 00…0 и 11…1.
• Код с проверкой на четность – код из слов
четного веса.
•Код без проверки – код из всех слов длины n.
•В некоторых случаях (например n = 19), не
существуют циклические коды, кроме
описанных выше четырех кодов.
31. Порождающая матрица циклического кода
1 g1 g 2 ... g n k 10 1 g1 ... g n k 2
G Т 0 0 1 ...
...
k n
0 ... ... 0
1
1
0
0
...
g n k 1
1
0
...
...
g n k 1
1
...
g1
g2
...
g n k 1
0
0
0
1
32. Проверочный многочлен циклического кода
• Так как порождающий многочлен циклическогокода g (x ) делит без остатка многочлен x n 1,
то
x 1 h( x) g ( x)
n
• Многочлен h(x) – проверочный многочлен
33. Проверочная матрица циклического кода
• Всякое кодовое слово можно представитькак c( x) a ( x) g ( x), deg a ( x) k 1
• Тогда
c ( x ) h( x ) a ( x ) g ( x ) h( x )
n
a( x) (1 x )
n
a ( x) a ( x) x
• поэтому
deg c( x) h( x) k 1
34. Проверочная матрица циклического кода
• Поэтому коэффициенты при степенях xстарше k-1 равны 0.
• Тогда
c0 hk c1 hk 1 ... ck h0 0
c1 hk c2 hk 1 ... ck 1 h0 0
c2 hk c3 hk 1 ... ck 2 h0 0
cn k 1 hk cn k hk 1 ... cn 1 h0 0
35. Проверочная матрица циклического кода
hk0
H 0
( n k ) n
0
hk 1
hk 2
...
h1
h0
0
hk
hk 1
...
h2
h1
h0
0
hk
...
...
...
h1
...
...
0
hk 1
hk 2
hk
0
0 ... 0
h0 ...
0
... h1 h0
0
...
36. Порождающий многочлен дуального кода
h x hk hk 1 x ... h0 x1
h ( x) x h( x )
*
k
k
37. Параметры циклического кода Хэмминга
n 2m 1• Длина кода
• Число информационных символов
k n m 2m 1 m
• Минимальное расстояние - 3
• Число исправляемых ошибок - 1






















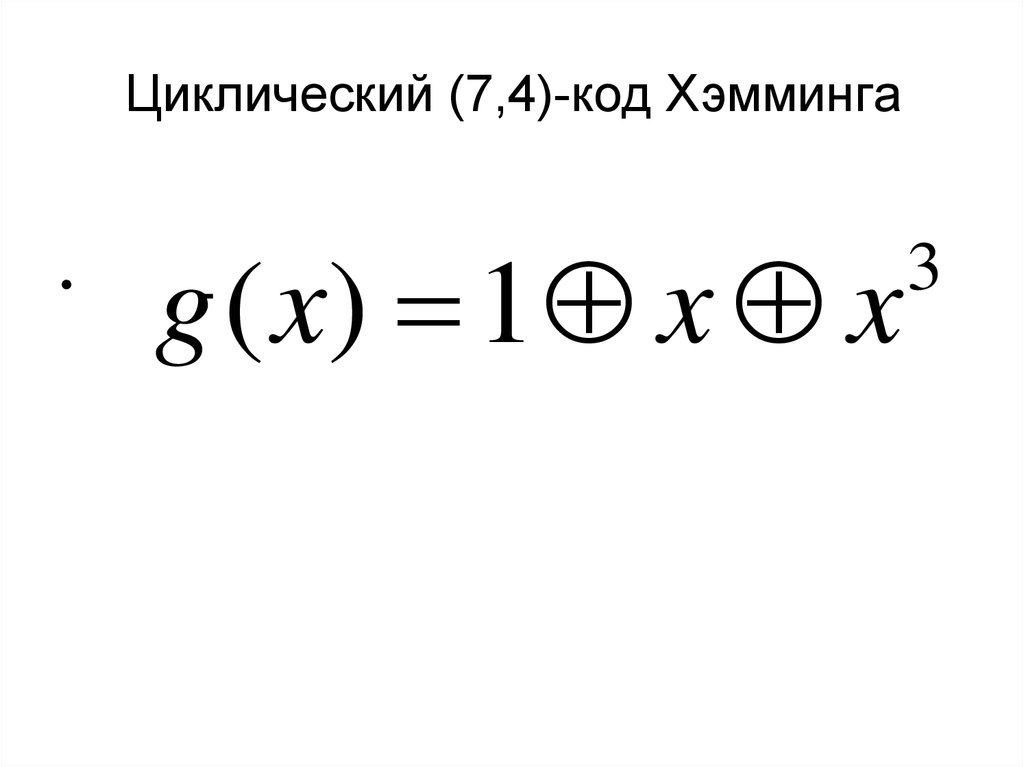










 Информатика
Информатика








