Тригонометрия. Тригонометрические функции двойного аргумента

1.

2. Формулы двойного и половинного аргумента

1.sin2x = 2 sinx·cosx;
2.cos2x = cos²x - sin²x;
3.cos2x = 1 – 2sin²x;
6.
4.cos2x = 2cos²x-1;
7.
5.
;

3. Основные тригонометрические тождества

1.

4.

Найдите значение выражения
.
1)
2)
4)
5)
6)
3)
sin2x = 2 sinx·cosx
cos2x = cos²x - sin²x

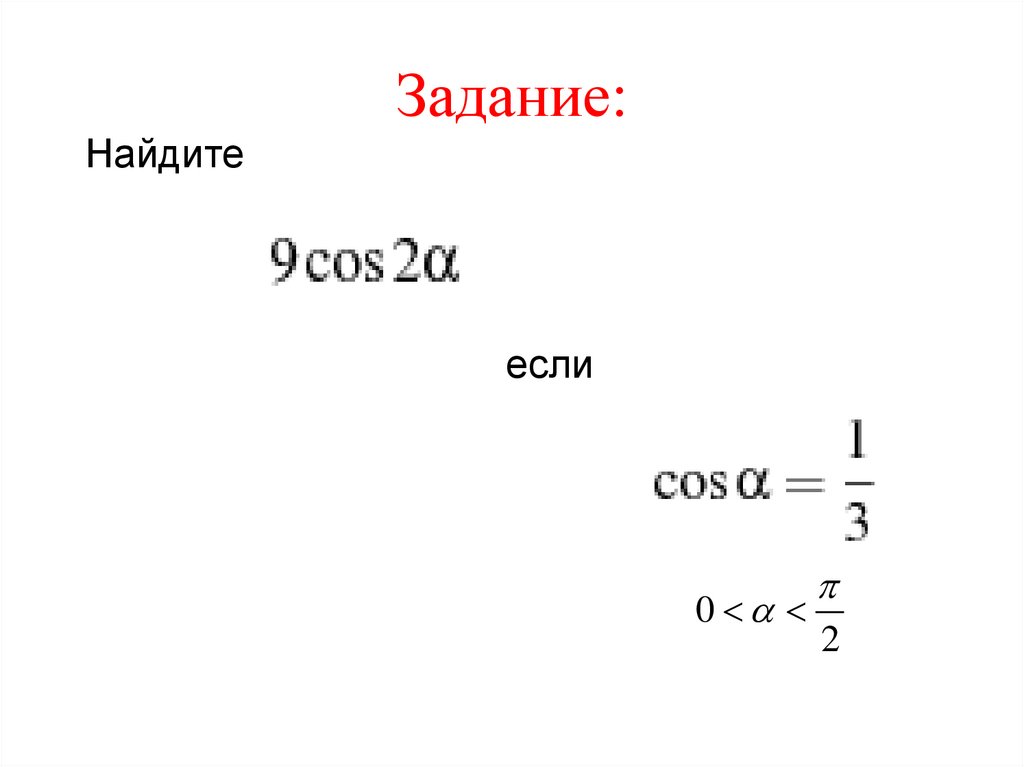
5. Задание:

Найдите
если
0
2

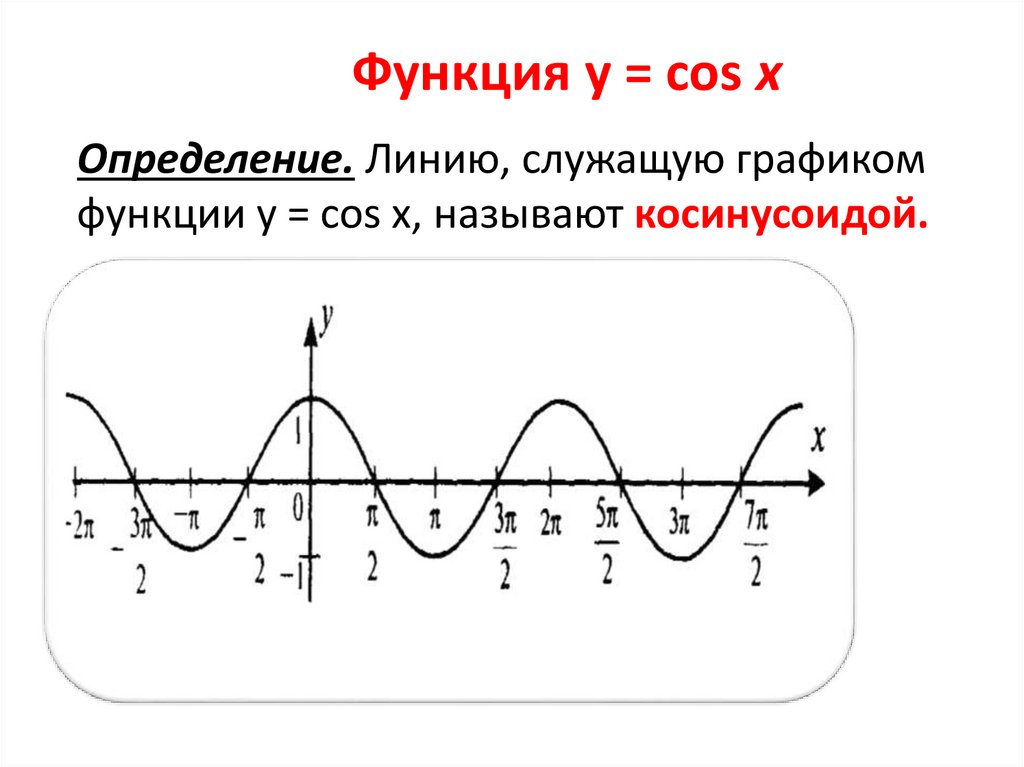
6. Функция y = cos x

Определение. Линию, служащую графиком
функции y = cos x, называют косинусоидой.

7. Свойства функции y = cos x.

Свойство 1. D(y) = (-∞;+∞).
Свойство 2. y = cos x – четная функция.
Свойство 3. Функция y = cos x убывает на отрезке [2πk; π + 2πk]
и возрастает на отрезке [π + 2πk; 2π + 2πk ], где k є Z.
Свойство 4. Функция ограничена и сверху и снизу (-1 ≤ cos t ≤
1).
Свойство 5. yнаим = -1; yнаиб = 1.
Свойство 6. Функция y = cos x периодическая, ее основной
период равен 2π.
Свойство 7. y = cos x – непрерывная функция.
Свойство 8. E(y) = [-1; 1].
Свойство 9. Функция выпукла вверх на отрезке [-0,5π+2πk;
0,5π+2πk],
выпукла вниз на отрезке [0,5π+2πk; 1,5π+2πk], где k є Z.

8. Функция y = tg x

Свойства функции:
График функции
1.
2.
3.
4.
5.
D(y) = (- π /2 + πn; π /2 + πn) ; n Z.
E(у) = R.
Функция периодическая; T = π.
Функция нечетная.
tg x = 0 при х = πn, n Z.
6. Функция возрастает на
(- π /2 + πn; π /2 + πn), n Z
7. tg x > 0
при πn < x < π /2 + πn, n Z;
tg x < 0
при - π /2 + πn < x < πn, n Z .
8. Функция не достигает наибольшего
и наименьшего значений.
9. Прямые π /2 + πn , n Z, являются
асимптотами графика функции.

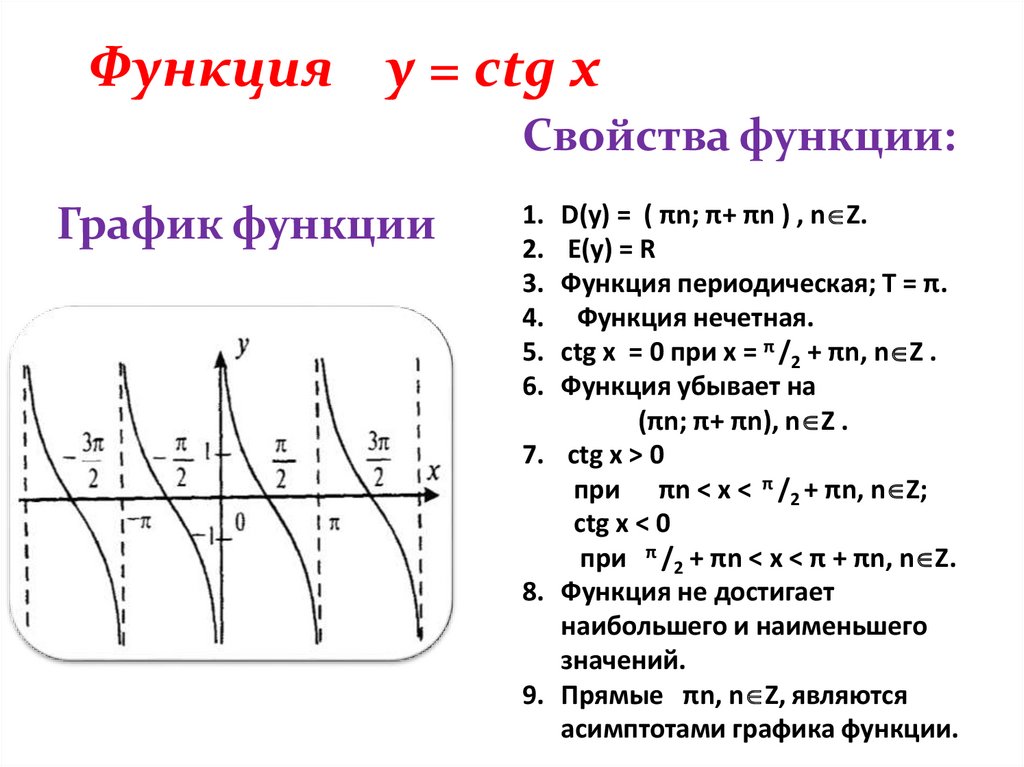
9. Функция y = ctg x

Свойства функции:
График функции
1.
2.
3.
4.
5.
6.
D(у) = ( πn; π+ πn ) , n Z.
E(у) = R
Функция периодическая; Т = π.
Функция нечетная.
ctg x = 0 при х = π /2 + πn, n Z .
Функция убывает на
(πn; π+ πn), n Z .
7. ctg x > 0
при πn < x < π /2 + πn, n Z;
ctg x < 0
при π /2 + πn < x < π + πn, n Z.
8. Функция не достигает
наибольшего и наименьшего
значений.
9. Прямые πn, n Z, являются
асимптотами графика функции.

10.

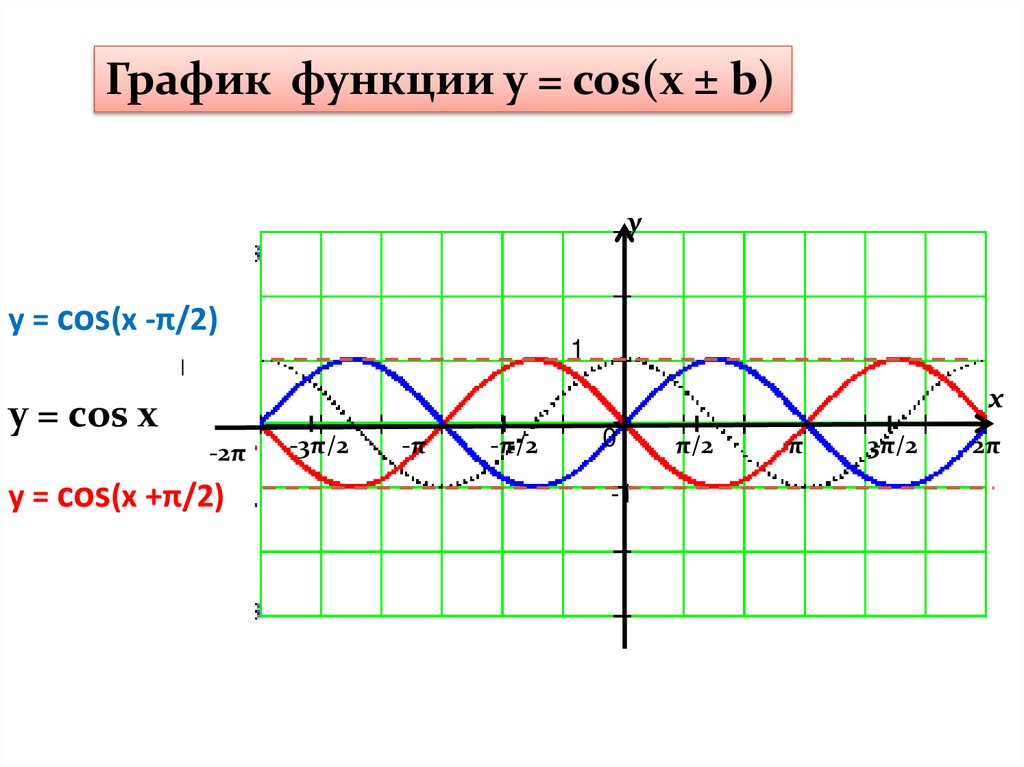
График функции y = cos(x ± b)
y
y = cos(x -π/2)
1
x
y = cos x
-2π
y = cos(x +π/2)
-3π/2
-π
-π/2
0
-1
π/2
π
3π/2
2π

11. Преобразование графиков тригонометрических функций

• График функции у = f (x+в) получается из графика функции у
= f(x) параллельным переносом на (-в) единиц вдоль оси
абсцисс
• График функции у = f (x)+а получается из графика функции
у = f(x) параллельным переносом на (а) единиц вдоль оси
ординат
тригонометрические
функции
11

12. Преобразование графиков тригонометрических функций путем сжатия и растяжения

График функции у =k f (x) получается из графика функции у = f(x)
путем его растяжения в k раз (при k>1) вдоль оси ординат
График функции у = k f (x) получается из графика функции у = f(x)
путем его сжатия в k раз (при 0<k<1) вдоль оси ординат
тригонометрические
функции
12

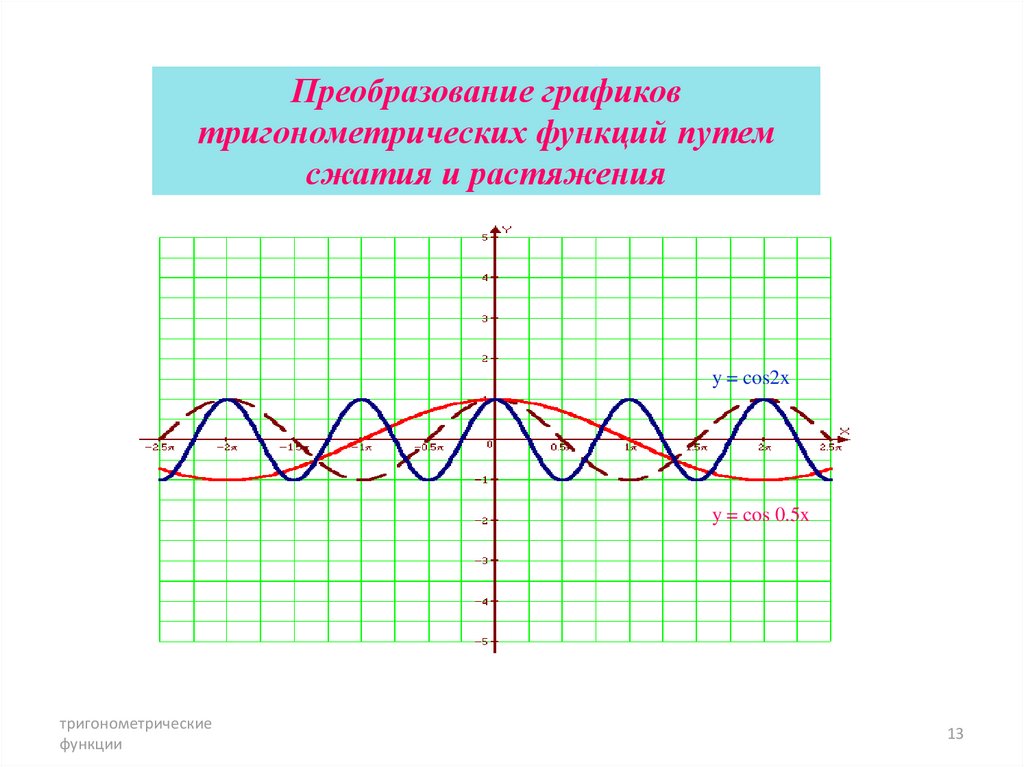
13. Преобразование графиков тригонометрических функций путем сжатия и растяжения

y = cos2x
y = cos 0.5x
тригонометрические
функции
13

14. Преобразование графиков тригонометрических функций путем сжатия и растяжения

Графики функций у = -f (kx) и у=-k f(x) получаются из графиков функций
у = f(kx) и y= k f(x) соответственно путем их зеркального отображения
относительно оси абсцисс
синус – функция нечетная, поэтому sin(-kx) = - sin (kx)
косинус –функция четная, значит cos(-kx) = cos(kx)
тригонометрические
функции
14

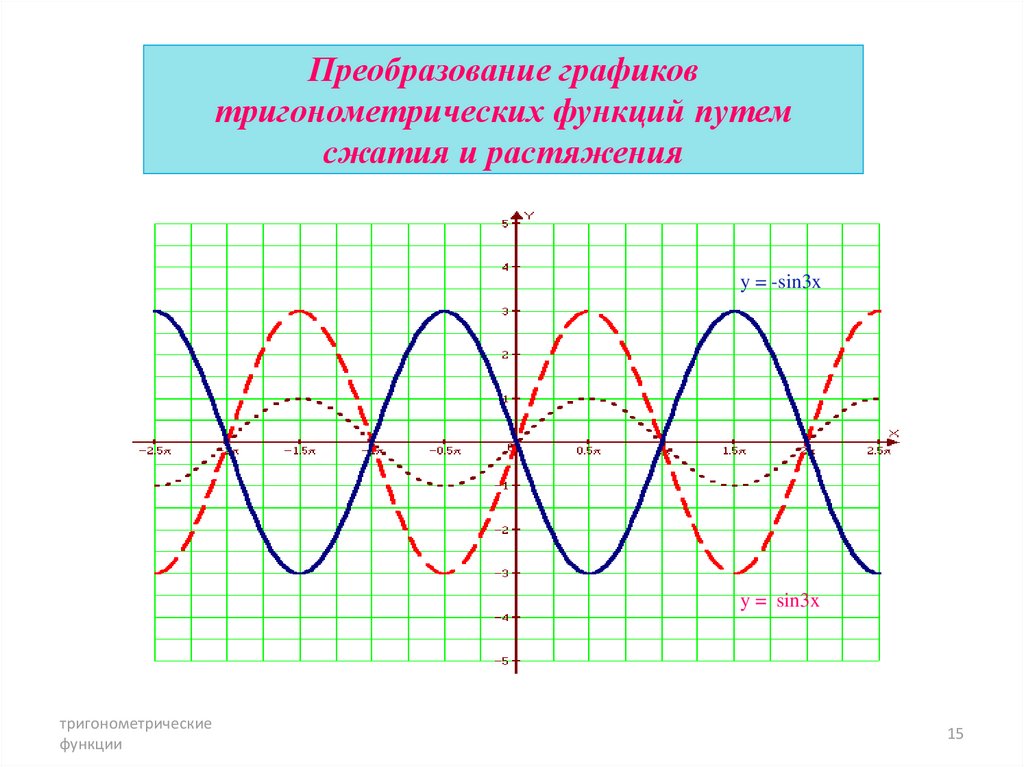
15. Преобразование графиков тригонометрических функций путем сжатия и растяжения

y = -sin3x
y = sin3x
тригонометрические
функции
15

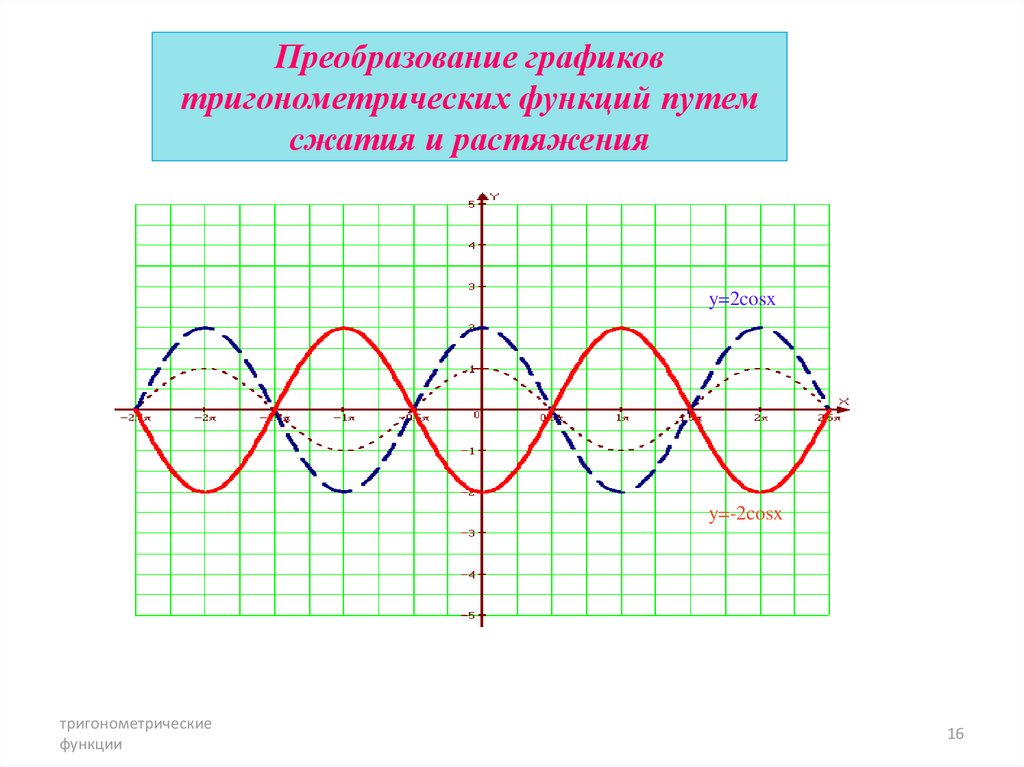
16. Преобразование графиков тригонометрических функций путем сжатия и растяжения

y=2cosx
y=-2cosx
тригонометрические
функции
16

17. Преобразование графиков тригонометрических функций путем сжатия и растяжения

График функции у = f (kx+b) получается из графика функции у = f(x)
путем его параллельного переноса на (-в/k) единиц вдоль оси абсцисс и
путем сжатия в k раз (при k>1) или растяжения в k раз ( при 0<k<1) вдоль
оси абсцисс
f ( kx+b) = f ( k( x+b/k))
тригонометрические
функции
17

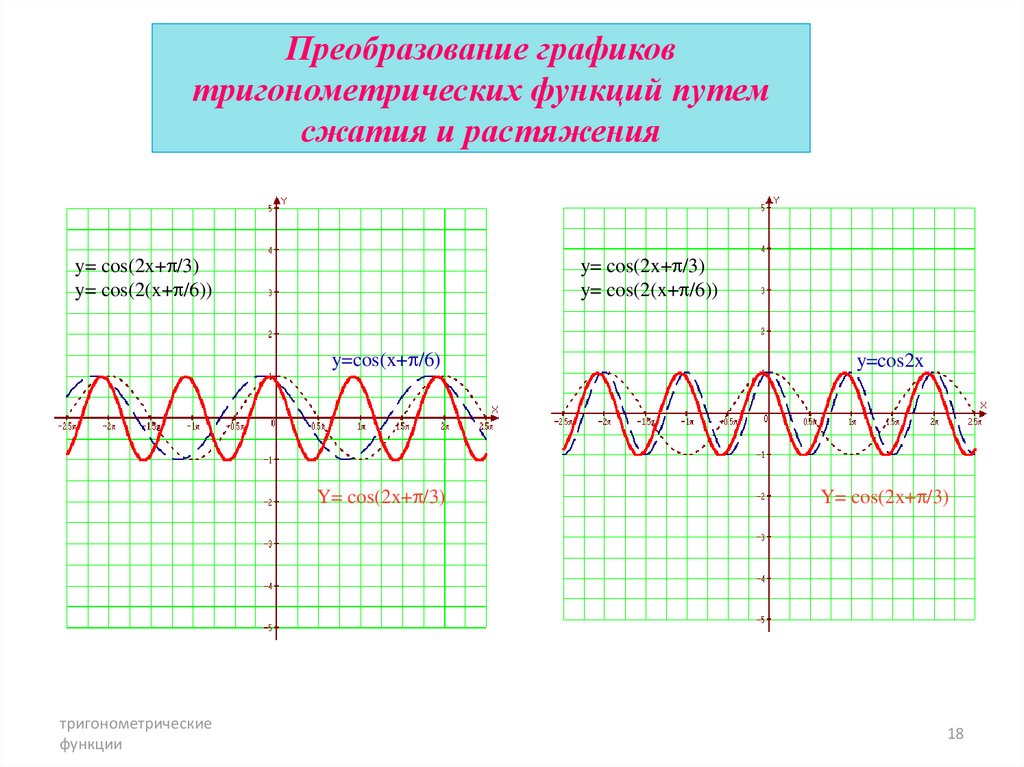
18. Преобразование графиков тригонометрических функций путем сжатия и растяжения

y= cos(2x+ /3)
y= cos(2(x+ /6))
тригонометрические
функции
y= cos(2x+ /3)
y= cos(2(x+ /6))
y=cos(x+ /6)
y=cos2x
Y= cos(2x+ /3)
Y= cos(2x+ /3)
18