Презентация по алгебре и началам математического анализа в 10 классе на тему _Тригонометрические функции, их свойства и графики_

1. Тригонометрические функции, их свойства и графики

2. Понятие функции

Если каждому значению x из некоторого
множества чисел поставлено в соответствие по
определенному правилу число y, то говорят, что
на этом множестве задана функция. При этом х
называют независимой переменной или
аргументом, а у – зависимой переменной или
функцией. Зависимость переменной у от
переменной х называют функциональной
зависимостью. Записывают y=f(x).

3. Область определения функции

Областью определения функции называют
множество всех допустимых значений
переменной x. Геометрически – это проекция
графика функции на ось Ох.

4. Множество значений функции

Множество значений функции — множество
всех значений, которые функция принимает на
области определения. Геометрически – это
проекция графика функции на ось Оy.

5. функции

6.

7.

8.

9.

10.

11.

12. Как найти область определения функции, заданной формулой?

Чтобы найти область определения функции
y=f(x), заданной формулой, нужно установить,
при каких значениях х выражение f(x) имеет
смысл, т. е. выполнимы все действия в правой
части формулы.

13.

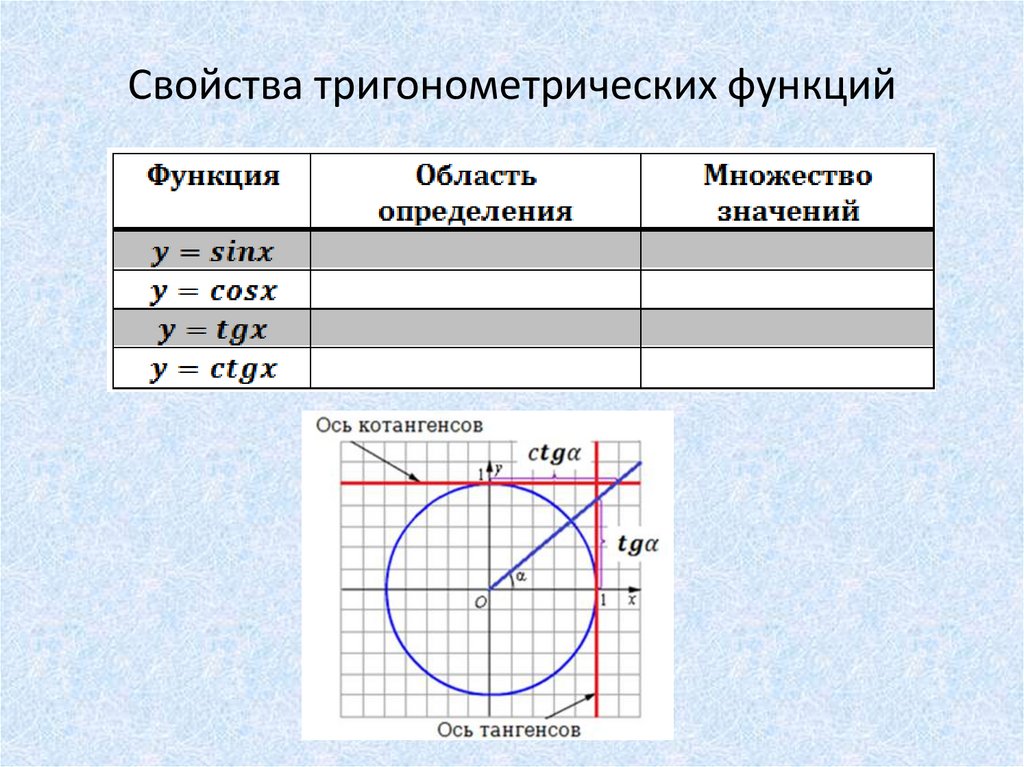
14. Свойства тригонометрических функций

15. Свойства тригонометрических функций

16.

1 2
x
y
М
1
0 2
0
-1
-y
-1 3
1
2
0
-x
М1
2
3
2
-1
2
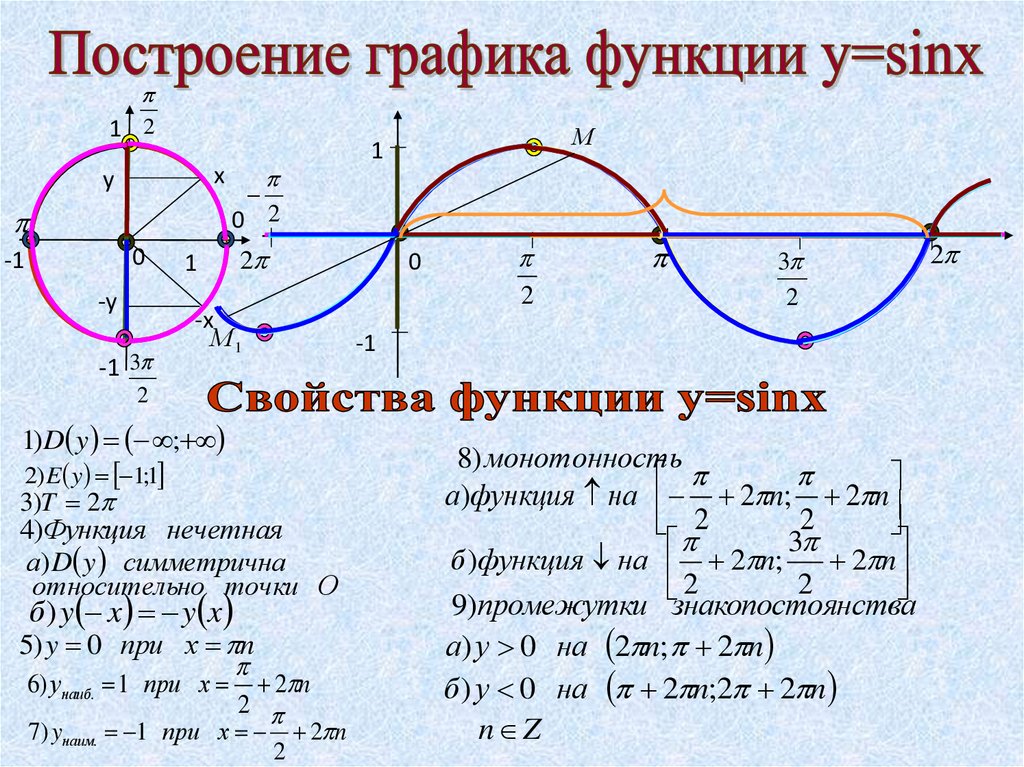
1) D y ;
2) E y 1;1
3)T 2
4)Функция нечетная
а) D y симметрична
относительно точки О
б ) y x y x
5) y 0 при х n
6) унаиб. 1 при х
2 n
2
7) yнаим. 1 при х
2
2 n
8) монотонность
а)функция на 2 n; 2 n
2
2
3
б )функция на 2 n;
2 n
2
2
9)промежутки знакопостоянства
а) у 0 на 2 n; 2 n
б ) у 0 на 2 n;2 2 n
n Z
2

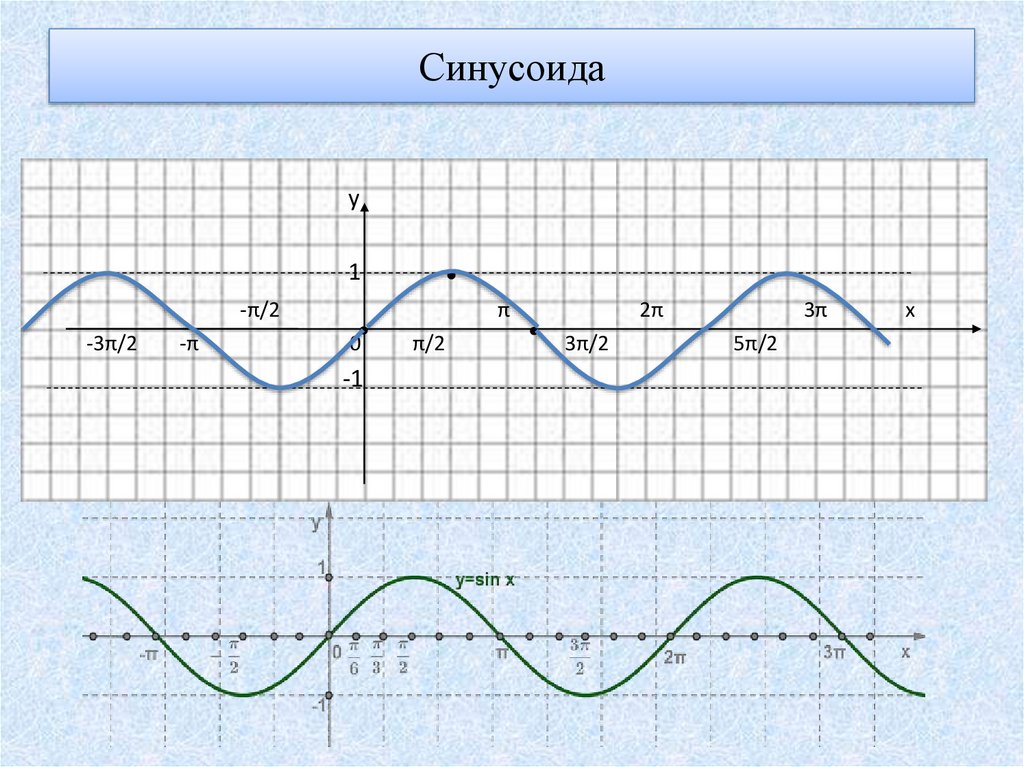
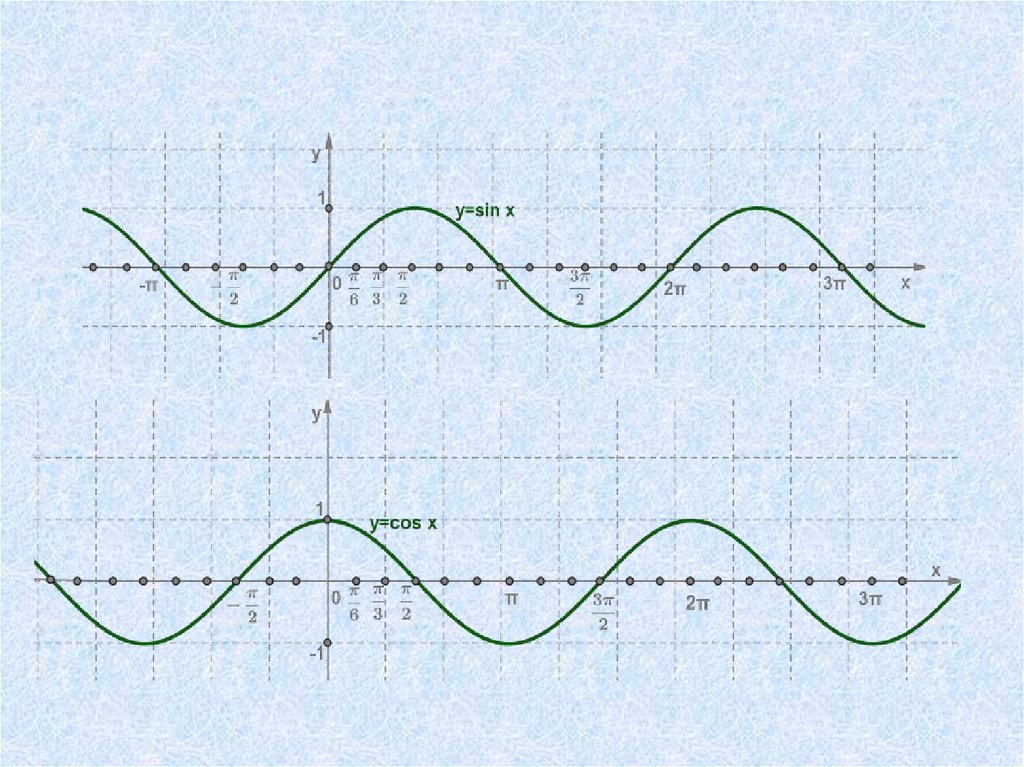
17. Синусоида

у
1
-π/2
-3π/2
-π
π
0
-1
π/2
2π
3π/2
3π
5π/2
х

18.

1 2
1
x
1 0
-1
y
0
2
2
0
-x
-1
2
-1
3 2
2
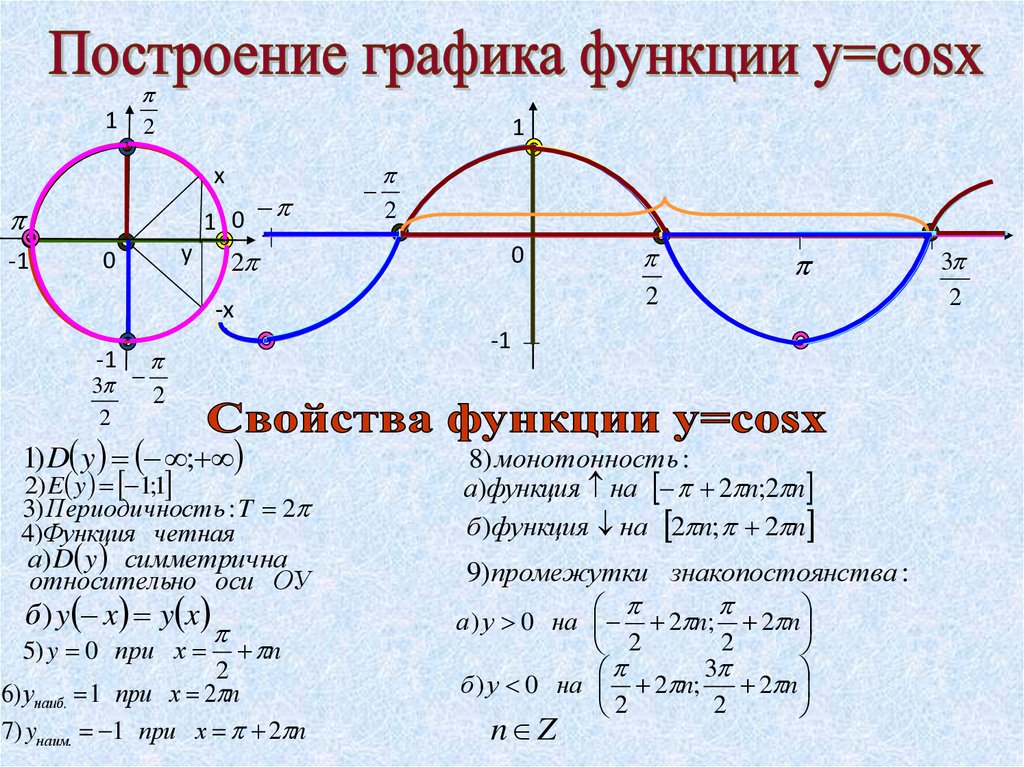
1) D y ;
2) E y 1;1
3) Периодичность : T 2
4)Функция четная
8) монотонность :
а)функция на 2 n;2 n
б )функция на 2 n; 2 n
б) y x y x
9)промежутки знакопостоянства :
а ) у 0 на 2 n; 2 n
а) D y симметрична
относительно оси ОУ
5) y 0 при х
n
2
6) унаиб. 1 при х 2 n
7) yнаим. 1 при х 2 n
2
2
3
б ) у 0 на 2 n;
2 n
2
2
n Z
3
2

19.

20. Преобразование графиков функций y=sin x и y=cos x

Параллельный перенос вдоль оси OY
Параллельный перенос вдоль оси OX
Растяжение (сжатие) в k раз вдоль оси OY
Растяжение (сжатие) в k раз вдоль оси OX
Симметрия относительно оси абсцисс
Пример построения графика сложной функции
20

21.

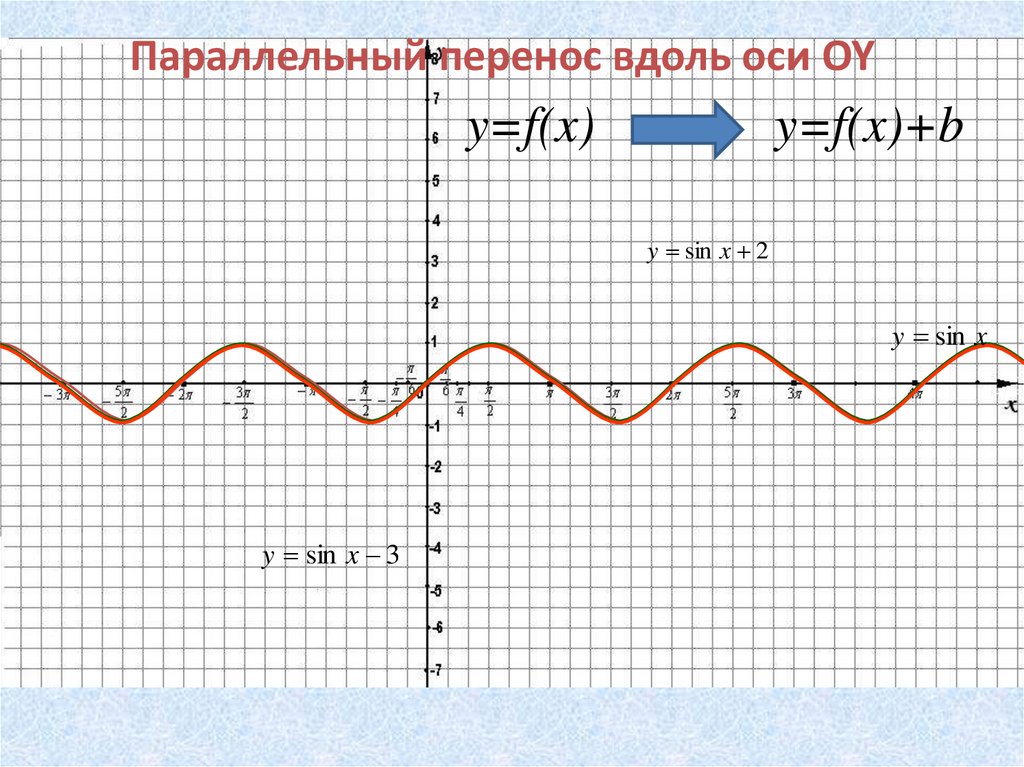
Параллельный перенос вдоль оси OY
y=f(x)
y=f(x)+b
y sin x 2
y sin x
y sin x 3

22.

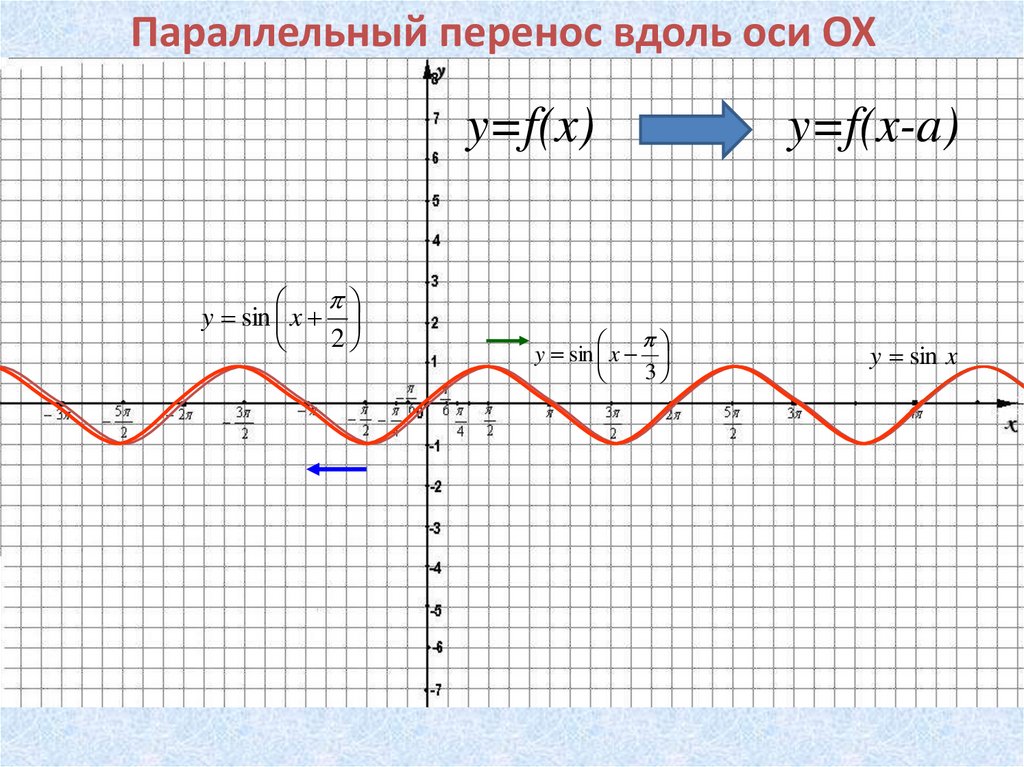
Параллельный перенос вдоль оси OX
y=f(x)
y sin x
2
y sin x
3
y=f(x-a)
y sin x

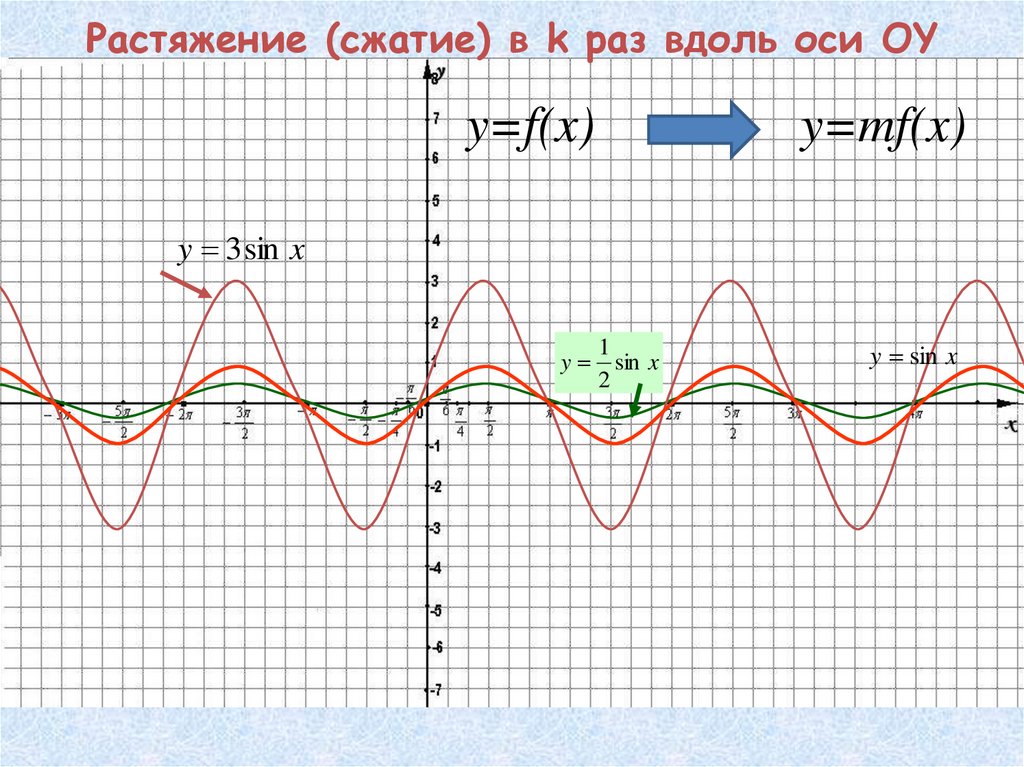
23. Растяжение (сжатие) в k раз вдоль оси OY

y=f(x)
y=mf(x)
y 3 sin x
y
1
sin x
2
y sin x

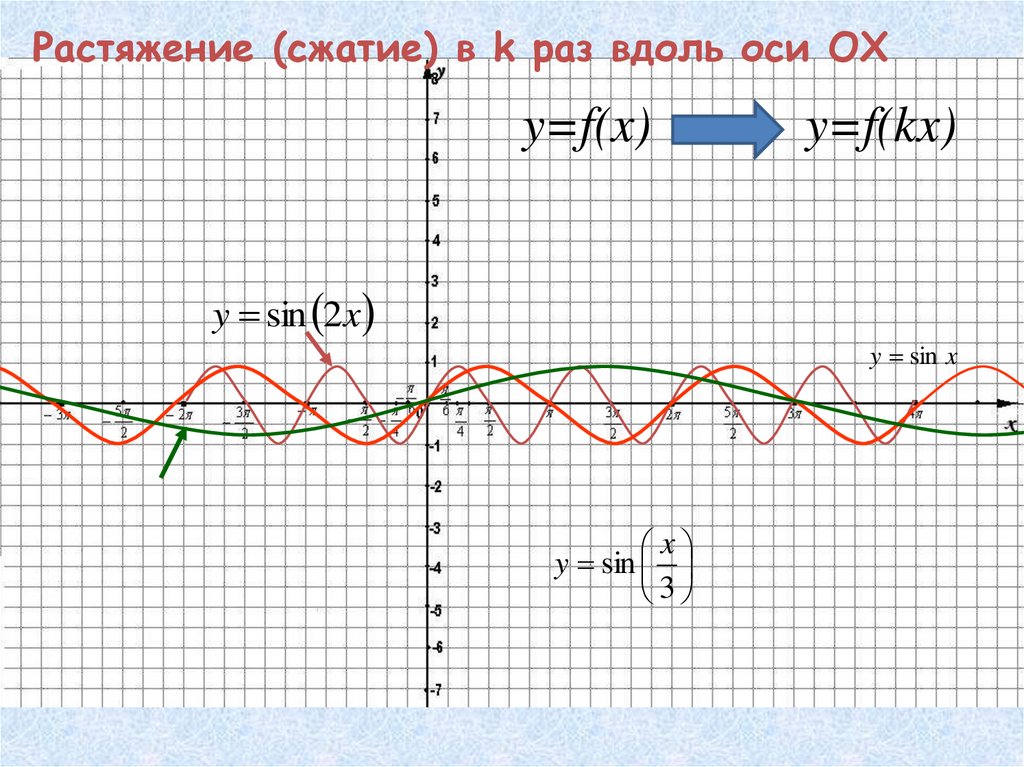
24. Растяжение (сжатие) в k раз вдоль оси OX

y=f(x)
y=f(kx)
y sin 2 x
y sin x
x
y sin
3

25.

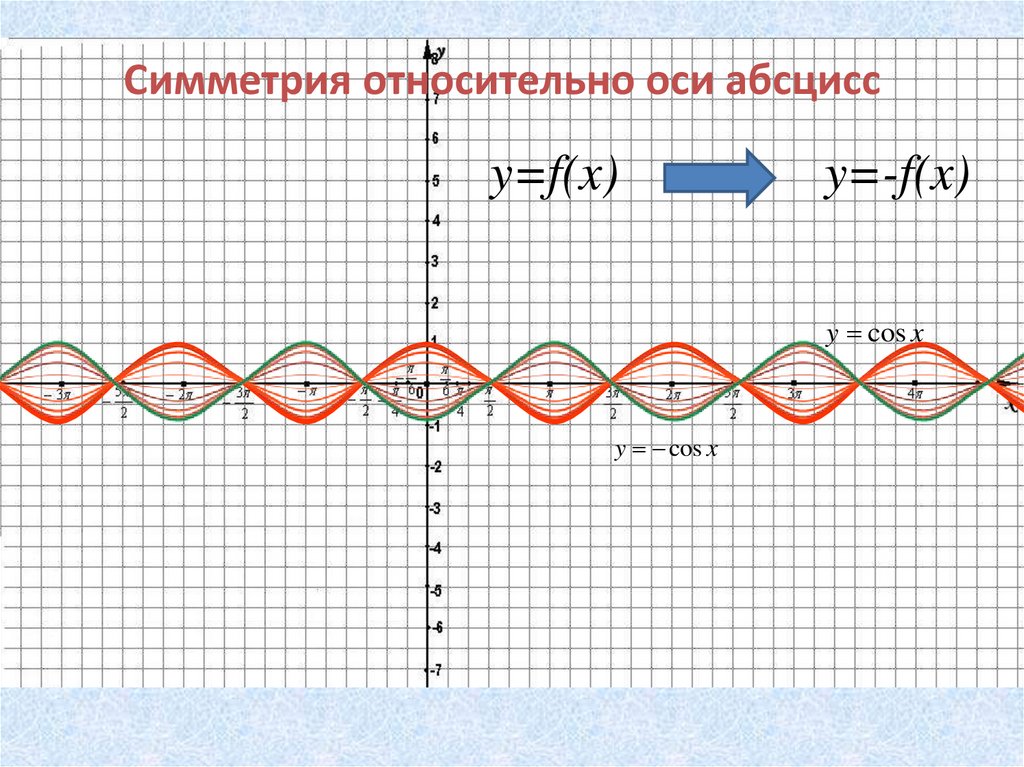
Симметрия относительно оси абсцисс
y=f(x)
y=-f(x)
y cos x
y cos x

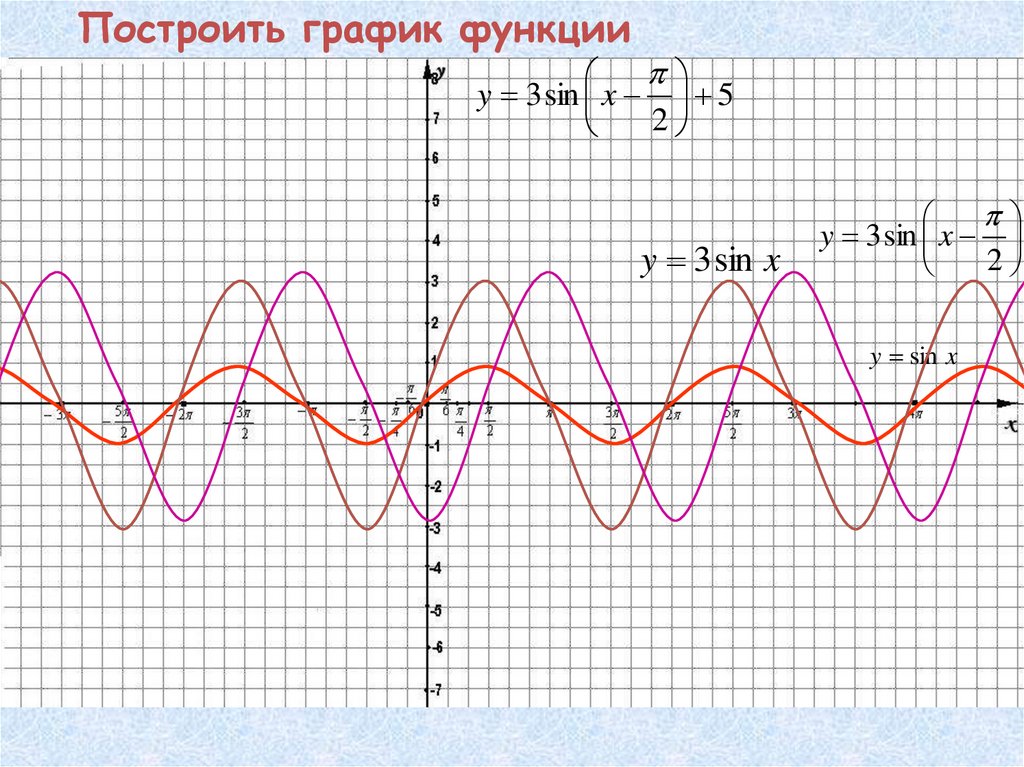
26. Построить график функции

y 3 sin x 5
2
y 3 sin x
y 3 sin x
2
y sin x

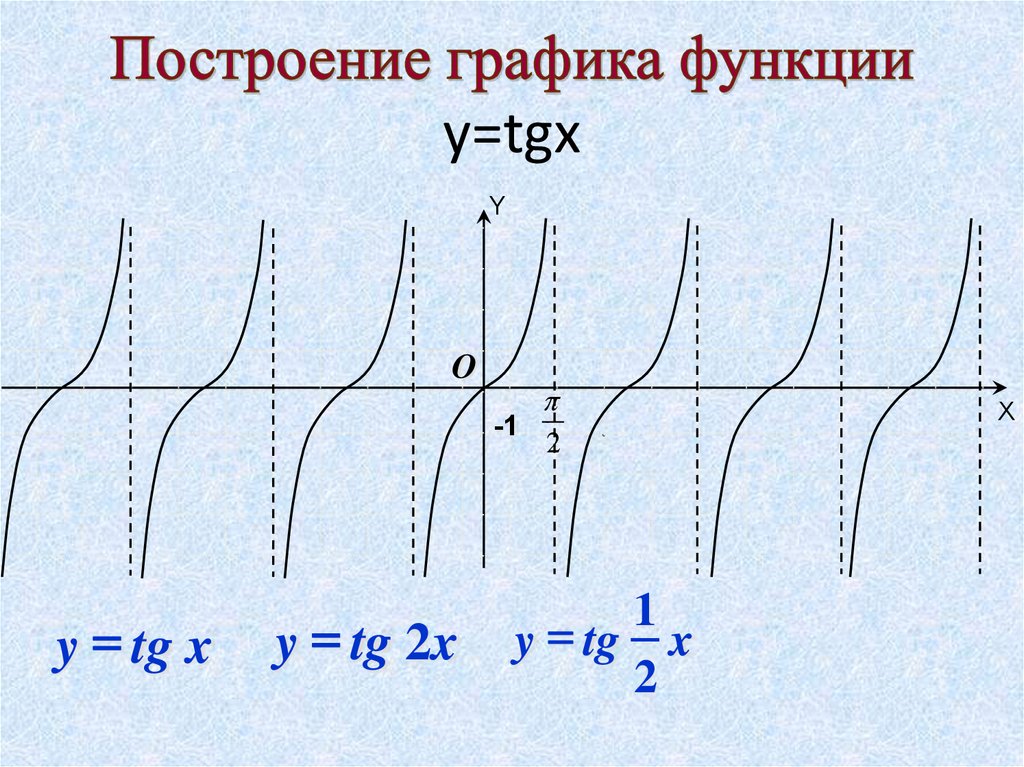
27. Построение графика функции y=tgx

y=tgx
Y
O
y tg x
y tg 2x
-1
2
1
y tg x
2
X

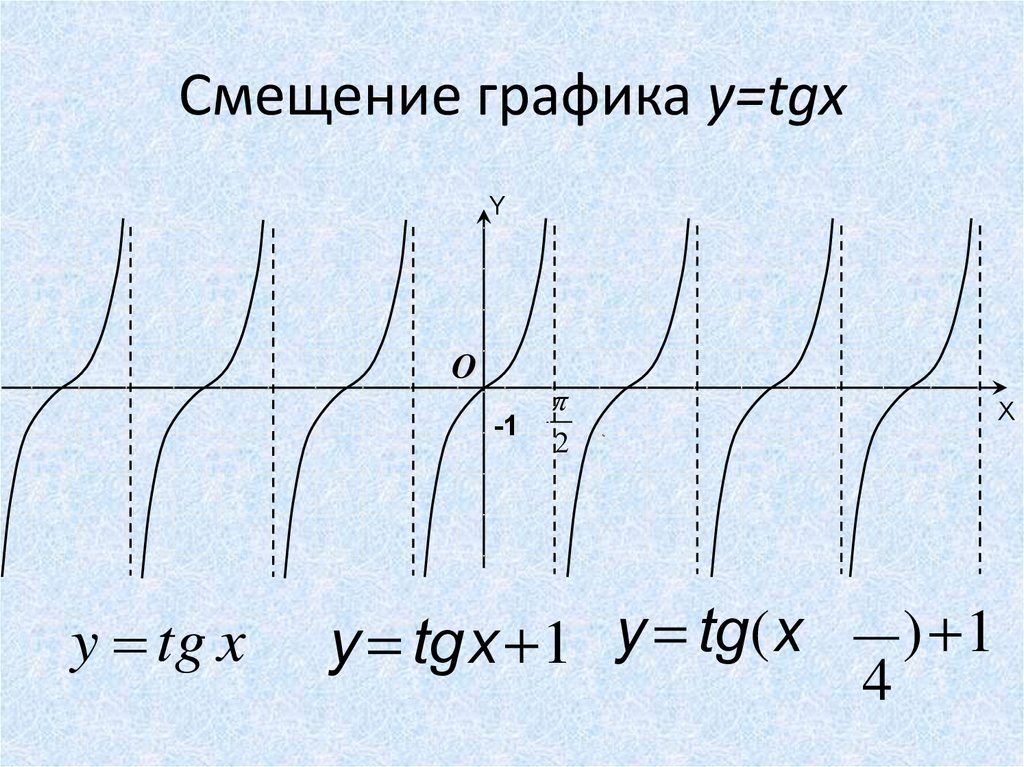
28. Смещение графика y=tgx

Y
O
-1
y tg x
2
X
p
y = tgx+1 y = tg(x - ) +1
4

29. Свойства графика функции y=tg x

1. Область определения: x≠π/2+πn, n∈Z
2. Множество значений: y∈(-∞;∞)
3.
4.
5.
6.
7.
8.
Функция периодическая Т=π
Функция нечетная
y=0, при x=πn, n∈Z
y>0, при x∈(πn; π/2+πn), n∈Z
y<0, при x∈(-π/2+πn; πn), n∈Z
Функция возрастает на интервалах: (-π/2+πn; π/2+πn), n∈Z

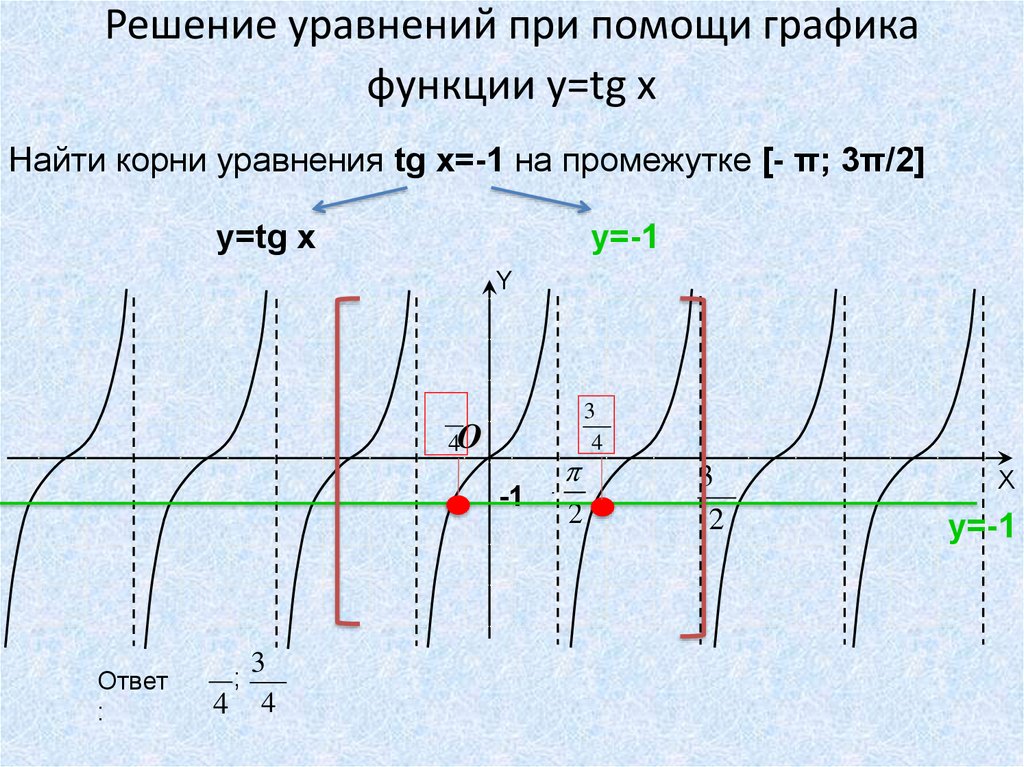
30. Решение уравнений при помощи графика функции y=tg x

Найти корни уравнения tg x=-1 на промежутке [- π; 3π/2]
y=tg x
y=-1
Y
-
-p
p
3p
;
Ответ
4 4
:
p
4O
-1
2
3p
4
3p
2
X
y=-1

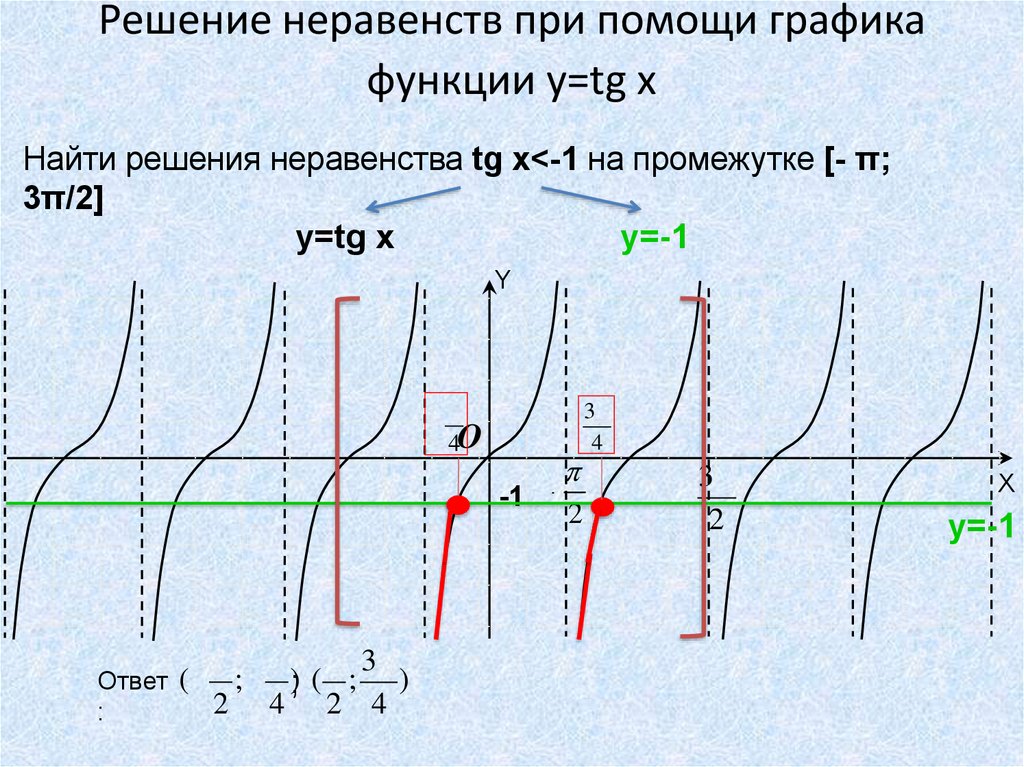
31. Решение неравенств при помощи графика функции y=tg x

Найти решения неравенства tg x<-1 на промежутке [- π;
3π/2]
y=tg x
y=-1
Y
-
-p
p p p 3p
(;- ); ( ; )
Ответ
2 4 2 4
:
p
4O
-1
2
3p
4
3p
2
X
y=-1

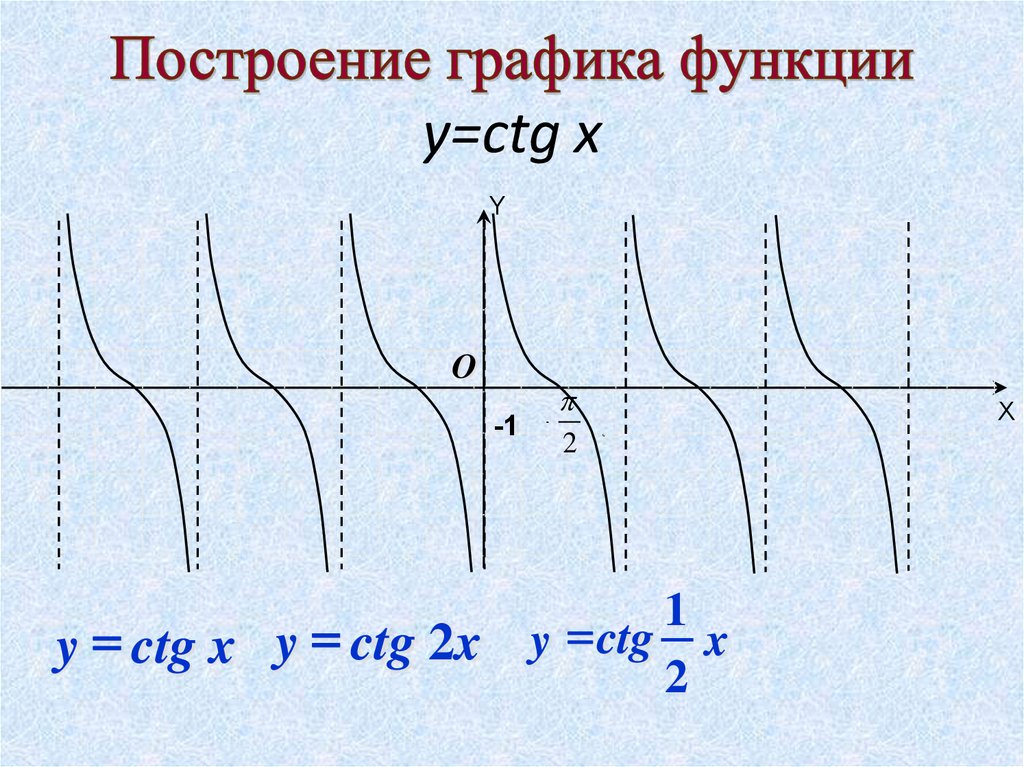
32. Построение графика функции y=ctg x

y=ctg x
Y
O
-1
y ctg x y ctg 2x
2
1
y ctg x
2
X

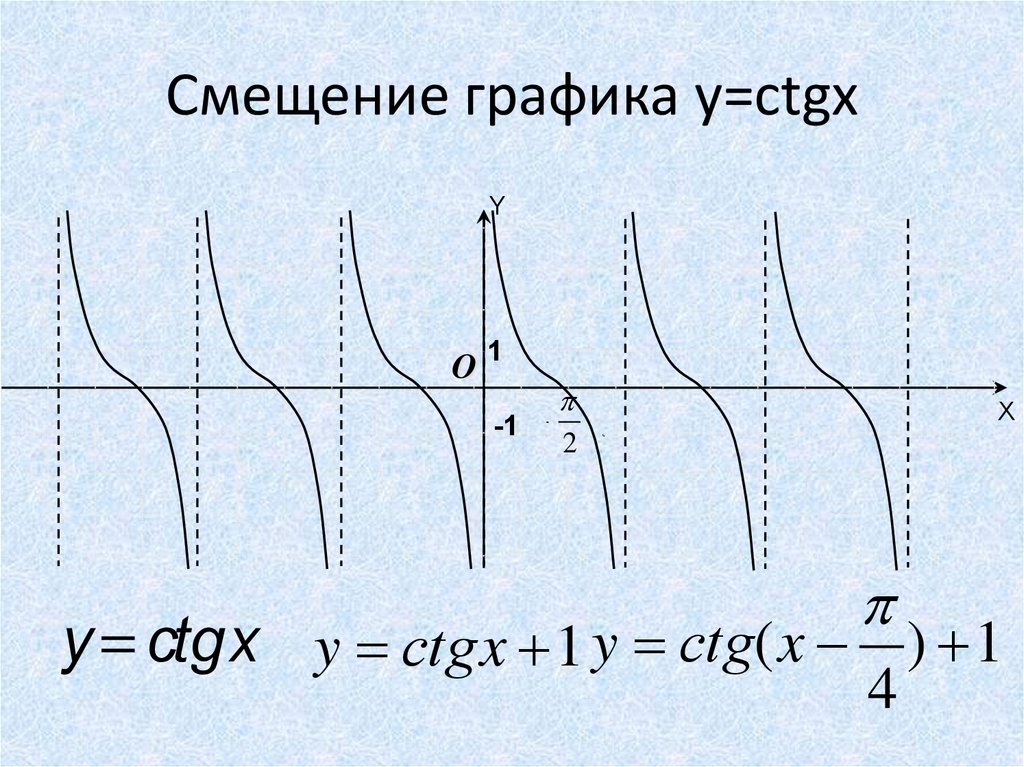
33. Смещение графика y=ctgx

Y
O1
-1
2
X
y = ctgx y сtg x 1 y сtg( x ) 1
4

34. Свойства графика функции y=ctg x

1. Область определения: x≠πn, n∈Z
2. Множество значений: y∈(-∞;∞)
3.
4.
5.
6.
7.
8.
Функция периодическая T=π
Функция нечетная
y=0, при x=π/2+πn, n∈Z
y>0, при x∈(0+πn; π/2+πn), n∈Z
y<0, при x∈(-π/2+πn; 0+πn), n∈Z
Функция убывает на интервалах (πn; π+πn), n∈Z

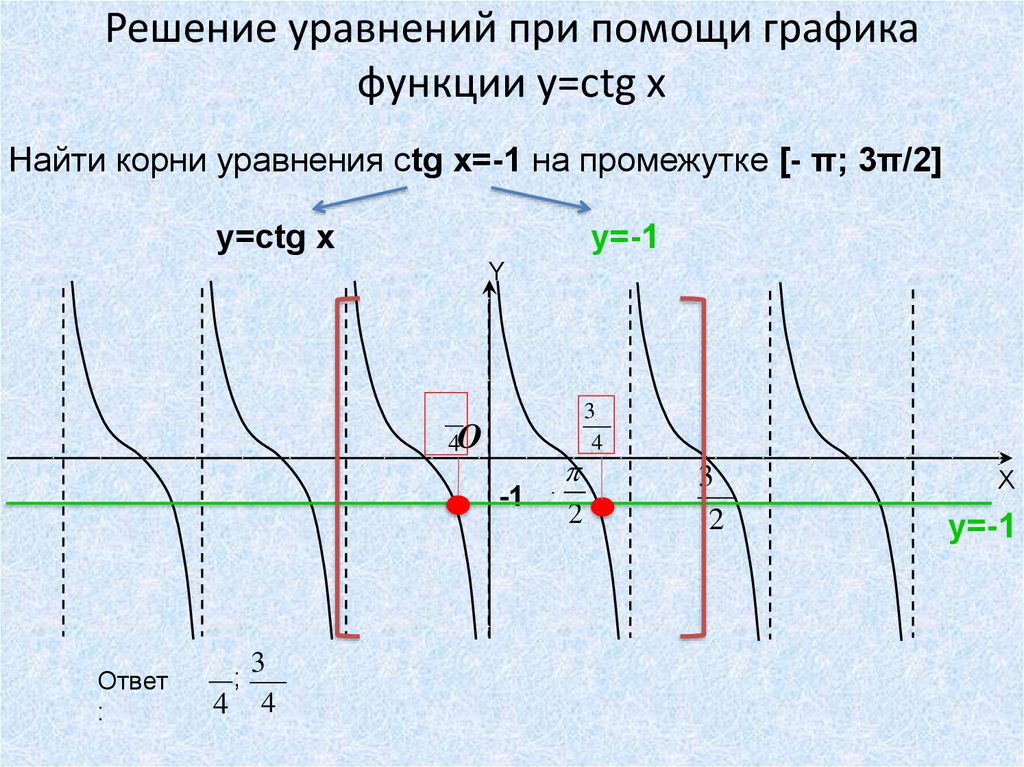
35. Решение уравнений при помощи графика функции y=сtg x

Найти корни уравнения сtg x=-1 на промежутке [- π; 3π/2]
y=сtg x
y=-1
Y
-
-p
p
3p
;
Ответ
4 4
:
p
4O
-1
2
3p
4
3p
2
X
y=-1

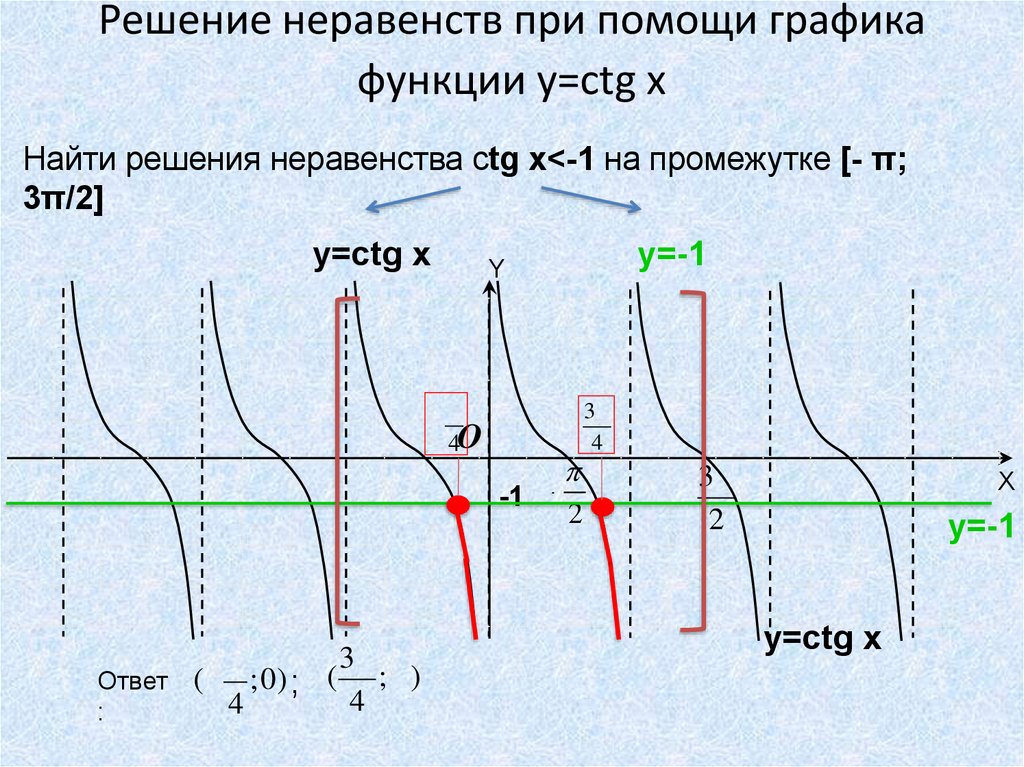
36. Решение неравенств при помощи графика функции y=ctg x

Найти решения неравенства ctg x<-1 на промежутке [- π;
3π/2]
y=сtg x
-
-p
3p
p
(
;p )
(;0)
Ответ
;
4
4
:
y=-1
Y
p
4O
-1
2
3p
4
3p
2
X
y=-1
y=сtg x