Практика ТО. Тема 17

1.

Практика ТО. Тема 17.
17.Синтез системы управления
организацией по экономическим критериям
17.1.Постановка задачи
17.2.Расчет базового примера
17.3.Адаптация к изменениям рынка
17.4.Задача управления организацией на
известном рынке

2.

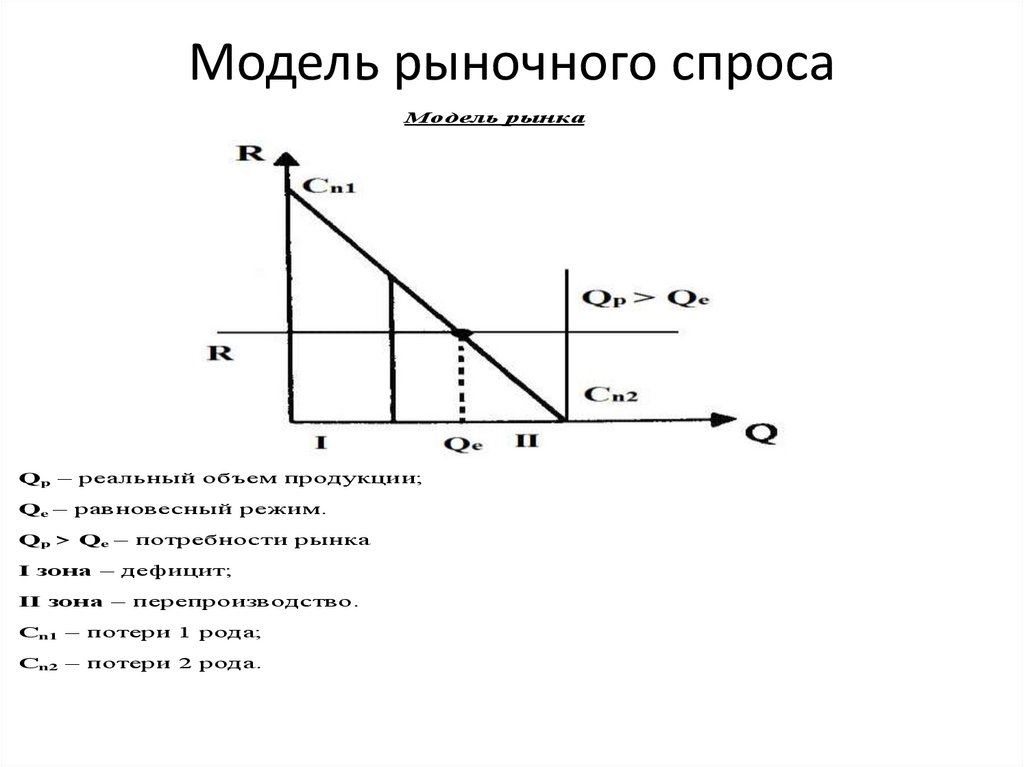
Модель рыночного спроса
Модель рынка
Qp – реальный объем продукции;
Qe – равновесный режим.
Qp > Qe – потребности рынка
I зона – дефицит;
II зона – перепроизводство.
Сn1 – потери 1 рода;
Сn2 – потери 2 рода.

3.

Оценки потерь двух видов
• Δ Q1 = Qe - Qp – недопроизводство => потери от
дефицита => упущенные возможности.
• Δ Q2 = Qр – Qе – размер перепроизводства.
D (pv)
O (pv)
D (pv) = O (pv)
• Δ Q = Q => Qе = Qр – точка равновесия.
• Сn1 (Δ Q1) = (Qе - Qр)(pv - pr), где:
• pv – продажная цена;
• pr – себестоимость.
• Сn2 (Δ Q2) = (Qр – Qе)Схр, где:
• Схр – стоимость хранения товара.

4.

Формализация цели фирмы
Определим цель фирмы
Цель фирмы: B (Qр) => max, где:
В – прибыль.
B (Qр) = Qр (pv - pr) – [Сn1(Δ Q1) + Сn2 (Δ Q2)] => max,
где:
Qр (pv - pr) – реальная прибыль;
[Сn1(Δ Q1) + Сn2 (Δ Q2)] – суммарные потери.
pv - pr = m – удельная прибыль (маржа)
Решение: (Q*,Pv*) => Bmax
B (Qр) = Qр (pv - pr) – [(Qе - Qр)(pv - pr) + (Qр – Qе)Схр]
=> max

5.

Исходные данные
• Условие задачи:
• Фирма работает на рынке с функцией спроса Q =
(1000+(10n)) – 6pv, где: n – номер в журнале.
• n = 19
• I часть:
• Задам функцию спроса
• Q = (1000+10*19) - 6pv = 1190 - 6pv
• Q = 1190 - 6pv
• pv = 80 руб/шт
• pr = 50 руб/шт
• Схр = 50 руб/шт

6.

Определение равновесного режима
Решение:
Вычисляем удельную прибыль - маржу (m)
m = pv - pr = 80 – 50 = 30 (руб/шт)
Рассчитываем параметры равновесного режима
(Qe)
Qе = 1190 - 6pv = 1190 – 6*80 = 710 (шт) – в равновесии
Вычисляем составляющие прибыли (B):
Сn1 (Δ Q1) – потери 1 рода,
Сn2 (Δ Q2) – потери 2 рода.

7.

Функция прибыли
1) Построим график зависимости потребностей 1 и 2 рода
2) Вывод
Равновесный режим гарантирует минимальные потери и соответствует
максимизации прибыли (В).
Прибыль является выпуклой функцией и стремится к максимуму.

8.

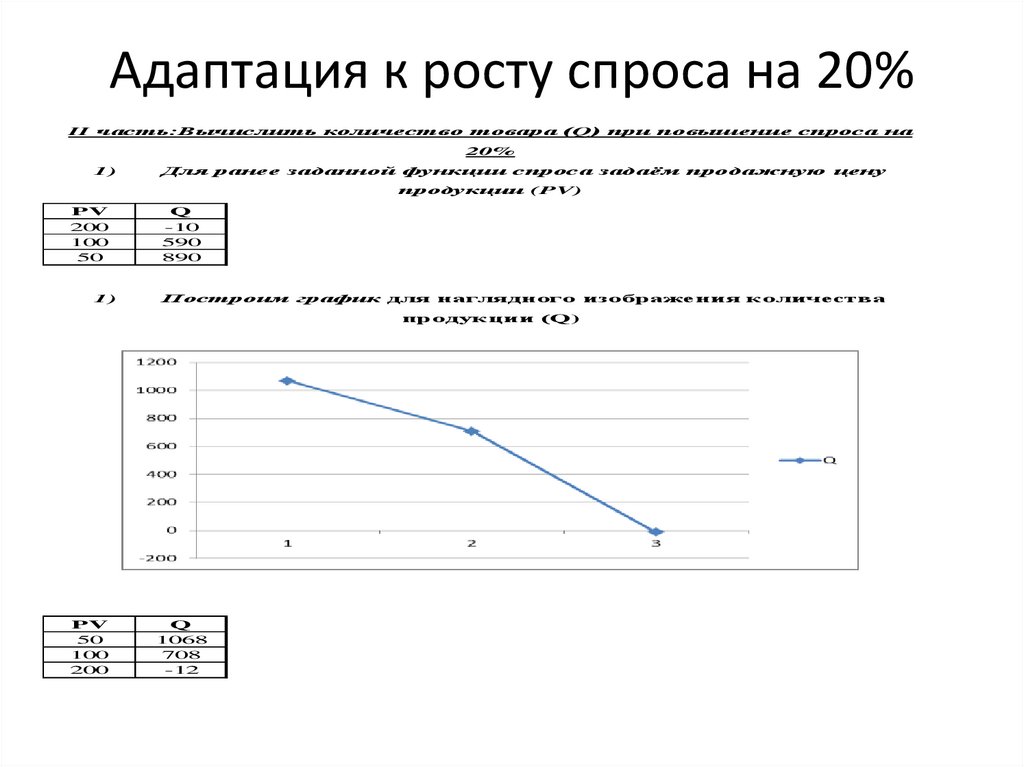
Адаптация к росту спроса на 20%
II часть:Вычислить количество товара (Q) при повышение спроса на
20%
1)
Для ранее заданной функции спроса задаём продажную цену
продукции (PV)
PV
200
100
50
1)
Q
-10
590
890
Построим график для наглядного изображения количества
продукции (Q)
PV
50
100
200
Q
1068
708
-12

9.

Решения менеджера
4) Вычислим количество продукции (Q)для равновесного режима рынка
Q = a – b*pv
1068 = a – b50
708 = a – b100
360 = 50b
b = 7,2
a = 1428
Q = 1428 – 7,2pv => pv = const = 80 руб/шт
5) Вычислим показатель равновесного режима (Qe)
Qe = 1428 – 7,2*80 = 852 (шт)
Сn1 – потери 1 рода,
Сn2 – потери 2 рода
6) Вычислим составляющие прибыли (B):

10.

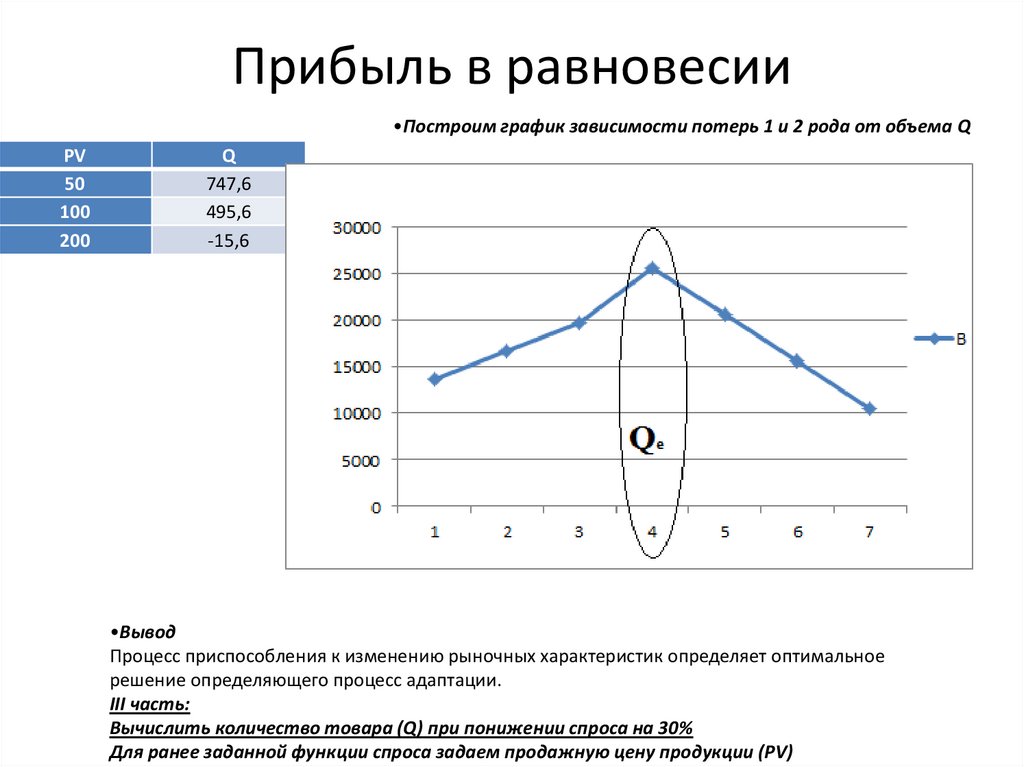
Прибыль в равновесии
•Построим график зависимости потерь 1 и 2 рода от объема Q
PV
50
100
200
Q
747,6
495,6
-15,6
•Вывод
Процесс приспособления к изменению рыночных характеристик определяет оптимальное
решение определяющего процесс адаптации.
III часть:
Вычислить количество товара (Q) при понижении спроса на 30%
Для ранее заданной функции спроса задаем продажную цену продукции (PV)

11.

Новый пример задачи
1)
2)
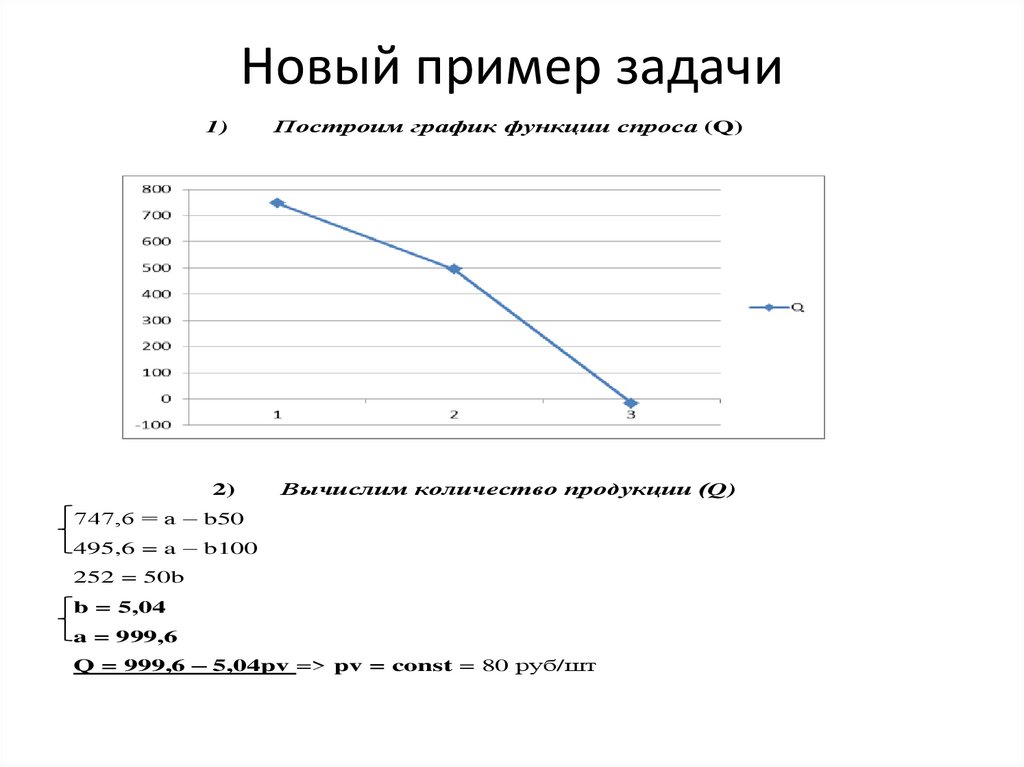
Построим график функции спроса (Q)
Вычислим количество продукции (Q)
747,6 = а – b50
495,6 = a – b100
252 = 50b
b = 5,04
a = 999,6
Q = 999,6 – 5,04pv => pv = const = 80 руб/шт

12.

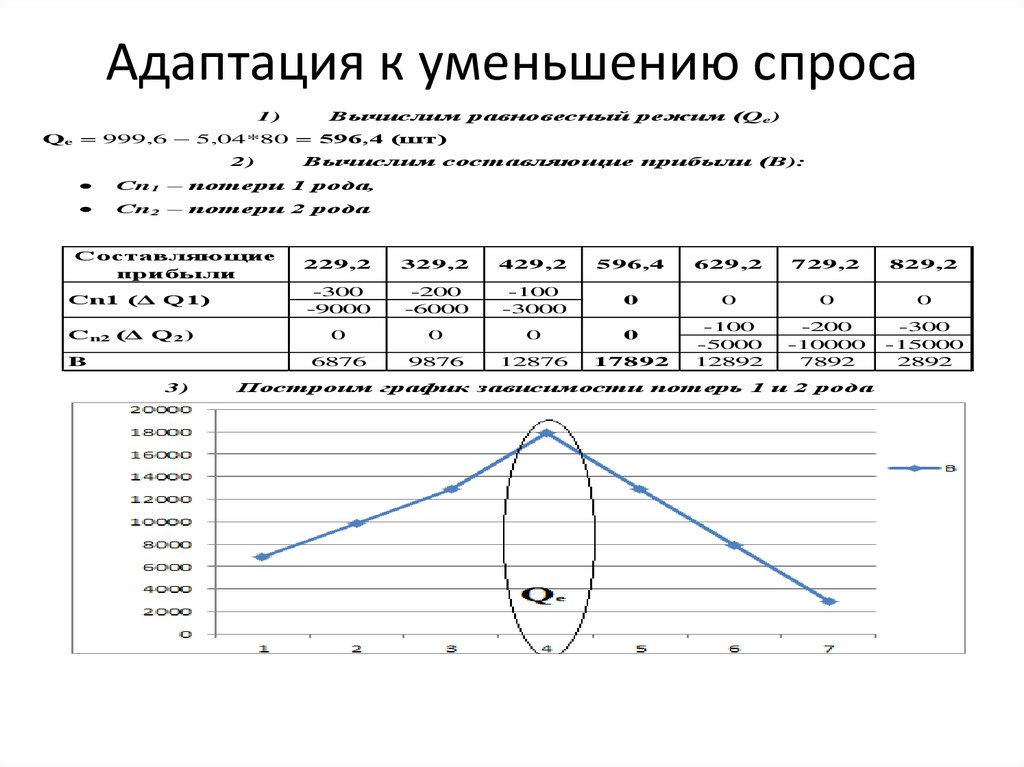
Адаптация к уменьшению спроса
1)
Вычислим равновесный режим (Qe)
Qe = 999,6 – 5,04*80 = 596,4 (шт)
2)
Вычислим составляющие прибыли (B):
Сn1 – потери 1 рода,
Сn2 – потери 2 рода
Составляющие
прибыли
Сn1 (Δ Q1)
Сn2 (Δ Q2 )
B
3)
229,2
329,2
429,2
596,4
629,2
729,2
829,2
-300
-9000
-200
-6000
-100
-3000
0
0
0
0
0
0
0
0
6876
9876
12876
17892
-100
-5000
12892
-200
-10000
7892
-300
-15000
2892
Построим график зависимости потерь 1 и 2 рода

13.

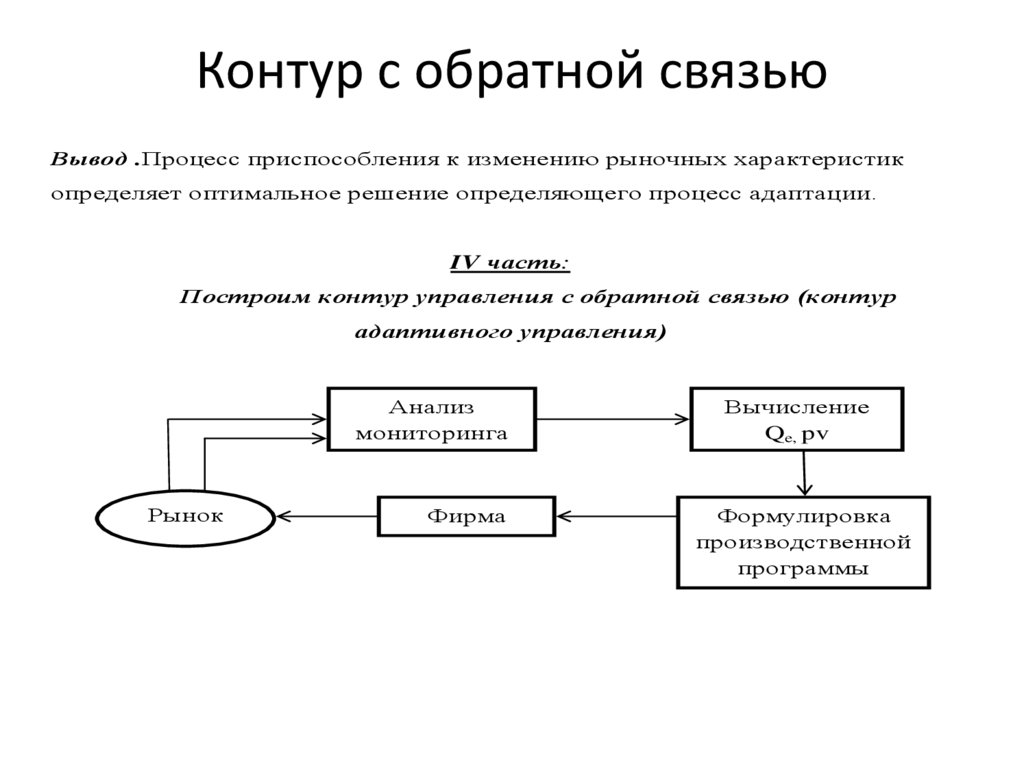
Контур с обратной связью
Вывод .Процесс приспособления к изменению рыночных характеристик
определяет оптимальное решение определяющего процесс адаптации.
IV часть:
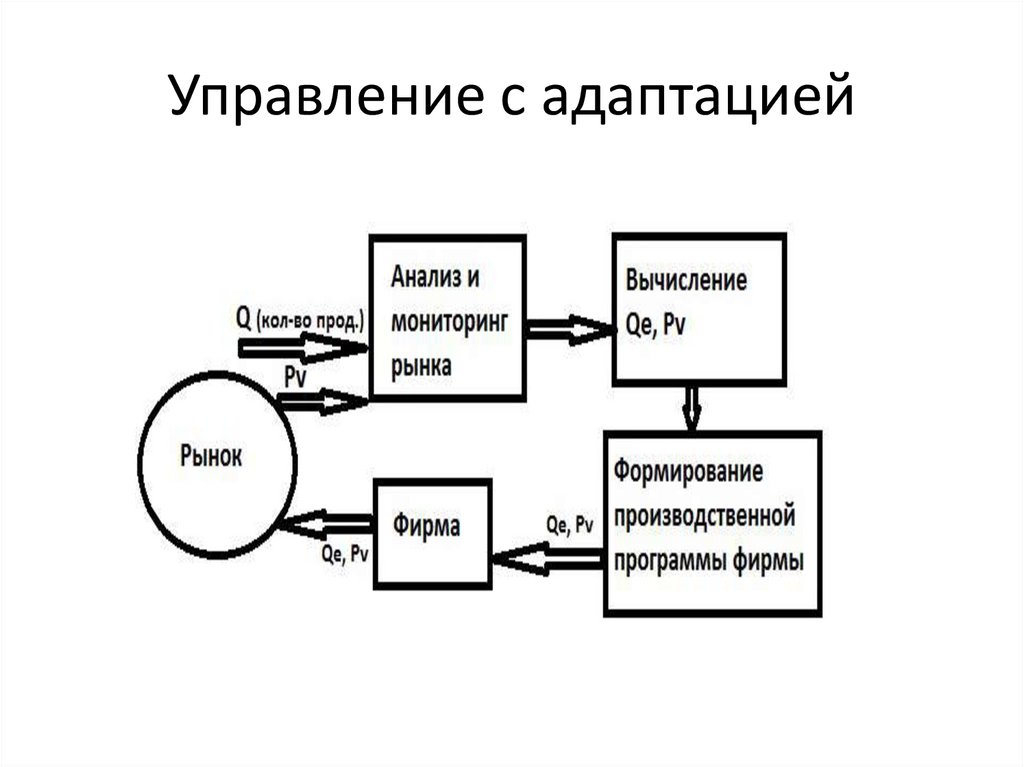
Построим контур управления с обратной связью (контур
адаптивного управления)
Анализ
мониторинга
Рынок
Фирма
Вычисление
Qe, pv
Формулировка
производственной
программы

14.

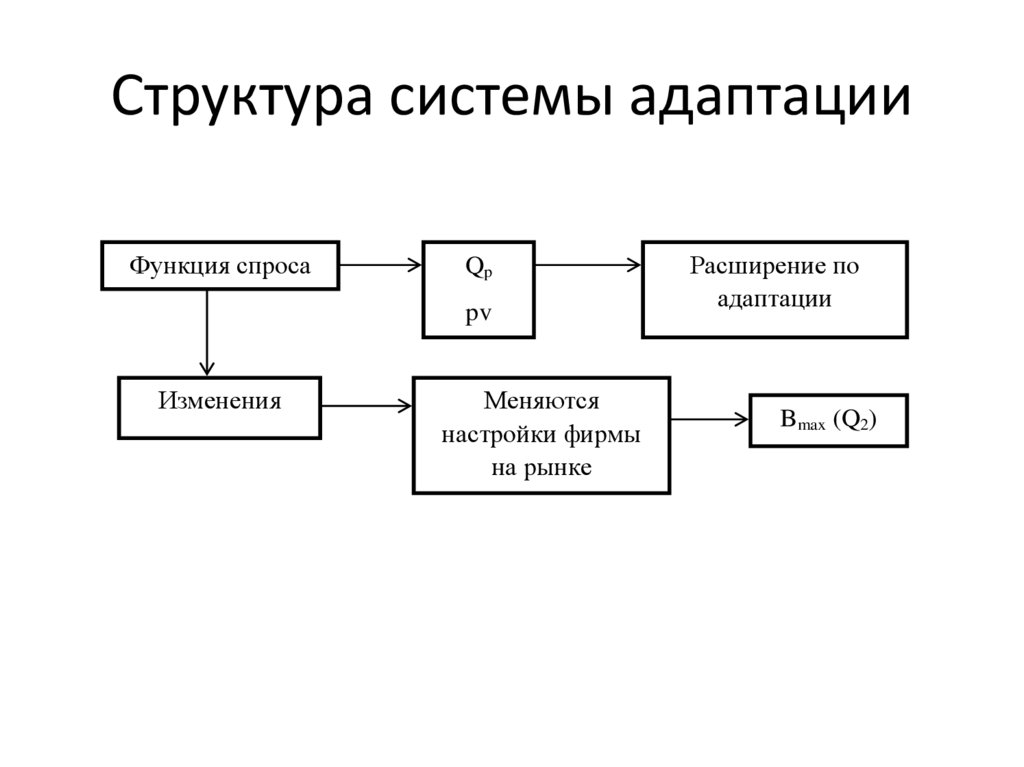
Структура системы адаптации
Функция спроса
Qp
pv
Изменения
Меняются
настройки фирмы
на рынке
Расширение по
адаптации
Bmax (Q2)

15.

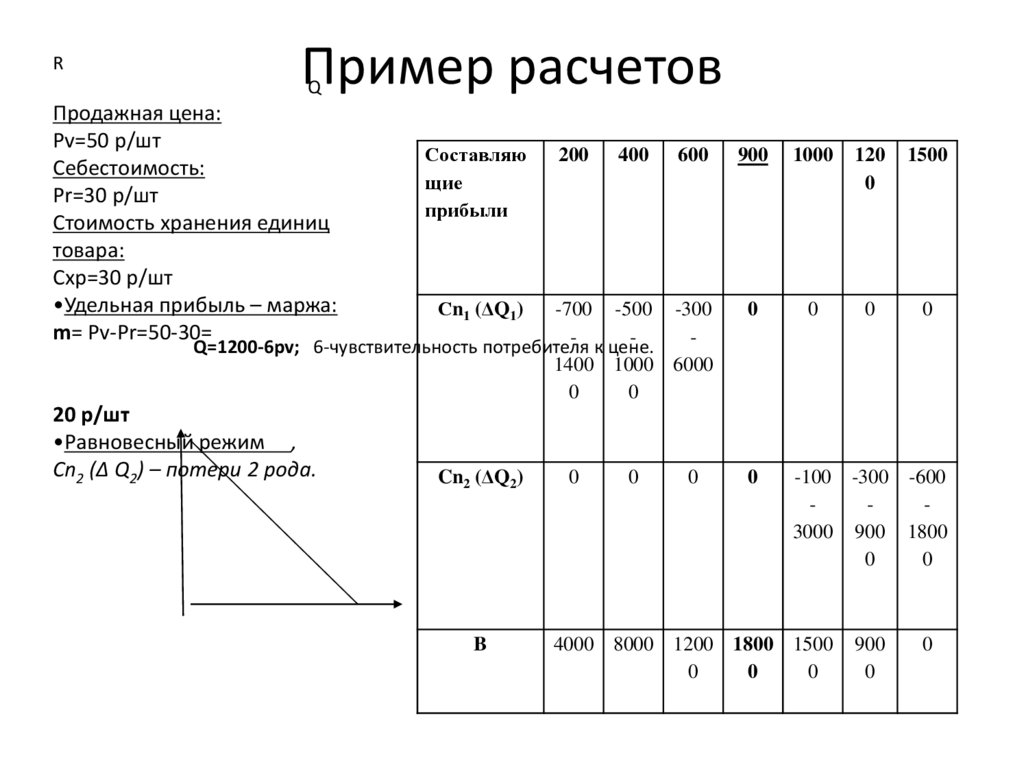
R
Пример расчетов
Q
Продажная цена:
Pv=50 р/шт
Себестоимость:
Pr=30 р/шт
Стоимость хранения единиц
товара:
Схр=30 р/шт
•Удельная прибыль – маржа:
m= Pv-Pr=50-30=
Составляю
щие
прибыли
200
400
600
Сn1 (ΔQ1)
-700 -500 -300
- к цене.
Q=1200-6pv; 6-чувствительность потребителя
1400 1000 6000
0
0
20 р/шт
•Равновесный режим ,
Сn2 (Δ Q2) – потери 2 рода.
Cn2 (ΔQ2)
B
0
0
0
900
1000
120
0
1500
0
0
0
0
0
-100 -300 -600
3000 900 1800
0
0
4000 8000 1200 1800 1500
0
0
0
900
0
0

16.

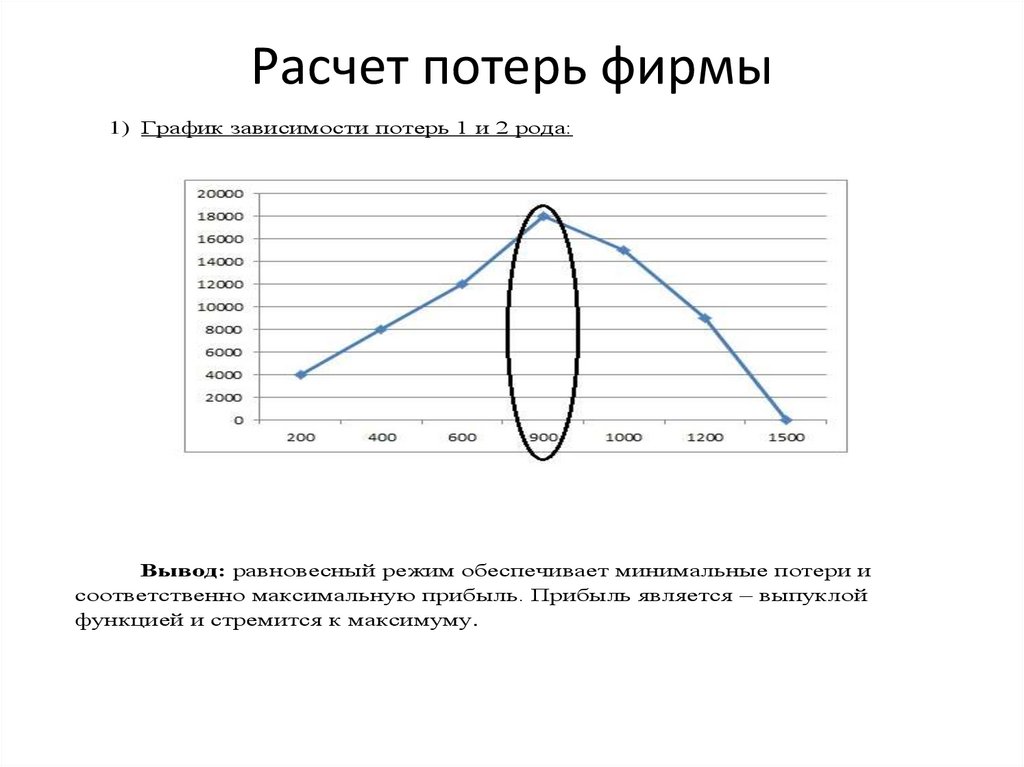
Расчет потерь фирмы
1) График зависимости потерь 1 и 2 рода:
Вывод: равновесный режим обеспечивает минимальные потери и
соответственно максимальную прибыль. Прибыль является – выпуклой
функцией и стремится к максимуму.

17.

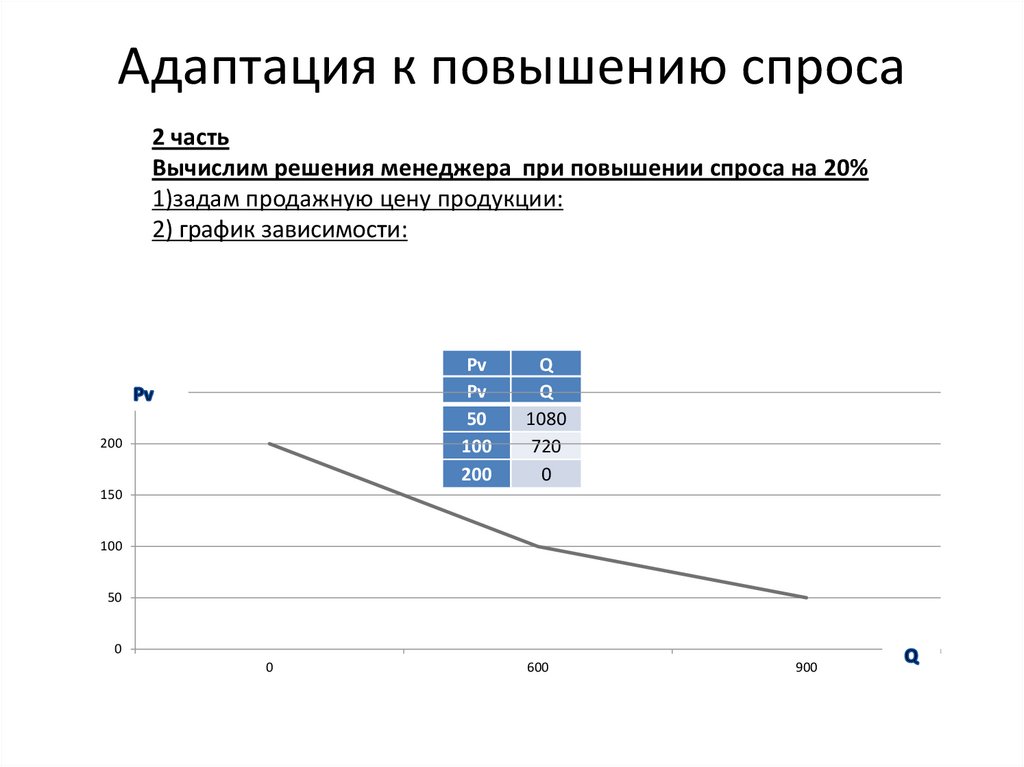
Адаптация к повышению спроса
2 часть
Вычислим решения менеджера при повышении спроса на 20%
1)задам продажную цену продукции:
2) график зависимости:
Pv
Pv
200
50
100
100
50
200
250
200
Q
Q
0
1080
600
720
900
0
150
100
50
0
0
600
900

18.

Решения менеджера
• 3) вычислим количество продукции, реализуемой для
максимума прибвли:
• Q = a – b*pv
• 1080 = a – b50
• 0 = a – b200
• 1080 = 150b
• b = 7,2
• a = 1440
• Q = 1440 – 7,2pv => pv = const = 50 руб/шт
• Равновесный режим:
• Qe=1440-7.2*50=1080 шт.

19.

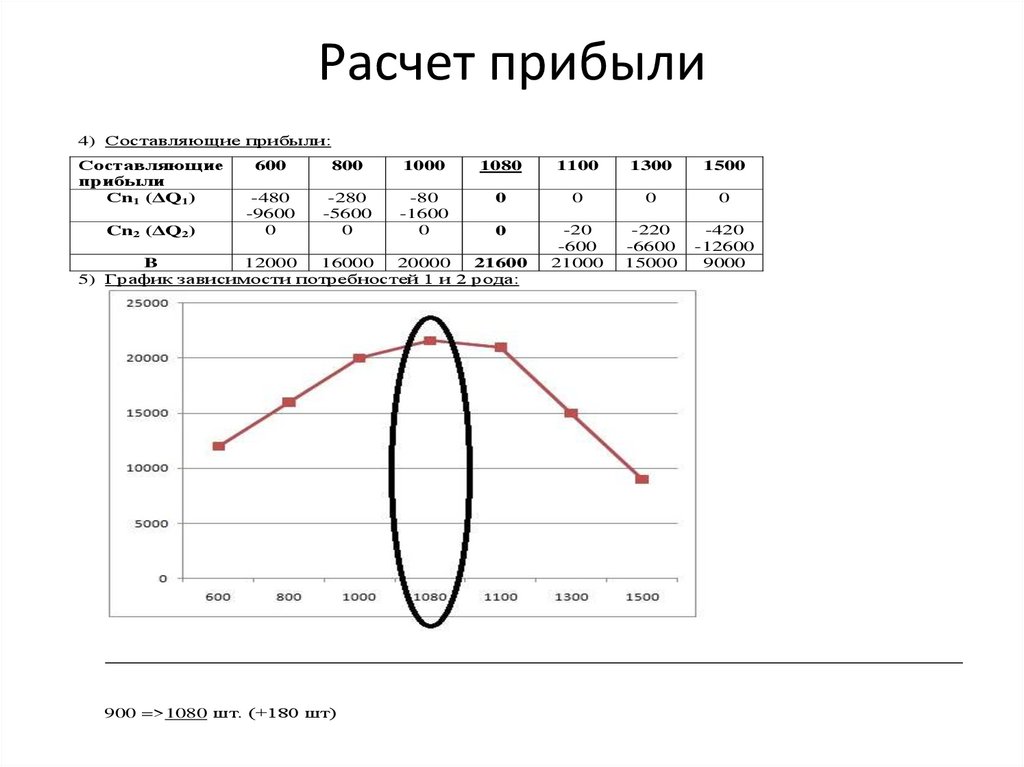
Расчет прибыли
4) Составляющие прибыли:
Составляющие
прибыли
Сn1 (ΔQ1)
Cn2 (ΔQ2)
600
800
1000
1080
1100
1300
1500
-480
-9600
0
-280
-5600
0
-80
-1600
0
0
0
0
0
0
-20
-600
21000
-220
-6600
15000
-420
-12600
9000
12000
16000
20000
B
21600
5) График зависимости потребностей 1 и 2 рода:
900 =>1080 шт. (+180 шт)

20.

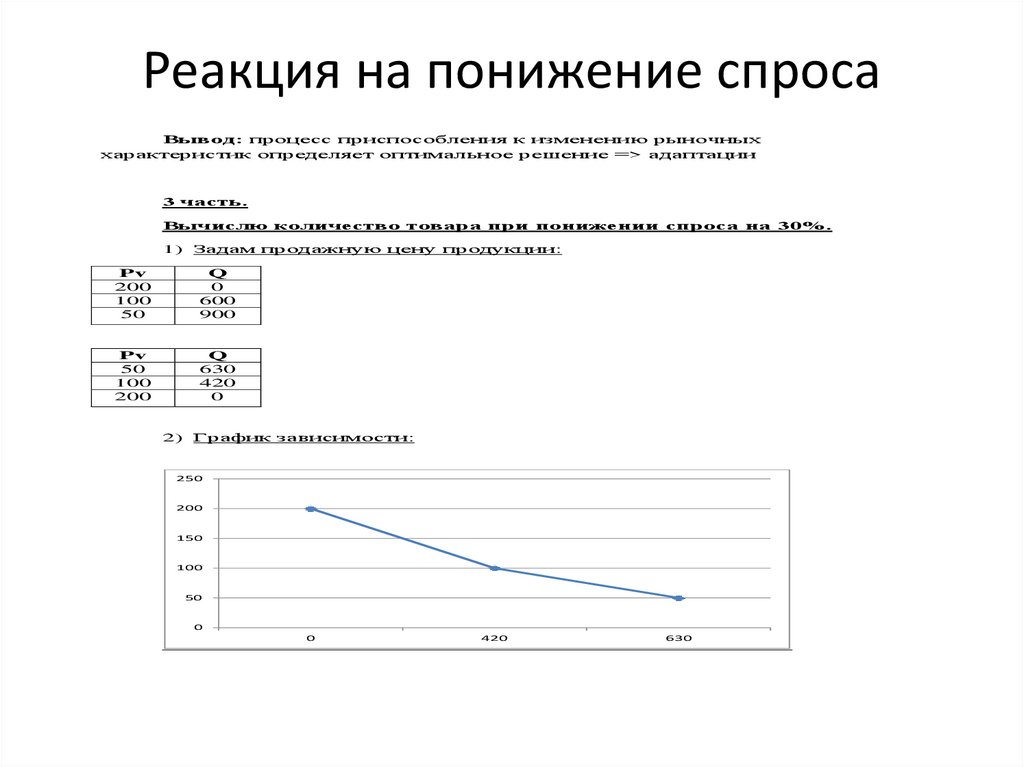
Реакция на понижение спроса
Вывод: процесс приспособления к изменению рыночных
характеристик определяет оптимальное решение => адаптации
3 часть.
Вычислю количество товара при понижении спроса на 30%.
1) Задам продажную цену продукции:
Pv
200
100
50
Q
0
600
900
Pv
50
100
200
Q
630
420
0
2) График зависимости:
250
200
150
100
50
0
0
420
630

21.

Оптимальные решения
• Вычисляем оптимальное количество производимой
продукции:
• 630 = а – b50
• 0 = a – b200
• 630 = 150b
• b = 4,2
• a = 840
• Q = 840 – 4,2pv => pv = const = 50 руб/шт
• равновесный режим:
• Qe=840-4.2*50=630 шт.

22.

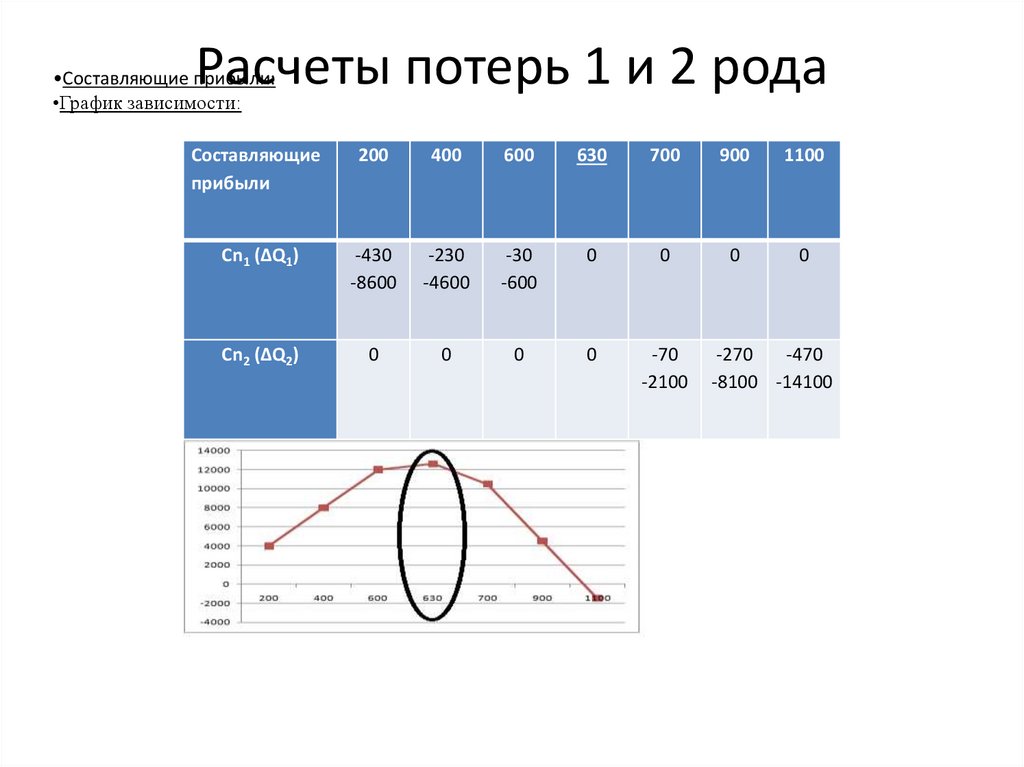
Расчеты потерь 1 и 2 рода
•Составляющие прибыли:
•График зависимости:
Составляющие
прибыли
200
400
600
630
700
900
1100
Сn1 (ΔQ1)
-430
-8600
-230
-4600
-30
-600
0
0
0
0
Cn2 (ΔQ2)
0
0
0
0
-70
-2100
-270
-470
-8100 -14100
B
4000
8000
12000
12600
10500
4500
-1500

23.

Управление с адаптацией

24.

Вывод формул расчета
Qp- реальный объем
Qe-равновесный режим
Q1=Qe-Qp-недопроизводство(потери от дефицита)
Q2=Qp-Qe-размер перепроизводства
Q=0 (Qp=Qe) - точка равновесия
Сп1( Q1) = (Qe-Qp) * (pv-pr) - размер потерь первого
рода
• Сп2( Q2) =(Qp-Qe) * Схр - потери второго рода
• Цель фирмы: В(Qp) -> max
• В(Qp)= Qp(pv-pr) - [Cn1( Q1)+Cn2( Q2)] -> max

25.

Настройка фирмы на спрос
Задача: Фирма работает на рынке с функцией спроса Q = (1000+10n)-6pv;
n-15 => Q=1150-6pv
pv=50 p/шт (продажная цена)
pr=30p/шт (себестоимость продаж)
Cxp=30p/шт (стоимость хранения единицы товара)
1) m= pv-pr = 50-30 = 20 р/шт (удельная прибыль или маржа)
2) Qe=1150 - 6*50=850 шт в равновесии можно продать
Составляющи
е прибыли
500
700
850
900
1000
Сп1( Q1)
-350;
-7000
-150;
-3000
0
0
0
Сп2( Q2)
0
0
0
-50;
-1500
-150;
-4500
В
10000
14000
17000
15500
12500

26.

Пример решения задачи адаптации
Фирма работает на рынке с функцией спроса:
Q=(1000+10n)-6 Pv, где n=23,
Q=1230-6 Pv.
(Pz)Себестоимость – 70р/шт.
(Pv)Продажная цена – 90р/шт.
(Схр) стоимость хранения-20р/шт.
Посчитаем прибыль фирмы:
1.m= Pv- Pz=90-70=20р/шт. маржа на единицу
продукции
• Рассчитаем потребность рынка в равновесном режиме.
• 2.Q e=1230-6*90=1230-540=690 штук в равновесии
можно реализовать.

27.

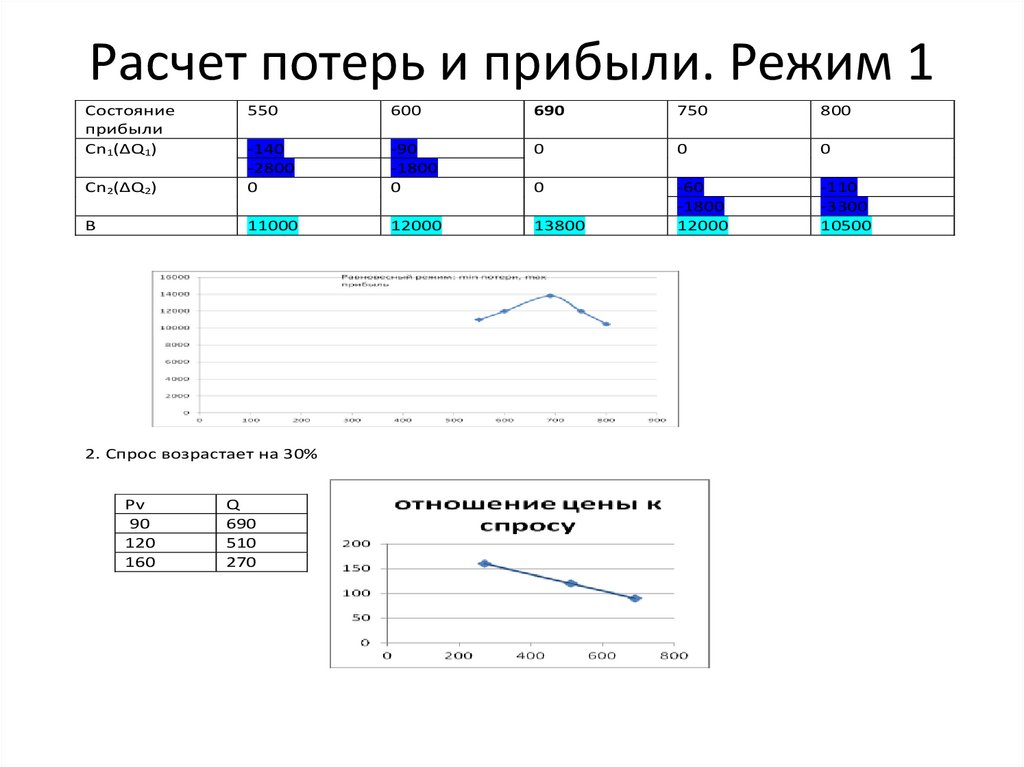
Расчет потерь и прибыли. Режим 1
Состояние
прибыли
Cn1(∆Q1)
550
600
690
750
800
-90
-1800
0
0
0
0
Cn2(∆Q2)
-140
-2800
0
0
B
11000
12000
13800
-60
-1800
12000
-110
-3300
10500
2. Спрос возрастает на 30%
Pv
90
120
160
Q
690
510
270

28.

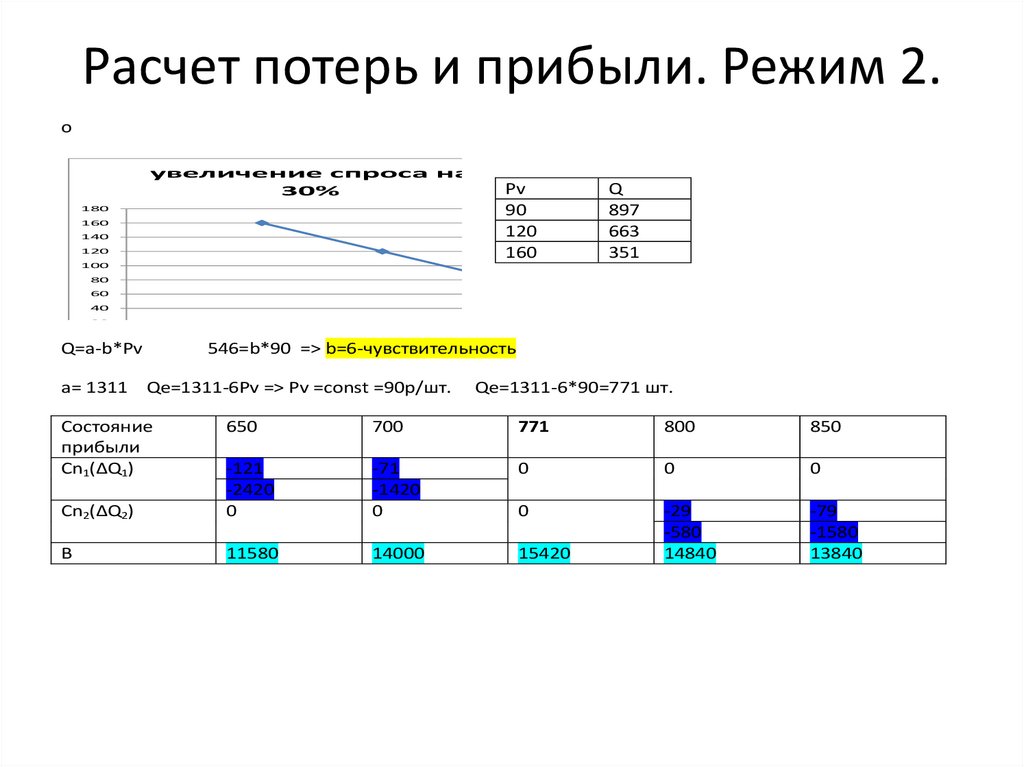
Расчет потерь и прибыли. Режим 2.
о
увеличение спроса на
30%
180
160
140
120
Pv
90
120
160
Q
897
663
351
100
80
60
40
20
0
0
Q=a-b*Pv
a= 1311
400
600
800
1000
546=b*90
=> b=6-чувствительность
200
Qe=1311-6Pv => Pv =const =90р/шт.
Состояние
прибыли
Cn1(∆Q1)
Qe=1311-6*90=771 шт.
650
700
771
800
850
-71
-1420
0
0
0
0
Cn2(∆Q2)
-121
-2420
0
0
B
11580
14000
15420
-29
-580
14840
-79
-1580
13840

29.

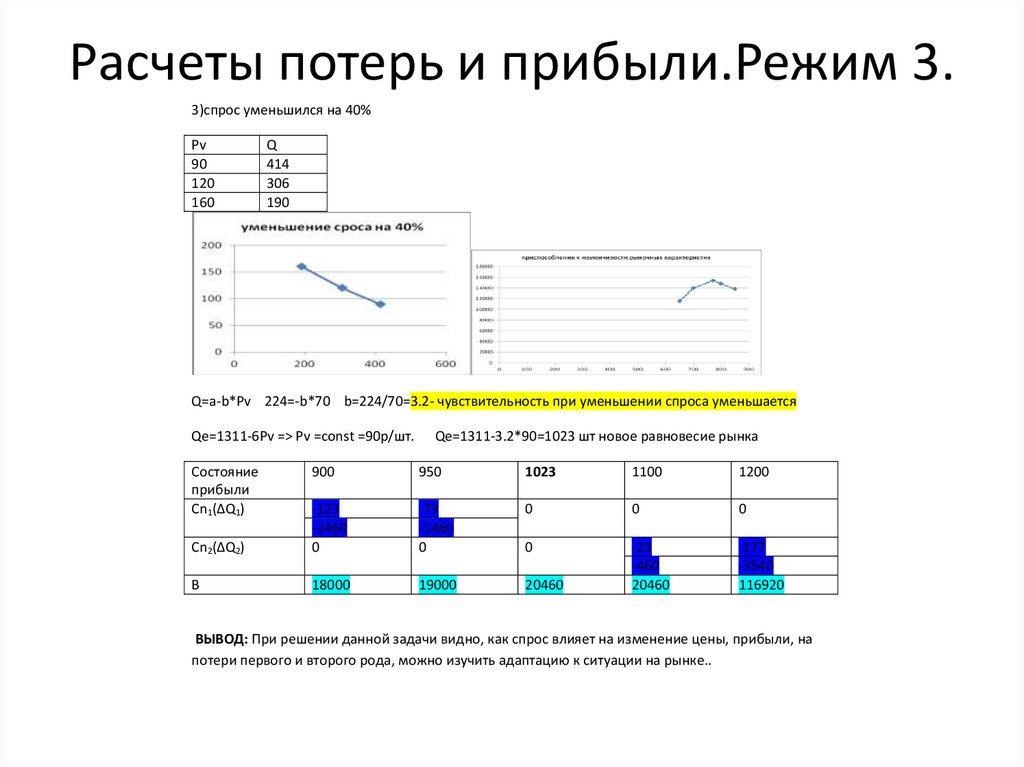
Расчеты потерь и прибыли.Режим 3.
3)спрос уменьшился на 40%
Pv
90
120
160
Q
414
306
190
Q=a-b*Pv 224=-b*70 b=224/70=3.2- чувствительность при уменьшении спроса уменьшается
Qe=1311-6Pv => Pv =const =90р/шт.
Состояние
прибыли
Cn1(∆Q1)
Qe=1311-3.2*90=1023 шт новое равновесие рынка
900
950
1023
1100
1200
-73
-1460
0
0
0
0
Cn2(∆Q2)
-123
-2460
0
0
B
18000
19000
20460
-23
-460
20460
-177
-3540
116920
ВЫВОД: При решении данной задачи видно, как спрос влияет на изменение цены, прибыли, на
потери первого и второго рода, можно изучить адаптацию к ситуации на рынке..

30.

Задание 17.1.
• Для любого интересующего Вас рынка:
• -определить таблицу связи p и Q
• Построить график и рассчитать функцию
спроса
• Найти равновесный режим, рассчитать потери
и прибыль по формулам
• Построить график прибыли
• Изменить спрос- рост и спад- рассчитать
потери и прибыль
• -сделать выводы об оптимальном режиме
работы организации на рынке

31.

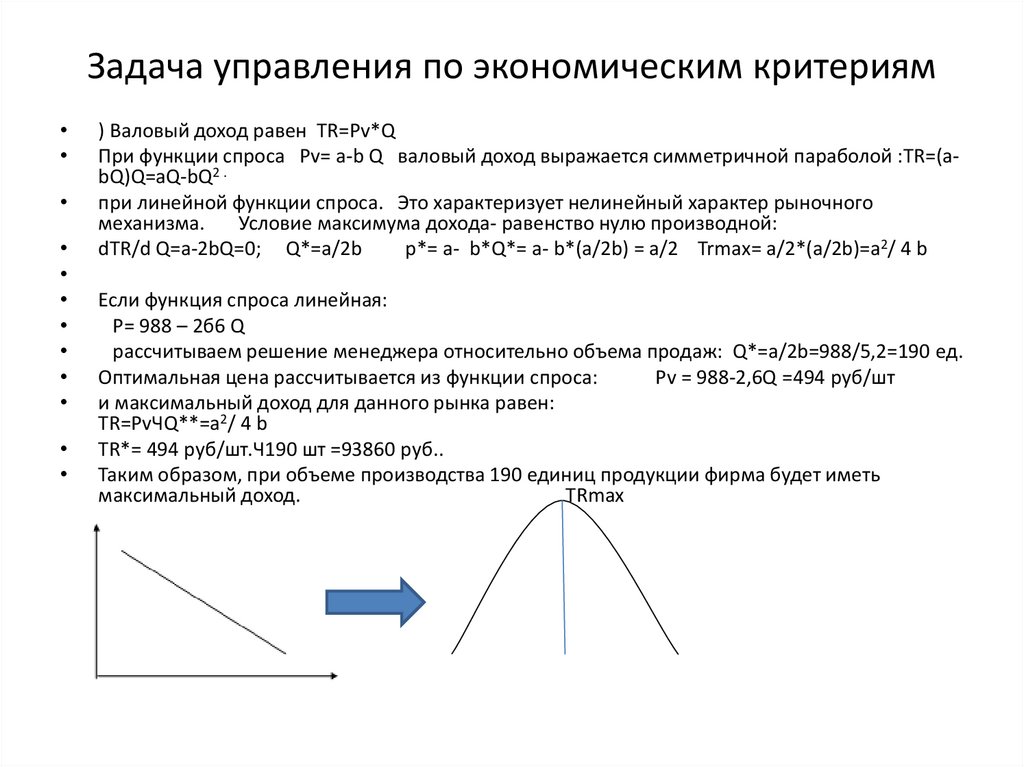
Задача управления по экономическим критериям
) Валовый доход равен TR=Pv*Q
При функции спроса Pv= a-b Q валовый доход выражается симметричной параболой :TR=(abQ)Q=aQ-bQ2 .
при линейной функции спроса. Это характеризует нелинейный характер рыночного
механизма.
Условие максимума дохода- равенство нулю производной:
dTR/d Q=a-2bQ=0; Q*=a/2b
p*= a- b*Q*= a- b*(a/2b) = a/2 Trmax= a/2*(a/2b)=a2/ 4 b
Если функция спроса линейная:
Р= 988 – 2б6 Q
рассчитываем решение менеджера относительно объема продаж: Q*=a/2b=988/5,2=190 ед.
Оптимальная цена рассчитывается из функции спроса:
Pv = 988-2,6Q =494 руб/шт
и максимальный доход для данного рынка равен:
TR=PvЧQ**=a2/ 4 b
TR*= 494 руб/шт.Ч190 шт =93860 руб..
Таким образом, при объеме производства 190 единиц продукции фирма будет иметь
максимальный доход.
TRmax

32.

Обеспечение максимального дохода
. Принятие решения, обеспечивающего максимальный доход фирмы на
заданном рынке и адаптацию к его изменениям.
Фирма работает на рынке с заданной функцией спроса :
pv
Q
225
525
825
850
550
350
Необходимо найти:
1) функцию спроса;
2) оптимальный объём производства (Q*);
3) оптимальную цену (pv*);
4) максимальный доход (TRmax);
5) объём производства, при котором доход будет равен нулю (Qкр);
6) если спрос упадёт на 20% (Q1*, pv1*, TRmax1);
7) если спрос упадёт на 10% (Q2*, pv2*, TRmax2);
8) выводы.

33.

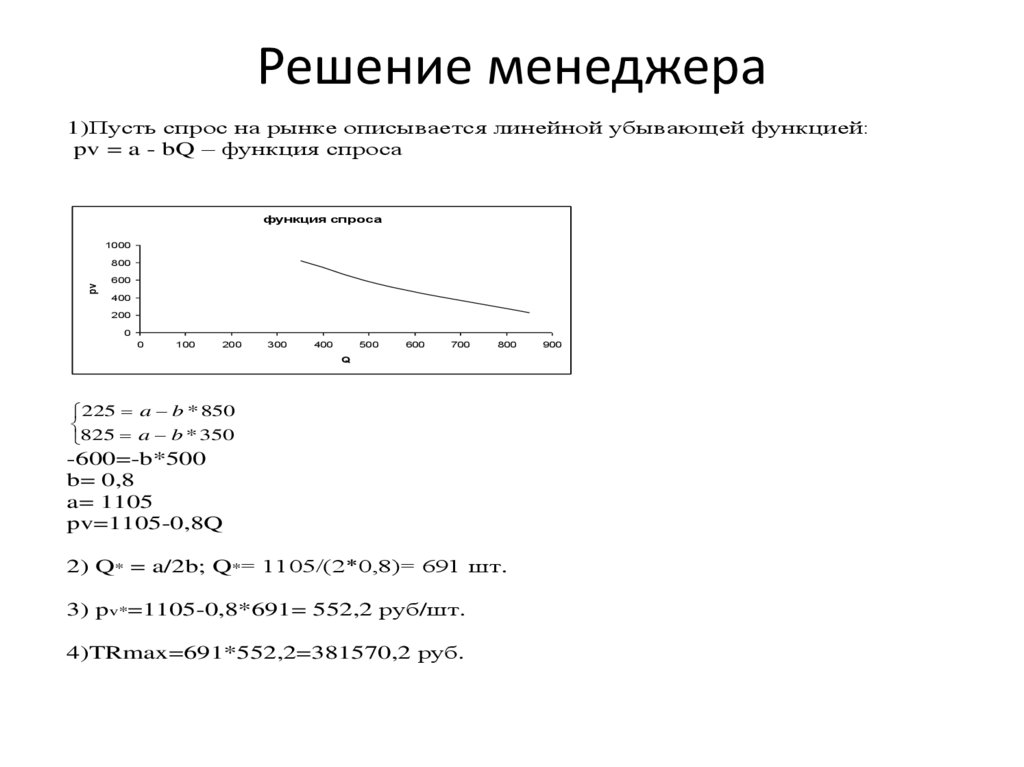
Решение менеджера
1)Пусть спрос на рынке описывается линейной убывающей функцией:
pv = a - bQ – функция спроса
функция спроса
1000
pv
800
600
400
200
0
0
100
200
300
400
500
600
700
800
Q
225 a b * 850
825 a b * 350
-600=-b*500
b= 0,8
a= 1105
pv=1105-0,8Q
2) Q* = a/2b; Q*= 1105/(2*0,8)= 691 шт.
3) pv*=1105-0,8*691= 552,2 руб/шт.
4)TRmax=691*552,2=381570,2 руб.
900

34.

Адаптивное решение 1
1382шт.
Зависимость дохода преприятия от количества
производимой продукции
500000
TR
400000
300000
200000
100000
0
0
200
400
600
800
1000
1200
1400
1600
Q
6) Если спрос упадёт на 20%, то функция будет иметь вид:
pv1
225
525
825
Q
680
440
280
225 a b * 680
825 a b * 280
-600=-b*400
b=0,7
a=1021
Q*=1021/(2*0,7)=729 шт.
pv=1021-0,7Q
pv=1021-0,7*729=510,7 руб/шт.
TRmax=729*510,7=372300, 3 руб.
Qкр=2*729=1458 шт.

35.

Адаптивное решение 2
.
Зависимость дохода преприятия от количества
производимой продукции при падении спроса на
20%
400000
TR
300000
200000
100000
0
0
500
1000
1500
2000
Q
7) Если спрос упадёт на 10%, функция будет иметь вид:
pv
225
525
825
Q
765
495
315
225 a b * 765
825 a b * 315
-600=-b*450
b=0,75
a=1061
Q*=1061/(2*0,75)=707 шт.
pv=1061-0,75*Q
pv=1061-0,75*707=530,75 руб/шт.
TRmax=707*530,75=375240,25 руб.
Qкр=2*707=1414 шт.
Зависимость дохода преприятия от количества
производимой продукции при падении спроса на
10%
400000
TR
300000
200000
100000
0
0
500
1000
1500
Q
8) Вывод. Из выше проведенного анализа предприятия можно узнать, какой
будет оптимальный объём производства при заданной функции спроса и
какова будет оптимальная цена. Не менее важно знать, сколько не нужно
производить, чтобы не получить доход, равный нулю (Qкр)!

36.

Задание 17.2.
• Для известной функции рыночного спроса
рассчитать оптимальные для max TR
решения:
• Вывести формулы расчета
• Рассчитать Q*
• Рассчитать р*
• Рассчитать TR max