Асимметричное шифрование. Эллиптические кривые

1.

Асимметричное
шифрование
Эллиптические кривые

2.

2
Односторонние функции с секретом
Определение. Эллиптической кривой E над полем F
называется множество точек (x, y), координаты которых
принадлежат полю и удовлетворяют кубическому
уравнению (общий вид):
y2 + a1xy+a3y = x3 + a2x2 + a4x + a6, ai ∈ F; (1)
В зависимости от характеристики поля уравнение (1)
приводится к разным каноническим формам:
• если характеристика поля p ≠ 2 и p ≠ 3, то
y2 = x3 + ax + b
• если характеристика поля p = 3, то
y2 = x3 + a2x2 + a4x + a6
• если же характеристика поля p = 2, то возможна одна из
форм:
y2 + y = x3 + ax + b или y2 + yх = x3 + ax + b

3.

3
Сингулярность и несингулярность
Над полем действительных чисел эллиптическая
кривая задается уравнением
y2 = x3 + axкривые
+ b. обладают
Только несингулярные
Для нахождения
точек
пересечения
необходимыми
характеристика
длякривой E с осью
криптографической
И уравнение:
абсцисс необходимо
решитьстойкости.
кубическое
3 + ax + b =на
именно они xиспользуются
0 практике.
Дискриминант этого уравнения вычисляется:
2
(a/3)3+(b/2)
Далее про них речьDне=пойдет,
т.к. не представляют
Если Dдля≠ криптографии.
0, то криваяВычисление
будет несингулярна,
т.е.
интерес
дискретного
логарифма(основная
кривая
не будет проблема)
иметь является
точекв общем
возврата и
смысле легко разрешимой
самопересечения,
в любойзадачей.
их точке можно провести
касательную.
Иначе, если D = 0, то в этом случае будут особые
точки и кривая будет являться сингулярной.

4.

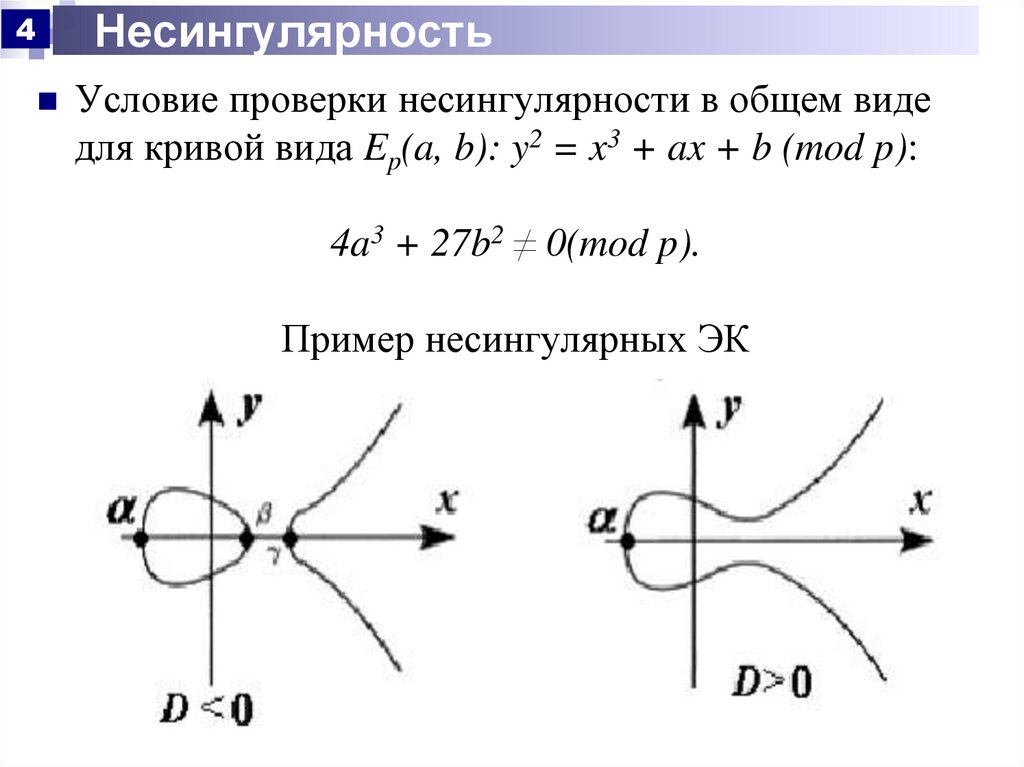
Несингулярность
4
Условие проверки несингулярности в общем виде
для кривой вида Ep(a, b): y2 = x3 + ax + b (mod p):
4a3 + 27b2 ≠ 0(mod p).
Пример несингулярных ЭК

5.

5
Операции в ЭК
Обратная
точке P(x, y) будет точка с координатами
(x,-y);
Точки на бесконечности (бесконечно удаленная точка)
кривой – O:
Точка принадлежит ЭК, тогда и
P+(-P) = O
только тогда, когда подставляя
Операция сложения 2 точек, таких что P ≠ ±Q:
Выполняется
через операции
соответствующие
значения
P+Q=R
удвоения
и сложения
точек.
координат
в уравнение
ЭК
Операция удвоения точки, когда P=Q:
Например:
13Рверное
= P + 2Р
+ 8Р =
получается
равенство.
P + P = 2P
P+2P+2(2(2P))
Формальная операция – скалярное умножение на
число: t○P = P + P + … + P
t раз
Также определяется 0○P = О и -t○P(x,y) = t○P(x, -y)

6.

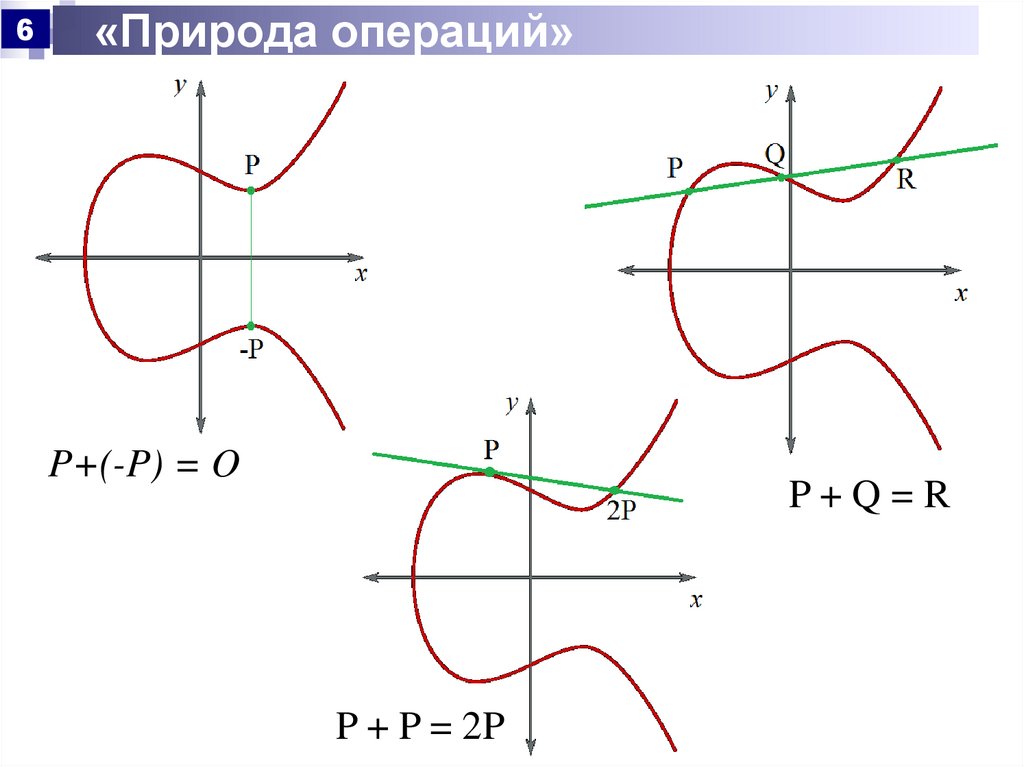
6
«Природа операций»
P+(-P) = O
P+Q=R
P + P = 2P

7.

Формулы для вычислений
7
Надо понимать, что на практике никто не рисует
Угловой
касательные
коэффициенти прямые через 2 точки и не
прямой/касательной
высчитывает
их координаты (это не реально). Для
этого выведены специальные формулы.
Очевидно! Если точки над которыми выполняются
операции принадлежат ЭК, то результирующая точка
также должна принадлежать этой же ЭК.

8.

Порядок ЭК
8
Число элементов группы точек эллиптической
кривой Ep(a, b) называют порядком этой группы.
Верхняя и нижняя границы для порядка группы
определяются теоремой Хассе.
Теорема Хассе. Для порядка NE группы точек
эллиптической кривой над полем GF(q) (q – число
элементов поля) справедливо неравенство: