B13. Задачи на движение по прямой

1. B13 ЕГЭ 2012г.

Задачи на движение по прямой.

2.

Из пункта A в пункт B одновременно выехали два автомобиля.
Первый проехал с постоянной скоростью весь путь. Второй
проехал первую половину пути со скоростью 24 км/ч, а вторую
половину пути — со скоростью, на 16 км/ч большей скорости
первого, в результате чего прибыл в пункт В одновременно с
первым автомобилем. Найдите скорость первого автомобиля.
Ответ дайте в км/ч.
S км
Х км/ч
S
2
S
2
(Х+16) км/ч
24 км/ч
t1 = t2
t
S
v

3.

Из пункта A в пункт B одновременно выехали два автомобиля.
Первый проехал с постоянной скоростью весь путь. Второй
проехал первую половину пути со скоростью 24 км/ч, а вторую
половину пути — со скоростью, на 16 км/ч большей скорости
первого, в результате чего прибыл в пункт В одновременно с
первым автомобилем. Найдите скорость первого автомобиля.
Ответ дайте в км/ч.
S
S
S 2
2 ;
x 24 x 16
S
S
S
; :S
x 2 24 2 ( x 16)
1
1
1
;
x 2 24 2 ( x 16)
48( x 16) x ( x 16) 24 x;
48 x 48 16 x 16 x 24 x;
2
x 8 x 48 16 0;
2
x 24(постор.корень);
x 32
В 13
3 2
3
10 х
х

4.

)
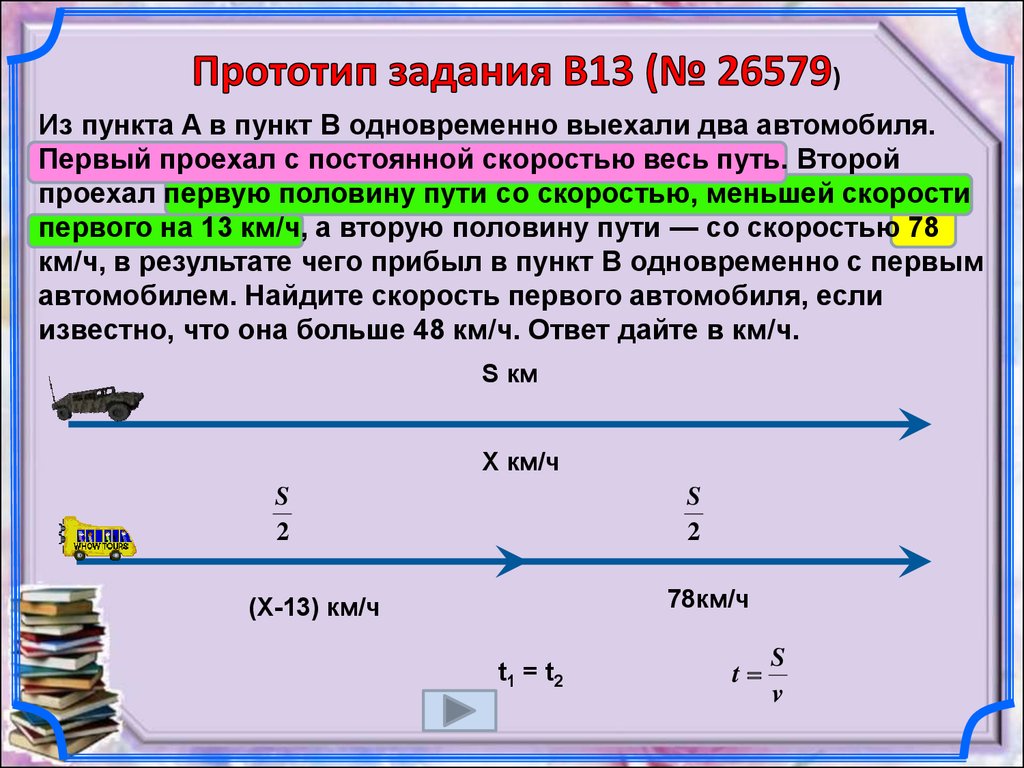
Из пункта A в пункт B одновременно выехали два автомобиля.
Первый проехал с постоянной скоростью весь путь. Второй
проехал первую половину пути со скоростью, меньшей скорости
первого на 13 км/ч, а вторую половину пути — со скоростью 78
км/ч, в результате чего прибыл в пункт В одновременно с первым
автомобилем. Найдите скорость первого автомобиля, если
известно, что она больше 48 км/ч. Ответ дайте в км/ч.
S км
Х км/ч
S
2
S
2
78км/ч
(X-13) км/ч
t1 = t2
t
S
v

5.

Из пункта A в пункт B одновременно выехали два автомобиля.
Первый проехал с постоянной скоростью весь путь. Второй
проехал первую половину пути со скоростью, меньшей
скорости первого на 13 км/ч, а вторую половину пути — со
скоростью 78 км/ч, в результате чего прибыл в пункт В
одновременно с первым автомобилем. Найдите скорость
первого автомобиля, если известно, что она больше 48 км/ч.
Ответ дайте в км/ч.
S
S
S
2 2;
x x 13 78
S
S
S
;
x 2( x 13) 2 78
2 78( x 13) 2 78 x x( x 13);
x 13 x 2 78 13 0
2
x 39( постор .корень),
1
x 52.
2
1
1
1
;
x 2( x 13) 2 78
В 13
5 2
3
10 х
х

6.

)
Из пункта А в пункт В, расстояние между которыми 75 км,
одновременно выехали автомобилист и велосипедист. Известно,
что за час автомобилист проезжает на 40 км больше, чем
велосипедист. Определите скорость велосипедиста, если известно,
что он прибыл в пункт В на 6 часов позже автомобилиста. Ответ
дайте в км/ч.
75 км
(X+40) км/ч
75км
X км/ч
t велосипедиста = t автомобилиста + 6
S
t
v

7.

Из пункта А в пункт В, расстояние между которыми 75 км,
одновременно выехали автомобилист и велосипедист.
Известно, что за час автомобилист проезжает на 40 км
больше, чем велосипедист. Определите скорость
велосипедиста, если известно, что он прибыл в пункт В на 6
часов позже автомобилиста. Ответ дайте в км/ч.
75
75
6;
x x 40
75( x 40) 75 x 6 x( x 40);
75 x 75 40 75 x 6 x 6 x 40;
2
6 x 6 x 40 75 40 0;
2
:6
x 40 x 25 20 0;
2
x 10
1
x 50(постор. корень)
2
В 13
1 0
3
10 х
х

8.

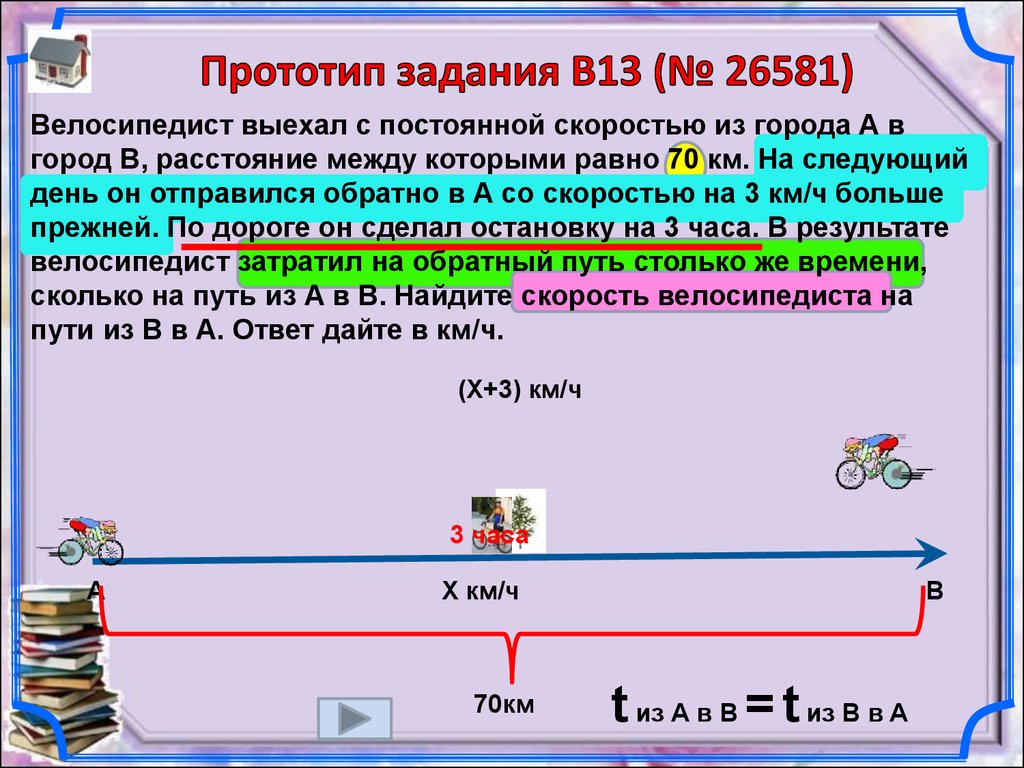
Велосипедист выехал с постоянной скоростью из города А в
город В, расстояние между которыми равно 70 км. На следующий
день он отправился обратно в А со скоростью на 3 км/ч больше
прежней. По дороге он сделал остановку на 3 часа. В результате
велосипедист затратил на обратный путь столько же времени,
сколько на путь из А в В. Найдите скорость велосипедиста на
пути из В в А. Ответ дайте в км/ч.
(X+3) км/ч
3 часа
А
X км/ч
70км
В
t из А в В = t из B в A

9.

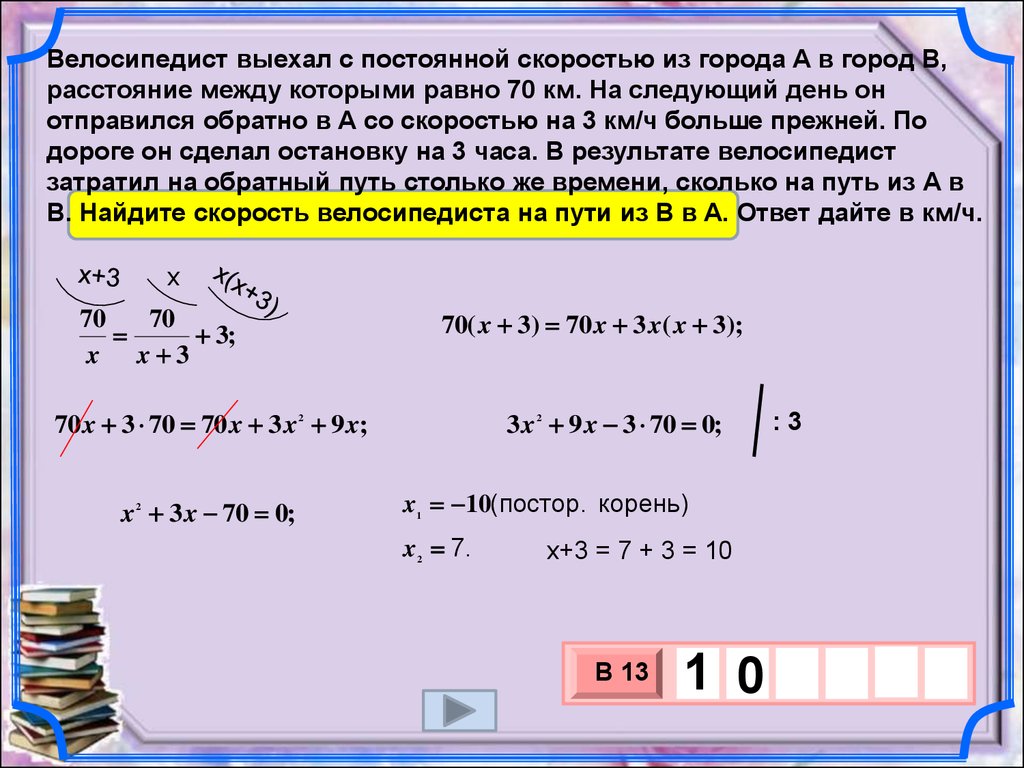
Велосипедист выехал с постоянной скоростью из города А в город В,
расстояние между которыми равно 70 км. На следующий день он
отправился обратно в А со скоростью на 3 км/ч больше прежней. По
дороге он сделал остановку на 3 часа. В результате велосипедист
затратил на обратный путь столько же времени, сколько на путь из А в
В. Найдите скорость велосипедиста на пути из В в А. Ответ дайте в км/ч.
x
70( x 3) 70 x 3 x( x 3);
70
70
3;
x x 3
70 x 3 70 70 x 3 x 9 x;
3 x 9 x 3 70 0;
2
x 3 x 70 0;
2
2
:3
x 10(постор. корень)
1
x 7.
2
x+3 = 7 + 3 = 10
В 13
1 0
3
10 х
х

10.

)
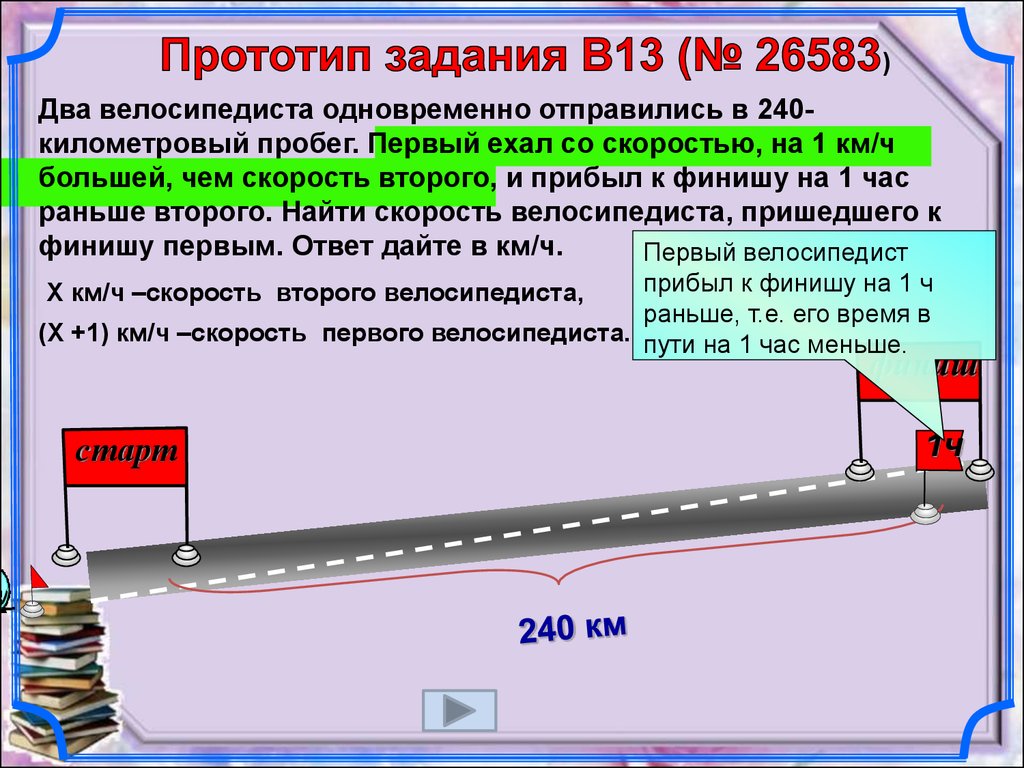
Два велосипедиста одновременно отправились в 240километровый пробег. Первый ехал со скоростью, на 1 км/ч
большей, чем скорость второго, и прибыл к финишу на 1 час
раньше второго. Найти скорость велосипедиста, пришедшего к
финишу первым. Ответ дайте в км/ч.
Первый велосипедист
прибыл к финишу на 1 ч
раньше, т.е. его время в
(Х +1) км/ч –скорость первого велосипедиста. пути на 1 час меньше.
Х км/ч –скорость второго велосипедиста,
финиш
старт
1ч

11.

Два велосипедиста одновременно отправились в 240километровый пробег. Первый ехал со скоростью, на 1 км/ч
большей, чем скорость второго, и прибыл к финишу на 1 час
раньше второго. Найти скорость велосипедиста, пришедшего к
финишу первым. Ответ дайте в км/ч.
240
х+1
<
240
=
+1
x
x x 240 0;
2
240 x x( x 1) 240( x 1);
x 16(постор. корень), x 15.
2
1
x + 1 = 16
t
t
S
v
Первый велосипедист прибыл к
финишу на 1 ч раньше, т.е. его
время в пути на 1час меньше.
240
х+1
240
х
В 13
1 6
3
10 х
х