Применение теории графов к решению задач

1. Применение теории графов к решению задач

2.

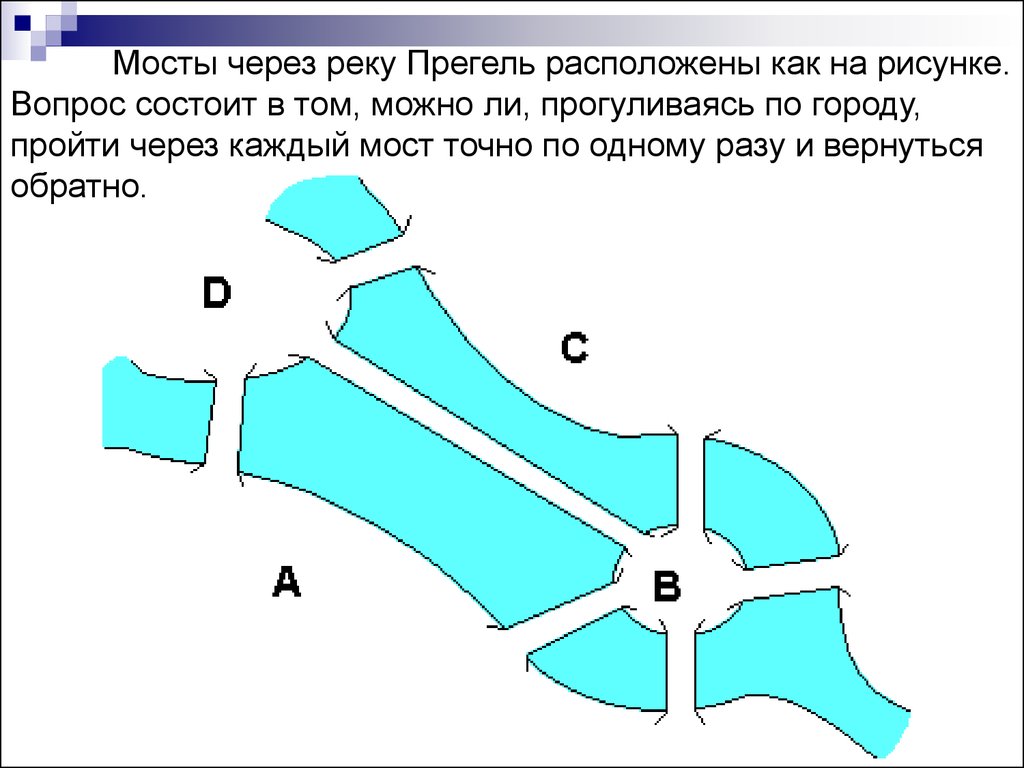
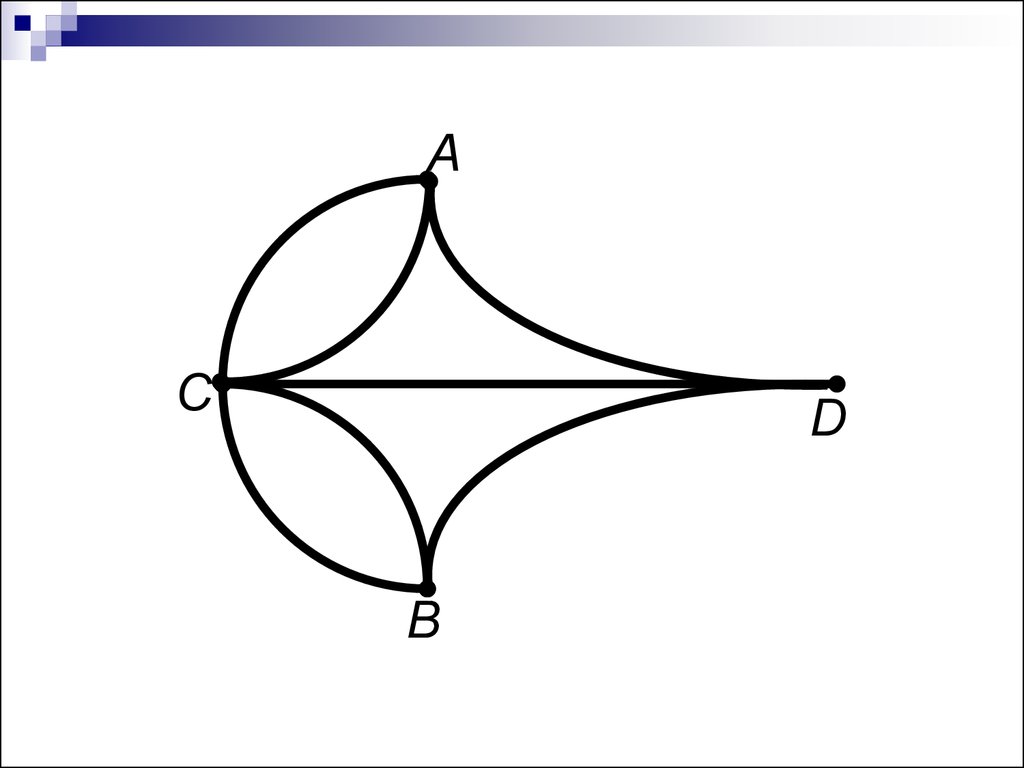
Мосты через реку Прегель расположены как на рисунке.
Вопрос состоит в том, можно ли, прогуливаясь по городу,
пройти через каждый мост точно по одному разу и вернуться
обратно.

3.

А
С
D
В

4.

На рисунке изображена решетка. Можно ли провести
непрерывную линию, пересекающую точно по разу
каждую сторону решетки?

5. Виды графов:

Неориентированный граф
Ориентированный граф
Граф-дерево или дерево возможностей
Граф с ребрами двух цветов

6. Неориентированные графы

7. Задача 1. В шахматном турнире участвовали 4 человека. Каждый спортсмен сыграл со всеми другими участниками соревнований по одному разу. Ско

Задача 1.
В шахматном турнире участвовали
4 человека. Каждый спортсмен
сыграл со всеми другими
участниками соревнований по
одному разу. Сколько всего было
сыграно партий?

8. В шахматном турнире участвовали 4 человека. Каждый спортсмен сыграл со всеми другими участниками соревнований по одному разу. Сколько всег

В шахматном турнире участвовали 4 человека.
Каждый спортсмен сыграл со всеми другими
участниками соревнований по одному разу.
Сколько всего было сыграно партий?
1
2
4
3

9. Задача 2. На лесной опушке встретились заяц, белка, лиса, волк, медведь и куница. Каждый, здороваясь, пожал каждому лапу. Сколько всего лапкоп

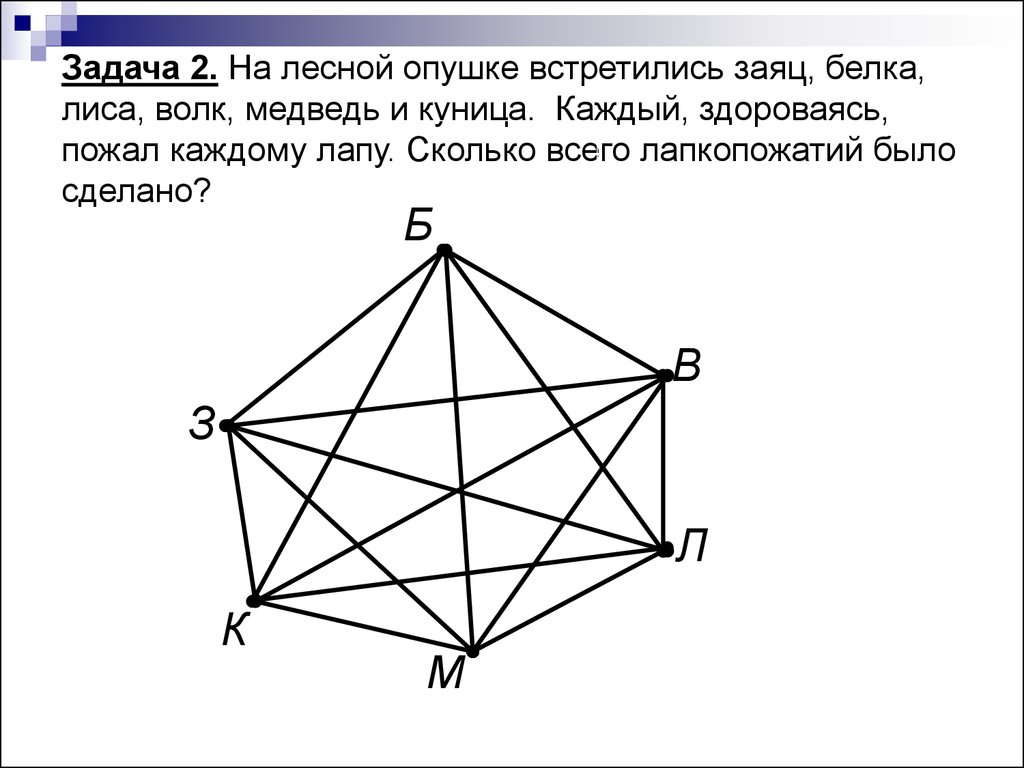
Задача 2. На лесной опушке встретились заяц, белка,
лиса, волк, медведь и куница. Каждый, здороваясь,
пожал каждому лапу. Сколько всего лапкопожатий было
сделано?
Б
В
З
Л
К
М

10. Задача 3. Несколько мальчиков встретились на вокзале, чтобы поехать за город в лес. При встрече все они поздоровались друг с другом за руку.

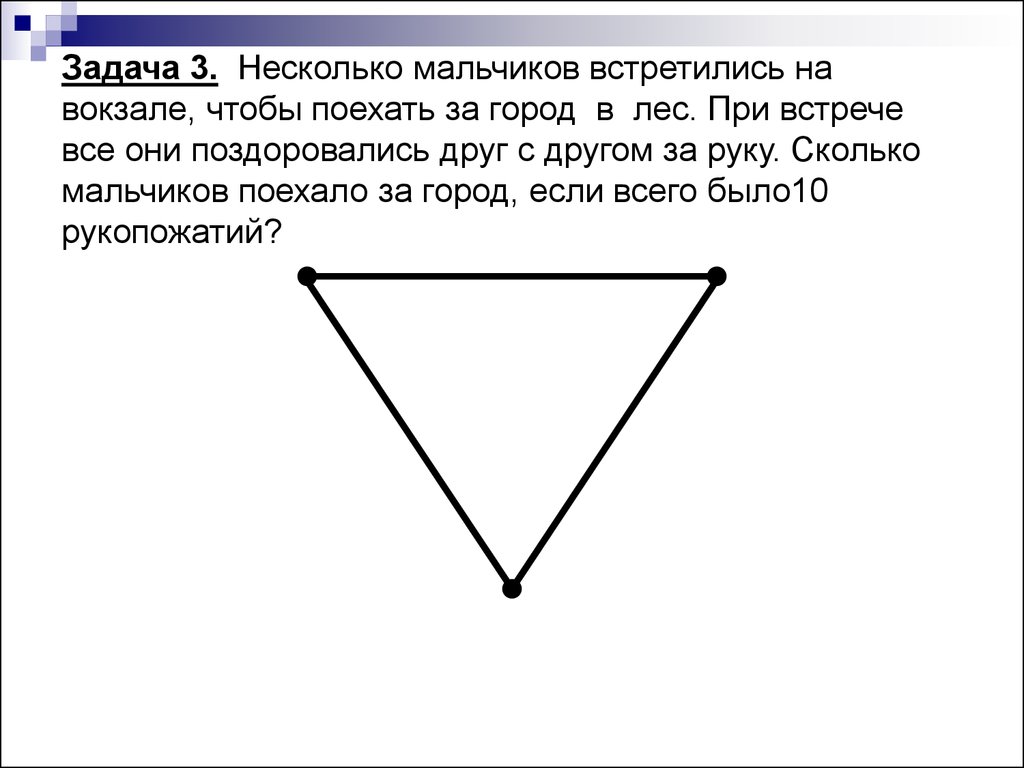
Задача 3. Несколько мальчиков
встретились на вокзале, чтобы
поехать за город в лес. При
встрече все они поздоровались
друг с другом за руку. Сколько
мальчиков поехало за город,
если всего было10 рукопожатий?

11. Несколько мальчиков встретились на вокзале, чтобы поехать за город в лес. При встрече все они поздоровались друг с другом за руку. Сколько м

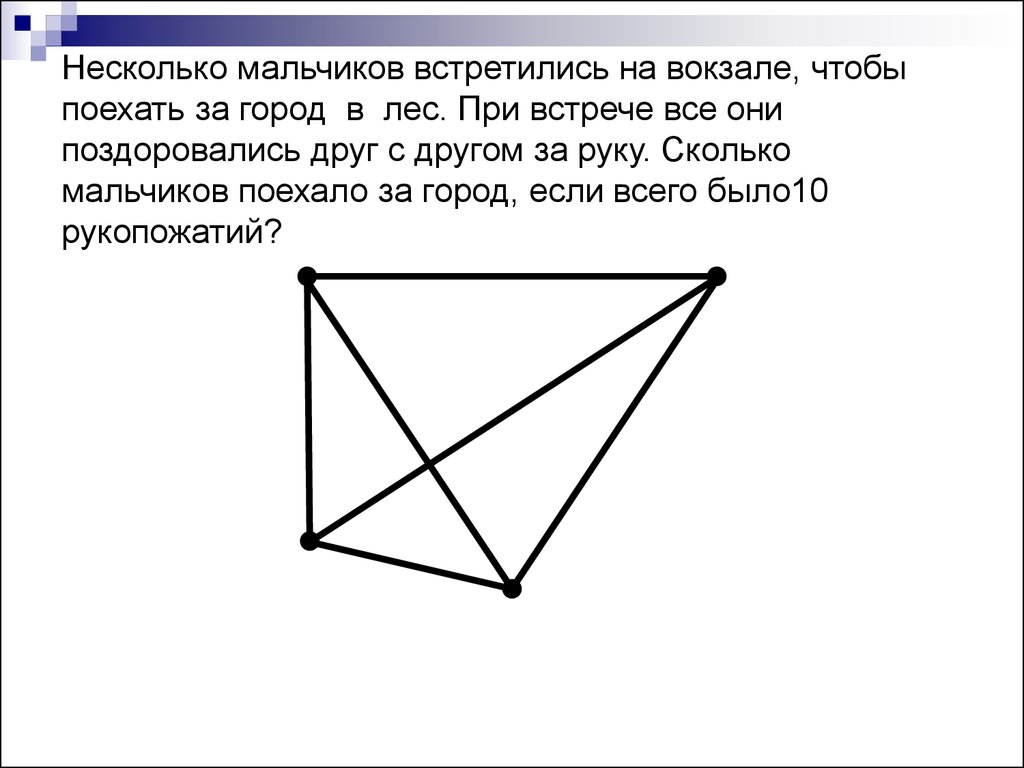
Несколько мальчиков встретились на вокзале, чтобы
поехать за город в лес. При встрече все они
поздоровались друг с другом за руку. Сколько
мальчиков поехало за город, если всего было10
рукопожатий?

12. Задача 3. Несколько мальчиков встретились на вокзале, чтобы поехать за город в лес. При встрече все они поздоровались друг с другом за руку.

Задача 3. Несколько мальчиков встретились на
вокзале, чтобы поехать за город в лес. При встрече
все они поздоровались друг с другом за руку. Сколько
мальчиков поехало за город, если всего было10
рукопожатий?

13. Несколько мальчиков встретились на вокзале, чтобы поехать за город в лес. При встрече все они поздоровались друг с другом за руку. Сколько м

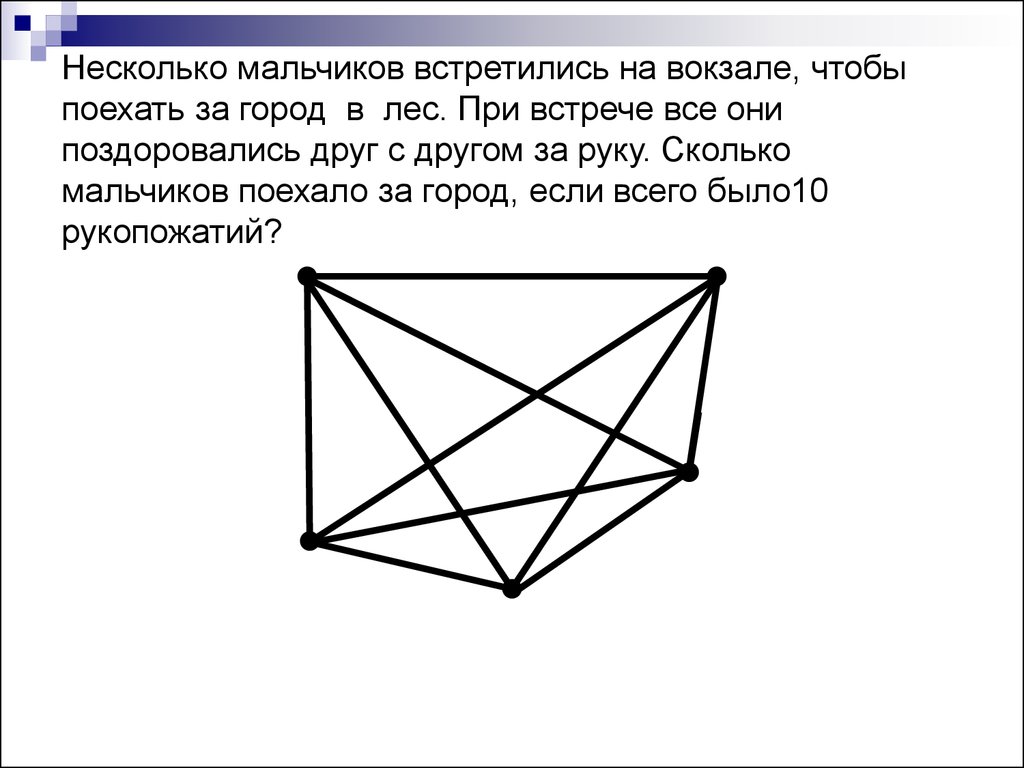
Несколько мальчиков встретились на вокзале, чтобы
поехать за город в лес. При встрече все они
поздоровались друг с другом за руку. Сколько
мальчиков поехало за город, если всего было10
рукопожатий?

14. Несколько мальчиков встретились на вокзале, чтобы поехать за город в лес. При встрече все они поздоровались друг с другом за руку. Сколько м

Несколько мальчиков встретились на вокзале, чтобы
поехать за город в лес. При встрече все они
поздоровались друг с другом за руку. Сколько
мальчиков поехало за город, если всего было10
рукопожатий?

15. Задача 4. В первенстве класса по шашкам 5 участников: Аня, Боря, Влад, Гриша, Даша. Первенство проводится по круговой системе – каждый из учас

Задача 4. В первенстве класса по шашкам 5
участников: Аня, Боря, Влад, Гриша, Даша.
Первенство проводится по круговой системе –
каждый из участников играет с каждым из
остальных один раз. К настоящему времени
некоторые игры уже проведены: Аня сыграла с
Борей, Владом и Дашей; Боря сыграл, как уже
говорилось, с Аней и еще с Гришей; Влад – с
Аней и Дашей, Гриша – с Борей, Даша – с
Аней и Гришей. Сколько игр проведено к
настоящему времени и сколько еще осталось?

16.

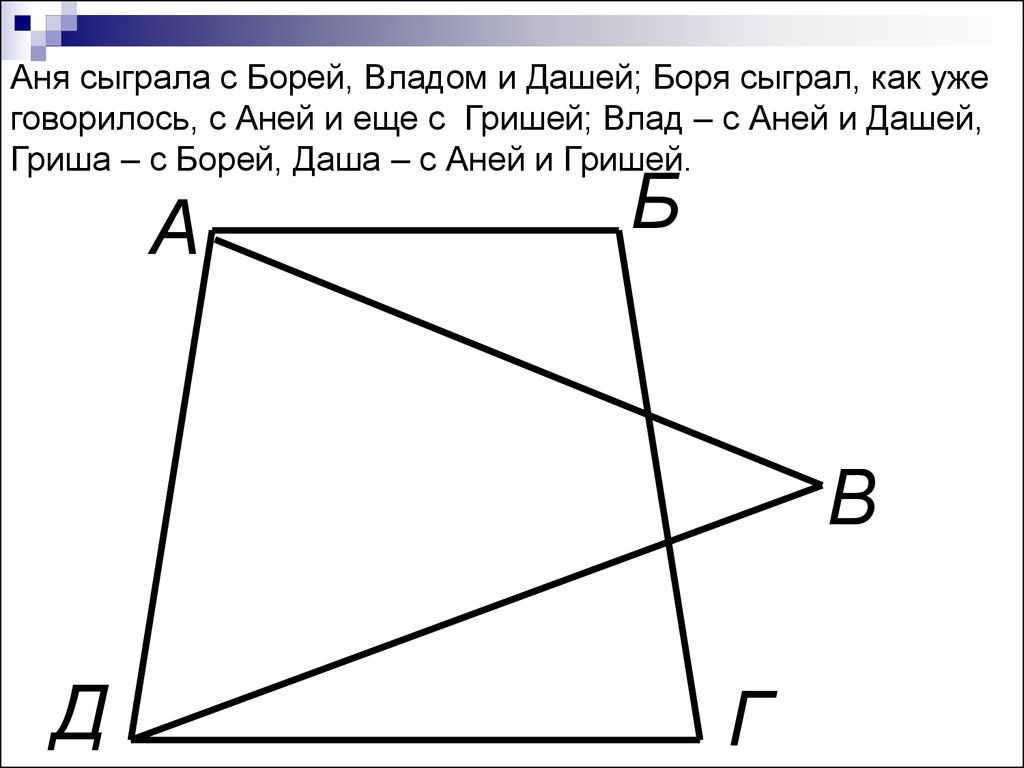
Аня сыграла с Борей, Владом и Дашей; Боря сыграл, как уже
говорилось, с Аней и еще с Гришей; Влад – с Аней и Дашей,
Гриша – с Борей, Даша – с Аней и Гришей.
А
Б
В
Д
Г

17. Задача 5. В стране алфавит 8 городов: А, Б, В, Г, Д, Е, Ж, З и восемь непересекающихся дорог между городами А и Б, Е и Д, Б и Ж, З и А, В и Г, Г и Д, Ж и З,

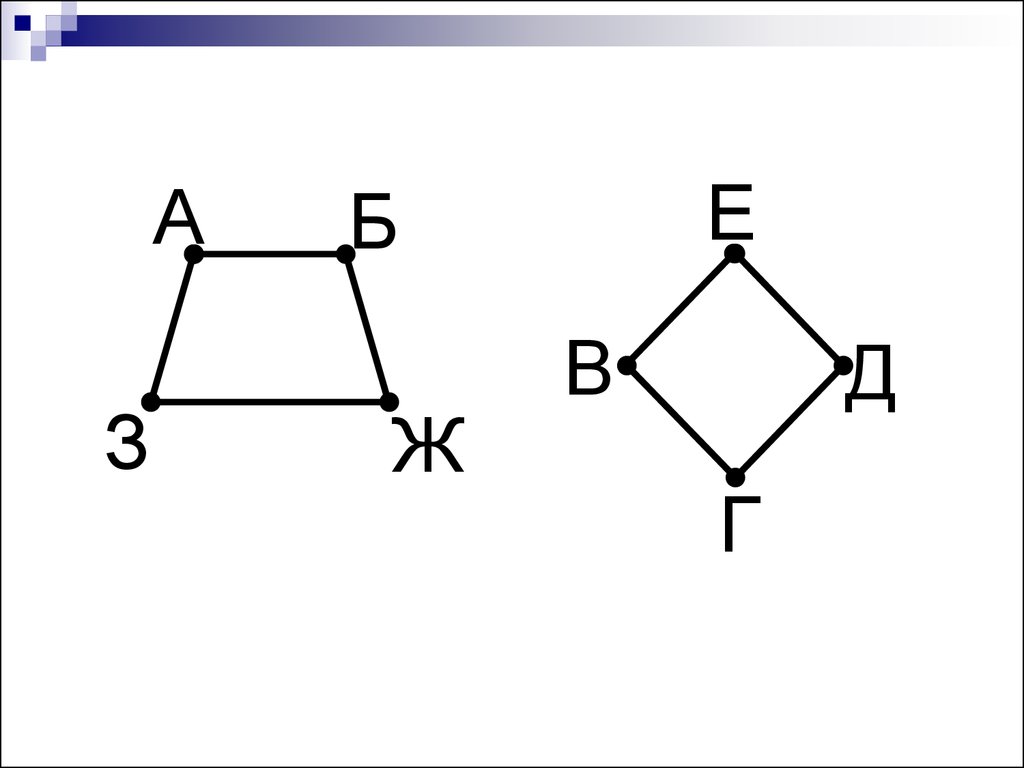
Задача 5. В стране алфавит 8
городов: А, Б, В, Г, Д, Е, Ж, З и
восемь непересекающихся
дорог между городами А и Б,
Е и Д, Б и Ж, З и А, В и Г, Г и Д,
Ж и З, В и Е. Можно ли по этим
дорогам проехать из А в Г?

18.

А
З
Е
Б
Ж
В
Д
Г

19. Ориентированные графы

20. Задача 6. Из лагеря вышли четыре туриста: Вася, Галя, Толя и Лена. Вася идет впереди Лены, Толя впереди Гали, а Лена впереди Толи. В каком поряд

Задача 6. Из лагеря вышли
четыре туриста: Вася, Галя, Толя
и Лена. Вася идет впереди Лены,
Толя впереди Гали, а Лена
впереди Толи. В каком порядке
идут дети?
Вася Лена
Толя Галя

21.

Вася идет впереди Лены, Толя впереди Гали, а
Лена впереди Толи.
Г
В
Т
Л

22. Задача 7. В детском лагере отдыха в одной комнате живут четыре девочки: Маша, Валя, Таня и Галя. Две из них ровесницы. Известно, что Таня старш

Задача 7. В детском лагере отдыха в
одной комнате живут четыре
девочки: Маша, Валя, Таня и Галя.
Две из них ровесницы. Известно, что
Таня старше Маши, которая моложе
Гали. Таня моложе Вали, которая
старше Гали. Кто ровесницы?
М
Г
Т
Г
В

23.

Таня старше Маши, которая моложе Гали.
Таня моложе Вали, которая старше Гали.
Т
В
М
М
Г
Г
В
Т

24. Задача 8. На пришкольном участке растут 8 деревьев: яблоня, тополь, береза, рябина, дуб, клен, лиственница и сосна. Рябина выше лиственницы, яб

Задача 8. На пришкольном участке
растут 8 деревьев: яблоня, тополь,
береза, рябина, дуб, клен,
лиственница и сосна. Рябина выше
лиственницы, яблоня выше клена,
дуб ниже березы, но выше сосны,
сосна выше рябины, береза ниже
тополя, а лиственница выше яблони.
Расположите деревья от самого
низкого к самому высокому.

25.

Рябина выше лиственницы, яблоня выше клена, дуб
ниже березы, но выше сосны, сосна выше рябины,
береза ниже тополя, а лиственница выше яблони.
Я
Т
Б
Д
Р
К
Л
С

26. Граф-дерево или дерево возможностей

27. Задача 9. В столовой на горячее можно заказать щуку, грибы и баранину, на гарнир – картофель и рис, а из напитков – чай и кофе. Сколько различ

Задача 9. В столовой на
горячее можно заказать щуку,
грибы и баранину, на гарнир –
картофель и рис, а из
напитков – чай и кофе.
Сколько различных вариантов
обедов можно составить из
указанных блюд?

28.

Г
Щ
Р
К
Ч
К Ч
К
Р
К
Ч
Б
К Ч
К
Р
К
Ч
К Ч
К

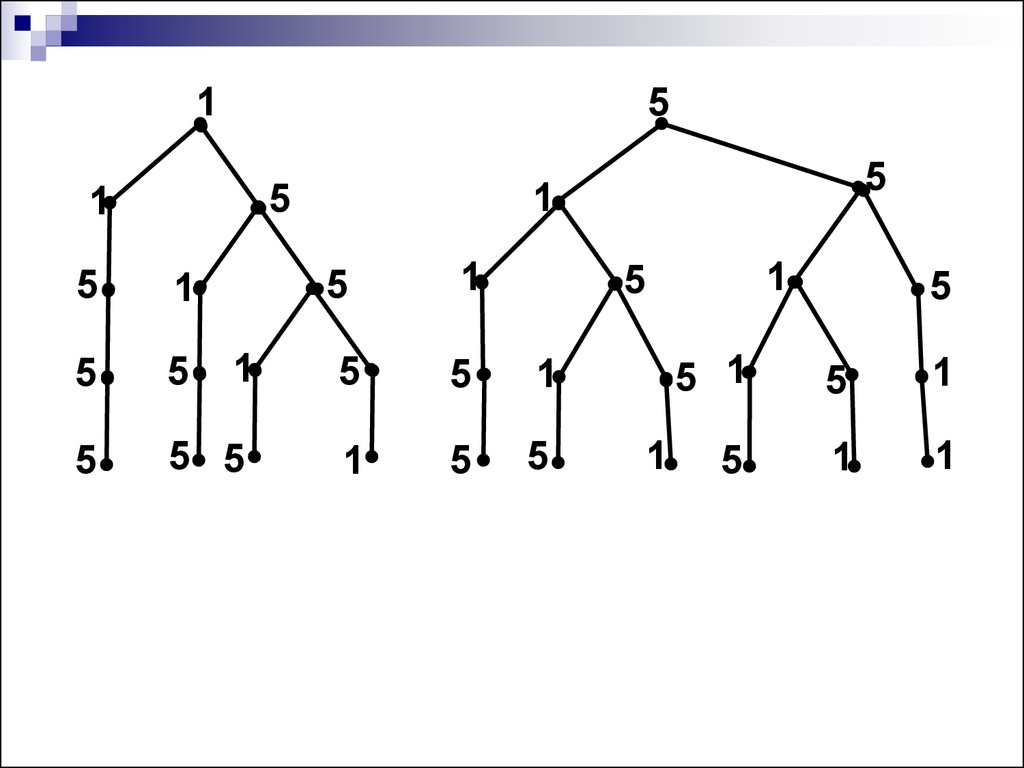
29. Задача 10. Из наборного полотна взяли 2 карточки с цифрой 1 и 3 карточки с цифрой 5. Сколько различных пятизначных чисел можно составить из эти

Задача 10. Из наборного
полотна взяли 2 карточки с
цифрой 1 и 3 карточки с
цифрой 5. Сколько различных
пятизначных чисел можно
составить из этих карточек?

30.

1
5
1
5
1
5
5
1
1
5
5
1
5
5
1
5
5
1
5
5 5
1
5
5
1
5
5 1
5
1
5
1
1

31. Граф с ребрами двух цветов

32. Задача 12. В одном классе учатся Иван, Петр и Сергей. Их фамилии Иванов, Петров и Сергеев. Установи фамилию каждого из ребят, если известно, чт

Задача 12. В одном классе учатся
Иван, Петр и Сергей. Их фамилии
Иванов, Петров и Сергеев. Установи
фамилию каждого из ребят, если
известно, что Иван не Иванов, Петр
не Петров и Сергей не Сергеев и что
Сергей живет в одном доме
Петровым.

33. Иван не Иванов, Петр не Петров, Сергей не Сергеев. Сергей живет в одном доме Петровым.

Иван
Иванов
Петр
Петров
Сергей
Сергеев

34. Задача 13. Три друга – Алеша, Сергей и Денис – купили щенков разной породы: щенка ротвейлера, щенка колли и щенка овчарки. Известно, что: щено

Задача 13. Три друга – Алеша, Сергей и
Денис – купили щенков разной породы:
щенка ротвейлера, щенка колли и щенка
овчарки. Известно, что: щенок Алеши
темнее по окрасу, чем ротвейлер, Леси и
Гриф; щенок Сергея старше Грифа,
овчарки и ротвейлера; Джек и ротвейлер
всегда гуляют вместе. У кого какой
породы щенок? Назовите клички щенков.

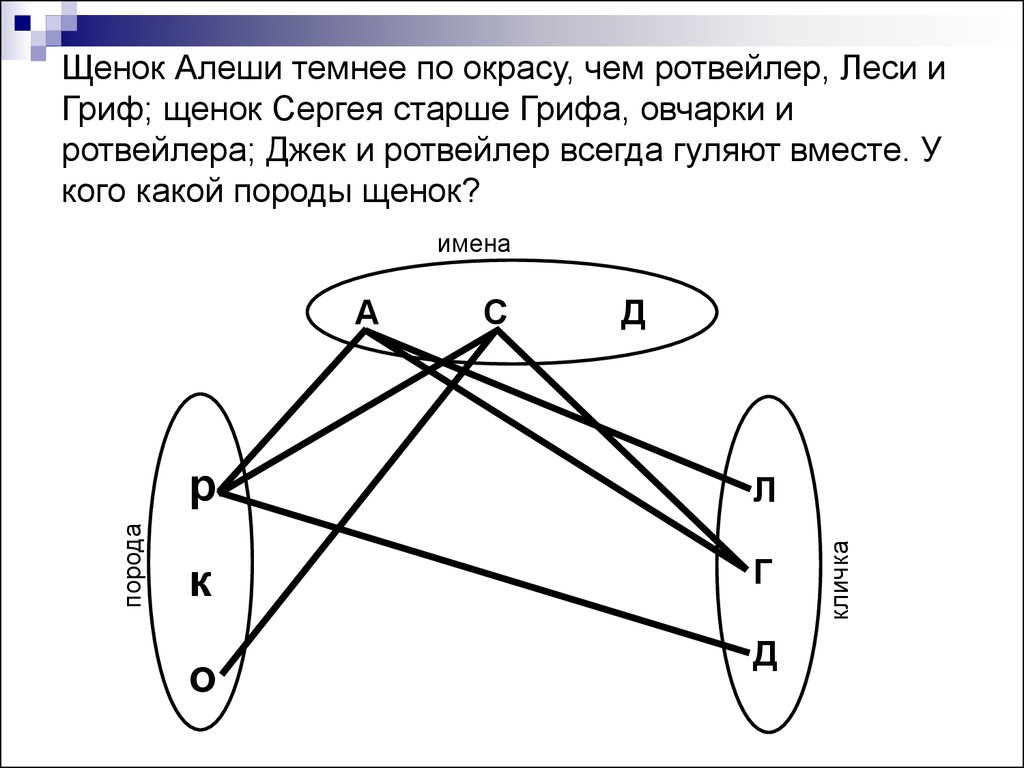
35. Щенок Алеши темнее по окрасу, чем ротвейлер, Леси и Гриф; щенок Сергея старше Грифа, овчарки и ротвейлера; Джек и ротвейлер всегда гуляют вме

Щенок Алеши темнее по окрасу, чем ротвейлер, Леси и
Гриф; щенок Сергея старше Грифа, овчарки и
ротвейлера; Джек и ротвейлер всегда гуляют вместе. У
кого какой породы щенок?
имена
С
Д
р
Л
к
Г
о
Д
кличка
порода
А

36. Щенок Алеши темнее по окрасу, чем ротвейлер, Леси и Гриф; щенок Сергея старше Грифа, овчарки и ротвейлера; Джек и ротвейлер всегда гуляют вме

Щенок Алеши темнее по окрасу, чем ротвейлер, Леси и
Гриф; щенок Сергея старше Грифа, овчарки и
ротвейлера; Джек и ротвейлер всегда гуляют вместе. У
кого какой породы щенок?
имена
С
Д
р
Л
к
Г
о
Д
кличка
порода
А

37. Щенок Алеши темнее по окрасу, чем ротвейлер, Леси и Гриф; щенок Сергея старше Грифа, овчарки и ротвейлера; Джек и ротвейлер всегда гуляют вме

Щенок Алеши темнее по окрасу, чем ротвейлер, Леси и
Гриф; щенок Сергея старше Грифа, овчарки и
ротвейлера; Джек и ротвейлер всегда гуляют вместе. У
кого какой породы щенок?
имена
С
Д
р
Л
к
Г
о
Д
кличка
порода
А