Применение граф – схем при решении задач

1.

МКОУ «Алцынхутинская средняя общеобразовательная
школа имени Г.О. Рокчинского»
«Применение граф – схем
при решении задач»
Манджарикова Тамара
Нохаевна – учитель математики

2.

I признак (СУС)
B
A
АВ = А1В1
B1
C
A1
А=А1
∆АВС = ∆А1В1С1
C1
АС = А1С1

3.

А
1
В
2
Дано:
АВ = ВД
<1 = <2
Доказать:
∆АВС = ∆ДВС
С
Д

4.

II признак (СУС)
L
K
L1
M
K1
<K = < K1
M1
KM = K1M1
< M = < M1
∆KLM = ∆ K1L1M1
Задание: Дано <1 = <2 и <3 = < 4. Доказать, что ∆АВД = ∆СВД
А
<1=<2
Д
1
2
4
3
С
ВД = ВД
В
∆АВД = ∆ СДВ
<3=<4

5.

III признак (СCС)
Е
Е1
Д
Д1
К1
К
ДЕ = Д1Е1 ДК = Д1К1 ЕК = Е1К1
∆ДЕК
В
= ∆Д1Е1К1
Задание: АВ=ДС, ВС=АД. Доказать ∆АВС = ∆СДА
АВ = ДС
А
ВС = АД
С
Д
∆АВС
= ∆СДА
АС = АС

6.

Решение задачи
В равнобедренном треугольнике АВС с основанием АС,
проведена биссектриса ВД, где точка М принадлежит ВД.
Докажите, что АМ=МС.
В
1 2
АВС - р/б
ВМ = ВМ
АВ = ВС
∆АВМ
М
ВД - бисс. В
<1=<2
= ∆СВМ
АМ = МС
А
Д
С
(против равных углов лежат равные
стороны.)

7.

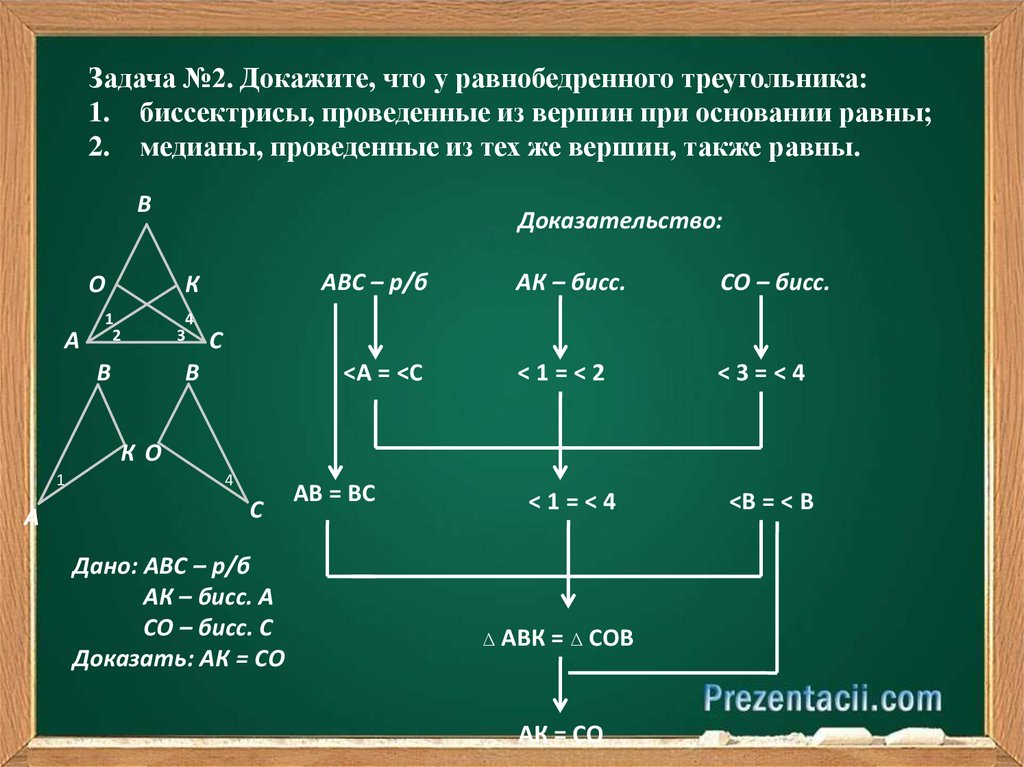
Задача №2. Докажите, что у равнобедренного треугольника:
1. биссектрисы, проведенные из вершин при основании равны;
2. медианы, проведенные из тех же вершин, также равны.
В
О
А
Доказательство:
АВС – р/б
К
1
2
В
4
3
АК – бисс.
СО – бисс.
<1=<2
<3=<4
С
В
<А = <С
КО
1
А
4
С
Дано: АВС – р/б
АК – бисс. А
СО – бисс. С
Доказать: АК = СО
АВ = ВС
<1=<4
∆
АВК = ∆ СОВ
АК = СО
<В = < В

8.

Самостоятельная работа

9.

Деформированное задание