Похожие презентации:
Электроника
1.
Нижегородский государственный технический университет им. Р.Е. АлексееваИнститут радиоэлектроники и информационных технологий
Кафедра «Электроника и сети ЭВМ»
Электроника
Лекции
К.т.н., доцент кафедры ЭСВМ
Калинина Н.А.
Kalinina_na@list.ru
2.
ФИЗИЧЕСКИЕ ОСНОВЫПОЛУПРОВОДНИКОВОЙ
ЭЛЕКТРОНИКИ
3.
Определяющие свойстваполупроводников
1.
2.
3.
4.
Удельное электрическое сопротивление ρ –
промежуточное положение между проводниками и
диэлектриками.
Высокая чувствительность их электропроводности
к добавлению примесей других веществ даже в
незначительных количествах.
Сильная, нелинейная, обратная зависимость
удельного сопротивления от температуры.
Зависимость удельного сопротивления от
различного рода излучений.
4.
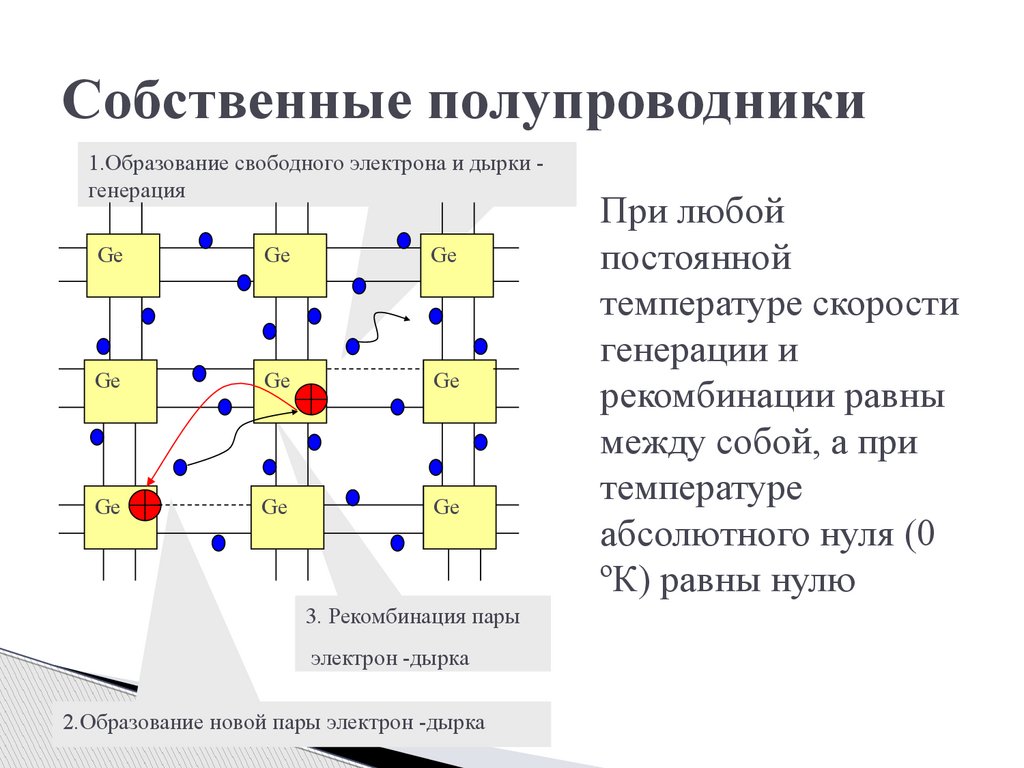
Собственные полупроводники1.Образование свободного электрона и дырки генерация
Ge
Ge
Ge
Ge
Ge
Ge
Ge
Ge
Ge
3. Рекомбинация пары
электрон -дырка
2.Образование новой пары электрон -дырка
При любой
постоянной
температуре скорости
генерации и
рекомбинации равны
между собой, а при
температуре
абсолютного нуля (0
ºК) равны нулю
5.
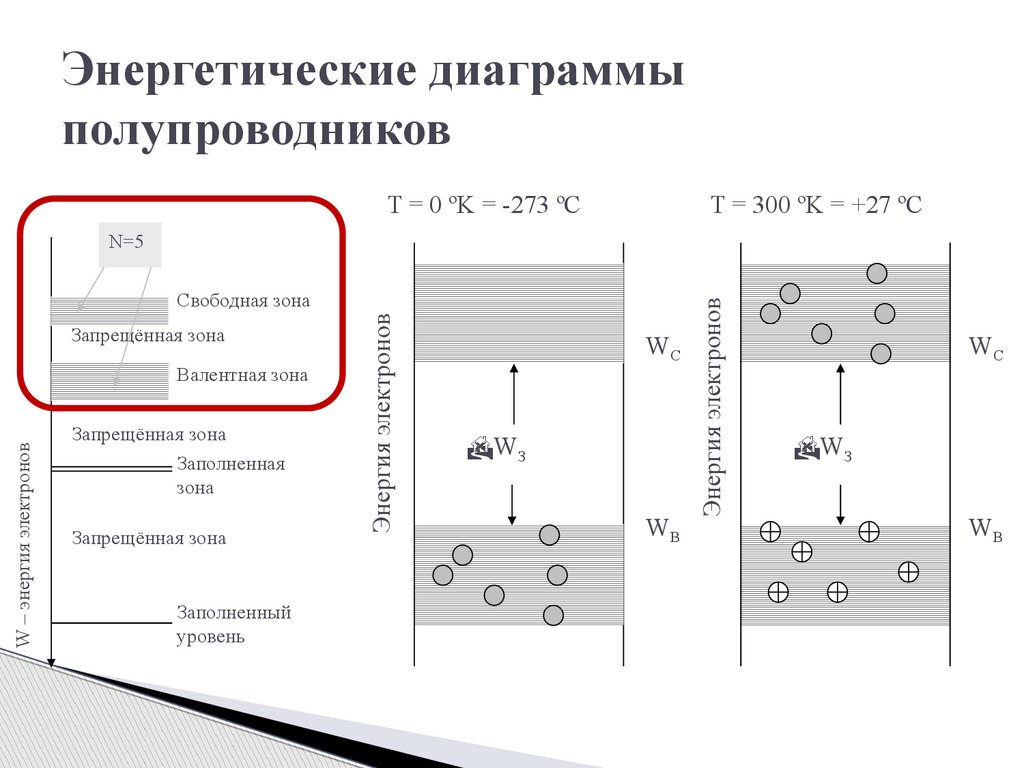
Энергетические диаграммыполупроводников
T = 0 ºK = -273 ºC
T = 300 ºK = +27 ºC
Запрещённая зона
W – энергия электронов
Валентная зона
Запрещённая зона
Заполненная
зона
Запрещённая зона
Заполненный
уровень
Энергия электронов
Свободная зона
WC
WЗ
WB
Энергия электронов
N=5
WC
WЗ
WB
6.
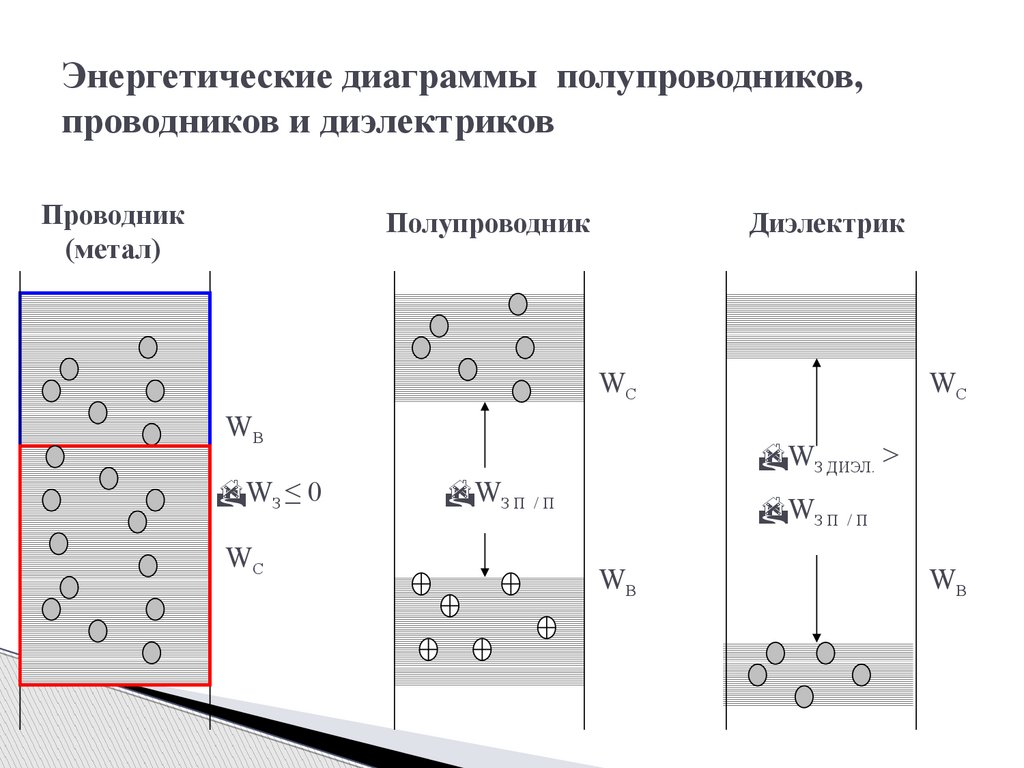
Энергетические диаграммы полупроводников,проводников и диэлектриков
Проводник
(метал)
Полупроводник
Диэлектрик
WC
WB
WЗ ≤ 0
WC
WC
WЗ ДИЭЛ. >
WЗ П / П
WЗ П / П
WB
WB
7.
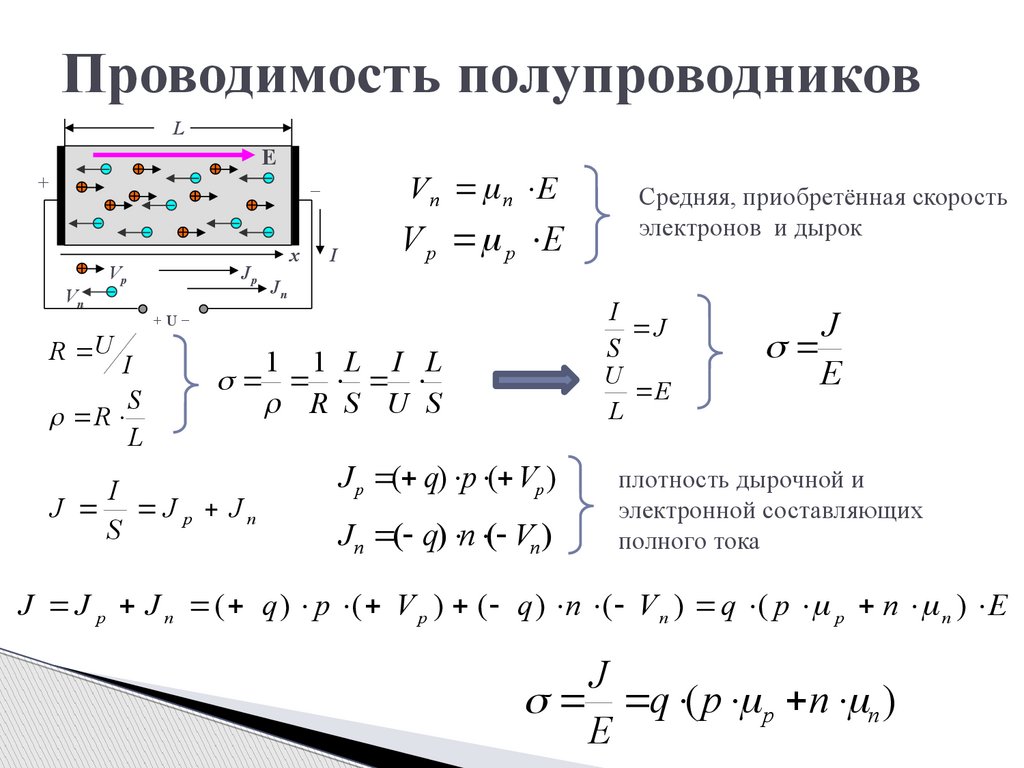
Проводимость полупроводниковL
E
+
V n n E
−
Vn
Vp
Jp
х
I
V p p E
Jn
I
J
S
U
E
L
+U−
R U
I
S
R
L
1 1 L I L
R S U S
I
J J p Jn
S
Средняя, приобретённая скорость
электронов и дырок
J p ( q) p ( Vp )
Jn ( q) n ( Vn )
J
E
плотность дырочной и
электронной составляющих
полного тока
J J p J n ( q ) p ( V p ) ( q ) n ( V n ) q ( p p n n ) E
J
q ( p p n n )
E
8.
Электропроводность собственныхполупроводников
Поскольку у собственных полупроводников
ni pi , то:
i q pi ( p n ) q ni ( p n )
Здесь и далее индекс i означает собственный
полупроводник.
9.
Функция распределенияФерми-Дирака
Вероятность заполнения электроном энергетического уровня с энергией W, при
заданной температуре T, количественно выражается функцией распределения
Ферми-Дирака: Fn(W) = 1/(1 + exp((W - WF) / kT ))
W
k – постоянная Больцмана
T – абсолютная температура
WF – уровень Ферми.
Энергия W
Fn(W
)
WF
Wз
T2>T1
T1
Fp(W
)
0
F(W)
0,5
Fn(W) + Fp(W) = 1,
T=0
1
Fp(W) – вероятность нахождения
дырки на энергетическом
уровне W.
Fp(W) = 1 - Fn(W),
Fp(W) = 1/(1 + exp((WF - W) / kT ))
Уровень Ферми – энергетический уровень равновероятный как для электрона, так и для дырки.
10.
Свойства функции распределенияФерми-Дирака
При T=0 функция Ферми превращается в
ступенчатую.
Для собственного полупроводника уровень Ферми
лежит в середине запрещённой зоны, т.к. функция
вероятности симметрична относительно него при
любой фиксированной температуре.
Функция Ферми имеет смысл только в валентной и
свободной зонах, т.к. в запрещённой зоне носители
заряда находиться не могут.
11.
Определение концентрации электронови дырок в собственном полупроводнике
Энергетические уровни зоны проводимости, а также и валентной
зоны распределены неравномерно, т.е. их плотность зависит от
энергии.
P(W) – число энергетических уровней в зоне проводимости,
попадающих в единичный, бесконечно малый энергетический
интервал dW. Т.е. P(W) – функция, характеризующая плотность
энергетических уровней.
dW·P(W) – число уровней в элементарной полосе dW.
Fn(W) – вероятностью заполнения энергетических уровней.
Тогда количество электронов, занимающих разрешённые
энергетические уровни в некоторой полосе dW
dni = P(W)·Fn(W)·dW.
12.
Определение концентрации электронов и дырок всобственном полупроводнике (продолжение)
Полное число электронов, приходящихся на 1 см3 вещества и
занимающих энергетическиеWуровни в полосе энергий от W1 до W2
ni P(W ) Fn (W )dW
будет равно:
2
W1
W
Аналогичным образом для концентрации
дырок валентной зоны
pi P(W ) F p (W )dW
получим:
W
2
1
В обоих случаях интегрирование ведётся по всей ширине зоны
проводимости (сonductivity)
или валентной (valency)
зоны.
W W
W
W
k T
В результате
k T
n i интегрирования
N C e
получим:
p
N
e
i
V
3
3
C
F i
2 mn k T 2
N C 2
2
h
F i
V
2 m p k T 2
N V 2
2
h
NС и NV – эфективная плотность состояний (на 1 см3) в зоне
проводимости и валентной зоне соответственно.
h = 4,14·10-15 эв·сек – постоянная Планка.
mn и mp – эффективная масса электрона и дырки соответственно.
13.
Определение концентрации электронов и дырок всобственном полупроводнике (продолжение)
В большинстве практических случаев можно считать, что
mn = mp = m – массе электрона в состоянии покоя. Тогда:
3
2
2 m k T
N C N V 2
2
h
Wc -Wv и учитывая,
далее, что ΔWз =
Положив
что в
собственном полупроводнике ni = pi , выражения для
концентрации электронов и дырок можно привести к
виду:
3
2
3
W
З
2 m k
ni p i 2
T 2 e 2 k T
2
h
14.
Определение концентрации электронов и дырок всобственном полупроводнике (продолжение)
При этих условиях уровень Ферми лежит точно
посередине запрещённой зоны, т.е.
WFi = (Wс-Wv) / 2.
Подставляя найденное значение концентрации n в
i
выражение для проводимости собственного
полупроводника придем к следующей
зависимости:
3
3
W
2 m k 2 2 2 k TЗ
i 2 q
n p
T e
2
h
2 m k
0 2 q
2
h
3
2
T
3
2
n p
i 0 e
WЗ
2 k T
15.
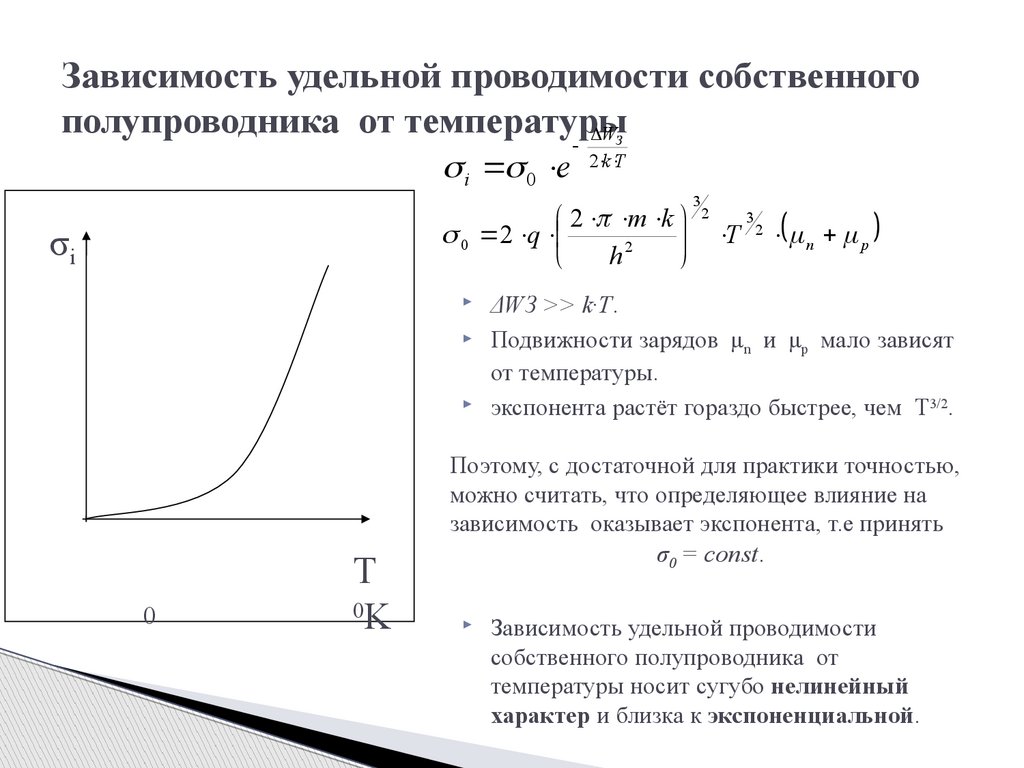
Зависимость удельной проводимости собственногополупроводника от температуры
W
i 0 e
З
2 k T
2 m k
0 2 q
h2
σi
0
T
0
K
3
2
T
3
2
n p
ΔWЗ >> k·T.
Подвижности зарядов μn и μp мало зависят
от температуры.
экспонента растёт гораздо быстрее, чем T3/2.
Поэтому, с достаточной для практики точностью,
можно считать, что определяющее влияние на
зависимость оказывает экспонента, т.е принять
σ0 = const.
Зависимость удельной проводимости
собственного полупроводника от
температуры носит сугубо нелинейный
характер и близка к экспоненциальной.
16.
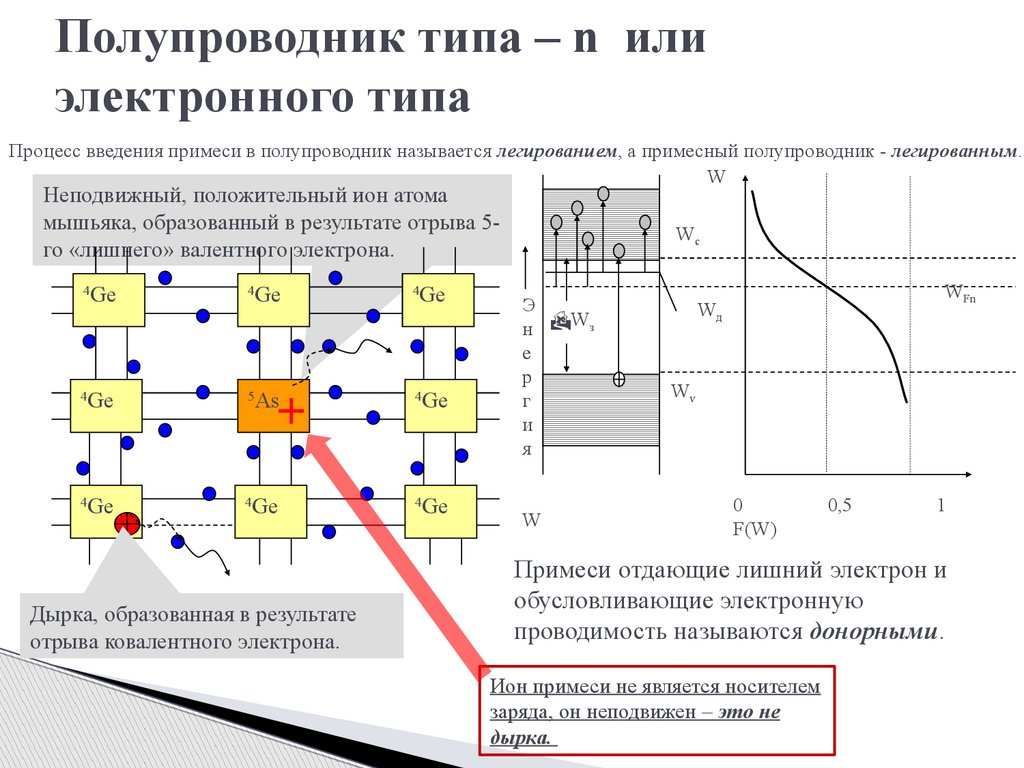
Полупроводник типа – n илиэлектронного типа
Процесс введения примеси в полупроводник называется легированием, а примесный полупроводник - легированным.
W
Неподвижный, положительный ион атома
мышьяка, образованный в результате отрыва 5го «лишнего» валентного электрона.
Ge
4
4
Ge
5
4
Ge
4
4
Ge
4
As
4
Ge
Ge
4
Ge
Дырка, образованная в результате
отрыва ковалентного электрона.
Ge
Wc
Э
н Wз
е
р
г
и
я
W
WFn
Wд
Wv
0
F(W)
0,5
1
Примеси отдающие лишний электрон и
обусловливающие электронную
проводимость называются донорными.
Ион примеси не является носителем
заряда, он неподвижен – это не
дырка.
17.
Уравнение n-полупроводникаКонцентрации электронов и дырок в полупроводнике типа n рассчитываются
также на основе статистики Ферми-Дирака.
n n N C e
WC WF n
k T
p n N V e
WF
n
WV
k T
где WFn – уровень Ферми в полупроводнике типа n, определяемый
Nд
выражением
WFn WC k T ln
NC
Величина Nд представляет собой концентрацию доноров. Из выражения
видно, что уровень Ферми лежит ниже уровня дна зоны проводимости.
Произведение концентраций электронов и дырок равно:
2
3
WV WC
WЗ
2
2
m
k
T
2
2 k T
n n p n N C N V e k T 2
e
n
i
h2
Уравнение полупроводника:
nn pn ni
2
18.
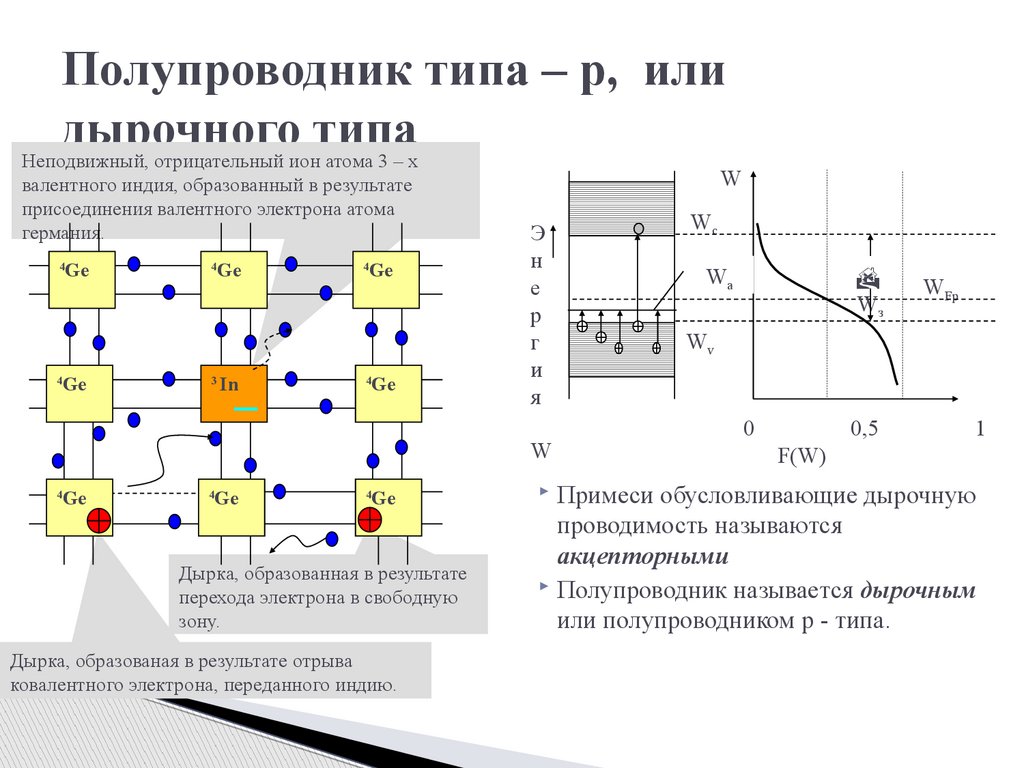
Полупроводник типа – p, илидырочного
типа
Неподвижный, отрицательный ион атома 3 – х
валентного индия, образованный в результате
присоединения валентного электрона атома
германия.
4
4
Ge
Ge
4
3
Ge
In
4
Ge
Ge
4
W
Э
н
е
р
г
и
я
W
4
Ge
4
Ge
Ge
4
Дырка, образованная в результате
перехода электрона в свободную
зону.
Дырка, образованая в результате отрыва
ковалентного электрона, переданного индию.
Wc
Wа
Wз
WFp
Wv
0
0,5
1
F(W)
Примеси обусловливающие дырочную
проводимость называются
акцепторными
Полупроводник называется дырочным
или полупроводником p - типа.
19.
Уравнение p-полупроводникаКонцентрации электронов и дырок в полупроводнике типа p рассчитываются
также на основе статистики Ферми-Дирака.
p p N V e
WF
p
WV
k T
n p N C e
WC WF p
k T
где WFp – уровень Ферми в полупроводнике типа p, определяемый выражением
N
WF p WV k T ln a
NV
Величина Nа представляет собой концентрацию акцепторов.
Так же как и для n – полупроводника, для полупроводников типа p справедливо
равенство:
n p p p ni
2
Это равенство означает, что произведение концентраций электронов и
дырок при данной температуре T для данного полупроводника постоянно и не
зависит от характера и количества примесей.
20.
Следствие из уравненияполупроводника
В силу симметрии выражений, определяющих концентрацию основных и неосновных
носителей заряда в примесных полупроводниках, независимо от типа проводимости, их
можно записать в следующем виде:
p N V e
W F WV
k T
n N C e
WC WF
k T
n p ni
2
где WF – уровень Ферми, определяемый для соответствующего типа полупроводника
Поделив эти выражения друг на друга, приняв при этом n = ni2 / p и p = ni2 / n, можно
WF WF i
WF i WF
привести их к следующему виду:
p n i e k T
n n i e k T
где WFi = (Wc - Wv) / 2 – уровень Ферми в собственном полупроводнике, а WF – уровень
Ферми в соответствующем примесном полупроводнике.
Учитывая, что энергия электрона (дырки) W = q·φ, последние выражения для дырок и
F i F
F F i
электронов соответственно можно привести к виду:
T
p n i e
n n i e T
φF i – потенциал Ферми в (вольтах) собственного полупроводника,
φF - потенциал Ферми в (вольтах) соответствующего собственного полупроводника,
φT = k·T/q – температурный потенциал (в вольтах). При комнатной
температуре φT =0,025В.
21.
Следствие из уравненияполупроводника (продолжение)
Заменим потенциал Ферми в собственном полупроводнике – φFi потенциалом
середины запрещённой зоны примесного полупроводника - φE, что
практически одно и то же, т.к. φFi ≈ φE.
F E
F
Тогда:
E
p n i e
T
n n i e
T
Из этих выражений непосредственно следует:
φFn = φE + φT · ln(n / n i ) – для полупроводников n – типа уровень Ферми
смещён от середины запрещённой зоны вверх по диаграмме к свободной зоне
на величину ln(n / n i ).
φFp = φE - φT · ln(p / n i ) – для полупроводников p – типа уровень Ферми
смещён от середины запрещённой зоны вниз по диаграмме к валентной зоне
на величину ln(p / n i ) .
22.
Электропроводность примесныхполупроводников
q p p q n n
в электронном полупроводнике n>>p,
σn ≈ q·n·μn
в дырочном полупроводнике p>>n,
σp ≈ q·p·μp
23.
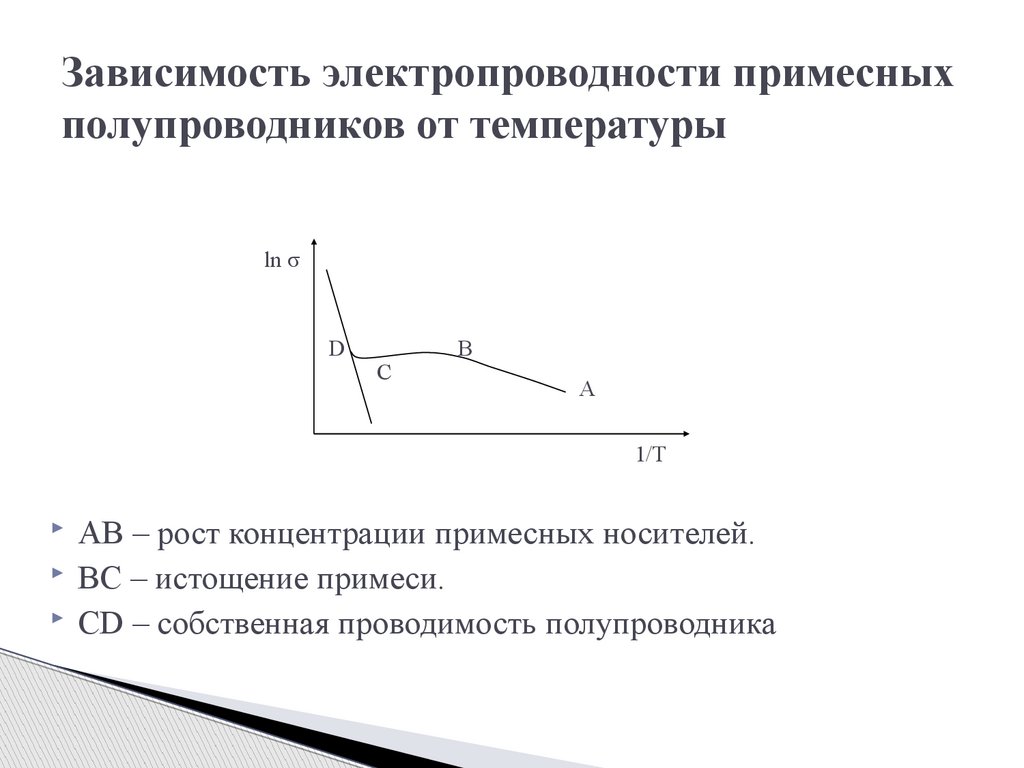
Зависимость электропроводности примесныхполупроводников от температуры
ln σ
D
C
B
A
1/T
AB – рост концентрации примесных носителей.
BC – истощение примеси.
CD – собственная проводимость полупроводника
24.
Электрический ток в примесномполупроводнике
Направленное перемещение под действием электрического поля –
дрейфовый ток.
jn др = q·n·μn·E
jp др = q·p·μp·E
Направленное перемещение носителей заряда вследствие разности
концентраций зарядов в смежных областях полупроводника –
диффузионный ток.
jn диф. = q·Dn·grad n
jp диф. = -q·Dp·grad p
Полная плотность электронного и дырочного тока :
J q n n E q Dn grad n q p p E q D p grad p
















 Физика
Физика








