Похожие презентации:
Сечение тел плоскостью. (11 класс)
1. СЕЧЕНИЕ ТЕЛ ПЛОСКОСТЬЮ
Урок геометрии в11 классе.
Рахмеева Л.А.
2.
Тема: Построение сеченийпризмы и пирамиды
Цели:
Знакомство с методами построения сечений многогранников плоскостью,
видов сечений.
Формирование умений и навыков при решении задач на построение.
Изучение методов и основных понятий, систематизация заданий и
упражнений на построение.
Практическое применение умений и навыков при решении задач на
построение.
1.
2.
3.
4.
Методы:
1.
2.
3.
Демонстрация наглядных и электронных пособий.
Выполнение практических работ.
Устный рассказ.
3.
Содержание урокаI. Сообщение учащимся темы, целей и задач урока.
II. Рассказ учителя о значении задач на построение сечений
многогранников в курсе геометрии.
III. Разбор и объяснение темы.
а) Виды сечений и их использование в различных областях науки.
(использование мультимедийной презентации)
б) Основные методы построения сечений в курсе геометрии 10-го
класса.
в) Разбор примера построения сечения пирамиды с использованием
наглядного пособия.
IV. Первичное закрепление.
а) Разбор задачи, выполненной учащимся в качестве
дополнительного задания.
б) Решение и разбор задачи на доске.
V. Подведение итогов урока. Объяснение домашнего задания.
4. Примеры сечения
Продольное сечениедетали.
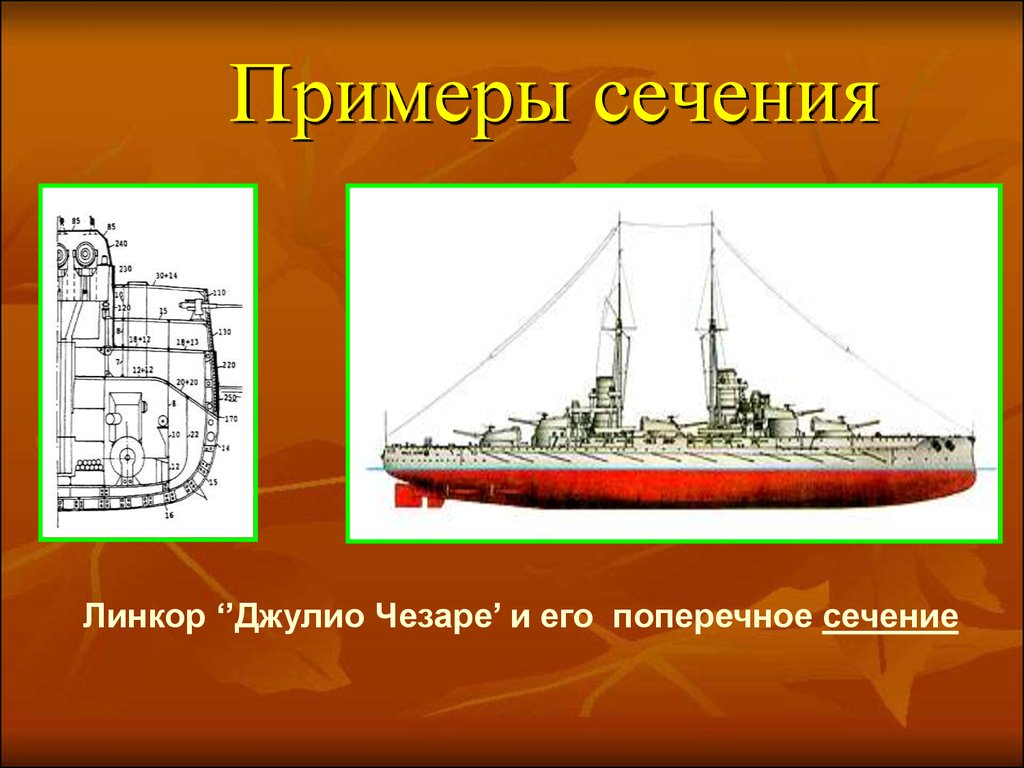
5. Примеры сечения
Линкор ‘’Джулио Чезаре’ и его поперечное сечение6. Примеры сечения
Трос биметаллический. Поперечное сечение.7. Примеры сечения
Вид внутринности дома всечении.
8. Примеры сечения
План крепости.Сечение по первому этажу.
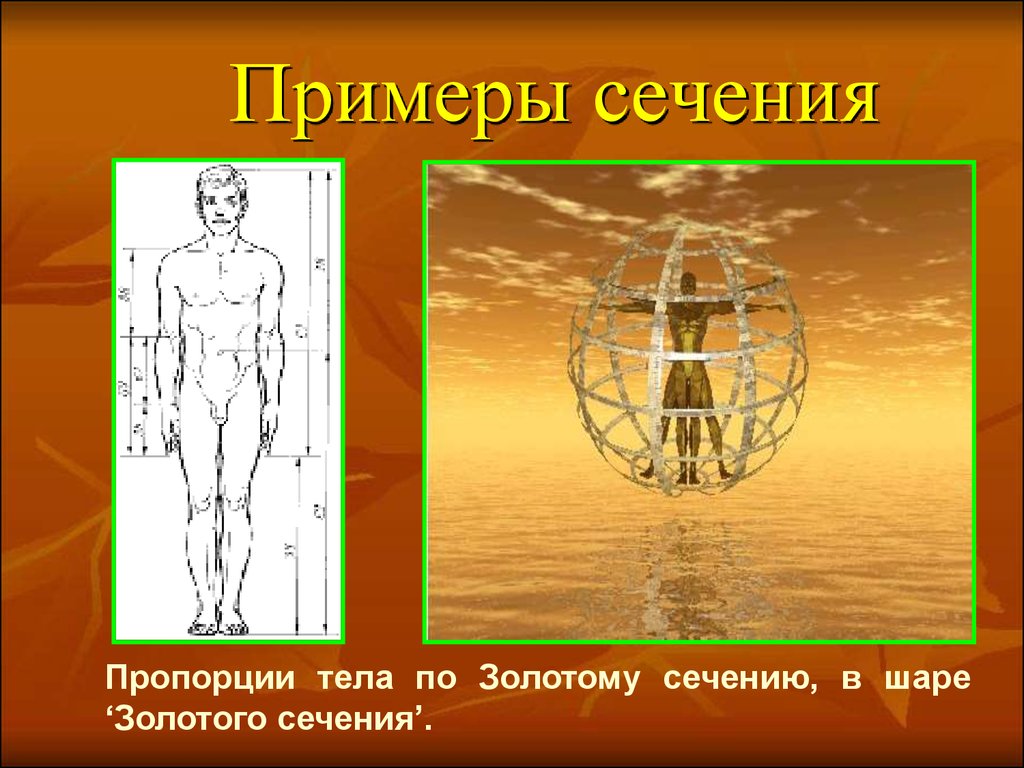
9. Примеры сечения
Пропорции тела по Золотому сечению, в шаре‘Золотого сечения’.
10.
Методы построения сечений1. Метод следов.
2. Метод внутреннего проектирования.
3. Комбинированный метод.
11.
ОПРЕДЕЛЕНИЕСечением поверхности геометрических
тел плоскостью называется плоская
фигура,
полученная
в
результате
пересечения
тела
плоскостью
и
содержащая точки, принадлежащие как
поверхности тела, так и секущей
плоскости.
12. Пример След секущей плоскости пересекает нижнюю грань многогранника
Сечение по трем точкамПример
След секущей плоскости
пересекает нижнюю грань
многогранника
13.
Демо - эскизПризма
Три
данные
точки на
боковых
ребрах
Сечение
Плоскость основания
14.
•Секущая плоскостьпересекает грани
многогранника по
прямым, а точнее по
отрезкам - разрезам.
•Так как секущая
плоскость идет
непрерывно, то разрезы
образуют замкнутую
фигуру-многоугольник.
•Полученный таким
образом многоугольник и
будет сечением тела.
15.
Шаг 1: Разрезаем грани KLBA иL
LMCB
• Проводим через
точки F и O прямую
FO.
F
K
• Отрезок FO есть
разрез грани KLBA
секущей плоскостью.
•Аналогичным образом
отрезок FG есть разрез
грани LMCB.
M
N
G
B
O
A
C
D
16.
Шаг2: Ищем след секущей плоскости на плоскостиоснования
L
F
• Проводим прямую АВ до
пересечения с прямой FO.
• Получим точку H, которая
принадлежит и секущей
плоскости, и плоскости
основания.
• Аналогичным образом
получим точку R.
• Через точки H и R
проводим прямую HR –
след секущей плоскости
H
M
K
N
G
B
O
A
C
R
D
17.
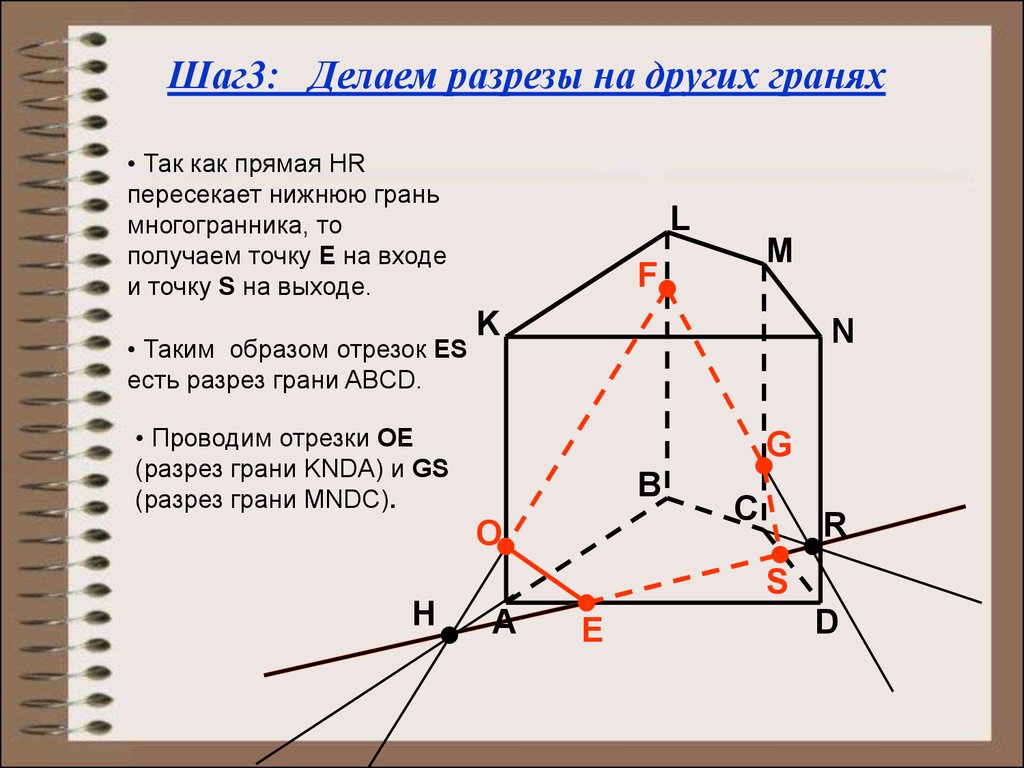
Шаг3: Делаем разрезы на других гранях• Так как прямая HR
пересекает нижнюю грань
многогранника, то
получаем точку E на входе
и точку S на выходе.
• Таким образом отрезок ES
есть разрез грани ABCD.
L
M
F
K
N
• Проводим отрезки ОЕ
(разрез грани KNDA) и GS
(разрез грани MNDC).
G
B
O
C
R
S
H
A
E
D
18.
Шаг4: Выделяем сечение многогранникаL
•Все разрезы
образовали
пятиугольник OFGSE,
который и является
сечением призмы
плоскостью,
проходящей через
точки O, F, G.
M
F
K
N
G
B
O
C
S
A
E
D
19.
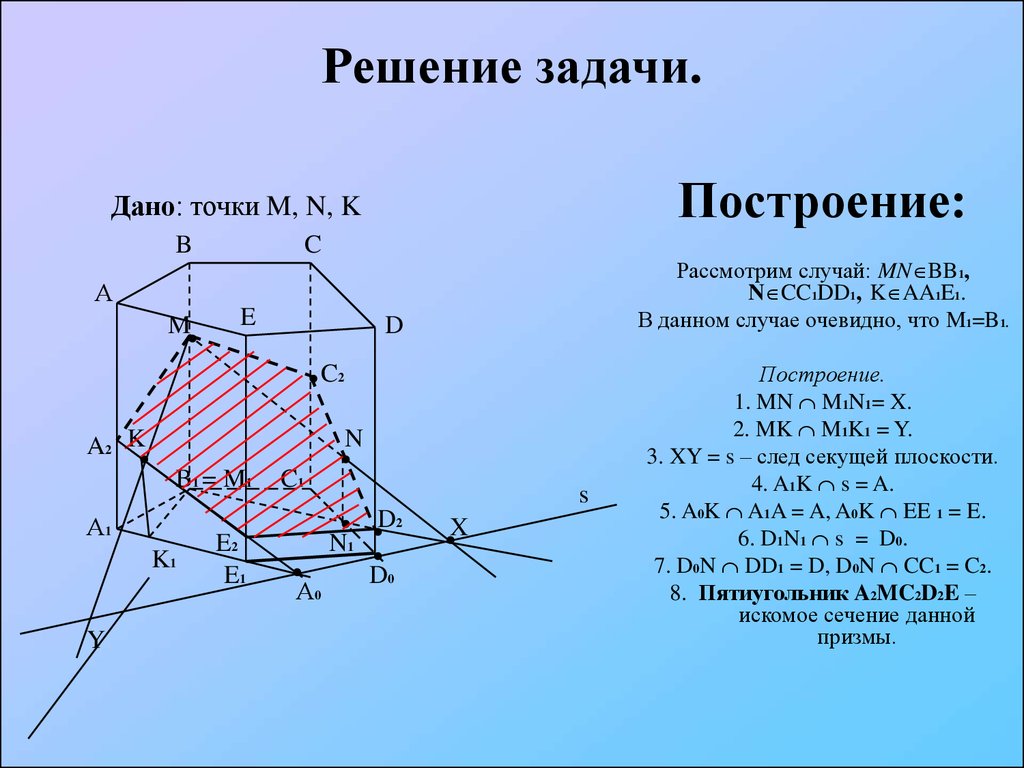
Решение задачи.Построение:
Дано: точки M, N, K
B
C
Рассмотрим случай: MN BB1,
N CC1DD1, K AA1E1.
В данном случае очевидно, что M1=B1.
А
M
E
D
C2
A2 K
N
B1 = M1
s
D2
А1
K1
Y
C1
E2
E1
N1
А0
D0
X
Построение.
1. MN M1N1= X.
2. MK M1K1 = Y.
3. XY = s – след секущей плоскости.
4. A1K s = A.
5. A0K A1A = A, A0K EE 1 = E.
6. D1N1 s = D0.
7. D0N DD1 = D, D0N CC1 = C2.
8. Пятиугольник A2MC2D2E –
искомое сечение данной
призмы.
20.
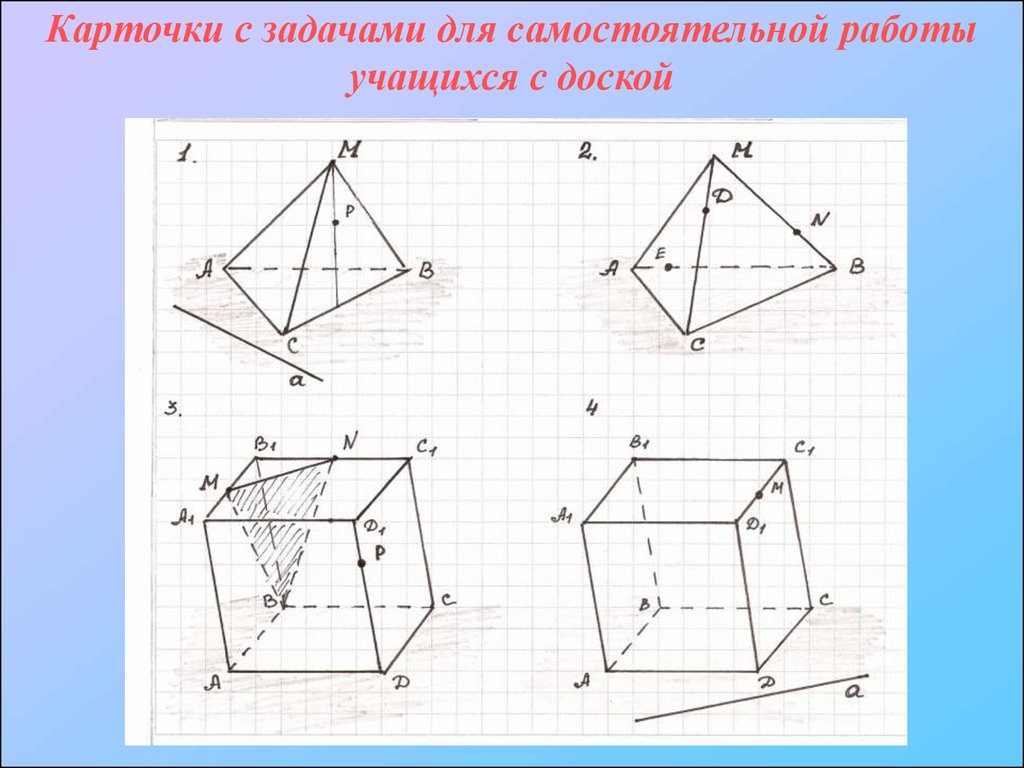
Карточки с задачами для cамостоятельной работыучащихся с доской
21.
Итог урокаа) Обобщение темы урока.
б) Вопросы по ведению урока.
в) Домашнее задание:
§ 4, пункт 14, задачи: 79, 81
















 Математика
Математика








