Построение сечений многогранников

1. Построение сечений многогранников

2.

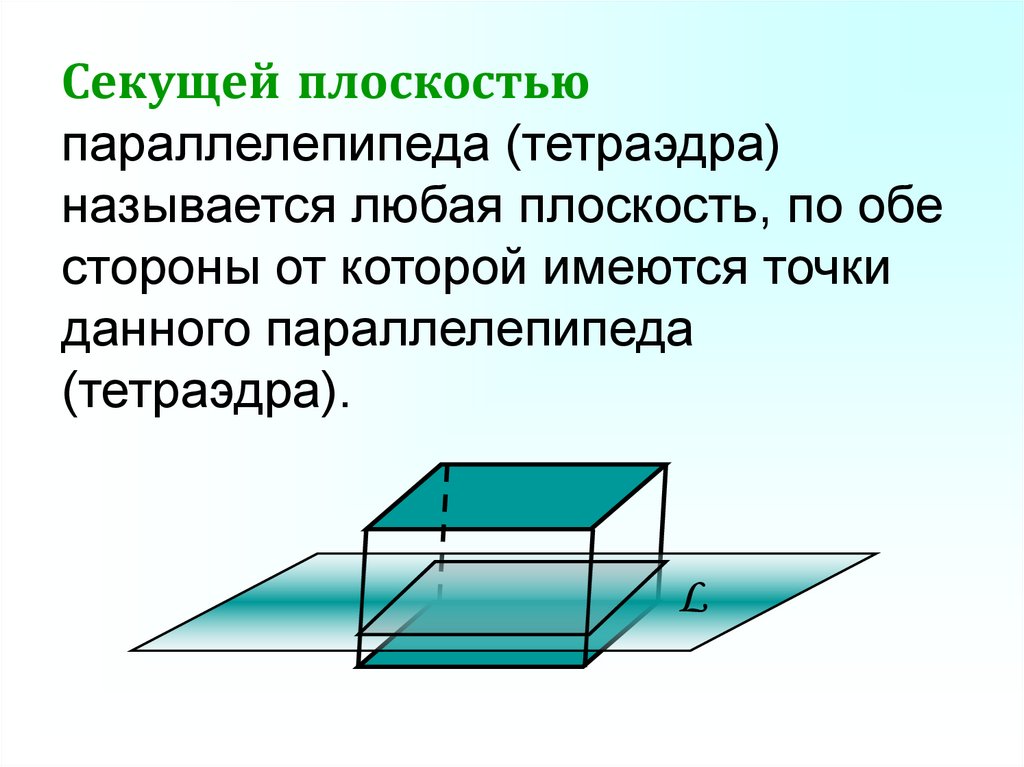
Секущей плоскостью
параллелепипеда (тетраэдра)
называется любая плоскость, по обе
стороны от которой имеются точки
данного параллелепипеда
(тетраэдра).
L

3.

Построить сечение многогранника
плоскостью – это значит указать
точки пересечения секущей плоскости с
ребрами многогранника и соединить эти
точки отрезками, принадлежащими граням
многогранника.
Для построения сечения многогранника
плоскостью нужно в плоскости каждой
грани указать 2 точки, принадлежащие
сечению, соединить их прямой и найти
точки пересечения этой прямой с ребрами
многогранника.

4.

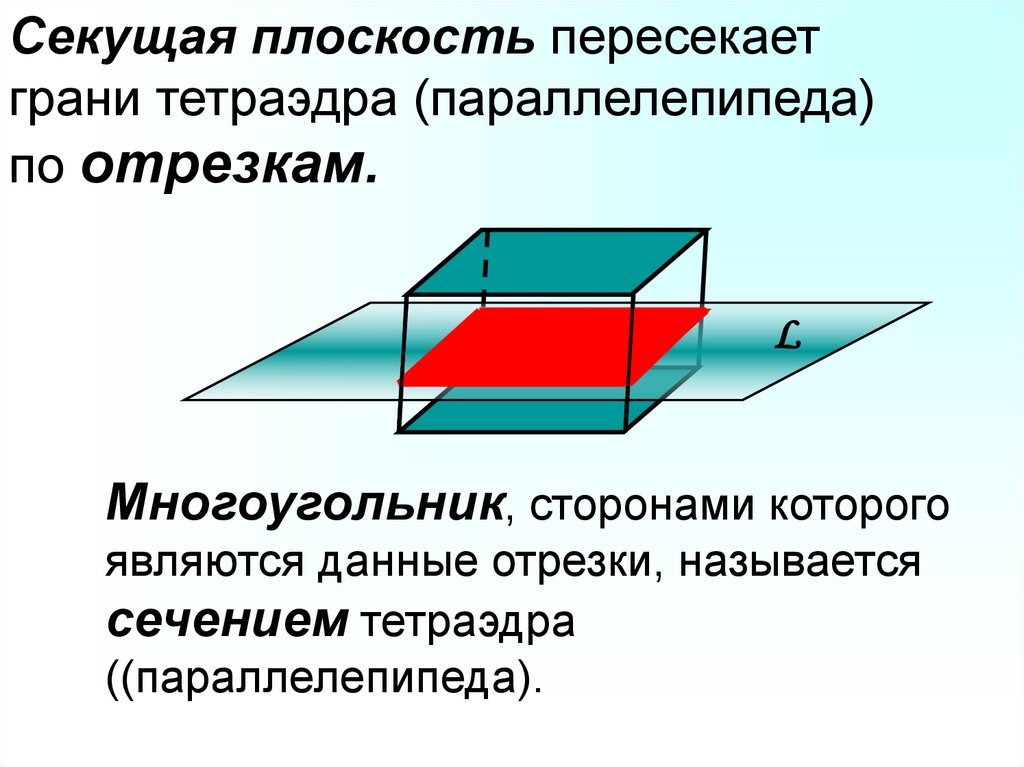
Секущая плоскость пересекает
грани тетраэдра (параллелепипеда)
по отрезкам.
L
Многоугольник, сторонами которого
являются данные отрезки, называется
сечением тетраэдра
((параллелепипеда).

5.

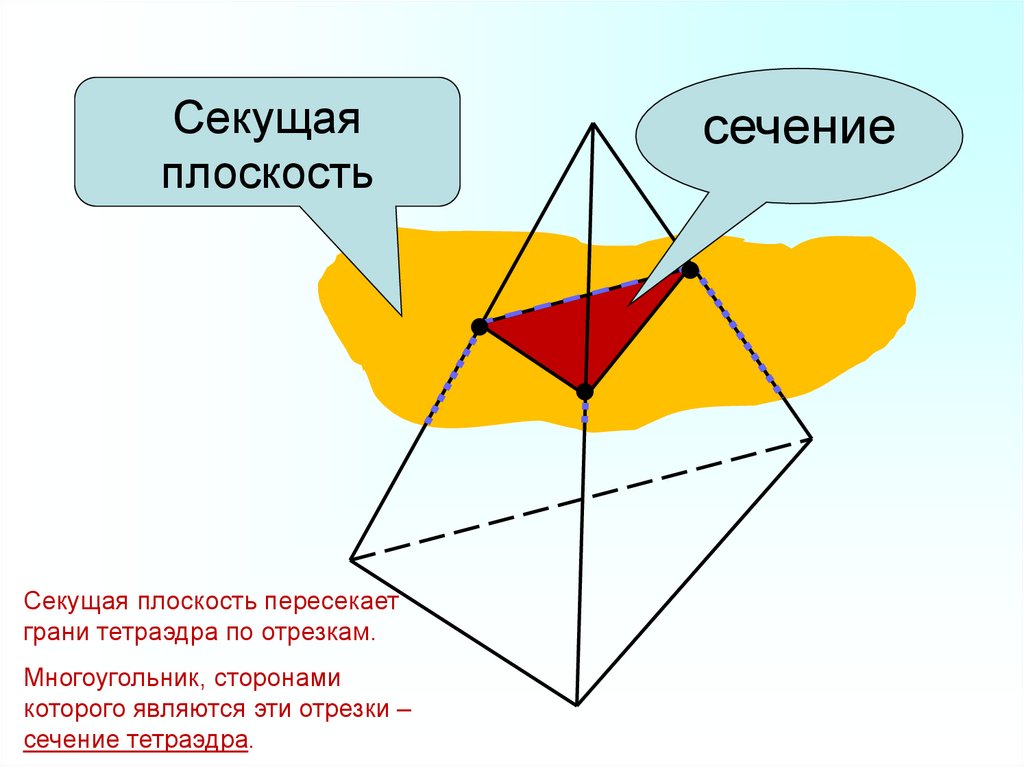
Секущая
плоскость
Секущая плоскость пересекает
грани тетраэдра по отрезкам.
Многоугольник, сторонами
которого являются эти отрезки –
сечение тетраэдра.
сечение

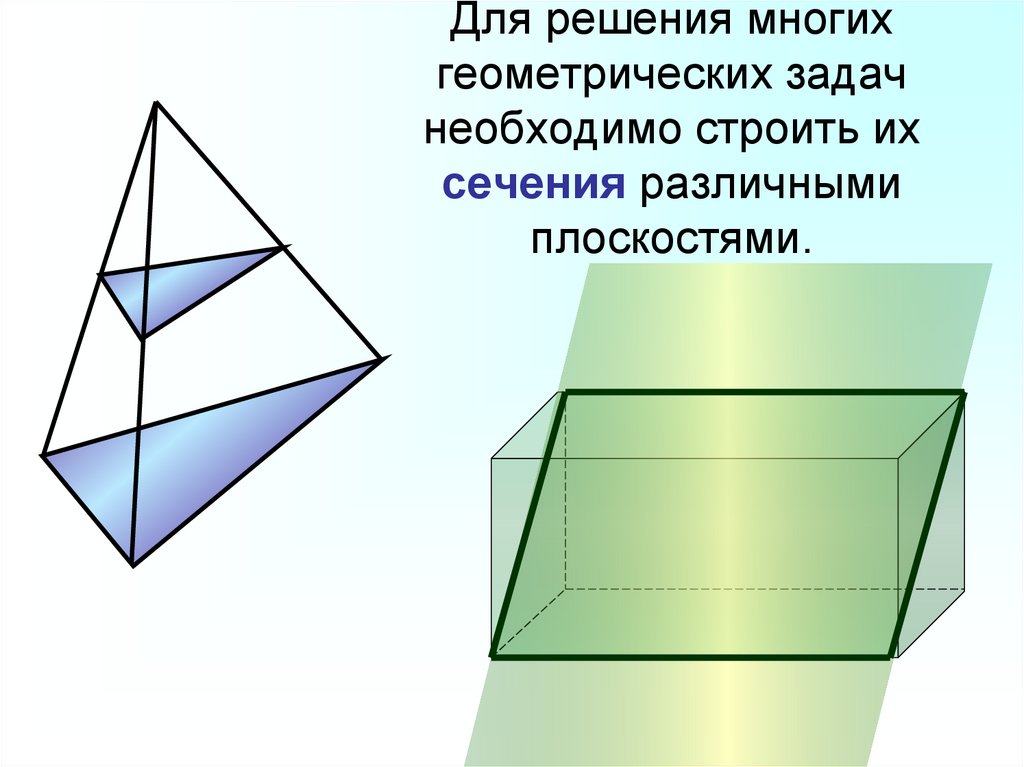
6. Для решения многих геометрических задач необходимо строить их сечения различными плоскостями.

7. При этом необходимо учитывать следующее:

Для построения сечения нужно построить
точки пересечения секущей плоскости с
ребрами и соединить их отрезками.
При этом необходимо учитывать
следующее:
1. Соединять можно только две точки, лежащие
в плоскости одной грани.
2. Секущая плоскость пересекает
грани по параллельным отрезкам.
параллельные
3. Если в плоскости грани отмечена только одна точка,
принадлежащая плоскости сечения, то надо построить
дополнительную точку. Для этого необходимо найти
точки пересечения уже построенных прямых с другими
прямыми, лежащими в тех же гранях.

8.

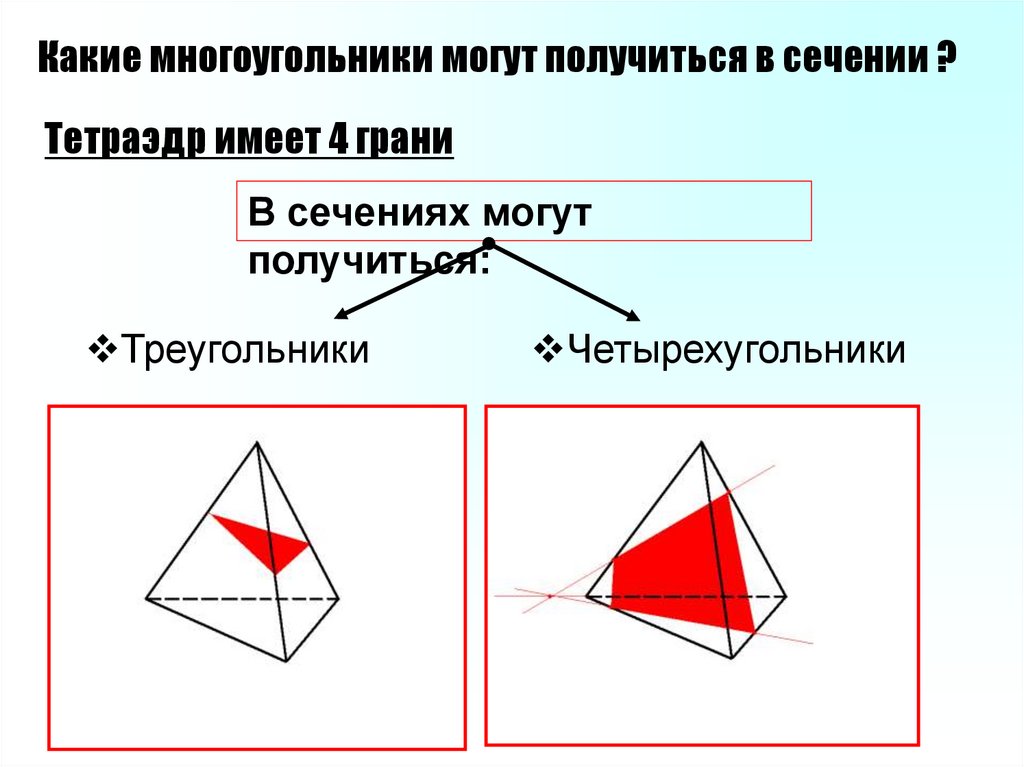
Какие многоугольники могут получиться в сечении ?
Тетраэдр имеет 4 грани
В сечениях могут
получиться:
Треугольники
Четырехугольники

9.

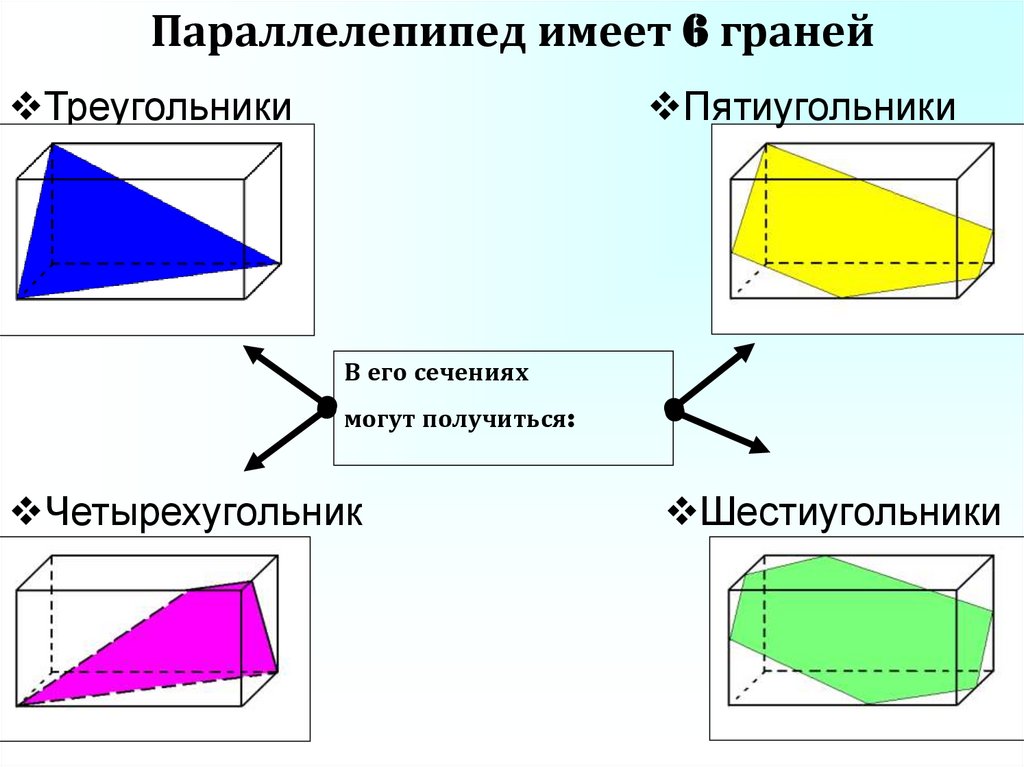
Параллелепипед имеет 6 граней
Треугольники
Пятиугольники
В его сечениях
могут получиться:
Четырехугольник
и
Шестиугольники

10. Блиц - опрос

• Задача блиц – опроса:
ответить на вопросы и
обосновать ответ с помощью
аксиом, теорем и свойств
параллельных плоскостей.

11.

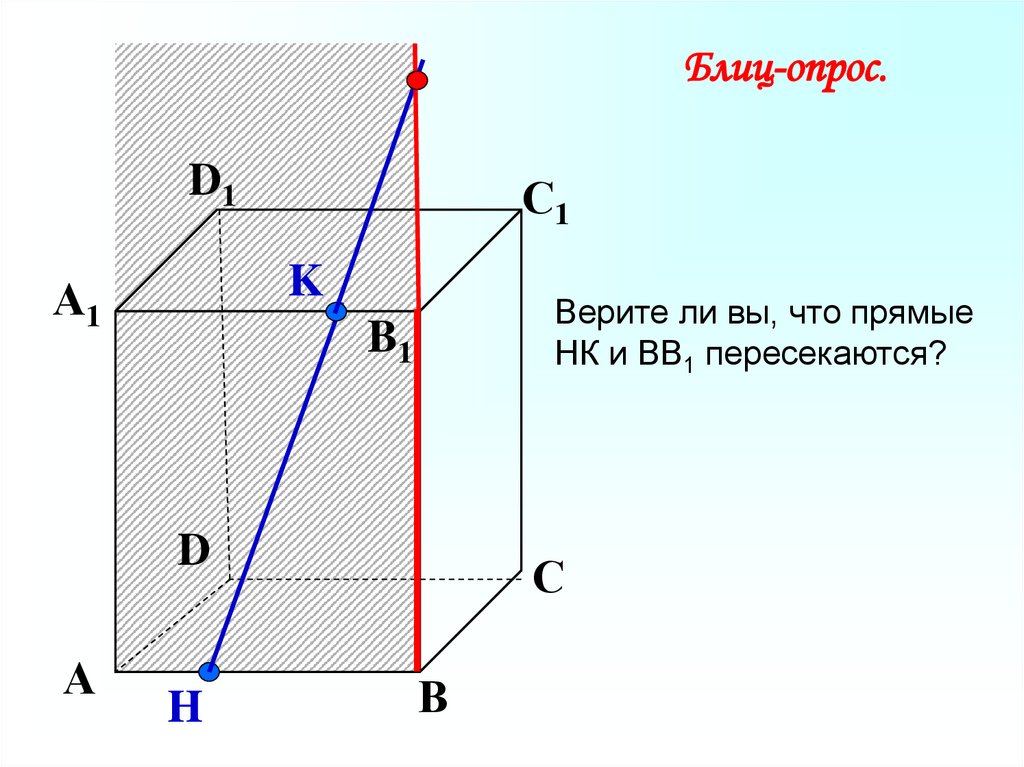
Блиц-опрос.
D1
С1
K
А1
Верите ли вы, что прямые
НК и ВВ1 пересекаются?
B1
D
А
H
С
В

12.

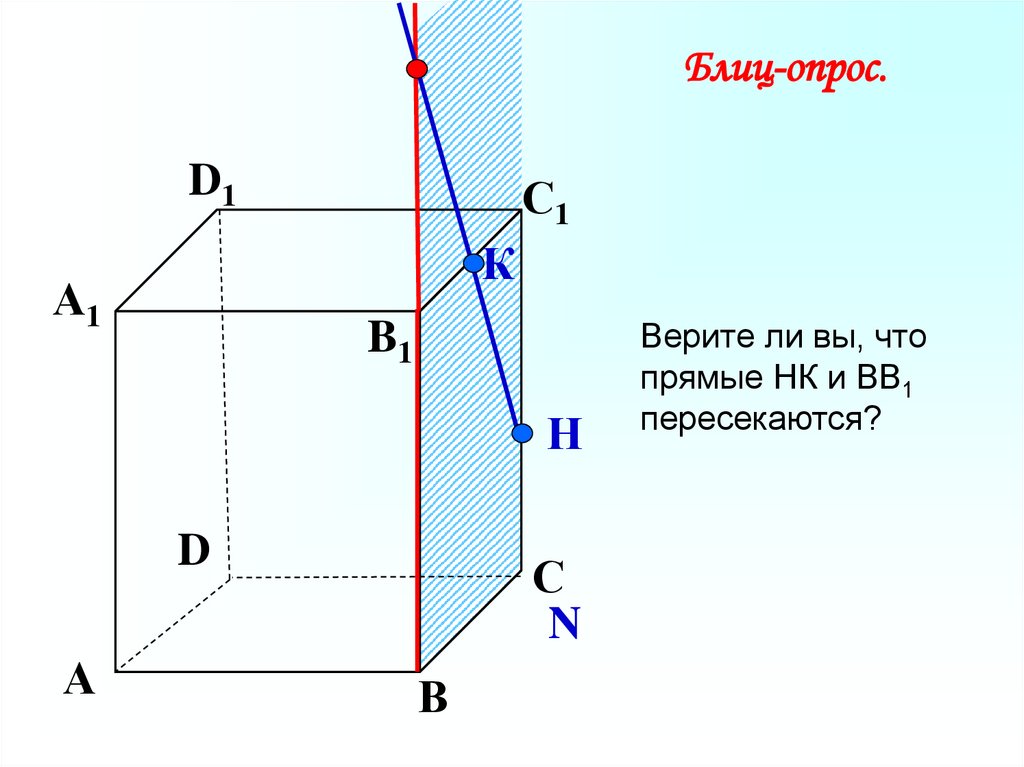
Блиц-опрос.
D1
С1
К
А1
B1
Н
D
А
С
N
В
Верите ли вы, что
прямые НК и ВВ1
пересекаются?

13.

Блиц-опрос.
D1
А1
К
А
С1
М
B1
Н
D
В
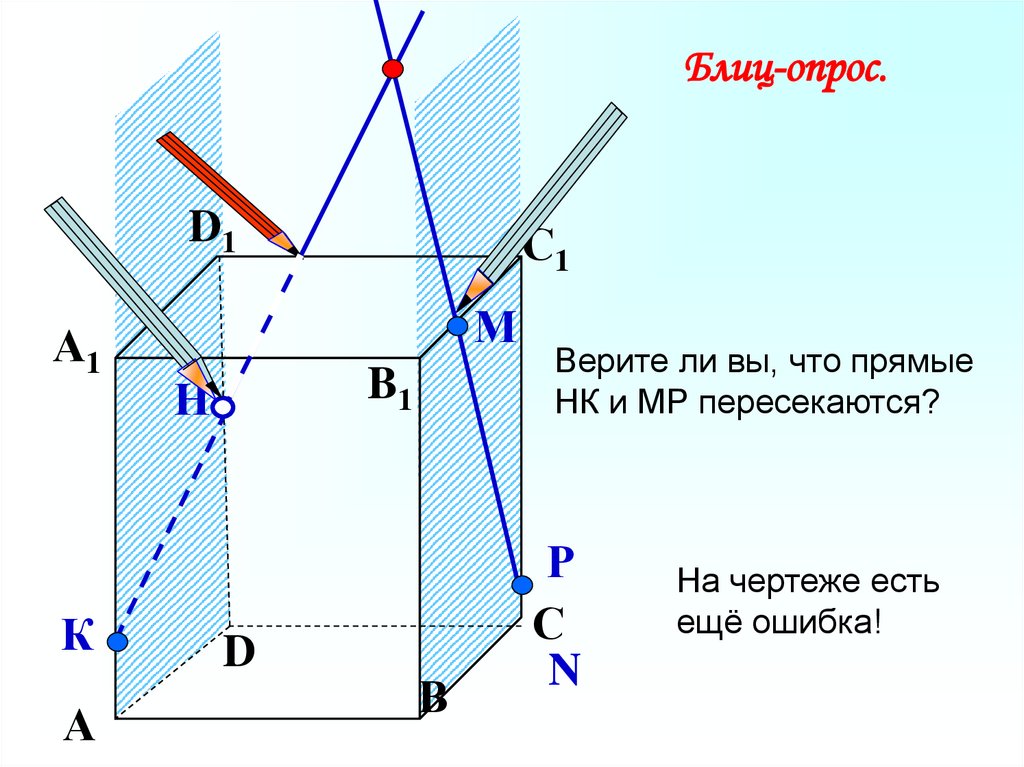
Верите ли вы, что прямые
НК и МР пересекаются?
Р
С
N
На чертеже есть
ещё ошибка!

14.

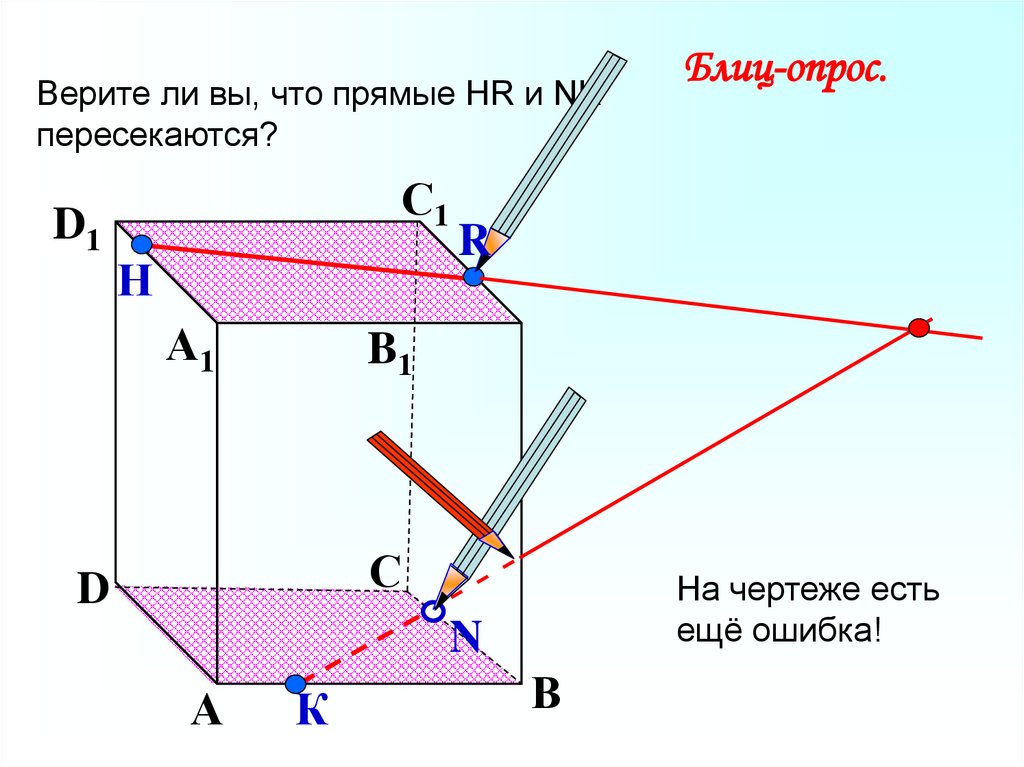
Верите ли вы, что прямые НR и NK
пересекаются?
D1
С1
Н
А1
R
B1
С
D
На чертеже есть
ещё ошибка!
N
А
Блиц-опрос.
К
В

15.

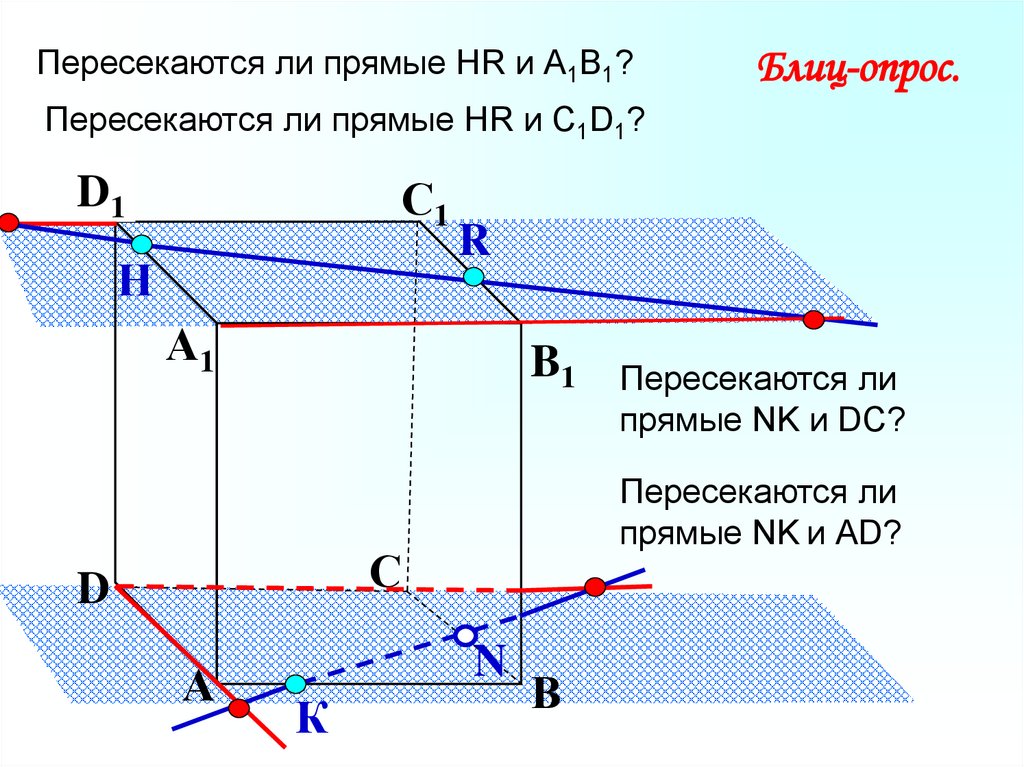
Пересекаются ли прямые НR и А1В1?
Блиц-опрос.
Пересекаются ли прямые НR и С1D1?
С1
D1
Н
R
А1
B1
Пересекаются ли
прямые NK и АD?
С
D
А
N
К
Пересекаются ли
прямые NK и DC?
В

16.

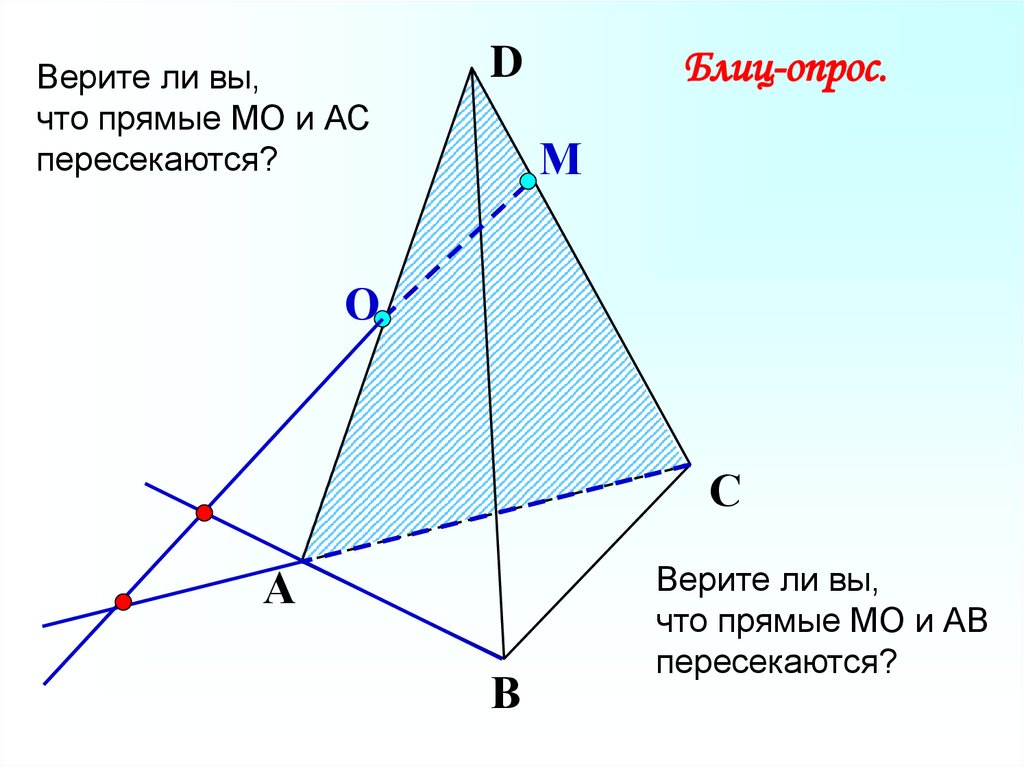
Верите ли вы,
что прямые МО и АС
пересекаются?
Блиц-опрос.
D
М
О
С
А
В
Верите ли вы,
что прямые МО и АВ
пересекаются?

17.

Умение решать задачи – практическое
искусство, подобное плаванию, или
катанию на лыжах … : научиться этому
можно лишь подражая избранным образцам
и постоянно тренируясь..
Д. Пойа

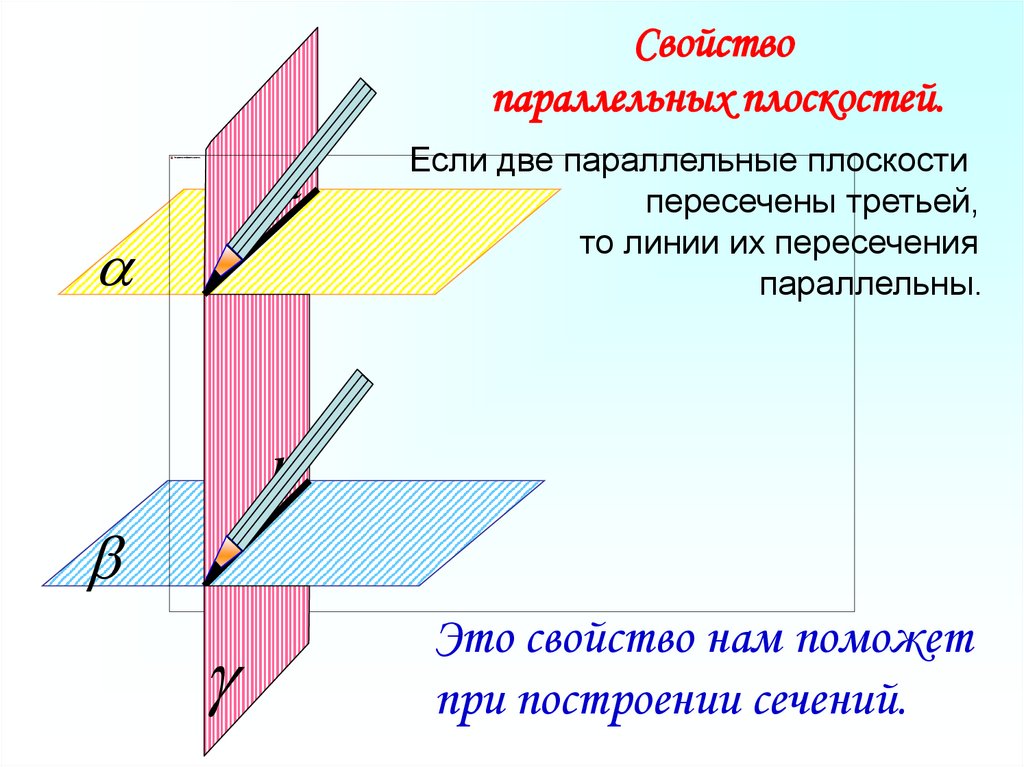
18.

Свойство
параллельных плоскостей.
а
Если две параллельные плоскости
пересечены третьей,
то линии их пересечения
параллельны.
b
Это свойство нам поможет
при построении сечений.

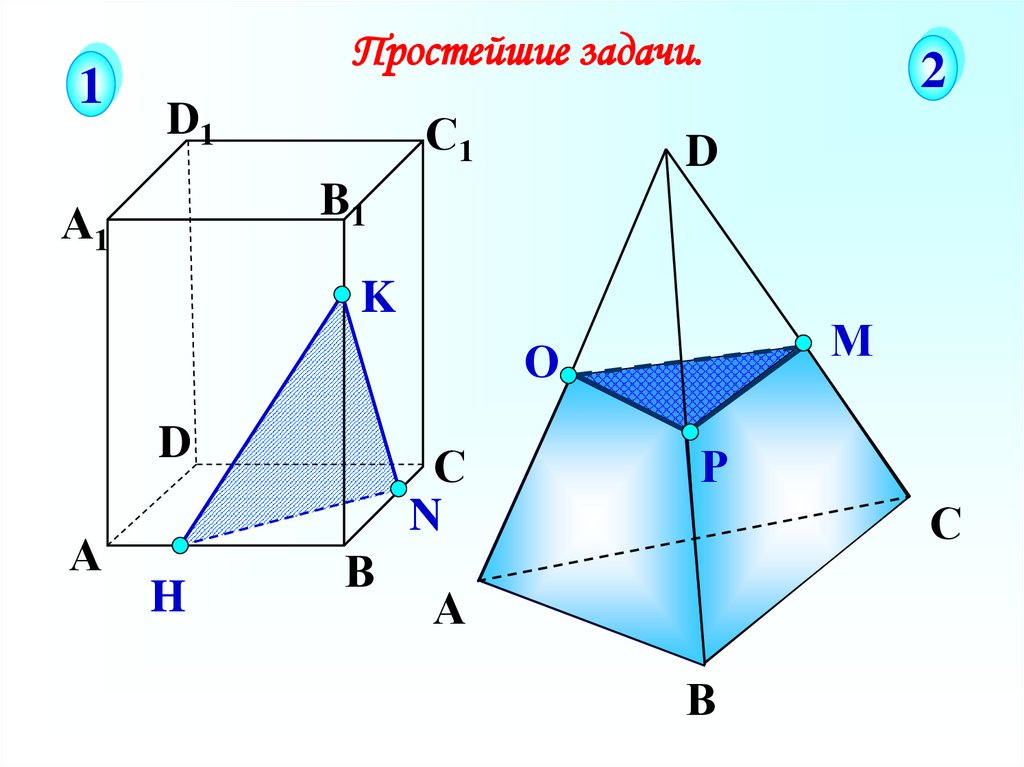
19.

1
Простейшие задачи.
D1
С1
D
B1
А1
K
М
О
D
А
2
H
С
N
В
Р
С
А
В

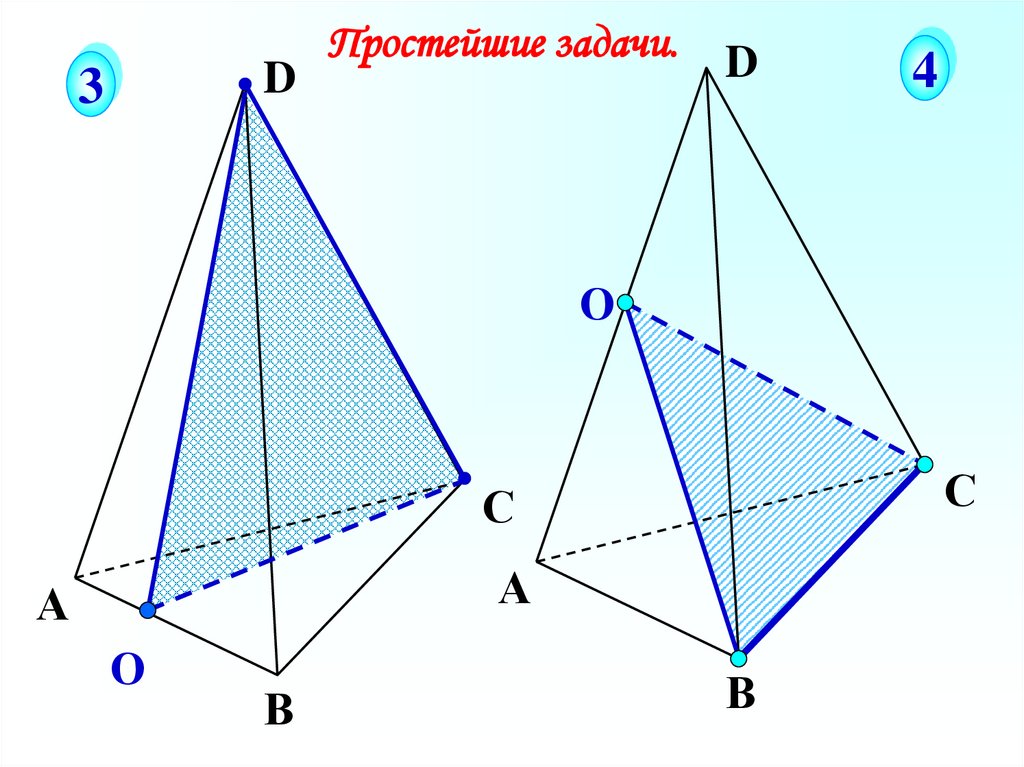
20.

D
3
Простейшие задачи.
D
4
О
С
С
А
А
О
В
В

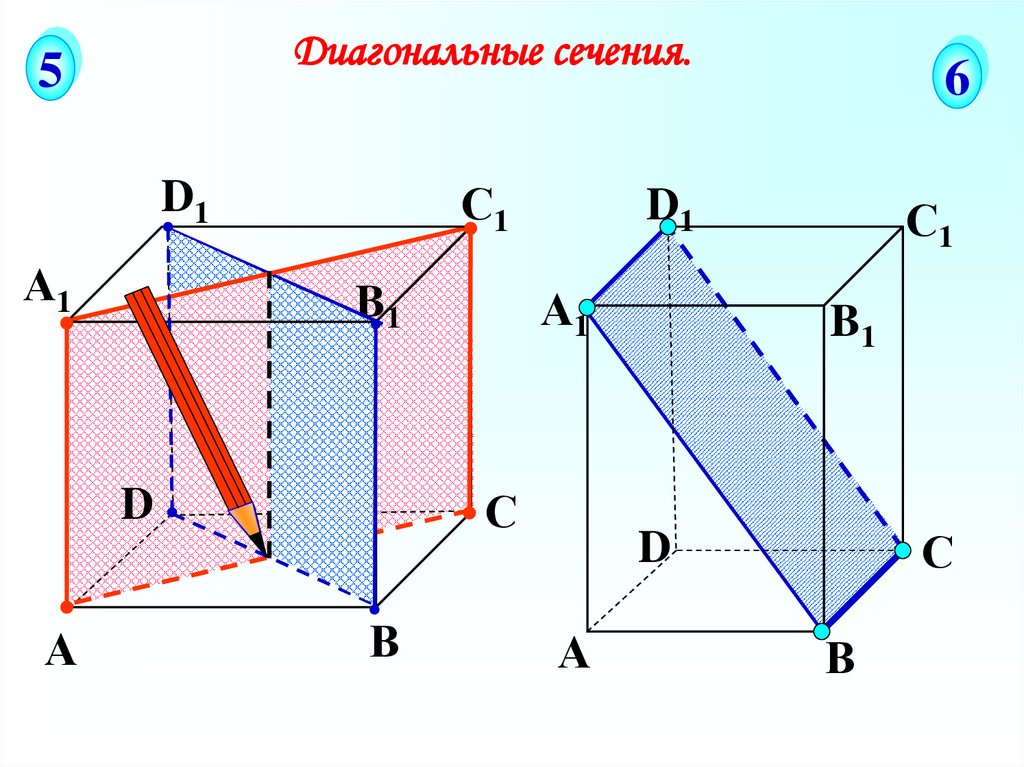
21.

Диагональные сечения.
5
С1
D1
А1
С
D
А
D1
А1
B1
В
6
С1
B1
С
D
А
В

22.

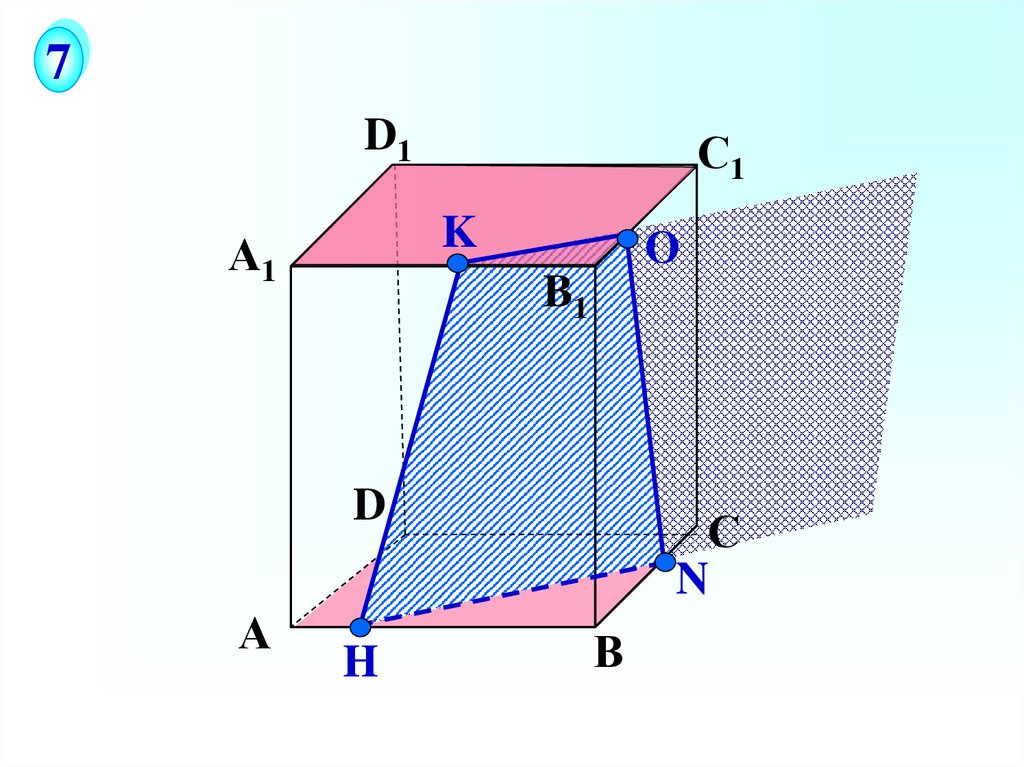
7
D1
С1
K
А1
О
B1
D
А
H
С
N
В

23. Аксиоматический метод

Метод следов
Суть метода заключается в построении
вспомогательной прямой, являющейся изображением
линии пересечения секущей плоскости с плоскостью
какой-либо грани фигуры . Удобнее всего строить
изображение линии пересечения секущей плоскости с
плоскостью нижнего основания. Эту линию называют
следом секущей плоскости. Используя след, легко
построить изображения точек секущей плоскости,
находящихся на боковых ребрах или гранях фигуры .

24.

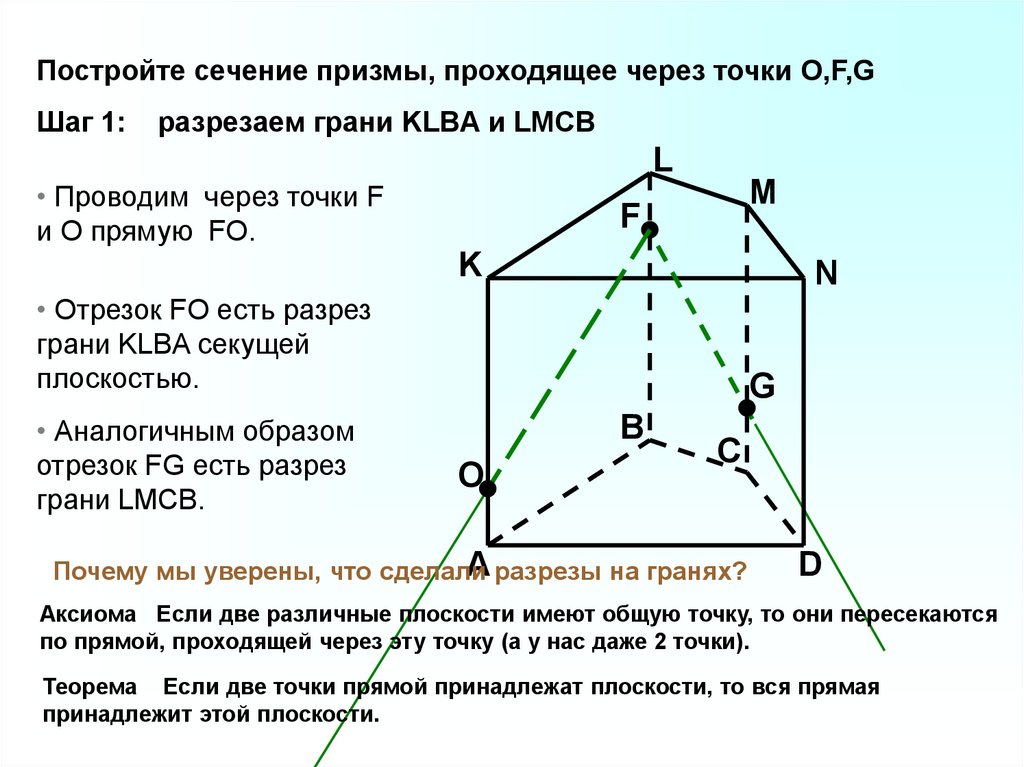
Постройте сечение призмы, проходящее через точки O,F,G
Шаг 1:
разрезаем грани KLBA и LMCB
L
• Проводим через точки F
и O прямую FO.
M
F
K
N
• Отрезок FO есть разрез
грани KLBA секущей
плоскостью.
• Аналогичным образом
отрезок FG есть разрез
грани LMCB.
G
B
O
C
A разрезы на гранях?
Почему мы уверены, что сделали
D
Аксиома Если две различные плоскости имеют общую точку, то они пересекаются
по прямой, проходящей через эту точку (а у нас даже 2 точки).
Теорема Если две точки прямой принадлежат плоскости, то вся прямая
принадлежит этой плоскости.

25.

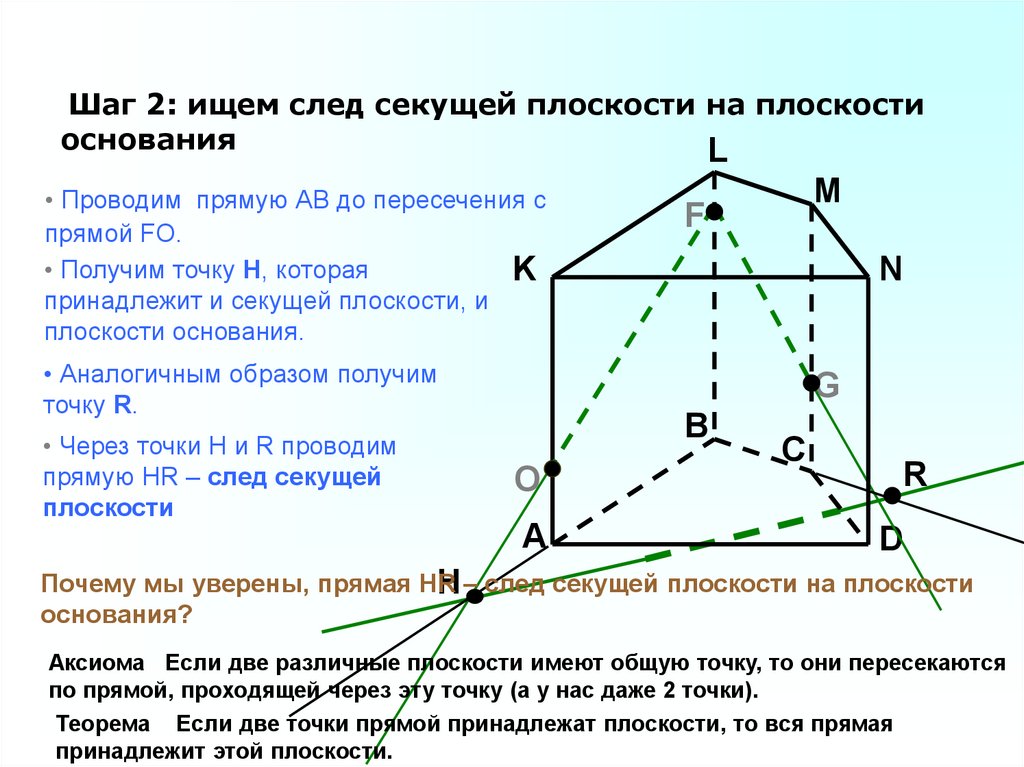
Шаг 2: ищем след секущей плоскости на плоскости
основания
L
• Проводим прямую АВ до пересечения с
прямой FO.
• Получим точку H, которая
K
принадлежит и секущей плоскости, и
плоскости основания.
• Аналогичным образом получим
точку R.
• Через точки H и R проводим
прямую HR – след секущей
плоскости
M
F
N
G
B
O
A
C
R
D
Почему мы уверены, прямая HR
H – след секущей плоскости на плоскости
основания?
Аксиома Если две различные плоскости имеют общую точку, то они пересекаются
по прямой, проходящей через эту точку (а у нас даже 2 точки).
Теорема Если две точки прямой принадлежат плоскости, то вся прямая
принадлежит этой плоскости.

26.

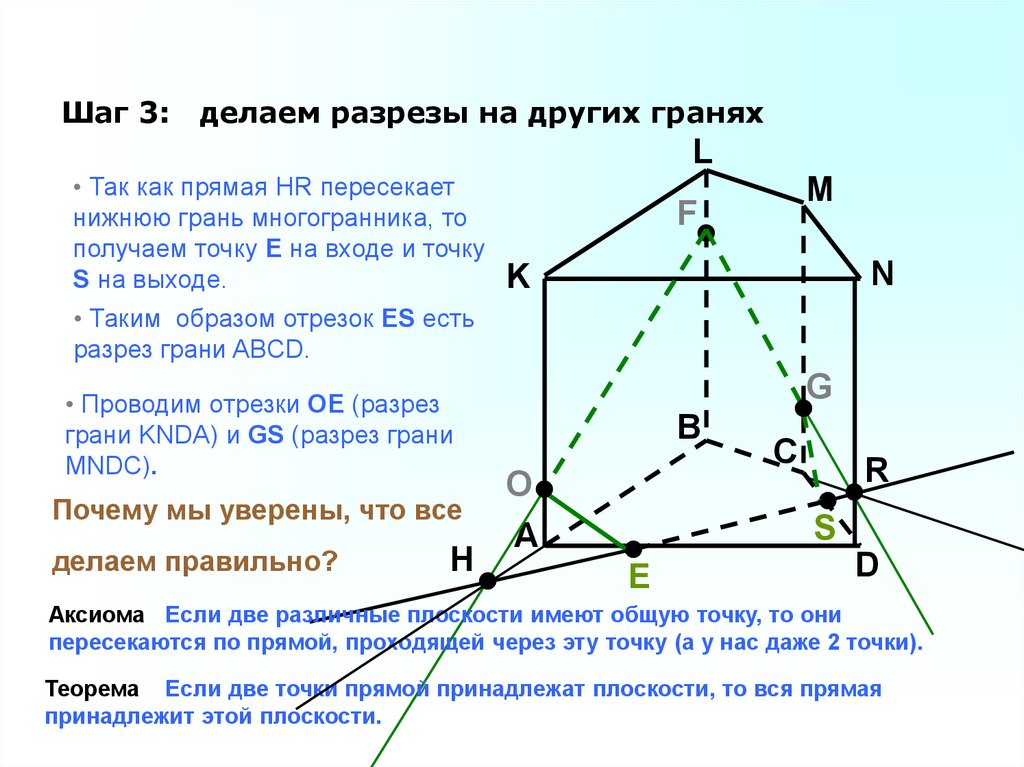
Шаг 3:
делаем разрезы на других гранях
L
• Так как прямая HR пересекает
нижнюю грань многогранника, то
получаем точку E на входе и точку
S на выходе.
M
F
N
K
• Таким образом отрезок ES есть
разрез грани ABCD.
• Проводим отрезки ОЕ (разрез
грани KNDA) и GS (разрез грани
MNDC).
Почему мы уверены, что все
делаем правильно?
H
G
B
O
A
C
R
S
E
D
Аксиома Если две различные плоскости имеют общую точку, то они
пересекаются по прямой, проходящей через эту точку (а у нас даже 2 точки).
Теорема Если две точки прямой принадлежат плоскости, то вся прямая
принадлежит этой плоскости.

27.

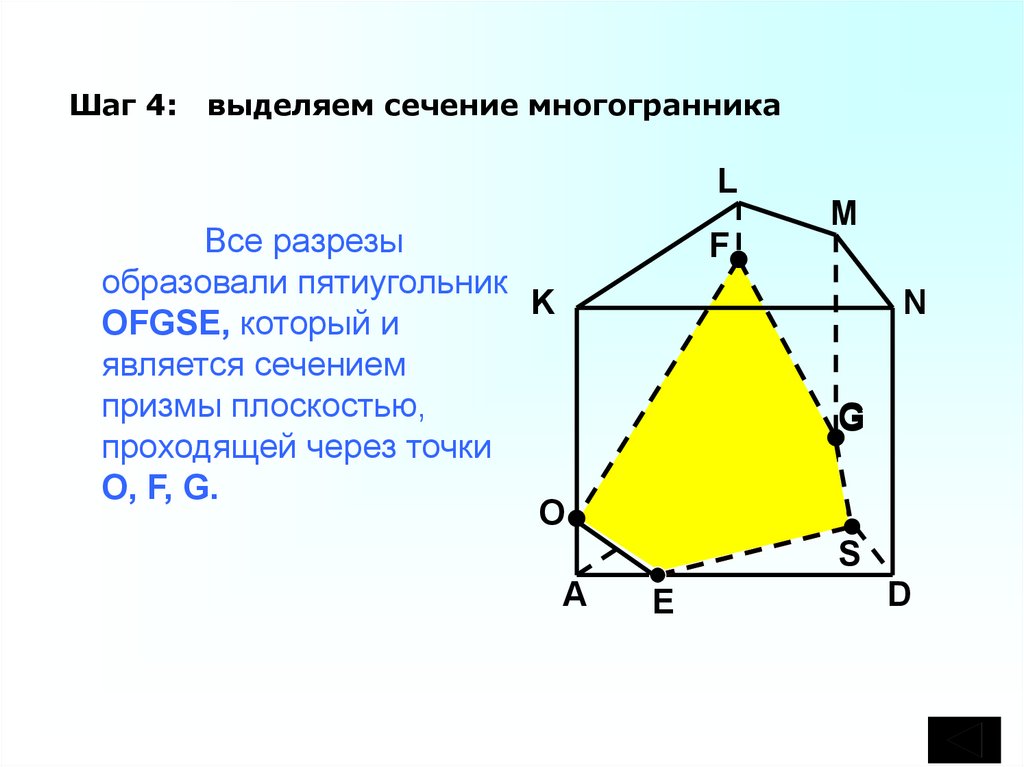
Шаг 4:
выделяем сечение многогранника
L
M
Все разрезы
образовали пятиугольник
K
OFGSE, который и
является сечением
призмы плоскостью,
проходящей через точки
O, F, G.
O
F
N
G
B
C
S
A
E
D

28.

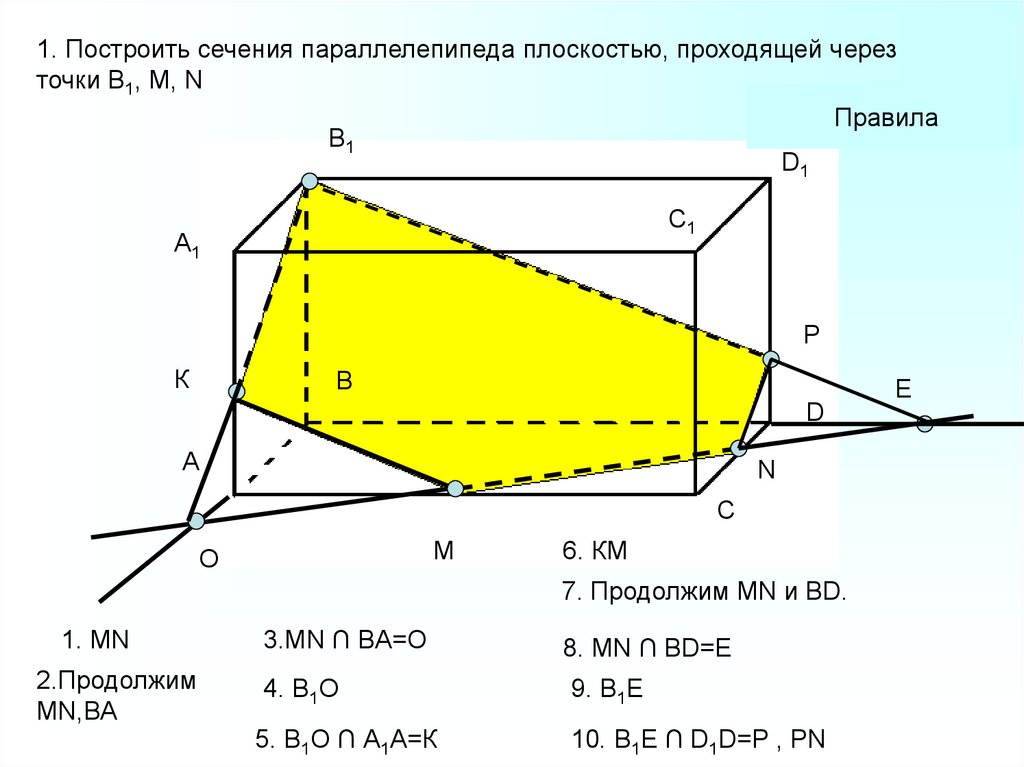
1. Построить сечения параллелепипеда плоскостью, проходящей через
точки В1, М, N
Правила
В1
D1
С1
A1
P
К
В
D
А
N
С
M
O
6. КМ
7. Продолжим MN и BD.
1. MN
2.Продолжим
MN,ВА
3.MN ∩ BA=O
8. MN ∩ BD=E
4. В1О
9. В1E
5. В1О ∩ А1А=К
10. B1Е ∩ D1D=P , PN
Е

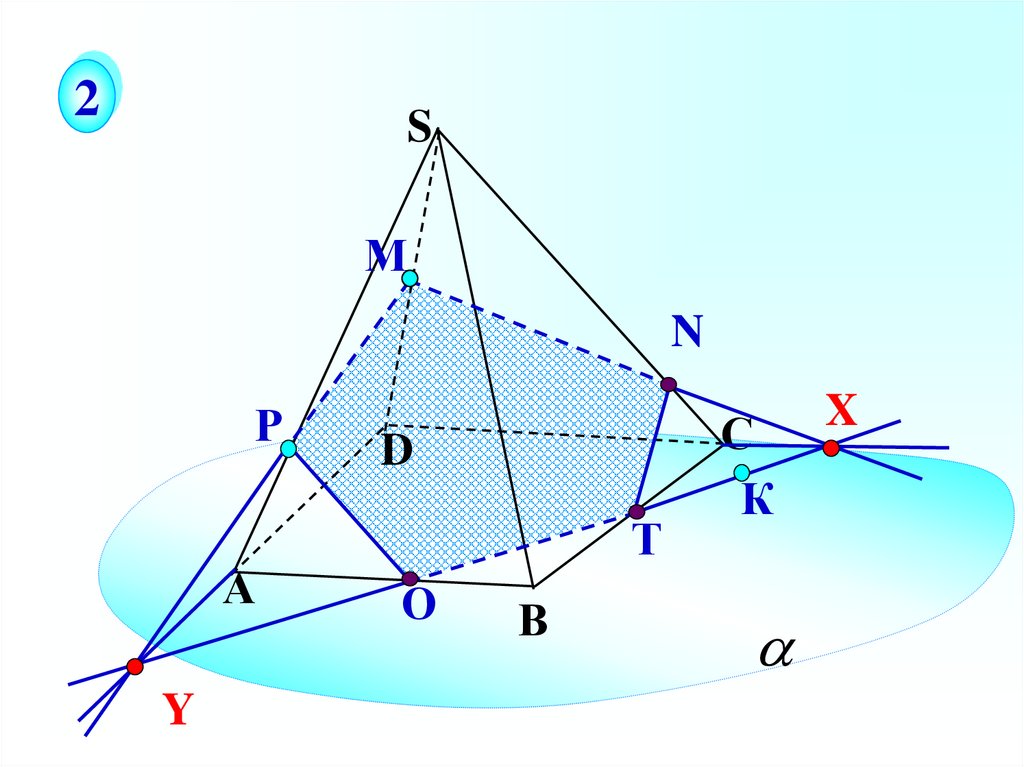
29.

2
S
М
N
Р
А
Y
D
Т
О
В
С
К
X

30. Правила для самоконтроля:

• Вершины сечения находятся только
на ребрах.
• Стороны сечения находятся только
на грани многогранника.
• Секущая плоскость пересекает грань
или плоскость грани, то только один
раз.

31.

Составить две
задачи на
построение сечений
многогранников с
использованием
полученных знаний.

32.

Если вы хотите научиться плавать, то
смело входите в воду, а если хотите
научиться решать задачи, то решайте
их
(Д. Пойа)