Программирование на языке Java

1. Программирование на языке Java

16. Решение уравнений
17. Вычисление площади (интеграла)
18. Вычисление длины кривой

2. Программирование на языке Java

Тема 16. Решение уравнений

3.

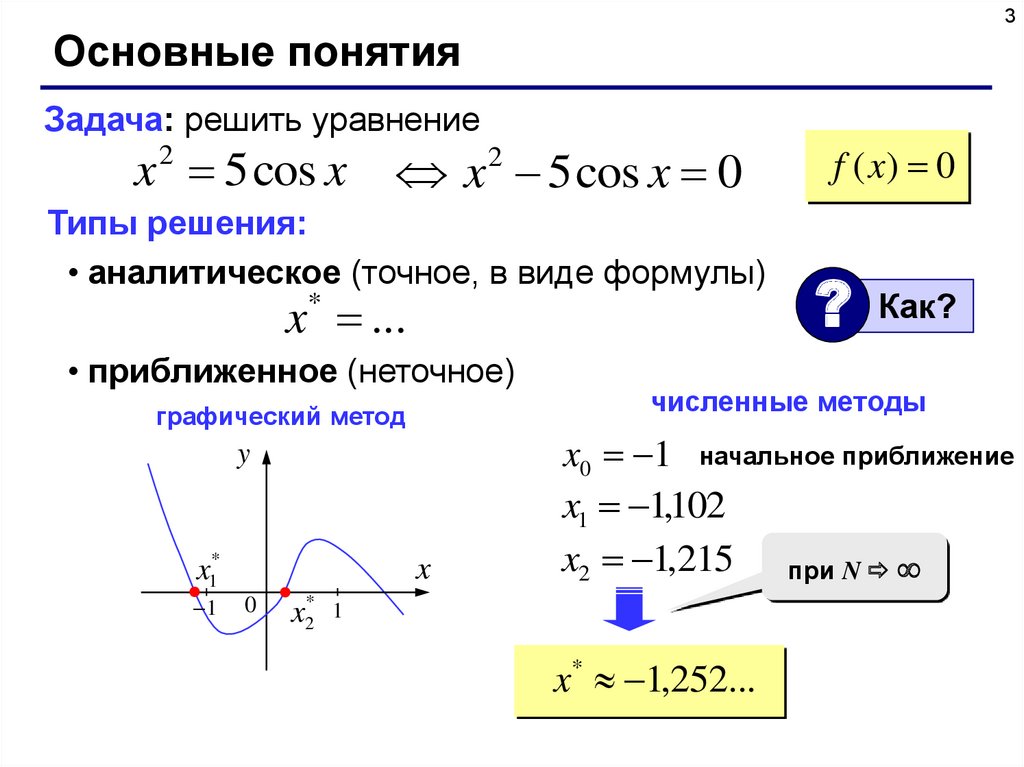
3
Основные понятия
Задача: решить уравнение
x 2 5 cos x
x 5 cos x 0
2
Типы решения:
• аналитическое (точное, в виде формулы)
x ...
*
• приближенное (неточное)
графический метод
y
x1*
1
x
0
x2*
f ( x) 0
?
Как?
численные методы
x0 1 начальное приближение
x1 1,102
x2 1,215 при N
1
x* 1,252...

4.

4
Численные методы
Идея: последовательное уточнение решения с помощью
некоторого алгоритма.
Область применения: когда найти точное решение
невозможно или крайне сложно.
1) можно найти хоть какое-то решение
2) во многих случаях можно оценить ошибку (то есть
можно найти решение с заданной точностью)
1) нельзя найти точное решение
x 1 4 sin( x 1) 0
x 1,3974
x 1,3974
2) невозможно исследовать решение при изменении
параметров
3) большой объем вычислений
4) иногда сложно оценить ошибку
5) нет универсальных методов

5.

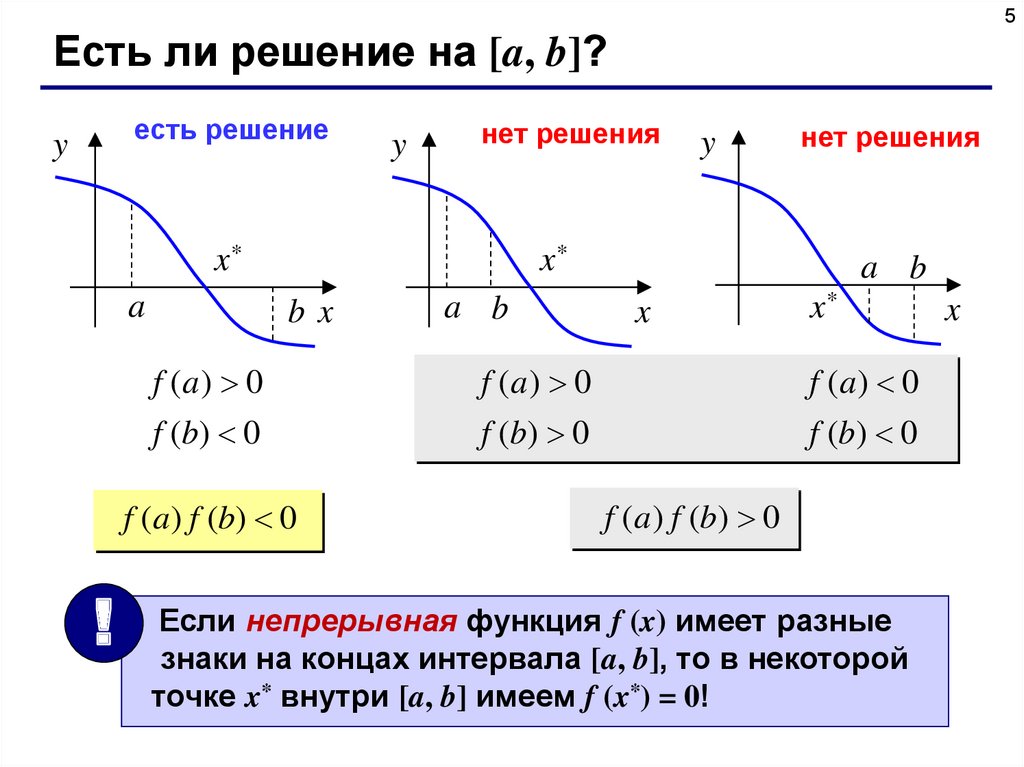
5
Есть ли решение на [a, b]?
есть решение
y
y
нет решения
x*
a
нет решения
x*
bx
a b
a b
x
x*
f (a) 0
f (a) 0
f (a) 0
f (b) 0
f (b) 0
f (b) 0
f (a) f (b) 0
!
y
f (a ) f (b) 0
Если непрерывная функция f (x) имеет разные
знаки на концах интервала [a, b], то в некоторой
точке x* внутри [a, b] имеем f (x*) = 0!
x

6.

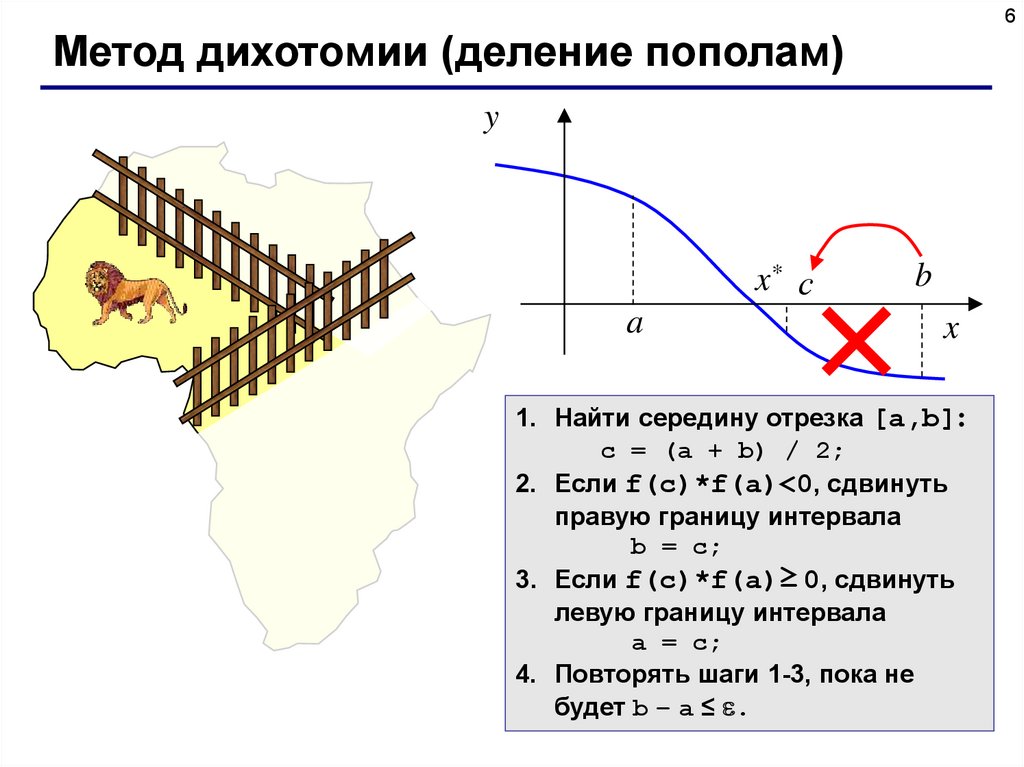
6
Метод дихотомии (деление пополам)
y
x* с
a
b
x
1. Найти середину отрезка [a,b]:
c = (a + b) / 2;
2. Если f(c)*f(a)<0, сдвинуть
правую границу интервала
b = c;
3. Если f(c)*f(a)≥ 0, сдвинуть
левую границу интервала
a = c;
4. Повторять шаги 1-3, пока не
будет b – a ≤ .

7.

7
Метод дихотомии (деления пополам)
• простота
• можно получить решение с заданной точностью
(в пределах точности машинных вычислений)
• нужно знать интервал [a, b]
• на интервале [a, b] должно быть только одно
решение
• большое число шагов для достижения высокой
точности
• только для функций одной переменной

8.

8
Метод деления отрезка пополам
Дано уравнение x 2 x 6 0 . Найти
приближенное решение уравнения на отрезке 0 до 10
с точностью до 7 знака после запятой. Подсчитать
количество итераций.
double a = 0, b = 10, c, eps = 1e-7;
int n = 0;
while (b - a > eps) {
c = (a + b) / 2;
if ((a*a + a - 6) * (c*c + c - 6) < 0)
b = c;
else
a = c;
n++;
}
printf("x = %.16f, n = %d",(a + b ) / 2, n);

9. Программирование на языке Java

Тема 17. Вычисление площади
(интеграла)

10.

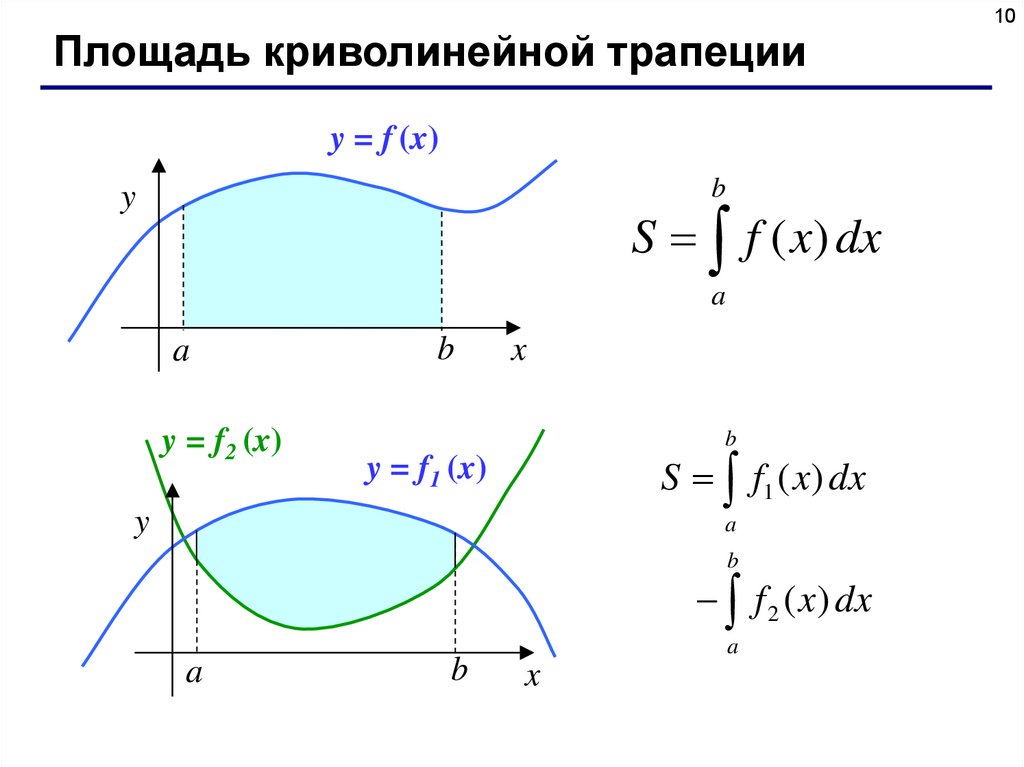
10
Площадь криволинейной трапеции
y = f (x)
b
y
S f ( x) dx
a
a
y = f2 (x)
b
x
b
S f1 ( x) dx
y = f1 (x)
y
a
b
f 2 ( x) dx
a
b
a
x

11.

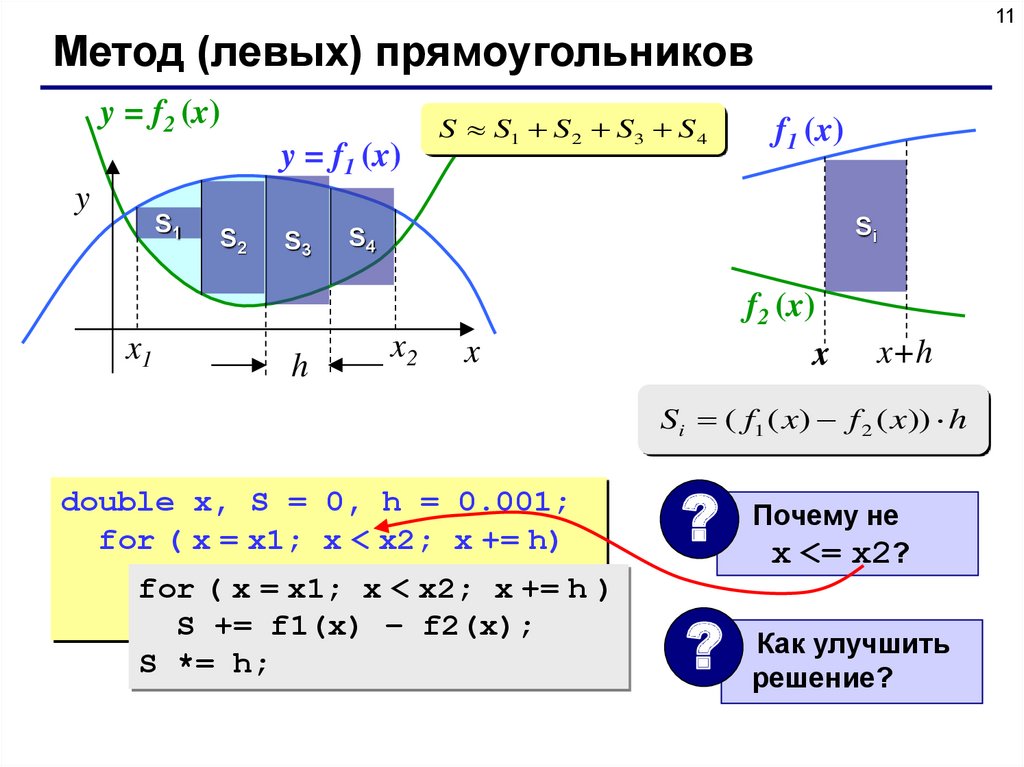
11
Метод (левых) прямоугольников
y = f2 (x)
y = f1 (x)
y
S1
x1
S2
S3
h
S S1 S 2 S3 S 4
f1 (x)
Si
S4
x2
f2 (x)
x
x
x+h
Si ( f1 ( x) f 2 ( x)) h
double x, S = 0, h = 0.001;
for ( x = x1; x < x2; x += h)
S +=
– f2(x));
for
( xh*(f1(x)
= x1; x < x2;
x += h )
S += f1(x) – f2(x);
S *= h;
?
?
Почему не
x <= x2?
Как улучшить
решение?

12.

12
Метод (правых) прямоугольников
y = f2 (x)
y = f1 (x)
S S1 S 2 S3 S 4
f1 (x)
y
S1
x1
S2
S3
h
Si
S4
x2
f2 (x)
x
x
x+h
Si ( f1 ( x h) f 2 ( x h)) h
double x, S = 0, h=0.001;
for ( x = x1; x < x2; x += h)
S +=
– f2(x+h));
for
( xh*(f1(x+h)
= x1; x < x2;
x += h )
S += f1(x+h) – f2(x+h);
S *= h;

13.

13
Метод (средних) прямоугольников
y = f2 (x)
y = f1 (x)
S S1 S 2 S3 S 4
f1 (x)
y
S1
x1
S2
S3
h
S4
f2 (x)
x2
Si
x x h x+h
x
2
h
h
S i f1 ( x ) f 2 ( x ) h
2
2
?
Какой метод точнее?
float x, S = 0, h=0.001;
for ( x = x1; x < x2; x += h)
h)
левые (правые):
S += h*(f1(x+h)
f1(x+h/2) –– f2(x+h));
f2(x+h/2);
O(h )
S *= h;
средние
O( h 2 )

14.

14
Метод трапеций
y = f2 (x)
f1 (x)
y = f1 (x)
y
S1
x1
S2
S3
h
Si
S4
x2
Si
f2 (x)
x
x
x+h
f1 ( x) f 2 ( x) f1 ( x h) f 2 ( x h)
h
2
for ( x = x1; x < x2; x += h )
SS =(
+= f1(x1)
f1(x) -– f2(x1)
f2(x) +
f1(x+h)
– f2(x+h);
+ f1(x2)
- f2(x2)
)/2.;
S *=
forh/2;
( x = x1+h; x < x2; x += h )
S += f1(x) – f2(x);
S *= h;
?
Как улучшить?
Ошибка
O( h 2 )

15. Программирование на языке Java

Тема 18. Вычисление длины
кривой

16.

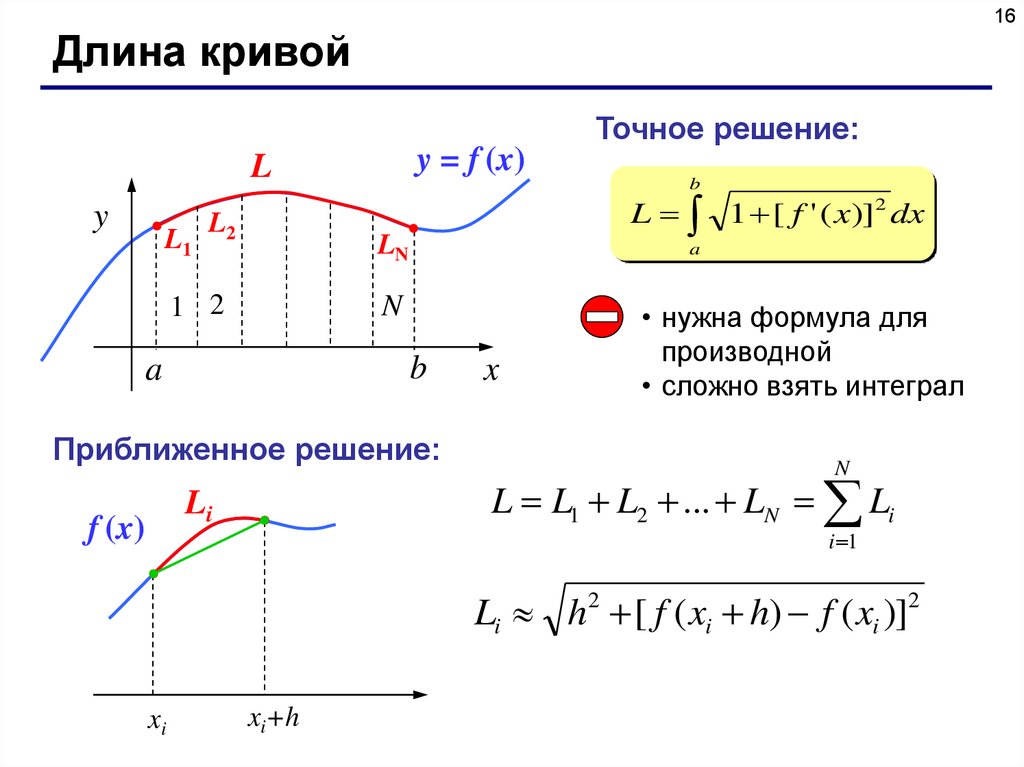
16
Длина кривой
Точное решение:
y = f (x)
L
y
L1
L2
b
L 1 [ f ' ( x)]2 dx
LN
a
N
1 2
b
a
Приближенное решение:
Li
f (x)
x
• нужна формула для
производной
• сложно взять интеграл
N
L L1 L2 ... LN Li
i 1
Li h2 [ f ( xi h) f ( xi )]2
xi
xi+h

17.

17
Длина кривой
Дана кривая y x . Найти длину кривой на
отрезке от 0 до 4.
2
double a = 0, b = 4;
double x, dy, h = 1e-6;
double h2 = h * h;
double L = 0;
for (x = a; x < b; x += h) {
dy = (x + h)*(x + h) - x * x;
L += Math.sqrt(h2 + dy * dy);
}
System.out.printf("L = %.16f", L);