Похожие презентации:
Численное интегрирование
1. ИНФОРМАТИКА
Тема 6.Численные методы решения задач.
2.
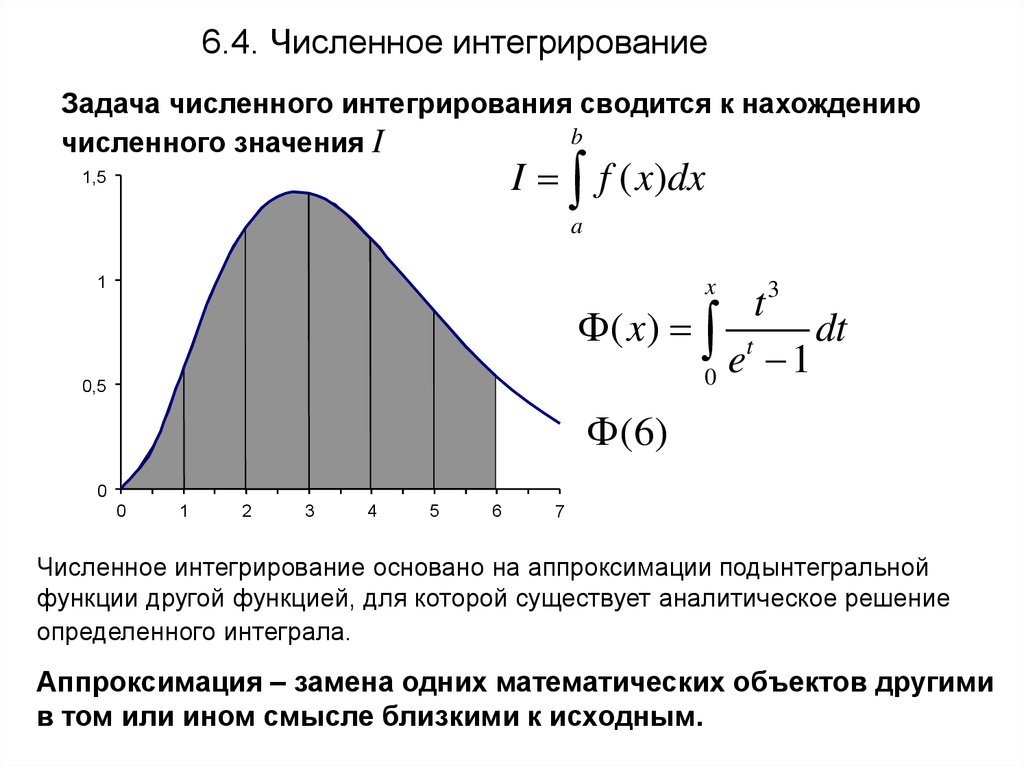
6.4. Численное интегрированиеЗадача численного интегрирования сводится к нахождению
b
численного значения I
I f ( x)dx
1,5
a
1
x
t3
( x ) t
dt
e 1
0
0,5
(6)
0
0
1
2
3
4
5
6
7
Численное интегрирование основано на аппроксимации подынтегральной
функции другой функцией, для которой существует аналитическое решение
определенного интеграла.
Аппроксимация – замена одних математических объектов другими
в том или ином смысле близкими к исходным.
3.
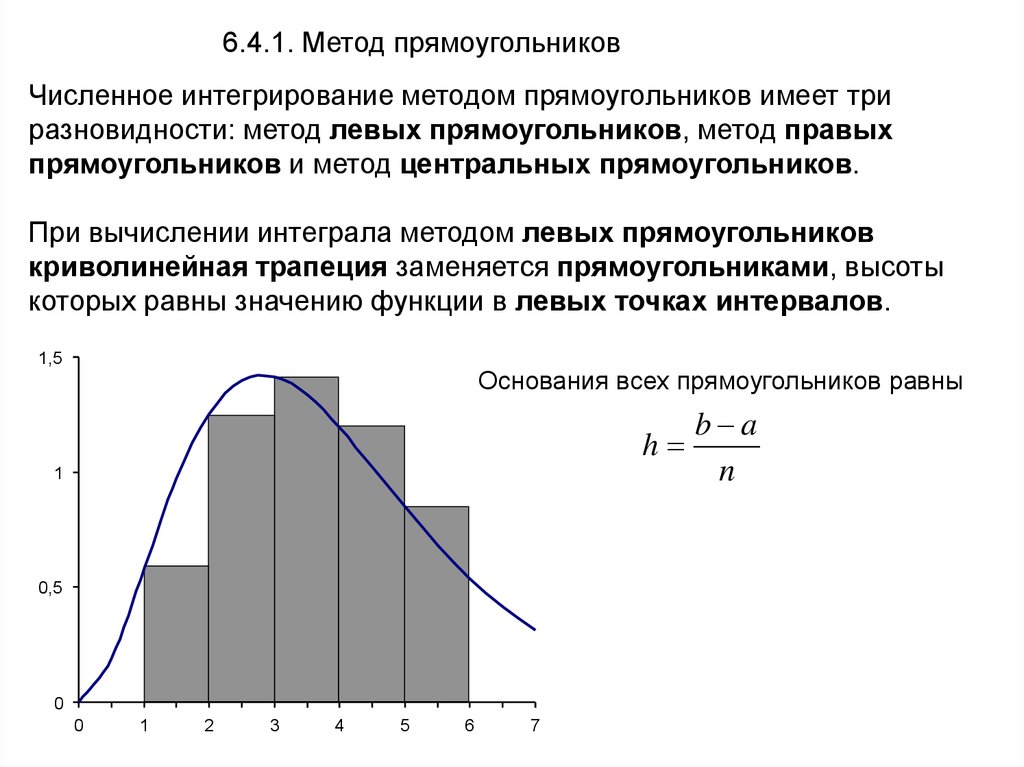
6.4.1. Метод прямоугольниковЧисленное интегрирование методом прямоугольников имеет три
разновидности: метод левых прямоугольников, метод правых
прямоугольников и метод центральных прямоугольников.
При вычислении интеграла методом левых прямоугольников
криволинейная трапеция заменяется прямоугольниками, высоты
которых равны значению функции в левых точках интервалов.
1,5
Основания всех прямоугольников равны
b a
h
n
1
0,5
0
0
1
2
3
4
5
6
7
4.
Метод левых прямоугольниковb
I f ( x)dx
a
n 6
[ a; b ]
S S1 S2 S3 S4 S5 S6
S1 h f (a)
S2 h f (a h)
S3 h f (a 2h)
S4 h f (a 3h)
S5 h f (a 4h)
S6 h f (a 5h)
S S1 S2 S3 S4 S5 S6
h f (a ) h f (a h) h f (a 2h) h f (a 3h) h f (a 4h) h f (a 5h)
h f (a ) f (a h) f (a 2h) f (a 3h) f (a 4h) f (a 5h)
Формула вычисления интеграла
методом левых прямоугольников
n 1
I ЛП h f (a i h)
i 0
b a
h
n
5.
Метод левых прямоугольниковПример. Вычислить интеграл методом левых прямоугольников
6
x3
I x
dx
e 1
0
a 0
b 6
n 6
h
x3
f ( x) x
e 1
6 0
1
6
03
13
23
33
43
53
I ЛП 1 0
1
2
3
4
5
e 1 e 1 e 1 e 1 e 1 e 1
1
8
27
64
125
2
3
4
5
0,582 1, 252 1, 415 1,194 0,848 5, 291
e 1 e 1 e 1 e 1 e 1
6.
Метод правых прямоугольниковПри вычислении интеграла методом правых прямоугольников
криволинейная трапеция заменяется прямоугольниками, высоты
которых равны значению функции в правых точках интервалов.
1,5
Основания всех прямоугольников равны
1
b a
h
n
0,5
0
0
1
2
3
4
5
6
7
7.
Метод правых прямоугольниковb
I f ( x)dx
a
n 6
[ a; b ]
S S1 S2 S3 S4 S5 S6
S1 h f (a h)
S2 h f (a 2h)
S3 h f (a 3h)
S4 h f (a 4h)
S5 h f (a 5h)
S6 h f (a 6h)
S S1 S2 S3 S4 S5 S6
h f (a h) h f (a 2h) h f (a 3h) h f (a 4h) h f (a 5h) h f (a 6h)
h f (a h) f (a 2h) f (a 3h) f (a 4h) f (a 5h) f (a 6h )
Формула вычисления интеграла
методом правых прямоугольников
n
I ПП h f (a i h)
i 1
b a
h
n
8.
Метод правых прямоугольниковПример. Вычислить интеграл методом правых прямоугольников
6
x3
I x
dx
e 1
0
a 0
b 6
n 6
h
x3
f ( x) x
e 1
6 0
1
6
13
23
33
43
53
63
I ПП 1 1
2
3
4
5
6
e 1 e 1 e 1 e 1 e 1 e 1
1
8
27
64
125
216
2
3
4
5
6
e 1 e 1 e 1 e 1 e 1 e 1
0,582 1, 252 1, 415 1,194 0,848 0,537 5,828
9.
Метод центральных прямоугольниковПри вычислении интеграла методом правых прямоугольников
криволинейная трапеция заменяется прямоугольниками, высоты
которых равны значению функции в центрах интервалов.
1,5
Основания всех прямоугольников равны
1
b a
h
n
0,5
0
0
1
2
3
4
5
6
10.
Метод центральных прямоугольниковb
I f ( x)dx
n 6
[ a; b ]
S S1 S2 S3 S4 S5 S6
h
3h
S1 h f a
S2 h f a
S3 h
2
2
a
7h
S4 h f a
2
9h
S5 h f a
2
5h
f a
2
11h
S6 h f a
2
S S1 S2 S3 S4 S5 S6
h
h f a h
2
h f
3h
f a h
2
5h
f a h
2
7h
f a h
2
9h
f a
h
2
11h
f a
2
h
3h
5h
7h
9h
11h
a
f
a
f
a
f
a
f
a
f
a
2
2
2
2
2
2
Формула вычисления интеграла методом
центральных прямоугольников
(2i 1) h
I ЦП h f a
2
i 1
n
b a
h
n
11.
Метод правых прямоугольниковПример. Вычислить интеграл методом центральных прямоугольников
6
x3
I x
dx
e 1
0
a 0
b 6
n 6
h
x3
f ( x) x
e 1
6 0
1
6
0,53
1,53
2,53
3,53
4,53
5,53
I ЦП 1 0,5
1,5
2,5
3,5
4,5
5,5
e 1 e 1 e 1 e 1 e 1 e 1
0,53
1,53
2,53
3,53
4,53
5,53
0,5
1,5
2,5
3,5
4,5
5,5
e 1 e 1 e 1 e 1 e 1 e 1
0,193 0,969 1,397 1,335 1,024 0,683 5,601
12.
6.4.2. Метод трапецийПри вычислении интеграла методом трапеций криволинейная
трапеция заменяется линейной функцией на каждом элементарном
отрезке.
1,5
1
Высоты всех трапеций равны
0,5
h
0
0
1
2
3
4
5
6
7
b a
n
13.
Метод трапецийb
I f ( x)dx
a
f (a ) f (a h )
S1
h
2
S4
[ a; b ]
n 6
S S1 S2 S3 S4 S5 S6
f ( a h ) f ( a 2h )
S2
h
2
S3
f (a 2h ) f (a 3h )
h
2
f ( a 3h ) f ( a 4h )
f (a 4h ) f (a 5h )
f (a 5h ) f (b)
h S5
h S6
h
2
2
2
S S1 S2 S3 S4 S5 S6
h
f (a ) 2 f (a h) 2 f (a 2h) 2 f (a 3h ) 2 f (a 4h ) 2 f (a 5h ) f (b)
2
Формула вычисления интеграла методом трапеций
n 1
h
I Тр f (a ) f (b) 2 f (a i h )
2
i 1
b a
h
n
14.
Метод трапецийПример. Вычислить интеграл методом трапеций
6
x3
I x
dx
e 1
0
a 0
b 6
n 6
h
x3
f ( x) x
e 1
6 0
1
6
13
1 03
63
23
33
43
53
I Тр 0
6
2 1
2
3
4
5
2 e 1 e 1
e 1 e 1 e 1 e 1 e 1
0,5 0 0,537 2 5, 291 0,5 11,119 5,559
15.
6.4.3. Метод парабол (Симпсона или Ньютона-Симпсона)При вычислении интеграла методом парабол криволинейная
2
трапеция заменяется квадратичной функцией y a x b x c
на каждом элементарном отрезке.
Y
y1
y a x2 b x c
y0
y2
0
x0
x1
I
X2
X0
x2
f ( x)dx
X
X2
2
(
a
x
b x c)dx
X0
16.
Метод параболI
X2
X0
X2
x2
1
1
2
3
2
f ( x)dx a x b x c dx a x b x c x
x0
3
2
X0
1
1
1
1
a x23 b x22 c x2 a x03 b x02 c x0
3
2
3
2
h
x2 x0
2
x0 x1 h x2 x1 h y0 f ( x0 ) y1 f ( x1 )
y 2 f ( x2 )
1
1
1
1
3
2
3
I a x2 b x2 c x2 a x0 b x02 c x0
3
2
3
2
a
b
a
b
( x1 h)3 ( x1 h) 2 c ( x1 h) ( x1 h)3 ( x1 h) 2 c ( x1 h)
3
2
3
2
a
b
( x1 h)3 ( x1 h)3 ( x1 h) 2 ( x1 h) 2 c ( x1 h) ( x1 h)
3
2
17.
Метод парабол1
1
1
1
I a x23 b x22 c x2 a x03 b x02 c x0
3
2
3
2
a
b
a
b
( x1 h)3 ( x1 h) 2 c ( x1 h) ( x1 h)3 ( x1 h) 2 c ( x1 h)
3
2
3
2
a
b
( x1 h)3 ( x1 h)3 ( x1 h) 2 ( x1 h) 2 c ( x1 h) ( x1 h)
3
2
( x1 h ) ( x1 h ) 2h
( x1 h )2 ( x1 h )2 ( x1 h ) ( x1 h ) ( x1 h ) ( x1 h ) 2 x1 2h
( x1 h)3 ( x1 h)3 ( x1 h) ( x1 h) ( x1 h)2 ( x1 h)( x1 h) ( x1 h ) 2
2h x12 2h x1 h 2 x12 h 2 x12 2h x1 h 2 2h 3x12 h 2
b
a
2
2
I 2h 3x1 h 2 x1 c
2
3
18.
Коэффициенты параболы определяются из условия прохожденияпараболы через три точки x0 ; f ( x0 ) x1 ; f ( x1 ) x2 ; f ( x2 )
a x02 b x0 c y0
2
a
x
1 b x1 c y1
a x 2 b x c y
2
2
2
x02
x12
x22
x0 1
x1 1
x2 1
x1 ( x1 h )2 ( x1 h ) ( x1 h ) 2 x12 ( x1 h )
x1 ( x1 h )2 x12 ( x1 h ) ( x1 h ) 2 ( x1 h )
x12 2h 2h ( x12 h 2 ) x12 4h 2h x12 2h x12 2h 3 4h x12 2h 3
2h
3
19.
y01 y1
y2
x0 1
x1 1 y0 h y2 h 2 y1 h h ( y0 y2 2 y1 )
x2 1
x02
2 x12
x22
y0 1
y1 1 4h x1 y1 2h x1 y0 h 2 y0 2h x1 y2 h 2 y2
y2 1
x02
3 x12
x22
x0
x1
x2
y0
y1 h 2 x1 ( y2 y0 ) h x12 ( y2 y0 ) 2h x12 y1 2h 3 y1
y2
1 h ( y0 y2 2 y1 ) y0 2 y1 y2
a
3
2h
2h 2
20.
2 4h x1 y1 2h x1 y0 h 2 y0 2h x1 y2 h 2 y2b
3
2h
4 x1 y1 2 x1 ( y0 y2 ) h ( y2 y0 )
2h 2
3 h 2 x1 ( y2 y0 ) h x12 ( y2 y0 ) 2h x12 y1 2h 3 y1
c
3
2 h
h x1 ( y2 y0 ) x12 ( y2 y0 ) 2 x12 y1 2h 2 y1
2h 2
I
4 x1 y1 2 x1 ( y0 y2 ) h ( y2 y0 )
1 y0 2 y1 y2
2
2
3
x
h
2 x1
1
h
3
2
h x1 ( y2 y0 ) x12 ( y2 y0 ) 2 x12 y1 2h 2 y1
h
I П y0 4 y1 y2
3
21.
Метод параболb
I f ( x)dx
a
h
S1 y0 4 y1 y2
3
S S1 S2 S3
[ a; b ]
n 6
S S1 S2 S3
h
S 2 y 2 4 y3 y 4
3
S3
h
y 4 4 y5 y 6
3
h
y0 4 y1 y2 y2 4 y3 y4 y4 4 y5 y6
3
h
y0 4 y1 2 y2 4 y3 2 y4 4 y5 y6
3
Формула вычисления интеграла методом парабол
h
I П y0 4 y1 2 y2 4 y3 2 y4 ... 2 yn 2 4 yn 1 yn
3
h
xn x0
n
(n кратно 2)
22.
Метод параболПример. Вычислить интеграл методом парабол
x0 0
n 6
x6 6
h
6 0
1
6
x3
f ( x) x
e 1
6
x3
I x
dx
e 1
0
1 03
13
23
33
43
53
63
IП 0
4 1
2 2
4 3
2 4
4 5
6
3 e 1
e 1
e 1
e 1
e 1
e 1 e 1
0 4 0,582 2 1, 252 4 1, 415 2 1,194 4 0,848 0,537 16,809
5,603
3
3
23.
6.4.4. Метод Симпсона 3/8При вычислении интеграла методом Симпсона 3/8 криволинейная
трапеция на каждом элементарном отрезке заменяется полиномом
третьей степени
y a x3 b x 2 c x d
I
X2
f ( x)dx
X0
X2
3
2
(
a
x
b
x
c x d )dx
X0
I 3/8
3h
y0 3 y1 3 y2 y3
8
Формула вычисления интеграла методом Симпсона 3/8
I 3/8
3h
y0 3 y1 3 y2 2 y3 3 y4 3 y5 ... 2 yn 3 3 yn 2 3 yn 1 yn
8
xn x0
h
n
(n кратно 3)
24.
Метод параболПример. Вычислить интеграл методом Симпсона 3/8
6
x3
I x
dx
e 1
0
x0 0
n 6
x6 6
h
6 0
1
6
x3
f ( x) x
e 1
3 03
13
23
33
43
53
63
IП 0
3 1
3 2
2 3
3 4
3 5
6
8 e 1
e 1
e 1
e 1
e 1
e 1 e 1
3 (0 3 0,582 3 1, 252 2 1, 415 3 1,194 3 0,848 0,537) 3 14,995
5,623
8
8
25.
6.4.5. Метод БуляПри вычислении интеграла методом Буля криволинейная трапеция
на каждом элементарном отрезке заменяется полиномом четвертой
степени
y a x 4 b x3 c x 2 d x e
I
X4
f ( x)dx
X0
X4
4
3
2
(
a
x
b
x
c
x
d x e)dx
X0
2h
IБ
7 y0 32 y1 12 y2 32 y3 7 y4
45
Формула вычисления интеграла методом Буля
IБ
2h
7 y0 32 y1 12 y2 32 y3 14 y4 32 y5 12 y6 32 y7 ... 32 yn 1 7 yn
45
h
xn x0
n
(n кратно 4)
26.
6.4.6. Сравнение различных методов по точности приближенияb
I f ( x)dx Q( f ) E ( f )
a
Q( f )
– численное значение интеграла,
полученное тем или иным методом
E( f )
– ошибка интегрирования, которая зависит от
вида функции f(x) и шага h
Степенью точности называют такое целое число n, что для всех
полиномов Pi(x) степени i ≤ n приближенная формула расчета
значения интеграла дает абсолютно точный числовой ответ.
27.
6.4.6. Сравнение различных методов по точности приближенияМетод
Расчетная формула
Левых
прямоугольников
h f0
h 2 f (c )
2
Правых
прямоугольников
h f1
h 2 f (c )
2
Центральных
прямоугольников
x x
h f 0 1
2
h3 f (2) (c)
24
Трапеций
h
( f0 f1 )
2
h3 f (2) (c)
12
Симпсона
h
( f0 4 f1 f 2 )
3
h5 f (4) (c)
90
Симпсона 3/8
3h
( f0 3 f1 3 f 2 f3 )
8
3h5 f (4) (c)
80
Буля
2h
(7 f0 32 f1 12 f 2 32 f3 7 f 4 )
45
8h7 f (6) (c)
945
Точность E ( f )
28.
6.4.7. Метод Гаусса-Лежандраy f ( x)
Постановка задачи: требуется найти площадь под кривой
Y
1 x 1
Y
y f ( x)
y f ( x)
-1
0
1
y1
y2
X
-1
x1
а)
0
x2
1
X
б)
( x x1 ) ( f ( x2 ) f ( x1 ))
y f ( x1 )
x2 x1
S
S
2 x2
2 x1
f ( x1 )
f ( x2 )
x2 x1
x2 x1
2
2
f ( x1 )
f ( x2 ) f ( x1 ) f ( x2 ) IТр
2
2
29.
6.4.7. Метод Гаусса-ЛежандраСогласно методу Гаусса-Лежандра приближенное значение
интеграла определяется с помощью весового суммирования
значений функции в двух точках по формуле
1
f ( x)dx f ( x )
1
1
2
f ( x2 )
1
Значения абсцисс x1 и x2 и весов ω1 и ω2 выбираются из
условия, что данная формула будет точной для четырех
функций: f(x)=1, x, x2, и x3.
30.
11dx 2
f ( x) 1
1
2
1
1
xdx 0 x
f ( x) x
1
1
2
x2
1
1
f ( x) x
2
2
x
dx
1
1
f ( x) x 3
2
1 x12 2 x22
3
3
3
3
x
dx
0
x
x
1
1
2
2
1
1 2 2
x x 0
2
2
1 1
2
2
2
1 x1 2 x2 3
3
3
1 x1 2 x2 0
31.
1 2 2x x 0
2
2
1 1
2
2
2
1 x1 2 x2 3
3
3
1 x1 2 x2 0
1 2
1 x1 2 x2
1 x13 2 x23
x12 x22
1 2 1
1
x
3
1
1
1
1 f ( x)dx f 3 f 3
2
1 x 2 x x x
3
2
1
2
2
2
1
2
2
1
1 f ( x)dx f 3
1
2
2
1
f
E2 ( f )
3
x1 x2
x1
1
3
x2
1
3
f (4) (c)
E2 ( f )
135
32.
Метод Гаусса-ЛежандраПример. Вычислить интеграл методом Гаусса-Лежандра по 2 точкам
1
dx
1 x 2
1
1
dx
1 x 2 ln( x 2) 1 ln(3) ln(1) ln(3) 1,09861
dx
2 1
1
1 x 2 2 1 2 1 2 1 0,33333 1,33333
1
dx
1 1
1
1 1
1 10
1 x 2 3 1 2 4 0 2 1 2 3 1 2 3 9 1,11111
1
1
dx
1
1
0,70291 0,38800 1,09091
1 x 2 1
1
2
2
3
3
33.
Метод Гаусса-ЛежандраЕсли требуется вычислить значение интеграла на интервале [a; b],
то требуется выполнить замену переменной
a b b a
x
t
2
2
b
a
b a
dx
dt
2
b a
a b b a b a
a b b a
f ( x)dx f
t
dt
f
t dt
2
2 2
2 1 2
2
1
1
1
2
Пример. Вычислить интеграл
0 2 2 0
x
t 1 t
2
2
5
6x
dx
0
a 0 b 2
f ( x) 6 x 5
2 0
dx
dt dt
2
5
5
1
1
5
5
6
x
dx
6
(1
t
)
dt
6
1
6
1
58,66667
0
1
3
3
2
1
34.
Метод Гаусса-ЛежандраЕсли требуется вычислить значение интеграла на интервале [a; b],
то требуется выполнить замену переменной
a b b a
x
t
2
2
b
a
b a
dx
dt
2
b a
a b b a b a
a b b a
f ( x)dx f
t
dt
f
t dt
2
2 2
2 1 2
2
1
1
1
1
Пример. Вычислить интеграл
sin( x)
0 x dx
a 0
b 1 f ( x)
1 0
1
0 1 1 0
1 t
dx
dt dt
t
2
2
2
2
2
1 t
sin
1
1
1
sin( x)
1
sin(0,5 0,5t )
2
dx
dt
dt 0,94604
0 x
1
t
2 1
1 t
1
2
x
sin( x)
x
35.
При вычислении интеграла методом Гаусса-Лежандра по тремточкам приближенное значение определяется по формуле
1
f ( x)dx f ( x )
1
1
2
f ( x2 ) 3 f ( x3 )
1
Значения абсцисс x1, x2 и x3 и весов ω1, ω2 и ω3 выбираются
из условия, что данная формула будет точной для шести
функций: f(x) = 1, x, x2, x3, x4, и x5.
x1 0,6
5
1
9
1
x2 0
8
2
9
x3 0,6
5
3
9
5
8
5
1 f ( x)dx 9 f ( 0,6) 9 f (0) 9 f ( 0,6)
f (6) (c)
E3 ( f )
15750
36.
Метод Гаусса-ЛежандраЧисло;
точек
Абсциссы
Весовые
коэффициенты
Точность
2
0,57735
1
3
0,774597
0
0,555556
0,888889
f (4) (c )
135
f (6) (c )
15750
4
0,861136
0,339981
0,347855
0,652145
f (8) (c)
3472875
0,236927
f (10) (c)
1237732650
5
0,9061798
0,538469
0
1
0,478629
0,568889
37.
6.4.8. Метод Монте-Карлоl
1
p
dAd
r
0 0
2 L
p
r
Николас Константин Метрополис,
Станислав Мартин Улам –
авторы статьи
«Метод Монте-Карло» (1950 г.)
r L
38.
6.4.8. Метод Монте-Карлоb
I f ( x)dx
a
u – случайная величина, равномерно распределенная на интервале [a; b]
b
M [ f (u )] f ( x) ( x)dx
( x)
a
– плотность распределения случайная величины u
1
b a
1 b
M [ f (u )]
f ( x)dx
b a a
( x)
b
f ( x)dx (b a) M [ f (u )]
a
39.
6.4.8. Метод Монте-Карлоb
f ( x)dx (b a) M [ f (u )]
a
Формула вычисления интеграла
простейшим методом Монте-Карло
b
a
b a N
f ( x)dx
f (ui )
N i 1
40.
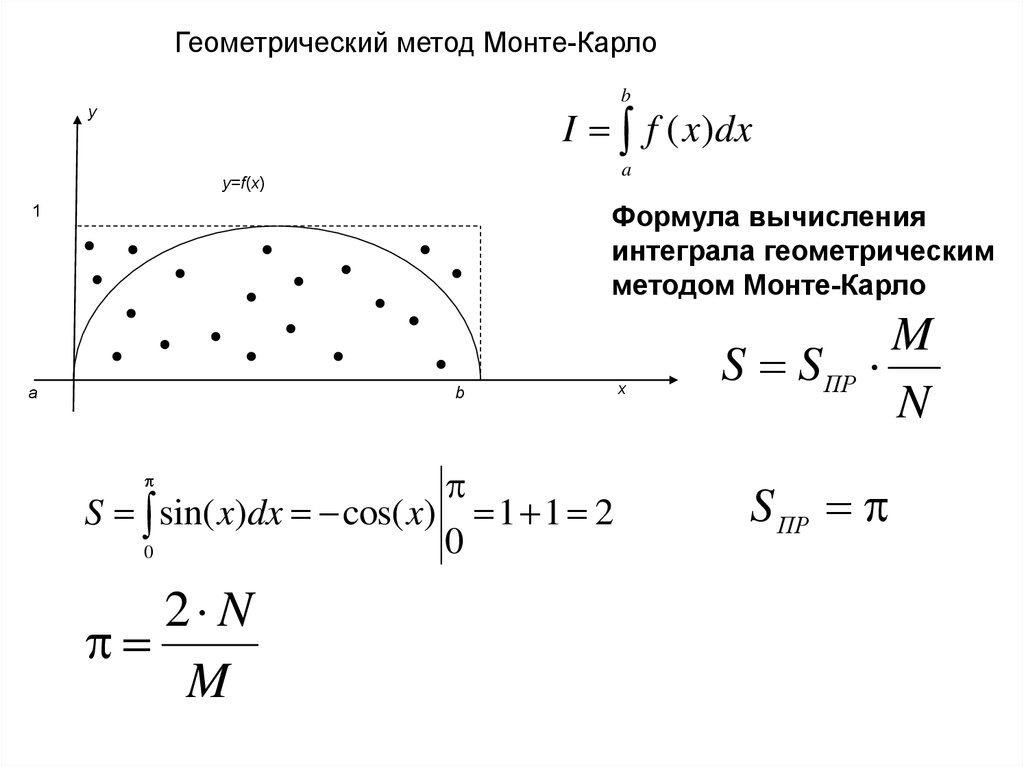
Геометрический метод Монте-Карлоb
I f ( x)dx
y
a
y=f(x)
Формула вычисления
интеграла геометрическим
методом Монте-Карло
1
a
b
S sin( x)dx cos( x) 1 1 2
0
0
2 N
M
x
M
S S ПР
N
S ПР
41.
Достоинства метода Монте-Карло:• простую структуру вычислительного алгоритма;
• вычисления значения интеграла можно прекратить в любой момент;
• погрешность вычислений не реагирует на размерность задачи;
• при вычислении многомерных интегралов метод Монте-Карло
остается единственным, способным выдать приближенное значение
за конечное время.
Недостатки метода Монте-Карло:
• при вычислении одномерных интегралов сходимость метода
уступает регулярным методам;
• для уменьшения погрешности на порядок, необходимо увеличить
количество испытаний на два порядка.
1
E
N
Простейший метод всегда точнее геометрического.
















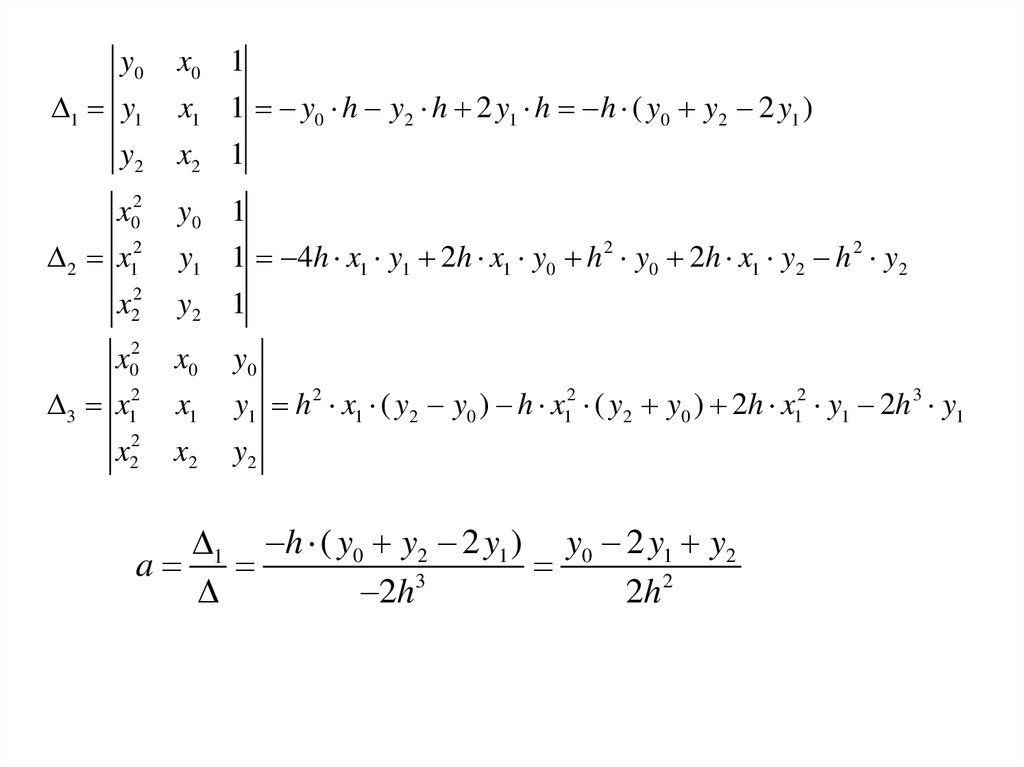
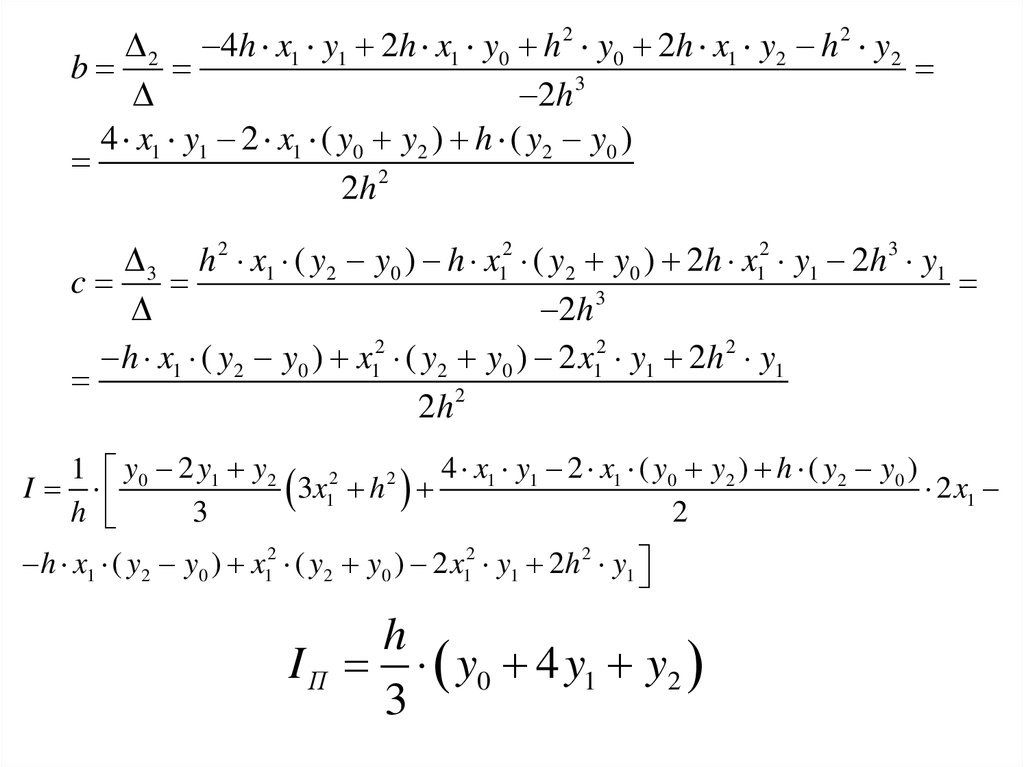










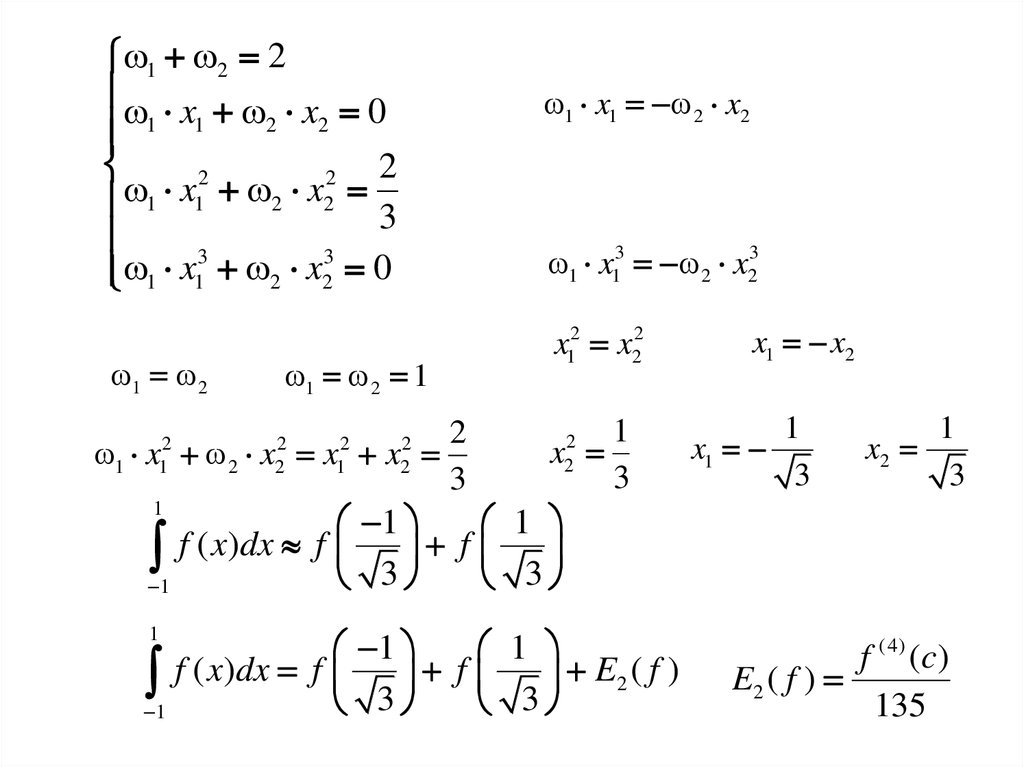









 Информатика
Информатика








