Похожие презентации:
Теория производства
1.
1Теория
производства
2.
2• 1. Виды производственных функций.
Функция Кобба-Дугласа. Отдача от
масштаба.
• 2. Результаты деятельности
фирмы. Закон убывающей
предельной производительности.
• 3. Понятие изоквант,
производственные множества и
технологическая эффективность.
Предельная норма технологического
замещения (MRTS).
• 4. Равновесие производителя. Кривая
«путь развития».
3.
31. Виды производственных
функций. Функция КоббаДугласа. Отдача от
масштаба
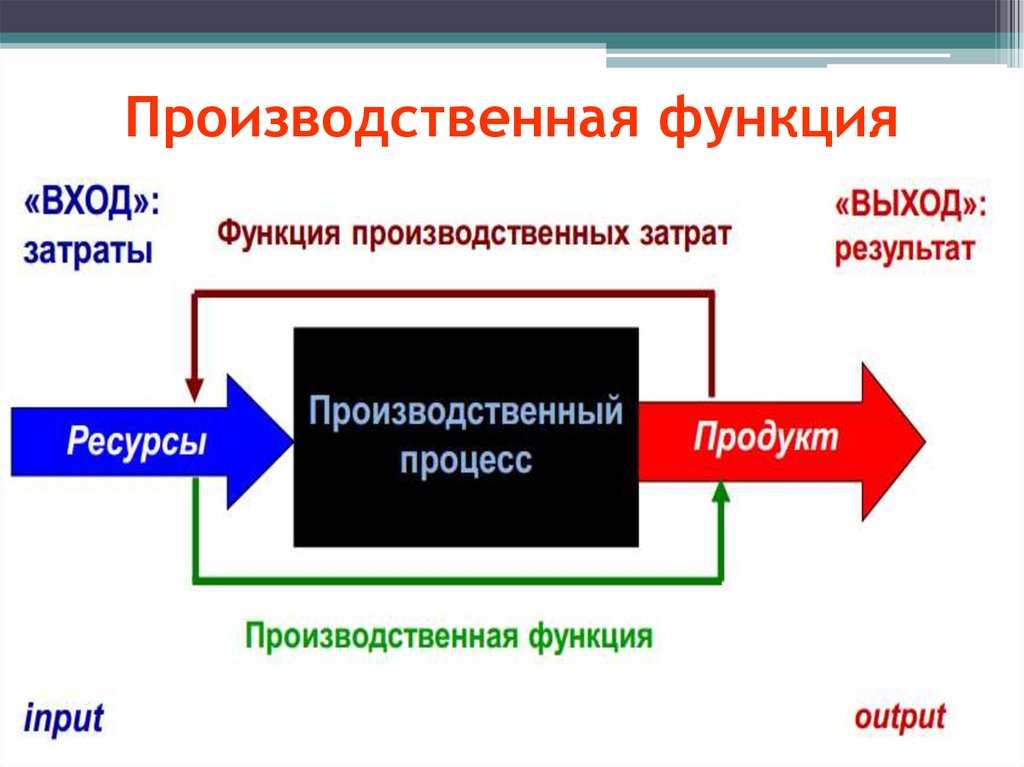
4. Производственная функция –
4Производственная функция –
функциональная взаимосвязь,
отображающая зависимость
между вводимой комбинацией
факторов производства и
объемом выпуска продукции
5. Производственная функция
6.
6В качестве независимых
переменных в
производственной функции
будут выступать значения
используемых факторов, а в
качестве зависимой
переменной – значения
объемов выпуска продукции.
7. Производственная функция
7Производственная функция
Производственная функция для различных видов
затрат для данной технологии:
Q = F(K,L,I,T)
где Q - выпуск,
K - капитал,
L - труд,
I – информация,
T – технология.
Производственная функция позволяет объединять
ресурсы в различных пропорциях, так что
определенного объема выпуска продукции можно
добиться различными способами.
8. Виды производственных функций
8Виды
производственных
функций
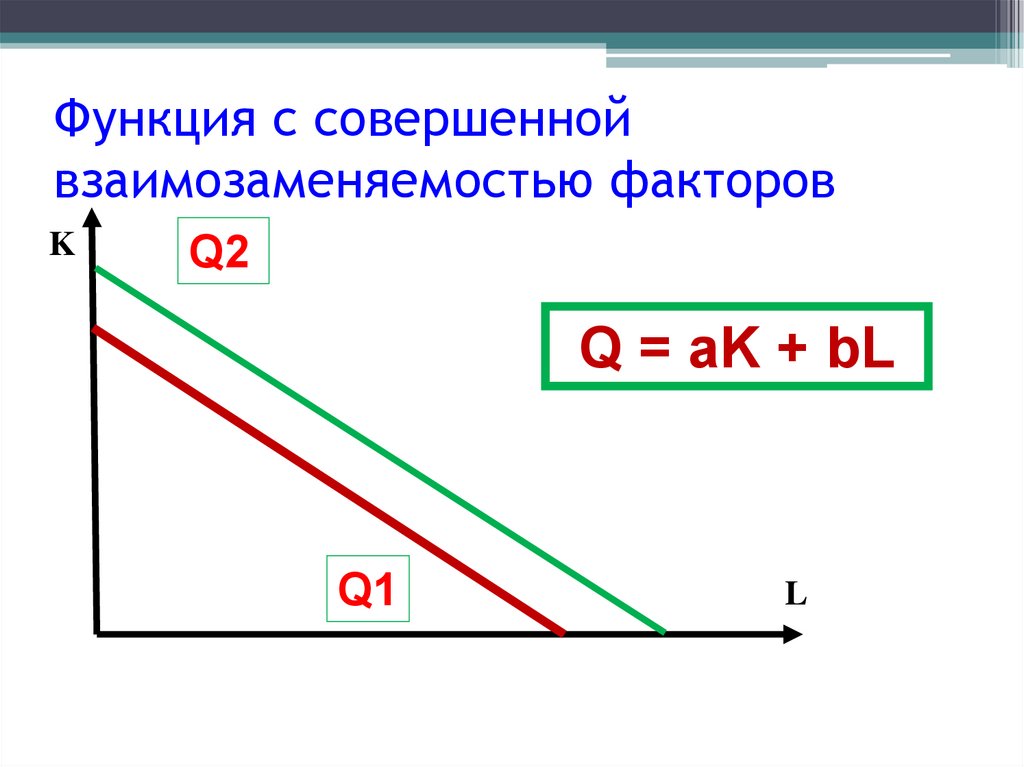
9. 1.Функция с совершенной взаимозаменяемостью факторов
91.Функция с совершенной
взаимозаменяемостью факторов
• Предположим, что труд и капитал совершенно
взаимозаменяемы: всех работников можно
заменить капиталом или использовать только
ручной труд.
• Производственная функция будет иметь вид:
Q = aK + bL
Представим данное выражение в виде:
Q b
K
L
a
a
Данная производственная функция описывается
линейной зависимостью.
10. Функция с совершенной взаимозаменяемостью факторов
KQ2
Q = aK + bL
Q1
L
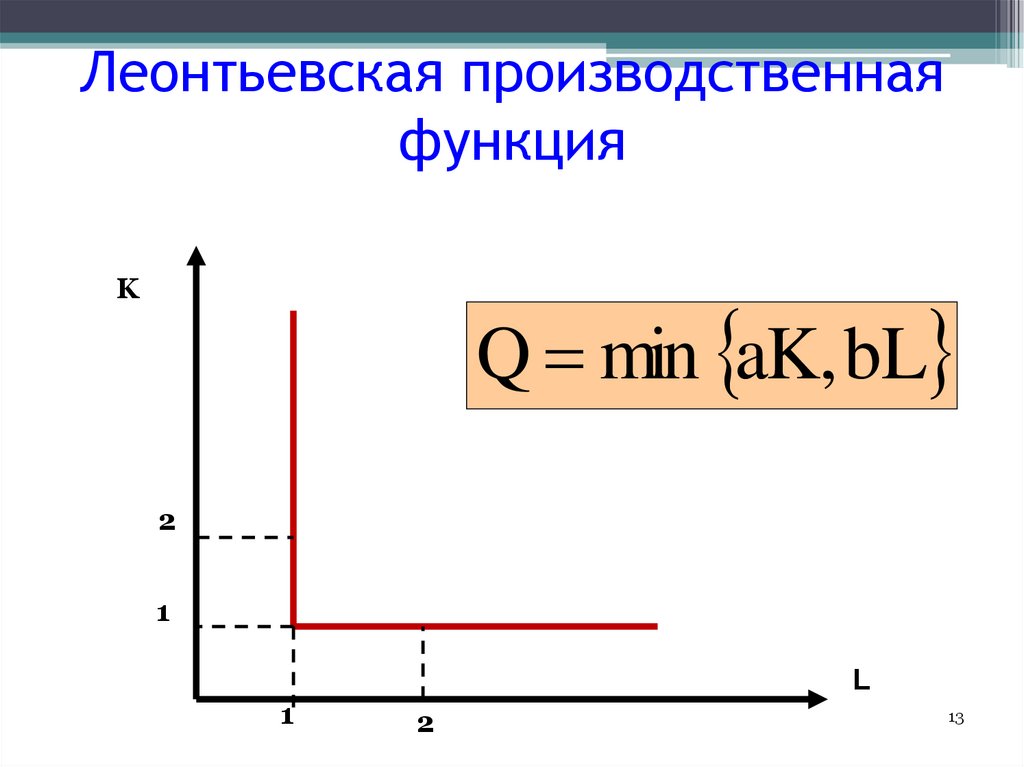
11. 2.Леонтьевская производственная функция
112.Леонтьевская производственная
функция
• Иногда факторы производства
абсолютно не заменяемы: пропорции
их использования строго
фиксированы.
• Используем пропорцию: L = 2K
12.
12• Такой производственный процесс
характеризуется производственной
функцией
фиксированных
пропорций – или леонтьевской
производственной функцией :
Q min aK, bL
a, b > 0
13.
Леонтьевская производственнаяфункция
K
Q min aK, bL
2
1
L
1
2
13
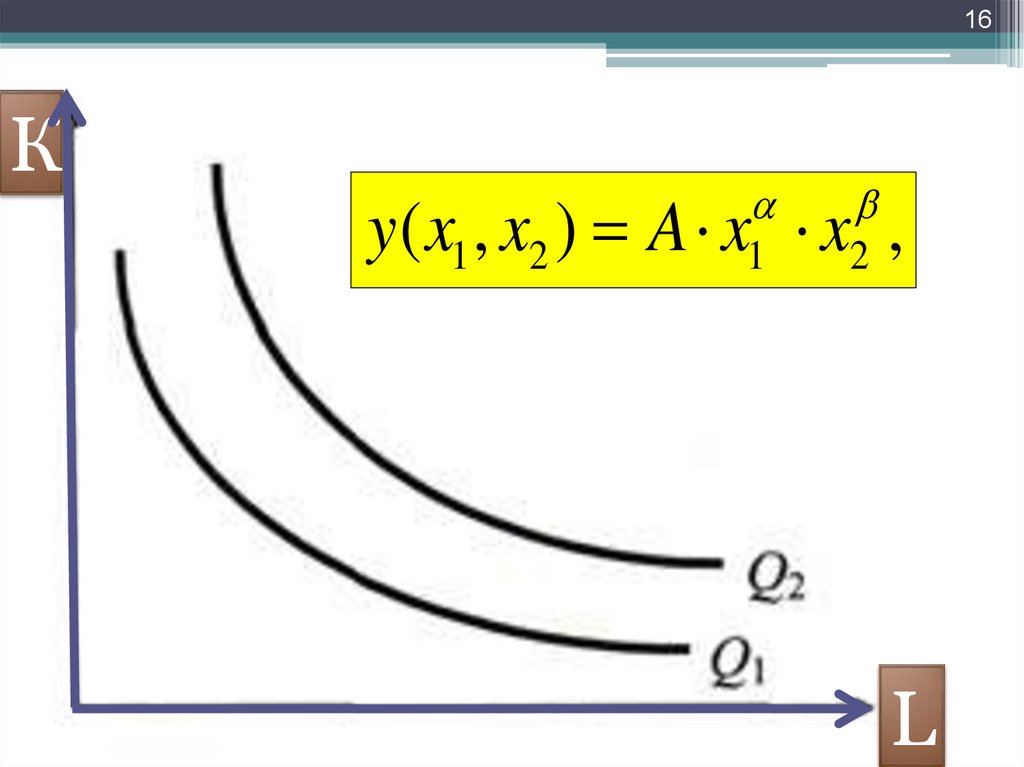
14. 3.Производственная функция Кобба-Дугласа (гипербола):
143.Производственная функция Кобба-Дугласа
(гипербола):
устанавливает зависимость величины
созданного общественного продукта от
совокупных затрат живого труда (Х1) и
суммарного объема применяемого
капитала (Х2) производственных
фондов. Она имеет следующий вид:
Q=АХ1α * Х2ᵦ,
где A – коэффициент, учитывающий
влияние факторов, не вошедших в это
уравнение,
α, ᵦ – показывают доли труда и
капитала в общем объеме затрат.
15.
15Производственная функция КоббаДугласа характеризует отдачу от
масштаба:
Если 1, то убывающая отдача от масштаба;
если
если
1,
то постоянная отдача от масштаба;
1,
то возрастающая отдача от масштаба.
16.
16К
1
2
y ( x1 , x2 ) A x x ,
L
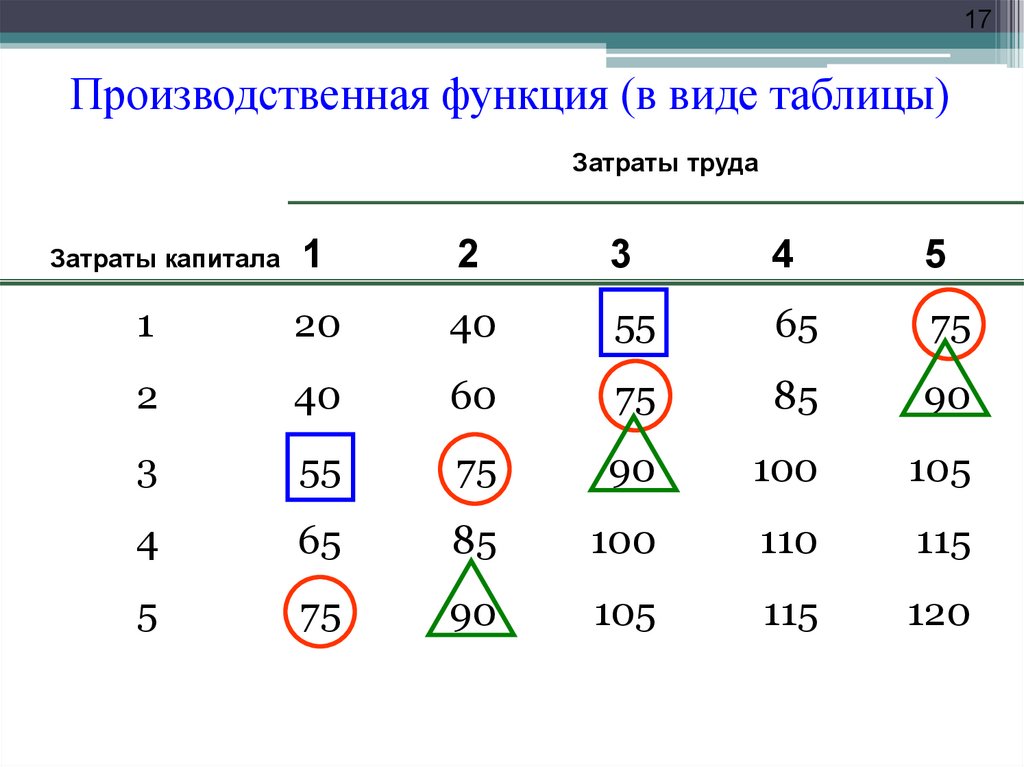
17. Производственная функция (в виде таблицы)
17Производственная функция (в виде таблицы)
Затраты труда
1
2
3
4
5
1
20
40
55
65
75
2
40
60
75
85
90
3
55
75
90
100
105
4
65
85
100
110
115
5
75
90
105
115
120
Затраты капитала
18. Производственная функция
18Производственная функция
• Ячейки
таблицы
показывают
максимальный (технически эффективный)
объем выпуска, который можно произвести за
год при каждой комбинации труда и капитала,
используемой на протяжении года.
• Данная
таблица
является
простейшим
примером производственной функции.
• Информацию, представленную в таблице
также можно изобразить графически при
помощи изоквант.
19.
1920. Измерение отношения между масштабом (размером) фирмы и выпуском
20Измерение отношения
между масштабом
(размером) фирмы и
выпуском
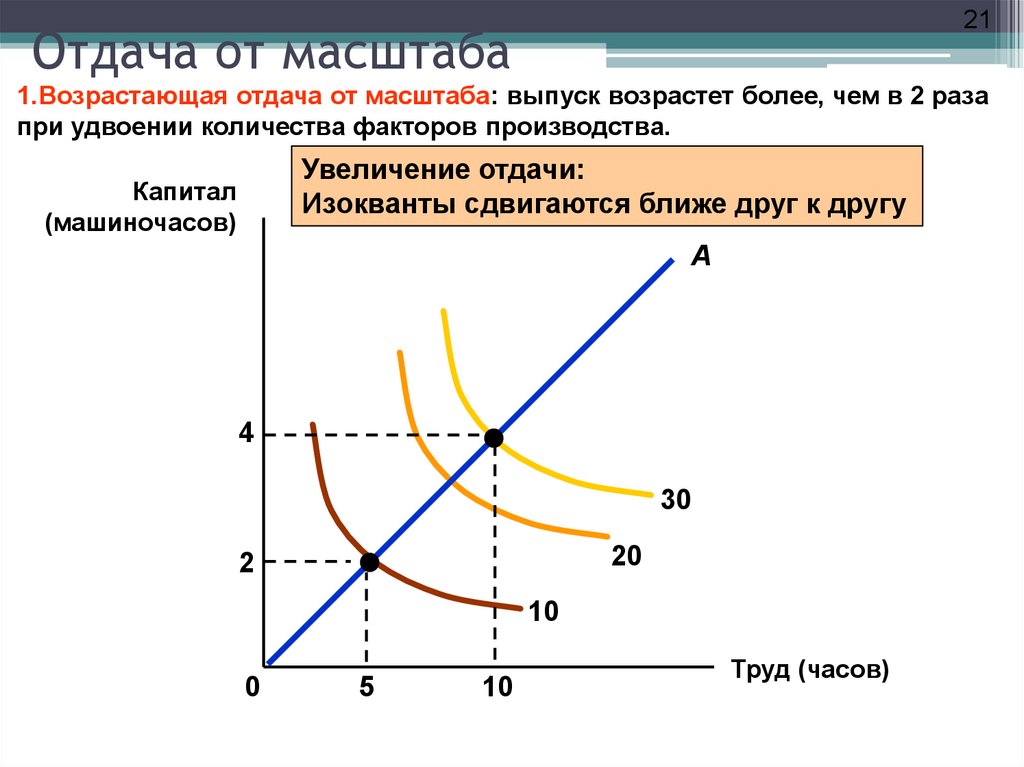
21. Отдача от масштаба
21Отдача от масштаба
1.Возрастающая отдача от масштаба: выпуск возрастет более, чем в 2 раза
при удвоении количества факторов производства.
Увеличение отдачи:
Изокванты сдвигаются ближе друг к другу
Капитал
(машиночасов)
A
4
30
20
2
10
0
5
10
Труд (часов)
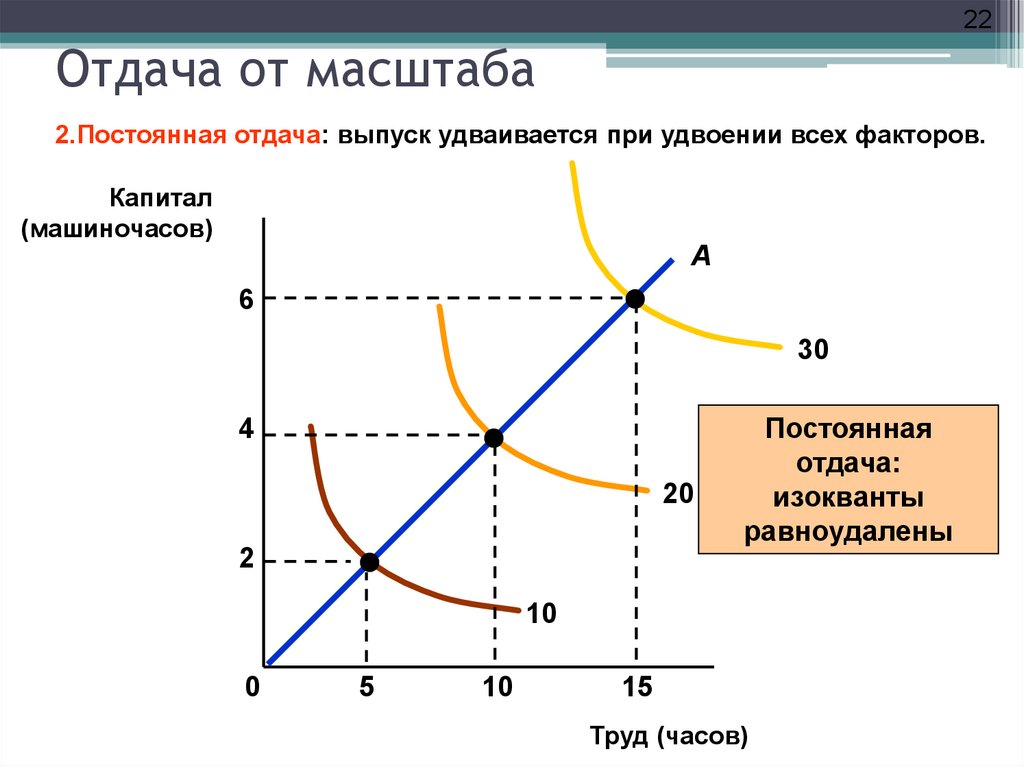
22. Отдача от масштаба
22Отдача от масштаба
2.Постоянная отдача: выпуск удваивается при удвоении всех факторов.
Капитал
(машиночасов)
A
6
30
4
20
2
Постоянная
отдача:
изокванты
равноудалены
10
0
5
10
15
Труд (часов)
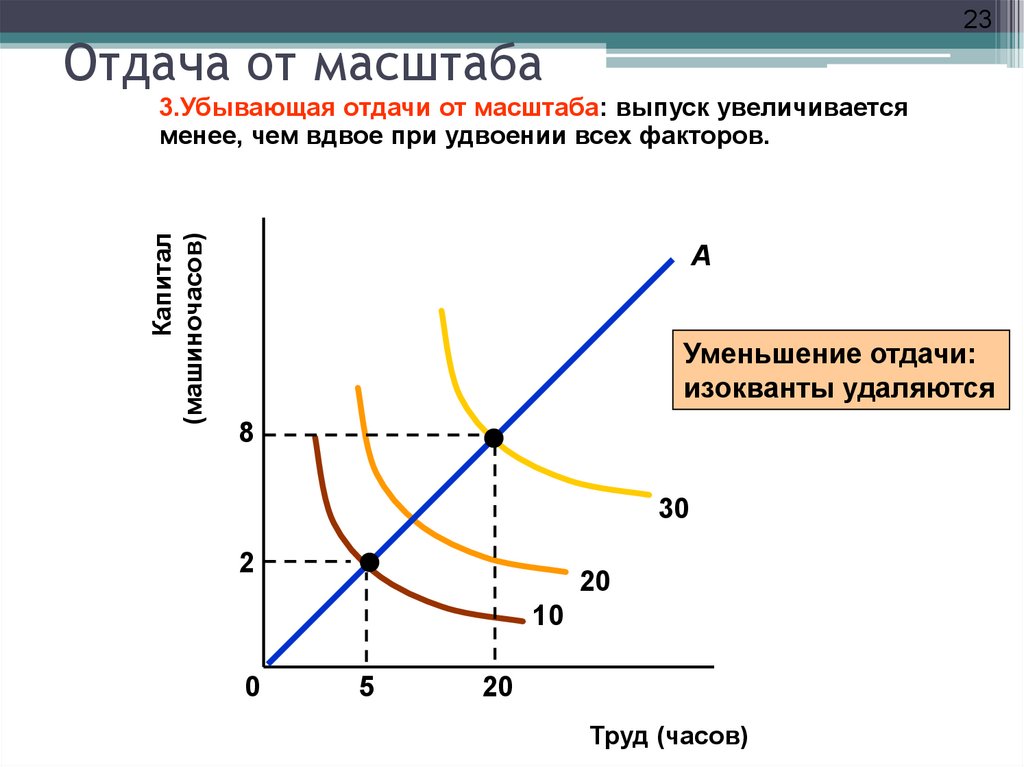
23. Отдача от масштаба
23Отдача от масштаба
Капитал
(машиночасов)
3.Убывающая отдачи от масштаба: выпуск увеличивается
менее, чем вдвое при удвоении всех факторов.
A
Уменьшение отдачи:
изокванты удаляются
8
30
2
20
10
0
5
20
Труд (часов)
24. Решая вопрос о приобретаемом количестве конкретного фактора производства, фирма должна сравнить выгоду, которую она получит в
24Решая вопрос о приобретаемом
количестве конкретного
фактора производства, фирма
должна сравнить выгоду,
которую она получит в
результате, с затратами.
25. Производство с одним переменным фактором (трудом)
25Производство с одним переменным
фактором (трудом)
• Наблюдения:
1) При использовании
дополнительных рабочих, выпуск (Q)
возрастает, достигает максимума,
и затем падает.
Совокупный продукт (Q) — это
количество
экономического
блага,
произведенное
с
использованием
некоторого
количества
переменного
фактора.
26. Средний продукт труда (APL) –характеризует производительность рабочей силы фирмы. Показывает, сколько продукции в среднем
26• Наблюдения:
2)
Средний продукт труда (APL),
или объем выпуска на рабочего,
повышается, а затем понижается.
Выпуск
Q
AP
L
Затраты труда L
Средний продукт труда (APL) –
характеризует производительность
рабочей силы фирмы. Показывает,
сколько продукции в среднем производит
каждый работник
27. Производство с одним переменным фактором (трудом)
27Производство с одним переменным
фактором (трудом)
• Наблюдения:
3) Предельный продукт труда
(MPL ) - дополнительный объем
выпуска продукции, создаваемый при
увеличении затрат труда на единицу :
Выпуск
Q
MPL
Затраты труда L
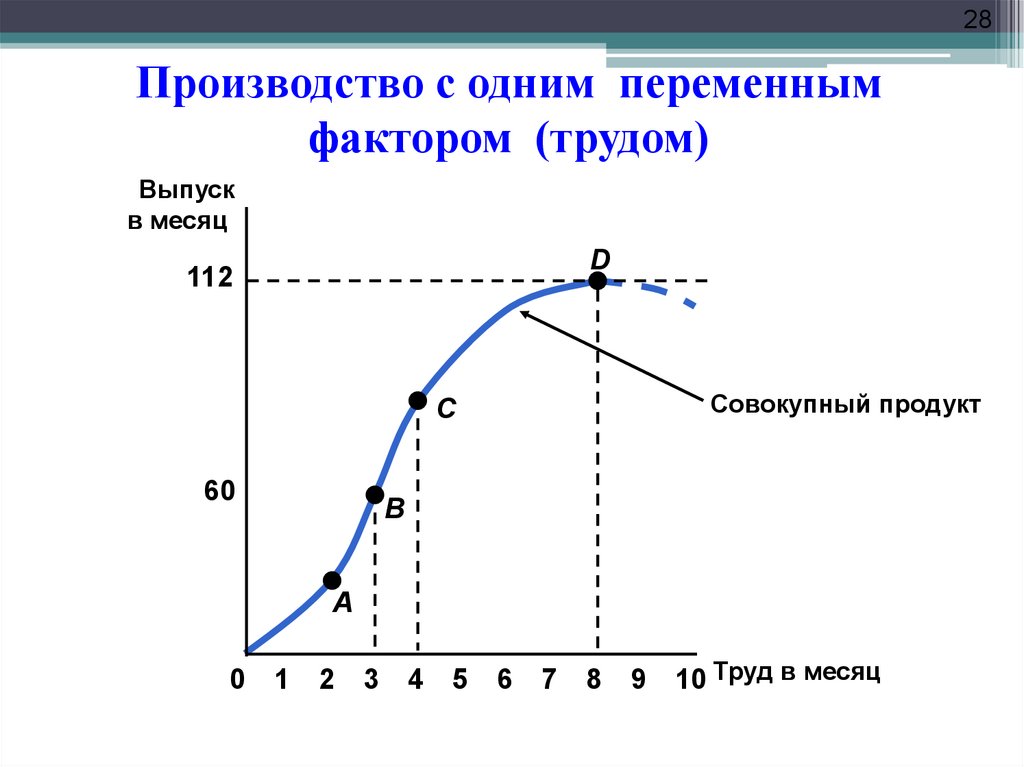
28. Производство с одним переменным фактором (трудом)
28Производство с одним переменным
фактором (трудом)
Выпуск
в месяц
D
112
Совокупный продукт
C
60
B
A
0 1
2 3
4
5 6
7 8
9
10 Труд в месяц
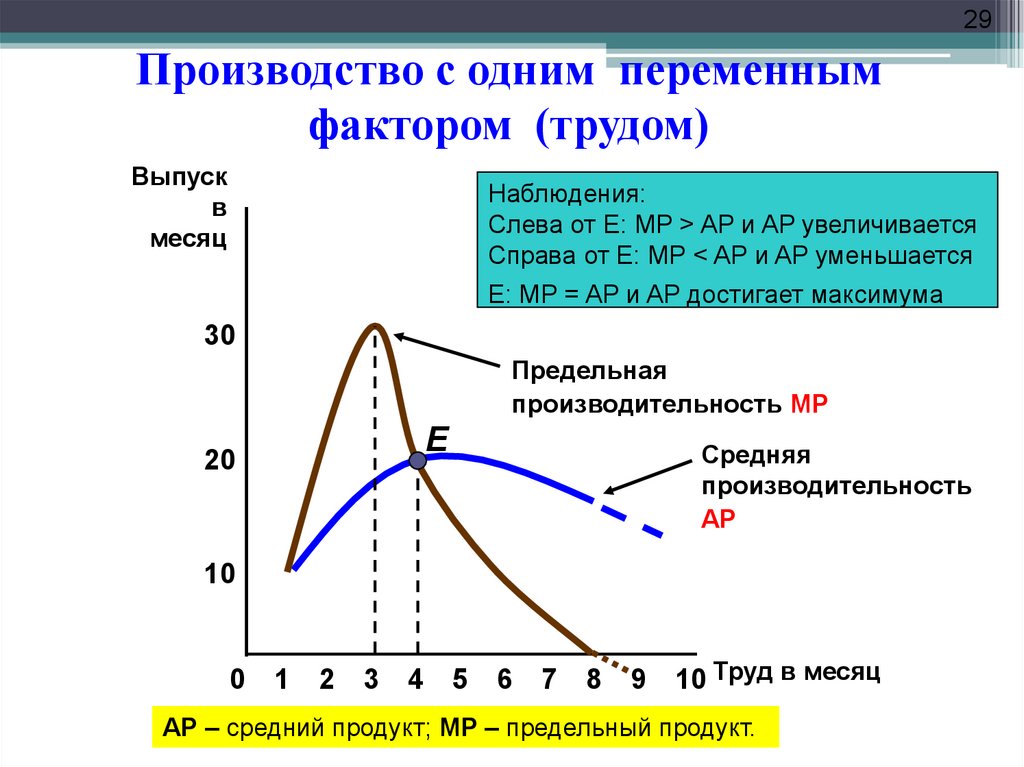
29. Производство с одним переменным фактором (трудом)
29Производство с одним переменным
фактором (трудом)
Выпуск
в
месяц
Наблюдения:
Слева от E: MP > AP и AP увеличивается
Справа от E: MP < AP и AP уменьшается
E: MP = AP и AP достигает максимума
30
Предельная
производительность MP
E
20
Средняя
производительность
AP
10
0 1
2 3
4
5 6
7 8
9
10 Труд в месяц
AP – средний продукт; MP – предельный продукт.
30. 2. Результаты деятельности фирмы. Закон убывающей предельной производительности
302. Результаты
деятельности фирмы.
Закон убывающей
предельной
производительности
31.
31Закон убывающей
предельной производительности:
при последовательном
увеличении производственного
фактора на единицу (и при
постоянстве остальных
факторов) приросты объемов
выпуска начиная с некоторого
момента уменьшаются
(MP понижается)
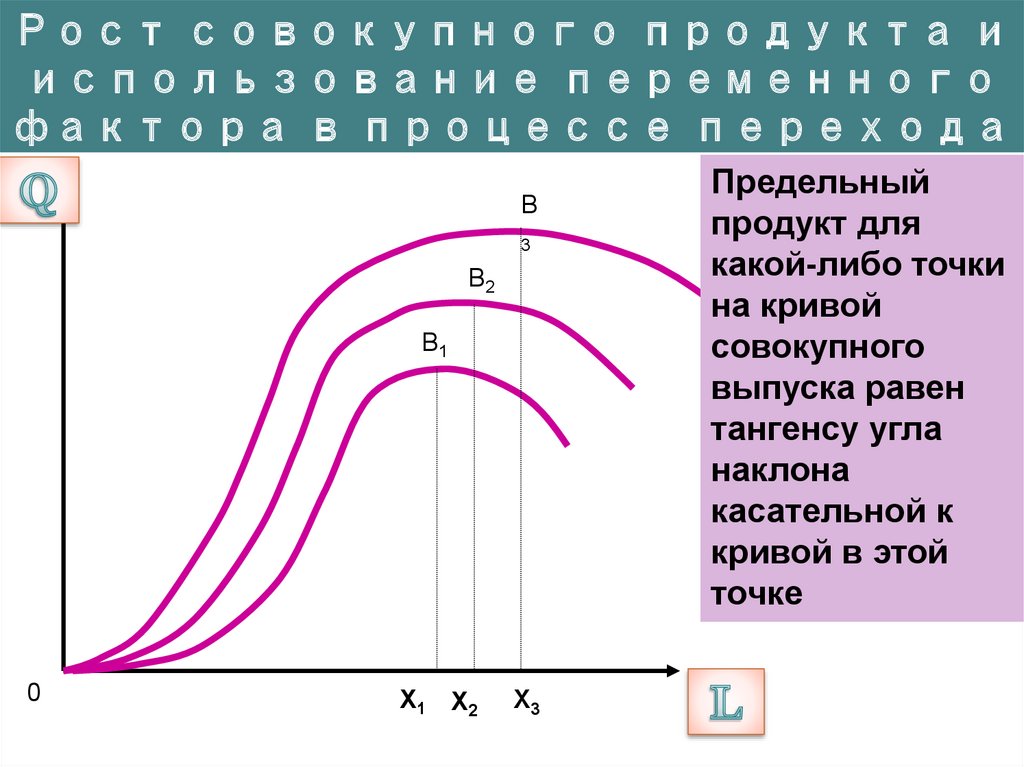
32.
Рост совокупного продукта ииспользование переменного
фактора в процессе перехода
ТР
к новым технологиям
Предельный
В
3
В2
В1
0
X1 X2
X3
продукт для
какой-либо точки
на кривой
совокупного
выпуска равен
тангенсу угла
наклона
касательной к
кривой в этой
точке
F
33.
33• Наем рабочих может продолжаться до тех пор,
пока предельный продукт их труда (МRРL) в
денежном выражении не сравняется с
величиной заработной платы (w)
дополнительного работника.
• Для предпринимателя заработная плата
дополнительного работника является
предельными издержками, –
дополнительными затратами на приобретение
одной дополнительной единицы труда.
• Прием последующих сотрудников
экономически не выгоден, поскольку величина
их предельного продукта (МRРL = МР х Р)
окажется ниже уровня их заработной платы (w).
34. Равновесие фирмы
34Равновесие фирмы
35. Равновесие фирмы
35Равновесие фирмы
Чтобы максимизировать прибыль,
каждый производитель (фирма) должен
использовать дополнительные
(предельные) единицы любого ресурса
до тех пор, пока каждая дополнительная
единица ресурса дает прирост
совокупного дохода, превышающий
прирост совокупных издержек.
36. Правило наименьших издержек
36Правило наименьших издержек
37. Правило наименьших издержек
37Правило наименьших издержек
— это условие, согласно которому
издержки минимизируются в том
случае, когда последний доллар
(евро,
рубль
и
так
далее),
затраченный на каждый ресурс,
дает
одинаковую
отдачу
—
одинаковый предельный продукт.
Правило
наименьших
обеспечивает равновесие
производителя.
издержек
положения
38.
38Степень использования ресурса в
производстве
определяется
разницей
между
доходом
(выручкой), которую он приносит,
и издержками, связанными с его
использованием.
Рациональный производитель стремится
максимизировать эту разность.
39. Правило максимизации прибыли
39Правило максимизации прибыли
• Ресурс
будет
находить
применение
в
производстве до тех пор, пока его предельная
производительность в денежном выражении
будет не ниже его цены МRР > Р.
Это означает, что
цена ресурсов измеряет предельную
производительность этих факторов.
• Предельный доход должен быть равен
предельным издержкам
МR=МС
40.
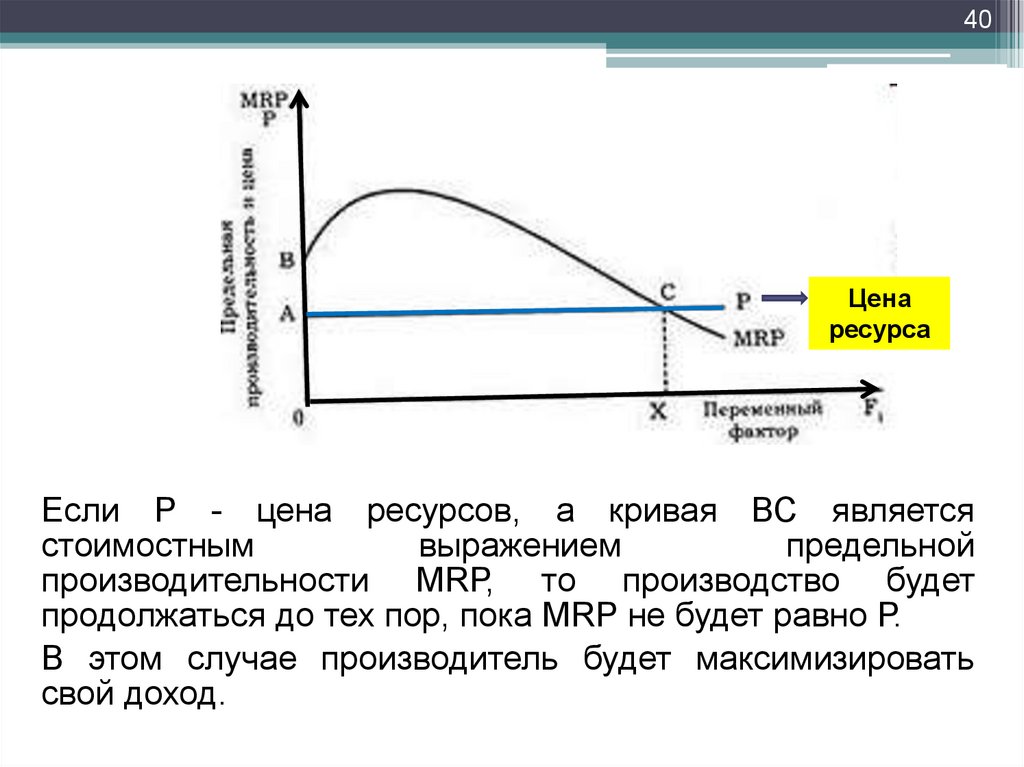
40Цена
ресурса
Если Р - цена ресурсов, а кривая ВС является
стоимостным
выражением
предельной
производительности МRР, то производство будет
продолжаться до тех пор, пока МRР не будет равно Р.
В этом случае производитель будет максимизировать
свой доход.
41.
413. Понятие изоквант,
производственные
множества и
технологическая
эффективность.
Предельная норма
технологического
замещения (MRTS)
42. Изокванта -
42Изокванта это кривая, отражающая все
возможные комбинации
факторов производства,
которые обеспечивают
одинаковый максимально возможный объем
производства
43. Являясь графической формой производственной функции, изокванта обладает теми же характеристиками, что и производственная
43Являясь графической формой производственной
функции, изокванта обладает теми же
характеристиками, что и производственная
функция.
• Во-первых, изокванта показывает
максимальный объем выпуска для
каждой отдельной комбинации факторов.
• Во-вторых, она имеет отрицательный
наклон, что свидетельствует о
разнонаправленном изменении
факторов: увеличение количества одного
фактора предполагает уменьшение
количества другого для неизменного
объема выпуска.
44.
44• В-третьих, являясь вогнутой
кривой, изокванта отражает
действие закона убывающей
отдачи: по мере увеличения
применения одного фактора и
относительном уменьшении другого
предельная производительность
первого снижается, а второго –
растет.
• В-четвертых, изокванты отражают
только экономическую область.
45.
45• Набор изоквант, или карта
изоквант, описывает
производственную функцию фирмы.
• Изокванты подчеркивают, насколько
различны могут быть комбинации
факторов при одном и том же
выпуске.
• Эта информация позволяет
производителю эффективно
реагировать на изменения на рынке,
меняя комбинацию затрат.
46. Производство с двумя переменными факторами (L,K)
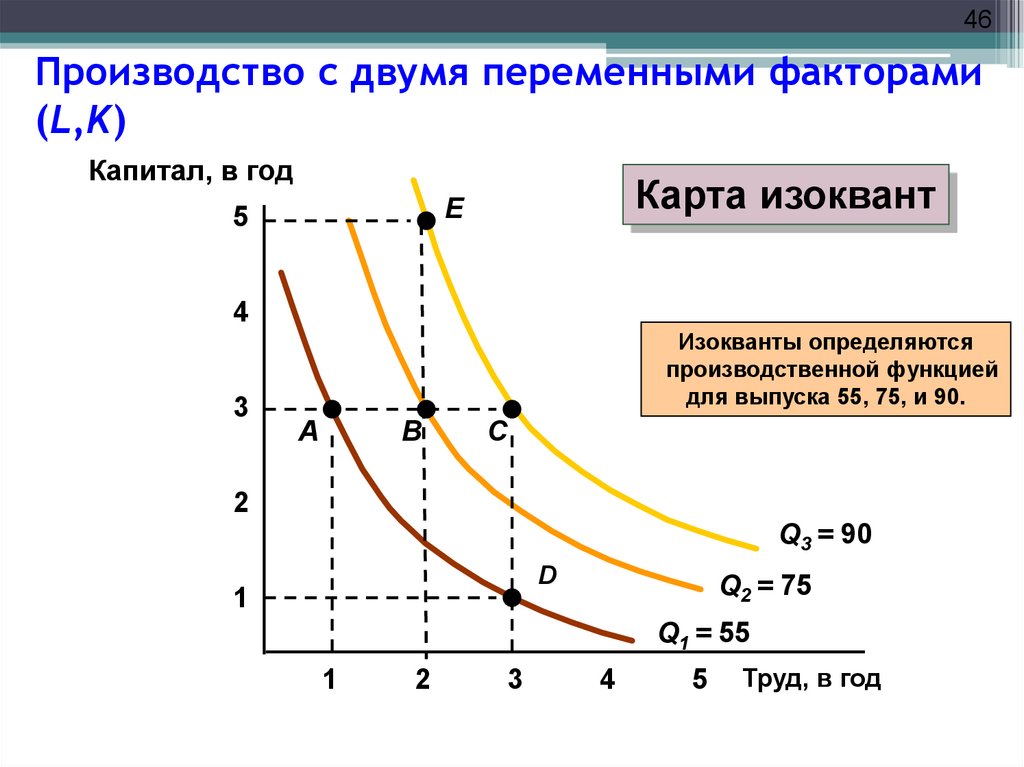
46Производство с двумя переменными факторами
(L,K)
Капитал, в год
Карта изоквант
E
5
4
3
Изокванты определяются
производственной функцией
для выпуска 55, 75, и 90.
A
B
C
2
Q3 = 90
D
1
Q2 = 75
Q1 = 55
1
2
3
4
5
Труд, в год
47. Технологическая (техническая) эффективность
47Способ производства признается
технологически эффективным, если не
существует другого способа, который бы
использовал для выпуска данного
объема продукции меньшее количество
хотя бы одного из факторов и не больше
— любого из остальных.
Она необходима, но недостаточна для
того, чтобы производство велось с
наименьшими издержками
(для экономически эффективного
производства).
48. Множество производственных возможностей –
48Множество производственных
возможностей –
это множество тех наборов товаров и
услуг, которые могут быть
произведены экономическим
субъектом (фирмой) при заданных
ограничениях на факторы
производства.
Кривая, ограничивающая множество
производственных возможностей, называется
кривой производственных
возможностей.
49. Предельная норма технологического замещения (MRTS) -
49показывает, как происходит техническое
замещение (субституция) одного ресурса
(капитала) другим (трудом).
MRTS - Изменение количества капитала/Изменение количества труда
MRTS K
L
(при постоянном уровне Q)
Наклон каждой изокванты показывает пропорции
замещения факторов, в то время как выпуск
остается прежним.
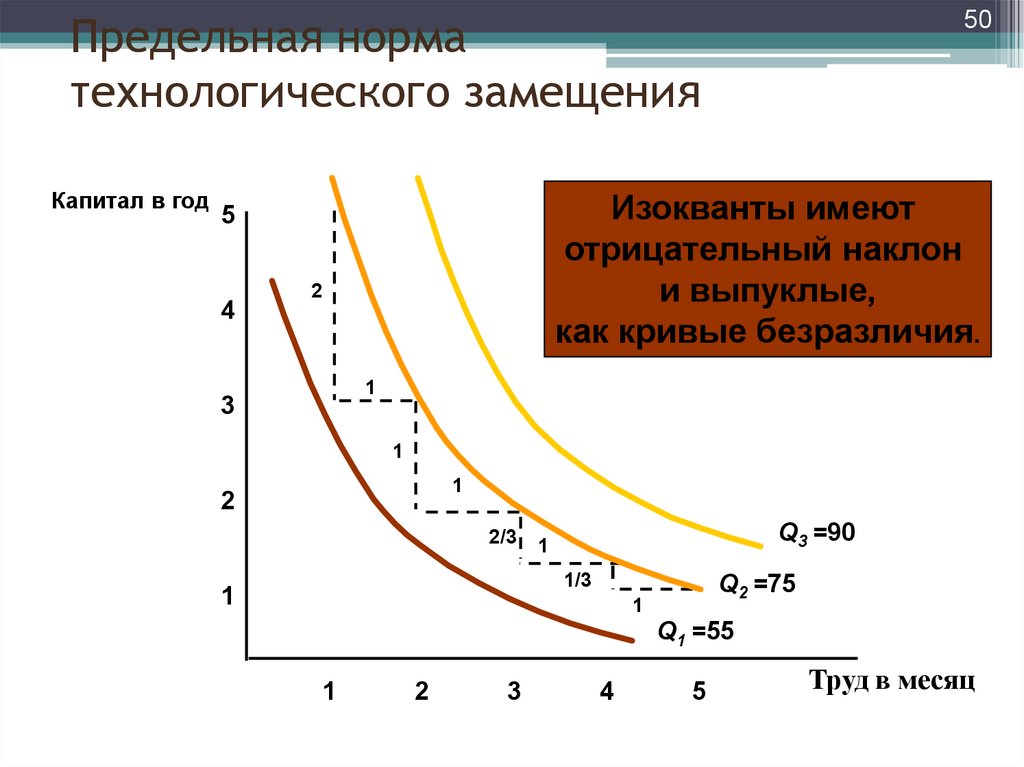
50. Предельная норма технологического замещения
Капитал в годИзокванты имеют
отрицательный наклон
и выпуклые,
как кривые безразличия.
5
4
50
2
1
3
1
1
2
2/3
Q3 =90
1
1/3
1
Q2 =75
1
Q1 =55
1
2
3
4
5
Труд в месяц
51. Предельная норма технологического замещения
511) Последовательное увеличение затрат
труда на одну единицу от 1 до 5, ведет к
снижению MRTS с 2 до 1/3.
2) Уменьшение MRTS происходит из-за
снижения отдачи от увеличения
количества фактора производства (труда)
и показывает, что изокванта выпукла.
52. Предельная норма технологического замещения
3)MRTS и предельная производительностьИзменение выпуска при изменении труда
равняется:
(MP L )( L)
52
53.
53и предельная производительность
Изменение выпуска при изменении
капитала равняется:
(MP K )( K)
54.
54Если
выпуск остается постоянным, а
труд увеличивается, то:
(MP L )( L) (MP K )( K) 0
55.
554. Равновесие
производителя.
Кривая «путь
развития»
56.
56• Анализ с помощью изоквант имеет для
производителя очевидные недостатки,
так как использует только натуральные
показатели затрат ресурсов и выпуска
продукции.
• Максимизировать выпуск при данных
издержках позволяет
прямая равных издержек, или
изокоста.
57. Равновесие производителя
57Равновесие производителя
▫
Два вида затрат: труд (L) и
капитал (K)
▫
Цена труда: заработная плата
(w)
▫
Цена капитала (r)
58.
58• Линия изокост C = wL + rK
Изокоста – линия,
показывающая все комбинации
L и K, которые могут быть
приобретены без изменения
бюджета затрат.
59.
59Линия изокост
• Перепишем C в виде линейного уравнения:
▫
K = C/r - (w/r)L
▫
Наклон изокост:
Отношение заработной платы к капитальным
издержкам K
w
L
r
Показывает норму, по которой капитал может
быть замещен трудом без перемен в размере
издержек.
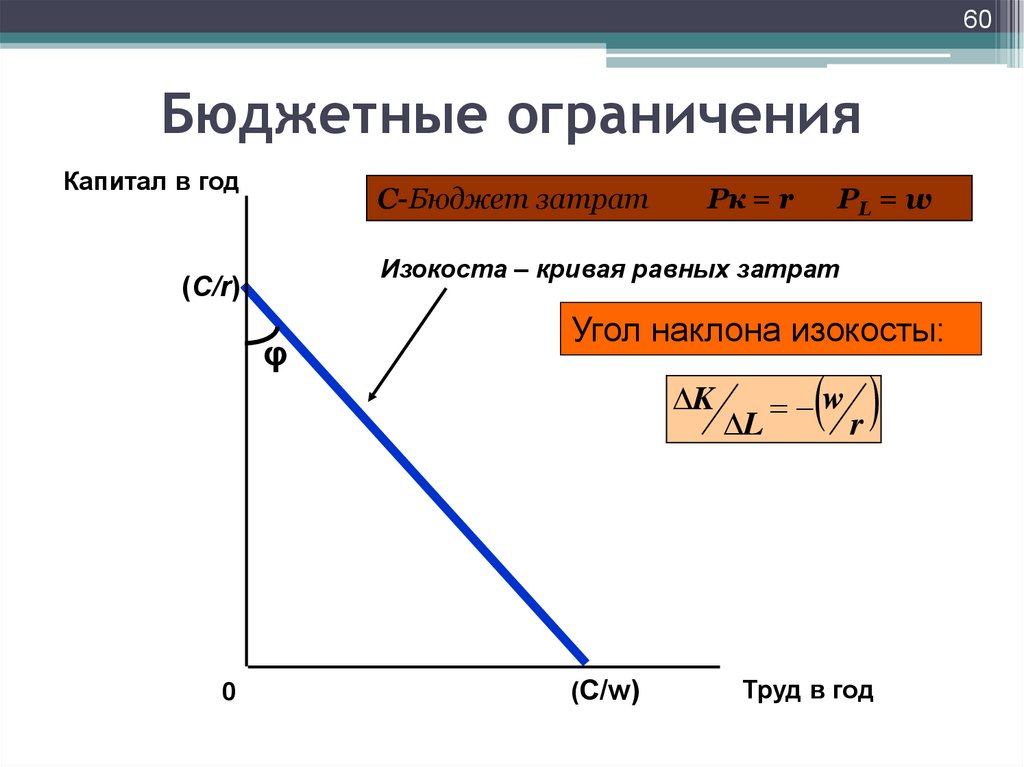
60. Бюджетные ограничения
60Бюджетные ограничения
Капитал в год
C-Бюджет затрат
Pк = r
Изокоста – кривая равных затрат
(С/r)
φ
Угол наклона изокосты:
K
0
PL = w
(C/w)
L
r
w
Труд в год
61.
61• Определим, как
минимизировать издержки
при заданном уровне выпуска.
Определим это, комбинируя
изокосты с изоквантами
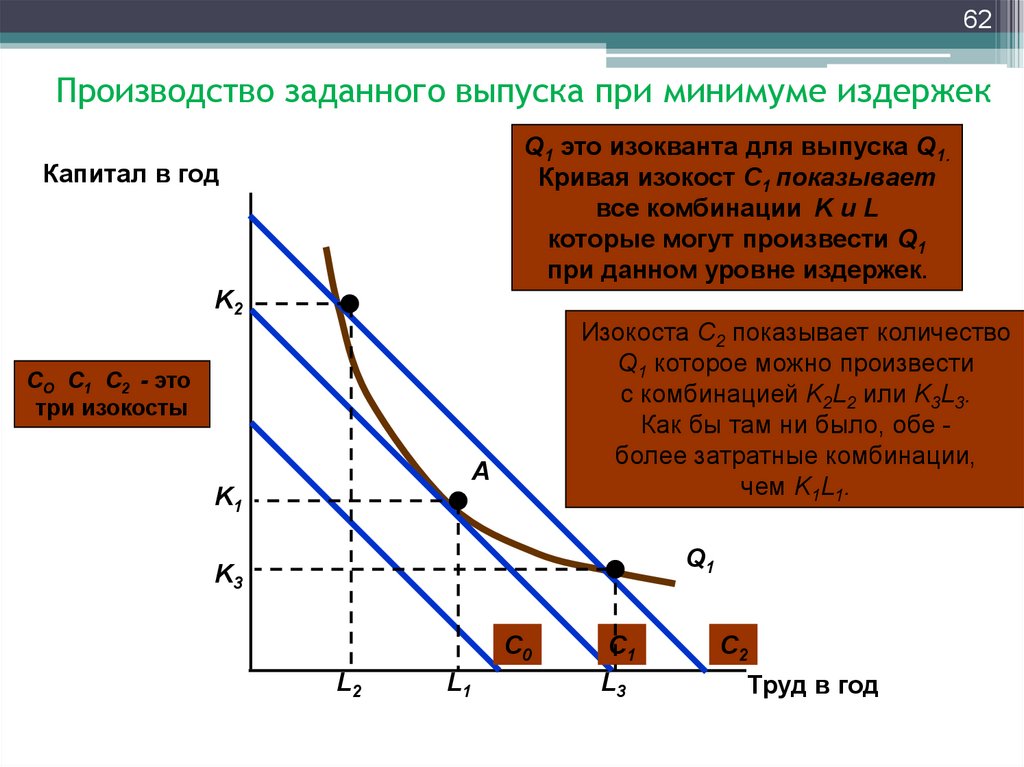
62. Производство заданного выпуска при минимуме издержек
62Производство заданного выпуска при минимуме издержек
Q1 это изокванта для выпуска Q1.
Кривая изокост C1 показывает
все комбинации K и L
которые могут произвести Q1
при данном уровне издержек.
Капитал в год
K2
Изокоста C2 показывает количество
Q1 которое можно произвести
с комбинацией K2L2 или K3L3.
Как бы там ни было, обе более затратные комбинации,
чем K1L1.
CO C1 C2 - это
три изокосты
A
K1
Q1
K3
C0
L2
L1
C1
L3
C2
Труд в год
63.
63• В случае изменения цен
факторов производства (труда
и капитала) произойдет
смещение изокосты в новое
положение и будет найдено
новое равновесие.
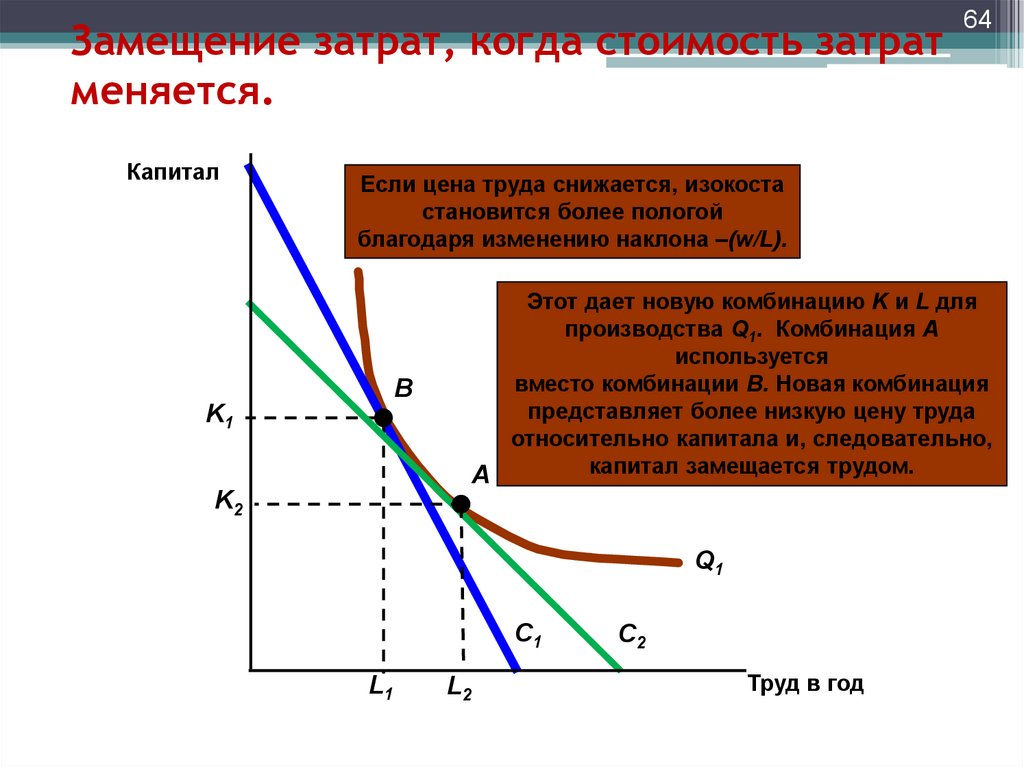
64. Замещение затрат, когда стоимость затрат меняется.
Капитал64
Если цена труда снижается, изокоста
становится более пологой
благодаря изменению наклона –(w/L).
Этот дает новую комбинацию K и L для
производства Q1. Комбинация А
используется
вместо комбинации В. Новая комбинация
представляет более низкую цену труда
относительно капитала и, следовательно,
капитал замещается трудом.
A
B
K1
K2
Q1
C1
L1
L2
C2
Труд в год
65. Равновесие производителя
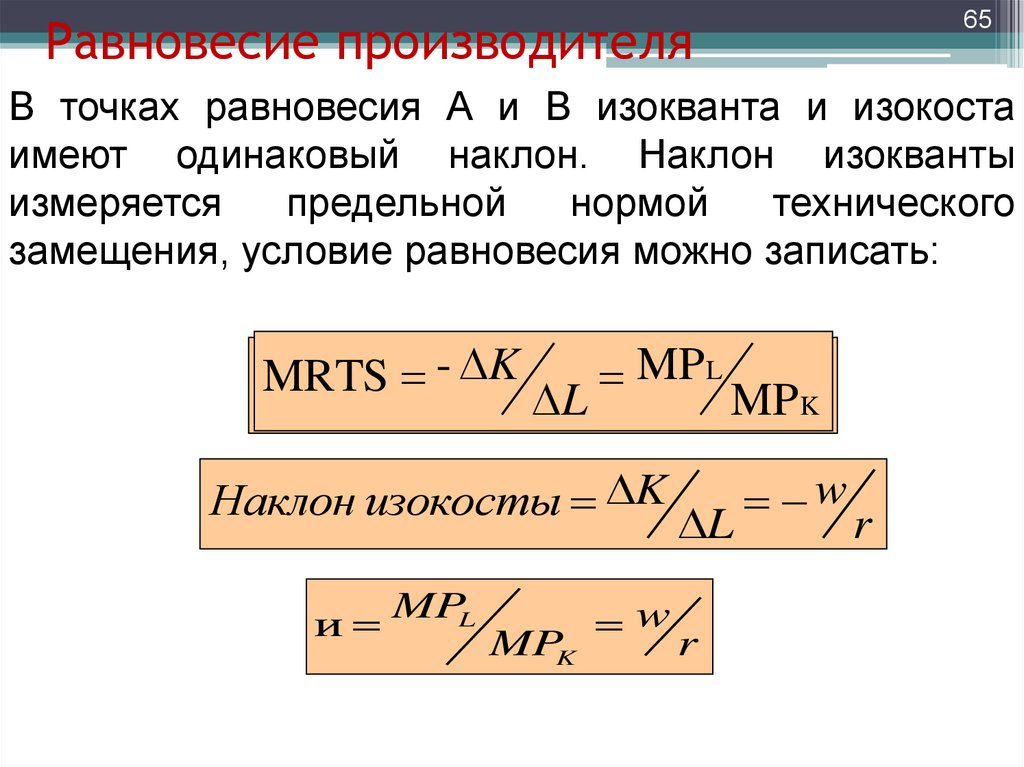
65Равновесие производителя
В точках равновесия А и В изокванта и изокоста
имеют одинаковый наклон. Наклон изокванты
измеряется
предельной
нормой
технического
замещения, условие равновесия можно записать:
MRTS - K
L
MP L
Наклон изокосты K
и
MPL
MPK
w
MP K
L
r
w
r
66.
66• Минимальная комбинация затрат может
быть выражена как:
MPL
▫
w
MPK
r
Минимальная комбинация затрат для
заданного выпуска – когда каждый доллар,
добавленный
в
ходе
производственного
процесса,
добавит
эквивалентный
объем
выпуска.
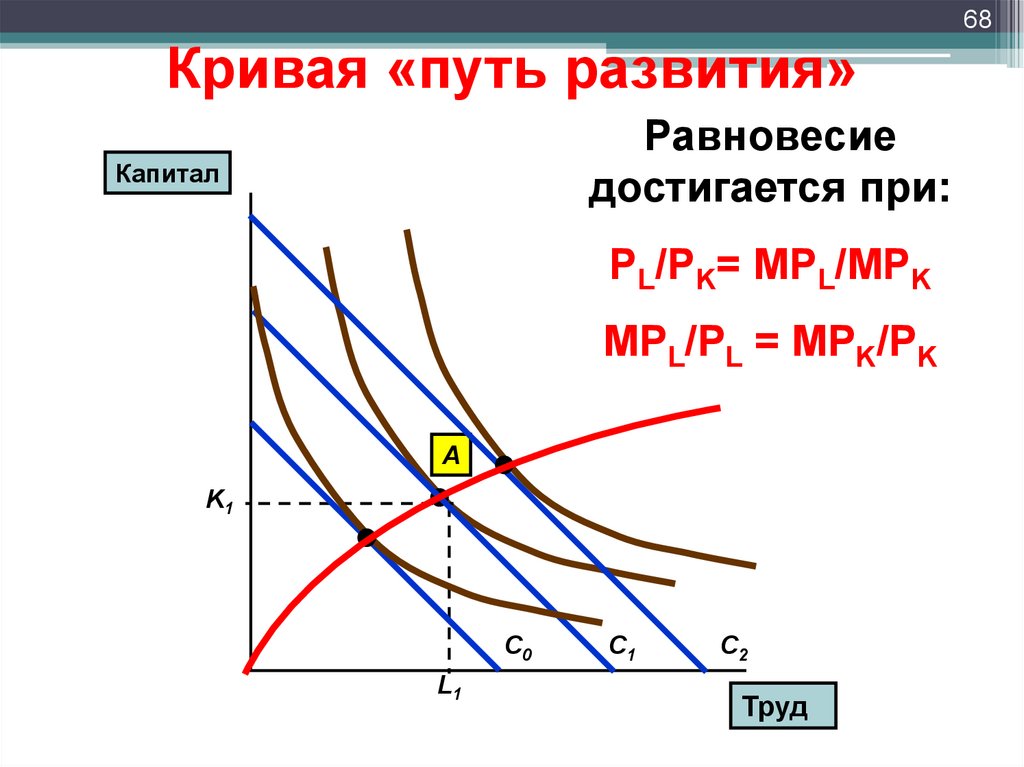
67. Кривая «путь развития»
67Кривая «путь развития»
• Предположим, что цены ресурсов
остаются неизменными, тогда как
бюджет производителя постоянно
растет.
• Равновесие производителя при этом
будет
смещаться
вместе
со
смещением изокост.
• Кривая
«путь
развития»
показывает траекторию смещения
равновесия производителя.
68.
68Кривая «путь развития»
Равновесие
достигается при:
Капитал
PL/PK= MPL/MPK
MPL/PL = MPK/PK
A
K1
C0
L1
C1
C2
Труд

















































 Экономика
Экономика








