Похожие презентации:
Описательная статистика для исследования экономических моделей
1.
Описательная статистикадля исследования
экономических моделей
Подготовила: к.п.н, доцент
Пьянкова Н.Г.
1
2.
Цель занятия:изучение функциональных
возможностей табличного процессора Excel 2007 и
приобретение навыков практической работы по
использованию средств описательной статистики для
исследования экономических моделей.
Задачи занятия:
Научиться
использовать
статистические
функции, а также пакет анализа данных,
используемых
для
описания
экономических
моделей.
2
3.
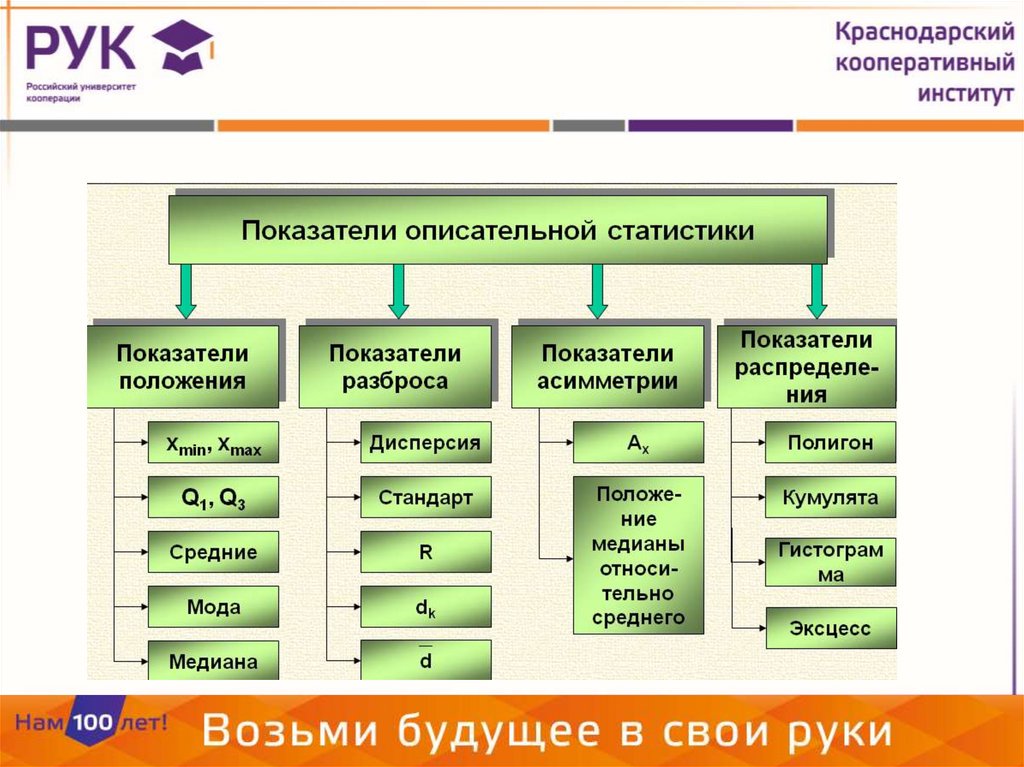
План лабораторного занятия:1. Функции MS Excel для оценки показателей положения
2. Функции MS Excel для оценки показателей разброса
3. Расчет средствами MS Excel показателя ассиметрии
4. Расчет средствами MS Excel показателя распределения
5. Пакет анализа данных
6. Задание для самостоятельной работы
3
4.
45.
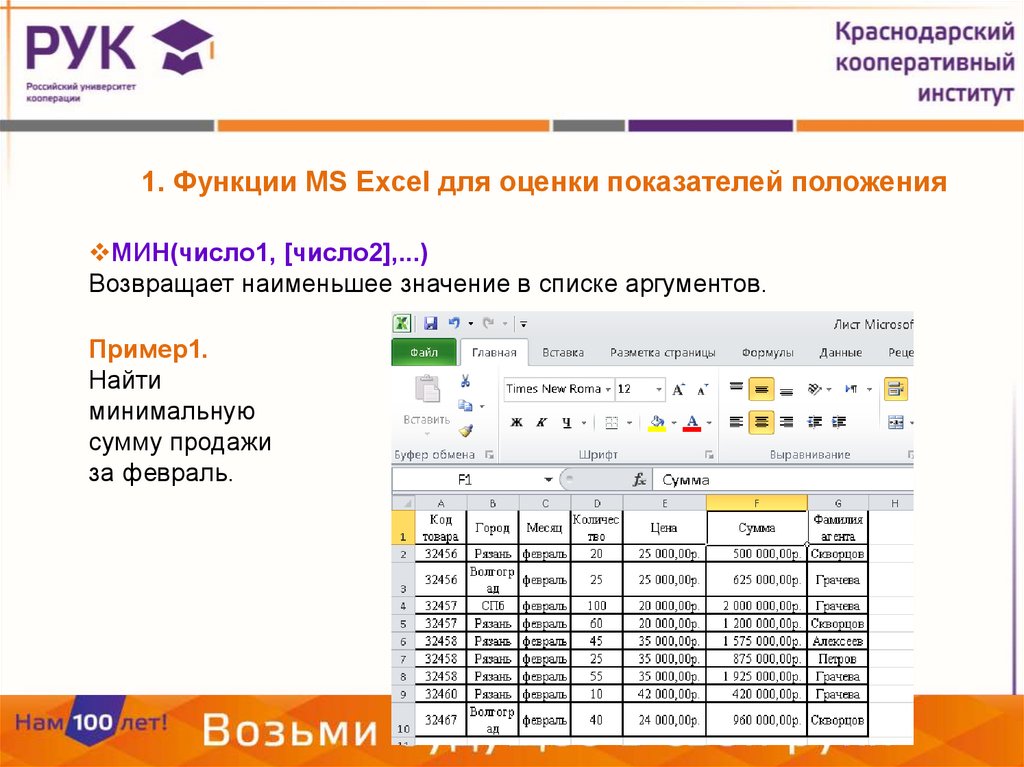
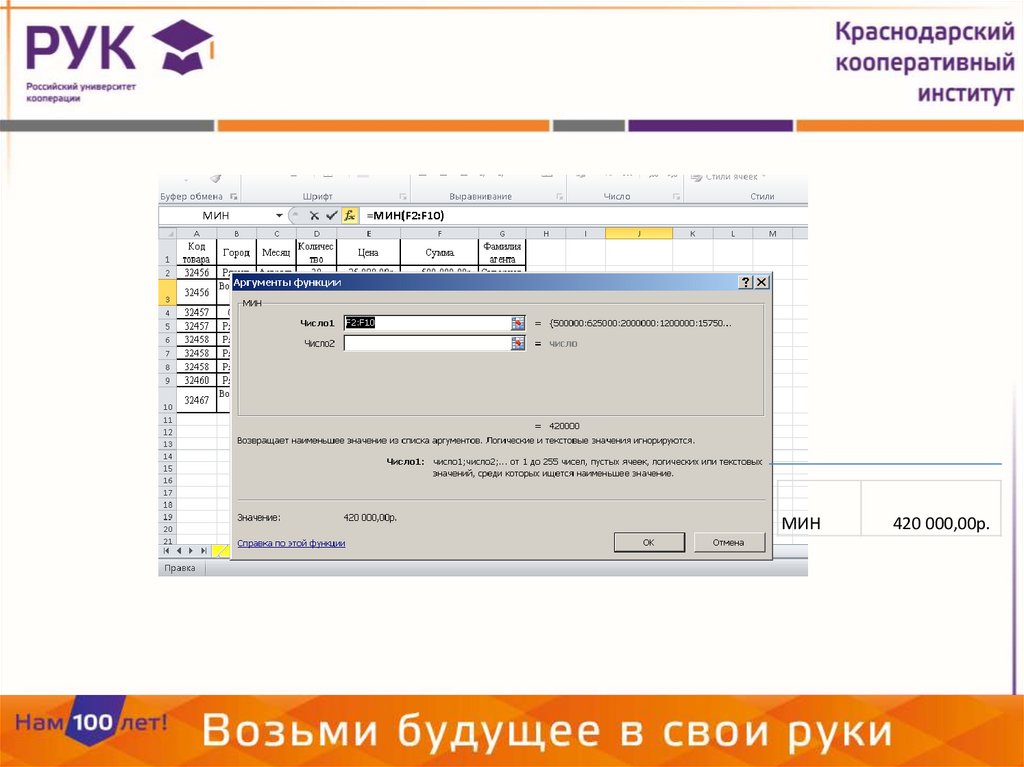
1. Функции MS Excel для оценки показателей положенияМИН(число1, [число2],...)
Возвращает наименьшее значение в списке аргументов.
Пример1.
Найти
минимальную
сумму продажи
за февраль.
5
6.
МИН420 000,00р.
6
7.
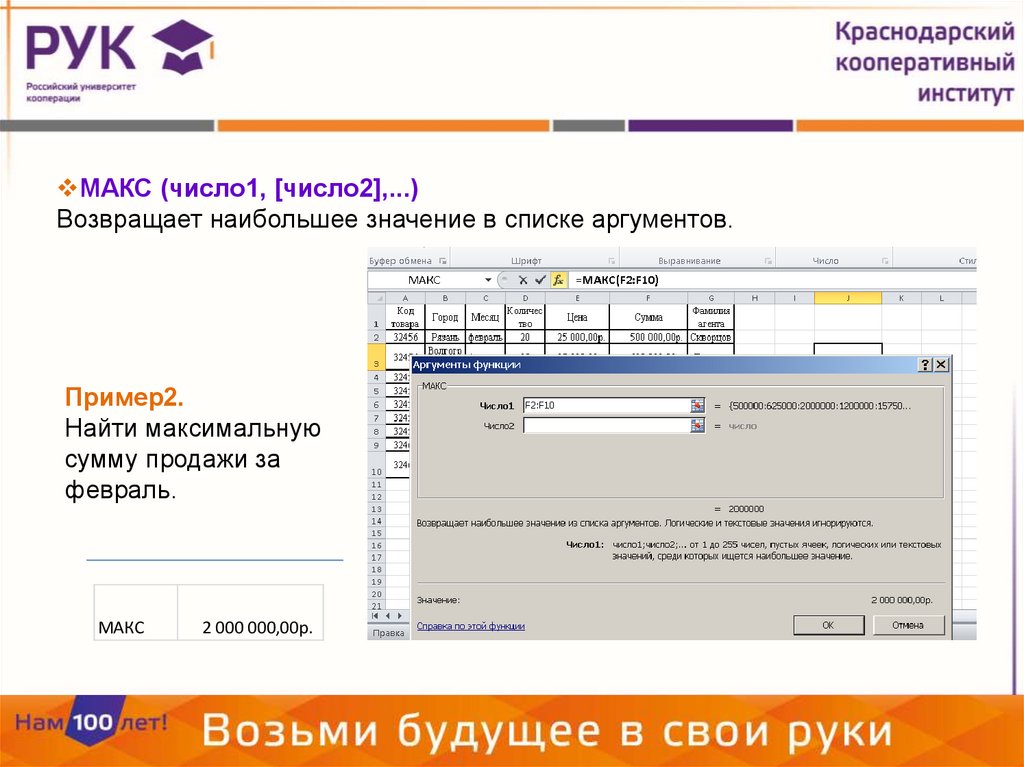
МАКС (число1, [число2],...)Возвращает наибольшее значение в списке аргументов.
Пример2.
Найти максимальную
сумму продажи за
февраль.
МАКС
2 000 000,00р.
7
8.
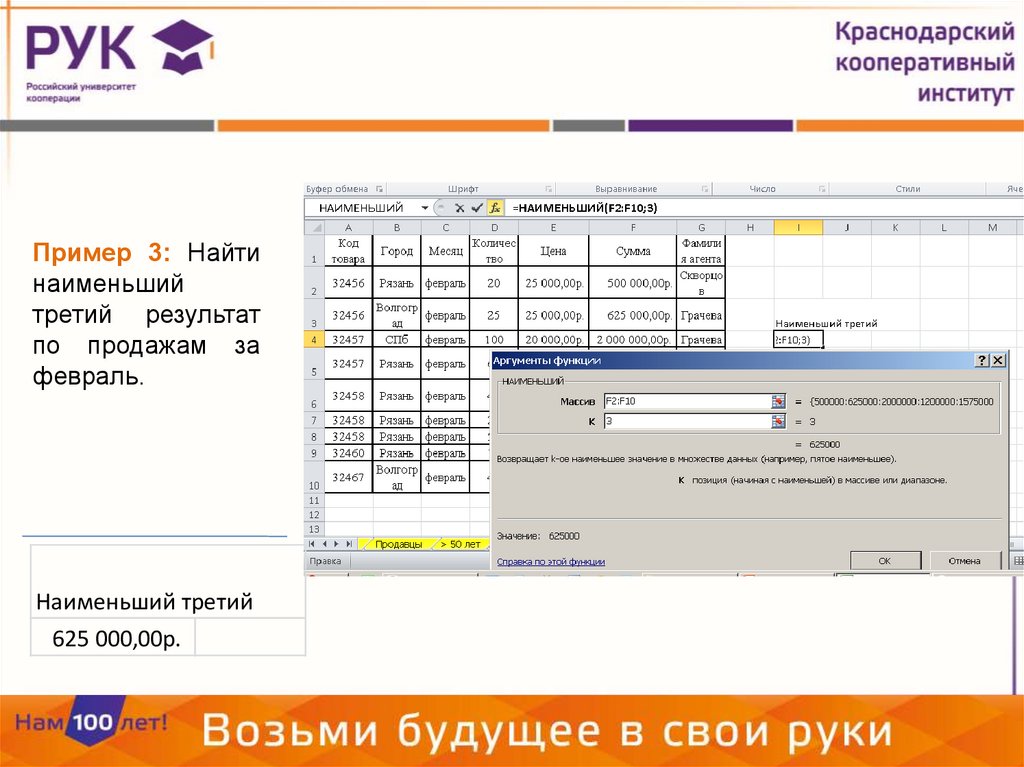
НАИМЕНЬШИЙ(массив, k)Возвращает k-ое наименьшее значение в множестве данных. Эта функция
используется для определения значения, занимающего заданное
относительное положение в множестве данных.
Замечание:
Если массив пуст, функция НАИМЕНЬШИЙ возвращает значение
ошибки #ЧИСЛО!.
Если k ≤ 0 или превышает число точек данных, функция НАИМЕНЬШИЙ
возвращает значение ошибки #ЧИСЛО!.
8
9.
Пример 3: Найтинаименьший
третий результат
по продажам за
февраль.
Наименьший третий
625 000,00р.
9
10.
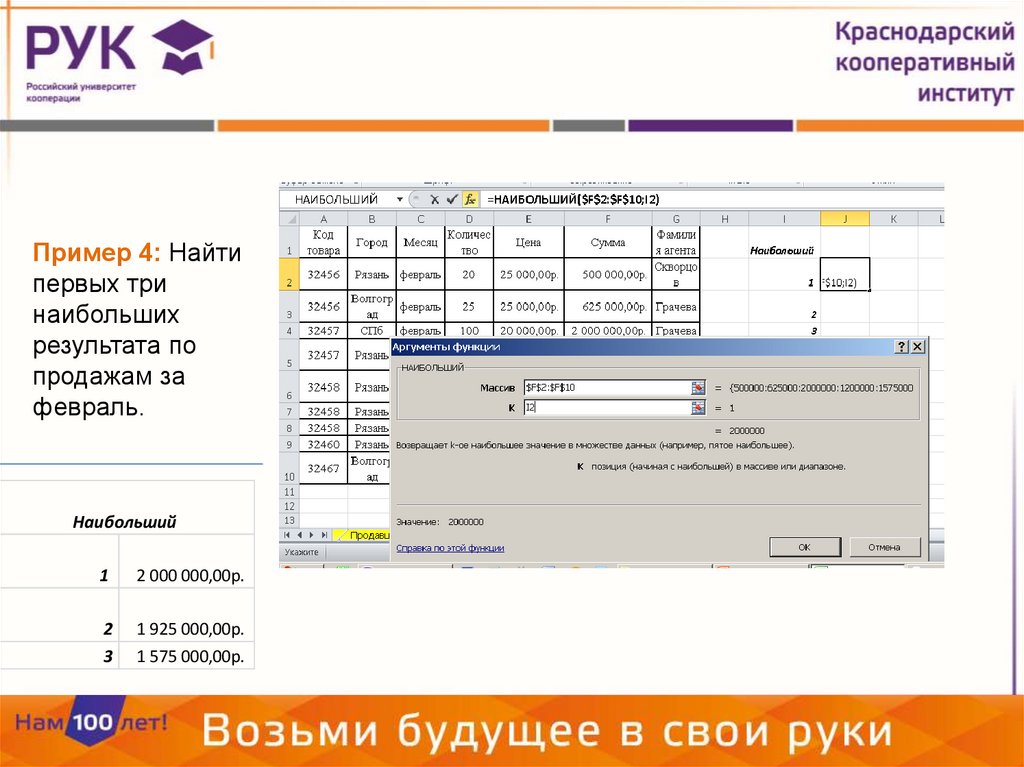
НАИБОЛЬШИЙ(массив, k)Возвращает k-ое по величине значение из множества данных. Эта
функция позволяет выбрать значение по его относительному
местоположению.
Замечание:
Если массив пуст, функция НАИБОЛЬШИЙ возвращает значение ошибки
#ЧИСЛО!.
Если k ≤ 0 или k больше, чем число точек данных, функция
НАИБОЛЬШИЙ возвращает значение ошибки #ЧИСЛО!.
10
11.
Пример 4: Найтипервых три
наибольших
результата по
продажам за
февраль.
Наибольший
1
2 000 000,00р.
2
1 925 000,00р.
3
1 575 000,00р.
11
12.
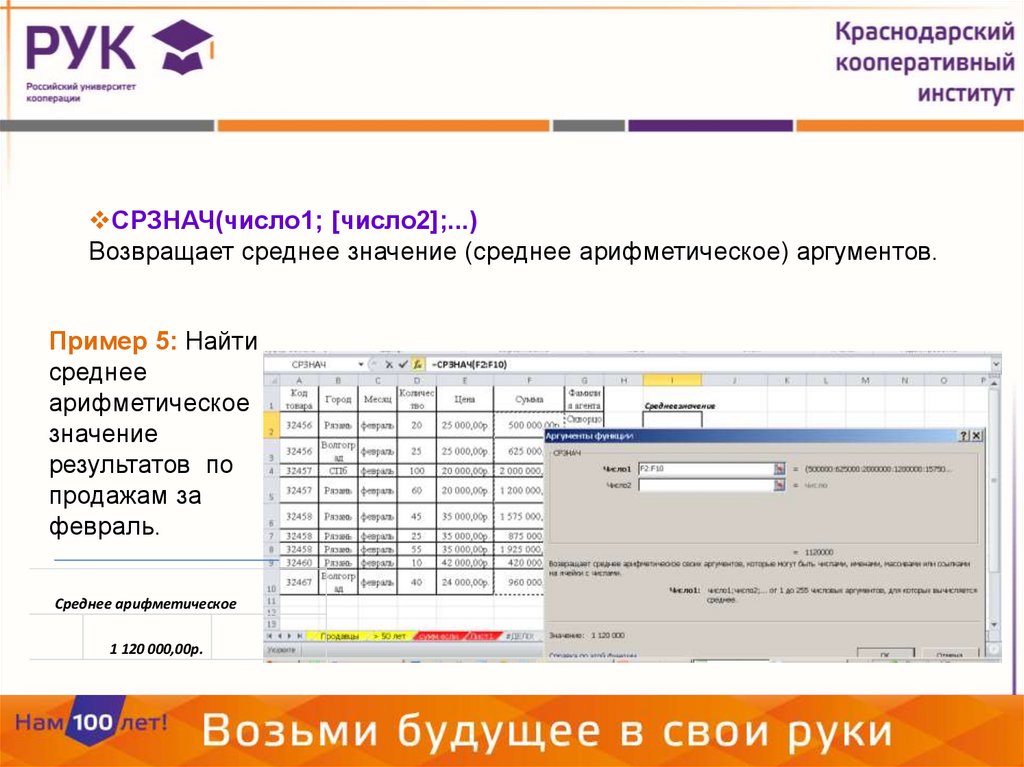
СРЗНАЧ(число1; [число2];...)Возвращает среднее значение (среднее арифметическое) аргументов.
Пример 5: Найти
среднее
арифметическое
значение
результатов по
продажам за
февраль.
Среднее арифметическое
1 120 000,00р.
12
13.
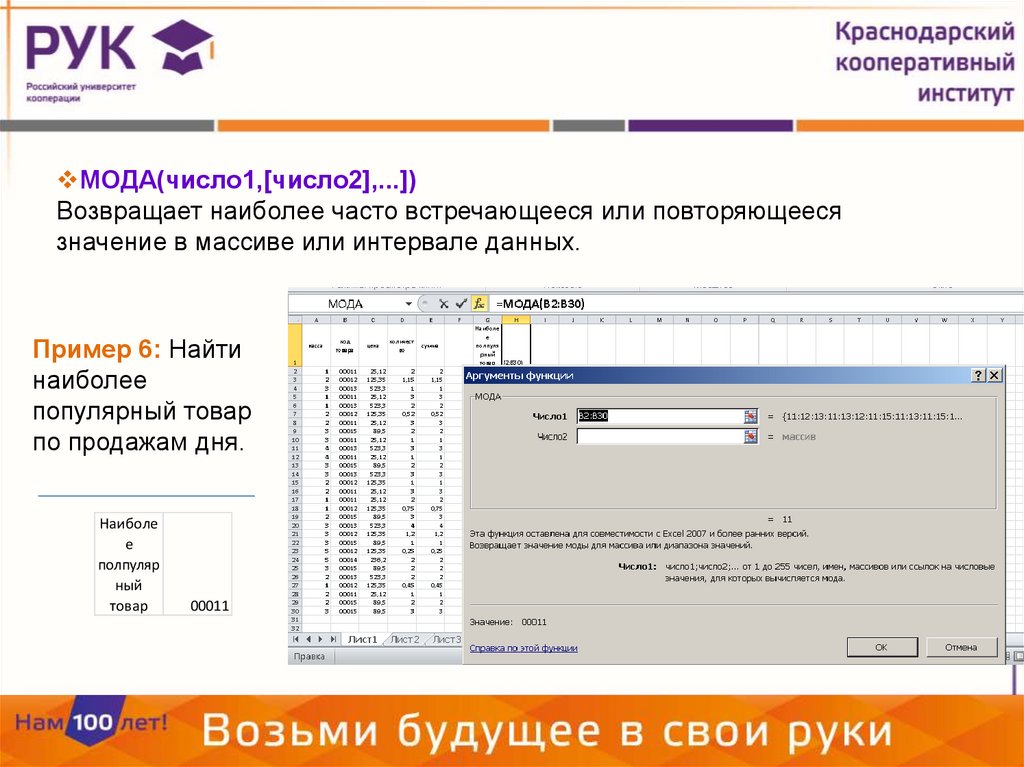
МОДА(число1,[число2],...])Возвращает наиболее часто встречающееся или повторяющееся
значение в массиве или интервале данных.
Пример 6: Найти
наиболее
популярный товар
по продажам дня.
Наиболе
е
полпуляр
ный
товар
00011
13
14.
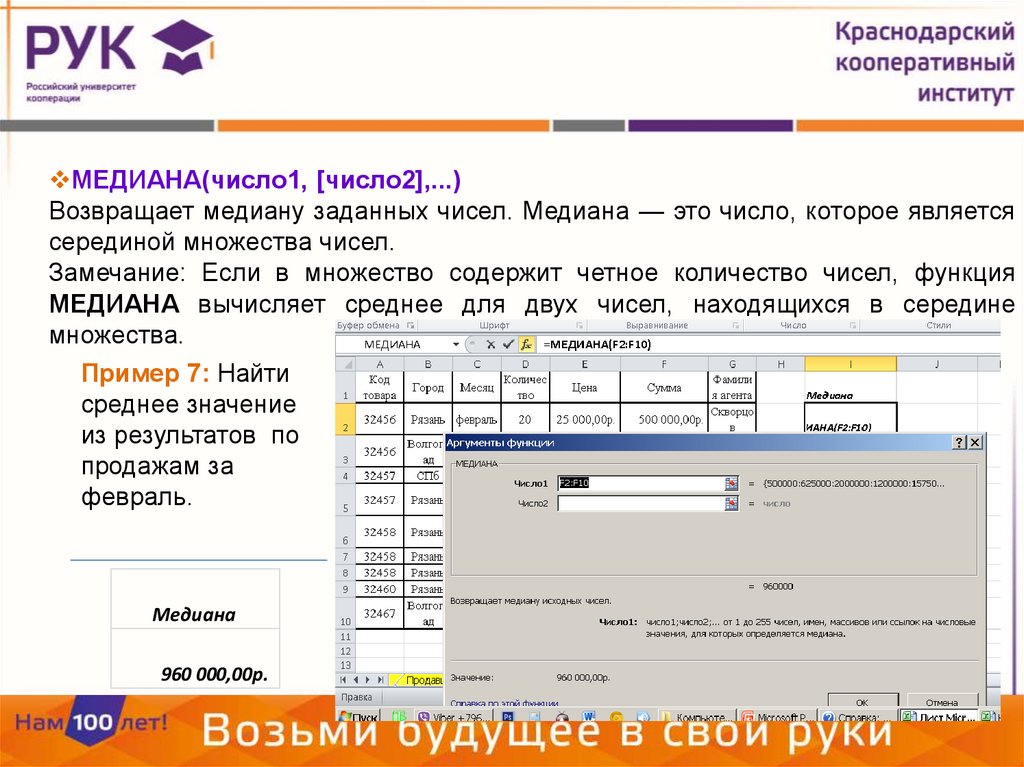
МЕДИАНА(число1, [число2],...)Возвращает медиану заданных чисел. Медиана — это число, которое является
серединой множества чисел.
Замечание: Если в множество содержит четное количество чисел, функция
МЕДИАНА вычисляет среднее для двух чисел, находящихся в середине
множества.
Пример 7: Найти
среднее значение
из результатов по
продажам за
февраль.
Медиана
960 000,00р.
14
15.
СРЗНАЧЕСЛИ(диапазон, условие, [диапазон_усреднения])Возвращает среднее значение (среднее арифметическое) всех ячеек в
диапазоне, которые соответствуют данному условию.
Аргументы:
Диапазон Обязательный. Одна или несколько ячеек для вычисления
среднего, включающих числа или имена, массивы или ссылки, содержащие
числа.
Условие Обязательный. Условие в форме числа, выражения, ссылки на
ячейку или текста, которое определяет ячейки, используемые при
вычислении среднего. Например, условие может быть выражено
следующим образом: 32, "32", ">32", "яблоки" или B4.
Диапазон_усреднения Необязательный. Фактическое множество ячеек
для вычисления среднего. Если этот параметр не указан, используется
диапазон.
15
16.
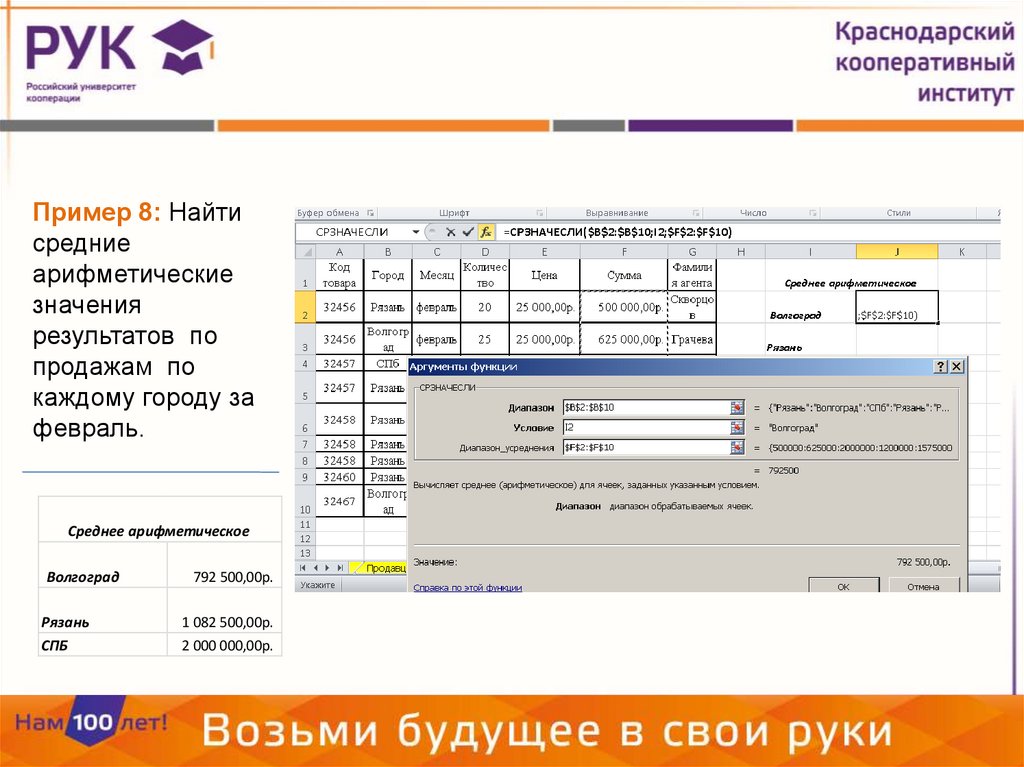
Пример 8: Найтисредние
арифметические
значения
результатов по
продажам по
каждому городу за
февраль.
Среднее арифметическое
Волгоград
792 500,00р.
Рязань
1 082 500,00р.
СПБ
2 000 000,00р.
16
17.
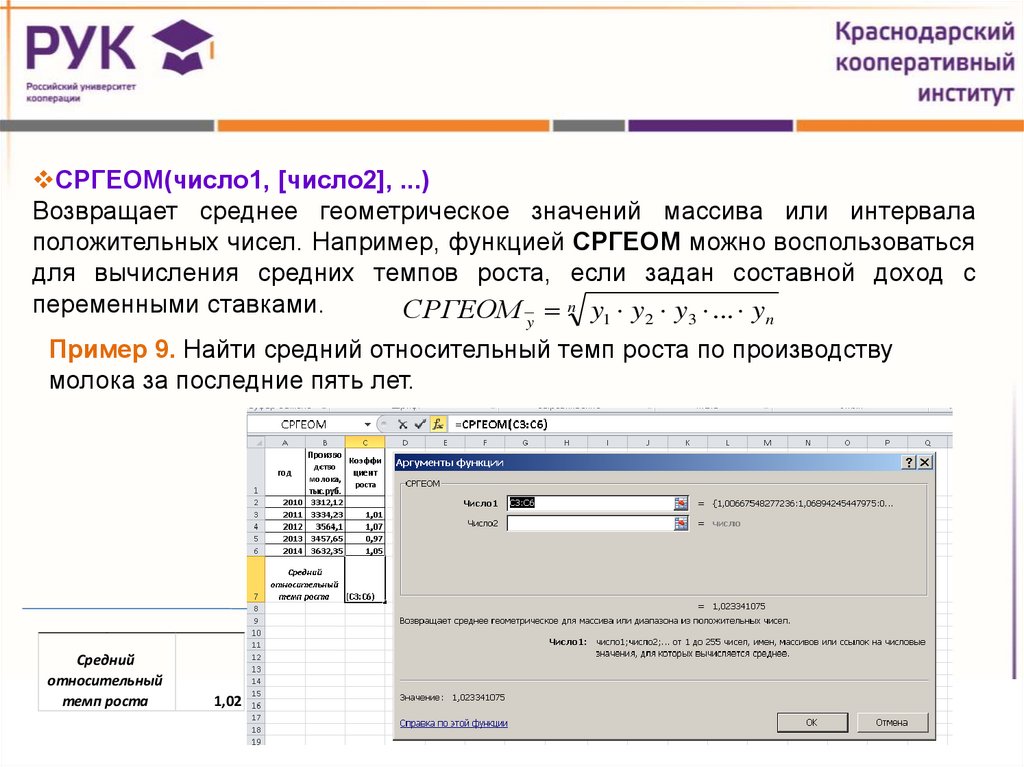
СРГЕОМ(число1, [число2], ...)Возвращает среднее геометрическое значений массива или интервала
положительных чисел. Например, функцией СРГЕОМ можно воспользоваться
для вычисления средних темпов роста, если задан составной доход с
переменными ставками.
СРГЕОМ y n y1 y2 y3 ... yn
Пример 9. Найти средний относительный темп роста по производству
молока за последние пять лет.
Средний
относительный
темп роста
1,02
17
18.
2. Функции MS Excel для оценки показателей разброса( xi x ) 2
n 1
i 1
Дисперсия – характеристика разброса, средняя величина квадрата
отклонения всех случайных величин в данном распределении.
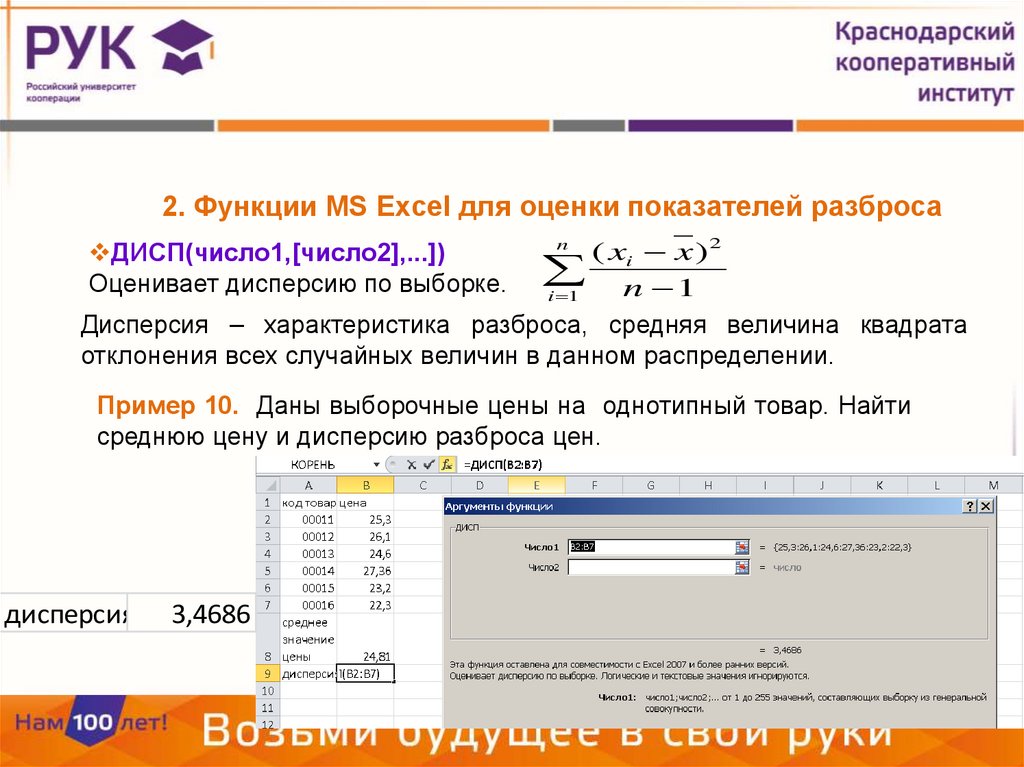
ДИСП(число1,[число2],...])
Оценивает дисперсию по выборке.
n
Пример 10. Даны выборочные цены на однотипный товар. Найти
среднюю цену и дисперсию разброса цен.
дисперсия
3,4686
18
19.
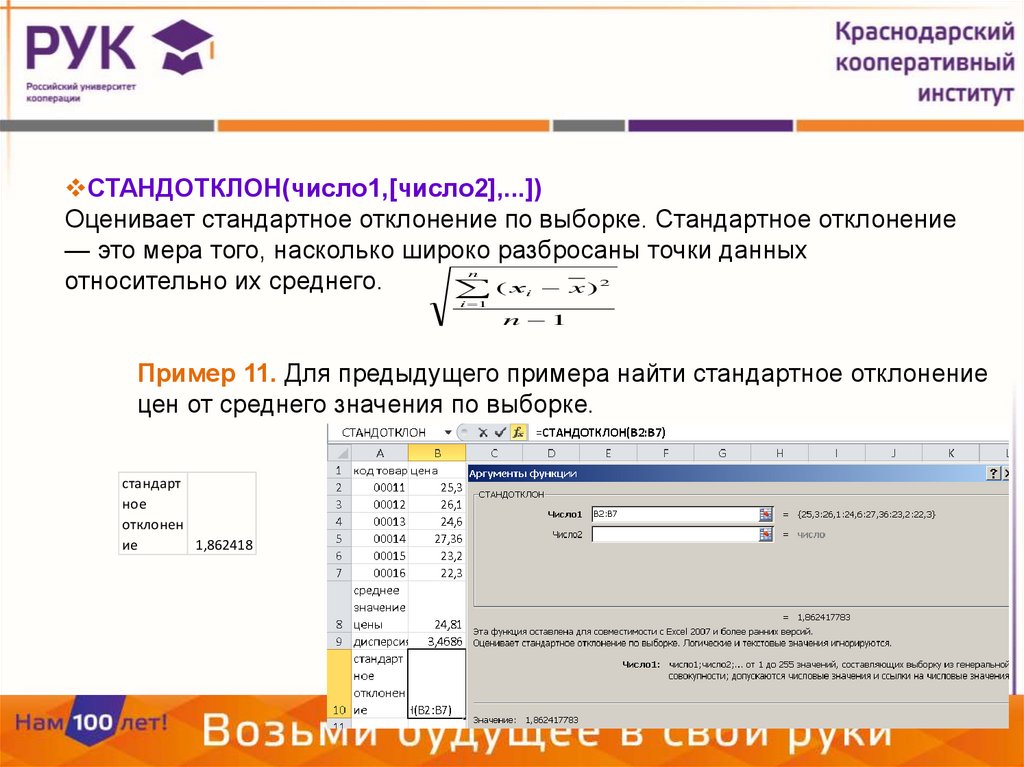
СТАНДОТКЛОН(число1,[число2],...])Оценивает стандартное отклонение по выборке. Стандартное отклонение
— это мера того, насколько широко разбросаны точки данных
относительно их среднего.
( х x)
n
2
i
i 1
n 1
Пример 11. Для предыдущего примера найти стандартное отклонение
цен от среднего значения по выборке.
стандарт
ное
отклонен
ие
1,862418
19
20.
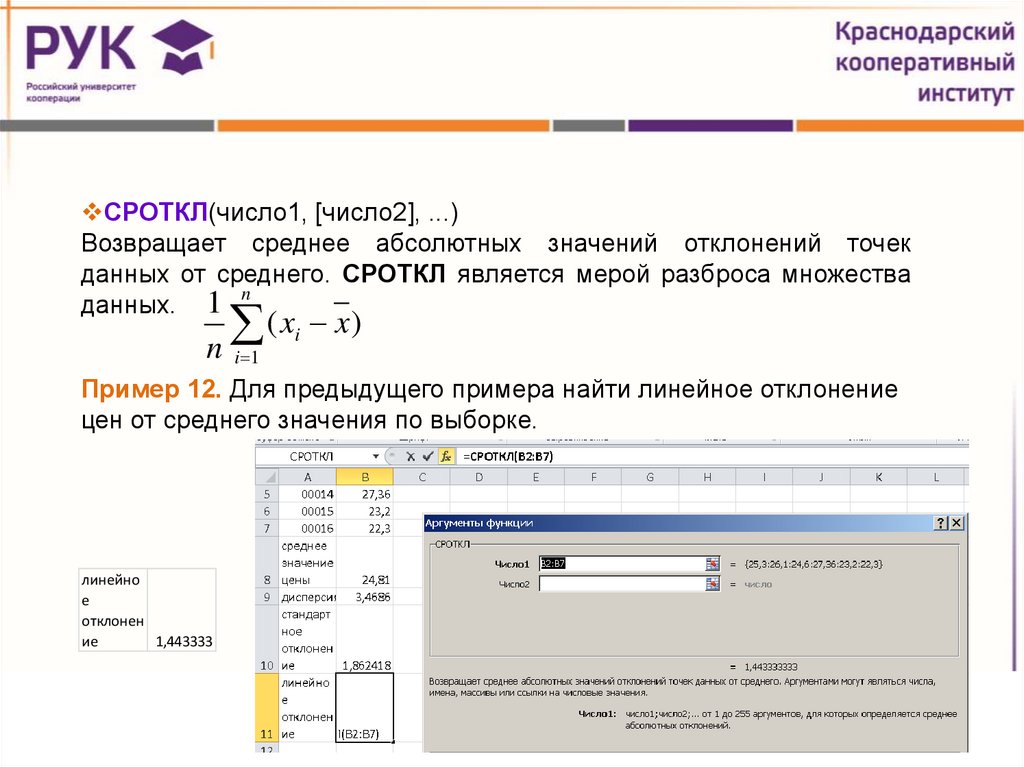
СРОТКЛ(число1, [число2], ...)Возвращает среднее абсолютных значений отклонений точек
данных от среднего. СРОТКЛ является мерой разброса множества
n
данных. 1
( x x)
n
i 1
i
Пример 12. Для предыдущего примера найти линейное отклонение
цен от среднего значения по выборке.
линейно
е
отклонен
ие
1,443333
20
21.
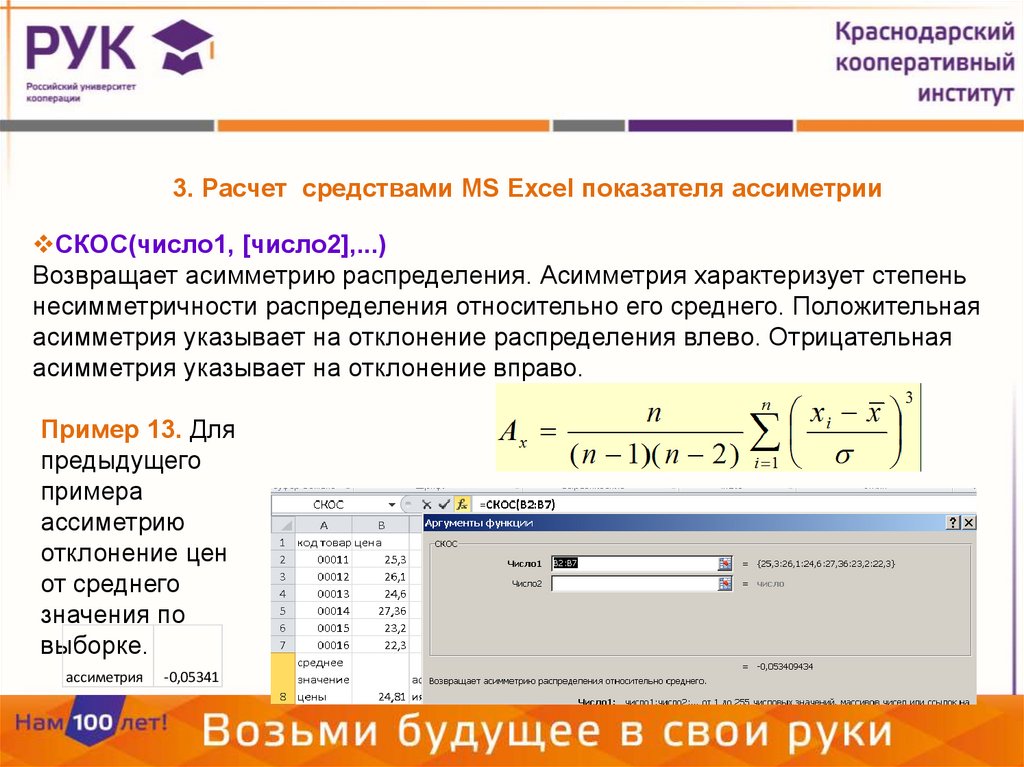
3. Расчет средствами MS Excel показателя ассиметрииСКОС(число1, [число2],...)
Возвращает асимметрию распределения. Асимметрия характеризует степень
несимметричности распределения относительно его среднего. Положительная
асимметрия указывает на отклонение распределения влево. Отрицательная
асимметрия указывает на отклонение вправо.
Пример 13. Для
предыдущего
примера
ассиметрию
отклонение цен
от среднего
значения по
выборке.
ассиметрия
-0,05341
21
22.
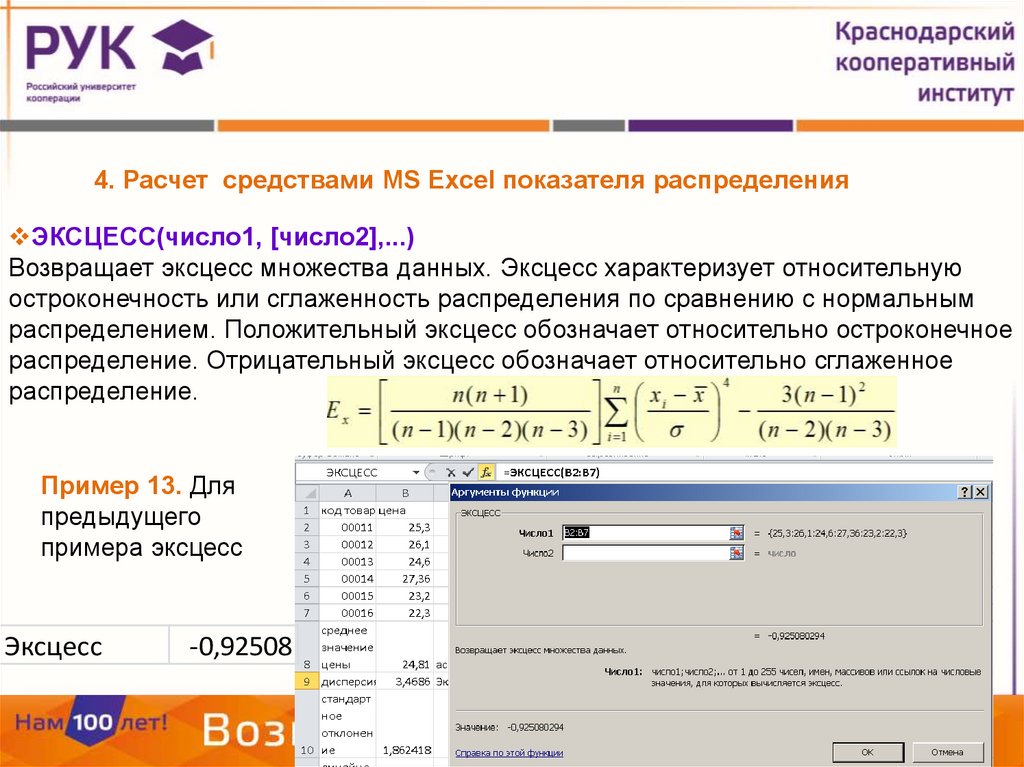
4. Расчет средствами MS Excel показателя распределенияЭКСЦЕСС(число1, [число2],...)
Возвращает эксцесс множества данных. Эксцесс характеризует относительную
остроконечность или сглаженность распределения по сравнению с нормальным
распределением. Положительный эксцесс обозначает относительно остроконечное
распределение. Отрицательный эксцесс обозначает относительно сглаженное
распределение.
Пример 13. Для
предыдущего
примера эксцесс
Эксцесс
-0,92508
22
23.
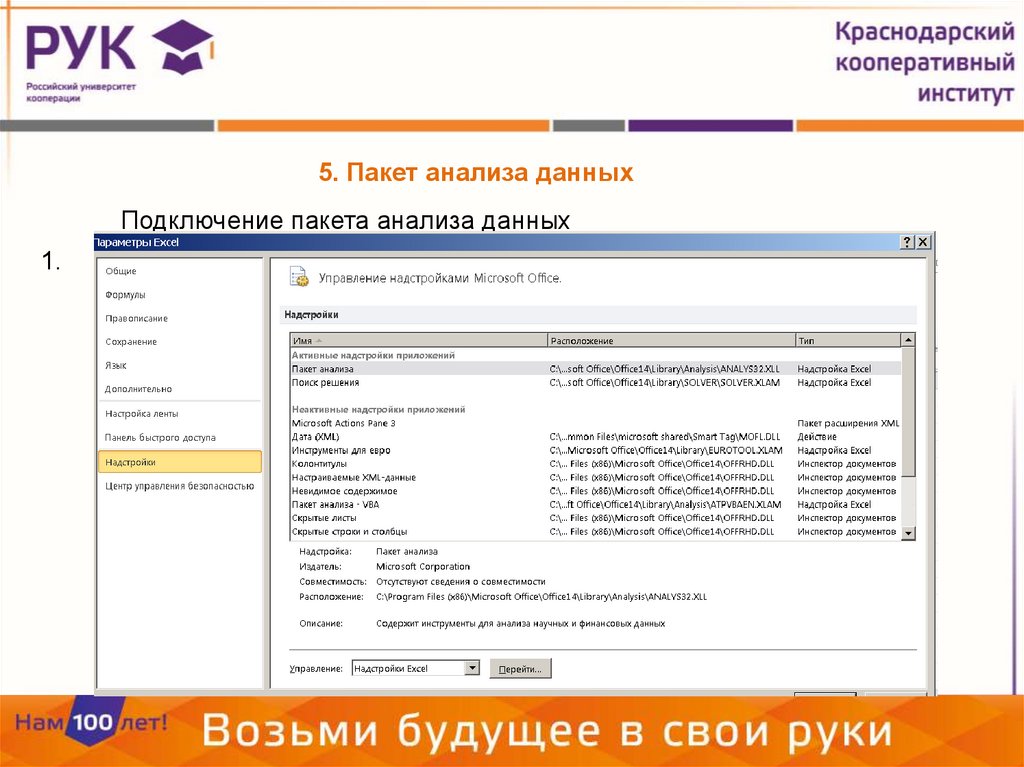
5. Пакет анализа данныхПодключение пакета анализа данных
1.
23
24.
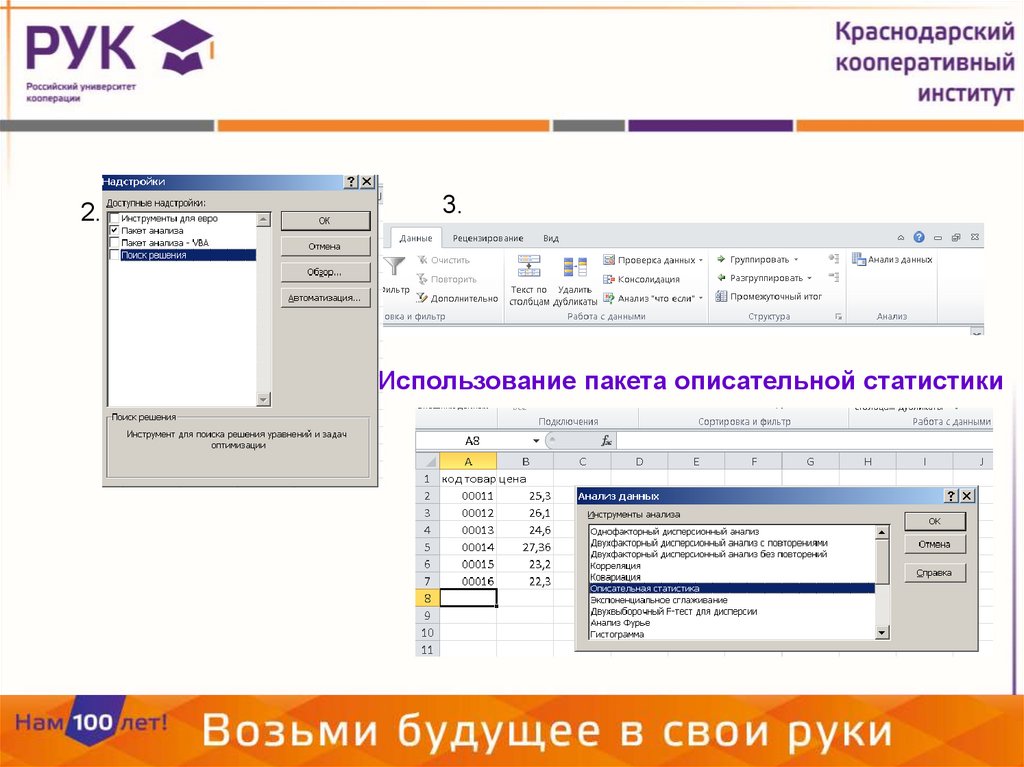
2.3.
Использование пакета описательной статистики
24
25.
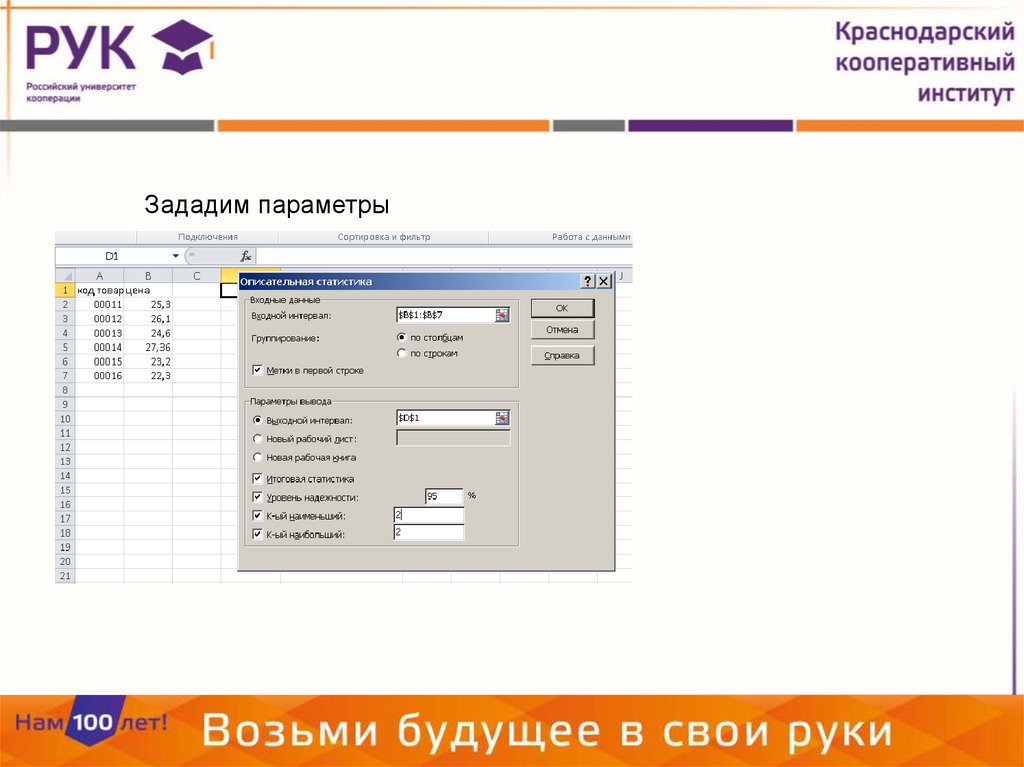
Зададим параметры25
26.
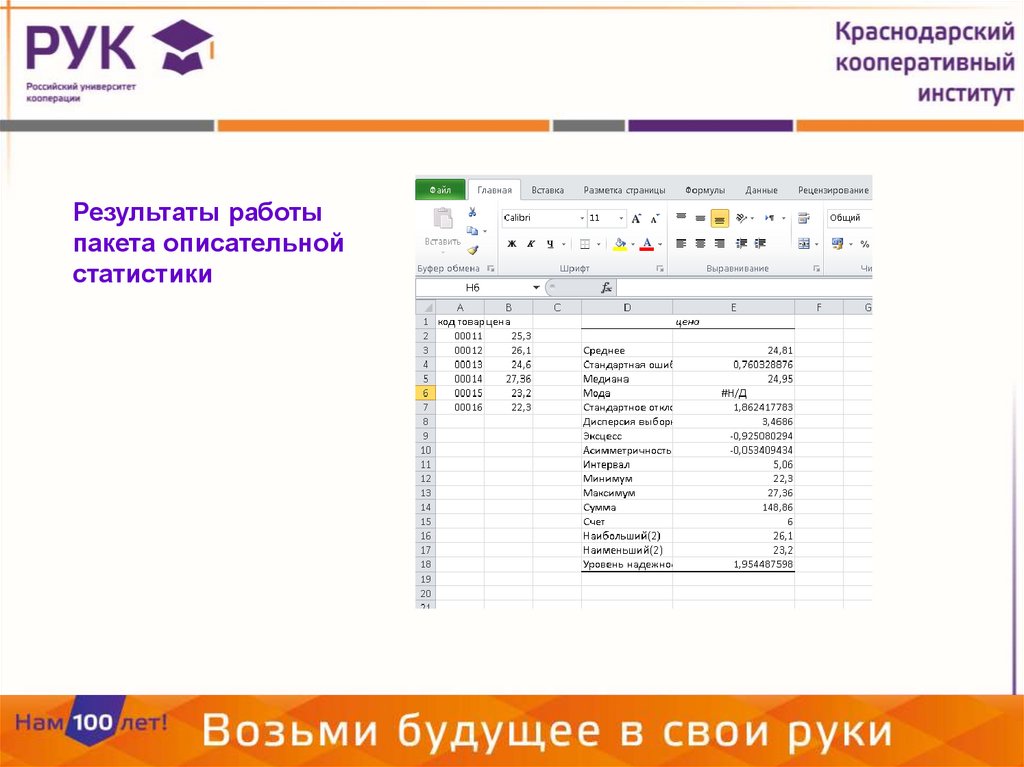
Результаты работыпакета описательной
статистики
26
27.
6. Задание для самостоятельной работы1. Проведите самостоятельно анализ цен по любому товару по семи
магазинам (или регионам). Для анализа используйте
функции
описательной статистики. Проанализируйте также цены с
использованием пакета анализа данных. Сохраняйте результаты
анализа по каждому параметру на отдельных листах.
27







 Математика
Математика Экономика
Экономика Программное обеспечение
Программное обеспечение








