Описательная статистика

1. Лекция 2

Тема: «Описательная
статистика»

2. План лекции:

Показатели
центральной
арифметическое, его свойства.
тенденции.
Мода,
медиана.
Квартили.
Соотношение
показателями центральной тенденции.
Среднее
между
Показатели изменчивости: размах, дисперсия, среднее
квадратическое отклонение, коэффициент вариации.
Свойства дисперсии.
Показатели ассиметрии и эксцесса.

3.

Показатели центральной тенденции.
Среднее арифметическое, его
свойства.

4.

Средняя арифметическая ( х ) – одна из основных
характеристик
центром
вариационного
распределения,
группируются
совокупности.
все
ряда,
вокруг
варианты
являющаяся
которого
статистической

5. Для негруппированных данных эта величина определяется как сумма всех членов совокупности деленная на их общее число n.

x1 x2 x3 ... xn 1
x
xi
n
n i 1
n
где:
xi
- значения вариант
n
x
- знак суммирования вариант в пределах от первой до n- й
варианты
i 1
n
i
- общее число вариант

6. Для данных, группируемых с учетом повторяемости или веса (pi) отдельных вариант средняя арифметическая, называемая взвешенной определяется

по формуле:
k
1
х xi pi
n i 1

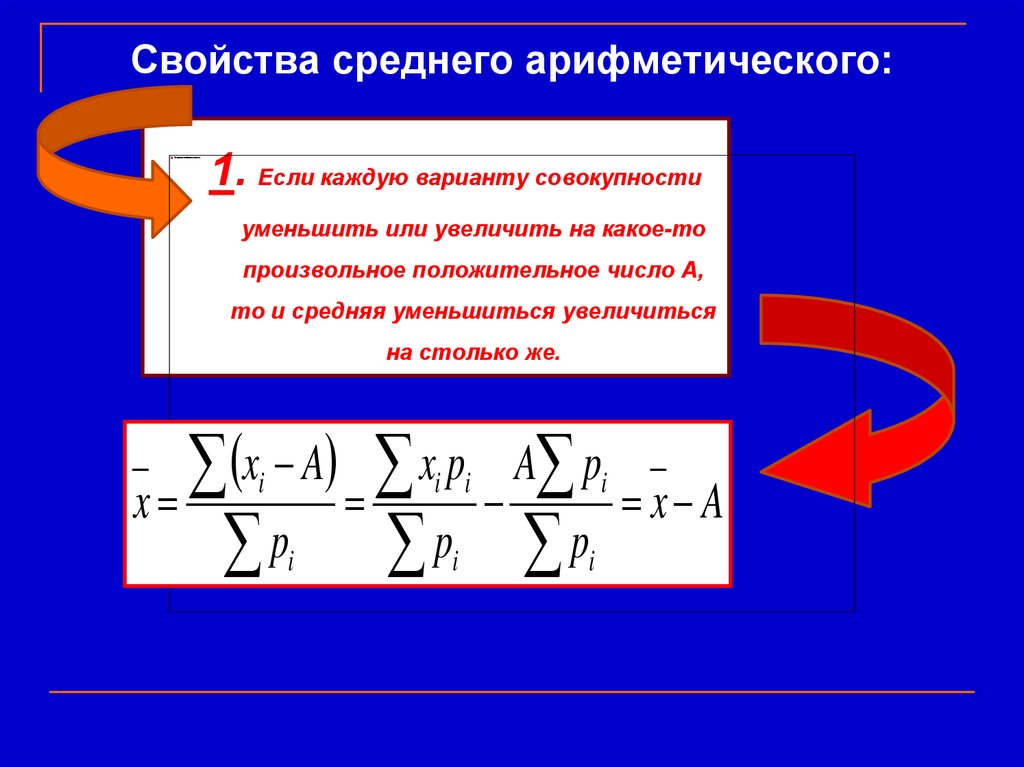
7. Свойства среднего арифметического:

1. Если каждую варианту совокупности
уменьшить или увеличить на какое-то
произвольное положительное число А,
то и средняя уменьшиться увеличиться
на столько же.
x A x p A p
x
x A
p p p
i
i i
i
i
i
i

8.

9.

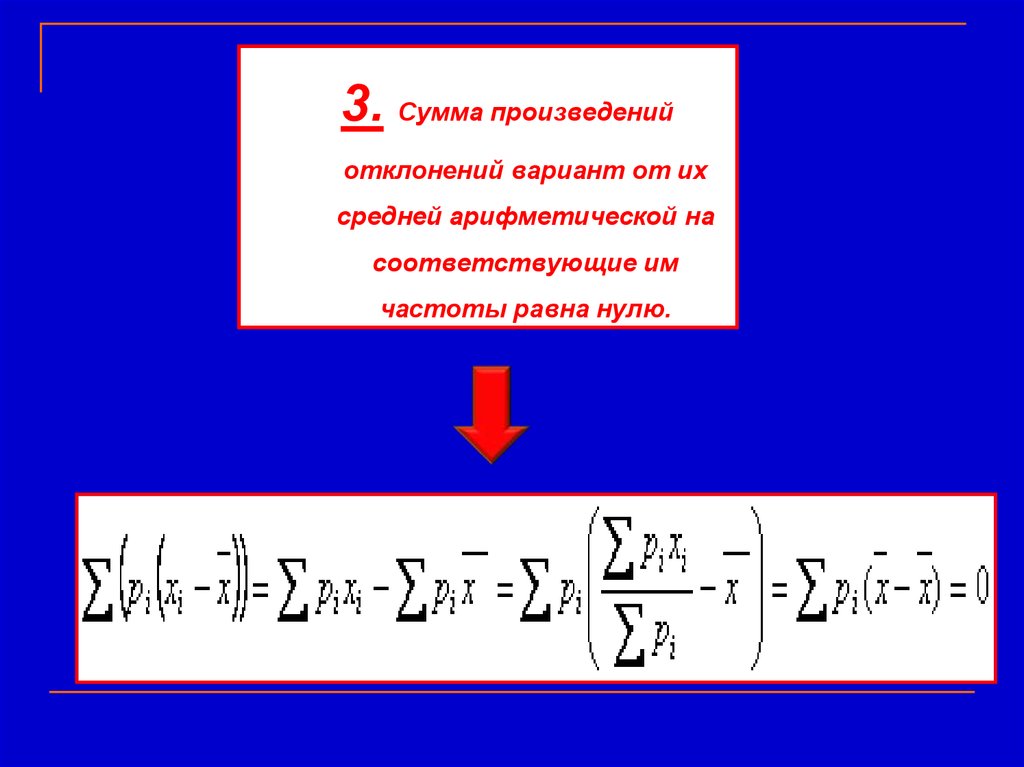
3. Сумма произведений
отклонений вариант от их
средней арифметической на
соответствующие им
частоты равна нулю.

10.

4. Сумма квадратов отклонений
вариант от их средней
арифметической меньше
суммы квадратов отклонений
тех же вариант от любой другой
величины А не равной х:
(х x) (x A)
2
i
i
2

11. Мода, медиана. Квартили. Соотношение между показателями центральной тенденции.

12.

Медиана эмпирического распределения (Me) (от лат.
Mediana – средняя) – средняя, относительно которой ряд
распределения делится на две половины: в обе стороны от
медианы располагается одинаковое число членов ряда
(вариант).
Если число членов ранжированного
центральная варианта и будет Me.
ряда
нечетное,
то
При четном числе членов ряда медиана определяется по
полусумме двух соседних вариант, расположенных в центре
ряда.

13. Если выборка распределена в вариационный ряд, медиана определяется как:

n
ps
Ме хМе i 2
pMe
хМе
р Ме
ps
нижняя граница интервала, в котором находится медиана или полусумма соседних классов;
частота медианного класса;
число накопленных частот, стоящих перед медианным классом;
i
величина классового интервала;
n
общее число наблюдений.

14. Мода (Mo) – величина, которая встречается в данной совокупности наиболее часто.

Класс с наибольшей частотой называется модальным.
p2 p1
Mo xн i
2 p2 p1 p3
где:
хн
р1
p3
i
- нижняя граница модального класса, т.е. класса с
наибольшей частотой ( p2 )
- частота класса, предшествующего модальному,
- частота класса, следующего за модальным,
- ширина классового промежутка.

15.

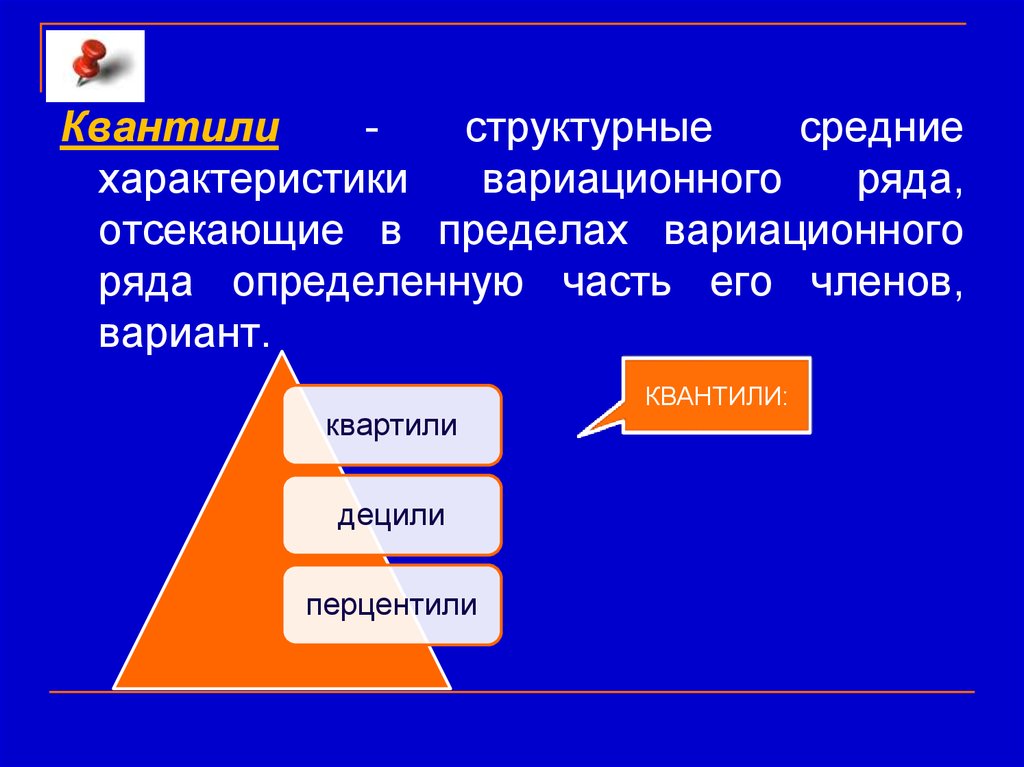
Квантили
структурные
средние
характеристики
вариационного
ряда,
отсекающие в пределах вариационного
ряда определенную часть его членов,
вариант.
квартили
децили
перцентили
КВАНТИЛИ:

16.

Квартиль – величина, отсекающая 1/4
членов ряда.
(3
квартиля делят весь вариационный ряд на четыре
равночисленные части (кварты)).
Дециль – величина, отделяющая 1/10
часть всех членов вариационного ряда.
(9 децилей делят весь вариационный ряд на десять равных
частей).
Перцентиль (процентиль)
сотые доли вариант.
отсекает
(99 децилей делят совокупность на 100 равных частей).

17.

Показатели изменчивости

18.

Лимиты (от лат limes - предел) – значения
максимальной и минимальной вариант, между
которыми распределяются все члены данной
совокупности.
xmax ; xmin

19.

Размах вариации – показатель,
характеризующий варьирование
признаков.
d xmax xmin

20.

Дисперсия (от лат. Dispersion - рассеяние)
или варианса (англ. Variance - изменение,
вариация) – важнейшая характеристика
вариационного ряда.
Дисперсия генеральной совокупности - σ²,
дисперсия выборки - S² .

21. Знак суммирования произведений отклонений вариант xi от их средней

k
S
2
( x x)
i 1
i
2
pi
n 1
k
i 1
Число степеней свободы - число
свободно варьирующих единиц или
элементов
в
составе
данной
ограниченной совокупности.
Знак суммирования произведений
отклонений вариант xi от их средней
pi
Частоты
n
Объем выборки
n 1
Число степеней свободы

22. Свойства дисперсии:

1.
Если каждую варианту
совокупности увеличить или
уменьшить на одно и то же
постоянное число А, то
дисперсия не изменится.
Т.о. дисперсию можно вычислить не только по значениям
признака, но и по их отклонениям от какой-нибудь
постоянной величины А.
1
1
2
2
Sx
[( xi A) ( x A)]
( xi x)
n 1
n 1
2

23.

2. Если каждую варианту
разделить или умножить на
одно и то же постоянное число
А, то дисперсия уменьшится
или увеличится в А2 раз.
2
x1 x
2
1
1
2
S
(
x
x
)
i
n 1 A A
A (n 1)
2

24.

Среднее квадратическое отклонение (Sx)
Характеризует величину и специфику варьирования признака.
Среднее квадратическое отклонение
=
Cтандартное отклонение (standard deviation – англ.)
Sx
p ( x x)
i
2
i
n 1
Чем сильнее варьирует признак, тем больше среднее квадратическое отклонение.
Дисперсия и среднее квадратическое отклонение выражаются в тех же единицах, что и
характеризуемый признак.

25.

Показатель, предложенный
К. Пирсеном –
обозначаемый буквой V
(или CV) называется
коэффициентом
вариации.
Sx
V
100%
x

26.

В качестве констант,
характеризующих
случайную величину, можно
использовать
математические ожидания
целых степеней случайной
величины.
Начальные моменты
k-й степени

27. Проверка нормальности распределения с помощью показателей асимметрии и эксцесса

Асимметрия или коэффициент асимметрии (термин был
впервые введен Пирсоном, 1895) является мерой
несимметричности распределения.
0
0
( 3)
0
0
( 2) ( 2)
( 3)
3
Где:
3
μ3 - равно ∑(xi- среднееx)
σ3 - стандартное отклонение (сигма), возведенное в
третью степень;
n - число наблюдений.

28. Асимметрия или коэффициент асимметрии (термин был впервые введен Пирсоном, 1895) является мерой несимметричности распределения.

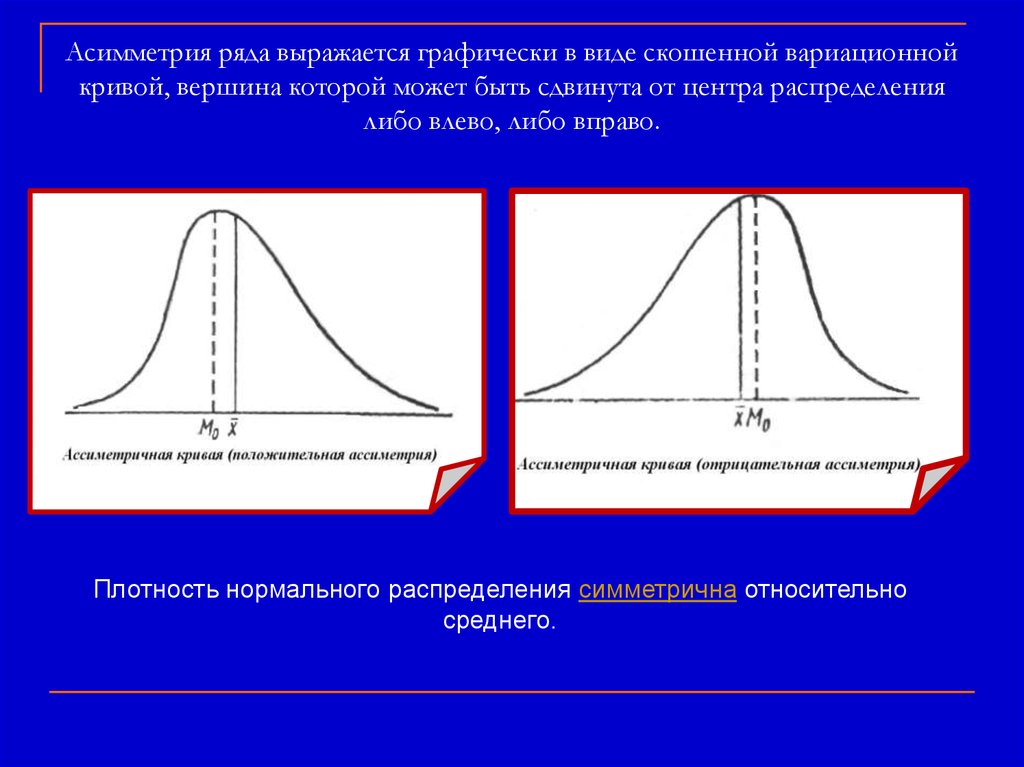
Асимметрия ряда выражается графически в виде скошенной вариационной
кривой, вершина которой может быть сдвинута от центра распределения
либо влево, либо вправо.
Плотность нормального распределения симметрична относительно
среднего.

29. Асимметрия или коэффициент асимметрии (термин был впервые введен Пирсоном, 1895) является мерой несимметричности распределения.

Коэффициент ассиметрии – величина
безразмерная, может принимать значения
от -∞ до +∞.
При симметричном распределении μ(3)=0 и
α=0.

30.

Асимметрию называют правосторонней или положительной,
если вершина кривой сдвинута влево от центра распределения;
она более пологая, сильно растянутая по оси абсцисс.
0
При
левосторонней,
наоборот,
вершина
или
отрицательной,
кривой
сдвинута
вправо
асимметрии,
от
центра
распределения, а ее пологая часть находится на левой стороне.
0

31. Асимметрия ряда выражается графически в виде скошенной вариационной кривой, вершина которой может быть сдвинута от центра распределения

Эксцесс
Термин был впервые введен Пирсоном, 1905.
Коэффициент эксцесса измеряет "пикообразность" распределения.
Оценка эксцесса (выборочный эксцесс) вычисляется по формуле:
0
( 4)
0
( 2) 2
0
( 4)
3 4 3
Где
Mj равен (xi-Meanx)j
n
- число наблюдений
4
- стандартное отклонение (сигма), возведенное в четвертую степень.

32.

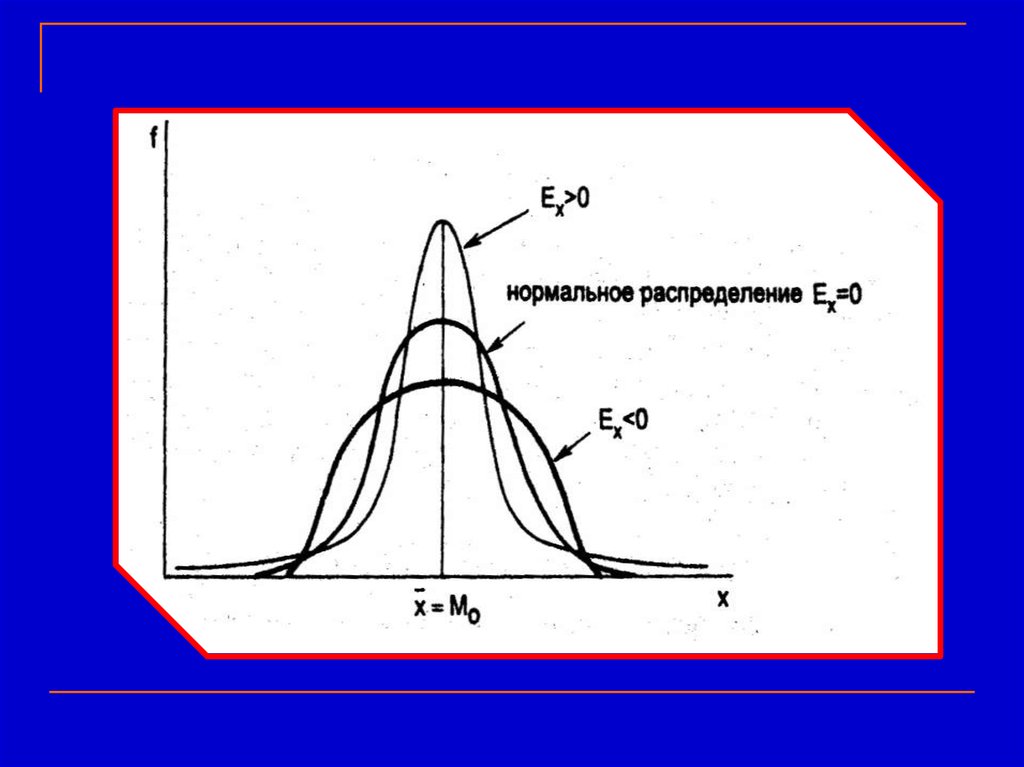
Если эксцесс значимо отличен от 0, то функция
плотности либо имеет более закругленный,
либо более острый пик, чем пик плотности
нормального распределения.
Функция плотности нормального
распределения имеет эксцесс равный 0.

33.

34. Эксцесс

Благодарю за внимание!