Похожие презентации:
Золотое сечение
1.
Золотое сечениеУчитель математики : Карпенко Е.В.
2.
«Довольно почестей Александрам! Да здравствуют Архимеды!»Сен-Симон А.
Пифагор (580-500 г.г.до н.э.)
Пропорции, т.е.
равенства отношений
изучались
пифагорейцами.
Евдокс развил учение о
пропорциях–одно из
величайших достижений
греческой математики.
Евдокс (408 – ок.355 г.г.до н.э.)
Леонардо да Винчи (1452-1519 г.г.)
Термин «золотое
сечение» ввёл Леонардо
да Винчи.
3.
Понятие «Золотое сечение»Золотое сечение - деление непрерывной
величины на две части в таком отношении,
при котором меньшая часть так относится к
большей, как большая ко всей величине.
a:b=b:c
или
с:b=b:а
4.
Эта пропорция равна:Золотое сечение в процентах
5.
Ряд ФибоначчиС историей золотого сечения связано
имя итальянского математика Леонардо
Фибоначчи.
Ряд чисел 0, 1, 1, 2, 3, 5, 8, 13, 21, 34,
55 и т.д. известен как ряд Фибоначчи.
Каждый член последовательности,
начиная с третьего, равен сумме двух
предыдущих, а отношение смежных
чисел ряда приближается к
отношению золотого деления.
Все исследователи золотого
деления в растительном и в животном
мире, искусстве, неизменно приходили к
ряду Фибоначчи как арифметическому
выражению закона золотого деления.
6.
«Золотая Пропорция» - главныйэстетический принцип эпохи Средневековья
Эпоха Возрождения ассоциируется с
именами таких «титанов», как Леонардо да
Винчи, Микеланджело, Рафаэль, Николай
Коперник, Альберт Дюрер, Лука Пачоли.
Имеется много авторитетных
свидетельств о том, что именно Леонардо
да Винчи(1452-1519) был одним из
первых, кто ввел сам термин «Золотое
Сечение».
Доказано, что во многих своих
произведениях Леонардо да Винчи
использовал пропорции золотого сечения,
в частности, в своей всемирно известной
фреске «Тайная вечеря» и
непревзойденной «Джоконде.
7.
«Витрувийский человек»Леонардо да Винчи
Разрабатывая правила изображения
человеческой фигуры, Леонардо да
Винчи пытался на основе литературных
сведений древности восстановить так
называемый «квадрат древних».
Он выполнил рисунок, в котором
показано, что размах вытянутых в
сторону рук человека примерно равен
его росту, вследствие чего фигура
человека вписывается в квадрат и в
круг.
При исследовании рисунка можно
заметить, что комбинация рук и ног в
действительности составляет четыре
различных позы.
Рисунок и текст иногда называют
каноническими пропорциями.
8.
Вклад Кеплерав теорию Золотого Сечения
Гениальный астроном Иоганн Кеплер
(1571-1630) был последовательным
приверженцем Золотого Сечения,
Платоновых тел и Пифагорейской
доктрины о числовой гармонии
Мироздания.
Считается, что именно Кеплер обратил
внимание на ботаническую
закономерность филлотаксиса и
установил связь между числами
Фибоначчи и золотой пропорцией,
доказав, что последовательность
отношений соседних чисел Фибоначчи:
1/1; 2/1; 3/2; 5/3 ;8/5; 13/8;…в пределе
стремится к золотой пропорции
9.
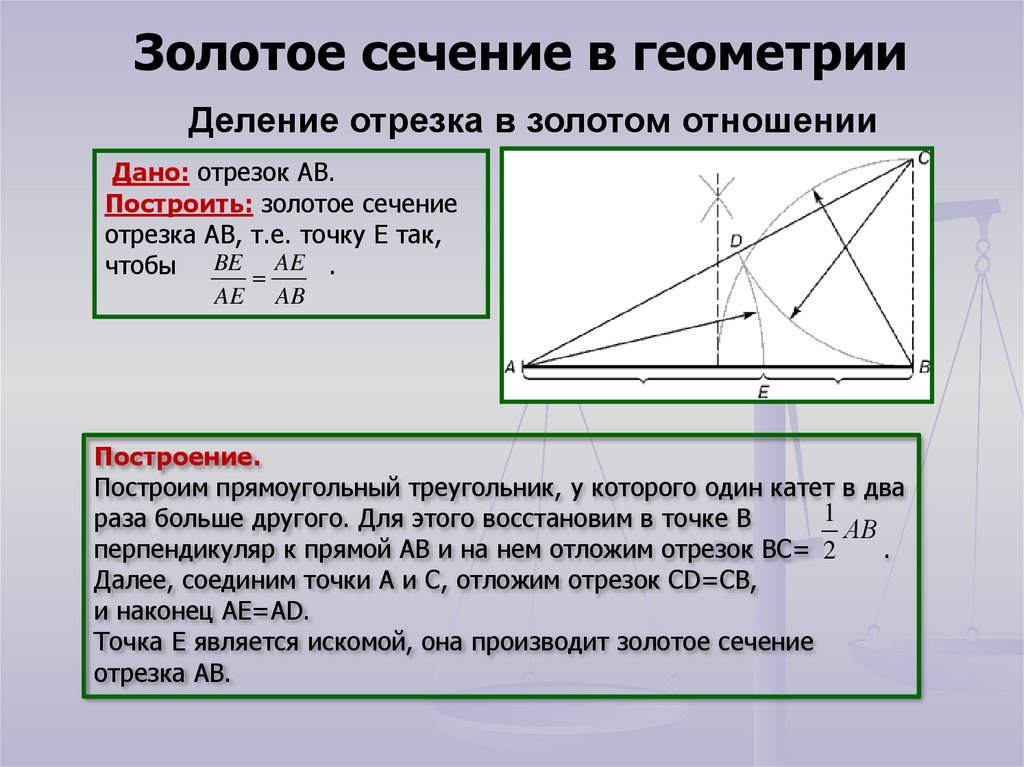
Золотое сечение в геометрииДеление отрезка в золотом отношении
Дано: отрезок АВ.
Построить: золотое сечение
отрезка АВ, т.е. точку Е так,
чтобы BE AE .
AE
AB
Построение.
Построим прямоугольный треугольник, у которого один катет в два
1
раза больше другого. Для этого восстановим в точке В
АВ
перпендикуляр к прямой АВ и на нем отложим отрезок ВС= 2
.
Далее, соединим точки А и С, отложим отрезок CD=CB,
и наконец AE=AD.
Точка Е является искомой, она производит золотое сечение
отрезка АВ.
10.
Золотой треугольникА
Золотым называется такой
равнобедренный треугольник,
основание и боковая сторона
которого находятся в золотом
отношении:
АВ
ВС
В
С
1 5
1,6180339887...
2
11.
Золотой прямоугольникАВ
ВС
Прямоугольник, стороны которого находятся
в золотом отношении, т.е. отношение длины
к ширине даёт число φ, называется
золотым прямоугольником.
12.
Золотая спиральПоследовательно отрезая от золотого прямоугольника
квадраты и вписывая в каждый по четверти окружности,
получаем золотую логарифмическую спираль.
Форма спирально завитой раковины привлекла
внимание Архимеда. Он изучал ее и вывел уравнение
спирали. Спираль, вычерченная по этому уравнению,
называется спираль Архимеда.
13.
ЗОЛОТАЯ СПИРАЛЬВопрос: Что общего в расположении полипептидных цепей
нуклеиновых кислот, лепестков розы, раковин моллюсков, рогов
млекопитающих, подсолнуха, далеких космических галактик?
Ответ: в основе их структуры лежит золотая (логарифмическая)
спираль. Эта спираль вписывается в золотой прямоугольник.
Носитель генетического кода - молекула ДНК - состоит из двух переплетенных
между собой спиралей.
14.
ЗОЛОТАЯ СПИРАЛЬРога животных растут по спирали
Спиралевидную форму имеют большинство раковин
15.
ЗОЛОТАЯ СПИРАЛЬЯВЛЕНИЕ ФИЛЛОТАКСИСА
Филлотаксисом называется своеобразное решетчатое расположение листьев,
семян, чешуек многих видов растений.
Ряды ближайших соседей в таких решетках разворачиваются по спиралям или
закручиваются винтовыми линиями вокруг цилиндра.
Семечки в подсолнухе расположены по логарифмическим спиралям. При этом
отношение числа левых и правых спиралей равно отношению соседних чисел
Фибоначчи . Можно встретить подсолнухи с отношением количества спиралей 34
/55 и 55/89.
16.
Золотое сечение в природе17.
Золотое сечение в природе18.
Определенные точки в композиции автоматически привлекают внимание.Таких точек 4, и расположены они на расстоянии 3/8 и 5/8 от краев
картины. Нарисовав сетку, получим эти точки в местах пересечения линий
(см. фотографию).
19.
«Золотое сечение»в живописи
20.
«Золотое сечение»в живописи
21.
ЗОЛОТОЕ СЕЧЕНИЕ В ИСКУССТВЕАРХИТЕКТУРА
Золотое сечение пронизывает всю историю искусства: пирамиды Хеопса,
знаменитый греческий храм Парфенон, большинство греческих скульптур
памятников, непревзойденная Джоконда Леонарда да Винчи, картины Рафаэля,
Шишкина, этюды Шопена, музыка Бетховена, Чайковского, стихи Пушкина … вот
далеко не полный перечень выдающихся произведений искусства, наполненных
чудесной гармонией основанной на золотом сечении.
На фотографии показаны здания, при делении основных масс конструкций которых
использовалось золотое сечение.
22.
«Есть в математике нечто вызывающее восторг»Хаусдорф Ф.
Сфинкс, охраняющий гробницу Тутанхамона
Пирамида Хеопса
Есть предположение, что
Пифагор понятие золотого
сечения позаимствовал у
египтян и вавилонян. И,
действительно пропорции
пирамиды Хеопса,
барельефы предметов
быта и украшений из
гробницы Тутанхамона
свидетельствуют, что
египетские мастера
пользовались
соотношением золотого
сечения при их создании.
23.
«Гёте удачно назвал благородный собор «окаменелой музыкой», …»Юнг Д.
Церковь Покрова Богородицы на Нерли 1165 год
«Простая» красота пропорций золотого сечения.
24.
«…, но, быть может, ещё лучше было бы назвать такой собор«окаменелой математикой»
Юнг Д.
Пропорции Покровского Собора на Красной площади в Москве
определяются восемью членами ряда золотого сечения: 1; d ; d 2 ;...; d 7 .
Многие члены ряда золотого сечения повторяются в затейливых
элементах храма многократно:
d d 2 1;
d 2 d 3 d ; d 3 d 4 d 2 ; и т.д.
25.
«Поистине живопись – наука и законная дочь природы…»Леонардо да Винчи
d2
1
d1
Сандро Ботичелли «Рождение Венеры» (около 1485 г).
Пропорции Венеры выполнены в золотом сечении.
26.
Античные храмы27.
Собор Парижской Богоматери28.
Русские храмы29.
Церковь«Рождественско –
преображенская»
30.
Кинотеатр«Родина»
31.
Уфимскаясоборная
мечеть
32.
«Золотое сечение»в живописи
33.
ПРОПОРЦИИ ТЕЛА ЧЕЛОВЕКА ИЗОЛОТОЕ СЕЧЕНИЕ
Существуют определенные правила, по которым изображают фигуру человека,
основанные на понятии пропорциональности размеров различных частей тела.
Идеальным, совершенным считается тело,
пропорции которого составляет золотое сечение.
Основные пропорции были определены
Леонардо да Винчи, и художники стали
сознательно их использовать.
Основное деление человеческого тела – это
деление точкой пупа. Отношение расстояния от
пупа до ступни к расстоянию от пупа до макушки
составляют золотое сечение.
Идеальной женской фигурой считается фигура
Афродиты Милосской (см. рисунок).
Интересно, что статистически средние размеры тел различных людей также подчинены
правилу золотого сечения (об этом свидетельствуют антропологические исследования
Цейзинга (1855 г.), который провел измерения почти 2000 человек.
.
34.
ПРОПОРЦИИ ЗОЛОТОГО СЕЧЕНИЯ ВПРИРОДЕ
Форма птичьих яиц описывается золотым сечением. Сегодня уже установлено, что при
такой конфигурации прочностные характеристики оболочки оказываются наиболее
высокими.
Совершенная форма тела стрекозы создана по законам золотого сечения: отношение
длины хвоста и корпуса равно отношению общей длины к длине хвоста.
35.
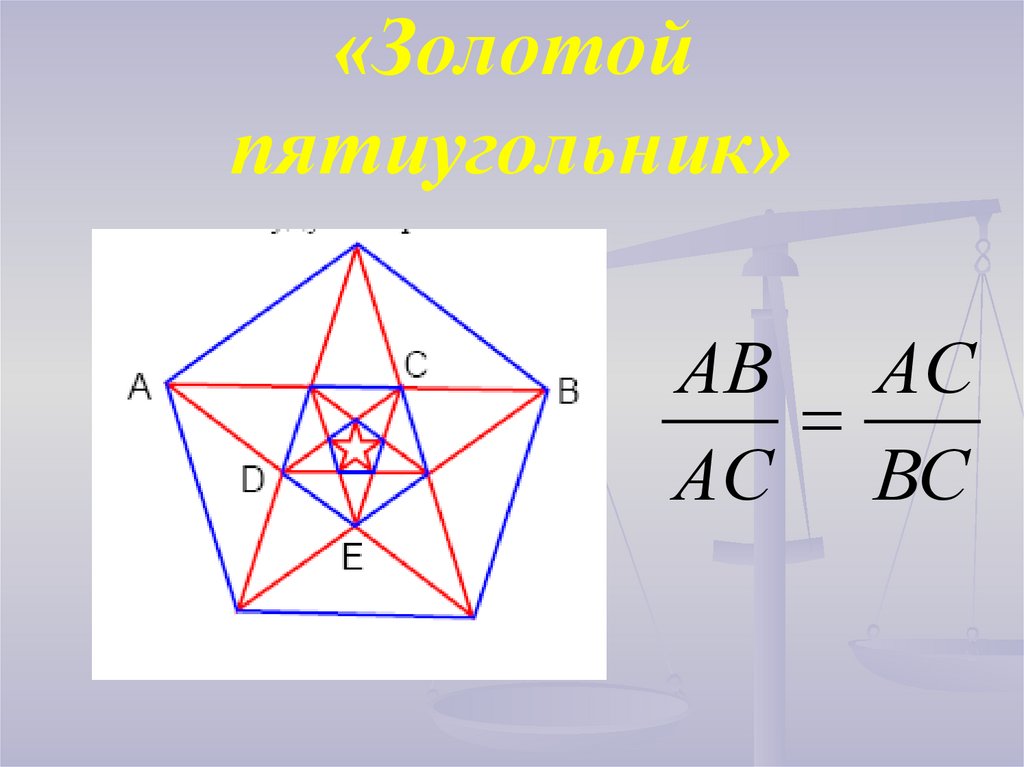
«Золотойпятиугольник»
АВ АС
АС ВС
36.
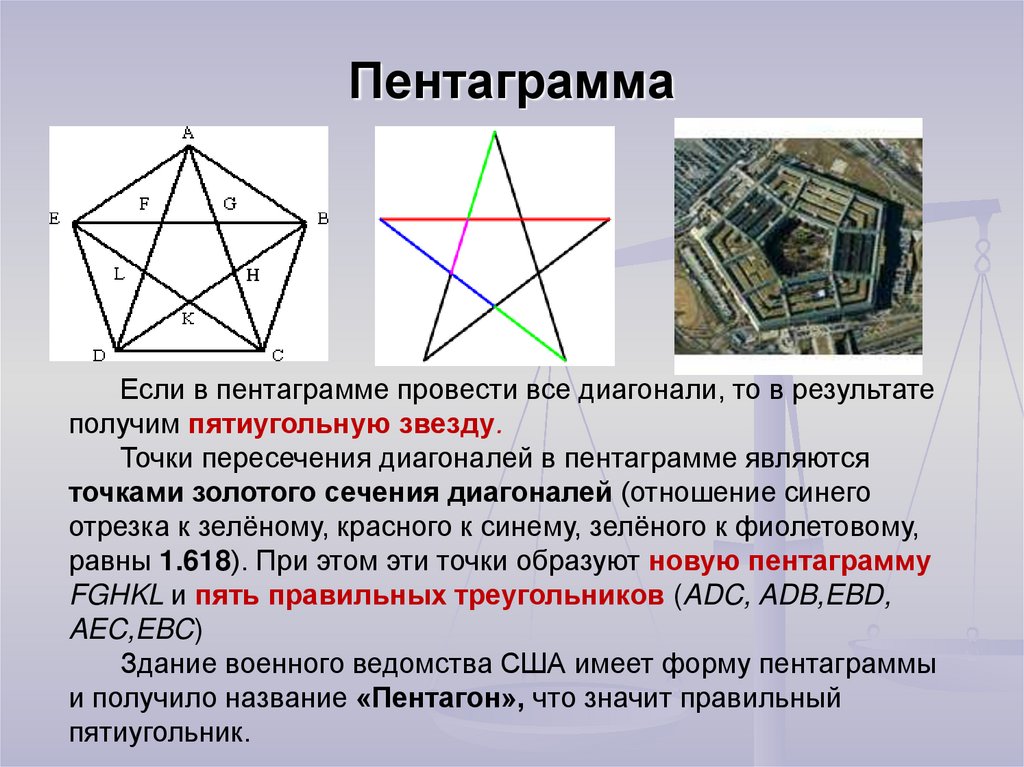
ПентаграммаЕсли в пентаграмме провести все диагонали, то в результате
получим пятиугольную звезду.
Точки пересечения диагоналей в пентаграмме являются
точками золотого сечения диагоналей (отношение синего
отрезка к зелёному, красного к синему, зелёного к фиолетовому,
равны 1.618). При этом эти точки образуют новую пентаграмму
FGHKL и пять правильных треугольников (ADC, ADB,EBD,
AEC,EBC)
Здание военного ведомства США имеет форму пентаграммы
и получило название «Пентагон», что значит правильный
пятиугольник.
37.
«Золотой пятиугольник»в природе
38.
«Золотые пропорции»человека
39.
СОХРАНИТЬ ЗЕМЛЮ- ЗНАЧИТСОХРАНИТЬ ЗОЛОТЫЕ ПРОПОРЦИИ
Земля как планета в
процессе развития оставила
себе явления, основанные на
"золотом сечении".
Например, соотношения
суши и воды на поверхности
Земли находятся в золотой
пропорции. Случайно ли это?
Наверное нет, так как за 4,5
миллиарда лет планета
должна была достичь
оптимального состояния. И
это выразилось в том, что, с
соотношение суши и воды на
ее поверхности стало
равным отношению золотой
пропорции.
38%
62%
суша
вода
40.
Числа управляютмировым порядком.
На числах основана
гармония
Вселенной.
Пифагор
41.
ПРАКТИЧЕСКИЕ ЗАДАНИЯ1. Разделите отрезок длиной 16 см в отношении “золотого сечения”.
Используйте числа Фибоначчи
1 вариант – 3 и 5
2 вариант - 2 и 3
2. Длина прямоугольника равна
20 см (1 вариант),
15 см(2 вариант).
Найдите такую ширину прямоугольника, чтобы отношение длины к ширине
составило “золотое сечение” Ф=1,6
Решите задачу, составив уравнение
3. Проверьте, насколько идеально одно из отношений вашей ладони:
отношение длины указательного пальца к длине двух его фаланг от конца
пальца.
Измерьте с помощью линейки указанные длины и найдите их отношение.
Округлите полученное число до десятых и сравните с Ф=1,6 (определите,
насколько оно больше или меньше числа Ф )
42.
ВыводЦелое всегда состоит из частей, части разной
величины находятся в определенном
отношении друг к другу и к целому. Принцип
золотого сечения – одно из замечательных
проявлений структурного и функционального
совершенства целого и его частей в
искусстве, науке, технике и природе.
43.
Самым древним музыкальным инструментом можносчитать Барабан. Разновидностей этого инструмента
огромное количество, от примитивных деревянных, до
современных барабанных установок.
Не найдётся на Земле такого места, где бы он
издревле не использовался, вначале, как сигнальное и
ритуальное приспособление, а теперь уже как
полноправный, чрезвычайно популярный музыкальный инструмент. Имеет ли
размер значение в данном случае? Конечно!
Важны не только длина, ширина и высота, но важны площади и объёмы.
Внутренние части субъекта должны собраться в Целое при определённом,
именно, Природном шаге.
При этом как части, так и целое отражаются Золотой Пропорцией.
Особенно важен внутренний объём барабана, его диаметр и толщина
которые, в идеале, рассчитываются с учётом особенностей шага Цветка
Жизни (так называемого - Цветка Пространства) и его Природных
Стандартов
44.
Следующий древний музыкальный инструментэто - Флейта. Самая древняя флейта найдена при
раскопках в Германии, и её возраст определён как
35000 - 40000 лет до нашей эры. Её диаметр 8 мм,
длина 21.8 мм и она имеет пять выходных отверстий,
благодаря которым возникает гармония сочетания
звуков.
Самым известным исполнителем чарующих звуков флейты, как мы знаем, был
Господь Кришна. Его завораживающая игра на флейте не только очаровывала
людей, но и сама Природа замирала, чтобы насладиться чарующими звуками этого
инструмента в руках Божественного исполнителя.
При изготовлении флейты или другого духового инструмента действуют те же
Природные, божественные Принципы Соразмерности и Золотой Пропорции
упомянутые выше.
Как при создании древних музыкальных инструментов, так и при
создании гармоничных инструментов в современности, необходимы знания
сакральной геометрии, математики, знание проявлений законов гармонии и
Золотой Пропорции, то есть всё то, что дают нам Природоподобные
Технологии, которые с аккумулировали в себе все необходимые знания, для
создания любых рукотворных объектов в их совершенной форме.
Вывод: ГДЕ ЕСТЬ ПРИРОДОПОДОБИЕ, ТАМ ЕСТЬ ЖИЗНЬ, ГАРМОНИЯ И
ПРОЦВЕТАНИЕ!!!









































 Математика
Математика








