Математические основы

1.

Для того чтобы правильно подобрать
инструмент,
необходимо
досконально
ознакомиться с ситуацией, выявить все
возможные факторы, причины и следствия,
собрать
максимум
информации
и
статистических
данных
по
изучаемой
проблеме. Здесь важно не просто наблюдать
за происходящим, но и грамотно оценить
обстоятельства
и
результаты,
уметь
пользоваться
теоретическими
и
статистическими данными.
Для сравнения различных материалов
используются
специфические
приемы,
которые
основываются
на
статистике,
математике, моделировании и пр. Одним из
таких методов является χ² Пирсона.

2.

Математическая статистика применяется для исследования различных
данных в процессе решения практических и теоретических задач. В
зависимости от поставленной цели подразделяется на таких 2 вида:
•теоретическую;
•прикладную (практическую).
Данное правило успешно применяется для оценки
воздействующих на исход исследования факторов. Здесь
наблюдается сочетание частот (количественное измерение
объекта исследования) с качественными
характеристиками. Фактически он позволяет сопоставить
опытные данные с теоретическими представлениями,
проанализировать сходства и различия, наличие
отклонений и пр.
χ² критерий Пирсона применяется в ходе анализа так
называемых таблиц сопряжения, которые содержат
сведения о частоте исходов в зависимости от
воздействующих параметров.
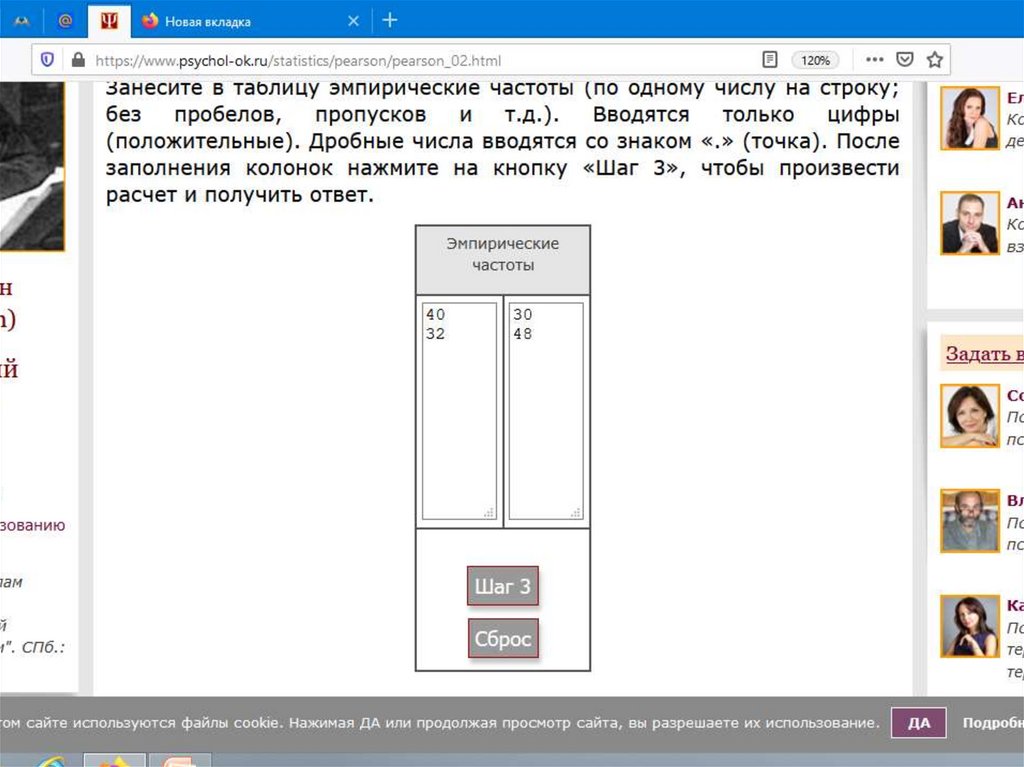
Таблицы сопряженности могут быть как простыми, так и
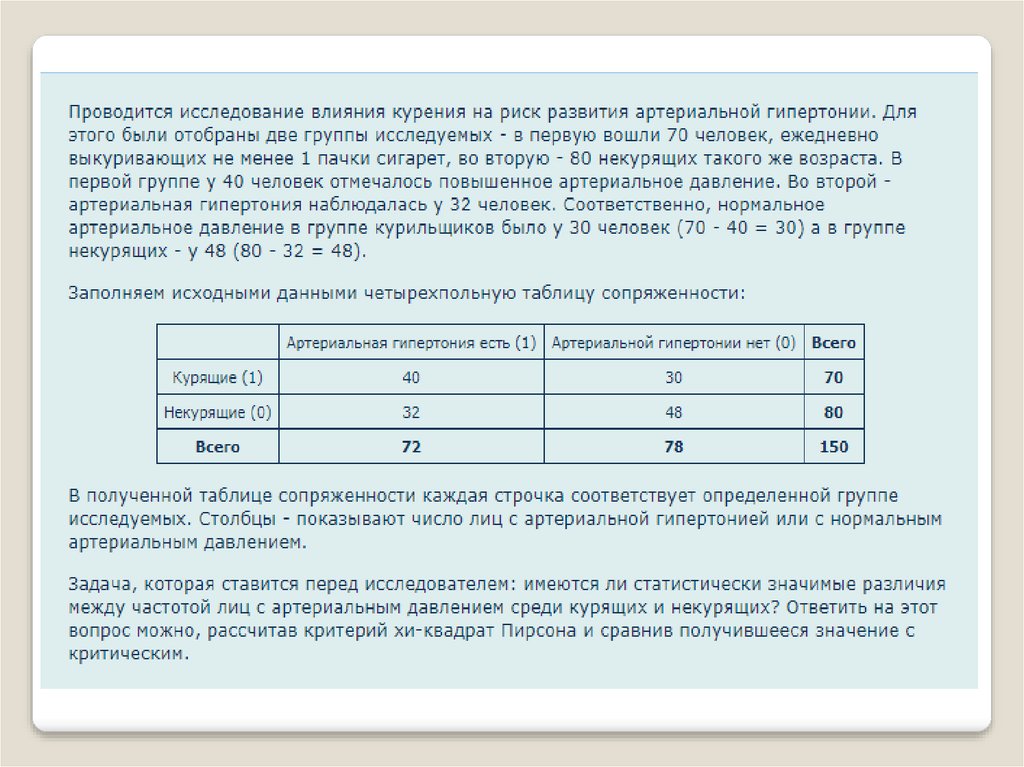
сложными. Приведем пример простейшего варианта.

3.

4.

Таблицы сопряженности позволяют представить полученные
сведения в более простом для анализа виде. Они напрямую
связывают факторы и результаты, уточняя связь статистически
данных, минимизируя случайные связи и погрешности.
Правила применения χ² Пирсона
Каждая методика применима в определенных случаях и имеет ряд
ограничений. В данном случае необходимо соблюдать следующие
требования:
Все показатели должны быть измерены в номинальной шкале.
Это значит, что все параметры должны быть качественными,
цельночисленными. Допустим, при оценке объектов исследования
целесообразно их подразделять по полу: мужчины и женщины, по
привычкам (курящие и некурящие), типу диагноза (хроническое
заболевание или сезонное) и пр. Притом важно изначально
правильно определять основные факторы: наличие/отсутствие
заболевания, пол, возраст и т.д.

5.

Количество наблюдений не менее 20. Данный
критерий является рекомендацией, но считается,
что чем больше опытов проведено (измерений,
наблюдений), тем выше точность исследования.
Ожидаемая частота при поверке основной
гипотезы должна быть более 5-10. Если параметр
менее 5-10, то исследователю придется сменить
тактику и использовать критерий Фишера.
Анализируемые и сравниваемые между собой
группы должны быть независимыми.
χ² Пирсона оценивает текущее положение, его
недопустимо применять для сравнения
результатов «до» и «после».

6.

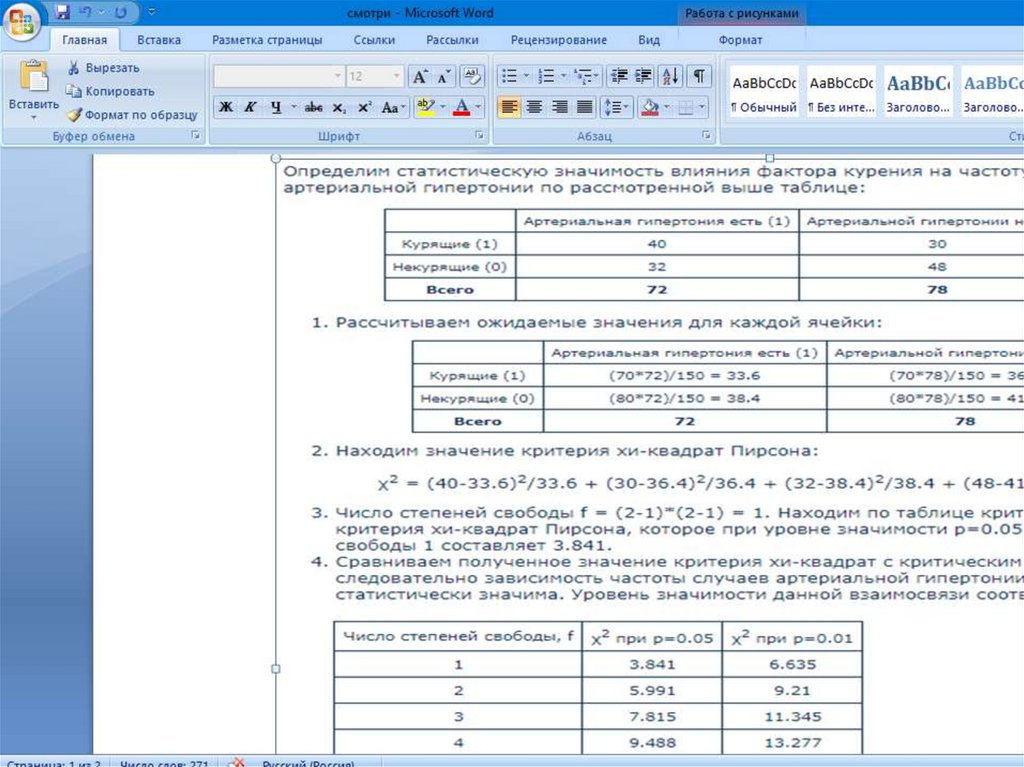
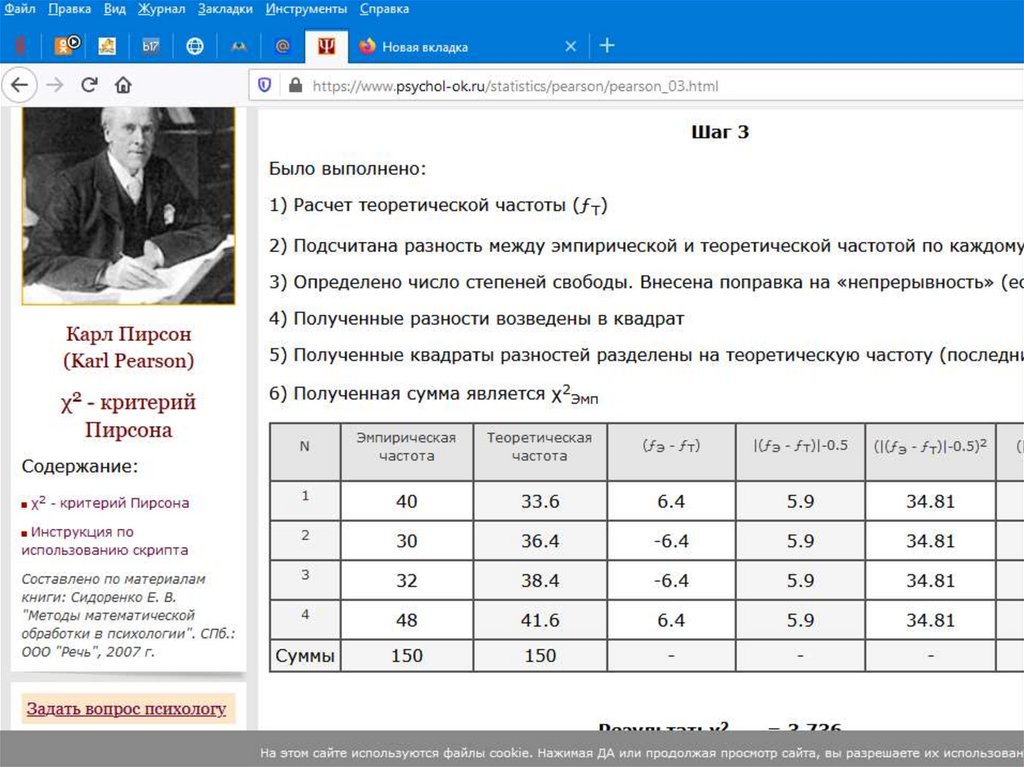
Алгоритм расчетов по методу χ² Пирсона
В основе действия данного принципа лежит сравнение
между существующими частотами (реальность) и
рассчитанными показателями (гипотетическими
частотами). Если различия между реальными и
«гипотетическими» данными малые, то исследователь
принимает за истину основную гипотезу. Если же
реальные и теоретические данные кардинально
разнятся, то нулевая (основная) гипотеза отвергается
из-за установления статистически значимых различий.
Чем выше значения χ² Пирсона, тем больше
вероятность того, что исследователю придется
отвергнуть нулевую идею. Притом важно учесть, что
изначально основная гипотеза считается истинной до
тех пор пока она не получит достойное опровержение.

7.

В основе методики χ² Пирсона лежат
следующие показатели:
•Ожидаемое количество наблюдений;
•Значение критерия χ²;
•Число степени свободы;
•Сравнение χ² с критической областью.

8.

9.

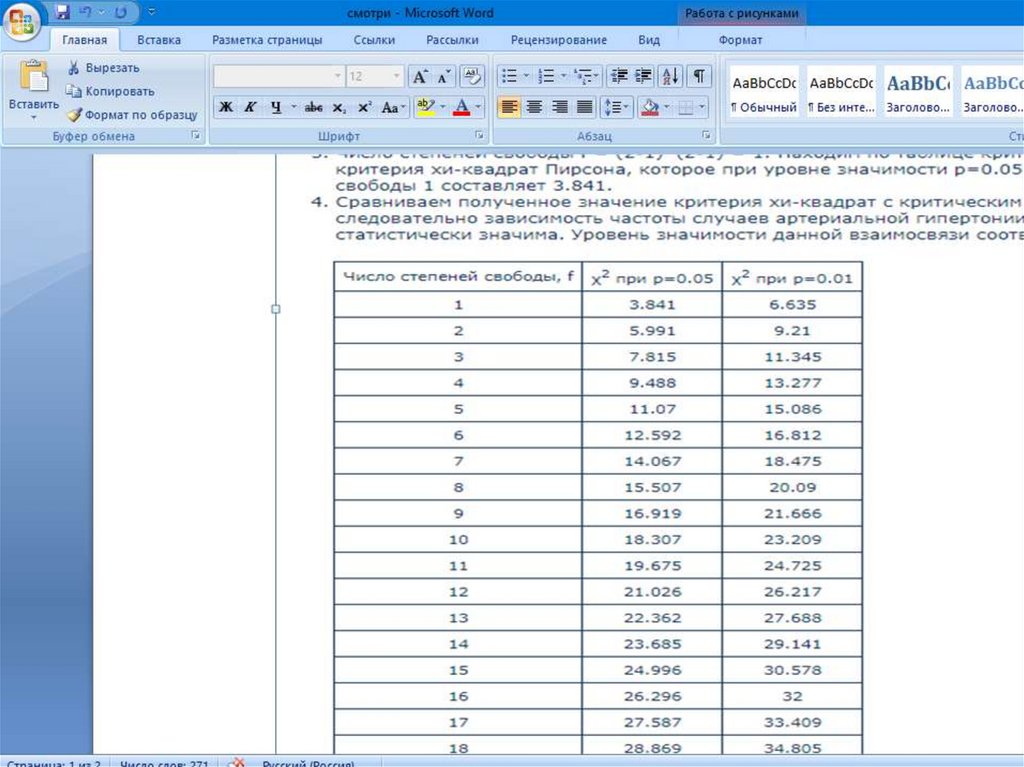
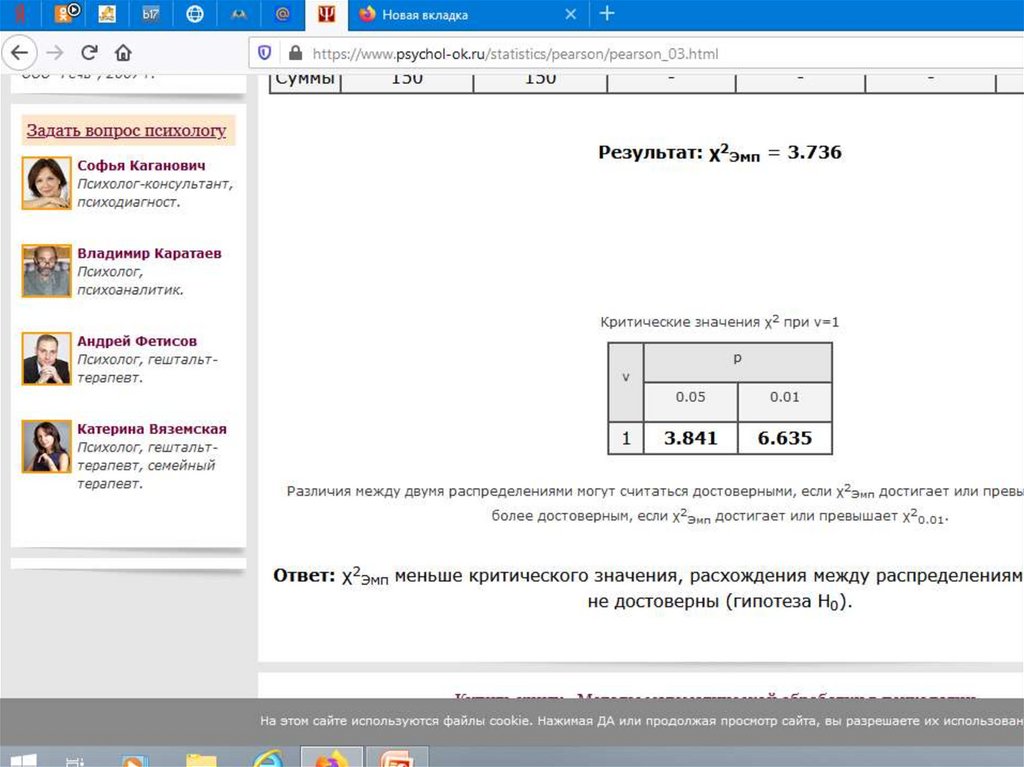
На чем основывается методика χ² критерия
Пирсона После сравнения полученного
результата χ² и критической области
исследователю необходимо грамотно
интерпретировать вывод.
Если χ² превосходит критическое
значение, то это свидетельствует о наличии
статистической связи между явлением и
результатом с учетом уровня значимости.
Методика χ² критерий Пирсона применима для
проверки простых и сложных гипотез. Главное,
учитывать все факторы и действовать согласно
установленным правилам.
Рассмотрим действие правила Пирсона на
конкретном примере.

10.

11.

12.

13.

14.

15.

16.

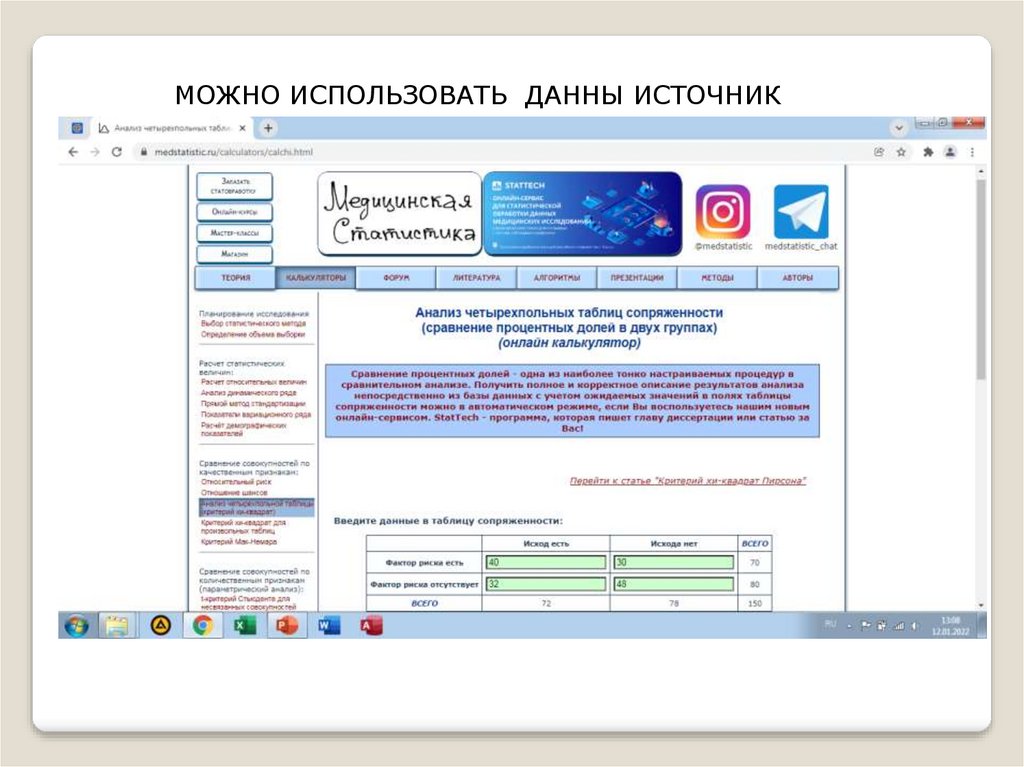
МОЖНО ИСПОЛЬЗОВАТЬ ДАННЫ ИСТОЧНИК

17.

t-критерий Стьюдента – общее название для
класса методов статистической проверки гипотез
(статистических критериев), основанных на
распределении Стьюдента.
Наиболее частые случаи
применения t-критерия
связаны с проверкой равенства
средних значений в двух выборках.
Уильям Госсет

18.

2. Для чего используется t-критерий Стьюдента?
t-критерий Стьюдента используется для определения
статистической значимости различий средних величин. Может
применяться как в случаях сравнения независимых выборок
(например, группы больных сахарным диабетом и группы
здоровых), так и при сравнении связанных совокупностей
(например, средняя частота пульса у одних и тех же пациентов до
и после приема антиаритмического препарата). В последнем случае
рассчитывается парный t-критерий Стьюдента
3. В каких случаях можно использовать t-критерий
Стьюдента?
Для применения t-критерия Стьюдента необходимо, чтобы
исходные данные имели нормальное распределение. Также имеет
значение равенство дисперсий (распределения) сравниваемых
групп (гомоскедастичность). При неравных дисперсиях
применяется t-критерий в модификации Уэлча (Welch's t).
При отсутствии нормального распределения сравниваемых выборок
вместо t-критерия Стьюдента используются аналогичные методы
непараметрической статистики, среди которых наиболее
известными является U-критерий Манна — Уитни.

19.

4. Как рассчитать t-критерий Стьюдента?
Для сравнения средних величин t-критерий
Стьюдента рассчитывается по следующей
формуле:
где М1 - средняя арифметическая первой
сравниваемой совокупности (группы), М2 средняя арифметическая второй
сравниваемой совокупности (группы), m1 средняя ошибка первой средней
арифметической, m2 - средняя ошибка второй
средней арифметической.

20.

5. Как интерпретировать значение t-критерия Стьюдента?
Полученное значение t-критерия Стьюдента необходимо правильно
интерпретировать. Для этого нам необходимо знать количество
исследуемых в каждой группе (n1 и n2). Находим число степеней
свободы f по следующей формуле:
f = (n1 + n2) - 2
После этого определяем критическое значение t-критерия
Стьюдента для требуемого уровня значимости (например, p=0,05) и
при данном числе степеней свободы f по таблице (см. ниже).
Сравниваем критическое и рассчитанное значения критерия:
•Если рассчитанное значение t-критерия Стьюдента равно или
больше критического, найденного по таблице, делаем вывод о
статистической значимости различий между сравниваемыми
величинами.
•Если значение рассчитанного t-критерия Стьюдента меньше
табличного, значит различия сравниваемых величин статистически
не значимы.

21.

6. Пример расчета t-критерия Стьюдента
Для изучения эффективности нового препарата
железа были выбраны две группы пациентов с
анемией. В первой группе пациенты в течение двух
недель получали новый препарат, а во второй группе получали плацебо. После этого было проведено
измерение уровня гемоглобина в периферической
крови. В первой группе средний уровень гемоглобина
составил 115,4±1,2 г/л, а во второй - 103,7±2,3 г/л
(данные представлены в формате M±m), сравниваемые
совокупности имеют нормальное распределение. При
этом численность первой группы составила 34, а
второй - 40 пациентов. Необходимо сделать вывод о
статистической значимости полученных различий и
эффективности нового препарата железа.

22.

Решение: Для оценки значимости различий
используем t-критерий Стьюдента, рассчитываемый
как разность средних значений, поделенная на сумму
квадратов ошибок:
После выполнения расчетов, значение t-критерия
оказалось равным 4,51. Находим число степеней
свободы как (34 + 40) - 2 = 72. Сравниваем
полученное значение t-критерия Стьюдента 4,51 с
критическим при р=0,05 значением, указанным в
таблице: 1,993. Так как рассчитанное значение
критерия больше критического, делаем вывод о том,
что наблюдаемые различия статистически значимы
(уровень значимости р<0,05).

23.

Число степеней
свободы, f
Значение t-критерия
Стьюдента при p=0.05
72-73
1.993