Логика_Профиль Задания 2 и 15 (3)

1.

1
Логические
основы
компьютеров

2.

2
Логика, высказывания
Логика (др.греч. λογικος) – это наука о том, как
правильно рассуждать, делать выводы,
доказывать утверждения.
Формальная логика отвлекается от
конкретного содержания, изучает только
истинность и ложность высказываний.
Аристотель
(384-322 до н.э.)
Логическое высказывание – это
повествовательное предложение, относительно
которого можно однозначно сказать, истинно оно
или ложно.

3.

4
Логика и компьютер
Двоичное кодирование – все виды информации
кодируются с помощью 0 и 1.
Задача – разработать оптимальные правила
обработки таких данных.
Почему «логика»?
Результат выполнения операции можно
представить как истинность (1) или ложность (0)
некоторого высказывания.
Джордж Буль разработал основы алгебры,
в которой используются только 0 и 1
(алгебра логики, булева алгебра).

4.

5
Вспомним известное…
Логическое выражение — это символическая
запись высказывания, которая может
содержать логические переменные и знаки
логических операций.
Логическая функция — это правило
преобразования входных логических значений
в выходные. Логическая функция задаётся
таблицей истинности.
Выражения:
A
A+A B
A (A+B)
A
0
0
1
1
B
0
1
0
1
F
0
0
1
1
функция

5.

6
Обозначение высказываний
A – Сейчас идет дождь.
B – Форточка открыта.
!
}
простые высказывания
(элементарные)
Любое высказывание может быть ложно (0)
или истинно (1).
Составные высказывания строятся из простых с
помощью логических связок (операций) «и», «или»,
«не», «если … то», «тогда и только тогда» и др.
AиB
A или не B
Сейчас идет дождь и открыта форточка.
Сейчас идет дождь или форточка закрыта.
если A, то B
Если сейчас идет дождь, то форточка открыта.
A тогда и только
тогда, когда B
Дождь идет тогда и только тогда, когда открыта
форточка.

6.

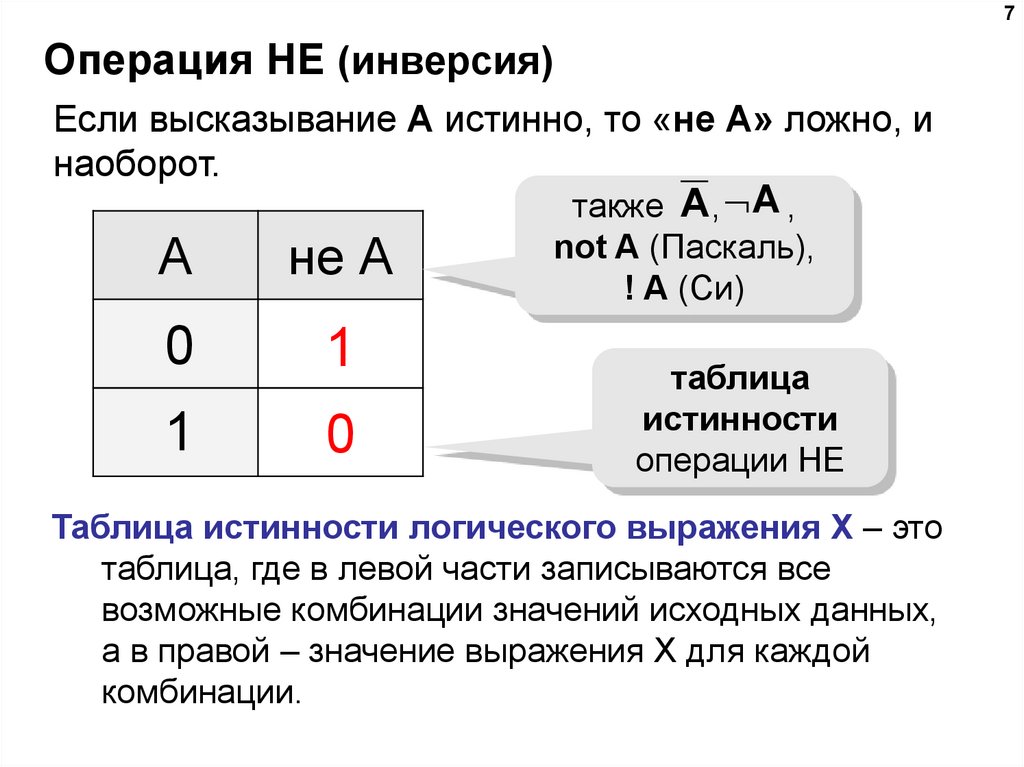
7
Операция НЕ (инверсия)
Если высказывание A истинно, то «не А» ложно, и
наоборот.
также A , A ,
А
не А
0
1
1
0
not A (Паскаль),
! A (Си)
таблица
истинности
операции НЕ
Таблица истинности логического выражения Х – это
таблица, где в левой части записываются все
возможные комбинации значений исходных данных,
а в правой – значение выражения Х для каждой
комбинации.

7.

8
Операция И
Высказывание «A и B» истинно тогда и только тогда,
когда А и B истинны одновременно.
AиB
A
B
220 В

8.

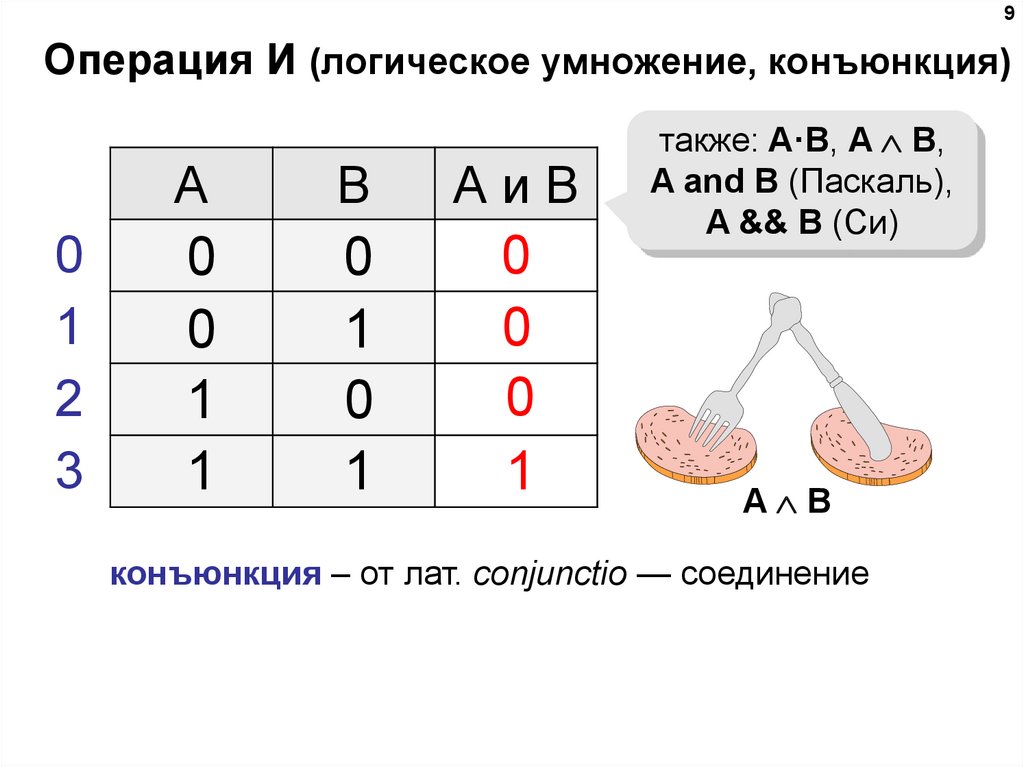
9
Операция И (логическое умножение, конъюнкция)
0
1
2
3
A
B
АиB
0
0
1
1
0
1
0
1
0
0
0
1
также: A·B, A B,
A and B (Паскаль),
A && B (Си)
A B
конъюнкция – от лат. conjunctio — соединение

9.

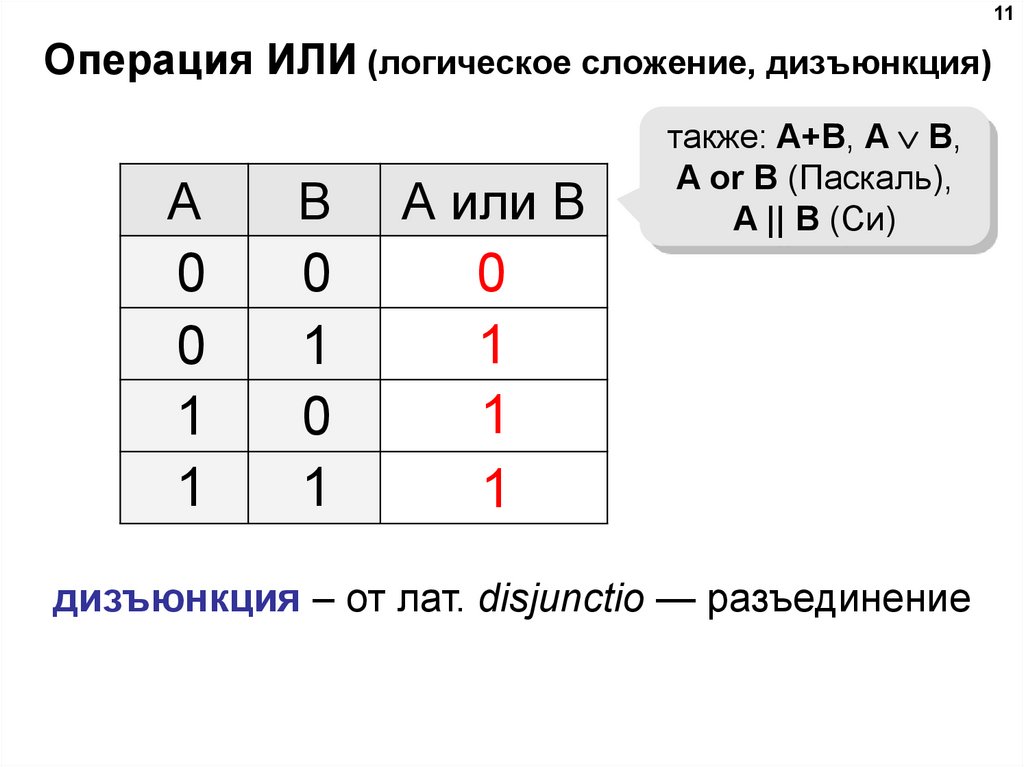
10
Операция ИЛИ (логическое сложение, дизъюнкция)
Высказывание «A или B» истинно тогда, когда
истинно А или B, или оба вместе.
A или B
A
B
220 В

10.

11
Операция ИЛИ (логическое сложение, дизъюнкция)
A
B
А или B
0
0
1
1
0
1
0
1
0
1
1
1
также: A+B, A B,
A or B (Паскаль),
A || B (Си)
дизъюнкция – от лат. disjunctio — разъединение

11.

12
Задачи
В таблице приведены запросы к поисковому серверу.
Расположите номера запросов в порядке возрастания
количества страниц, которые найдет поисковый
сервер по каждому запросу. Для обозначения логической
операции «ИЛИ» в запросе используется символ |, а для
логической операции «И» – &.
1) принтеры & сканеры & продажа
2) принтеры & продажа
3) принтеры | продажа
4) принтеры | сканеры | продажа
1234

12.

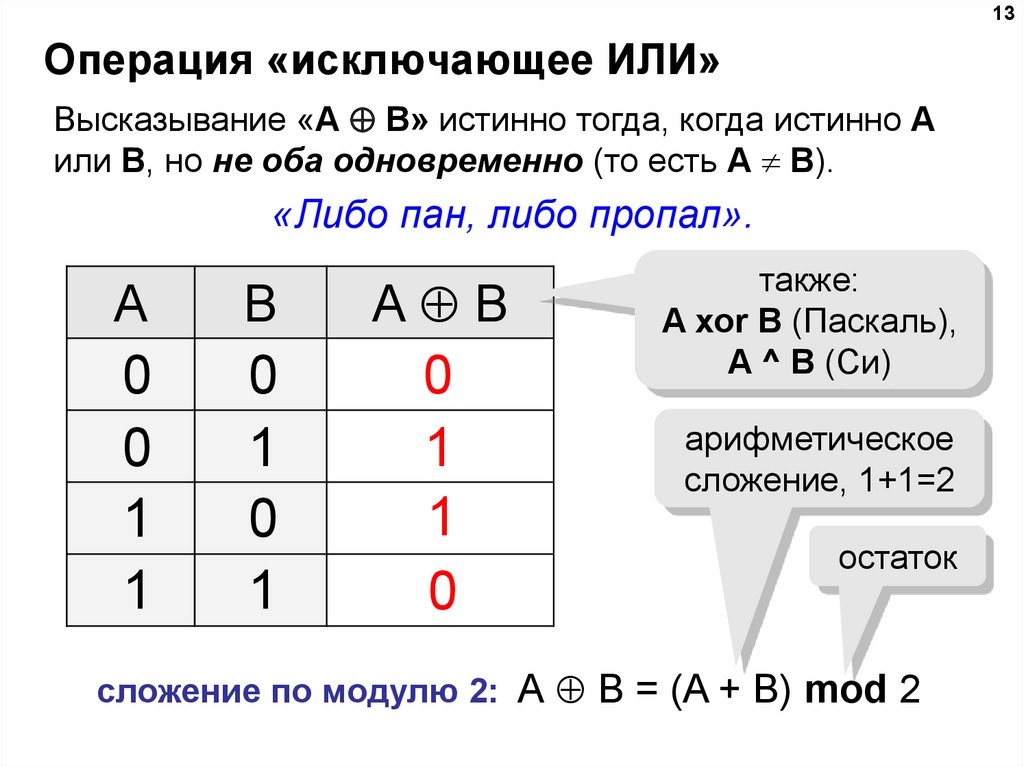
13
Операция «исключающее ИЛИ»
Высказывание «A B» истинно тогда, когда истинно А
или B, но не оба одновременно (то есть A B).
«Либо пан, либо пропал».
A
B
А B
0
0
1
1
0
1
0
1
0
1
1
0
также:
A xor B (Паскаль),
A ^ B (Си)
арифметическое
сложение, 1+1=2
остаток
сложение по модулю 2: А B = (A + B) mod 2

13.

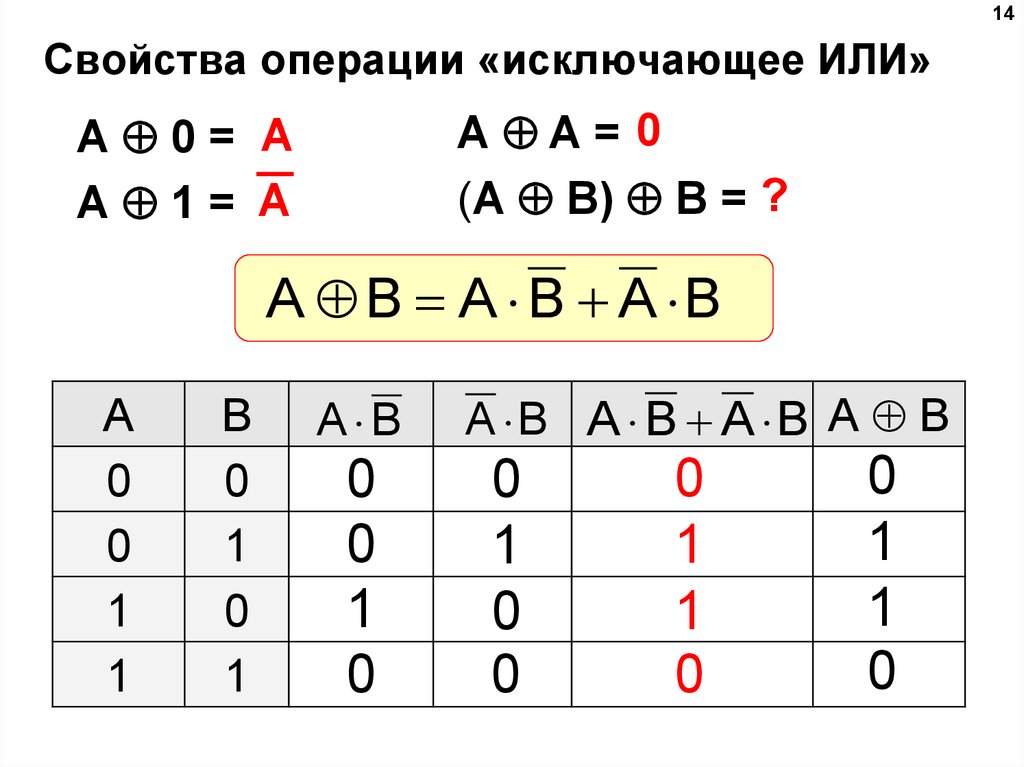
14
Свойства операции «исключающее ИЛИ»
A A= 0
(A B) B = ?
A 0= A
A 1= A
A B A B A B
A
0
0
1
1
B
0
1
0
1
A B
0
0
1
0
A B A B A B А B
0
1
0
0
0
1
1
0
0
1
1
0

14.

15
Импликация («если …, то …»)
Высказывание «A B» истинно, если не
исключено, что из А следует B.
A – «Работник хорошо работает».
B – «У работника хорошая зарплата».
A
0
0
1
1
B
0
1
0
1
А B
1
1
0
1
A B A B

15.

16
Импликация («если …, то …»)
«Если Вася идет гулять, то Маша сидит дома».
A – «Вася идет гулять».
A
B
А
B
B – «Маша сидит дома».
A B 1
?
А если Вася не идет
гулять?
Маша может пойти гулять
(B=0), а может и не пойти (B=1)!
0
0
1
1
0
1
0
1
1
1
0
1

16.

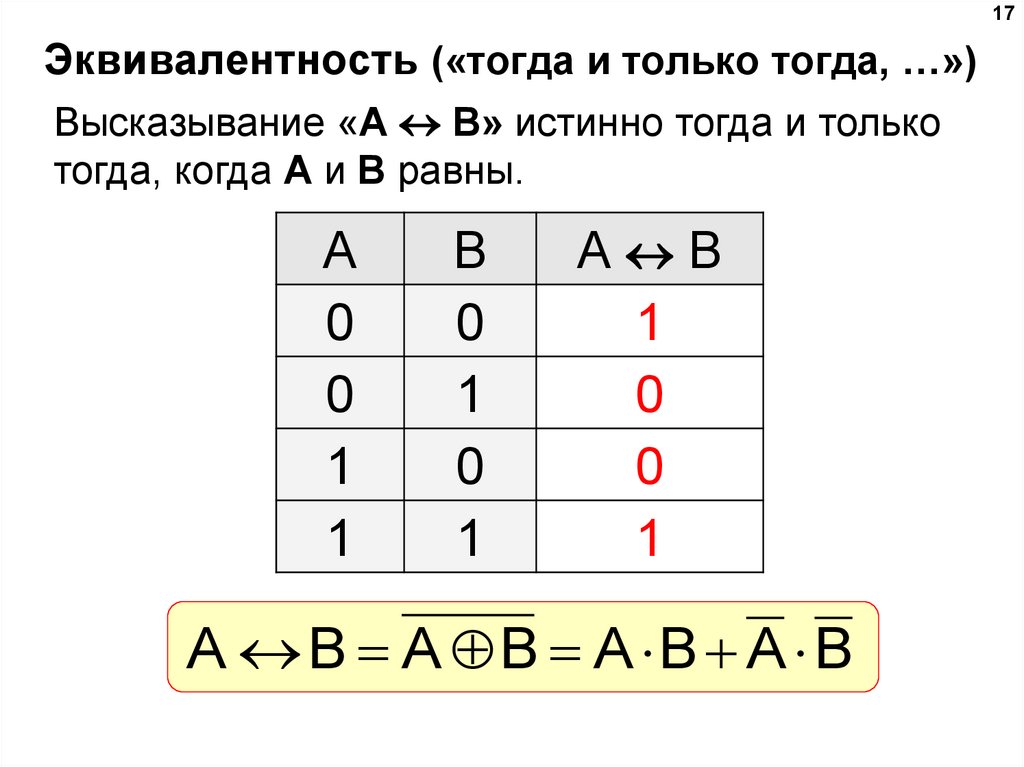
17
Эквивалентность («тогда и только тогда, …»)
Высказывание «A B» истинно тогда и только
тогда, когда А и B равны.
A
0
0
1
1
B
0
1
0
1
А B
1
0
0
1
A B A B A B A B

17.

19
Логические
основы
компьютеров

18.

20
Формализация
Прибор имеет три датчика и может работать, если два из
них исправны. Записать в виде формулы ситуацию
«авария».
A – «Датчик № 1 неисправен».
B – «Датчик № 2 неисправен».
Формализация – это
переход к записи на
C – «Датчик № 3 неисправен».
формальном языке!
Аварийный сигнал:
X – «Неисправны два датчика».
X – «Неисправны датчики № 1 и № 2» или
«Неисправны датчики № 1 и № 3» или
«Неисправны датчики № 2 и № 3».
логическая
формула
X A B A C B C
!

19.

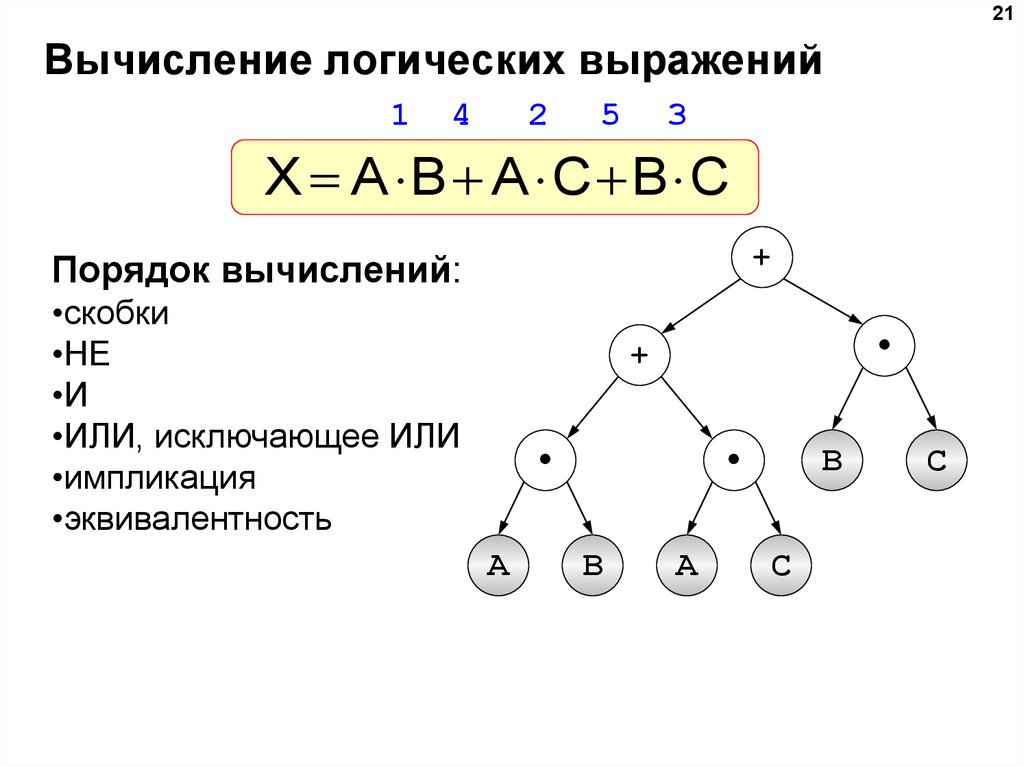
21
Вычисление логических выражений
1
4
2
5
3
X A B A C B C
+
Порядок вычислений:
•скобки
•НЕ
•И
•ИЛИ, исключающее ИЛИ
•импликация
•эквивалентность
+
A
B
A
B
С
C

20.

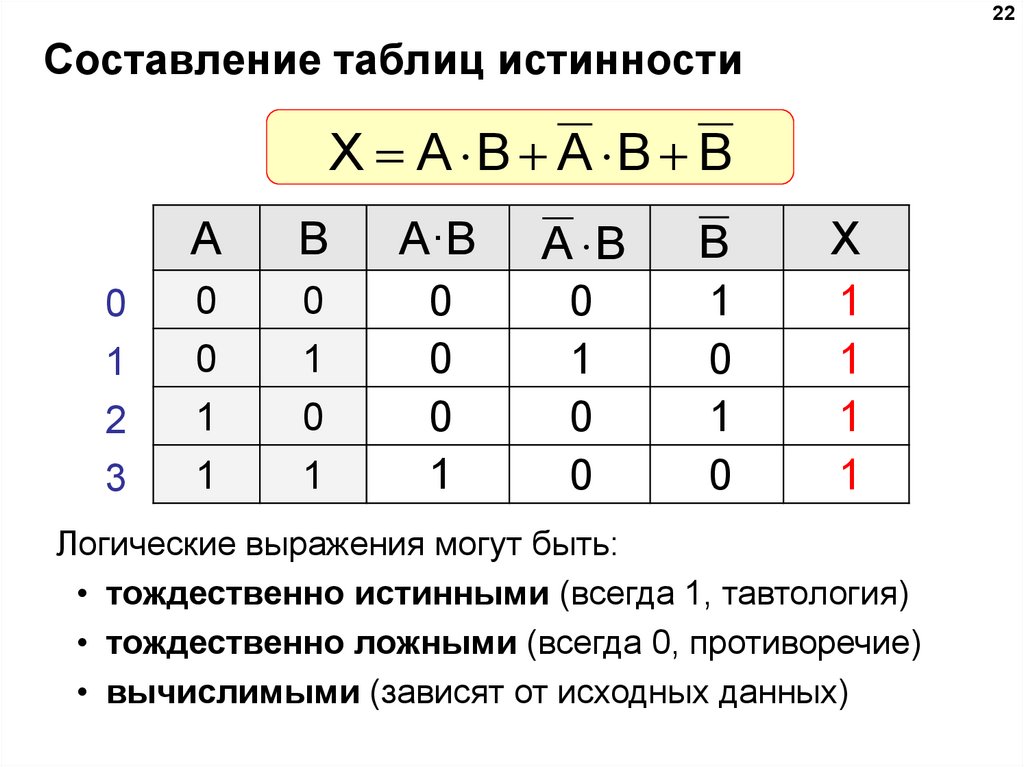
22
Составление таблиц истинности
X A B A B B
0
1
2
3
A
B
A·B
A B
B
X
0
0
1
1
0
1
0
1
0
0
0
1
0
1
0
0
1
0
1
0
1
1
1
1
Логические выражения могут быть:
• тождественно истинными (всегда 1, тавтология)
• тождественно ложными (всегда 0, противоречие)
• вычислимыми (зависят от исходных данных)

21.

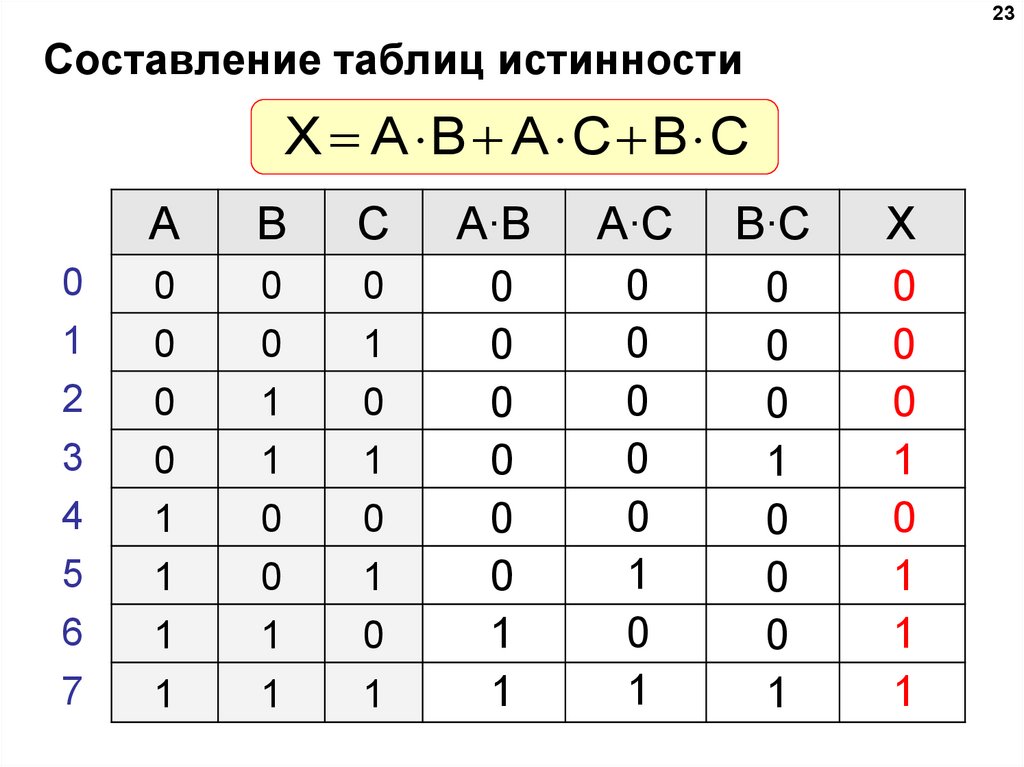
23
Составление таблиц истинности
X A B A C B C
0
1
2
3
4
5
6
7
A
B
C
A∙B
A∙C
B∙C
X
0
0
0
0
1
1
1
1
0
0
1
1
0
0
1
1
0
1
0
1
0
1
0
1
0
0
0
0
0
0
1
1
0
0
0
0
0
1
0
1
0
0
0
1
0
0
0
1
0
0
0
1
0
1
1
1

22.

24
Задачи
Задача 1. При каких значениях логических переменных
истинно выражение:
X1 X 2 X 3 X 4 X 5
Решение. Все сомножители равны 1:
X 1 X 4 1,
X2 X3 X5 1
Задача 2. При каких значениях логических переменных
ложно выражение:
X1 X 2 X 3 X 4 X 5
Решение. Все слагаемые равны 0:
X 1 X 3 X 5 0,
X2 X4 1

23.

25
Задачи
Задача 3. Запишите любое логические выражение,
соответствующее таблице истинности:
в полной
X Y Z F
23 = 8 строк
Полная таблица?
?
1 0 0 1
0 0 0 0
1 1 1 0
истинно при X = 1, Y = Z = 0
X Y Z 1
F X Y Z

24.

26
Задачи
Задача 4. Запишите любое логические выражение,
соответствующее таблице истинности:
X
1
0
1
Y
0
0
1
Z
0
0
1
F
0
1
1
ложно при X = 1, Y = Z = 0
X Y Z 0
F X Y Z

25.

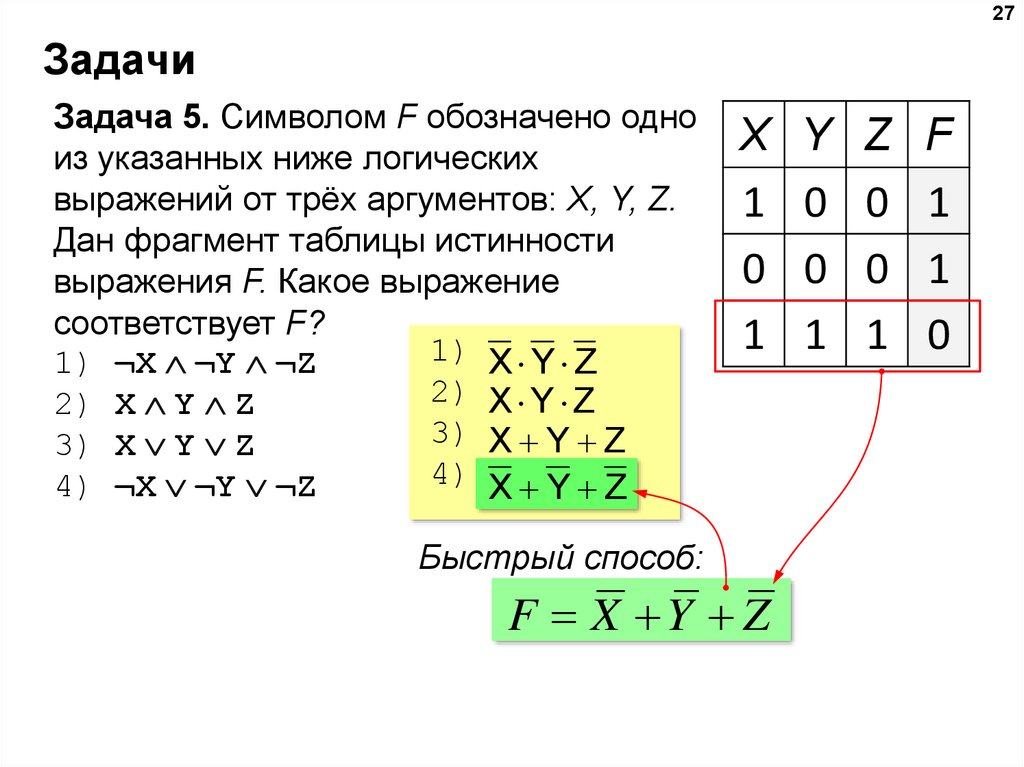
27
Задачи
Задача 5. Символом F обозначено одно
из указанных ниже логических
выражений от трёх аргументов: X, Y, Z.
Дан фрагмент таблицы истинности
выражения F. Какое выражение
соответствует F?
1) X Y Z
1) ¬X ¬Y ¬Z
2) X Y Z
2) X Y Z
3) X Y Z
3) X Y Z
4) X Y Z
4) ¬X ¬Y ¬Z
X
1
0
1
Быстрый способ:
F X Y Z
Y
0
0
1
Z
0
0
1
F
1
1
0

26.

28
Задачи
Упрощённый способ подбора:
1) один нуль операция «ИЛИ»
2) получить 0, применив «НЕ» к
слагаемым:
X Y Z 0
1 1 1
1) одна единица операция «И»
2) получить 1, применив «НЕ» к
сомножителям:
X Y Z 1
0 1 0
X
1
0
1
Y
0
0
1
Z
0
0
1
F
1
1
0
X
1
0
1
Y
0
1
1
Z
1
0
1
F
0
1
0

27.

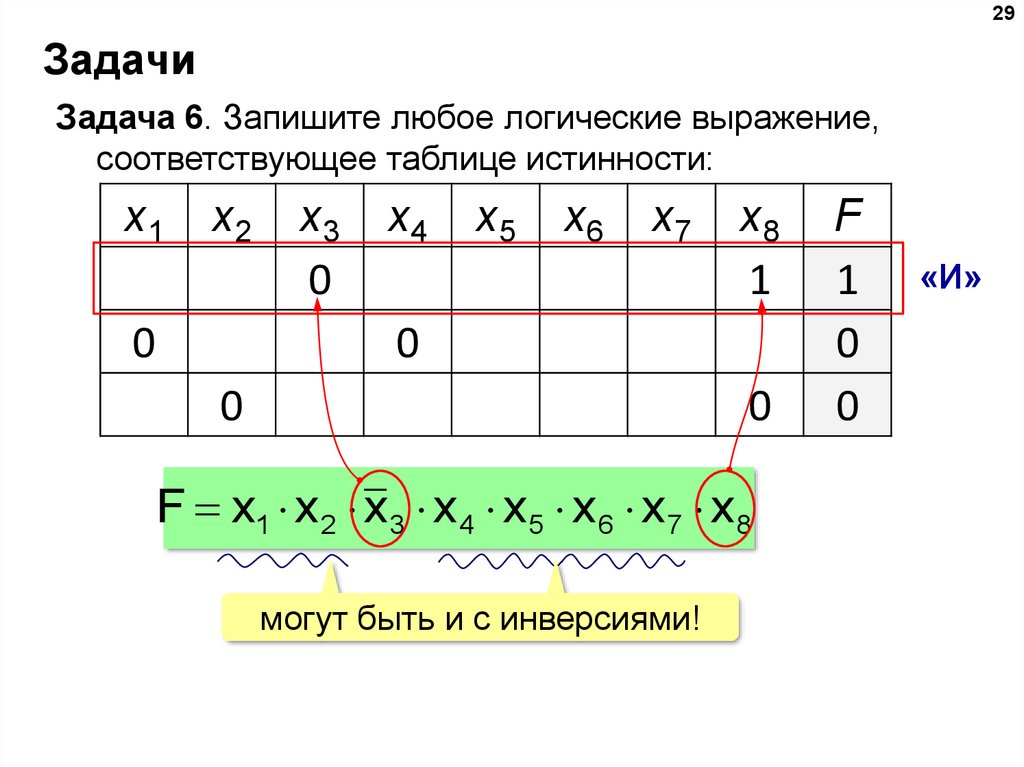
29
Задачи
Задача 6. Запишите любое логические выражение,
соответствующее таблице истинности:
x1
x2
0
x3
0
x4
x5
x6
x7
x8
1
0
0
0
F x1 x 2 x 3 x 4 x 5 x 6 x 7 x 8
могут быть и с инверсиями!
F
1
0
0
«И»

28.

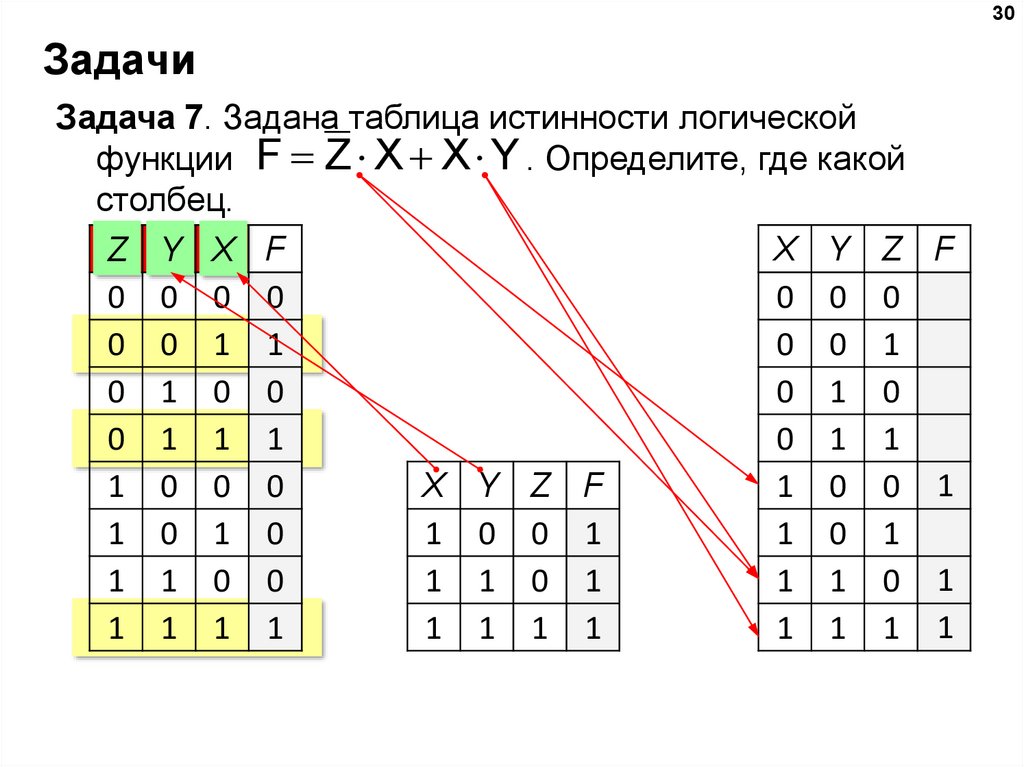
30
Задачи
Задача 7. Задана таблица истинности логической
функции F Z X X Y . Определите, где какой
столбец.
?
? X
? F
X Y Z
Z Y
0 0 0 0
0 0 0
0 0 1 1
0 0 1
0 1 0 0
0 1 0
0 1 1 1
0 1 1
1 0 0 0
X Y Z F
1 0 0
1 0 1 0
1 0 0 1
1 0 1
1 1 0 0
1 1 0 1
1 1 0
1 1 1 1
1 1 1 1
1 1 1
F
1
1
1

29.

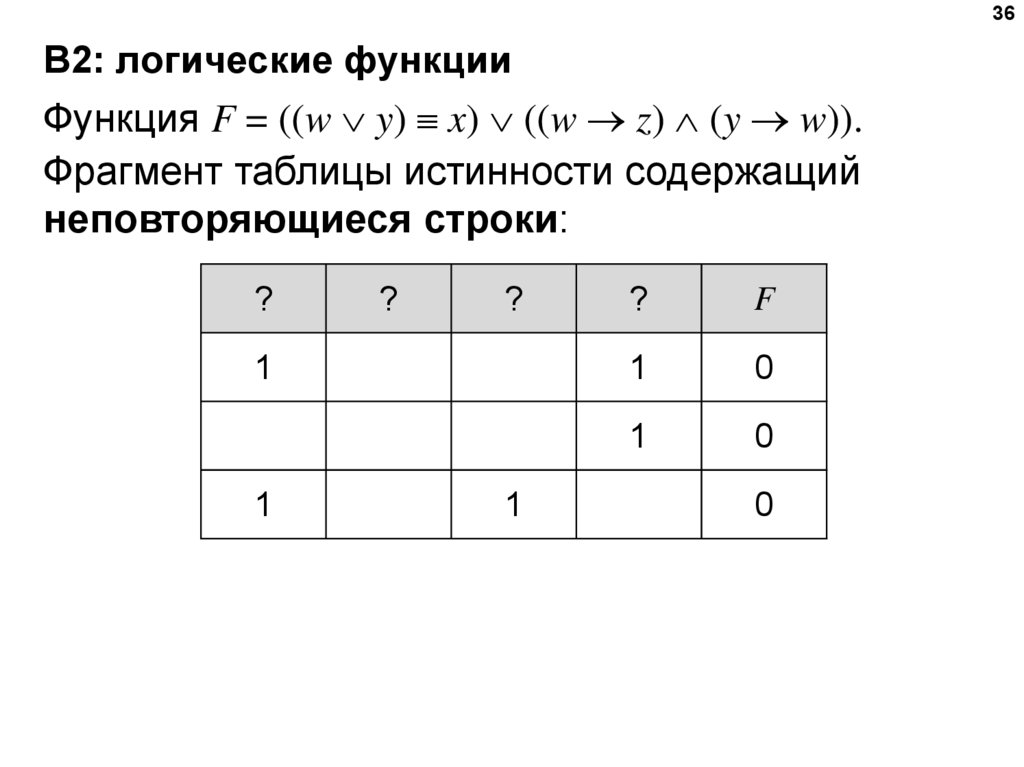
31
B2: логические функции
x1
1
!
x2
0
x3
x4
0
1
x5
x6
x7
x8
1
1
F
0
1
1
Все варианты – простые И или ИЛИ!
1) «в лоб» – подставлять в формулы…
2) если все «ИЛИ» один ноль
проверяем строку, где F = 0
x2 без инверсии, x8 с инверсией
3) если все «И» одна единица

30.

32
B2: логические функции
Заданы все строки таблицы истинности, для
которых функция x w ( y z ) истинна.
Определите, в каких столбцах x, y, z, w.
x
?
1
1
1
y
?
0
1
1
?z
0
0
w
?
0
0
F
1
1
1
0
1
x w ( y z) 1
x 1, w 0
y z 1 y 1 или z 0

31.

33
B2: логические функции (СДНФ)
Заданы все строки таблицы истинности, для
которых функция x ( y z w y z ) истинна.
Определите, в каких столбцах x, y, z, w.
w
?
0
0
1
?x
1
1
1
?z
0
1
0
y
?
F
1
0
1
1
1
1
x ( y z w y z) 1
x 1
y z w y z 1
y z w y z (w w ) 1
y z w 1
y z w 1
y z w 1
y
0
z
1
1
1
0
0
w
F
0
1
0
1
1
1

32.

34
B2: логические функции
Все нулевые строки x y z x
Определите, в каких столбцах x, y и z.
?z
0
0
0
?x
0
0
1
?y
0
1
1
F
0
0
0
y z.
F x y z x y z
x 0 F z y z z
z 0
x y
z F
0 0 0 0
y {0, 1}
0
1
1
1
0
0
0
0
x 1 F y y z y z
y 1, z 0

33.

35
B2: логические функции
(Демо-2019) Дана часть таблицы истинности для
функции x y ( y z ) w . Определите, в каких
столбцах x, y, z, w.
y 0 x (0 z ) w 0
?z
y
?
x
?
w
?
F
0
1
0
1
0
1
0
1
1
1
1
1
0
0
0
столбец с тремя 1
нет строки с тремя 0
нет столбца с тремя 0
2 строки с тремя 1
z 1 x 1
w 1, z 1, x 1
x
1
0
1
y
0
1
1
z
1
0
0
w
1
1
1
F
0
0
0
y 1 (1 z ) w 0
w 1, z 0, x {0, 1}

34.

36
B2: логические функции
Функция F = ((w y) x) ((w z) (y w)).
Фрагмент таблицы истинности содержащий
неповторяющиеся строки:
?
?
?
1
1
1
?
F
1
0
1
0
0

35.

37
B2: логические функции
F = ((w y) x) ((w z) (y w)).
Строим все строки, где F = 0:
w = 0: F = (y x) + (y 0) = 0.
y = 1, x = y = 0, z = {1, 0}
x
y
z
w
F
0
1
0
0
0
0
1
1
0
0

36.

38
B2: логические функции
F = ((w y) x) ((w z) (y w)).
Строим все строки, где F = 0:
w = 1: F = (1 x) + (1 z) = 0.
x = 0, z = 0, y = {1, 0}
x
y
z
w
F
0
1
0
0
0
0
1
1
0
0
0
0
0
1
0
0
1
0
1
0

37.

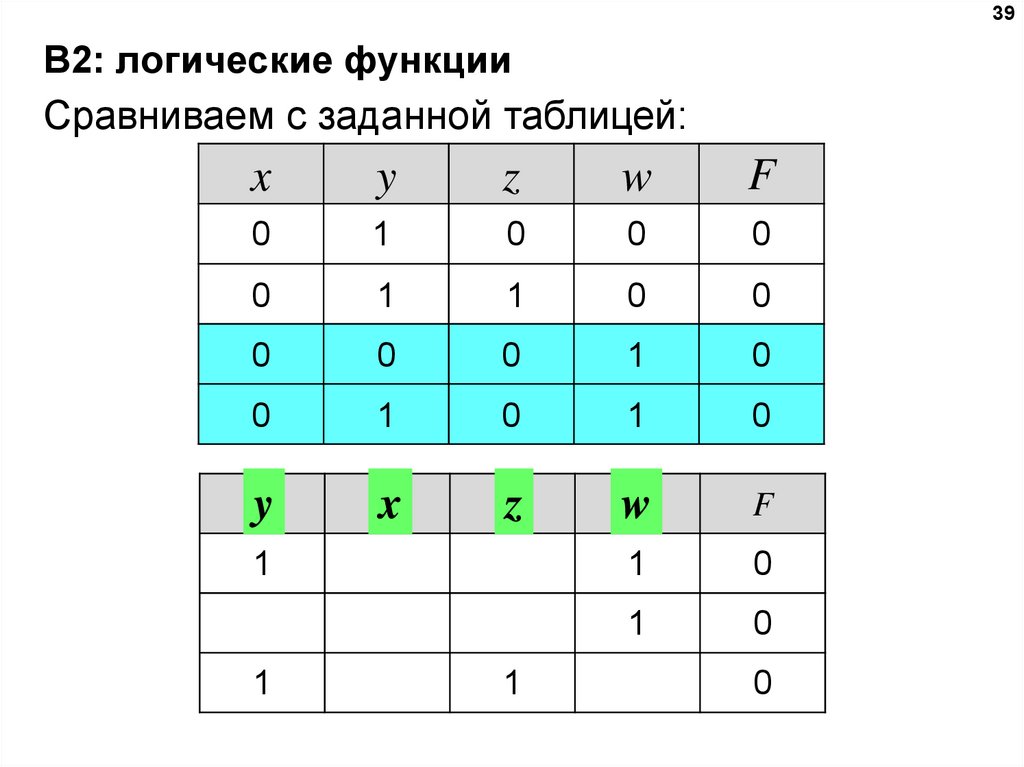
39
B2: логические функции
Сравниваем с заданной таблицей:
x
y
z
w
F
0
1
0
0
0
0
1
1
0
0
0
0
0
1
0
0
1
0
1
0
?
y
?
x
?z
?
w
F
1
0
1
0
1
1
1
0

38.

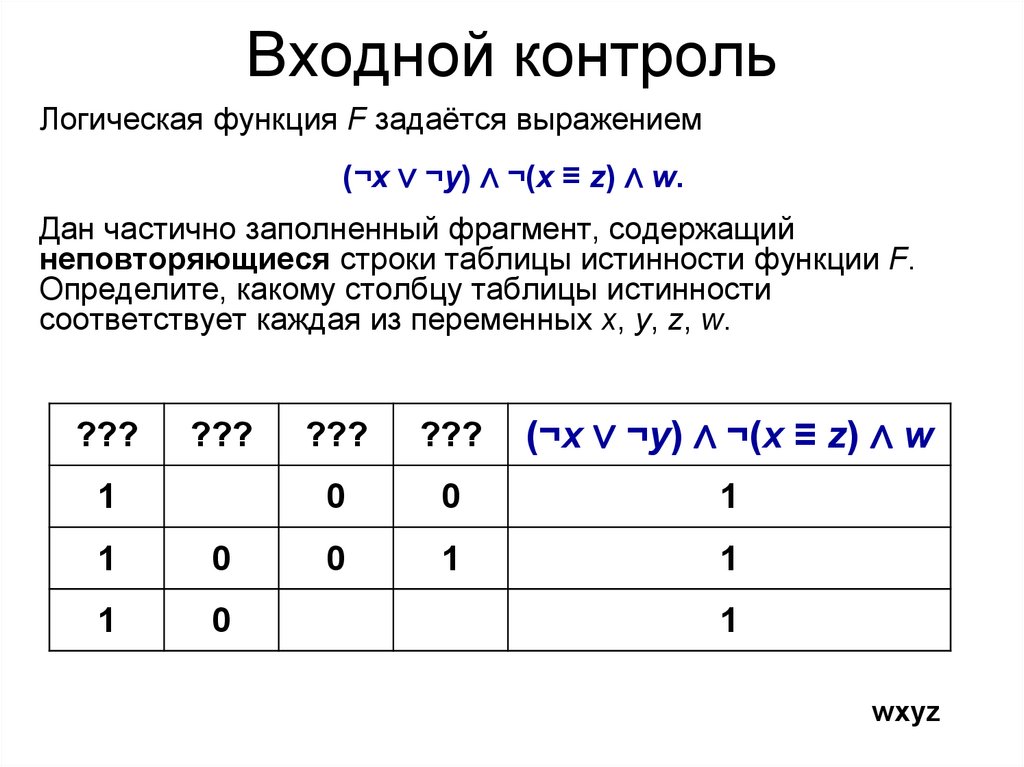
Входной контроль
Логическая функция F задаётся выражением
(¬x ∨ ¬y) ∧ ¬(x ≡ z) ∧ w.
Дан частично заполненный фрагмент, содержащий
неповторяющиеся строки таблицы истинности функции F.
Определите, какому столбцу таблицы истинности
соответствует каждая из переменных x, y, z, w.
???
???
1
1
0
1
0
???
???
(¬x ∨ ¬y) ∧ ¬(x ≡ z) ∧ w
0
0
1
0
1
1
1
wxyz

39.

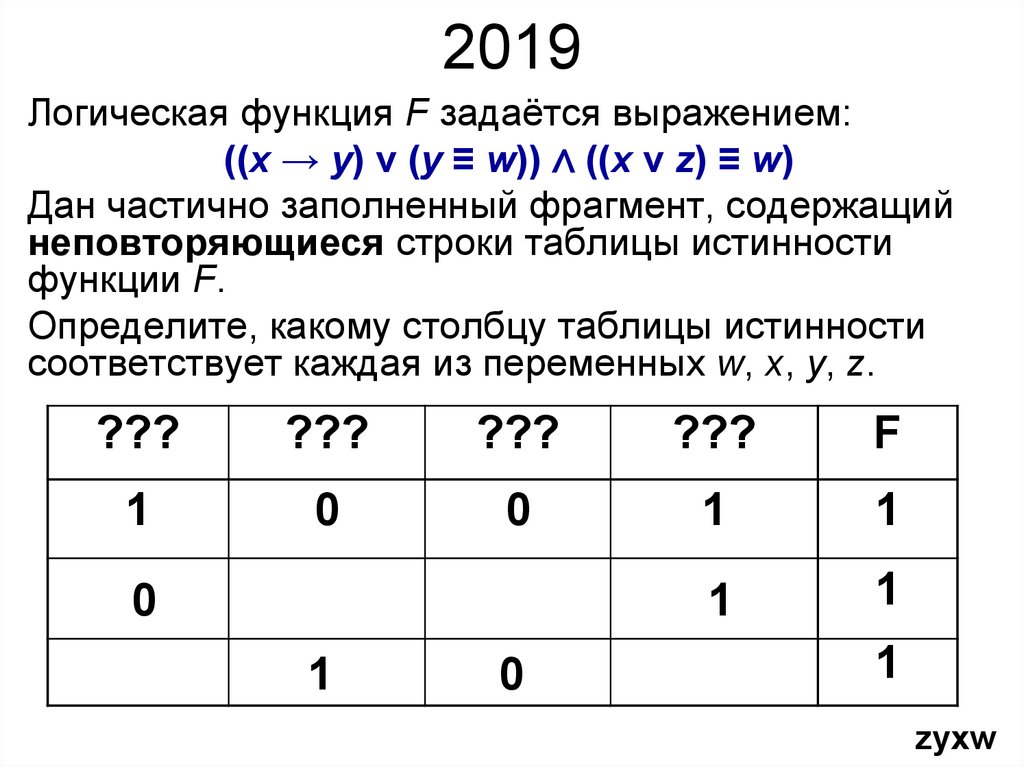
2019
Логическая функция F задаётся выражением:
((x → y) v (y ≡ w)) ∧ ((x v z) ≡ w)
Дан частично заполненный фрагмент, содержащий
неповторяющиеся строки таблицы истинности
функции F.
Определите, какому столбцу таблицы истинности
соответствует каждая из переменных w, x, y, z.
???
???
???
???
F
1
0
0
1
1
1
1
0
1
0
1
zyxw

40.

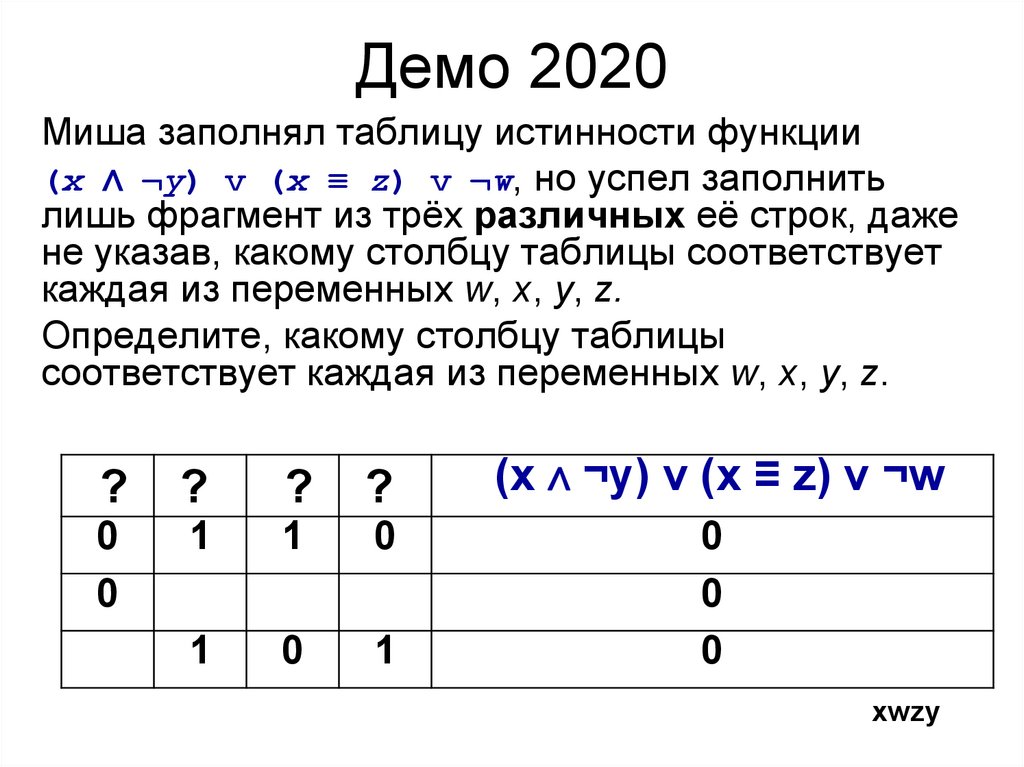
Демо 2020
Миша заполнял таблицу истинности функции
(x ∧ ¬y) v (x ≡ z) v ¬w, но успел заполнить
лишь фрагмент из трёх различных её строк, даже
не указав, какому столбцу таблицы соответствует
каждая из переменных w, x, y, z.
Определите, какому столбцу таблицы
соответствует каждая из переменных w, x, y, z.
?
?
?
?
0
0
1
1
0
1
0
1
(x ∧ ¬y) v (x ≡ z) v ¬w
0
0
0
xwzy

41.

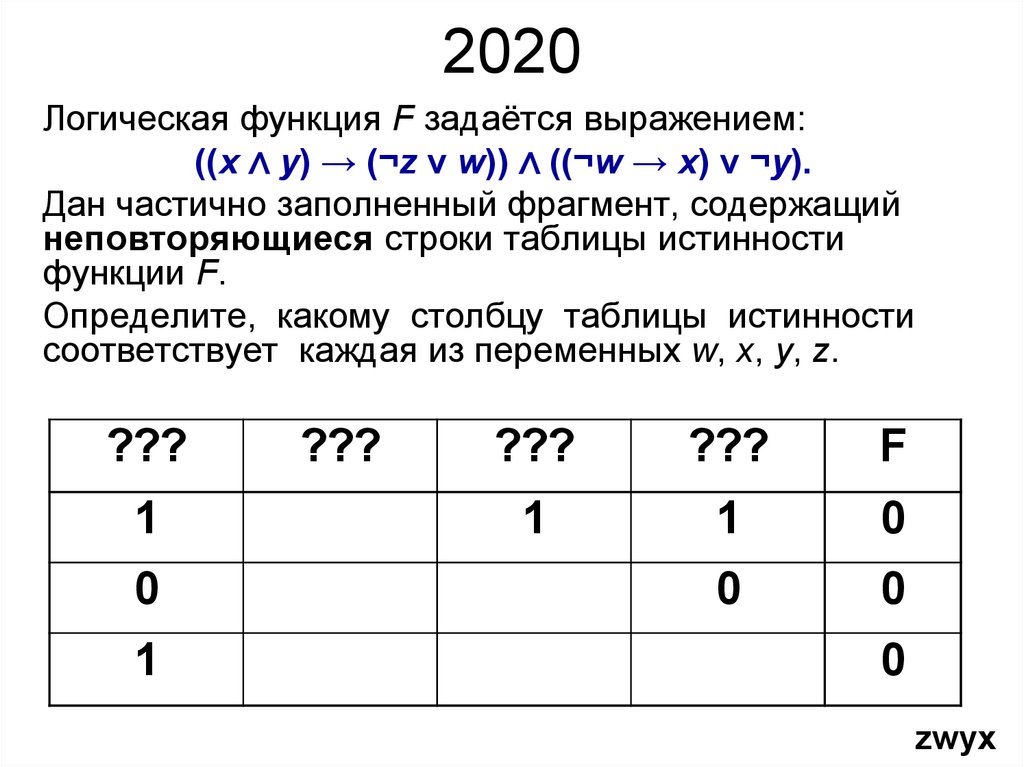
2020
Логическая функция F задаётся выражением:
((x ∧ y) → (¬z v w)) ∧ ((¬w → x) v ¬y).
Дан частично заполненный фрагмент, содержащий
неповторяющиеся строки таблицы истинности
функции F.
Определите, какому столбцу таблицы истинности
соответствует каждая из переменных w, x, y, z.
???
1
0
1
???
???
???
F
1
1
0
0
0
0
zwyx

42.

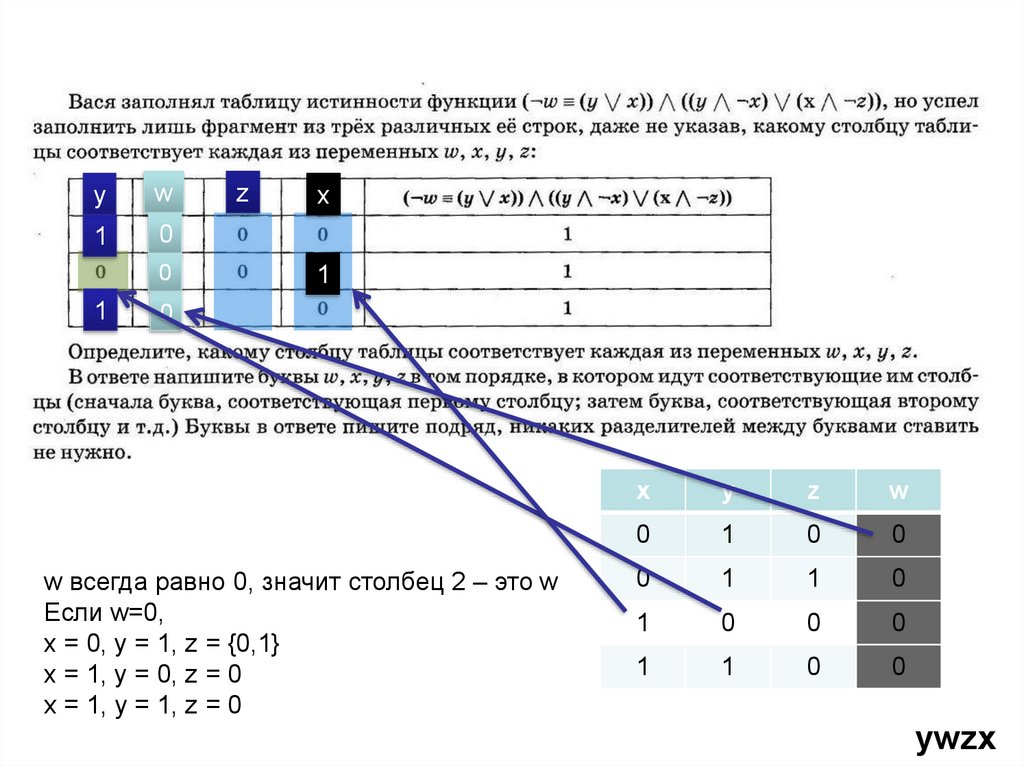
y
w
1
0
0
1
z
x
1
0
w всегда равно 0, значит столбец 2 – это w
Если w=0,
x = 0, y = 1, z = {0,1}
x = 1, y = 0, z = 0
x = 1, y = 1, z = 0
x
y
z
w
0
1
0
0
0
1
1
0
1
0
0
0
1
1
0
0
ywzx

43.

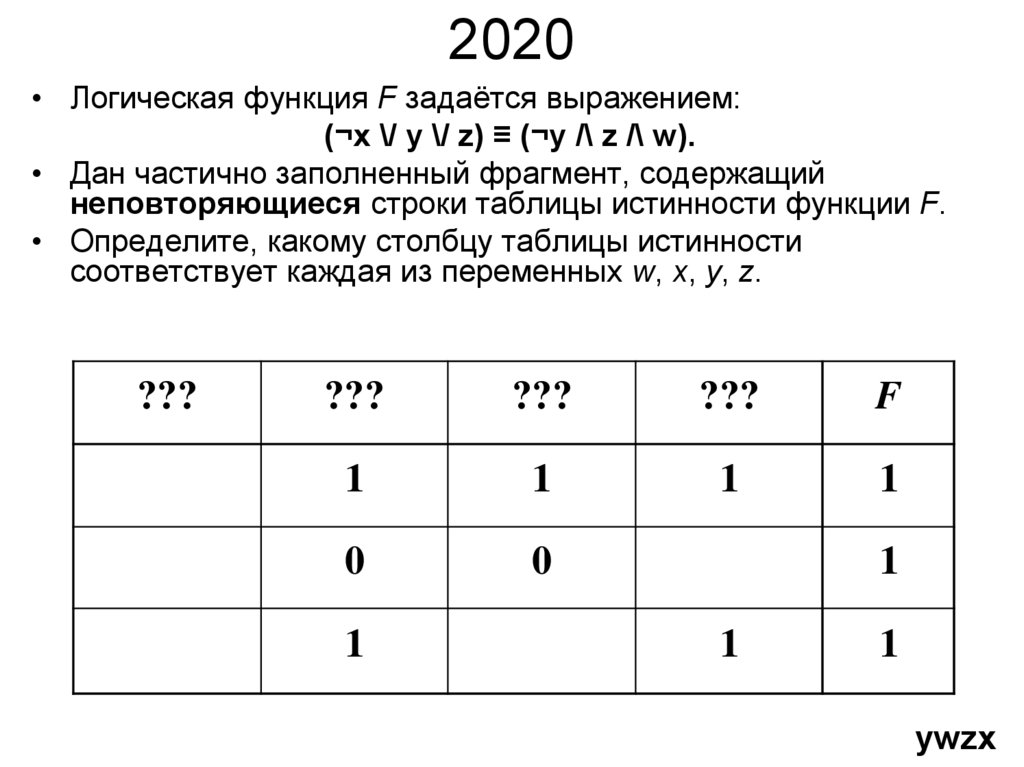
2020
• Логическая функция F задаётся выражением:
(¬x \/ y \/ z) ≡ (¬y /\ z /\ w).
• Дан частично заполненный фрагмент, содержащий
неповторяющиеся строки таблицы истинности функции F.
• Определите, какому столбцу таблицы истинности
соответствует каждая из переменных w, x, y, z.
???
???
???
???
F
1
1
1
1
0
0
1
1
1
1
ywzx

44.

46
Логические
основы
компьютеров
Упрощение логических
выражений

45.

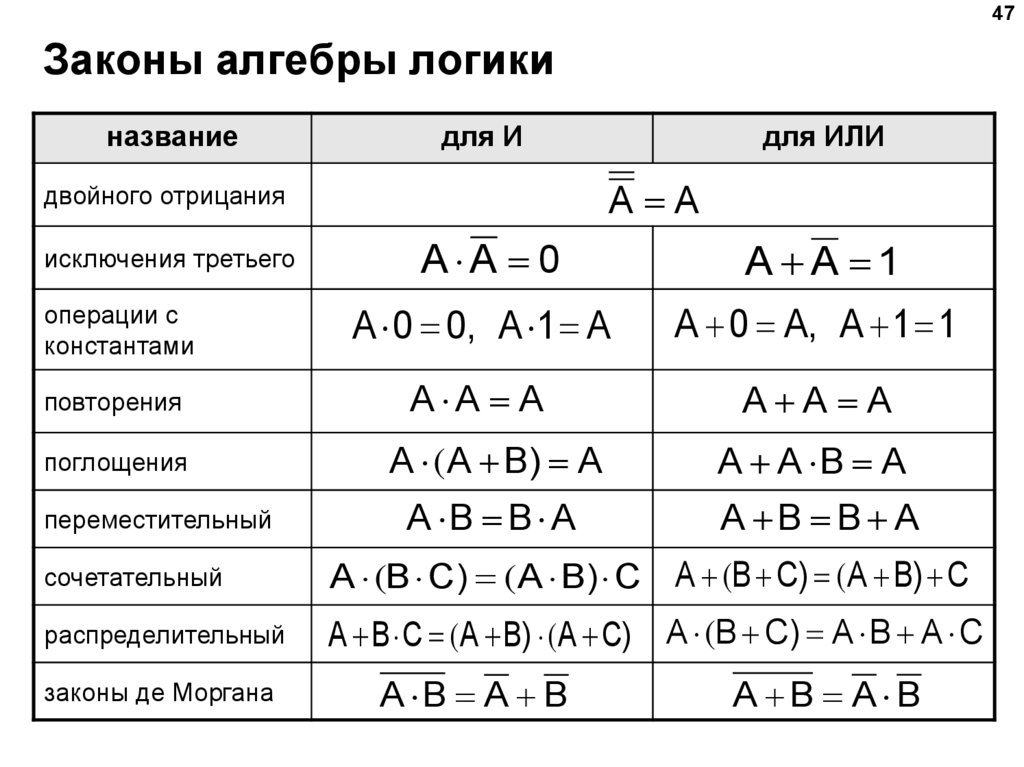
47
Законы алгебры логики
название
для И
для ИЛИ
A A
двойного отрицания
A A 0
A A 1
операции с
константами
A 0 0, A 1 A
A 0 A, A 1 1
повторения
A A A
A A A
исключения третьего
поглощения
переместительный
A ( A B) A
A A B A
A B B A
A B B A
сочетательный
A (B C) ( A B) C A (B C) ( A B) C
распределительный
A B C ( A B) ( A C)
A (B C) A B A C
законы де Моргана
A B A B
A B A B

46.

48
Упрощение логических выражений
Шаг 1. Заменить операции на их выражения
через И, ИЛИ и НЕ:
A B A B A B
A B A B
A B A B A B
Шаг 2. Раскрыть инверсию сложных выражений по
формулам де Моргана:
A B A B,
A B A B
Шаг 3. Используя законы логики, упрощать выражение,
стараясь применять закон исключения третьего.

47.

49
Упрощение логических выражений
Q M X H M X H (M M ) X H X H
X (B A) (A B) (A C)
( B A) (A B) (A C)
формула де Моргана
( B A) A B (A C)
( B A A A ) B (A C)
B A B (A C)
B A (A C)
B A
раскрыли
распределительный
исключения третьего
повторения
поглощения

48.

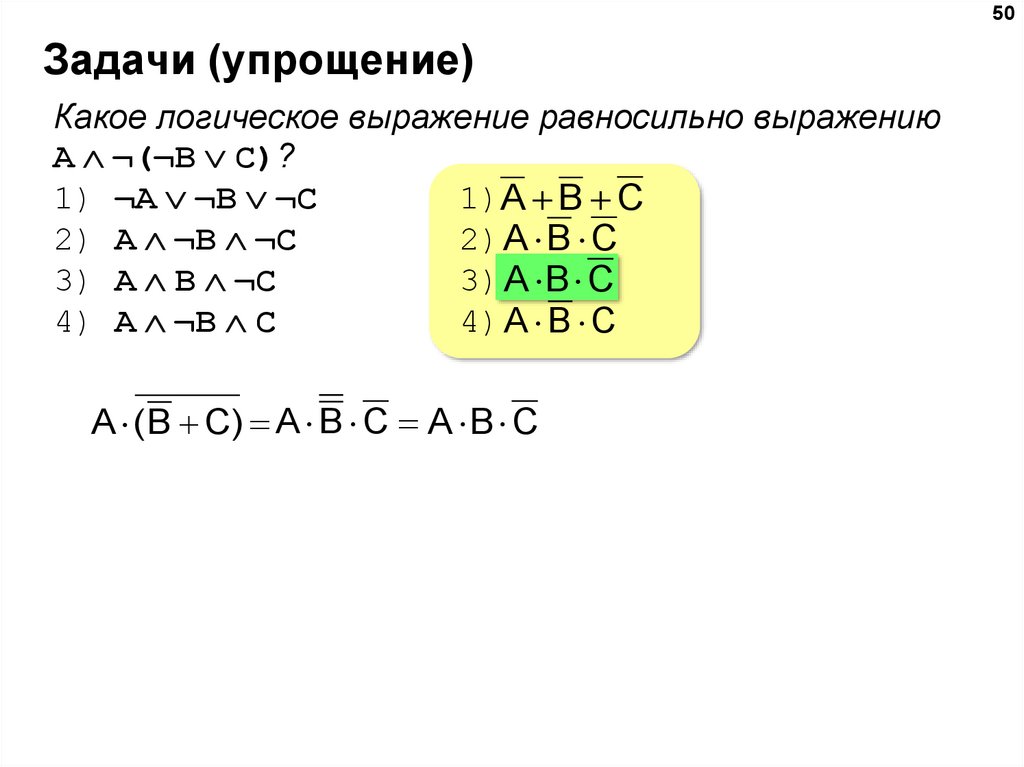
50
Задачи (упрощение)
Какое логическое выражение равносильно выражению
A ¬(¬B C)?
1) ¬A ¬B ¬C
1)A B C
2) A ¬B ¬C
2) A B C
3) A B ¬C
3) A B C
4) A ¬B C
4) A B C
A ( B C) A B C A B C

49.

51
Логические
основы
компьютеров
Множества и логика

50.

52
15 (повышенный уровень,
время – 3 мин)
Тема: Основные понятия математической логики.
Что проверяется:
Знание основных понятий и законов математической логики
1.5.1. Высказывания, логические операции, кванторы,
истинность высказывания.
• 1.1.7. Умение вычислять логическое значение сложного
высказывания по известным значениям элементарных
высказываний.

51.

53
Постановка задачи
На числовой прямой даны два отрезка: P = [37; 60] и Q =
[40; 77]. Укажите наименьшую возможную длину такого
отрезка A, что выражение
(x P) → (((x Q) ¬(x A)) → ¬(x P))
истинно при любом значении переменной х.
Элементами множеств А, P и Q являются
натуральные числа, причём
P = {2, 4, 6, 8, 10, 12} и Q = {4, 8, 12, 116}.
Известно, что выражение
(x P) → (((x Q) ¬(x A)) → ¬(x P))
истинно при любом значении переменной х.
Определите наименьшее возможное значение суммы
элементов множества A.

52.

54
Постановка задачи
Для какого наибольшего натурального числа А
выражение
¬ДЕЛ(x, А) (ДЕЛ(x, 6) ¬ДЕЛ(x, 4))
тождественно истинно (то есть принимает
значение 1 при любом натуральном значении
переменной х)?
Определите наименьшее натуральное число A,
такое что выражение
(x & 53 0) ((x & 41 = 0) (x & A 0))
тождественно истинно?

53.

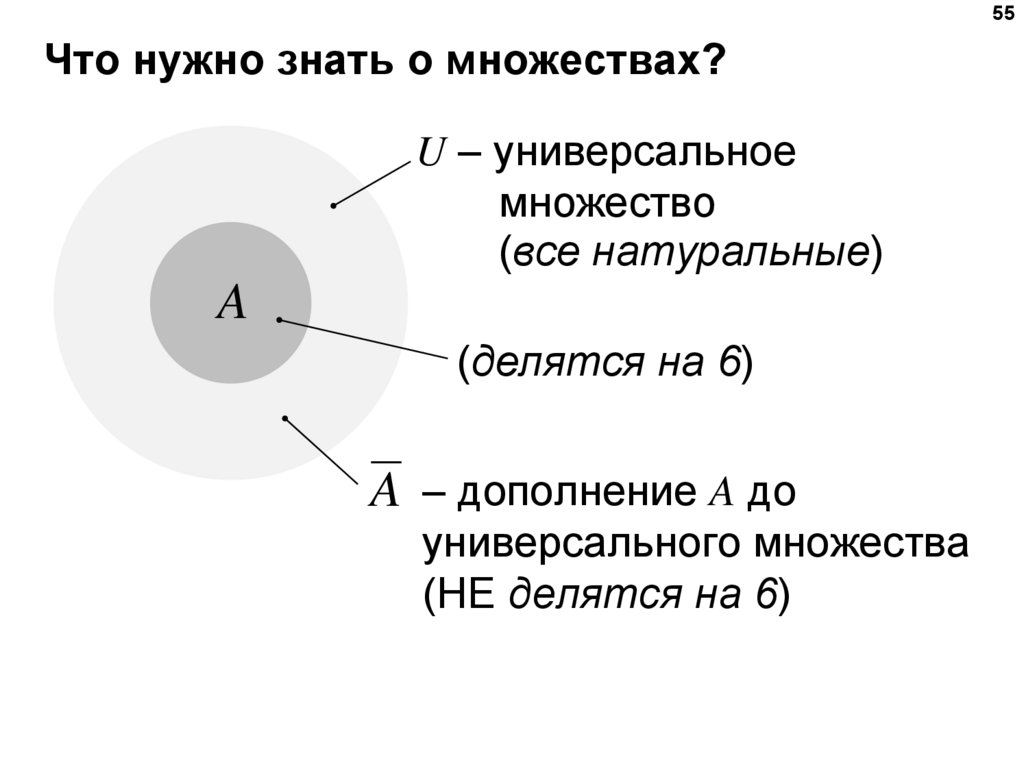
55
Что нужно знать о множествах?
U – универсальное
множество
(все натуральные)
A
(делятся на 6)
A – дополнение A до
универсального множества
(НЕ делятся на 6)

54.

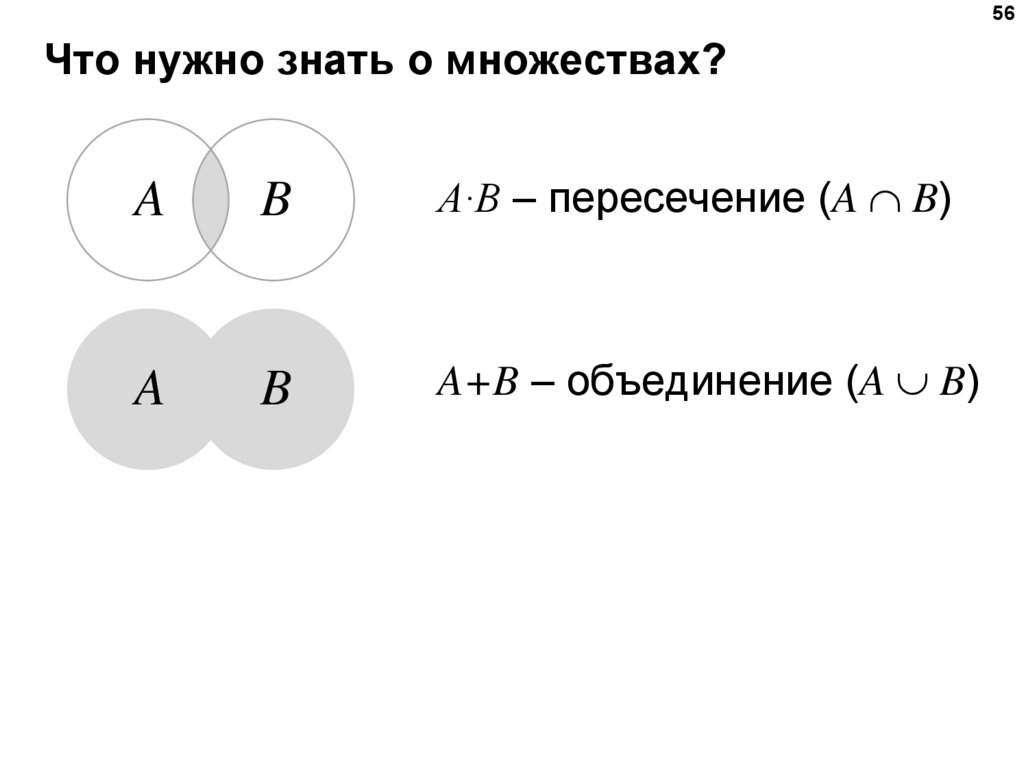
56
Что нужно знать о множествах?
A
B
A·B – пересечение (A B)
A
B
A+B – объединение (A B)

55.

57
Множества и логические функции
Множество задаётся логической функцией
x A
A
A(x) = 1
A( x) 1 x A
x A
A
A
B
A( x) B( x) 1 x A·B
A
B
A( x) B( x) 1 x A+B

56.

58
Задача дополнения (I)
Задача 1. Каким должно быть множество A для того,
чтобы множество A + B совпадало с универсальным
множеством U?
A B U A( x) B( x) 1 для всех x
это решение!
B B U A B
B ( x) 1
это условие
?
A
Есть ли другие решения?
определяет нужное
множество A
A включает B
(A B)
C B B U Amin B

57.

59
Задача дополнения (II)
Задача 2. Каким должно быть множество A для того,
чтобы множество A B совпадало с универсальным
множеством U?
A B U A( x) B( x) 1 для всех x
B B U A B A B
B( x ) 1
это условие
это решение!
?
A
Есть ли другие решения?
определяет нужное
множество A
A включает B
(A B)
C B B U ( A ) min B
A B
Amax B

58.

60
Общий подход к решению
1. Свести задачу к одной из базовых задач
Задача 1. A B 1
B A 1
Задача 2. A B 1 B A 1
2. Использовать готовое решение:
Задача 1. Amin B
Задача 2. Amax B

59.

61
Задачи с отрезками
На числовой прямой даны два отрезка:
P = [37; 60] и Q = [40; 77]. Укажите наименьшую
возможную длину такого отрезка A, что
выражение
(x P) → (((x Q) ¬(x A)) → ¬(x P))
истинно при любом значении переменной х.
Вводим утверждения:
P = (x P), Q = (x Q),
Заданное условие:
P (Q A P )
A = (x A)

60.

62
Задачи с отрезками
Упрощение выражения:
P (Q A P ) P (Q A P)
P Q A P
P Q A
A B 1 Задача 1
Решение:
P Q
Amin B P Q P Q
P = [37; 60], Q = [40; 77]
Amin = [40; 60]
длина 20

61.

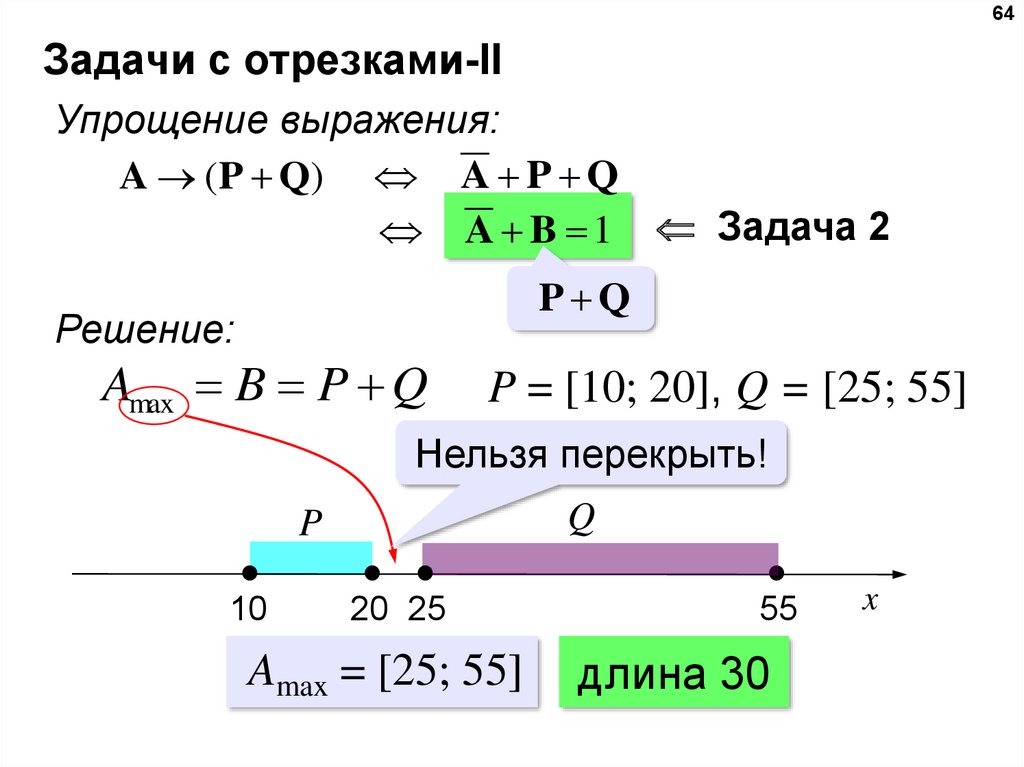
63
Задачи с отрезками-II
На числовой прямой даны два отрезка:
P = [10; 20] и Q = [25; 55]. Укажите наибольшую
возможную длину такого отрезка A, что
выражение
(x A) → ((x P) (x Q))
истинно при любом значении переменной х.
Вводим утверждения:
P = (x P), Q = (x Q),
Заданное условие:
A ( P Q)
A = (x A)

62.

64
Задачи с отрезками-II
Упрощение выражения:
A ( P Q) A P Q
A B 1 Задача 2
P Q
Решение:
Amax B P Q
P = [10; 20], Q = [25; 55]
Нельзя перекрыть!
Q
P
10
20 25
Amax = [25; 55]
55
длина 30
x

63.

65
Задачи с отрезками-III
На числовой прямой даны два отрезка:
P = [10; 20] и Q = [25; 55]. Укажите наименьшую
возможную длину такого отрезка A, что
выражение
((x P) (x Q)) → (x A)
истинно при любом значении переменной х.
Вводим утверждения:
P = (x P), Q = (x Q),
Заданное условие:
( P Q) A
A = (x A)

64.

66
Задачи с отрезками-III
Упрощение выражения:
( P Q) A A P Q
A B 1
Задача 1
P Q
Решение:
Amin B P Q
P
10
P = [10; 20], Q = [25; 55]
Нужно перекрыть!
Q
20 25
Amin = [10; 55]
55
длина 45
x

65.

67
Множества чисел
Элементами множеств А, P и Q являются
натуральные числа, причём
P = {2, 4, 6, 8, 10, 12} и Q = {4, 8, 12, 116}.
Известно, что выражение
(x P) → (((x Q) ¬(x A)) → ¬(x P))
истинно при любом значении переменной х.
Определите наименьшее возможное значение суммы
элементов множества A.
Вводим утверждения:
P = (x P), Q = (x Q),
Заданное условие:
P (Q A P )
A = (x A)

66.

68
Множества чисел
Упрощение выражения:
P (Q A P ) P (Q A P)
P Q A P
P Q A
A B 1 Задача 1
Решение:
P Q
Amin B P Q P Q
P = {2, 4, 6, 8, 10, 12}, Q = {4, 8, 12, 116}
Amin = {4, 8, 12}
сумма 24

67.

69
Множества чисел-II
Элементами множеств А, P и Q являются
натуральные числа, причём
P = { 2, 4, 6, 8, 10, 12, 14, 16, 18, 20}
Q = { 3, 6, 9, 12, 15, 18, 21, 24, 27, 30 }.
Известно, что выражение
((x A) → ¬(x P)) (¬(x Q) → ¬(x A))
истинно при любом значении переменной х.
Определите наибольшее возможное количество
элементов множества A.
Вводим утверждения:
P = (x P), Q = (x Q),
Заданное условие:
( A P ) ( Q A)
A = (x A)

68.

70
Множества чисел-II
Упрощение выражения:
(A P) (Q A) ( A P) (Q A)
A Q P Q A P A
A Q P Q A
A P Q
A B 1 Задача 2
Решение:
Amax B P Q
P Q
P = { 2, 4, 6, 8, 10, 12, 14, 16, 18, 20}
Q = { 3, 6, 9, 12, 15, 18, 21, 24, 27, 30 }
Amax = { 3, 9, 15, 21, 24, 27, 30 }
7 шт.

69.

71
Множества чисел Python
На числовой прямой даны отрезки A = [70; 90], B = [40; 60] и C = [0; N] и
функция
F(x) = ( (x A) (x B) ) ( (x C) (x A) )
При каком наименьшем числе N функция F(x) истинна более чем для 30
целых чисел x?

70.

72
Делимость

71.

73
Делимость
Для какого наибольшего натурального числа a
выражение
¬ДЕЛ(x, a) (ДЕЛ(x, 6) ¬ДЕЛ(x, 4))
тождественно истинно (то есть принимает
значение 1 при любом натуральном значении
переменной х)?
DN – множество чисел, делящихся на N
A = Da – множество чисел, делящихся на a
Вводим утверждения:
DN = (x DN), A = (x A)
Заданное условие: A (D6 D4 )

72.

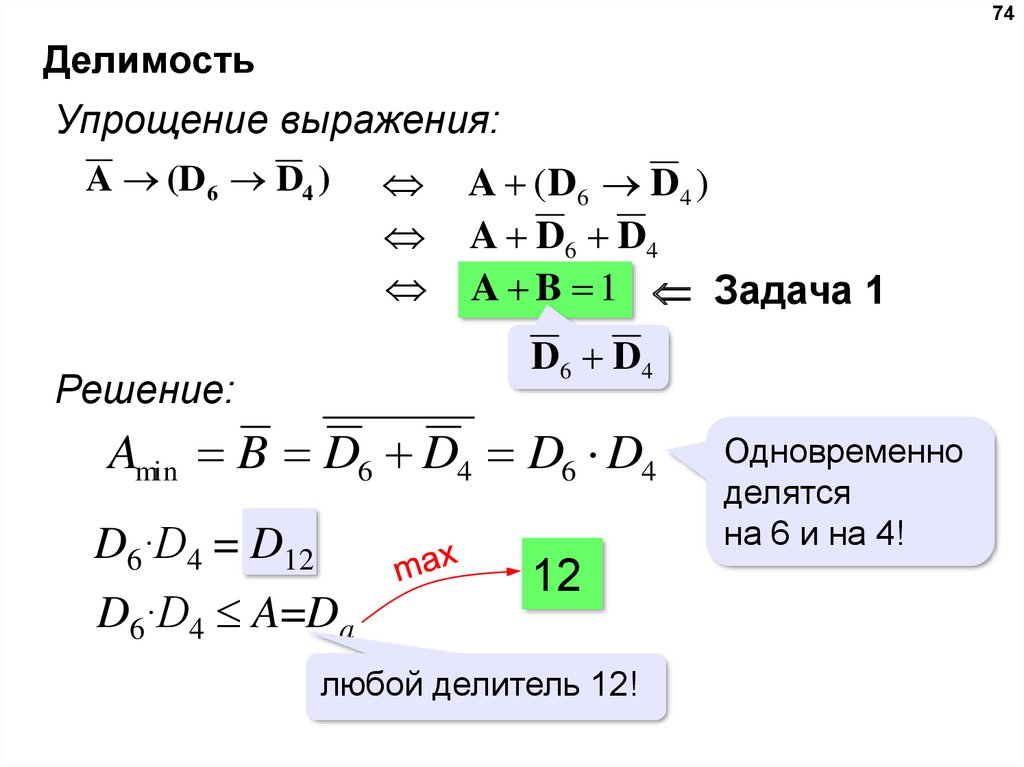
74
Делимость
Упрощение выражения:
A (D6 D4 )
A (D6 D4 )
A D6 D4
A B 1 Задача 1
D6 D 4
Решение:
Amin B D6 D4 D6 D4
D6·D4 = D12
D6·D4 A=Da
12
любой делитель 12!
Одновременно
делятся
на 6 и на 4!

73.

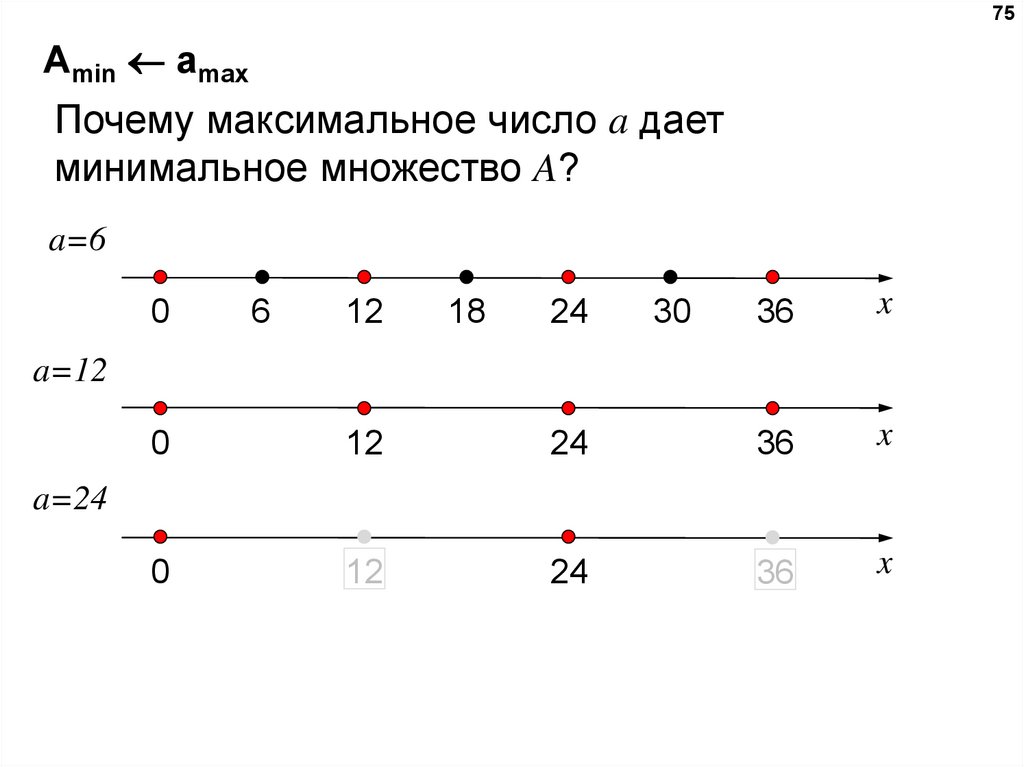
75
Amin amax
Почему максимальное число a дает
минимальное множество A?
a=6
0
6
12
18
24
30
36
x
a=12
0
12
24
36
x
0
12
24
36
x
a=24

74.

76
Делимость-II
Для какого наибольшего натурального числа a
выражение
¬ДЕЛ(x, a) (¬ ДЕЛ(x, 21) ¬ДЕЛ(x, 35))
тождественно истинно?
DN – множество чисел, делящихся на N
A = Da – множество чисел, делящихся на a
Вводим утверждения:
DN = (x DN), A = (x A)
Заданное условие:
A (D21 D35 )

75.

77
Делимость-II
Упрощение выражения:
A (D21 D35 )
A D21 D35
A B 1 Задача 1
D21 D35
Решение:
Amin B D21 D35
D21+D35 = Da
D21+D35 < Da
Делятся
D21 D35 на 21 или на 35!
нет такого a!
max
Общий делитель 21 и 35!
7

76.

78
Делимость-III
Для какого наименьшего натурального числа a
выражение
ДЕЛ(x, a) (¬ ДЕЛ(x, 21) ДЕЛ(x, 35))
тождественно истинно?
DN – множество чисел, делящихся на N
A = Da – множество чисел, делящихся на a
Вводим утверждения:
DN = (x DN), A = (x A)
Заданное условие:
A (D21 D35 )

77.

79
Делимость-III
Упрощение выражения:
A (D21 D35 )
A D21 D35
A B 1 Задача 2
D21 D35
Решение:
Amax B D21 D35
D21 D35 Da
нет такого a!
D21 D35 A Da
Не делятся
на 21 или
делятся на 35!

78.

80
Делимость-III
Переход к другой импликации:
!
A D21 D35 ( A D21 ) D35
Если число делится на a и на 21, оно должно
делиться на 35!
Делится на A и на 21:
x a k 21 m 3 7 m
Делится на 35:
x 35 q 5 7 q
k, m – натуральные
a 5 r
min
Этот сомножитель
добавляется с
помощью A!
5

79.

81
Делимость-IV
Для какого наименьшего натурального числа a
выражение
(ДЕЛ(x, a) ДЕЛ(x, 21)) ДЕЛ(x, 18)
тождественно истинно?
DN – множество чисел, делящихся на N
A = Da – множество чисел, делящихся на a
Вводим утверждения:
DN = (x DN), A = (x A)
Заданное условие:
(A D21 ) D18

80.

82
Делимость-IV
(A D21 ) D18
!
Если число делится на A и на 21, оно должно
делиться на 18!
Делится на A и на 21:
x a k 21 m 3 7 m
Делится на 18:
x 18 q 2 3 3 q
Эти сомножители
добавляются с
помощью A!
a 2 3 3 r
min
18

81.

83
Делимость-V
Для какого наименьшего натурального числа a
выражение
¬ДЕЛ(x, 18) (¬ДЕЛ(x,21) ¬ДЕЛ(x, a))
тождественно истинно?
DN – множество чисел, делящихся на N
A = Da – множество чисел, делящихся на a
Вводим утверждения:
DN = (x DN), A = (x A)
Заданное условие:
D18 ( D21 A )

82.

84
Делимость-IV
D18 ( D21 A )
D18 D21 A
A B 1 Задача 2
D18 D21
Решение:
Amax B D18 D21
D18 D21 Da
нет такого a!
D18 D21 A Da
!
Нельзя перекрывать
другие числа!
Делятся
на 18 или
на 21!
Варианты:
A D18 , D36 , ...
A D21, D42 , ...

83.

(демо-2021) Для какого наибольшего натурального
числа А формула
¬ДЕЛ(x,А) (ДЕЛ(x,6) ¬ДЕЛ(x,9))
тождественно истинна (то есть принимает значение
1 при любом натуральном значении переменной х)?
Ответ: 18
85

84.

86
Линейное (и нелинейное)
программирование
Задание 15

85.

87
Постановка задачи
Укажите наименьшее целое значение А, при котором
выражение
(y + 2x < A) ∨ (x > 20) ∨ (y > 30)
истинно для любых целых положительных значений x и y.
Укажите наименьшее целое значение А, при котором
выражение
(y + 2x < A) ∨ (3y +2x > 120) ∨ (3y – x > 30)
истинно для любых целых положительных значений x и y.
Укажите наибольшее целое значение А, при котором
выражение
(y – x 5) ∨ (A < 2x3 + y) ∨ (A < y2 + 16)
истинно для любых целых положительных значений x и y.

86.

88
Задача 1.
Укажите наименьшее целое значение А, при котором
выражение
(y + 2x < A) ∨ (x > 20) ∨ (y > 30)
истинно для любых целых положительных значений x и y.
не зависит от A
(y + 2x < A) ∨ (x > 20) ∨ (y > 30)
истинно
ложно
(x > 0) (x 20) (y 30) (y > 0)

87.

89
Задача 1. Аналитическое решение
(x > 0) (x 20) (y 30) (y > 0)
(y + 2x < A)
A > y + 2x для (x > 0) (x 20) (y 30) (y > 0)
A > max(y + 2x)
для (x > 0) (x 20) (y 30) (y > 0)
только x
только y
максимум линейной функции при линейных
ограничениях
!
Задача линейного программирования!
A > max(y + 2x) = max(y) + 2·max(x)
A > 30 + 2·20 = 70
Amin = 71

88.

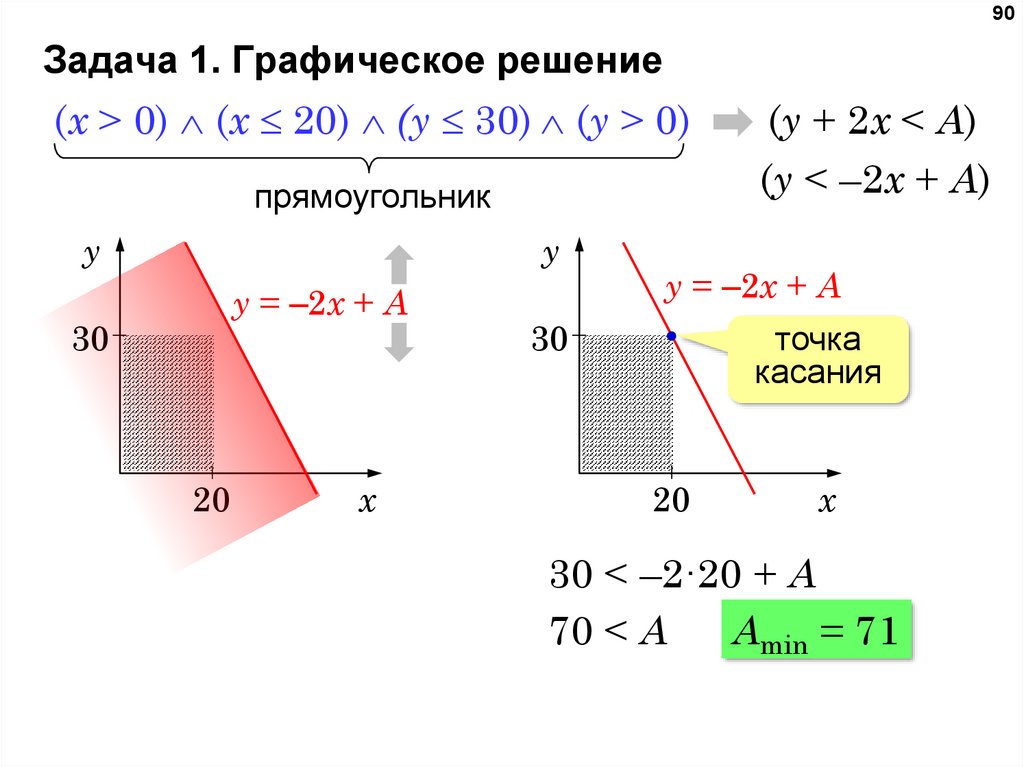
90
Задача 1. Графическое решение
(x > 0) (x 20) (y 30) (y > 0)
прямоугольник
y
y
y = –2x + A
30
20
x
(y + 2x < A)
(y < –2x + A)
y = –2x + A
30
точка
касания
20
x
30 < –2·20 + A
70 < A
Amin = 71

89.

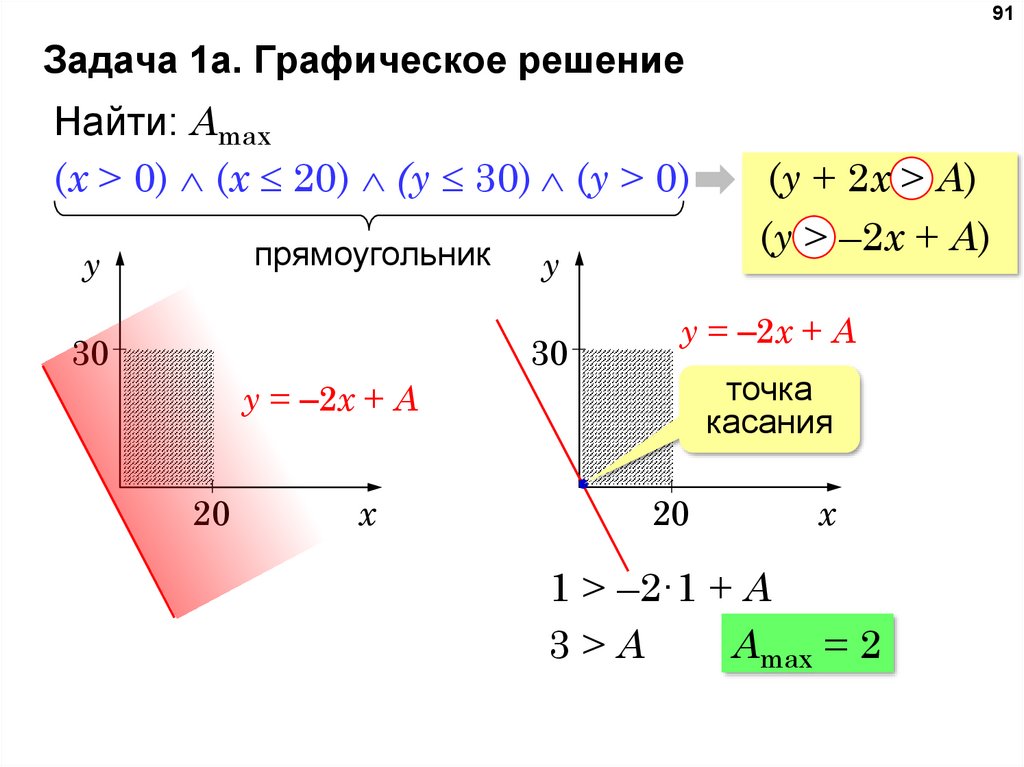
91
Задача 1a. Графическое решение
Найти: Amax
(x > 0) (x 20) (y 30) (y > 0)
прямоугольник
y
30
y
30
y = –2x + A
точка
касания
y = –2x + A
20
x
(y + 2x > A)
(y > –2x + A)
20
x
1 > –2·1 + A
3>A
Amax = 2

90.

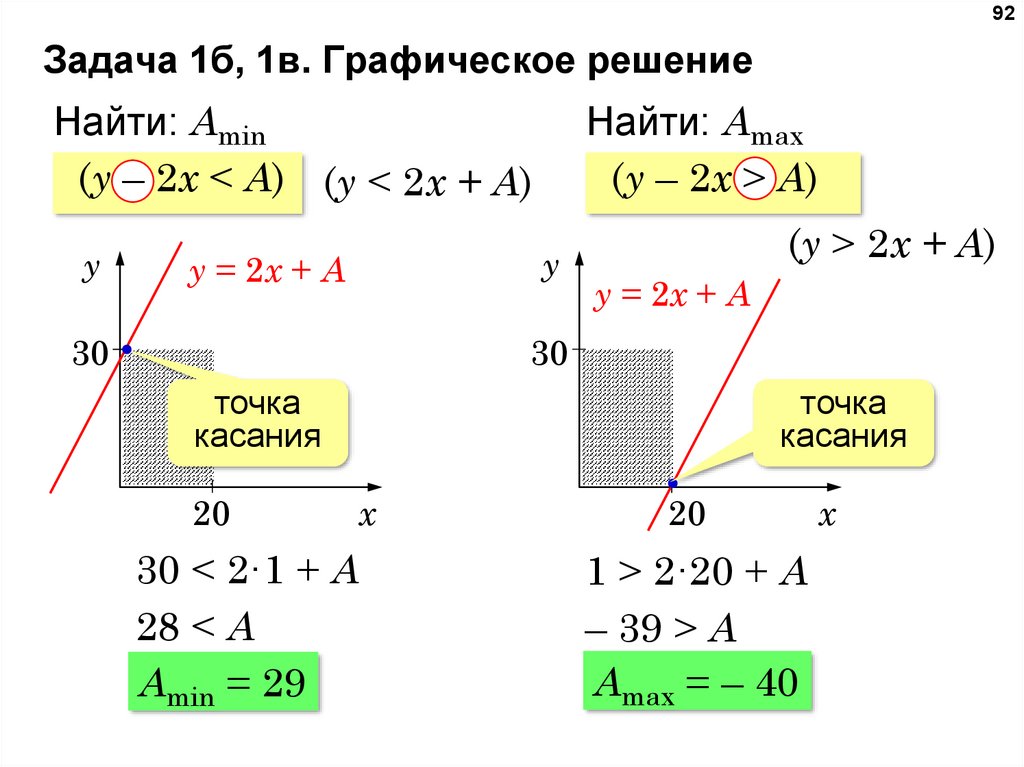
92
Задача 1б, 1в. Графическое решение
Найти: Amin
(y – 2x < A) (y < 2x + A)
y
Найти: Amax
(y – 2x > A)
y
y = 2x + A
(y > 2x + A)
y = 2x + A
30
30
точка
касания
20
точка
касания
x
30 < 2·1 + A
28 < A
Amin = 29
20
1 > 2·20 + A
– 39 > A
Amax = – 40
x

91.

93
Задача 1.
Укажите наименьшее целое значение А, при котором
выражение
(5k + 6n > 57) ∨ ((k ≤ A) (n < A))
истинно для любых целых положительных значений k и n.
Ответ: 10

92.

94
Задача 2.
Укажите наименьшее целое значение А, при котором
выражение
(5x + 3y 60) ∨ ((A > x) (A > y))
истинно для любых целых неотрицательных
значений x и y.
не зависит от A
((A > x) (A > y)) ∨ (5x + 3y 60)
истинно
ложно
(x 0) (5x + 3y = 60) (y 0)

93.

95
Задача 2. Аналитическое решение
(x 0) (5x + 3y = 60) (y 0)
(A > x)
(A > y)
A > max(x) при (x 0) (5x + 3y = 60) (y 0)
A > max(y) при (x 0) (5x + 3y = 60) (y 0)
A > max(x) при (5x = 60) xmax = 12
A > max(y) при (3y = 60) ymax = 20
A > max(x) = 12
A > max(y) = 20
Amin = 21

94.

96
Задача 2. Графическое решение
(x 0) (5x + 3y = 60) (y 0)
отрезок
y
A
20
A > max(x) = 12
A > max(y) = 20
5x + 3y = 60
12
A
(A > x)
квадрат
(A > y)
Amin = 21
x

95.

97
Решение в стиле Python
Ответ: 21

96.

98
Задача 3.
Укажите наименьшее целое значение А, при котором
выражение
(y +3x 19) ∨ (A > 2x + 16) (A > 3y)
истинно для любых целых положительных значений x и y.
не зависит от A
(A > 2x + 16) (A > 3y) ∨ (y + 3x 19)
истинно
ложно
(x > 0) (y + 3x = 19) (y > 0)

97.

99
Задача 3. Аналитическое решение
(x > 0) (y + 3x = 19) (y > 0)
(A > 2x + 16)
и (A > 3y)
A > max(2x + 16)
A > max(3y)
прямая
y = – 3x + 19
max(2x + 16)
при (x > 0) (y + 3x = 19)
A > max
(y > 0)
max(3y)
ymax при x = 1
возрастающие при
x > 0, y > 0
отрезок
ymax = – 3·1+ 19 = 16
xmax при y = 1
xmax= (19 – 1) / 3 = 6
max(2·6 + 16)
A > max
= max(28, 48)
max(3·16)
Amin = 49

98.

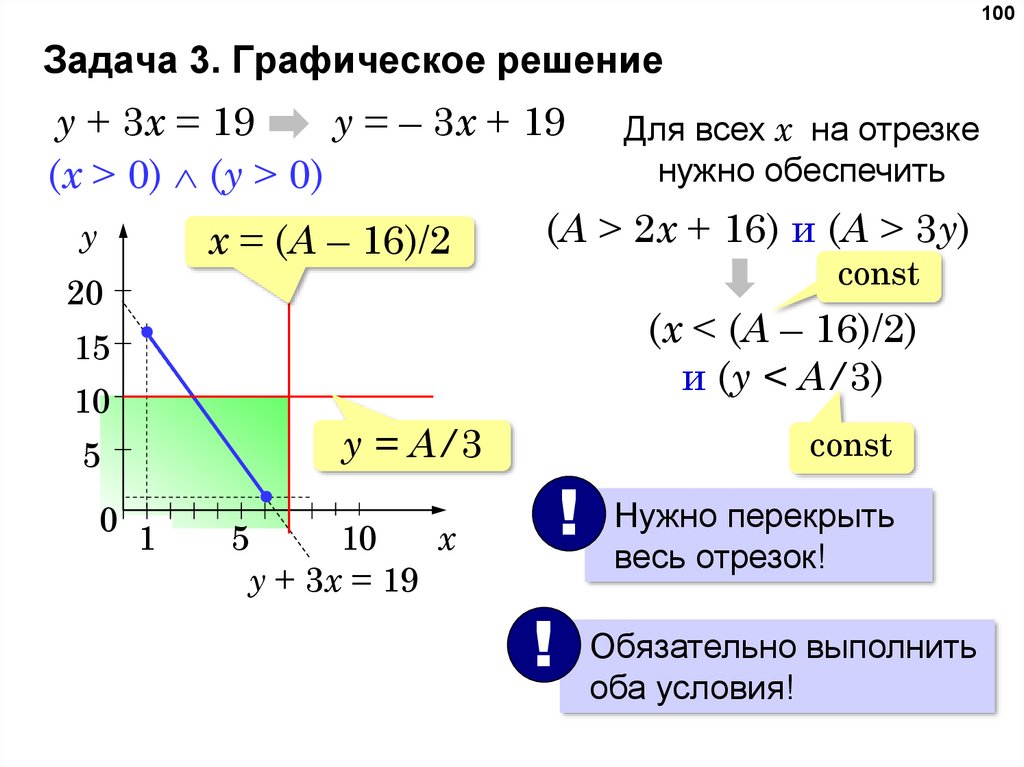
100
Задача 3. Графическое решение
y + 3x = 19
y = – 3x + 19 Для всех x на отрезке
нужно обеспечить
(x > 0) (y > 0)
(A > 2x + 16) и (A > 3y)
y
x = (A – 16)/2
const
20
(x < (A – 16)/2)
и (y < A/3)
15
10
y = A/3
5
0
1
x
5
10
y + 3x = 19
const
!
!
Нужно перекрыть
весь отрезок!
Обязательно выполнить
оба условия!

99.

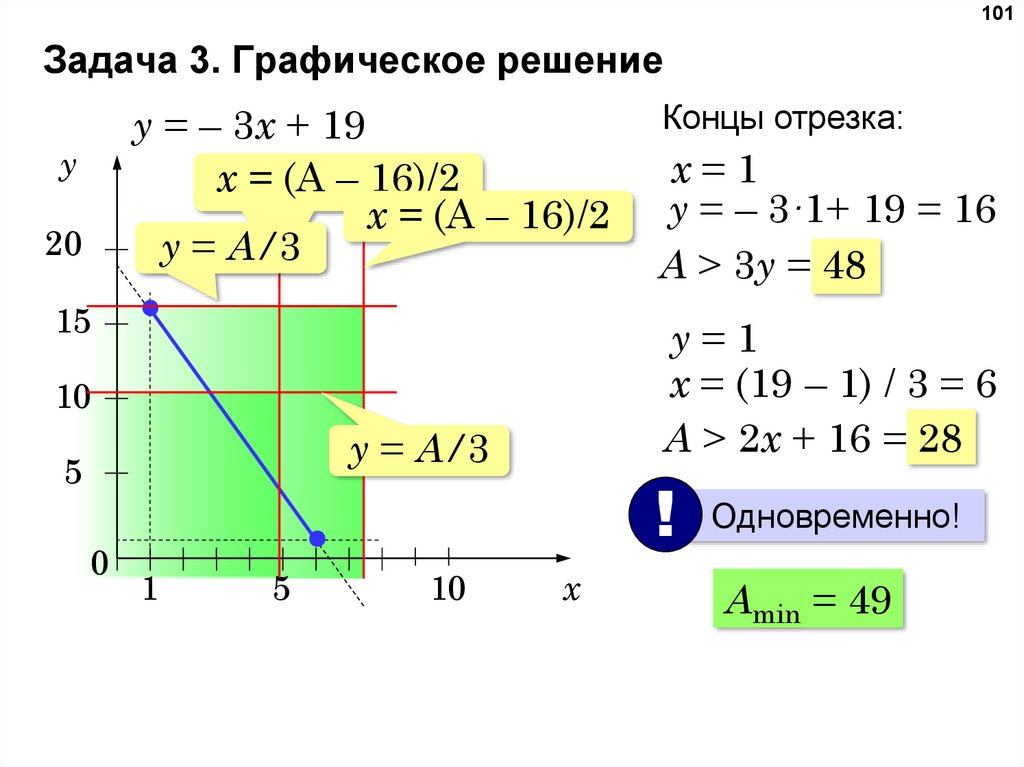
101
Задача 3. Графическое решение
y = – 3x + 19
x = (A – 16)/2
x = (A – 16)/2
y = A/3
y
20
15
y = A/3
0
1
5
10
x=1
y = – 3·1+ 19 = 16
A > 3y = 48
y=1
x = (19 – 1) / 3 = 6
A > 2x + 16 = 28
10
5
Концы отрезка:
!
x
Одновременно!
Amin = 49

100.

127
Побитовые логические операции
Определите наименьшее натуральное число a,
такое что выражение
(x & 53 0) ((x & 41 = 0) (x & a 0))
тождественно истинно.?
Вводим множества:
ZN = {x: x & N = 0}
Z N {x : x & N 0}
Вводим утверждения:
ZN = (x ZN), A = (x Za)
Заданное условие:
Z53 (Z 41 A)
Число a
определяет
множество Za или
условие A.

101.

128
Побитовые логические операции
Что такое Z53:
биты 5 4 3 2 1 0
53 = 110101
x = abcdef
x & 53 = ab0d 0f = 0
Что такое Z:53
биты 5 4 3 2 1 0
53 = 110101
x = abcdef
x & 53 = ab0d 0f 0
Биты 5, 4, 2, 0 числа x
нулевые!
Среди битов 5, 4, 2, 0 числа
x есть ненулевые!

102.

129
Главная ошибка
После упрощения:
биты 5 4 3 2 1 0
21 = 010101
11 = 001011
Вывод:
Z 21 Z11 A 1
Натуральные
числа!
21 or 11 or a 1
a 21 or 11
a 21 or 11 20
!
?
Логические
значения!
Это ИНОГДА
проходит!
Это min или max?

103.

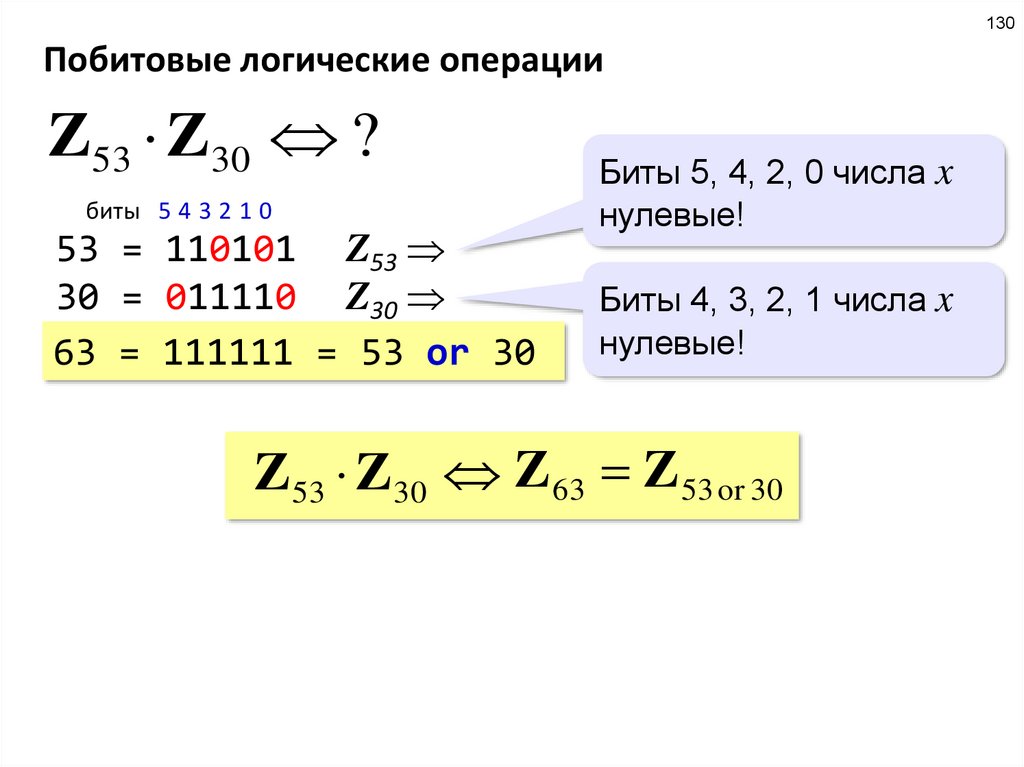
130
Побитовые логические операции
Z53 Z30 ?
биты 5 4 3 2 1 0
53 = 110101 Z53
30 = 011110 Z30
63 = 111111 = 53 or 30
Биты 5, 4, 2, 0 числа x
нулевые!
Биты 4, 3, 2, 1 числа x
нулевые!
Z53 Z30 Z 63 Z 53 or 30

104.

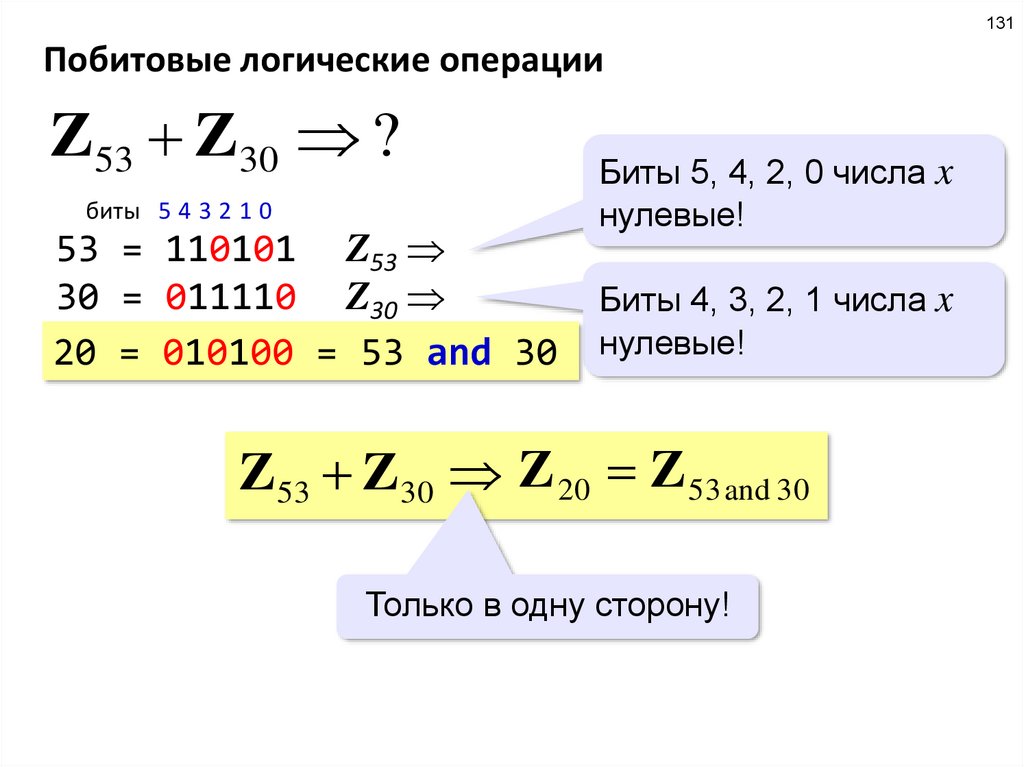
131
Побитовые логические операции
Z53 Z30 ?
биты 5 4 3 2 1 0
53 = 110101 Z53
30 = 011110 Z30
20 = 010100 = 53 and 30
Биты 5, 4, 2, 0 числа x
нулевые!
Биты 4, 3, 2, 1 числа x
нулевые!
Z53 Z30 Z 20 Z 53 and 30
Только в одну сторону!

105.

132
Побитовые логические операции
Z b Z c Z b or c
Z b Z c Z b and c
Двойственность
операций И и ИЛИ
только для левой
части импликации!

106.

134
Побитовые логические операции
Биты 4, 2 и 0
нулевые!
Биты 4 и 0 нулевые!
Zb Z c 1
биты 4 3 2 1 0
Zb : 21 = 10101
!
биты 4 3 2 1 0
Z c : 17 = 10001
Множество единичных битов c входит во
множество единичных битов b!
Z 21 Z 7 0
?
биты 4 3 2 1 0
Zb : 21 = 10101
биты 4 3 2 1 0
1
Z c : 7 = 00111

107.

135
Побитовые логические операции
Zb ( A Z c ) ?
Z b ( A Z c ) ( Z b A) ( Z b Z c )
Вариант 1:
Zb Z c 1
!
a – любое!
Вариант 2:
Zb Z c 0 Zb A 1
!
Множество единичных битов a входит во
множество единичных битов b!

108.

136
Побитовые логические операции
Метод А.В. Здвижковой (г. Армавир):
!
Строим импликацию так, чтобы избавиться
от всех инверсий!
Z53 (Z 41 A)
Z 53 (Z 41 A )
Z 53 Z 41 A
Z41 A Z53
(Z 41 A) Z53

109.

137
Побитовые логические операции
(Z 41 A) Z53
Биты 5, 3, 0
нулевые!
Решение:
Логическое
ИЛИ между
битами!
биты 5 4 3 2 1 0
41 = 101001
a = ??????
1 1
53 = 110101
amin = 101002 = 20
Биты 5, 4, 2, 0
нулевые!
?
Другие a?

110.

138
Побитовые логические операции-II
Определите наибольшее натуральное число a,
такое что выражение
(x & a 0) ((x & 20 = 0) (x & 5 0))
тождественно истинно.
Вводим множества:
ZN = {x: x & N = 0}
Z N {x : x & N 0}
Вводим утверждения:
ZN = (x ZN), A = (x Za)
Заданное условие:
A (Z 20 Z5 )

111.

139
Побитовые логические операции-II
Упрощение выражения (до суммы):
A (Z 20 Z5 ) A (Z 20 Z5 )
A Z 20 Z5 Z20 Z5 A
Импликация без инверсий:
Решение:
(Z 20 Z5 ) A
Биты 4, 2 нулевые!
биты 4 3 2 1 0
Z 20 : 20 = 10100
Z 5 : 5 = 00101
amax = 101012 = 21
a = 1, 4, 5, 16, 17, 20, 21
Биты 2, 0 нулевые!
?
?
Другие a?
Сколько?
23 – 1 = 7

112.

140
Побитовые логические операции-III
Определите наибольшее натуральное число a,
такое что выражение
(x & a 0) ((x & 12 = 0) (x & 21 = 0))
тождественно истинно.
Вводим множества:
ZN = {x: x & N = 0}
Z N {x : x & N 0}
Вводим утверждения:
ZN = (x ZN), A = (x Za)
Заданное условие:
A (Z12 Z 21 )

113.

141
Побитовые логические операции-III
Упрощение выражения:
!
От него
ничего не
зависит!
A (Z12 Z 21 ) A Z12 Z 21
Z12 (A Z21)
Решение:
(Z12 A) (Z12 Z21)
биты 4 3 2 1 0
Z12 : 12 = 1100
Z21 : 21 = 1101011
?
Z12 A
0
amax = 11002 = 12
Другие a?
a = 4, 8, 12
22 – 1 = 3

114.

142
Побитовые логические операции-IV
Определите наименьшее натуральное число a,
такое что выражение
( (x & 28 0) (x & 45 0))
((x & 48 = 0) (x & a 0))
тождественно истинно.
Вводим множества: ZN = {x: x & N = 0}
Z N {x : x & N 0}
Вводим утверждения:
ZN = (x ZN), A = (x Za)
Заданное условие:
( Z 28 Z 45 ) (Z 48 A )

115.

143
Побитовые операции–IV
Упрощение выражения:
( Z 28 Z 45 ) (Z 48 A )
Решение:
(Z28 Z45 ) (Z48 A)
Z 48 A Z 28 Z 45
биты 5 4 3 2 1 0
Z 28 : 28 = 11100
Z 45 : 45 = 101101
Z61
= 111101
Z 28 Z 45 :
Z 48 : 48 = 110000
Z 61 :
11 1
a = ??????
= 111101
Логическое ИЛИ
между битами!
?
Другие a?
amin = 11012 = 13

116.

144
Побитовые логические операции (V)
(А.Г. Гильдин). Определите наименьшее
натуральное число a, такое что выражение
(x & 19 = 0) (x & 38 0)
((x & 43 = 0) ((x & a = 0) (x & 43 = 0)))
тождественно истинно.
Вводим множества: ZN = {x: x & N = 0}
Z N {x : x & N 0}
Вводим утверждения:
ZN = (x ZN), A = (x Za)
Заданное условие:
Z19 Z38 (Z 43 ( A Z 43 ))

117.

145
Побитовые логические операции (V)
Упрощение выражения:
Z19 Z38 (Z 43 ( A Z 43 ))
Z19 Z38 Z 43 A Z 43
Z19 Z38 Z 43 A
Z 43 ( A Z19 Z38 )
(Z 43 A) (Z 43 Z19 Z38 )
?
Что с этим
делать?

118.

146
Побитовые логические операции
Zb (A Zc Zd ) ?
(Z b A) (Z b Z c ) (Z b Z d )
Вариант 1:
Zb Z c 0
Zb A
Вариант 2:
Zb Z c 1
(Z b A) (Z b Z d )
Zb A Z d (Z b Z d ) A
Z b or d A

119.

147
Побитовые логические операции (V)
(Z 43 A) (Z 43 Z19 Z38 )
0
Z 43 Z19 0
!
биты 5 4 3 2 1 0
Z 43 : 43 = 101011
Z19 : 19 = 10011
Z 43 A
?
Какие подходят?
Не влияют на
решение!
Все, у которых единицы
только в разрядах 5, 3, 1 и 0!
a = 1, 2, 3, 8, 9, 10, 11,
32, 33, 34, 35, 40, 41, 42, 43
24 – 1 = 15

120.

148
Побитовые логические операции (VI)
(М.В. Кузнецова). Определите наименьшее
натуральное число a, такое что выражение
(( (x & 13 0) (x & a 0)) (x & 13 0)
((x & a 0) (x & 39 = 0))
тождественно истинно.
Вводим множества: ZN = {x: x & N = 0}
Z N {x : x & N 0}
Вводим утверждения:
ZN = (x ZN), A = (x Za)
Заданное условие:
(( Z13 A ) Z13 ) A Z 39

121.

149
Побитовые логические операции (V)
Упрощение выражения:
(( Z13 A ) Z13 ) A Z 39
Z13 A Z13 A Z 39
(Z13 Z13 ) ( A Z13 ) A Z 39
A A Z 39 Z13
A Z 39 Z13 Z13 ( A Z 39 )
Z13 (A Z39 ) (Z13 A) (Z13 Z39 )
Z13 A
Решение:
биты 5 4 3 2 1 0
13 =
1101
1
39 = 1100111
!
0
Не влияет на
решение!
a = 1, 4, 5, 8, 9, 12, 13

122.

150
Побитовые логические операции (V)
Вариант с другими числами:
(( Z53 A) Z53 ) A Z 21 Z53 ( A Z 21 )
(Z53 A) (Z53 Z 21 )
Решение:
биты 5 4 3 2 1 0
53 = 110101
21 = 10101
!
Множество единичных
битов числа 21 входит во
множество единичных
битов числа 53!
!
Всегда 1!
a – любое!

123.

151
Побитовые логические операции (VI)
Определите наименьшее натуральное число a,
такое что выражение
((x & 23 0) (x & 45 0))
((x & a 0) (x & 23 0))
тождественно истинно.
Вводим множества: ZN = {x: x & N = 0}
Z N {x : x & N 0}
Вводим утверждения:
ZN = (x ZN), A = (x Za)
Заданное условие:
( Z 23 Z 45 ) ( A Z 23 )

124.

152
Побитовые логические операции (V)
Упрощение выражения:
( Z 23 Z 45 ) ( A Z 23 ) Z 23 Z 45 A Z 23
(Z 23 A) (Z 23 Z 23 ) Z 45
A Z 23 Z 45
A (Z 23 Z 45 )
(A Z 23 ) (A Z 45 )
( A Z 23 ) amin 23
или
( A Z 45 ) amin 45

125.

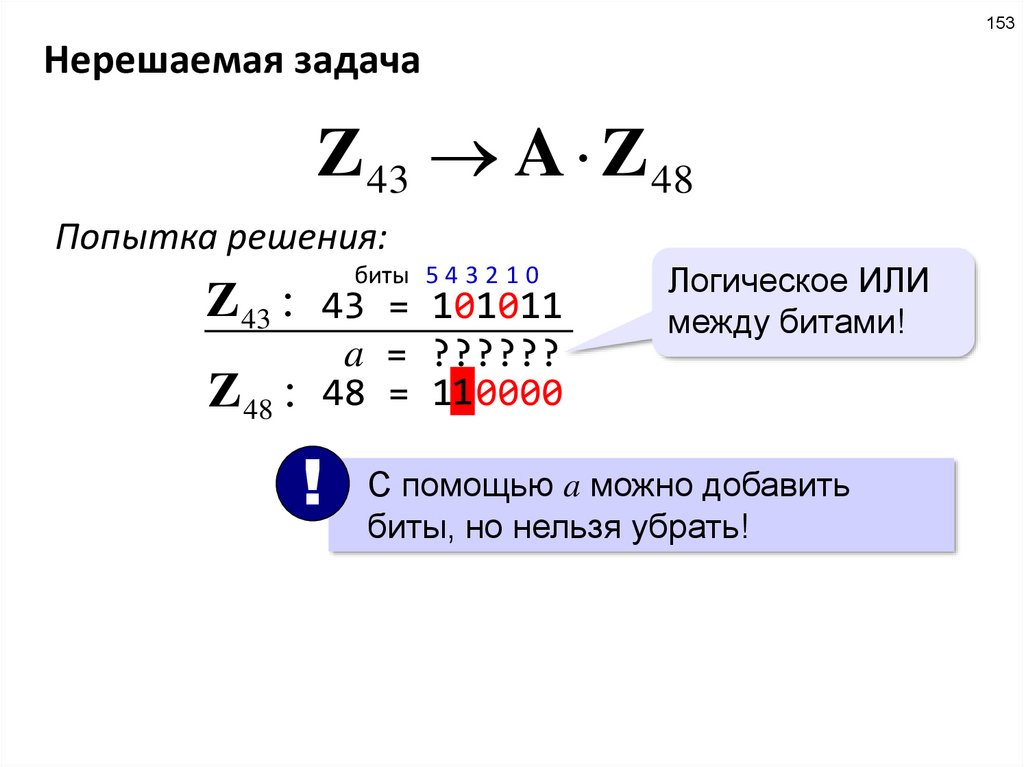
153
Нерешаемая задача
Z 43 A Z 48
Попытка решения:
биты 5 4 3 2 1 0
Z 43 : 43 = 101011
Z 48 :
a = ??????
1
48 = 110000
!
Логическое ИЛИ
между битами!
С помощью a можно добавить
биты, но нельзя убрать!

126.

154
Новая задача
Определите наименьшее (и наибольшее)
натуральное число a, такое что выражение
(x & 125 1) ((x & 34 = 2) (x & a = 0))
тождественно истинно.
!
Вводим множества:
ZN = {x: x & N = 0}
Z N {x : x & N 0}
Вводим утверждения:
ZN = (x ZN), A = (x Za)
?
Что дальше?
Не ноль!

127.

155
Преобразование выражений
(x & b = c) = ?
(x & b c) = ?
Вариант 1:
(x & 10 = 1) = 0?
Единичные биты числа c
= 1 не входят во
множество единичных
битов числа b = 10!
биты 3 2 1 0
10 = 1010
x = abcd
x & 10 = a0c 0 = 1

128.

156
Преобразование выражений
(x & b = c) = ?
Вариант 2:
(x & 23 = 3) = ?
биты 4 3 2 1 0
23 = 10111
x = abcde
x & 23 = a0cde = 3
(x & b c) = ?
Единичные биты числа
c = 3 входят во множество
единичных битов числа b = 23!
a=c=0
d=e=1
( x & b c) Z b c Z c1 Z c2 Z cq
( x & b c) Z b c Z c1 Z c2 Z cq
Z 20 1
Z1 0
Z2 0
Все биты числа c!

129.

157
Новая задача
(x & 125 1) ((x & 34 = 2) (x & a = 0))
Раскрываем импликацию:
(x & 125 1) (x & 34 2) (x & a = 0)
Эквивалентные замены:
( x & 125 1) Z124 Z1
( x & 34 2) Z 32 Z 2
Z124 Z1 Z 32 Z 2 A
Переход к импликации:
Z124 Z32 Z1 Z 2 A 1
( Z124 Z 32 ) ( Z1 Z 2 A)

130.

158
Новая задача
( Z124 Z 32 ) ( Z1 Z 2 A)
Z124 (Z1 Z 2 A)
124 or 32 = 124
(Z124 Z1 ) (Z124 Z2 ) (Z124 A)
=0
=0
Z124 A
amin 2 4
2
amax 124
?
биты 6 5 4 3 2 1 0
124 = 1111100
1 =
1
2 =
10
Сколько всего?
25 – 1 = 31

131.

Задание 15
Введём выражение M & K, обозначающее поразрядную
конъюнкцию M и K (логическое «И» между
соответствующими битами двоичной записи).
Определите наибольшее натуральное число A, такое
что выражение
(((X & A ≠ 0) (X & 12 = 0)) ((X & A = 0) (X & 21 ≠ 0)))
((X & 21 = 0) (X & 12 = 0))=1
тождественно истинно (то есть принимает
значение 1 при любом натуральном значении
переменной X)?
Ответ 12

132.

Решение:

133.

Задание 15
Введём выражение M & K, обозначающее поразрядную
конъюнкцию M и K (логическое «И» между
соответствующими битами двоичной записи).
Определите наименьшее натуральное число A, такое
что выражение
(X & 49 0) ((X & 33 = 0) (X & A 0))
тождественно истинно (то есть принимает
значение 1 при любом натуральном значении
переменной X)?
Ответ 16

134.

если X & 49 = 0, то исходное выражение истинно, независимо от значения числа А;
значит, значение числа А влияет на решение задачи только при выполнении
условия:
X &49 0.
тогда исходное выражение может быть представлено в виде:
1 ((X & 33 = 0) (X & A 0))
Для того чтобы это выражение было истинным, необходимо, чтобы выражение
(X & 33 = 0) (X & A 0)
было истинным, при этом, если X & 33 0, то это выражение истинно независимо от
значения числа А (импликация из 0 в 1).
следовательно, значение числа А влияет на принимаемое исходным выражением
значение только при одновременном соблюдении двух условий:
1. X & 49 0
2. X & 33 = 0
исходное выражение принимает следующий вид:
1 (1 (X & A 0))
для того чтобы это выражение приняло значение 1, необходимо, чтобы выполнилось
третье условие:
3. X & A 0.
4910 =
1100012
3310 =
1000012
X
010000
условия 1 и 2 выполняются, если пятый бит числа Х равен 1.
значит условие № 3 выполняется, если пятый бит числа А равен 1
число А минимально, если младшие разряды этого числа равны 0

135.

Задание 15
Введём выражение M & K, обозначающее
поразрядную конъюнкцию M и K (логическое
«И» между соответствующими битами
двоичной записи). Определите наибольшее
натуральное число A, такое что выражение
(X & A ≠0 ) ((X & 20 = 0) (X & 5 ≠ 0))
тождественно истинно (то есть принимает
значение 1 при любом натуральном значении
переменной X)?
Ответ 21

136.

введём обозначения:
P = (X & 20 = 0),
Q = (X & 5 = 0), A = (X & A = 0)
перепишем исходное выражение и преобразуем его, используя свойство импликации и
закон де Моргана :
таким образом, нужно выбрать максимальное A, такое что при выполнении условий P и Q
автоматически выполняется и условие A
теперь попробуем понять, что означают условия типа X & 20 = 0 и X & 20 ¹ 0; побитовая
конъюнкция (операция «И») применяется к соответствующим битам чисел X и 20, где 20
выполняет роль маски;
запишем числа в двоичной системе; учитывая, что 20 = 16 + 4 = 24 + 22, в двоичном коде
числа 20 будут равны 1 (установлены) только биты с номерами 4 и 2:
номер бита
4 3 2 10
X=
20 =
abcde
10100
X & 20 =
a0c00
после выполнения побитовой операции «И» остаются только те биты числа X, для которых
соответствующие биты маски равны 1, остальные (соответствующие нулевым битам
маски) обнуляются; поэтому
условие X & 20 ¹ 0 означает, что среди битов {4, 2} числа X есть ненулевой
условие X & 20 = 0 означает, что биты {4, 2} числа X нулевые
итак, условие P обозначает, что биты {4, 2} числа X нулевые
поскольку Q = (X & 5 = 0) и 5 = 4 + 1 = 22 + 20, условие Q означает, что биты 2 и 0 – нулевые
что же следует из выполнения P и Q одновременно? только то, что биты {4, 2, 0} числа X –
нулевые;
максимальное натуральное число, которое при выполнении побитового «И» с такой маской
даст 0, это число, которое в этих битах имеет 1, а в остальных – нули, то есть число
101012 = 21

137.

Задание 15
Элементами множеств А, P, Q являются
натуральные числа, причём
P = {2, 4, 6, 8, 10, 12, 14, 16, 18, 20},
Q = {3, 6, 9, 12, 15, 18, 21, 24, 27, 30}.
Известно, что выражение
( (x P) → (x A) ) (¬(x A) → ¬(x Q) )
истинно (т. е. принимает значение 1) при
любом значении переменной х.
Определите
наименьшее
возможное
количество элементов в множестве A.
Ответ 3

138.

166
Поразрядные конъюнкции
Определите наименьшее натуральное число a, такое что
выражение
( x & 125 ≠1) ((x & 34 = 2) (x & a = 0))
тождественно истинно (то есть принимает значение 1 при
любом натуральном значении переменной x)?
Ответ: 4