Логические основы компьютеров

1.

ЛОГИЧЕСКИЕ
ОСНОВЫ
КОМПЬЮТЕРОВ
1

2.

Базовые логические
операции
2

3.

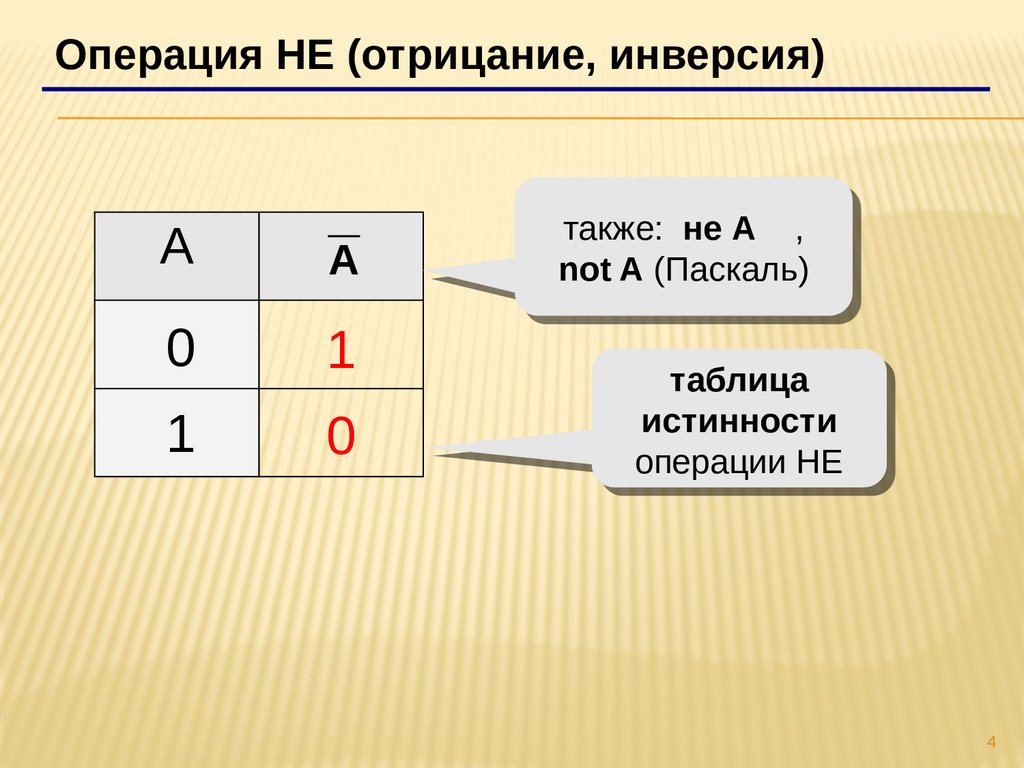
1.Инверсия (Операция НЕ,
отрицание)
Инверсия истинна тогда, когда само высказывание ложно, и
ложна, когда высказывание истинно.
3

4.

Операция НЕ (отрицание, инверсия)
А
A
0
1
1
0
также:
также: не
неАА ,,
not
notAA(Паскаль)(Паскаль)ППаскаль))
аскаль))
таблица
таблица
истинности
истинности
операции
операции НЕ
НЕ
4

5.

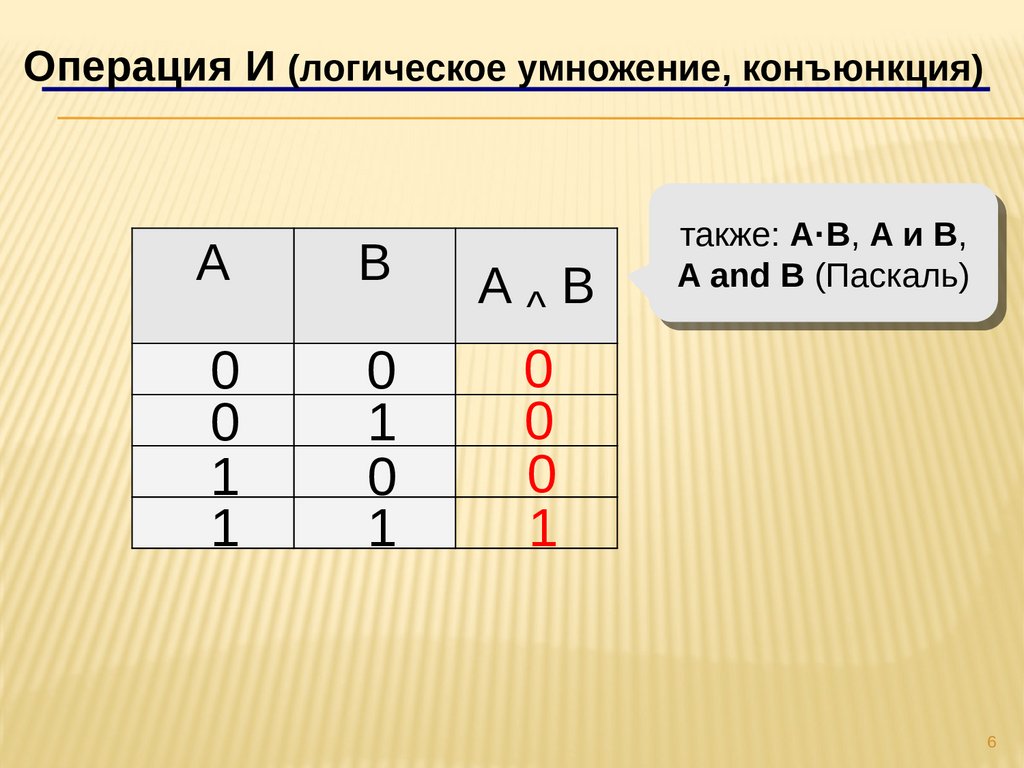
2.Конъюнкция (Операция И,
логическое умножение) ^
Конъюнкция (логическое умножение) двух и более высказываний
истинно тогда и только тогда, когда все простые высказывания,
входящие в неё истинны.
5

6.

Операция И (логическое умножение, конъюнкция)
A
B
А^B
0
0
1
1
0
1
0
1
0
0
0
1
также:
также: A·B,
A·B, AAии B,
B,
AAand
and BB (Паскаль)(Паскаль)ППаскаль))
аскаль))
6

7.

3.Дизъюнкция (Операция ИЛИ,
логическое сложение)
Дизъюнкция – это логическое сложение (союз ИЛИ) двух или более
высказываний, ложно тогда и только тогда, когда все простые
высказывания, входящие в неё ложны.
7

8.

Операция ИЛИ (логическое сложение, дизъюнкция)
A
B
А B
0
0
1
1
0
1
0
1
0
1
1
1
также:
также: A+B,
A+B,
AAили
или B,
B,
AAor
or BB (Паскаль)(Паскаль)ППаскаль))
аскаль))
8

9.

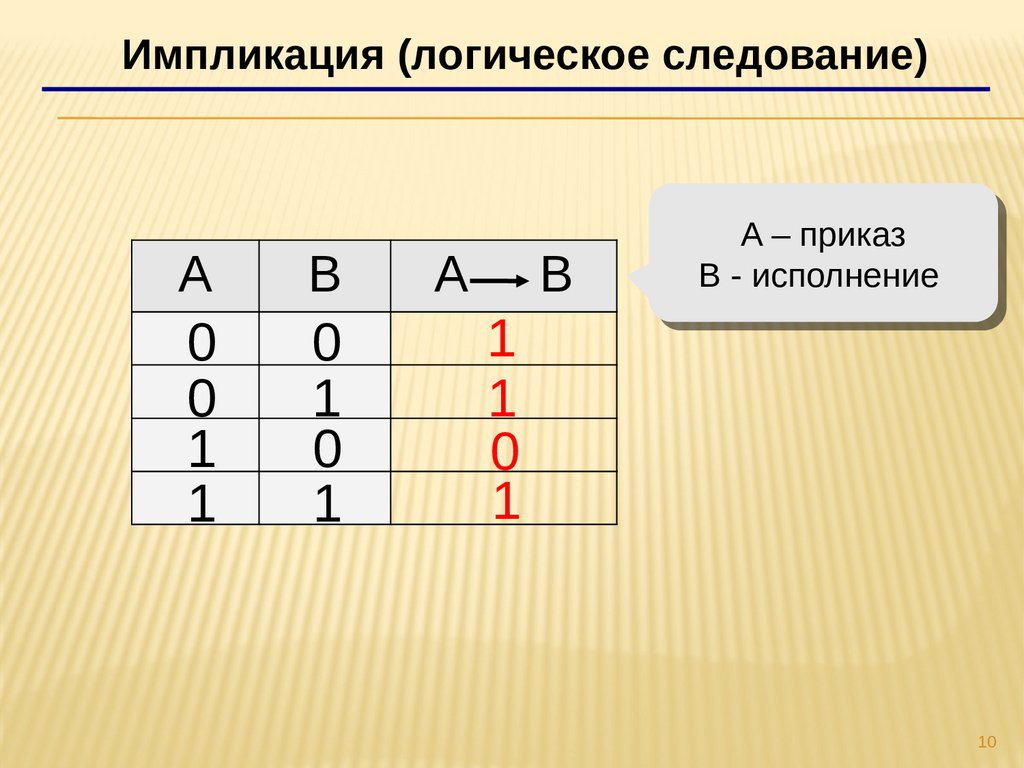
4.Импликация (логическое
следование)
Импликация (логическое следствие) – это сложное логическое
выражение, которое является ложным тогда и только тогда, когда
условие истинно, а следствие ложно.
9

10.

Импликация (логическое следование)
A
B
0
0
1
1
0
1
0
1
А
B
AA–– приказ
приказ
BB-- исполнение
исполнение
1
1
0
1
10

11.

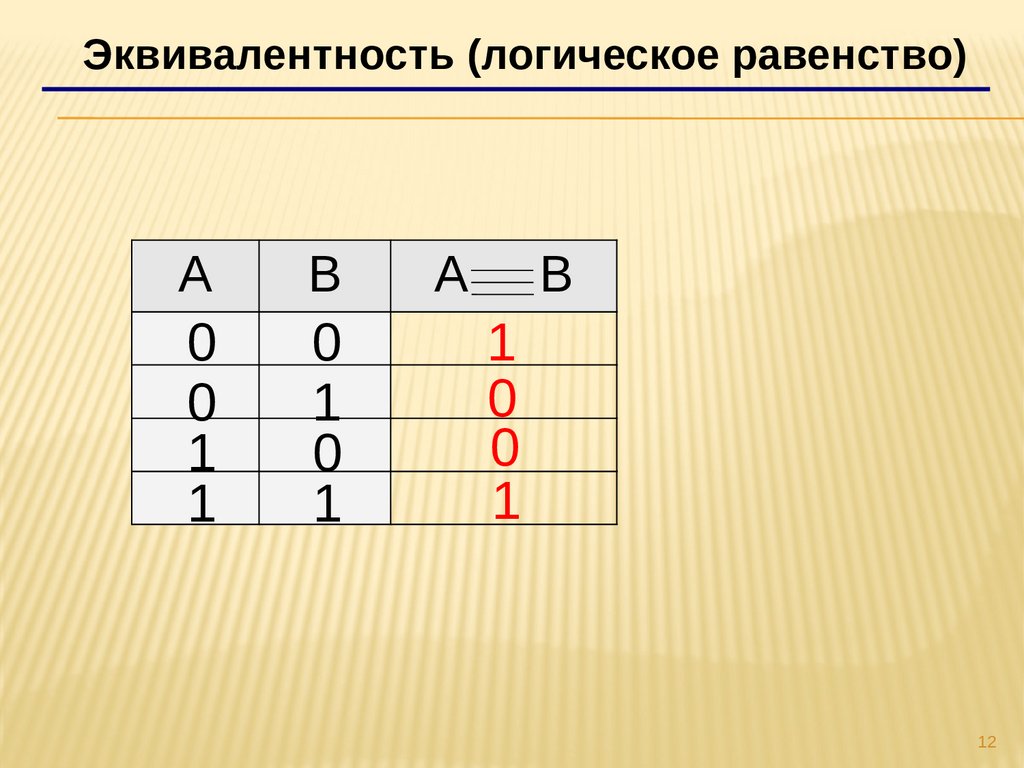
5.Эквивалентность
(логическое равенство)
Эквивалентность – это сложное логическое высказывание, которое
является истинным только при одинаковых значениях истинности
простых выражений, входящих в него.
11

12.

Эквивалентность (логическое равенство)
A
B
0
0
1
1
0
1
0
1
А
B
1
0
0
1
12

13.

ПОРЯДОК ВЫПОЛНЕНИЯ ОПЕРАЦИЙ:
1. Инверсия (Отрицание
)
2. Конъюнкция (Умножение ^)
3. Дизъюнкция (Сложение
)
4. Импликация (Следование
)
5. Эквивалентность (Равенство
)
13

14.

Таблица истинности
14

15.

Таблица истинности - это такая таблица, в которой
показываются все выходные состояния элемента для
любых комбинации входных сигналов. С помощь)ю
таблиц истинности можно определять) истинностное
значение любого высказывания для всех возможных
случаев значений истинности составляющих его
высказываний.

16.

Количество строк в ТИ находится по
формуле:
где n-количество переменных
Количество столбцов:
R=n+k
где k-количество простых логических
операций в формуле
16

17.

A и B – входные сигналы
F - выход
17

18.

ПОСЛЕДОВАТЕЛЬНОСТЬ
ПОСТРОЕНИЯ ТАБЛИЦЫ
ИСТИННОСТИ
18

19.

20.

Составление таблиц истинности (пример 1)
X A B
A
B
0
0
1
1
0
1
0
1
B
1
0
1
0
X
1
0
1
1
20

21.

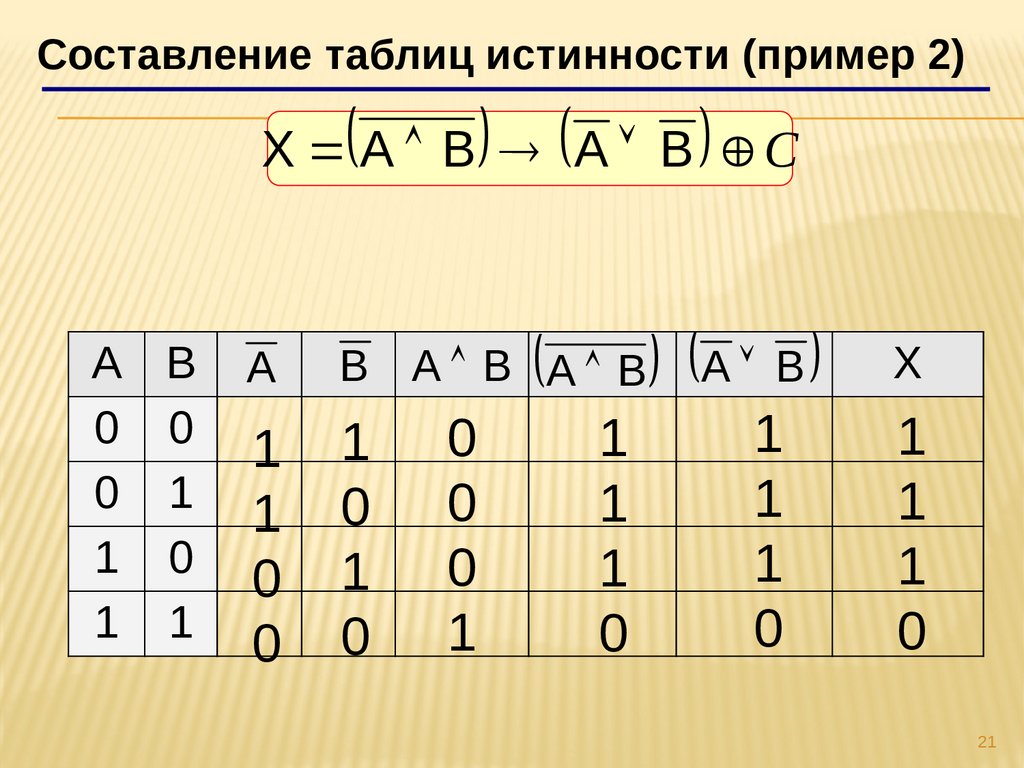
Составление таблиц истинности (пример 2)
X A B A B C
A B
0 0
0 1
1 0
1 1
A
B А В A B
1
1
0
0
1
0
1
0
0
0
0
1
1
1
1
0
A B
1
1
1
0
X
1
1
1
0
21

22.

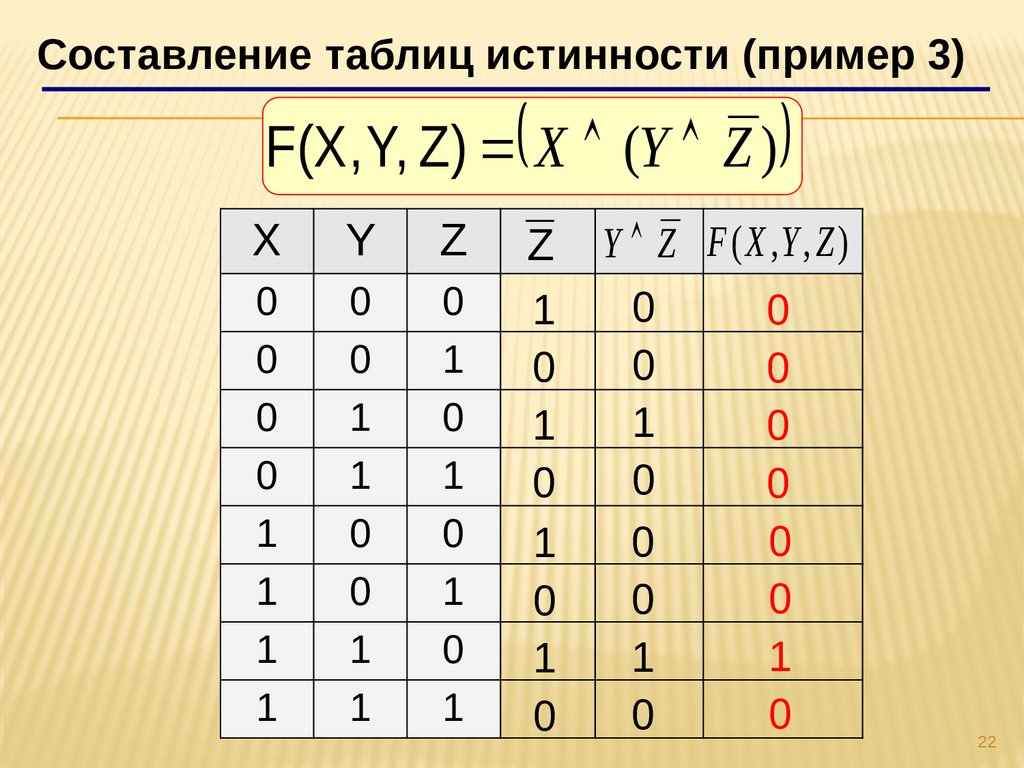
Составление таблиц истинности (пример 3)
F(Паскаль)X, Y, Z) X (Y Z )
X
Y
Z
0
0
0
0
1
1
1
1
0
0
1
1
0
0
1
1
0
1
0
1
0
1
0
1
Z
1
0
1
0
1
0
1
0
Y Z F ( X ,Y , Z )
0
0
0
0
1
0
0
0
0
0
0
0
1
1
0
0
22