Похожие презентации:
Алгебра – арифметика пяти действий
1. Индивидуальный проект АЛГЕБРА – АРИФМЕТИКА ПЯТИ ДЕЙСТВИЙ
Выполнил студент группы МО-18-1Юсупов Никита
Руководитель:
преподаватель математики
Дудаева Ф.В.
2. «Алгебра есть не что иное,как математический язык, приспособленный для обозначения отношений между количествами». И. Ньютон
Алгебра - часть математики, котораяизучает общие свойства действий над
различными величинами.
3. Цель:
• Формирование компетентности в сфере самостоятельнойпознавательной деятельности, навыков самостоятельной
работы с различными источниками знаний, овладение
методами научной творческой работы.
• Формирование умений неординарно мыслить, собирая
разнообразную информацию, обобщать, видеть главное,
представлять его в различной форме.
• Развитие кругозора, мышления, творческих задатков
учащихся.
4. Пять математических действий
• Алгебру нередко называют «арифметикойсеми действий»,желая подчеркнуть,что к
четырем общеизвестным математическим
операциям она присоединяет три
новых:возведение в степень и два ему
обратных действия.
• Наши алгебраические беседы о пяти
математических действиях:сложении,вычинии,умножении,делении и возведении в
степень.
5. Сложение (+ )
• Алгебре предшествовала арифметика, каксобрание постепенно накопленных практич.
+ — решения повседневных
правил для
житейских задач. Эти правила арифметики
сводились к сложению, вычитанию,
умножению и делению чисел, вначале только
целых, а затем - постепенно и в очень
медленном развитии - и дробных.
6. Сложение в египетской арифметике
В таблицах сложения каждый из реальных предметов (это могут бытьживотные, собираемые в стадо, камни, складываемые для постройки, и т.д.)
замещался идеальным объектом "единица", который фиксировался знаком I
(вертикальная черта). Набор предметов изображался здесь как система единиц
(для "десятков", "сотен", "тысяч" и т.д. в египетской арифметике существовали
свои знаки, фиксирующие соответствующие идеальные объекты).
Оперирование с предметами, объединяемыми в совокупность (сложение), и
отделение от совокупности предметов или их групп (вычитание) изображались
в правилах действия над "единицами", "десятками", "сотнями" и т.д.
Прибавление, допустим, к пяти единицам трех единиц производилось
следующим образом: изображался знак III (число "три"), затем под ним
писалось еще пять вертикальных черточек IIIII (число "пять"), а затем все эти
черточки переносились в одну строку, расположенную под двумя первыми. В
результате получалось восемь черточек, обозначающих соответствующее число.
Древние египтяне обозначали сложение знаком – рисунком шагающих ног.
7.
Название «слагаемое» впервые встречается в работах математиков 13 века, апонятие «сумма» только в 15 веке. До этого времени суммой называли
результат любого из четырех арифметических действий.
Впервые знаки «+» и «-» в печати появились в книге «Быстрый и красивый
счет для всего купечества». Автором этой книги является чешский математик
Ян Видман, а написал ее в 1489 году.
В 15 – 16 веках вместо знака сложения использовали латинскую букву «Р»начальную букву слова «плюс».
Для сложения употреблялось также латинское слово «еt», что означает
«и».Так как это слово приходилось писать часто, то его стали сокращать:
писали одну букву «t», которая постепенно превратилась в знак «+».
• В 1701 году императорским указом была учреждена в Сухаревой башне
математически-навигацкая школа, где преподавал Л. Ф. Магницкий. По
поручению Петра I он написал известный учебник арифметики (1703).
Учебник Магницкого для того времени был исключительно добротным и
содержательным. Автор тщательно отобрал всё лучшее, что было в
существовавших тогда учебниках, и изложил материал об арифметических
действиях «сложение» и «вычитание» ясно, с многочисленными примерами и
пояснениями.
8. Вычитание
Создание современной алгебраической символики относится к 14 – 17 векам;
оно определялось успехами практической арифметики. В различных странах
стихийно появляются математические знаки для некоторых действий, как
«сложение» и «вычитание».
Мы знаем, что существует мнение, что знаки «+» и «-» возникли в торговой
практике. Виноторговец черточками отмечал, сколько мер вина он продал
из бочки. Приливая в бочку новые запасы, он зачеркивал столько
расходных черточек, сколько мер восстанавливал. Легенда гласит о том, что
именно так произошли знаки сложения и вычитания в 15 веке.
Но уже в 3 веке до нашей эры в Греции использовали перевернутую
греческую букву пси.
Итальянский математик Л.Пачоли употреблял вместо знака вычитания букву
m (от латинского minus).
В 16 веке для обозначения действия вычитания стали применять знак «-».
Чтобы этот знак отличить от тире, в 17 веке знак «-» стали обозначать
знаком ÷. Такой знак встречается у великого русского математика Леонтия
Магницкого в книге «Арифметика». Примеры: 6 ÷ 2; 17 ÷ 12.
9. Умножение (× ∙)
• Умножение для натуральных чисел появилось в качестве, так сказать,пакетного сложения. Свойства и взаимосвязь операций открывались
постепенно.
• С развитием понятия натурального числа как результата счёта предметов в
обиход включаются действия над числом. Действия сложения и вычитания
возникают сначала как действия над самими совокупностями в форме
объединения двух совокупностей в одну и отделения части совокупности.
Умножение, по-видимому, возникло в результате счёта равными частями (по
два, по три и т.д.), деление — как деление совокупности на равные части. Лишь
в многовековом опыте сложилось представление об отвлечённом характере
этих действий, о независимости количественного результата действия от
природы предметов, составляющих совокупности, о том, что, например, два
предмета и три предмета составят пять предметов независимо от природы этих
предметов. Тогда стали разрабатывать правила действий, изучать их свойства,
создавать методы для решения задач, т. е. начинается развитие науки о числе.
10. История возникновения знака умножения
• В Европе долгое время произведение называли суммой умножения.Название «множитель» упоминается в работах 11 века, а «множимое» в 13
веке.Европейские математики 16 века для обозначения действий
умножения применяли букву М , начальную букву в латинском слове,
которое обозначало увеличение, умножение (мультипликация).
• Слово «мультфильм» произошло от этого слова.
• В 16 – 17 веках единого символа умножения не было. Некоторые математики
обозначали умножение косым крестиком х, а другие применяли для этого
точку. В 17 веке мохно было насчитать около десятка математических знаков
для действия умножения.
• Знак умножения крестиком ввел в 1631 году английский математик
Вильям Оутред. А в 18 веке большинство математиков уже пользовались
знаком умножения х.
• В России впервые дал названия компонентам умножения Леонтий
Филипович Магницкий только в начале 18 века.
11. Русский способ умножения
В старинной «Арифметике» Магницкого,о которой мы раньше упоминали,
необходимость знания таблицы
умножения воспета в таких - надо
сознаться, чуждых для современного
слуха - стихах:
Аще кто не твердит
таблицы и гордит,
Не может познати
числом что множати
И во всей науки,
несвобод от муки,
Колико не учит
туне ся удручит
И в пользу не будет аще ю забудет.
Автор этих стихов, очевидно, не знал или
упустил из виду, что существует способ
перемножать числа и без знания
таблицы умножения. Способ этот, ие
похожий на наши школьные приемы,
употребителен в обиходе великорусских
крестьян и унаследован ими от глубокой
древности. Сущность его в том, что
умножение любых двух чисел сводится к
ряду последовательных делений одного
числа пополам при одновременном
удвоений другого числа.
Вот пример:
32•13
16•26
8•52
4•104
2•208
1•416
12. Великий русский математик МагницкийЛ.Ф. – основоположник арифметических действий в России, автор книги «Арифметика»
13. «Крестьянский» способ умножения
Египтяне построили арифметику преимущественно аддитивного характера, т.е.
ее основное направление состоит в сведении всех умножений к повторным
сложениям. Например, умножение на 13 получается умножением сначала на 2,
затем на 4, затем на 8 и сложением результатов умножения на 4 и на 8 с
первоначальным числом:
Например, для вычисления 13 х 11 писали: *1 11
1
17+
2 22
2
34+
*4 44
4
68
*8 88
8
136
и складывали все числа, отмеченные звездочкой, что дает 143.
16
272+
Дальше рассмотрим примеры, которые еще за тысячелетия до нас египтяне
пользовались приемом умножения, довольно сходным с нашим
«крестьянским», который неведомыми путями он как бы перекочевал из
древней Страны Пирамид в современную русскую деревню. Если бы обитателю
земли фараонов предложили перемножить, например, 19•17, он произвел бы
это действие следующим образом: (см.выше)
14. Способ умножения из страны пирамид
«Наставление, как достигнуть знания всех темных вещей... Всехтайн, сокрытых в вещах»
«Составлено при царе Верхнего и Нижнего Египта Ра-а-усе,
дающем жизнь, по образцу древних сочинений времен царя Раен-мата писцом Аамесом».
В этом интересном документе, насчитывающем за собою около 40 веков и
свидетельствующем о еще более глубокой древности, мы находим четыре
примера умножения, выполненные по способу, живо напоминающему наш
русский народный способ. Вот эти примеры (точки впереди чисел обозначают
число единиц множителя; знаком+мы отметили числа, подлежащие
сложению):(8 х 8)
(9 х 9)
(8 х 365)
(7 х 2801)
•8
• 9+
•365
• 2801+
••16
••18
••730
•• 5602+
••••32
••••36
••••1460
••••11204+
••••2920
итог •• 19607
15. Мгновенное умножение чисел
три девятки.В следующей витрине выставлено наибольшее из всех трехзначных чисел: 999. Оно без
сомнения гораздо удивительнее, чем его перевернутое изображение - 666 - знаменитое
«звериное число» Апокалипсиса, вселявшее нелепый страх многим суеверным людям, но
по арифметическим свойствам ничем не выделяющееся среди прочих чисел. Любопытная
особенность числа 999 проявляется при умножении на него всякого другого трехзначного
числа. Тогда получается шестизначное произведение; первые три цифры его есть
умножаемое число, только уменьшенное на 1-цу, а остальные три цифры(кроме последней)
- «дополнения» первых до 9. Например:
572
573 х 999 = 572427
999
или
573000
573 х 999 = 573 х (1000 – 1) = 573
______
572427
ЧИСЛО ШЕХЕРАЗАДЫ – 1001.
Замечательнее то, что при умножении на него трехзначного числа получается результат,
состоящий из самого умноженного числа, только написанного дважды, например:
873•1001=873873;
207•1001=207207, и т. д.
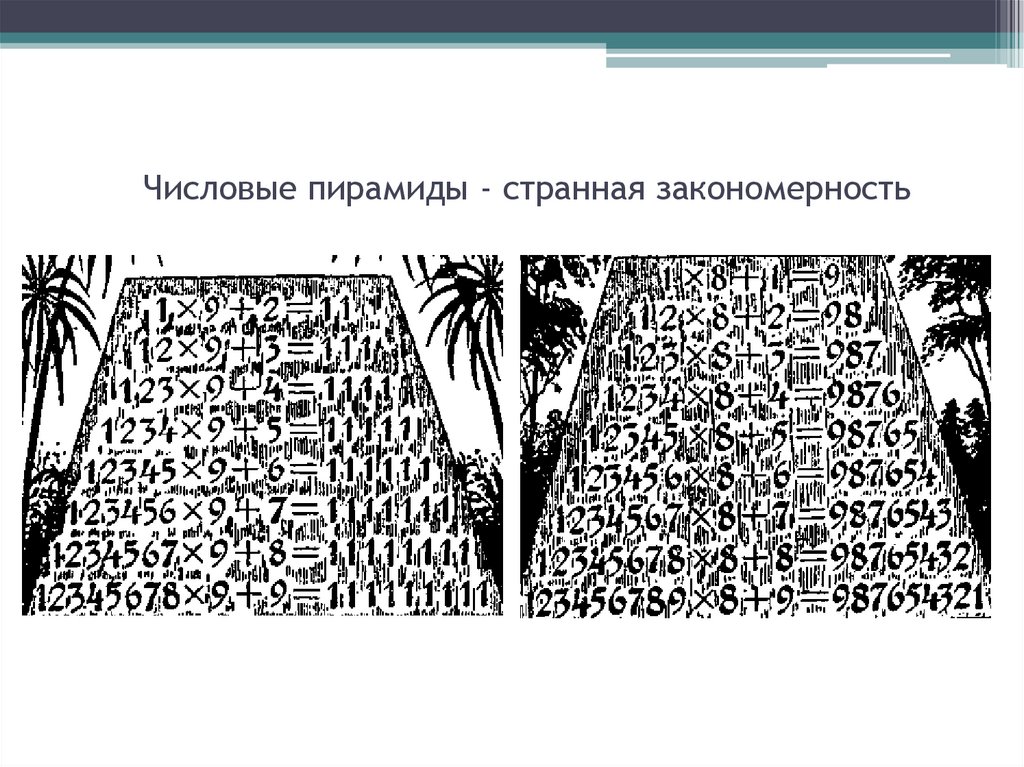
16. Числовые пирамиды - странная закономерность
17. Деление (/ : ÷)
Счёт предметов на самых ранних ступенях развития культуры привёл ксозданию простейших понятий арифметики натуральных чисел. Только на
основе разработанной системы устного счисления возникают письменные
системы счисления и постепенно вырабатываются приёмы выполнения над
натуральными числами четырёх арифметических действий ,из которых только
деление ещё долго представляло большие трудности. На протяжении
тысячелетий действие деления не обозначали знаками. Его просто
называли и записывали словами.
Индийские математики первыми стали обозначать деление начальной
буквой из названия этого действия – Д.
Итальянский математик Фибоначчи в 13 веке обозначал деление чертой, но
до него это обозначение ввели арабы. Фибоначчи впервые применил
термин «частное».
Знак двоеточия (:) для деления появился только в конце 17 века.
В России в начале 18 века названия «делимое», «делитель», «частное»,как
и компоненты сложения, вычитания и умножения впервые ввел Леонтий
Филипович Магницкий.
18. Разделение на части (дробь)
Другое важное практическое действие — разделение на части — со временемабстрагировалось в четвёртую арифметическую операцию — деление.
Потребности измерения (количества зерна, длины дороги и т.п.) приводят к
появлению названий и обозначений простейших дробных чисел и к
разработке приемов выполнения арифметических действий над дробями.
Делить на 10 частей сложно, поэтому десятичные дроби, удобные в сложных
вычислениях, появились сравнительно поздно. Первые дроби обычно имели
знаменатели 2, 3, 4, 8 или 12. Это единичные дроби, которые возникли
2000 лет тому назад. Например, у римлян стандартной дробью была унция
(1/12). Средневековые денежные и мерные системы несут на себе явный
отпечаток древних недесятичных систем: 1 английский пенс = 1/12
шиллинга, 1 дюйм = 1/12 фута, 1 фут = 1/3 ярда и т. д.
В русском языке слово «дробь» появилось в 8 веке, имело значение
дробить, ломать на части. В первоначальных изданиях учебников математики дроби назывались «ломанные числа», а само слово «дробь» ввел в
1202 году итальянец Фибоначчи. Названия «числитель» и«знаменатель»
ввел в 13 веке греческий ученый, математик, монах Максим Плануд.
19. Трудное дело - деление
«Трудное дело - деление» гласила старинная
латинская поговорка; оно и в самом деле было
трудно, если принять во внимание утомительные
методы, какими выполнялось тогда это действие.
Нужды нет, что способы эти носили подчас довольно
игривые названия: под веселым названием
скрывался длиннейший ряд запутанных
манипуляций. В XVI веке кратчайшим и
удобнейшим способом считалось, например,
деление «лодкой, или галерой». Знаменитый
итальянский математик того времени Николай
Тарталья (XVI век в своем обширном учебнике
арифметики писал о нем следующее.
«Второй способ деления называется в
Венециилодкой или галерой, вследствие некоторого
сходства фигуры, получающейся при этом, потому
что при делении некоторых родов чисел
составляется фигура, похожая на лодку, а в других на галеру, которая в самом деле красиво выглядит;
галера получается иной раз хорошо отделанная и
снабженная всеми принадлежностями выкладывается из чисел так, что она действительно
представляется в виде галеры с кормою и носом,
мачтою, парусами и веслами». На рисунке числовая «галера».
20. Возведение в степень
• Вызвана ли потребность в этом новом действии практической жизнью?Безусловно.
• Современная запись показателя степени введена Декартом в его "Геометрии"
(1637), правда, только для натуральных степеней, больших 2. Позднее Ньютон
распространил эту форму записи на отрицательные и дробные показатели
(1676).
• Древнеегипетская письменность основывалась на иероглифах. Система
счисления того периода также уступала вавилонской. Египтяне пользовались
непозиционной десятичной системой, в которой числа от 1 до 9 обозначались
соответствующим числом вертикальных черточек, а для последовательных
степеней числа 10 вводились индивидуальные символы. Последовательно
комбинируя эти символы, можно было записать любое число. С появлением
папируса возникло, так называемое, иератическое письмо – скоропись,
способствовавшее, в свою очередь, появлению новой числовой системы.
Теория о степенях возникла благодаря И. Ньютону в 1676 году.
21. Пятое действие. Так ли оно важно?
Геометрический подход к алгебраическим проблемам сковывал дальнейшее
развитие науки, так как, например, нельзя было складывать величины разных
размерностей (длины и площади или площади и объемы, где обычно
приходится возвышать числа во вторую и третью степень). Нельзя было
говорить о произведении более чем трех множителей и т. д.
• Отказ от геометрической трактовки наметился у Диофанта Александрийского,
жившего в III в. В его книге "Арифметика" появляются зачатки буквенной
символики и специальные обозначения для степеней неизвестного вплоть до
шестой. Были у него и обозначения для степеней с отрицательными
показателями, обозначения для отрицательных чисел, а также знак равенства
(особого знака для сложения еще не было), краткая запись правил умножения
положительных и отрицательных чисел.
• На дальнейшее развитие алгебры сильное влияние оказали разобранные
Диофантом задачи, приводящие к сложным решениям со степенями.
22. Степени в реальной действительности
Сила всемирного тяготения, электростатическое и магнитное взаимодействия,свет, звук – ослабевают пропорционально второй степени расстояния.
Продолжительность обращения планет вокруг Солнца (и спутников вокруг
планет) связана с расстояниями от центра обращения также степенной
зависимостью: вторые степени времен обращения относятся между собой, как
третьи степени расстояний.
Более высокие показатели степени также существуют, и не только в
алгебраических задачниках, но и на практике.
Никто, пожалуй, не пользуется так широко пятым математическим действием,
как астрономы.Исследователям вселенной на каждом шагу приходится
встречаться с огромными числами,сотоящими из одной – двух значащих цифр
и длинного ряда нулей. Например, до туманности Андромеды, написанное
обычным порядком, представляется таким числом км:
8050000000000000000 км.
А если выражать небесные расстояния не в км, а в см, то число удлиняется
пятью нулями: 805000000000000000000000 см = 80,5 · 10²².
23. Использование степенного изображения в задачах
Сколько весит воздух?Четырьмя единицами
Определим, во сколько раз масса
земного шара больше массы всего
окружающего его воздуха .
Поверхность земного шара 510
млн.кв.км, в степенном изображении
5,1 • 10 кв.км = 5,1 • 10¹ кв. см.
Атмосфера Земли весит
5100000000000000000 кг = 5,1 • 10¹ т,
масса земного шара весит 6 • 10²¹т.
Чтобы определить, во сколько раз наша
планета тяжелее ее воздушной оболочки,
произведем деление:
6 • 10²¹ : 5,1 • 10¹ ≈ 1000000, то есть
воздух весит около миллиона т.
Четырьмя единицами, не употребляя
никаких знаков математических
действий, написать возможно большее
число.
Приходящее на ум решение – 1111 – не
отвечает требованию задачи, так как
число 11¹¹ во много раз больше.
• Тремя двойками.
Можно написать 222 или 22², но
правильно и больше число
2²²=4194304.
• Трема тройками: 3³³
• Четырьмя двойками: 22²².
24. Вывод:
Открытия арифметических действий русскихматематиков , особенно умножения, не являются ни
копией,ни модификацией каких- либо известных на
сегодня способов этих действий, поэтому
заслуживают особого внимания и специальных
исследований.
25. Используемая литература и ресурсы:
• 1. «Занимательная алгебра», Я.И.Перельман, Москва 1950 г.• 2. «Я познаю мир», энциклопедия по математике,А.П.Савин,
Москва 2000г.
• 3. «Занимательные задачи», Москва «Посвещение», 1967г.
• 4. http://www.aspirahtov.net/sorum./index.php.topic=1190
• 5. http://ru.wikipedia.orq/wi//История математики.
• 6.http://www.rshebnik.ru/history/02/01/
• 7.http://www.bodhi.ru/book/perelman_ zanim_arifmetika.html.
























 Математика
Математика








