Похожие презентации:
Задачи линейного программирования и их решение в современных вычислительных средах. Лекция №12
1.
Задачи линейногопрограммирования и их решение в
современных вычислительных
средах
Лекция №12
2.
Математическое программированиеМатематическое программирование занимается изучением
проблем принятия решений, которые могут быть математически
сформулированы как задачи нахождения максимума (минимума)
функции многих переменных, при заданной системе ограничений
на основные переменные задачи.
Функция, для которой определяется точка максимума или
минимума (оптимума), называется целевой функцией. Часто она
обозначается буквами F или С.
С(x1, x2, …, xn) max (min) Функции С и G могут быть как линейными, так
и нелинейными. Ограничения могут быть
G1(x1, x2, …, xn)≥0
нестрогими неравенствами (≥ или/и ≤) или
….
равенствами.
Кроме того, могут быть специфические
Gm(x1, x2, …, xn)≥0
ограничения. Например, целочисленность
одной или нескольких переменных х.
3.
Линейное программированиеЛинейное программирование (ЛП) – раздел математического
программирования, изучающий методы решения задач
математического программирования в случае линейной целевой
функции и линейных ограничений.
Основные математические предположения ЛП:
1. Линейность целевой функции (ЦФ) и ограничений.
2. Определенность (детерминированность) – предполагается,
что все параметры модели известны точно или могут быть
оценены.
3. Делимость – предполагается, что все основные переменные
задачи могут принимать произвольные вещественные
значения в определенном диапазоне (бесконечно делимы).
Основателем линейного программирования является советский
математик Леонид Витальевич Канторович (1939г.).
4.
Формулирование задачи линейногопрограммирования состоит из следующих
этапов:
• Понять проблему, составить описательную модель
задачи.
• Выбрать основные переменные задачи.
• Выбрать некоторую количественную меру эффективности
для целевой функции.
• Представить эту меру эффективности как линейную
функцию относительно основных переменных.
• Представить все ограничения как линейные уравнения
или неравенства относительно основных переменных.
• Собрать количественные данные или сделать
соответствующие оценки для всех параметров модели.
5.
Целевая функция задачи ЛПC=С(x1, x2, …, xn)=c1x1+c2x2+….+cnxn
:
Или:
.
n
С cjxj
j 1
n – число переменных модели.
6.
Формы задачи ЛП• Каноническая.
• Стандартная (нормальная).
• Общая.
(2)
(3)
7.
Каноническая форма задачи ЛПЦФ => максимум.
Ограничения канонической модели –линейные
равенства + условие положительности всех
переменных:
a1,1 x1 a1, 2 x2 ... a1, n xn b1
...
am ,1 x1 am , 2 x2 ... am , n xn bm
x j 0, j 1,2,..., n
Или в сокращенной записи:
n
ai , j x j bi
,
j 1
x j 0
i=1, 2, …, m,
J=1, 2, …, n.
8.
Стандартная (нормальная) форма задачи ЛП1. ЦФ => максимум.
Ограничения–линейные неравенства (≤) + условие
положительности всех переменных:
a1,1 x1 a1, 2 x2 ... a1, n xn b1
...
am ,1 x1 am , 2 x2 ... am , n xn bm
x j 0, j 1,2,..., n
Или в сокращенной записи:
n
ai , j x j bi
,
j 1
x j 0
i=1, 2, …, m,
J=1, 2, …, n.
9.
Стандартная (нормальная) форма ЛП2. ЦФ => минимум.
Ограничения–линейные неравенства (≥) + условие
положительности всех переменных:
a1,1 x1 a1, 2 x2 ... a1, n xn b1
...
am ,1 x1 am , 2 x2 ... am , n xn bm
x j 0, j 1,2,..., n
Или в сокращенной записи:
n
ai , j x j bi
,
j 1
x j 0
i=1, 2, …, m,
J=1, 2, …, n.
10.
Общая (смешанная) форма задачи ЛП• Требуется найти максимум или минимум ЦФ.
• Ограничения неравенства с разными
соотношениями (≥, ≤) и равенства.
• Условие положительности может отсутствовать или
иметь место для некоторых переменных.
Если все или некоторые ограничения в системе заданы
неравенствами, то задачу можно свести к
канонической путём преобразования неравенств в
уравнения с помощью введения дополнительных
переменных. Неравенство со знаком ≥ можно
преобразовать в неравенство со знаком ≤ умножением
обеих его частей на (-1).
11.
Решение (план, программа) задачи ЛП• Множество всевозможных числовых значений x1, x2, …, xn,
удовлетворяющих системе ограничений,
называется решением этой системы. Решение системы
также часто называется планом, и немного реже –
программой, но именно отсюда и пошло название
«линейное (или математическое) программирование».
• Оптимальным решением задачи линейного
программирования называется решение системы, при
которых функция цели в оптимум.
• Решение задачи линейного программирования
называется вырожденным, если в нём некоторые
переменные равны нулю. В противном случае решение
является невырожденным.
12.
Методы решения задачи ЛПГрафический метод –
для случае двух
переменных х1 и х2 (n=2)
Симплекс-метод
13.
Примеры формулировки задачилинейного программирования
14.
Пример 1. Задача использования сырьяДля изготовления двух видов продукции П1 и П2 требуется
четыре вида ресурсов (сырья): S1 , S2 , S3 , S4 .
Запасы сырья – соответственно, b1, b2 , b3 , b4 единицы. На
производство единицы продукции Пj требуется ai,j единиц
сырья Si, j=1, 2; i=1, …, 4.
Доход от реализации одной единицы
продукции П1 равен c1
П2
у.е.,
а
доход
от
реализации
одной
единицы
продукции П2 равен c2 у. е.
Требуется узнать, сколько единиц П1 и сколько единиц П2
нужно изготовить из имеющегося запаса сырья, чтобы получить
максимальный доход.
15.
Пример 1. Задача использования сырьяДля удобства анализа данные представим в виде таблицы:
Виды
сырья
Запасы
сырья
S1
S2
b1
b2
a1,1
aП2,1
a1,2
a2,2
S3
S4
b3
b4
a3,1
a4,1
a3,2
a4,2
с1
с2
Доход от
реализаци
и единицы
продукции
Виды продукции
П1
2
П2
16.
Пример 1. Задача использования сырьяОбозначим:
х1 –количество изготовляемых единиц продукции П1,
х2 –количество изготовляемых единиц продукции П2.
Тогда ЦФ равна:
C=С(x1, x2)=c1x1+c2x2.
Ограничения на расход сырья запишутся в виде:
a1,1 x1 a1, 2 x2 b1
a x a x b
2,1 1 2, 2 2
2
a3,1 x1 a3, 2 x2 b3
a4,1 x1 a4, 2 x2 b4
В левой части i-го ограничения записан общий расход
сырья Si на производство продукции двух видов, а в правой
части – запас сырья Si. Кроме того, количество продукции
не может быть отрицательным: x1≥0, x2≥0.
17.
Пример 2. Транспортная задачаНа двух станциях отправления A1 и A2 имеется,
соответственно, a1 и a2 единиц некоторого груза. Этот груз
следует доставить в три пункта назначения B1, B2, B3, и в
каждый из них должно быть завезено, соответственно,
b1, b2, b3 единиц этого груза. Стоимость перевозки одной
единицы груза из пункта Ai в пункт Bk равна ci,k. Составить
такой план перевозок, чтобы суммарная стоимость
перевозок была минимальной.
Считать, что количество всего груза на двух пунктах
отправления равно потребности в грузе на всех трех пунктах
назначения, то есть:
a1 + a2 = b1 + b2 + b3.
18.
Пример 2. Транспортная задачаРасположим исходные данные этой задачи в виде таблицы:
Пункт
Пункт назначения Запас груза
отправления B
B2
B3
1
A1
с1,1
A2
с2,1
Потребность b1
в грузе
с1,2
с2,2
b2
с1,3
с2,3
b3
a1
a2
19.
Пример 2. Транспортная задачаОбозначим: xi,k – количество перевезенного груза из пункта
Ai в пункт Bk . Тогда ЦФ (которую нужно минимизировать)
равна:
2
3
C ci , k xi , k
i 1 k 1
Ограничения:
3
x
k 1
i,k
2
x
i 1
i,k
ai , i 1,2
bk , k 1,2,3
xi , k 0, i 1,2; k 1,2,3
20.
Основные теоремы линейногопрограммирования
• Теорема 1. Множество всех допустимых решений
системы ограничений задачи линейного
программирования является выпуклым.
Множество решений задачи линейного
программирования определяется совокупностью линейных
ограничений, поэтому такое множество геометрически
представляет собой выпуклый многогранник или
неограниченную многогранную область, за исключением тех
случаев, когда система ограничений несовместна.
Выпуклое множество: если две точки принадлежат
множеству, то любая точка на линии, соединяющей две
исходные точки, также принадлежит этому множеству.
21.
Основные теоремы линейногопрограммирования
• Теорема 2. Если существует, и притом единственное,
оптимальное решение задачи линейного
программирования, то оно совпадает с одной из угловых
точек множества допустимых решений.
Эта теорема позволяет сделать вывод, что поиски
оптимального решения можно ограничить перебором
конечного числа угловых точек.
22.
Графический метод решения задачи ЛП.Применяется только для случаях двух
переменных: х1 и х2
Пусть ограничения имеют вид:
a1,1 x1 a1, 2 x2 b1
a x a x b
2,1 1
2, 2 2
2
...
am ,1 x1 am , 2 x2 bm
Кроме того, переменные x1 и х2 – неотрицательные.
Надо найти значения x1 и х2, на которых ЦФ
С =с1х1+с2х2
принимает оптимальное значение.
23.
Графический метод решения задачи ЛП.Общий подход
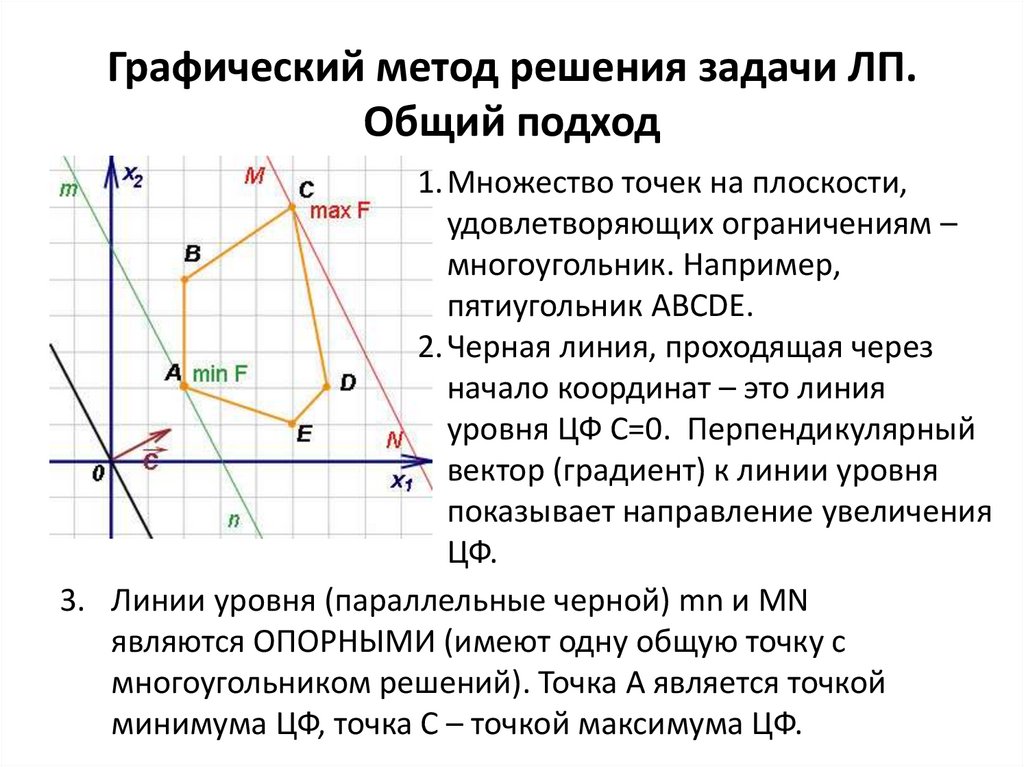
1. Множество точек на плоскости,
удовлетворяющих ограничениям –
многоугольник. Например,
пятиугольник АВСDE.
2. Черная линия, проходящая через
начало координат – это линия
уровня ЦФ С=0. Перпендикулярный
вектор (градиент) к линии уровня
показывает направление увеличения
ЦФ.
3. Линии уровня (параллельные черной) mn и MN
являются ОПОРНЫМИ (имеют одну общую точку с
многоугольником решений). Точка А является точкой
минимума ЦФ, точка С – точкой максимума ЦФ.
24.
Примеры решения задач ЛП графическимметодом
25.
Пример 1Пусть ограничения имеют вид:
x1 4 x2 4
x x 6
1
2
x1 2
x2 0
Надо найти значения x1 и х2, на которых ЦФ
С =х1+3х2
принимает максимальное значение.
26.
Решение графическим методом1. Желтым цветом изображены
линии, полученные из
ограничений. Множество
допустимых значений –
четырехугольник АВСD.
2. Черная линия, проходящая через
начало координат – это линия
уровня ЦФ С=0.
Перпендикулярный вектор к линии
уровня (градиент) показывает
направление увеличения ЦФ.
3. Перемещая линию уровня в направлении градиента,
найдем опорные прямые. Точка А является точкой
минимума ЦФ, точка В – точкой максимума ЦФ. Подставляя
в ЦФ координаты точки В x1=2, x2=4, найдем максимальное
значение ЦФ: Cmax=14.
27.
Пример 2Пусть ограничения имеют вид:
2 x1 x2 6
x 2x 6
1
2
x2 1
x1 0
Надо найти значения x1 и х2, на которых ЦФ
С =5х1+6х2
принимает минимальное значение.
28.
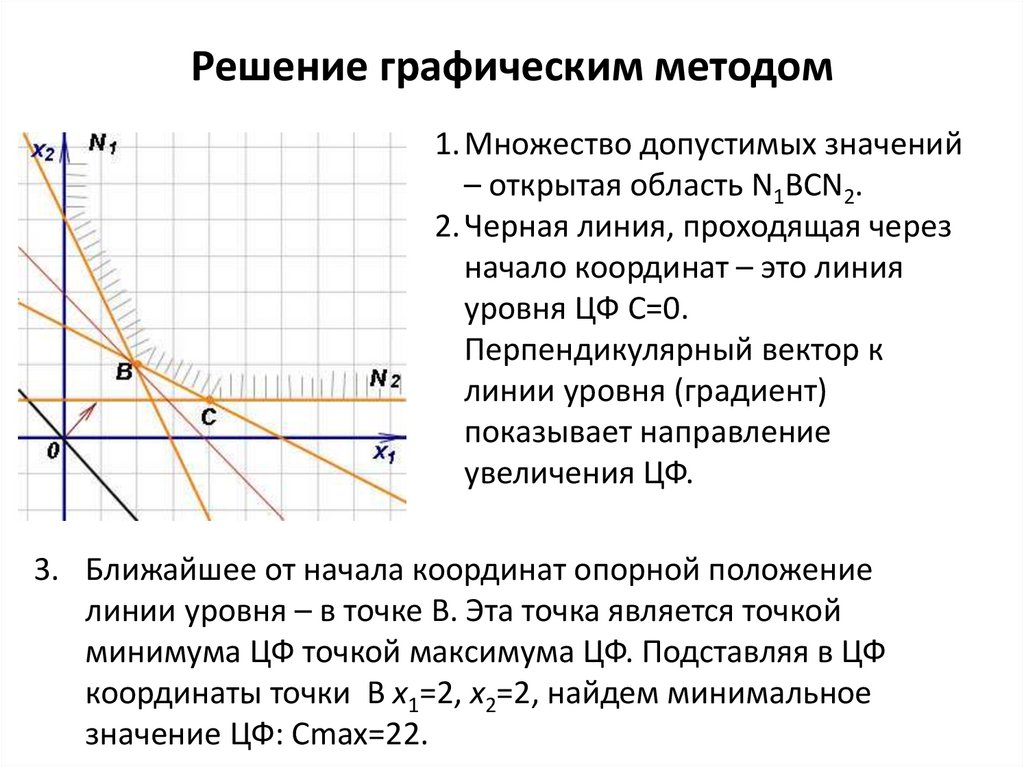
Решение графическим методом1. Множество допустимых значений
– открытая область N1ВСN2.
2. Черная линия, проходящая через
начало координат – это линия
уровня ЦФ С=0.
Перпендикулярный вектор к
линии уровня (градиент)
показывает направление
увеличения ЦФ.
3. Ближайшее от начала координат опорной положение
линии уровня – в точке B. Эта точка является точкой
минимума ЦФ точкой максимума ЦФ. Подставляя в ЦФ
координаты точки В x1=2, x2=2, найдем минимальное
значение ЦФ: Cmax=22.
29.
Симплекс-метод решения задачи ЛПСимплекс метод - это метод последовательного перехода
от одного базисного решения (вершины многогранника
решений) системы ограничений задачи линейного
программирования к другому базисному решению до тех
пор, пока функция цели не примет оптимального значения
(максимума или минимума).
Симплекс метод был предложен американским
математиком Р.Данцигом в 1947 году, с тех пор для нужд
промышленности этим методом нередко решаются задачи
линейного программирования с тысячами переменных и
ограничений.
30.
Инструменты решения задач ЛПExcel: Поиск
решения
Matlab: функция
linprog
Mathcad: блок
Given и функции
нахождения
оптимума



























 Математика
Математика








