Похожие презентации:
Двойственные задачи линейного программирования
1. 5.7.Двойственные задачи ЛП
2.
С каждой задачей линейногопрограммирования тесно связана другая
линейная задача, называемая
двойственной к исходной.
Пусть дана задача ЛП.
Максимизировать линейную функцию
f ( x) c1 x1 c2 x2 cn xn max (5.9)
3.
При ограниченияхa11 x1 a12 x2 a1n xn b1 ,
a21 x1 a22 x2 a2 n xn b2 ,
a x a x a x b ,
mn n
m
m1 1 m 2 2
x j 0, j 1, n
Или в матричном виде
f ( x) (c, x) max
Ax b
x 0
(5.10)
4.
Двойственная к ней задачаформулируется следующим образом
Минимизировать линейную
функцию
z ( y ) b1 y1 b2 y2 bm ym min (5.11)
при ограничениях
5.
a11 y1 a21 y2 am1 ym c1 ,a12 y1 a22 y2 am 2 ym c 2 ,
(5.12)
a y a y a y c ,
mn m
n
1т 1 2 т 2
y j 0, j 1, m
или в матричном виде
z ( y ) (b, y ) min
AT y c
y 0
6.
Задачи (5.9), (5.10) и (5.11), (5.12)образуют пару взаимодвойственных
задач, и любая из них может
рассматриваться как исходная.
Решать исходную или двойственную
задачу – вопрос лишь удобства
Математические модели двойственных
задач могут быть симметричными и
несимметричными. В табл. 5.13, 5.14
приведены их матричные формы записи
7.
5.7.1.Симметричные задачиВ симметричных задачах система
ограничений как исходной, так и
двойственной задачи задается
неравенствами, причем на
двойственные переменные налагается
условие неотрицательности.
8.
9.
5.7.2. Несимметричные задачиВ несимметричных двойственных
задачах система ограничений исходной
задачи задается в виде равенств, а в
двойственной - в виде неравенств,
причем в последней переменные могут
быть и отрицательными.
10.
11.
Пример 5.11. Даны прямые задачи.Построить двойственные к ним задачи.
a)
f ( x) x1 2 x 2 5 x3 max;
2 x1 2 x 2 4 x3 18,
5 x - 3 x 6 x 19,
1
2
3
2 x1 x 2 3 x3 20,
x1 , x 2 , x3 0.
12.
Решение. Рассматриваемая задачаотносится к симметричным двойственным
задачам на отыскание максимального
значения целевой функции.
Используем общие правила
составления двойственных задач. Так
как в задаче на максимум ограничения
неравенства должны иметь вид « < », то
умножим второе ограничениенеравенство на -1.
Исходная задача запишется в виде
13.
f ( x) x1 2 x 2 5 x3 max;2 x1 2 x 2 4 x3 18,
- 5 x 3 x - 6 x 19,
1
2
3
2 x1 x 2 3 x3 20,
x1 , x 2 , x3 0.
14.
Найдем соответствующуюдвойственную задачу (строка 1, табл.
5.13). Введем вектор двойственных
переменных размерности 3 (по числу
уравнений системы ограничений) .
y ( y1 , y2 , y3 ) .
Т
Соответствующие векторы и матрица
ограничений имеет вид:
15.
c (1, - 2, 5)b (18, - 19, 20)
4
2 2
A 5 3 6
2 1 3
2
2 5
T
A 2 3
1
4 6 3
16.
Запишем двойственную задачу. Найтиминимум функции
g ( y ) (b, y ) 18 y1 19 y 2 20 y 3 min
2 y1 5 y 2 2 y 3 1,
2 y1 1
2 5
2 y 3 y y 2,
1
2
3
3
1 y2 2
2
4 6 3 y 5
4 y1 6 y 2 3 y 3 5,
3
y1 , y 2 , y 3 0.
17.
Укажем еще один метод, позволяющийзначительно облегчить процесс
построения двойственных задач.
Каждому ограничению прямой задачи
поставим в соответствие двойственные
переменные.
2 x1 2 x 2 4 x3 18,
- 5 x1 3 x 2 - 6 x3 19,
2 x x 3 x 20,.
1
2
3
x1 , x 2 , x 3 0
y1
y2
y3
18.
Чтобы получить, например, первоеограничение двойственной задачи, надо
найти сумму произведений элементов,
стоящих в столбце x1 , на
соответствующие двойственные
переменные. Результат 2 y1 5 y2 2 y3 .
Считаем, что эта сумма не меньше c1 1 :
2 y1 5 y 2 2 y 3 1.
Аналогично составляются и остальные
ограничения двойственной задачи.
19.
b)f ( x) 3 x1 4 x 2 6 x3 min;
2 x1 3 x 2 x3 8,
3 x 2 x 2 x 10,
1
2
3
5 x1 - 4 x 2 x3 7,
x1 , x 2 , x3 0.
20.
Решение. Каждому ограничениюпрямой задачи поставим в соответствие
двойственные переменные
2 x1 3 x 2 x3 8,
3 x1 2 x 2 2 x3 10,
5 x - 4 x x 7,
1
2
3
y1
y2
y3
21.
Составим двойственную задачу:g ( y ) 8 y1 10 y 2 7 y 3 max;
2 y1 - 3 y 2 5 y 3 3,
3 y 2 y 4 y 4,
1
2
3
y1 - 2 y 2 y 3 6,
y1 , y 3 0.
Переменная y 2 , соответствующая
ограничению-равенству
3 x1 2 x 2 2 x3 10
может быть любого знака.
22.
5.7.3. Первая теорема двойственностиЕсли из двух задач (исходной и
двойственной) одна имеет решение, то
другая задача также имеет решение,
причем максимальное значение целевой
функции исходной задачи и минимальное
значение двойственной задачи численно
равны
f max zmin .
23.
Если же одна из задач не имеетоптимального решения, то система
ограничений двойственной задачи
противоречива
5.7.4. Экономическая интерпретация
двойственной задачи.
Пусть ( x1, x2 , , xn ) - оптимальное
решение прямой задачи, а ( y1, y2 , , ym )
оптимальное решение двойственной
задачи
24.
На основании первой теоремыдвойственности ( f max z min ) можно
записать
f max b1 y1 b2 y2 bm ym .
Найдем
f max
y j , f max y j b j .
b j
25.
Учитывая, что функция f max линейная,получим
f max y j b j . (5.13)
Из последней формулы следует:
значения переменных y j в оптимальном
решении двойственной задачи
представляют собой оценки влияния
свободных членов b j системы
ограничений прямой задачи на величину
f max .
26.
Пример 5.12. Для производства двухвидов продукции предприятие использует
четыре вида сырья S1 , S 2 , S3 , S 4 .
S1
Затраты сырья на единицу каждого вида
продукции, прибыль и запасы сырья даны
в табл.
27.
Составить план производства,обеспечивающий предприятию
максимальную прибыль.
Математическая модель прямой
задачи
Обозначим через x1 , x2 - количество
единиц продукции, соответственно I и II
видов.
Тогда задача заключается в следующем:
28.
максимизировать целевую функциюf ( x) 7 x1 5 x 2
при ограничениях
2 x1 3 x 2 19
2 x x 13
2
1
3 x 2 15
3 x
18
1
x1 , x 2 0
29.
Запишем задачу в матричном виде.f ( x) (c, x) max,
A x b,
x 0,
где
x ( x1 , x 2 ) T - вектор неизвестных,
с (7, 5)
- вектор коэффициентов
целевой функции,
b (19, 13, 15, 18) T - вектор правых частей
системы ограничений,
30.
22
A
0
3
3
1
3
0
- матрица коэффициентов
системы ограничений.
Решение прямой задачи дает
оптимальный план выпуска продукции I и
II видов.
Поставим в соответствие прямой
задаче двойственную задачу.
31.
Пример 5.13. Предприятию необходимоопределить минимальное суммарное
количество сырья каждого из видов
S1 , S 2 , S3 , S 4 ,
применив прежнее условие примера 5.12.
Математическая модель
двойственной задачи
В качестве переменных двойственной
задачи возьмем y1 , y2 , y3 , y4 ,
представляющие собой условные оценки
запасов сырья
32.
Представим двойственную задачу вматричном виде
g ( x) (b, y ) min,
T
A y c,
y 0,
(5.14)
где y ( y1 , y 2 , y 3 , y 4 ) - вектор
двойственных переменных;
3 1 3 0
T
- транспонированная
A
2 2 0 3
матрица
коэффициентов системы ограничений
33.
Раскрывая соотношение (5.14) можносформулировать двойственную задачу
так:
найти минимум целевой функции
z ( y ) (b, y ) 19 y1 13 y2 15 y3 18 y4 ,
при ограничениях
3 y1 y2 3 y3 7,
2 y 2 y 3 y 5,
2
4
1
y j 0, j 1, 4.
34.
Чтобы найти решение этих задачрешим одну из них – прямую, т.к. система
ограничений этой задачи содержит лишь
неравенства « < ». Решение находим
симплексным методом.
Приведем задачу к каноническому виду
35.
2 x1 3 x2 x319
2 x x x
13
1
2
4
3 x2
x 5 15
x6 18
3 x1
x j 0, j 1,6
f ( x) 7 x1 5 x 2 0 x3 0 x 4 0 x 5 0 x6
36.
Запишем систему ограничений ввекторном виде
A1 x1 A2 x2 A3 x3 A4 x4 A5 x5 A6 x6 A0 (5.14)
где
2
3
2
1
A1 , A 2 , A 3
0
3
3
0
1
0
0
1
, A 4 , A 5
0
0
0
0
0
0
19
0
0
13
, A 6 , A 0 .
1
0
15
0
1
18
37.
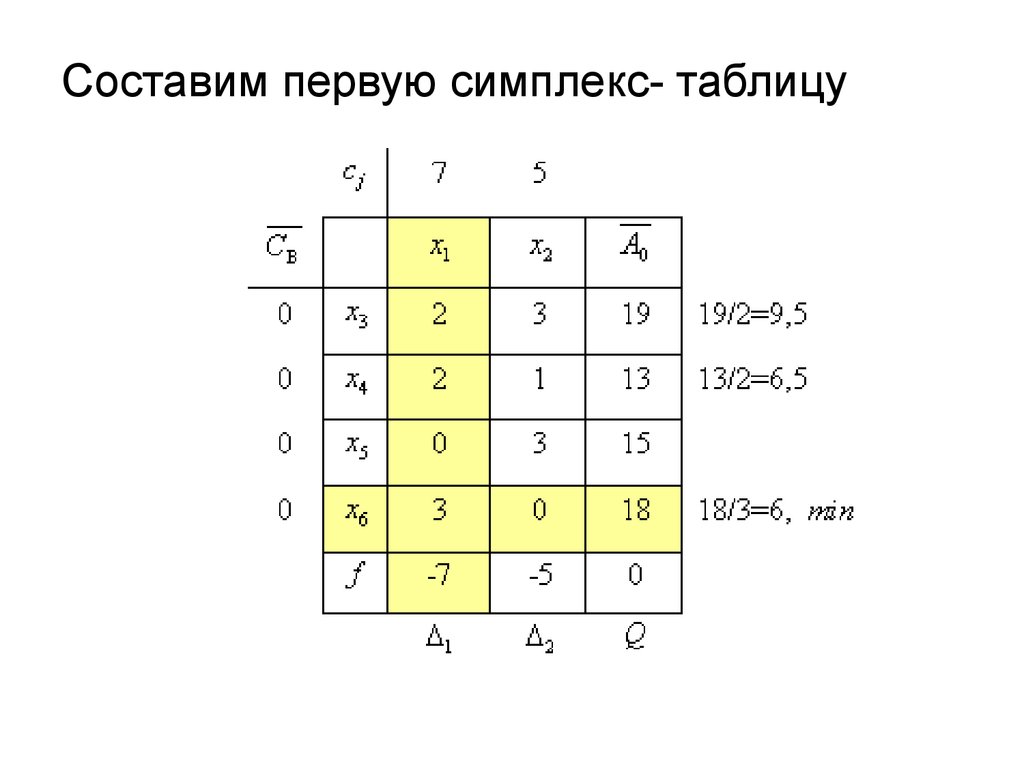
Составим первую симплекс- таблицу38.
Поскольку отыскивается максимумзадачи, то критерий оптимальности для
плана не выполнен, т.к. в f - строке
имеются отрицательные оценки.
Дальнейшие результаты пошагового
решения задачи представлены в табл.
5.15 – 5.17.
39.
40.
41.
42.
В последней таблице f - строка несодержит отрицательных оценок, что
свидетельствует об оптимальности
полученного решения:
x * ( x1 , x 2 , x3 , x 4 , x 5 , x6 ) (5, 3, 0, 0, 6, 3),
f max f ( x * ) (C В A0 ) 0 3 5 3 0 6 7 5 50 (ед.).
43.
Оптимальное решение двойственнойзадачи может быть получено из
оптимального решения прямой задачи.
Так как прямая задача имеет решение,
то на основании теоремы о
двойственности двойственная задача
также разрешима. Ее решение может
быть найдено из формулы
1
y CВ D ,
*
44.
гдеD - матрица, составленная из
компонент векторов, входящих в
последний базис, при котором получен
оптимальный план исходной задачи.
В нашем примере в последней
симплекс-таблице базисными
переменными являются
x6 , x2 , x5 , x1 .
45.
Соответствующие этим переменнымвекторы A 6 , A 2 , A 5 , A1 в разложении (5.14)
используются для формирования
столбцов матрицы D
0
0
D ( A6 , A2 , A5 , A1 )
0
1
3 0 2
1 0 2
.
3 1 0
0 0 3
46.
Вычислим0,75 2,25
0,5
0,5
1
D
1,5
1,5
0,25 0,75
Так как
C B (0, 5, 0, 7) ,
1
0
0
1
0
1
0
.
0
0
то
y CВ D (0,75; 2,75; 0; 0)
*
47.
При этом минимальное значениецелевой функции двойственной задачи
z min z ( y * ) (b, y * )
19 0,75 13 2,75 15 0 18 0 50 (ед.)
совпадает с максимальным значением
прямой задачи.
f
max
48.
Проведем анализ полученногооптимального решения двойственной
задачи.
Рассмотрим экономическое
содержание двойственных оценок.
Предположим, что запасы сырья
увеличены на 1единицу.
Пользуясь формулой (5.13), найдем
49.
f max y3 b3 0 1 0;f max y4 b 4 0 1 0.
Нулевые оценки S3 и S 4 означают,
что данное сырье не полностью
используется (является недефицитным)
и дальнейшее его увеличение не
повлияет на оптимальный план выпуска
продукции и сумму прибыли.
50.
f max y1 b1 0,75 1 0,75 (ед );f max y2 b 2 2,75 1 2,75 (ед ).
Если увеличить запасы сырья S на
1
1 (ед.), то прибыль увеличится на 0,75
(ед.).
Если увеличить запасы сырья S на
2
1 (ед.), то прибыль увеличится на 2,75
(ед.).
51.
Запасы сырья S1 и S 2 полностьюиспользуются в оптимальном плане,
являются дефицитными и сдерживают
рост целевой функции.
52.
Здесь следует отметить, что оценкипозволяют судить об эффекте не любых,
а лишь сравнительно небольших
изменений объема ресурсов. При резких
изменениях сами оценки могут стать
другими.




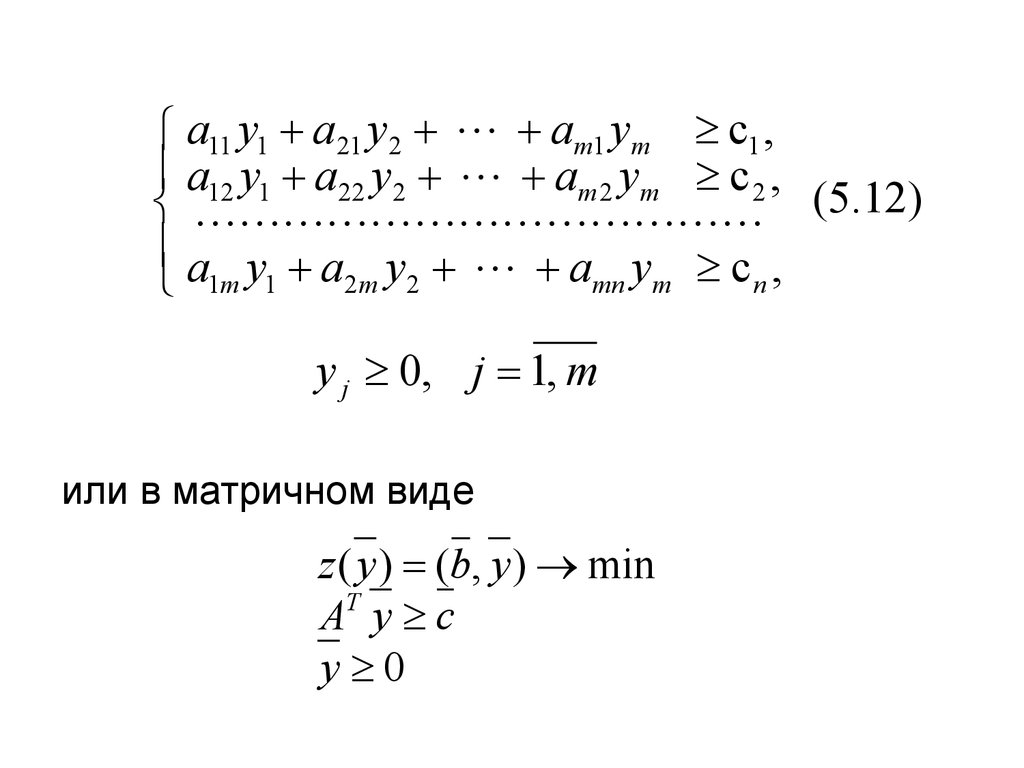







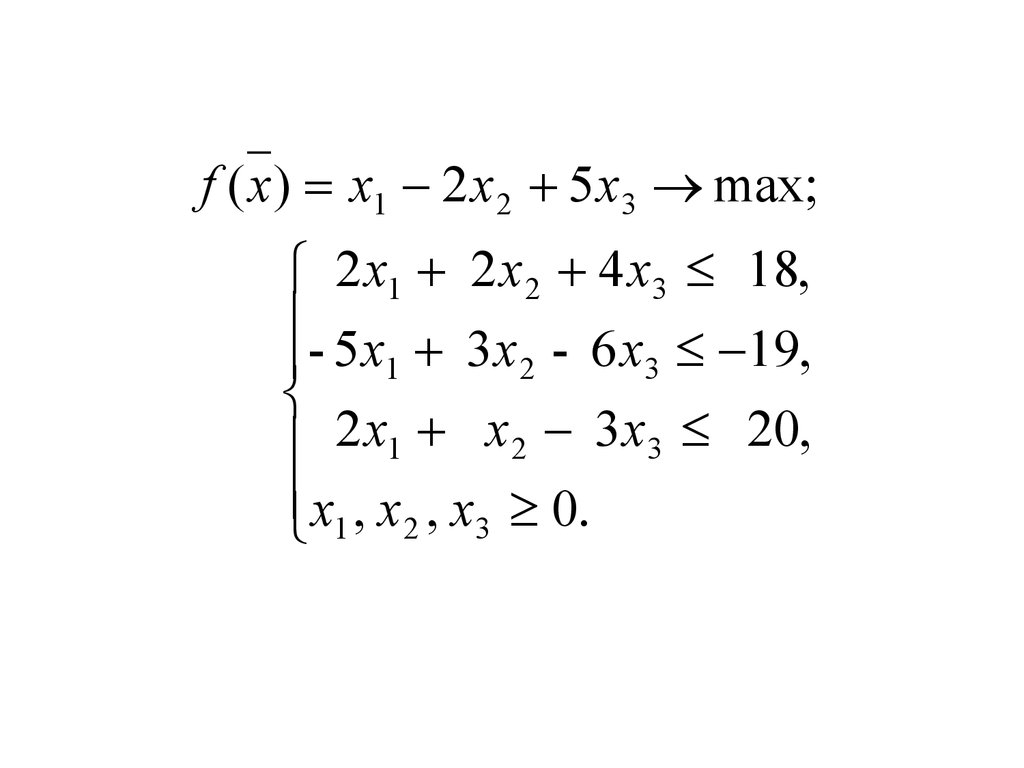





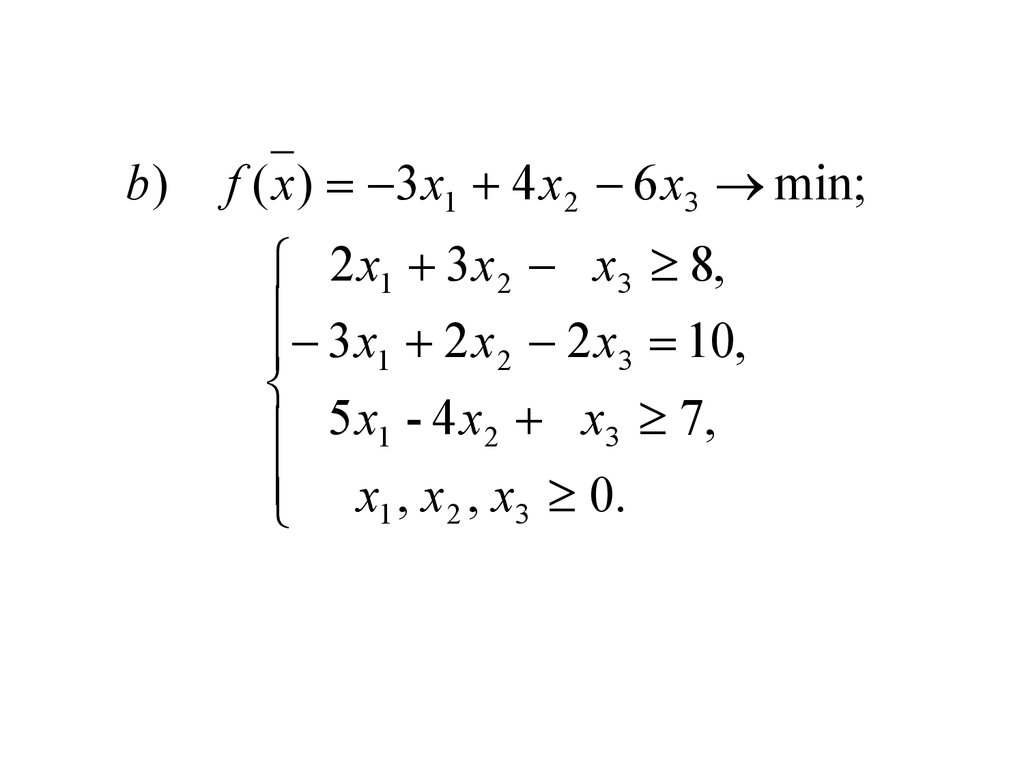















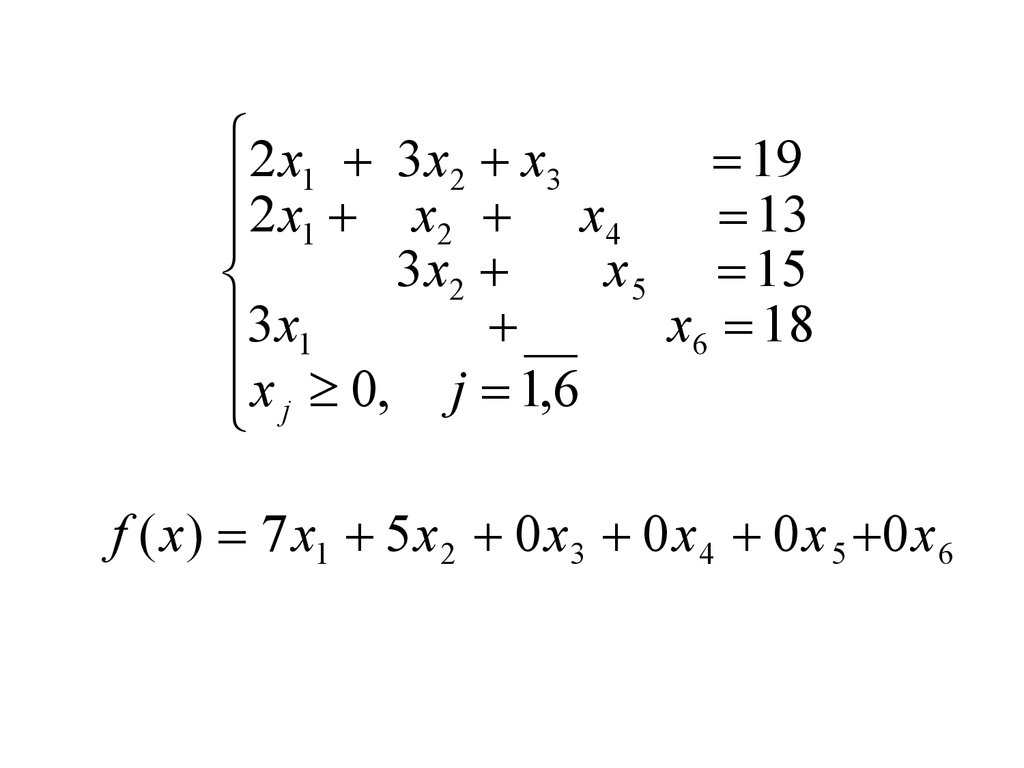
















 Математика
Математика Программирование
Программирование








