Кинематика материальной точки. Физические модели

1. Физика

Лекция 1
Кинематика. Динамика.

2. Кинематика материальной точки. Физические модели. Пространство и время. Прямолинейное движение точки. Скорость и ускорение. Прямая и обрат

Кинематика материальной точки.
Физические модели. Пространство и время.
Прямолинейное движение точки. Скорость и
ускорение. Прямая и обратная задачи кинематики.
Движение точки по окружности.
Динамика материальной точки.
Основные понятия динамики:
масса, импульс, сила.
Законы Ньютона и следствия из них. Понятие
состояния в классической механике. Виды сил:
сила трения, сила тяжести, сила тяготения.
Элементы теории относительности

3. Физика – наука, изучающая наиболее общие законы движения и взаимодействия материальных тел в неживой природе. Физических модели: Материал

Физика – наука, изучающая наиболее общие законы
движения и взаимодействия материальных тел в
неживой природе.
Физических модели:
Материальная точка – материальное тело, размерами
которого можно пренебречь.
Абсолютно твердое тело – материальное тело,
состоящее из очень большого числа материальных
точек. Расстояние между любыми двумя из них
остается всегда неизменным.
Сплошная среда – материальное тело, состоящее из
очень большого числа материальных точек.
Расстояние между любыми двумя из них может
изменяться по определенному закону под воздействием
внешних и внутренних причин.

4.

Кинематика
Движение - это изменение положения
исследуемого
материального
тела
относительно других тел с течением
времени.
Тело или система неподвижных
относительно
друг
друга
тел
называются системой отсчета.

5.

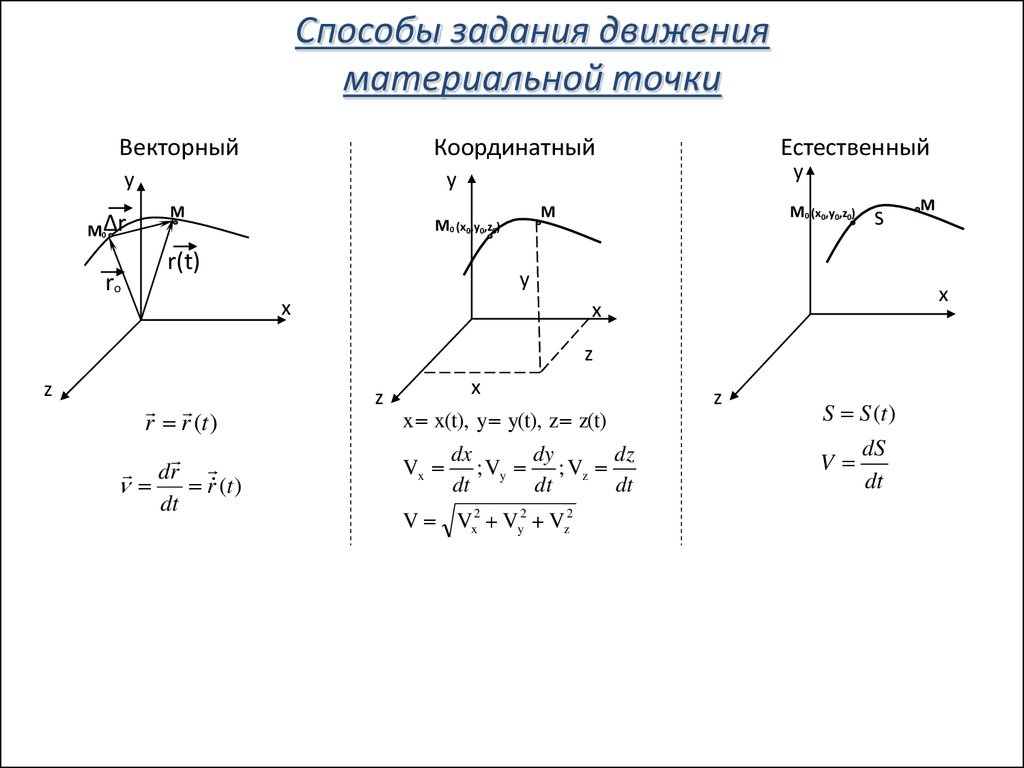
Способы задания движения
материальной точки
Векторный
Координатный
y
M0∆r
ro
Естественный
y
y
M
M0 (x0,y0,z0)
r(t)
M
M0 (x0,y0,z0)
M
y
x
x
x
z
z
r r (t )
dr
r (t )
dt
z
x
x x(t), y y(t), z z(t)
dx
dy
dz
Vx ; Vy ; Vz
dt
dt
dt
V Vx2 Vy2 Vz2
z
S S (t )
V
dS
dt

6.

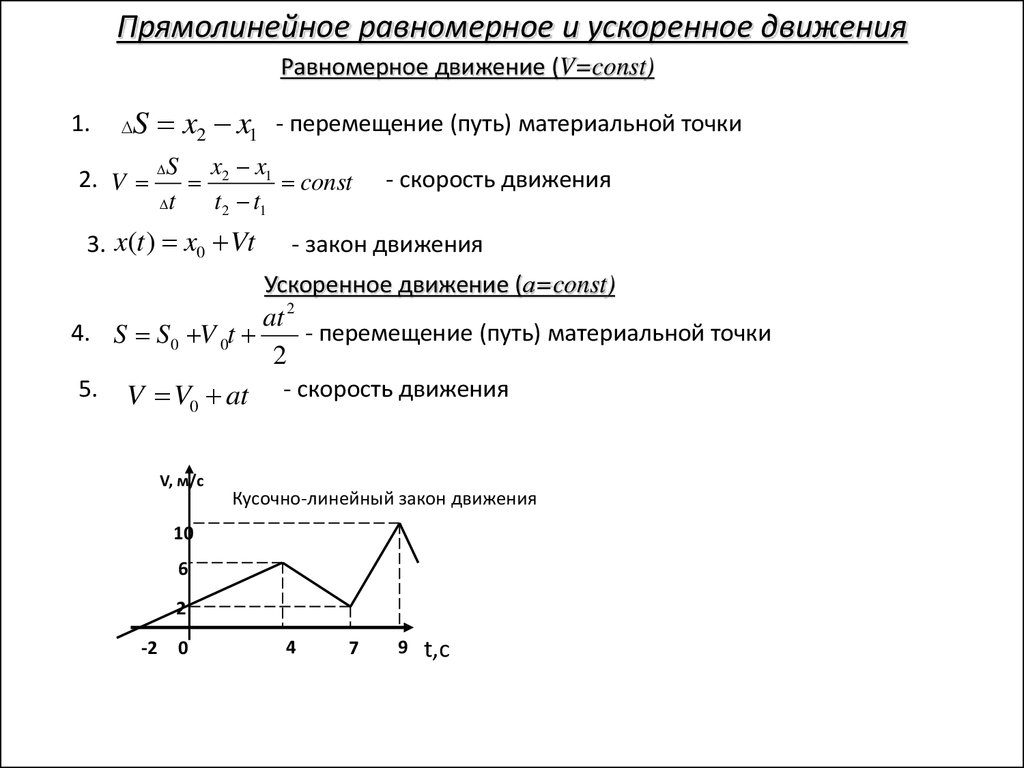
Прямолинейное равномерное и ускоренное движения
Равномерное движение (V=const)
1.
S x2 x1 - перемещение (путь) материальной точки
2. V
S x2 x1
const
t
t 2 t1
3. x(t ) x0 Vt
- скорость движения
- закон движения
Ускоренное движение (а=const)
at 2
4. S S0 V 0t
- перемещение (путь) материальной точки
2
5. V V at - скорость движения
0
V, м/с
Кусочно-линейный закон движения
10
6
2
-2
0
4
7
9
t,c

7. Кинематика движения точки по окружности. Основные кинематические параметры.

0 0t
t2
2
d
d
,
dt
dt
, 0 t , T
2
Связь между угловыми и линейными параметрами
V R
dV
R
dt
V2
an
2 R
R
a

8.

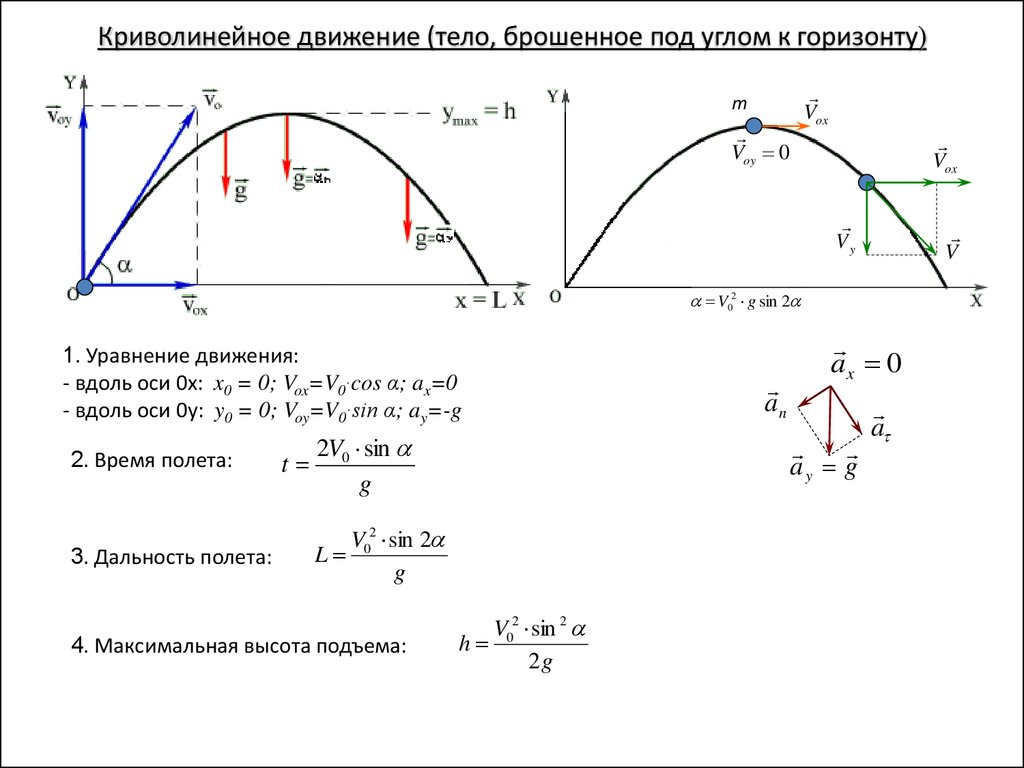
Криволинейное движение (тело, брошенное под углом к горизонту)
Vox
m
Voy 0
Vox
Vy
V
V02 g sin 2
1. Уравнение движения:
- вдоль оси 0х: x0 = 0; Vox=V0·cos α; ax=0
- вдоль оси 0у: y0 = 0; Voy=V0·sin α; ay=-g
2. Время полета:
3. Дальность полета:
t
2V0 sin
g
ay g
V02 sin 2
L
g
4. Максимальная высота подъема:
an
ax 0
V02 sin 2
h
2g
a

9.

Динамика
Динамика – раздел механики в котором изучаются
причины движения и взаимодействия материальных тел.
Основные понятия
Масса – количественная мера материи.
m
Импульс – количественная мера движения
материального тела.
p = m∙v
Сила – количественная мера действия на
материальное тело со стороны других тел.
F

10.

1 закон Ньютона.
Всякая материальная точка будет находиться в
состоянии покоя или прямолинейного равномерного
движения до тех пор, пока это состояние не будет
изменено воздействием со стороны других тел.
Следствия
Способность тел сохранять свое первоначальное
состояние называется инертностью.
Состояние материальной точки определяется
значением координаты и величиной импульса
(x,y,z; px ,py ,pz).

11.

2 закон Ньютона.
Изменение
импульса
пропорционально
приложенной движущей силе и происходит по
направлению той прямой, по которой эта сила
dp
действует.
F
dt
Следствия
1. Если на тело действует несколько сил, то их
действие можно заменить действием
результирующей силы.
F Fi
2. Если масса тела постоянна, то тогда
dp d ( m ) m d
F
m a
dt
dt
dt
некоторой

12.

3 закон Ньютона.
Действию всегда есть равное и противоположное
противодействие, иначе – взаимодействия двух тел
друг на друга между собой равны и направлены в
противоположные стороны
F 12 F 21
Следствия
1.Силы всегда возникают парами.
2.Силы при взаимодействии равны по величине,
противоположны по направлению, но приложены к
разным телам.
3.Системы отсчета, в которых выполняется законы
Ньютона, называются инерциальными.

13.

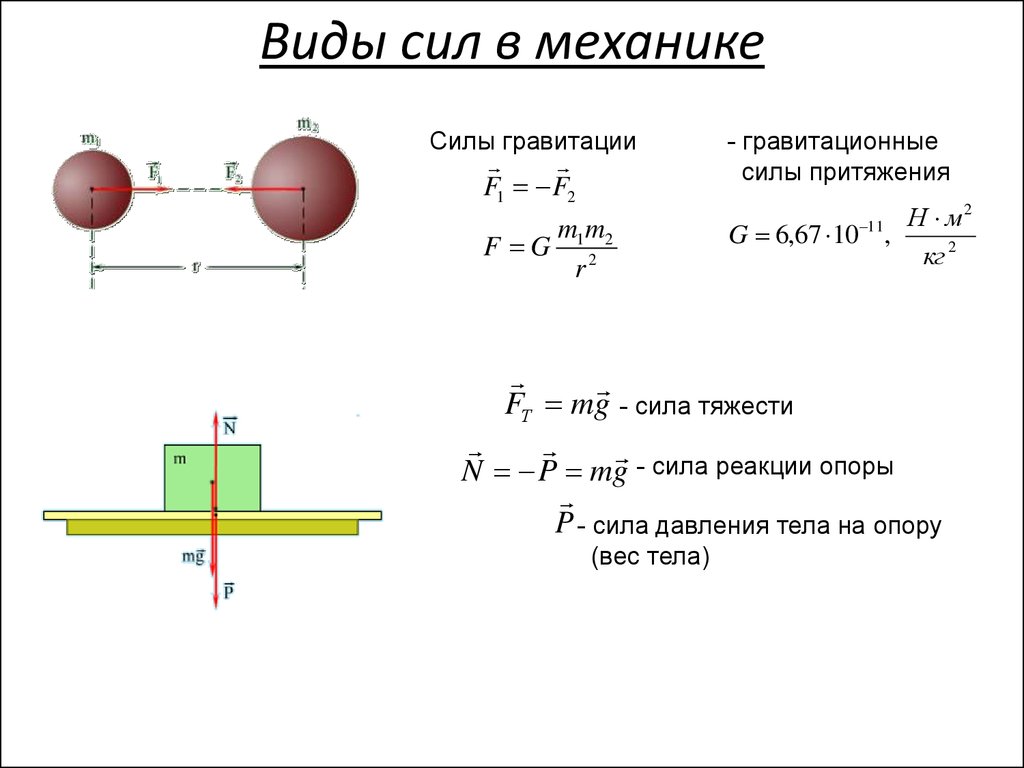
Виды сил в механике
Силы гравитации
F1 F2
F G
m1m2
r2
- гравитационные
силы притяжения
Н м2
G 6,67 10 ,
кг 2
11
FТ mg - сила тяжести
- сила реакции опоры
N P mg
P - сила давления тела на опору
(вес тела)

14.

Силы трения
Fò ð kN
Fò ð kN

15. Элементы теории относительности

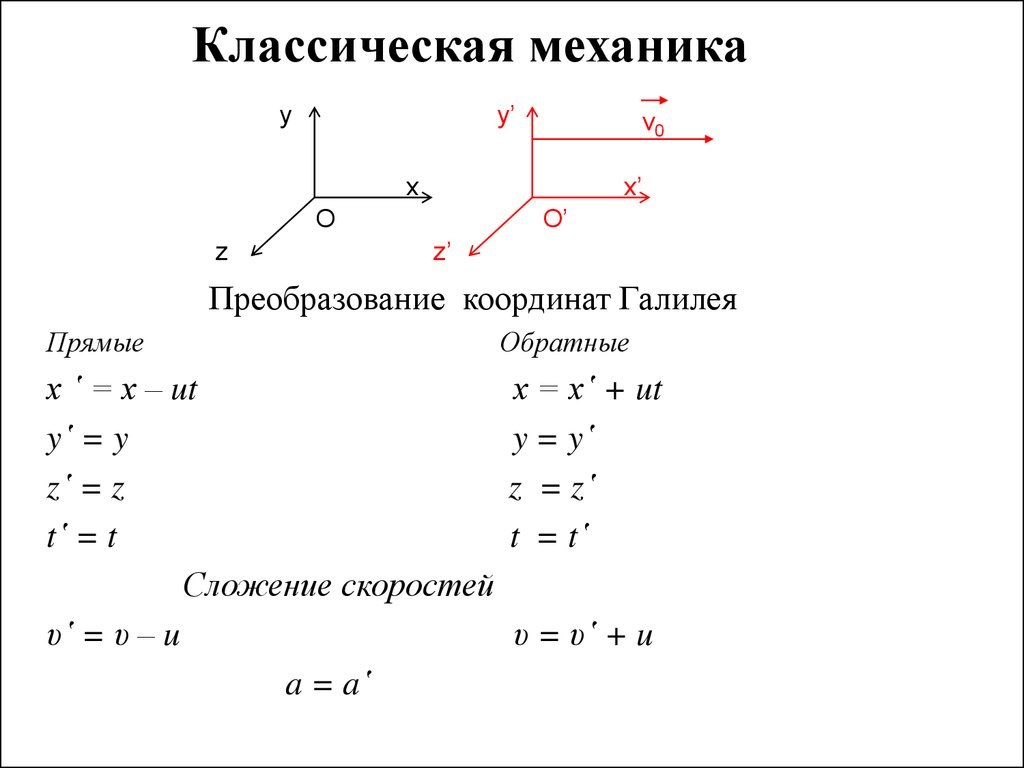
16. Классическая механика

y’
y
v0
x’
x
O’
O
z
z’
Преобразование координат Галилея
Прямые
х ῾ = х – ut
y῾ = y
z῾ = z
t῾ = t
Сложение скоростей
υ῾ = υ – u
a = a῾
Обратные
х = х῾ + ut
y = y῾
z = z῾
t = t῾
υ = υ῾ + u

17. Принцип относительности Галилея. Никакими механическими опытами нельзя установить движется или покоится инерциальная система.

18. Релятивистская механика

19.

Постулаты Специальной Теории
Относительности Эйнштейна
• Принцип относительности:
Все законы природы одинаковы во
всех инерциальных системах отсчета
• Принцип постоянства скорости света:
Скорость света в вакууме одинакова
во всех инерциальных системах отсчета
и не зависит от движения источников и
приемников света
c = 3·108 м/с

20.

Преобразования Лоренца
x'
x v0 t
1 v /c
2
0
x
2
x' v 0 t'
1 v /c
2
0
y' y
y y'
z' z
z z'
t'
t - (v 0 /c ) x
2
1 v 02 /c 2
t
2
t' (v 0 /c 2 ) x'
1 v 02 /c 2

21.

y’
y
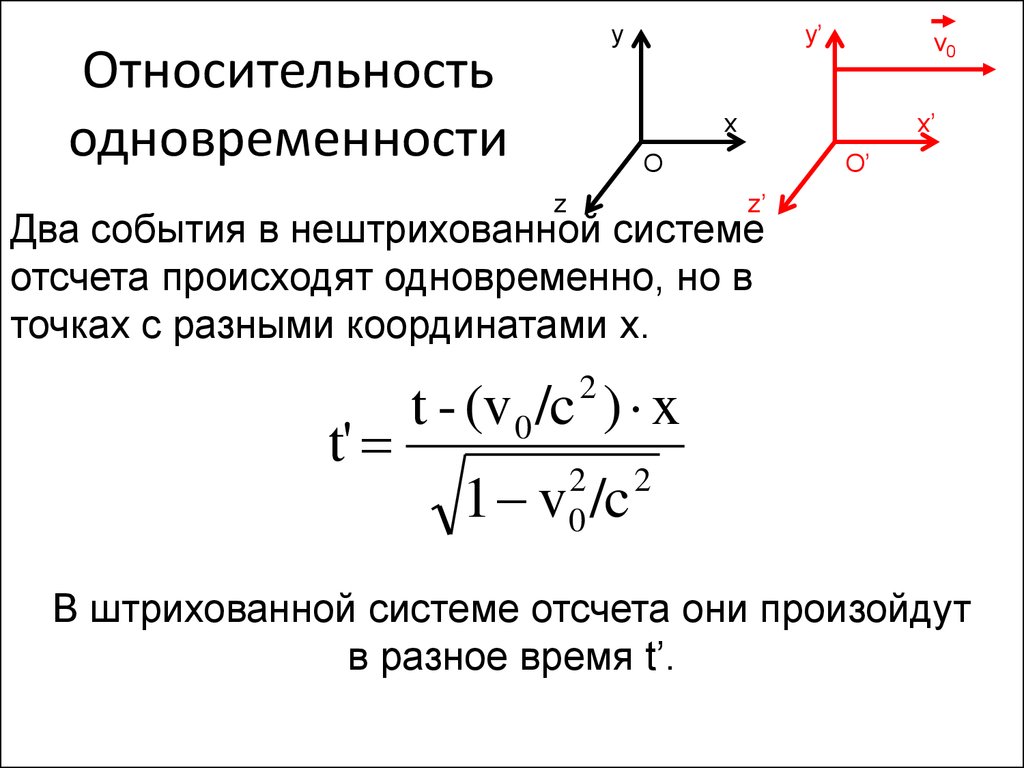
Относительность
одновременности
v0
x’
x
O’
O
z’
z
Два события в нештрихованной системе
отсчета происходят одновременно, но в
точках с разными координатами x.
t'
t - (v 0 /c ) x
2
1 v /c
2
0
2
В штрихованной системе отсчета они произойдут
в разное время t’.

22.

Относительность длины
Рассмотрим стержень, неподвижный в нештрихованной
системе отсчета. Его длина Δx = xконца - xначала
y’
y
v0
x’
x
O’
O
z
z’
Если в штрихованной системе отсчета (где стержень
движется) одновременно (t’=const)
x' v 0 t'
замерить x’конца и x'начала, то с учетом, что x
2 2
Δx' Δx 1 v /c
2
0
1 v 0 /c
2

23.

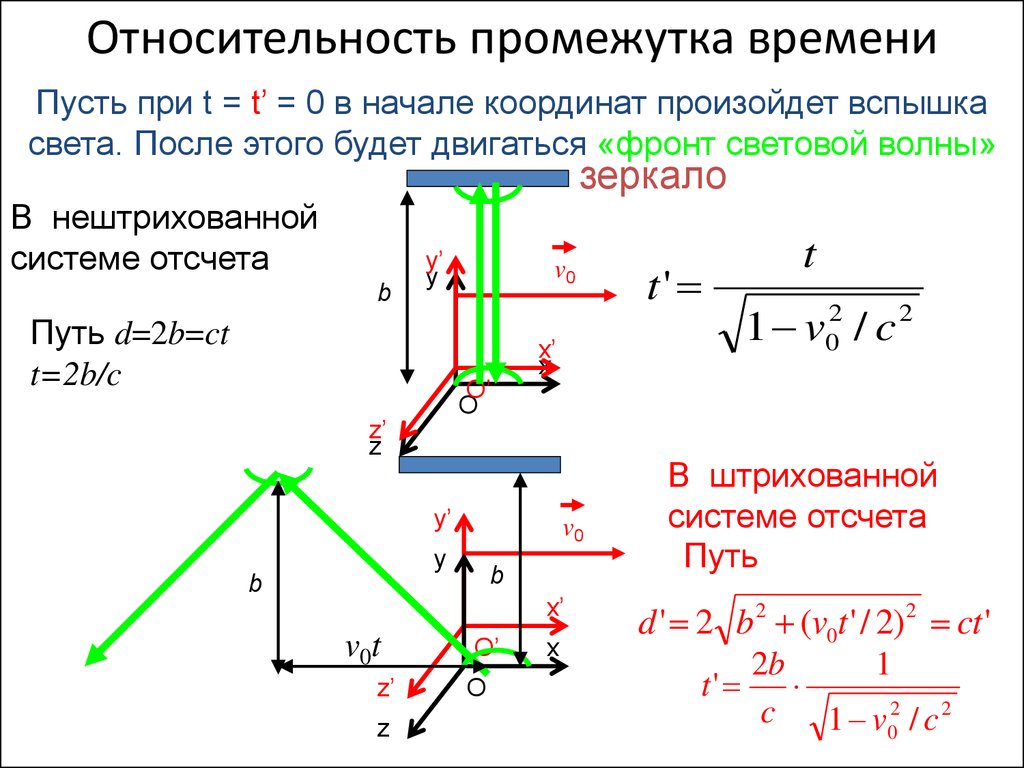
Относительность промежутка времени
Пусть при t = t’ = 0 в начале координат произойдет вспышка
света. После этого будет двигаться «фронт световой волны»
зеркало
В нештрихованной
системе отсчета
b
y’
y
Путь d=2b=ct
t=2b/c
v0
O’
O
z’
z
x’
x
y’
v0
y
b
b
x’
v0 t
z’
z
O’
O
x
t'
t
1 v02 / c 2
В штрихованной
системе отсчета
Путь
d ' 2 b 2 (v0t ' / 2) 2 ct '
2b
1
t'
c
1 v02 / c 2

24.

25. Ускорение

Преобразование скоростей
x
x' v 0 t'
1 v /c
2
0
2
t
t' (v0 /c 2 ) x'
1 v02 /c 2
v'x v 0
vx
v'x v 0
1 2
c
Ускорение
dx
vx
dt