Похожие презентации:
Основные теоремы дифференциального исчисления
1.
Если дифференцируемая на промежуткеХ функция y=f(x) достигает
наибольшего или наименьшего
значения во внутренней точке х0 этого
промежутка, то производная функции
в этой точке равна 0:
f ( x0 ) 0
2.
Пусть функция y=f(x) дифференцируема напромежутке Х и в точке x0 X
принимает наименьшее значение.
Тогда f ( x0 x ) f ( x0 )
x0 x X
Величина y f ( x0 x) f ( x0 ) 0
если
Следовательно
y
0 при x 0
x
y
0 при x 0
x
3.
Переходим в этих неравенствах соответственнок пределу справа и слева:
y
lim
0
x 0
x
и
y
lim
0
x 0
x
По условию функция y=f(x) дифференцируема в
точке х0, следовательно ее предел при x 0
не должен зависеть от способа стремления Δх к
нулю, т.е.
y
y
lim
lim
0
x 0
x x 0 x
f ( x0 ) 0
4.
В точке наибольшего или наименьшегозначения, достигаемого внутри промежутка
Х, касательная к графику функции
параллельна оси Х.
5.
Пусть функция y=f(x) удовлетворяетследующим условиям:
1. Непрерывна на отрезке [a,b].
2. Дифференцируема на интервале (a,b).
3. На концах отрезка принимает равные
значения: f(a)=f(b).
Тогда внутри отрезка существует по
крайней мере одна такая точка ξ, в
которой производная равна нулю:
f ( ) 0
6.
По теореме Вейерштрасса, функция, непрерывнаяна отрезке, достигает на нем своего наибольшего
М и наименьшего m значений.
Если оба этих значения достигаются на концах
отрезка,то они по условию равны: М= m, а это
значит, что функция постоянна на [a,b]. Тогда
f ( x) 0 во всех точках этого отрезка.
Если же хотя бы одно из этих значений
достигается внутри отрезка, то по теореме
Ферма, производная функции в этой точке
равна нулю:
f ( x) 0
7.
Найдется хотя бы одна точка, в которойкасательная к графику функции
параллельна оси Х, в этой точке
производная функции будет равна нулю.
8.
yy f (x)
a
1
2
b
x
9.
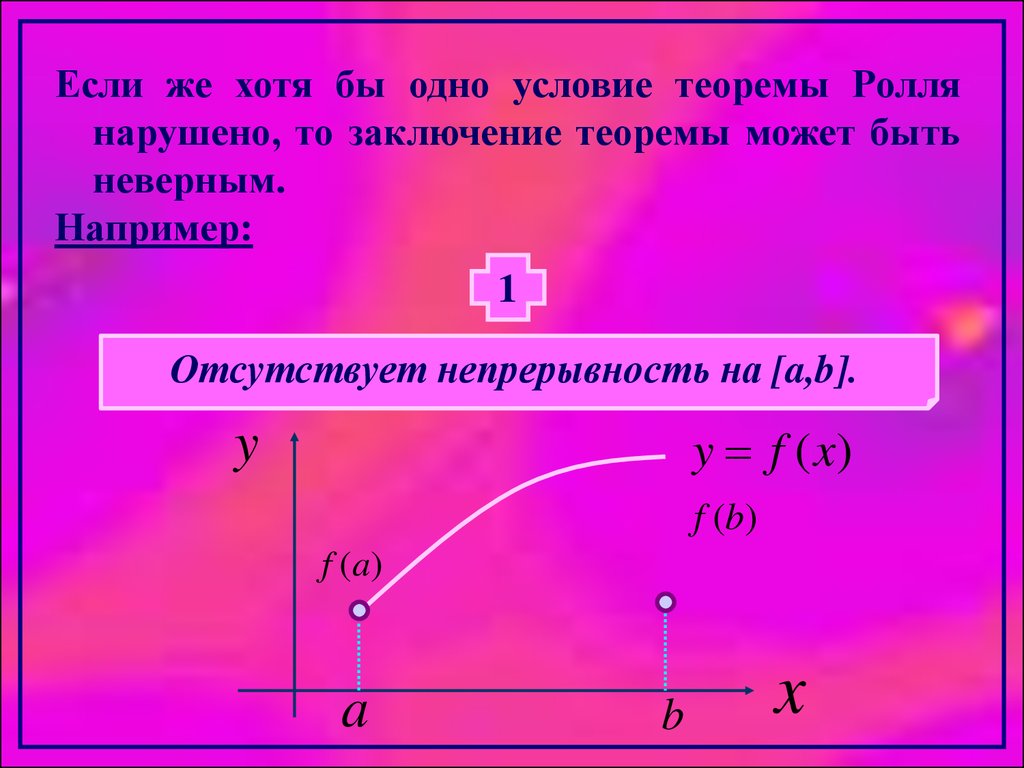
Если же хотя бы одно условие теоремы Роллянарушено, то заключение теоремы может быть
неверным.
Например:
1
Отсутствует непрерывность на [a,b].
y f (x)
y
f (b)
f (a)
a
b
x
10.
2Отсутствует дифференцируемость на (a,b).
y f (x)
y
f (a)
a
f (b)
b
x
11.
3f (a) f (b)
f (b)
y
f (a )
y f (x)
a
b
x
12.
Пусть функция y=f(x) удовлетворяетследующим условиям:
1. Непрерывна на отрезке [a,b].
2. Дифференцируема на интервале (a,b).
13.
Тогда внутри отрезка существует покрайней мере одна такая точка ξ, в
которой производная функции равна
частному от деления приращения
функции на приращение аргумента на
этом отрезке:
f (b) f (a)
f ( )
b a
14.
Введем новую функцию g(x):f (b) f (a)
g ( x) f ( x)
( x a)
b a
Эта функция удовлетворяет всем условиям
теоремы Ролля:
Она непрерывна на [a,b], дифференцируема на
(a,b) и на концах отрезка принимает равные
значения:
f (b) f (a)
g (b) f (b)
(b a)
b a
15.
g (b) f (b) f (b) f (a) f (a)f (b) f (a)
g (a) f (a)
(a a)
b a
g ( a) f (a)
Следовательно, по
точка
g (a) g (b)
теореме Ролля существует
( a, b )
такая, что
0
g ( ) 0
16.
илиf (b) f (a)
g ( ) f ( )
( a) 0
b a
f (b) f (a)
g ( ) f ( )
0
b a
отсюда
f (b) f (a)
f ( )
b a
17.
Эту теорему часто записывают в виде:f ( ) (b a) f (b) f (a)
18.
yB
y f (x)
A
a
b
x
19.
Если перемещать прямую АВпараллельно начальному положению,
то найдется хотя бы одна точка
( a, b )
в которой касательная к графику
функции y=f(x) и хорда АВ, проведенная
через концы дуги АВ будут
параллельны.
20.
Если производная функции y=f(x) равна 0на некотором промежутке Х, то эта
функция постоянна на всем
промежутке.
21.
Возьмем на промежутке Х [a,х], тогда по теоремеЛагранжа
f ( ) ( x a) f ( x) f (a)
По условию теоремы f ( ) 0
0 ( x a ) f ( x) f ( a )
0 f ( x) f ( a )
То есть
f ( x) f ( a )







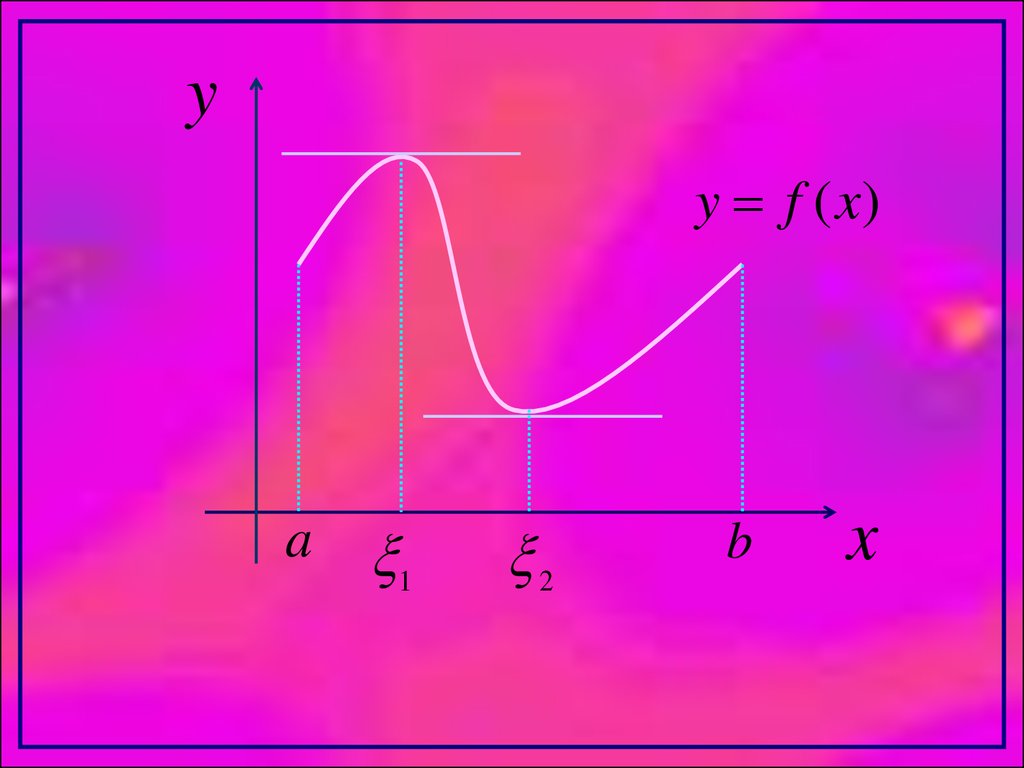












 Математика
Математика








