Похожие презентации:
Гипербола
1.
ГИПЕРБОЛОЙ называется множествоточек плоскости, абсолютная величина
разности расстояний от каждой из которых
до двух заданных точек, называемых
фокусами, есть величина постоянная
(меньшая, чем расстояние между фокусами)
2.
yM ( x, y)
2b
F1
F2
2a
x
3.
Введем обозначения:F1 (c;0)
F2 ( c;0)
F1F2 2c
a – действительная полуось гиперболы
b – мнимая полуось гиперболы
Для любой
гиперболе,
равенство:
точки М(х,у), принадлежащей
по определению выполняется
F1M MF2 2a
4.
Прямые, проходящие через начало координат иимеющие угловые коэффициенты
b
a
b
и
a
называются асимптотами гиперболы.
Асимптоты делят плоскость на 4 области, в двух
из которых расположена гипербола.
Точки гиперболы по мере удавления от оси у
приближаются к асимптотам, т.е. расстояние
между точками гиперболы и асимптотой при
увеличении х уменьшается и стремится к нулю.
5.
ТЕОРЕМАДля того, чтобы точка М(х,у)
принадлежала гиперболе, необходимо и
достаточно, чтобы ее координаты
удовлетворяли уравнению
x2 y2
2 1
2
a
b
где
b c a
2
2
2
2
6.
Покажем, что координаты точки, принадлежащейгиперболе, удовлетворяют уравнению (2).
Т.к. точка М(х,у) принадлежит гиперболе, то по
определению гиперболы, должно выполнятся
условие
F1M F2 M 2a
Выразим каждое расстояние по
расстояния между двумя точками:
F1 ( c;0)
M ( x; y)
формуле
F1M ( x c) y
2
2
7.
F2 (c;0)F2 M ( x c) y
2
M ( x; y)
2
Тогда:
F1M F2 M ( x c) y ( x c) y 2a
2
2
2
2
( x c) y ( x c) y 2a
2
2
2
2
8.
( x c) y 2a ( x c) y2
2
2
2
Возводим в квадрат обе части выражения:
( x c) y 4a 4a ( x c) y ( x c) y
2
2
2
2
2
2
2
x 2cx c 4a 4a ( x c) y x 2cx c
2
2
2
2
2
a ( x c) y cx a
2
2
2
2
2
9.
Возводим в еще раз квадрат:a 2a cx c x a x 2a xc a c a y
4
2
2
2
2
2
2
2 2
c x a x a y a c a
2
2
2
2
2
2
2 2
4
x (c a ) a y a (c a )
2
2
2
b
2
2
2
2
Делим все выражение на
2
2
b
2
ab
2
2
2
2
10.
22
x
y
1
2
2
a
b
11.
Отношение фокусного расстояния кдлине действительной оси гиперболы
называется
ЭКСЦЕНТРИСИТЕТОМ
2c c
2a a
12.
c aДля гиперболы
c
a b
b
2
1 2
2
a
a
a
2
2
2
2
2
Следовательно, для гиперболы
1
Чем меньше отношение мнимой и действительной
полуосей, тем меньше эксцентриситет и тем более
гипербола будет прижата к оси х, и наоборот.








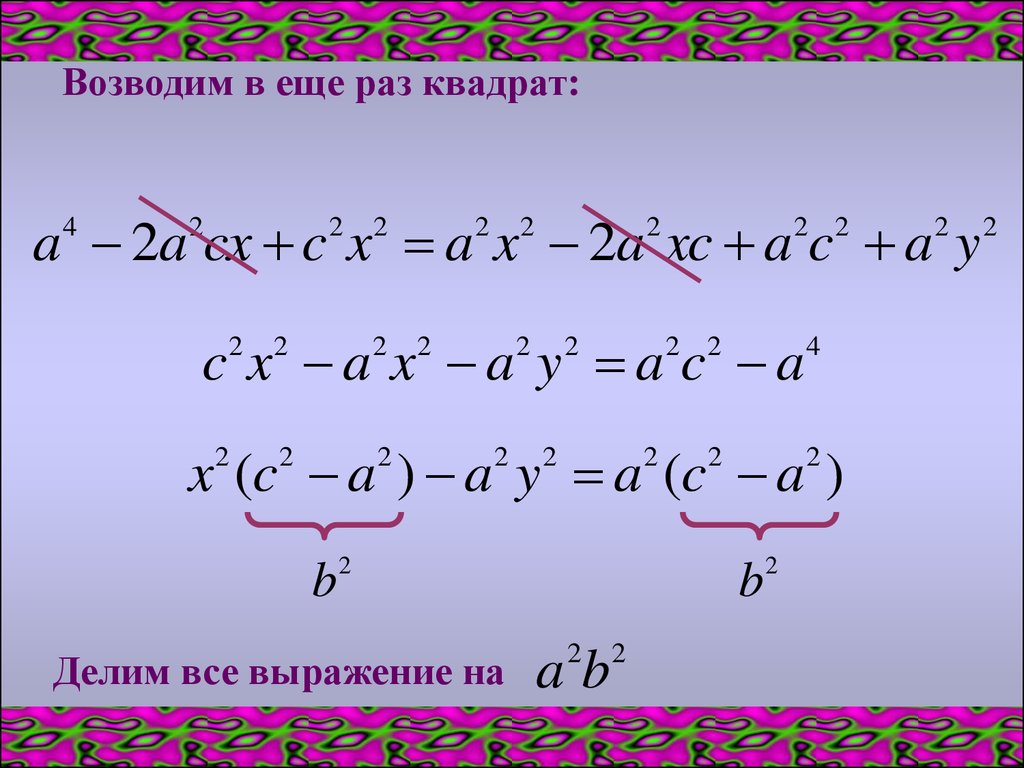



 Математика
Математика








