Похожие презентации:
Кривые второго порядка
1. Кривые второго порядка
Общее уравнение кривой второго порядкаОкружность
Эллипс
Гипербола
Парабола
2. Общее уравнение кривой второго порядка
К кривым второго порядка относятся: эллипс, частным случаемкоторого является окружность, гипербола и парабола.
Они задаются уравнением второй степени относительно x и y:
Ax 2 2Bxy Cy 2 2Dx 2Ey F 0
Общее уравнение кривой
второго порядка
В некоторых частных случаях это уравнение может определять
также две прямые, точку или мнимое геометрическое место.
3. Окружность
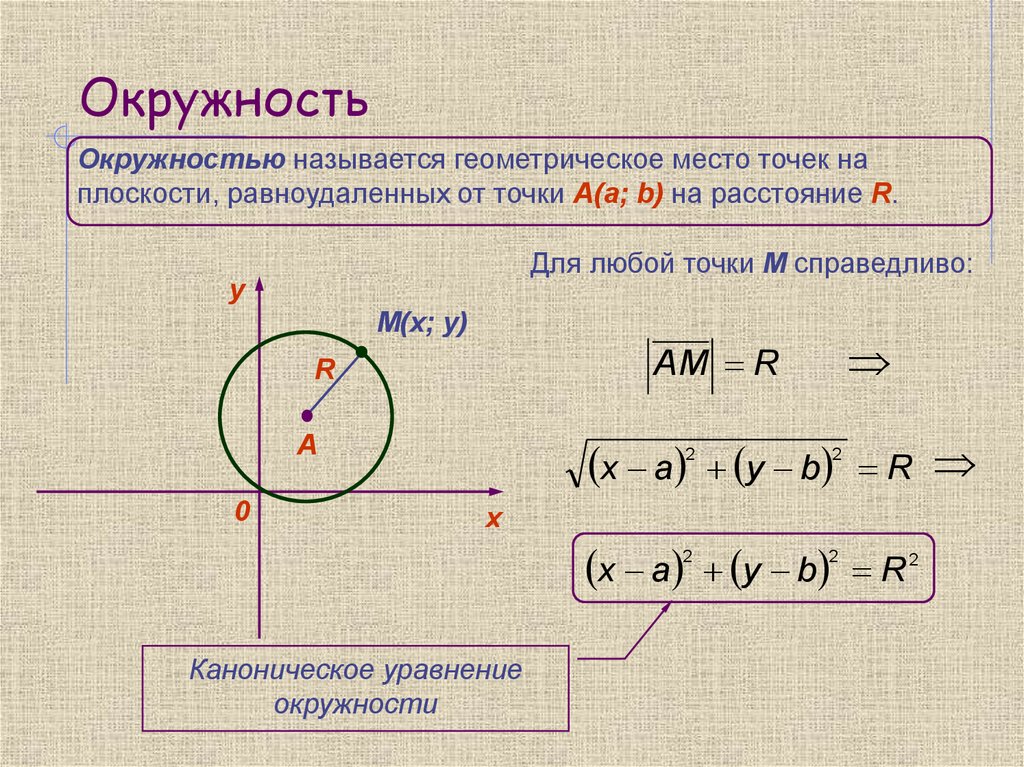
Окружностью называется геометрическое место точек наплоскости, равноудаленных от точки А(a; b) на расстояние R.
Для любой точки М справедливо:
y
М(x; y)
А
0
AM R
R
2
x a y b
R
2
x a y b
R2
2
х
2
Каноническое уравнение
окружности
4. Эллипс
Эллипсом называется геометрическое место точек, суммарасстояний от каждой из которых до двух точек той же плоскости
F1 и F2, называемых фокусами, есть величина постоянная,
равная 2а.
Зададим систему координат и начало координат выберем в
середине отрезка [F1 F2]
r1 r2 2a
y
F1( c; 0);
M(x; y)
r2
r1
r1 F1M
x c
r2 F2M
x c
2
y2
F
F1
-c
F2 (c; 0)
0
c2
х
2
y2
5. Эллипс
x c2
x c
y2
2
y 2 2a
x c y 2a 2 a x xc c y y
2
2
x c
2
4a
y 4a 4a
2
x c
2
2
2
2
2
22
x c
2
y
2
x c
2
22
2
a cb x a y a (ba : (ca22)b2 )
22
2
2
2
x2 y 2
2 1
2
a
b
2
22
a 2 x 2 2a 2 xc a 2c 2 a 2 y 2 a 4 2a 2 xc x 2c 2
2
y2
y 2 4a 2 x 2 2 xc c 2 x 2 2 xc c 2
22
2
4a
a xx
cc
yy 4a
4
xc
a xc : 4
22
2
2
b2
Каноническое уравнение
эллипса
6. Эллипс
yb
Fмалая
F полуось
2c
1 2
F
F1
-c
M(x; y)
r2
r1
-а
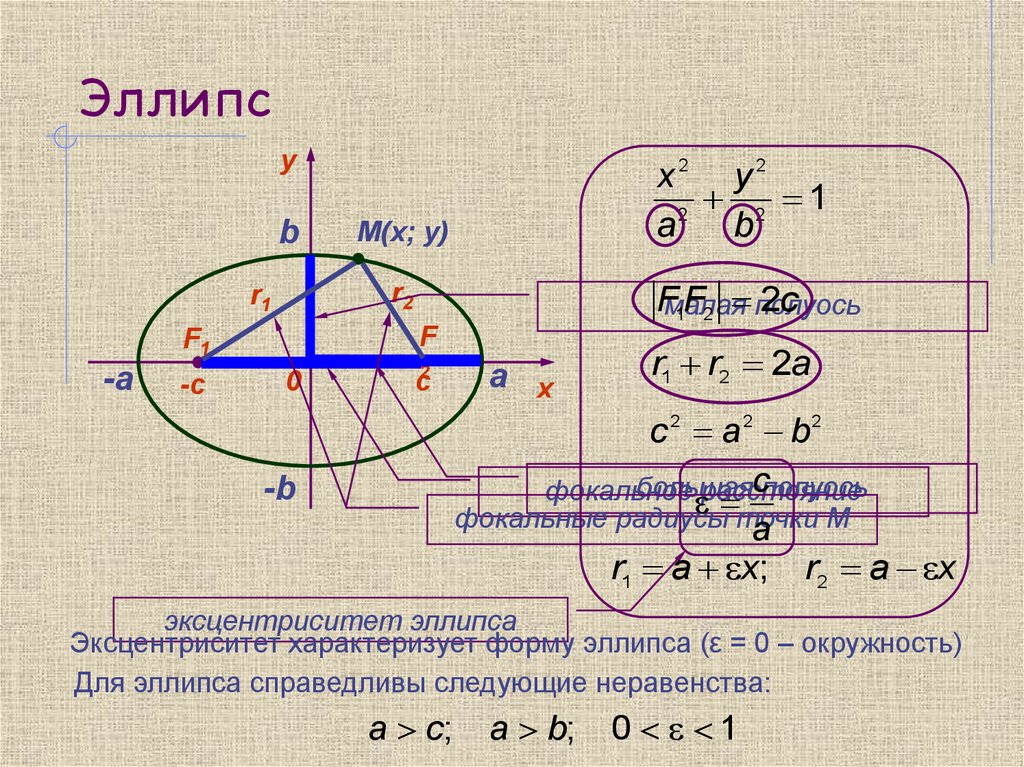
x2 y 2
2 1
2
a
b
0
c2
а х
r1 r2 2a
c 2 a2 b2
cполуось
большая
фокальное
расстояние
фокальные радиусы точки
М
a
r1 a x; r2 a x
-b
эксцентриситет эллипса
Эксцентриситет характеризует форму эллипса (ε = 0 – окружность)
Для эллипса справедливы следующие неравенства:
a c;
a b;
0 1
7. Пример
Составить уравнение эллипса, фокусы которого лежат вточках F1(-4; 0) F2(4; 0), а эксцентриситет равен 0,8.
c 4
c
0.8
a
c 2 a2 b2
b 2 a 2 c 2 25 16 9
Каноническое уравнение эллипса:
y
3
-5
0
-3
c
4
a
5
0 .8
5 х
x2 y 2
1
25 9
b 3
8. Гипербола
Гиперболой называется геометрическое место точек, разностьрасстояний от каждой из которых до двух точек той же плоскости
F1 и F2, называемых фокусами, есть величина постоянная,
равная 2а.
y
r1 r2 2a
M(x; y)
F1( c; 0);
r1
F
F1
-c
0
2
c
r2
х
F2 (c; 0)
r1 F1M
x c
r2 F2M
x c
2
2
y2
y2
9. Гипербола
x c2
y2
x c
2
y 2 2a
x c
2
y2
x c
2
y 2 2a
После тождественных преобразований уравнение примет вид:
c ab2 2 x 2 a2 y 2 a2 (bc22 : (a22b) 2 )
2
x2 y 2
2 1
2
a
b
b2
Каноническое уравнение
гиперболы
10. Гипербола
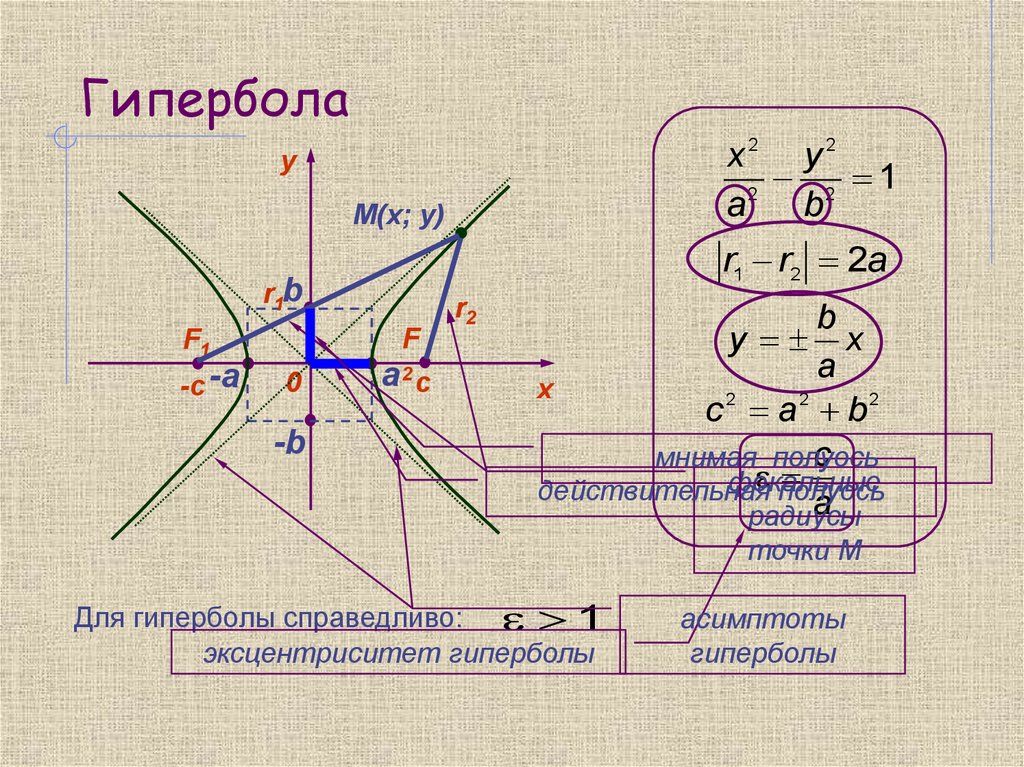
x2 y 22 1
2
a
b
y
M(x; y)
r1 r2 2a
r1b
F
F1
-c -а
0
-b
а2 c
r2
b
y x
a
х
c 2 a2 b2
c
мнимая полуось
полуось
фокальные
действительная
a
радиусы
точки М
Для гиперболы справедливо: 1
эксцентриситет гиперболы
асимптоты
гиперболы
11. Пример
Составить уравнение гиперболы, проходящей через точкуА(6; -4), если ее асимптоты заданы уравнениями:
6
y
x
3
b
6
a
3
3b 6a
x2 y 2
62 ( 4)2
2 1 2
1
Точка А лежит на гиперболе
2
2
a
b
a
b
36b 2 16a 2 a 2b 2
2
3b 6a
b2 a2
Решим систему:
3
2
2
2 2
2
2
2 2
36b 16a a b
36
b
16
a
a
b
2 2
2
2
b a
a 2 3
a
12
3
2
2
b 8
b 2 2
24a 2 16a 2 a 4
3
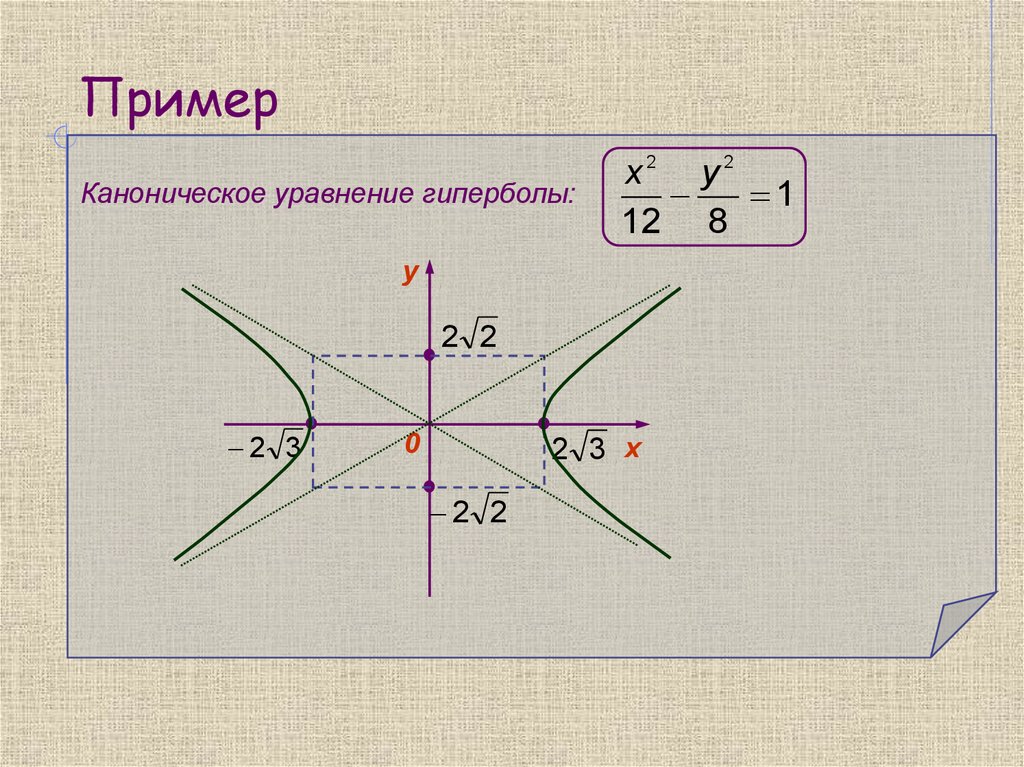
12. Пример
Каноническое уравнение гиперболы:x2 y 2
1
12 8
y
2 2
2 3
2 3 х
0
2 2
13. Парабола
Параболой называется геометрическое место точек наплоскости, для каждой из которых расстояние до некоторой
фиксированной точки той же плоскости
p
p
x
,
называемой
фокусом,
равно
расстоянию
до
прямой:
F ( ;0)
2
2
y
r d
d
M(x; y)
r
p
2
0
p
2
p 0
2
F
p
F ( ; 0)
2
х
p
r FM x y 2
2
d x
p
2
14. Парабола
каноническоеуравнение параболы
2
p
p
2
x
y
x
2
2
2
2
p
p
x 2 px
y 2 x 2 px
4
4
y
y 2 2px
директриса параболы
p
r x
d
M(x; y)
r
2
фокальный радиус
F
p
2
0
p
2
х
фокус параболы
Эксцентриситет параболы: 1
15. Преобразование общего уравнения к каноническому виду
Ax 2Bxy Cy 2Dx 2Ey F 02
2
Составим из коэффициентов уравнения два определителя:
A B
B C
A B D
B C E
D E
Дискриминант
уравнения
F
Дискриминант старших
0
членов уравнения 0
0
Эллипс
Точка
0
Гипербола
Пара пересекающихся
прямых
0
Парабола
Пара параллельных
прямых
16. Преобразование общего уравнения к каноническому виду
Общее уравнение кривой называется пяти-членным, если 2Bxy=0:Ax 2 Cy 2 2Dx 2Ey F 0
Приведение пяти-членного уравнения к каноническому виду
рассмотрим на примере:
16 x 2 25y 2 32x 50y 359 0
16x 2 32x 25y 2 50y 359 0
16 x 2 2x 25 y 2 2y 359
16 x 2 2x 1 25 y 2 2y 1 359 16 25
16 x 1 25 y 1 400
2
2
x 1
2
25
y 1
2
16
1
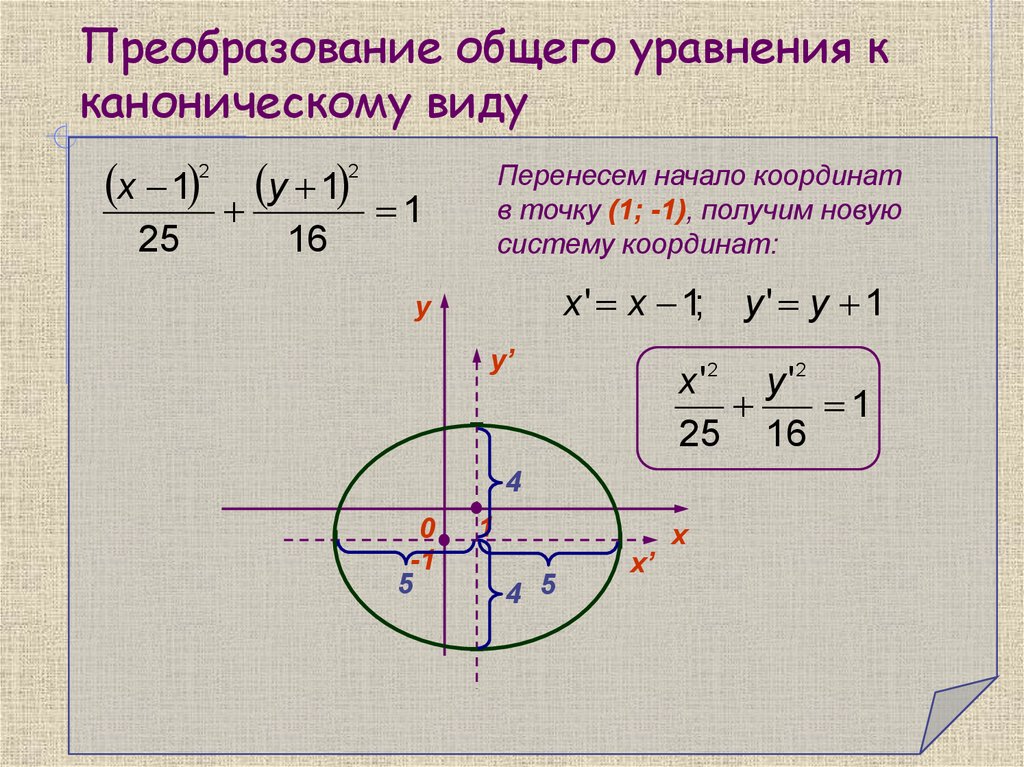
17. Преобразование общего уравнения к каноническому виду
x 12
25
y 1
Перенесем начало координат
в точку (1; -1), получим новую
систему координат:
2
16
1
x ' x 1;
y
y’
x '2 y '2
1
25 16
4
0
-1
5
1
4 5
y' y 1
x’
х
18. Преобразование общего уравнения к каноническому виду
Если слагаемое 2Bxy в общем уравнении не равно нулю, то дляприведения уравнения к каноническому виду необходимо
повернуть оси координат на угол α. При этом зависимость между
старыми координатами и новыми определяются формулами:
x x ' cos y ' sin
y x ' sin y ' cos
Угол α удовлетворяет условию:
2B
tg 2
A C
В случае, если A = C, то
2 90 0 45 0













 Математика
Математика








