Нахождение оптимального сочетания пар объектов по заданным параметрам

1. НАХОЖДЕНИЕ ОПТИМАЛЬНОГО СОЧЕТАНИЯ ПАР ОБЪЕКТОВ ПО ЗАДАННЫМ ПАРАМЕТРАМ

УГАТУ, ФИРТ
Студентка 3 курса:.
Руководитель: к.т.н. Верхотурова Г.Н.
Уфа–2013

2.

АКТУАЛЬНОСТЬ
Существует проблема нахождения оптимального
сочетания пар объектов по заданным параметрам
Например, подбор игроков в команду, по
определенным качествам или выбор в
соответствии с позицией рейтинга наиболее
привлекательного задания (темы дипломных
проектов в группе, задания на курсовую работу)
Эти задачи могут быть решены с помощью
теории графов, а именно, нахождения
максимального паросочетания в двудольном
графе

3.

ПРИМЕНЕНИЕ ТЕОРИИ ГРАФОВ
Теория графов находит применение, например, в
геоинформационных системах (ГИС)
Существующие или вновь проектируемые дома,
сооружения, кварталы и т.п. рассматриваются как
вершины, а соединяющие их дороги, инженерные
сети, линии электропередач и т.п. - как рёбра
графа
Применение различных вычислений,
производимых на таком графе, позволяет,
например, найти кратчайший объездной путь
или ближайший продуктовый магазин,
спланировать оптимальный маршрут

4. ПОСТАНОВКА ЗАДАЧИ

Студентам в группе раздали темы на курсовую
работу. Чем выше рейтинг студента, тем наиболее
интересную тему он может выбрать (студенты – левая
доля графа, курсовые работы – правая доля графа)
Найти оптимальное (все студенты взяли курсовую
работу) сочетание пар объектов по заданным
параметрам
Создать программу, реализующую нахождение
максимального паросочетания в двудольном графе

5.

ПАРОСОЧЕТАНИЕ
Паросочетанием в графе называется такое
подмножество его рёбер, что никакие два ребра
не смежны
Максимальное паросочетание – это
паросочетание, в котором максимальное
возможное количество рёбер

6.

АЛГОРИТМ КУНА
Левую долю будем называть студентами, а правую
курсовыми работами.
Выбираем непересекающиеся рёбра произвольным
образом, пока есть такая возможность.
Построим граф, в котором от студентов ведёт только
одно ребро – к курсовой, которую они выбрали.
Назовём эти рёбра красными. Остальные рёбра
оставим прежними.
Ищем путь в графе от студента, который не выбрал
курсовую, к свободным темам, такой, что красные и
не красные рёбра в этом пути чередуются. Если
такой путь найти не удаётся, завершаем алгоритм.
Поменяем все красные рёбра в найденном пути на
не красные, а не красные – на красные.
Если ещё остались студенты и темы, возвращаемся к
п.3

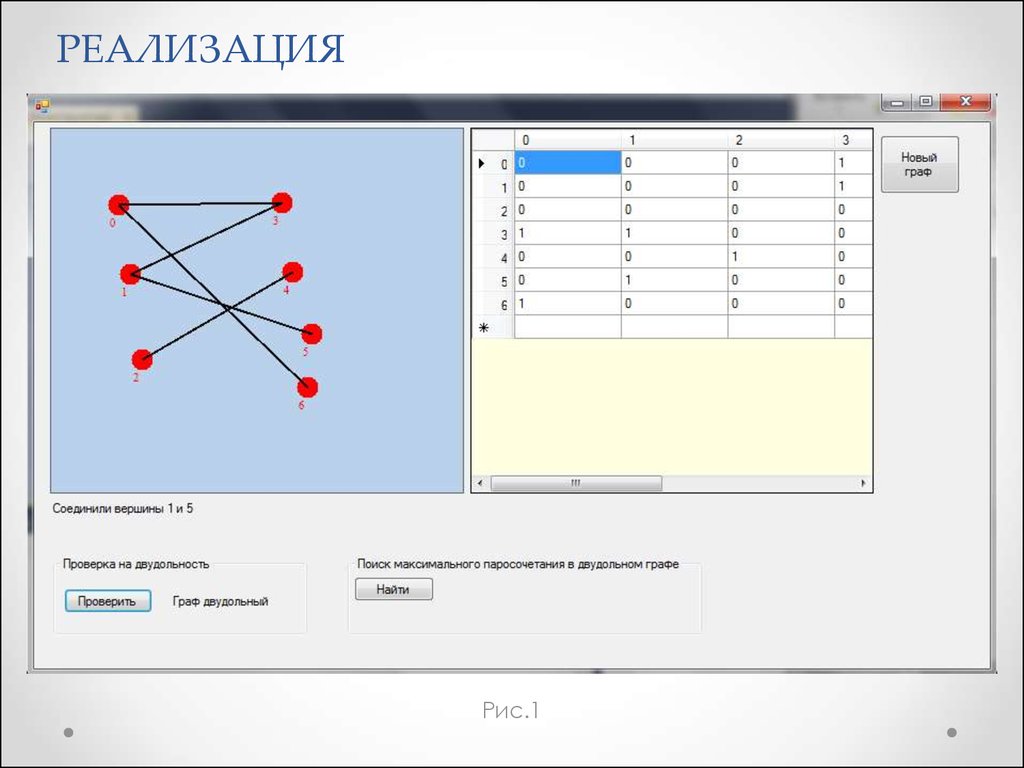
7. РЕАЛИЗАЦИЯ

Рис.1

8. РЕАЛИЗАЦИЯ

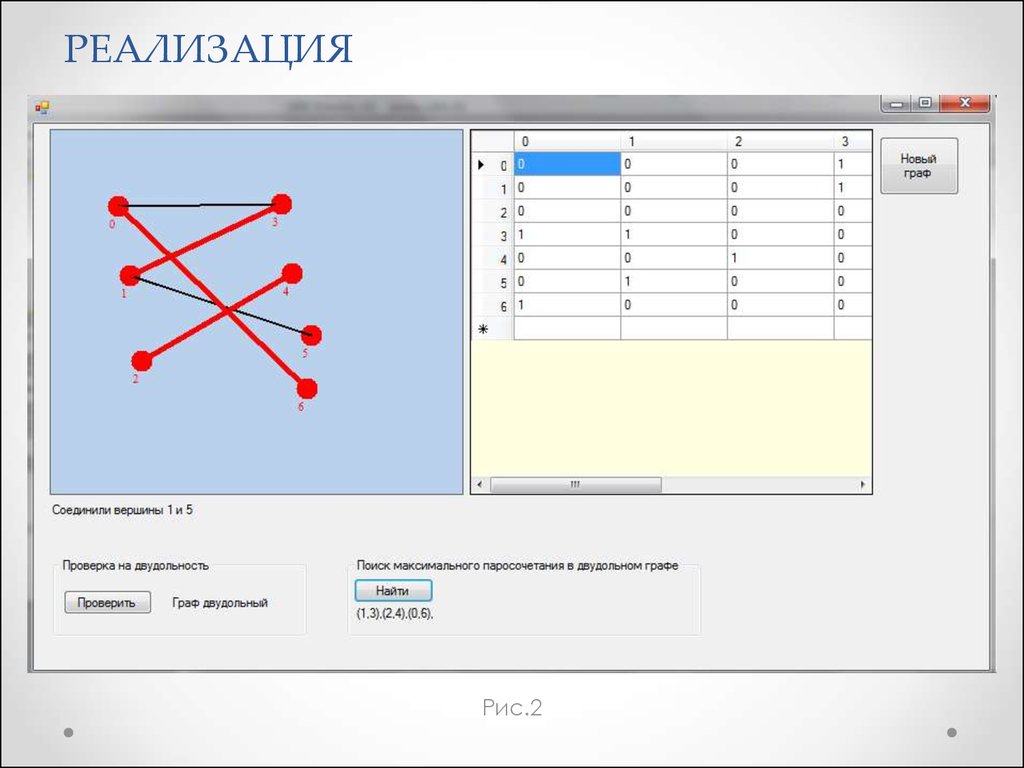
Рис.2

9.

РЕЗУЛЬТАТЫ РАБОТЫ
Создана программа на языке
программирования С++, реализующая
построение двудольного графа и
находящая максимальное паросочетание в
нем по заданному признаку
Найдено оптимальное (все студенты взяли
курсовую работу) сочетание пар объектов
по заданным параметрам

10.

СПАСИБО ЗА ВНИМАНИЕ