Похожие презентации:
Степени с рациональными показателями, их свойства
1.
Разгадайте ребуси определите тему урока:
«Степень»
2.
Государственное бюджетное профессиональноеобразовательное учреждение Свердловской области
«Талицкий лесотехнический колледж им. Н.И.Кузнецова»
Урок №8
Степени с рациональными
показателями, их свойства
Практику отправить на проверку , тест не надо он
дан для самопроверки.
Выполнила преподаватель
Кудина Л.В.
Талица 2015
3.
«Пусть кто-нибудьпопробует вычеркнуть
из математики
степени, и он увидит,
что без них далеко не
уедешь»
М.В.Ломоносов
4.
Цели урока:-обобщить и систематизировать знания по
данной теме;
-закрепить и усовершенствовать навыки
применения свойств степеней;
-развить навыки выполнения простейших
преобразований содержащих корни.
Задачи урока:
- повышение вычислительной культуры студентов;
- проверка уровня усвоения темы;
-развитие интереса к предмету;
- воспитание навыков контроля и самоконтроля.
5.
Определение степени числас натуральным показателем.
Степенью действительного числа а с
натуральным показателем п называется
произведение п множителей, каждый из
которых равен а.
n
1
a a a a ... a
5∙5∙5∙5∙5∙5∙5= 57
5 – основание степени,
7- показатель степени
a a
6.
an
Читается:
«а в степени n»
«n- я степень числа а».
По определению степени:
а¹ = а, а²=а ∙ а, а³= а ∙ а ∙ а.
n
а = а ∙ а…а
Проговорить:
4
n раз
3 = 3 ∙ 3 ∙ 3 ∙ 3=81;
0³=0 ∙ 0 ∙ 0= 0;
(-6)³=(-6) ∙(-6) ∙(-6)=-216;
9¹=9.
7.
Степеньс отрицательным показателем
Если п- целое отрицательное число,
причём α ≠ 0, то
1
a n
a
0
a 1
n
а
п
1
п
а
Степень числа 0 определена только
для положительных показателей.
8.
Определение степени числас рациональным показателем.
Степенью действительного числа а с
рациональным показателем
т
r
п
(m- целое, n-натуральное) называется
число
п
а
т
а
т
п
9.
Представьте степень с дробнымпоказателем
в виде корня:
2
1.
2
2.
1
3
3.
4.
5.
3
3
3
8 1
1, 5
2
1
3
1
3
2
1
3
3
не имеет смысла
5а 2 5 а
2
2
3
х у 3 х у
10.
Представьте корень в видестепени с дробным показателем:
1
2
4
9
2.
7
7
а а
1
3
3.
3 2 2
2
1
1.
4.
5.
b b b b b
2
х у
3
4
9
1, 5
x y x y
3
2
1,5
11.
Свойства степеней1.a a a
n
m
n m
2.a : a a
n
m
3. a
n m
a
b 0
n m
4. a b a b
n
n
a 0
n m
n
a
a
5. n
b
b
n
n
12.
Упростить выражения:(устно)
1) х
5
х
6
=
х
11
3)( у) ( у) = у
3
5
2)
8
х х х х
3
6
7
4
=
х
4) ( у) ( у) = у
2
3
х
6) 2 = х
х
3
5
5) х х = х
t9
3
3 2 7
2
4
2
3
=
t
=
8) х у а у х х а у
7) t 6
2
5
2
а
а
а
6
5
=а
9) х ( х х ) = 1 10)
8
4
4
а а а
3
2
20
13.
Упростить выражения:(устно)
(а ) = а
3 4
5 8
(х ) х = х
4 5
12
(b )
6
=b
34
b
3
4
t t 5 = t 10
( 5 )
t
7
27
9
y 2
10
( 4) = y
y
3 2 9
( 7 ) = b14
b
(k 2 k 8 k 5 k )10 (k 2 k )2 = k 166
(3 xy)3 27 x
2
2
5 =
y
x y
14.
Решить примеры самостоятельно:1)a a b : a
2) 4 49 7 : 1966
3) 499 312 : 3 49 9
5
4
4 32
4) 10
8
3
4
125 0,2
5)
2
25
6
3
9
15.
Проверьте правильность решений:1)a a b : a a 4 a 5 b 5 : a 9
5
4
9
a b : a a b 1 b b
9
5
0
9
5
5
5
2) 4 49 : 196 196 : 196 196
7
7
6
3) 49 3 : 3 49
9
12
9
6
499 312
3
9 9 3
3 49
27
16.
4 322 2
4) 10
3 10
8
2
6
2
27 30
27
2 2
2
30
30
2
2
1 1
3
2 3
2
8
3
2 6
5 3
12
15
4
1
5
3
4
9
1
125 0,2
5
5
5
5)
2
2
2
4
25
5
5
3 3
4
5
17.
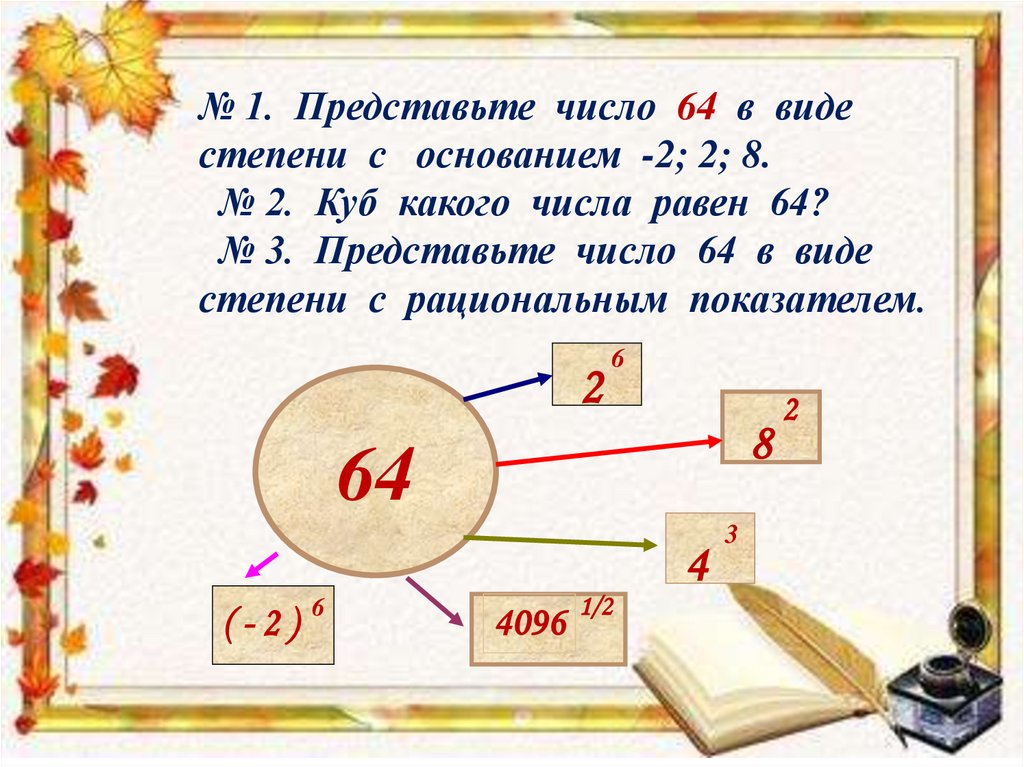
№ 1. Представьте число 64 в видестепени с основанием -2; 2; 8.
№ 2. Куб какого числа равен 64?
№ 3. Представьте число 64 в виде
степени с рациональным показателем.
2
6
8
64
4
(-2)
6
4096
1/2
3
2
18.
Самостоятельная работаВариант 1
1)
2)
1)
18 2
3
Вариант 2
25
5
11 )
2)
(-2
)
∙
54 32 8 162
6
3)
2 2
4) (2- 3 )
32
2
3) ( 2 3)( 2 3)
4) 36а 3 81а 5
при а =1/2
1
3
5) -0,064 ∙ 0,49
1
2
1
3
3
4
5) 125 ∙ 16 -36
1
2
19.
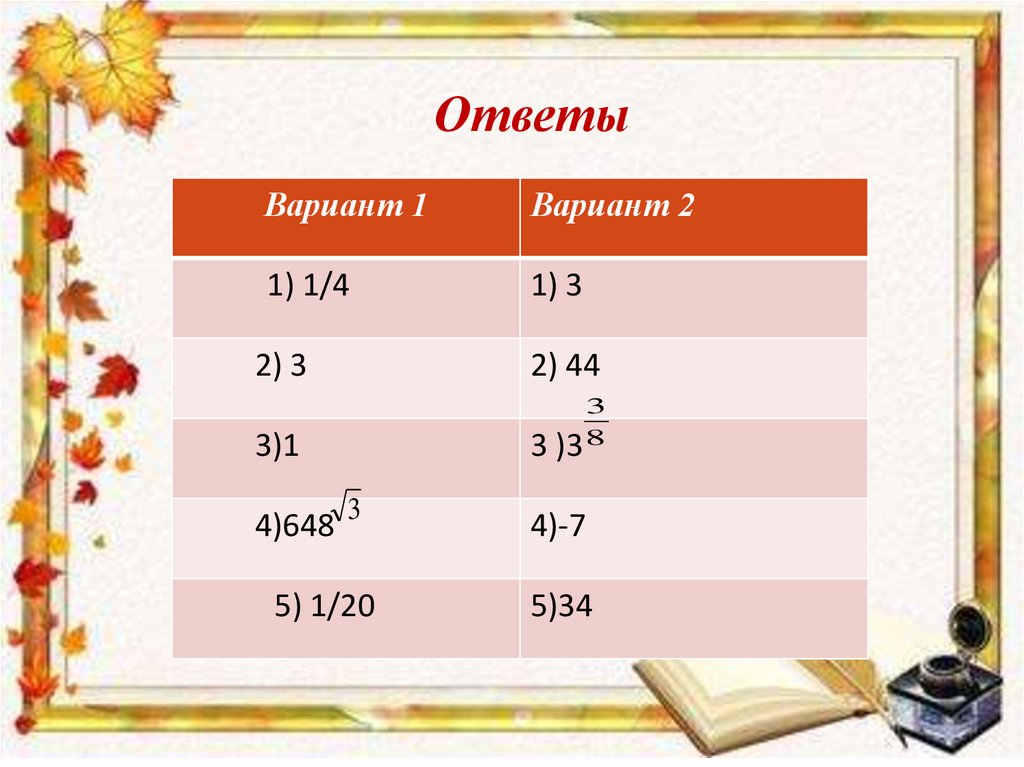
ОтветыВариант 1
Вариант 2
1) 1/4
1) 3
2) 3
2) 44
3
)3 8
3)1
3
4)648 3
4)-7
5) 1/20
5)34
20.
Оформление практики.1.В тетради писать № Урока, тему.
2.Вариант
3.Задание (Текст задания)
4.Выбрать правильные ответы.
21.
Практика (отправить на проверку)Вариант-1
1. Для каждого выражения из верхней строки укажите
тождественно равное ему выражение из нижней строки
А) а-8 ∙ а2; Б) а-8:а2; В) (а-8)2
1)а-16; 2) а-10; 3) а-6; 4) а-4
Ответ: АБВ-
2. Представьте выражение х -8 ∙ х 10:х 4 в виде степени с
основанием х
1)х8; 2) х -2; 3) х--6; 4) х 6;
Вариант-2
1.Для каждого выражения из верхней строки укажите
тождественно равное ему выражение из нижней строки
А) b-6:b-2; Б) (b-6)-2 В) b-6 ∙ b-3;
1) b12; 2)b-2; 3) b-4 ; 4)b-9;
Ответ: АБВ2.Представьте выражение а8 :а4 ∙ а-9 в виде степени с
основанием а
1)а4; 2) а7; 3) а-13; 4) а-5;
22.
Любопытные фактыиз мира степеней
нервных клеток и
Наш мозг состоит из 2 ∙
способен ежедневно запоминать 8,6 ∙
единиц информации. К концу жизни наша
память может хранить около
единиц
информации.
23.
Хотя мы и используем арабскиецифры, но древние славяне тоже
умели записывать большие числа,
для этого у них были
специальные названия для
3
большого счета: «Тысяща»-10
«Тьма»-10 6
«Легион»-1012
«Леорд»-10 24
Ворон»-10 48 49
«Колода»-10
24.
Степень с основанием10 применяетсяпри записи больших чисел:
Миллиард
109
Септиллион
1042
Биллион
1012
Септиллиард
1045
Биллиард
1015
Октиллион
1048
Триллион
1018
Октиллиард
1051
Триллиард
1021
Нониллион
1054
Квадриллион
1024
Нониллиард
1057
Квадриллиард 1027
Дециллион
1060
Квинтиллион 1030
Дециллиард
1063
Гугол
Вигинтиллион
10100
10120
Вигинтиллиард
10123
Центиллион
10600
Квинтиллиард 1033
Секстиллион
1036
Секстиллиард 1039
25.
Источники:Учитель математики Филобок Т.В. «Степень с натуральным,
целым и рациональным показателем. Свойства степеней».
http://ppt-online.org/9261 Удивительный мир степеней.























 Математика
Математика








