Похожие презентации:
«Теорема о четырёх красках»
1.
«Теорема о четырёх красках»Автор: учащийся 7а класса Гладченко Макар
Учитель: Лопатина И.С.
2022
2.
Цель:узнать, что такое теорема о четырех красках
3.
Задачи:Изучить историю теоремы о четырех
красках.
Преобразовать теорему в графы.
Познакомиться с инструкцией игры
“Четыре краски”.
4.
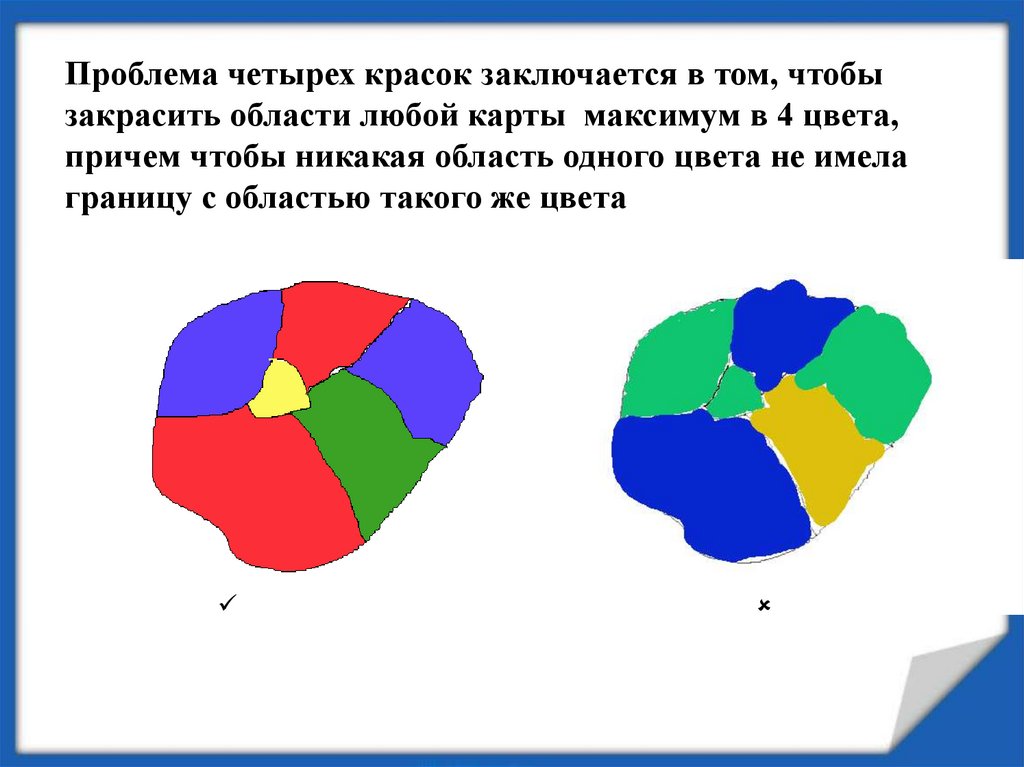
Проблема четырех красок заключается в том, чтобызакрасить области любой карты максимум в 4 цвета,
причем чтобы никакая область одного цвета не имела
границу с областью такого же цвета
5.
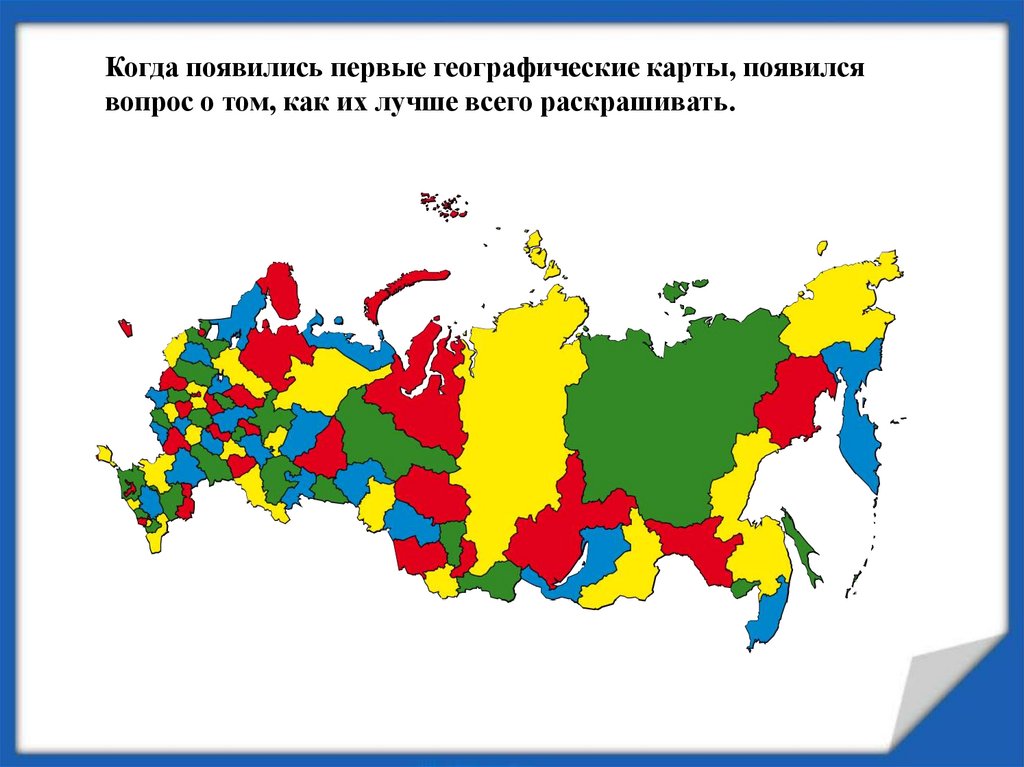
Когда появились первые географические карты, появилсявопрос о том, как их лучше всего раскрашивать.
6.
В 1852 году при раскрашиваниикарты Британии студент Френсис
Гутри выдвинул эту гипотезу:
любую карту можно раскрасить
четырьмя цветами, при условии,
чтобы никакие две смежные области
(имеющие общую границу) не
оказались окрашенными в один и тот
же цвет
Проблема возникла в том, чтобы
решить, верна ли гипотеза.
(1831-1899)
7.
Альфред Кемпев 1879 опубликовал
решение проблемы по
его мнению
Перси.Дж.Хивуд.
В 1889 опровергнул это решение
8.
Питер ТэйтВ 1880 предложил еще одно доказательство проблемы четырёх
красок, которое опровергли в 1891
9.
Кеннет Аппель и ВольфгангХакен
В 1971 окончательно доказали
теорему при помощи компьютера
10.
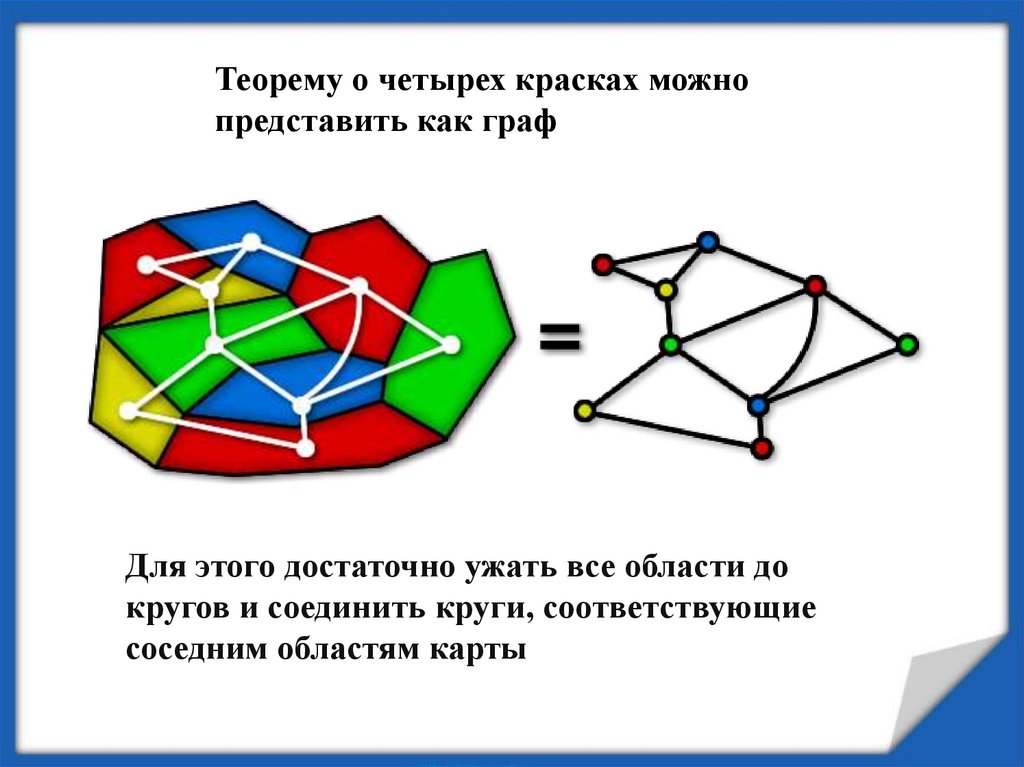
Теорему о четырех красках можнопредставить как граф
Для этого достаточно ужать все области до
кругов и соединить круги, соответствующие
соседним областям карты
11.
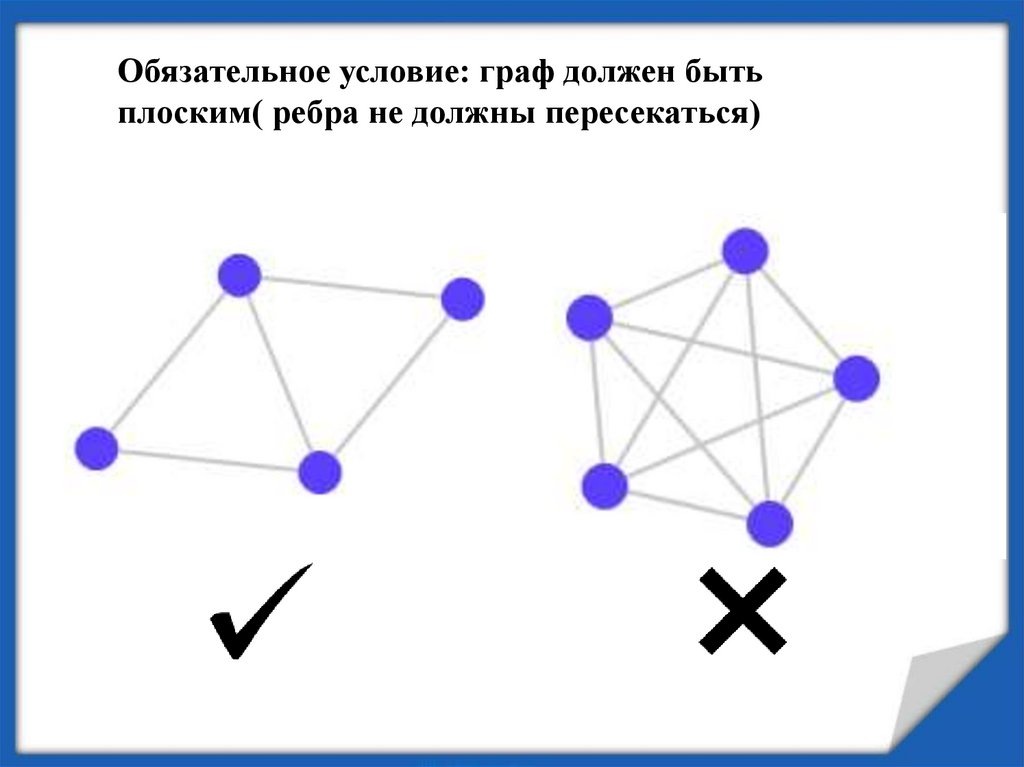
Обязательное условие: граф должен бытьплоским( ребра не должны пересекаться)
12.
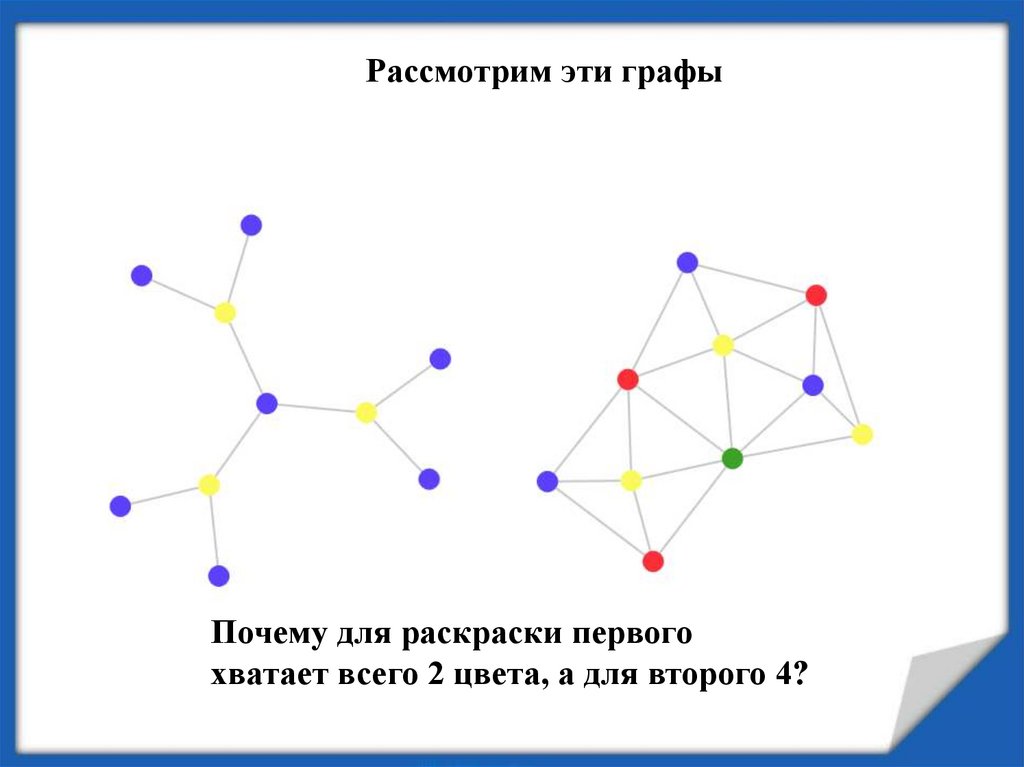
Рассмотрим эти графыПочему для раскраски первого
хватает всего 2 цвета, а для второго 4?
13.
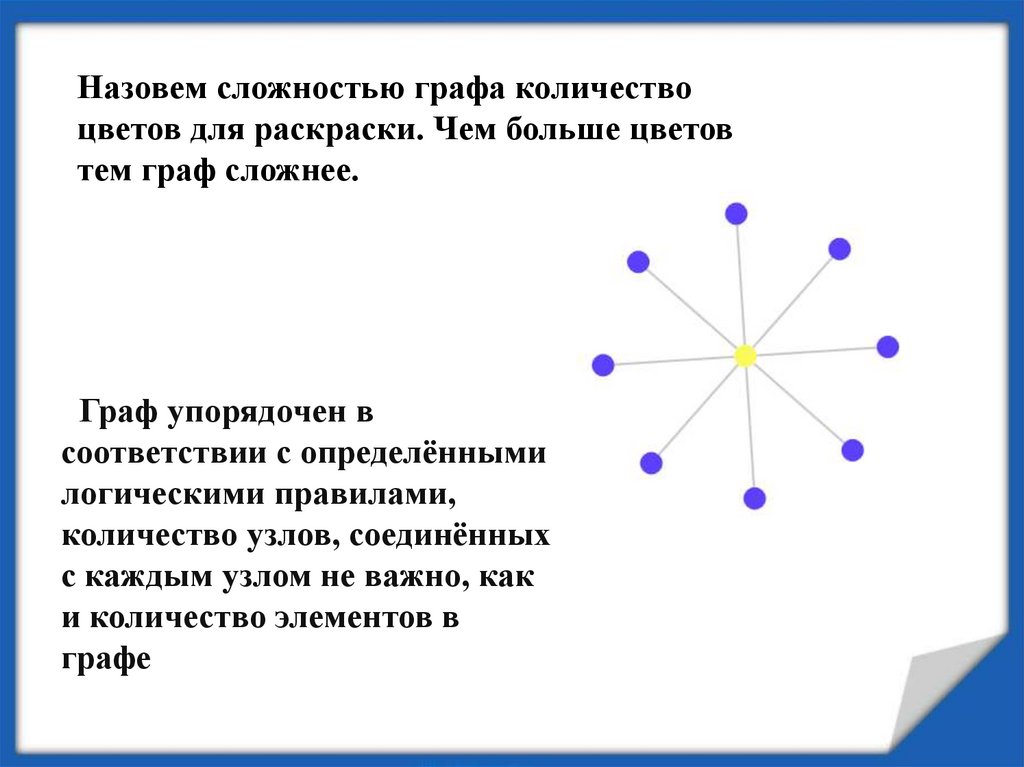
Назовем сложностью графа количествоцветов для раскраски. Чем больше цветов
тем граф сложнее.
Граф упорядочен в
соответствии с определёнными
логическими правилами,
количество узлов, соединённых
с каждым узлом не важно, как
и количество элементов в
графе
14.
15.
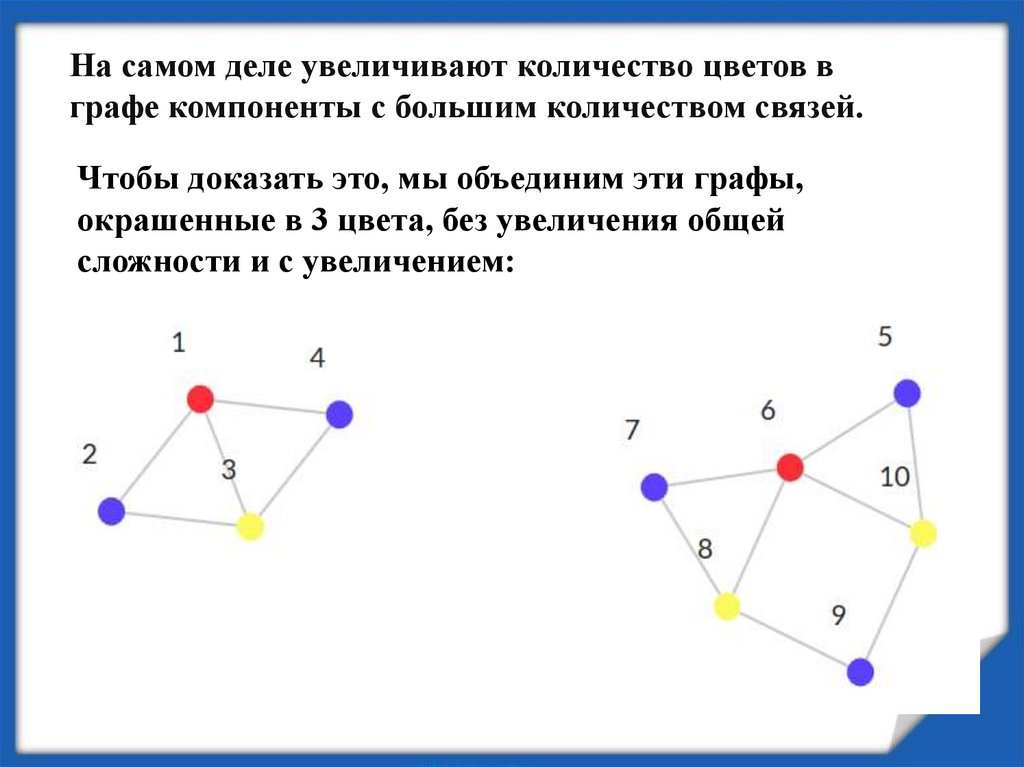
На самом деле увеличивают количество цветов вграфе компоненты с большим количеством связей.
Чтобы доказать это, мы объединим эти графы,
окрашенные в 3 цвета, без увеличения общей
сложности и с увеличением:
16.
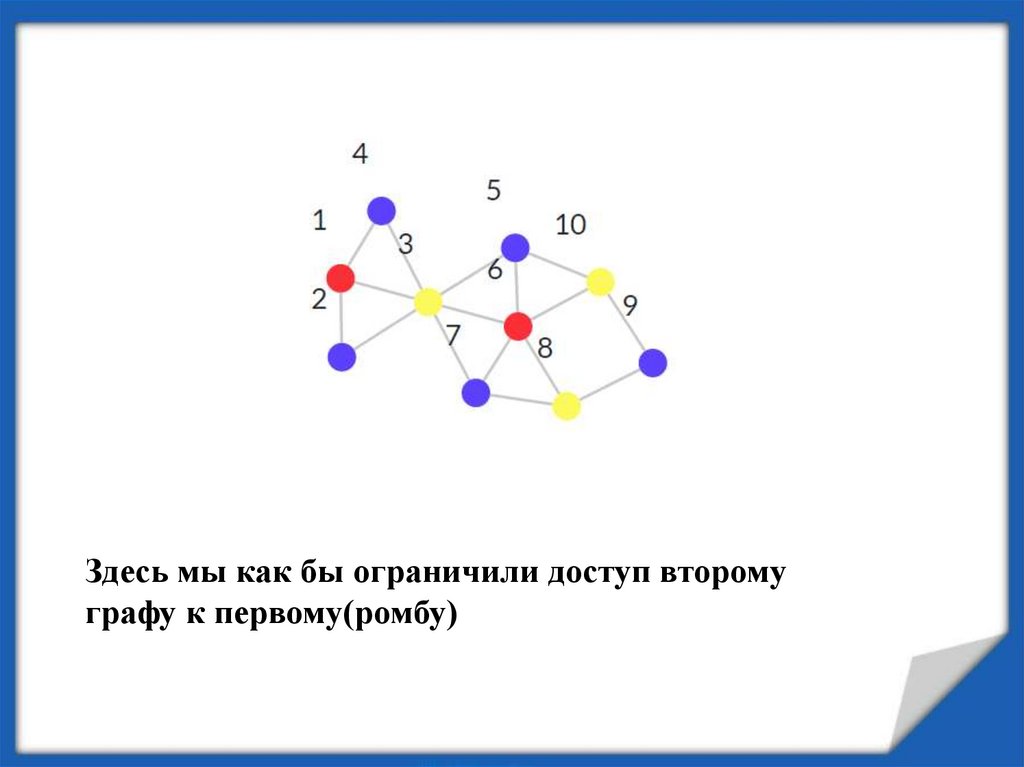
Здесь мы как бы ограничили доступ второмуграфу к первому(ромбу)
17.
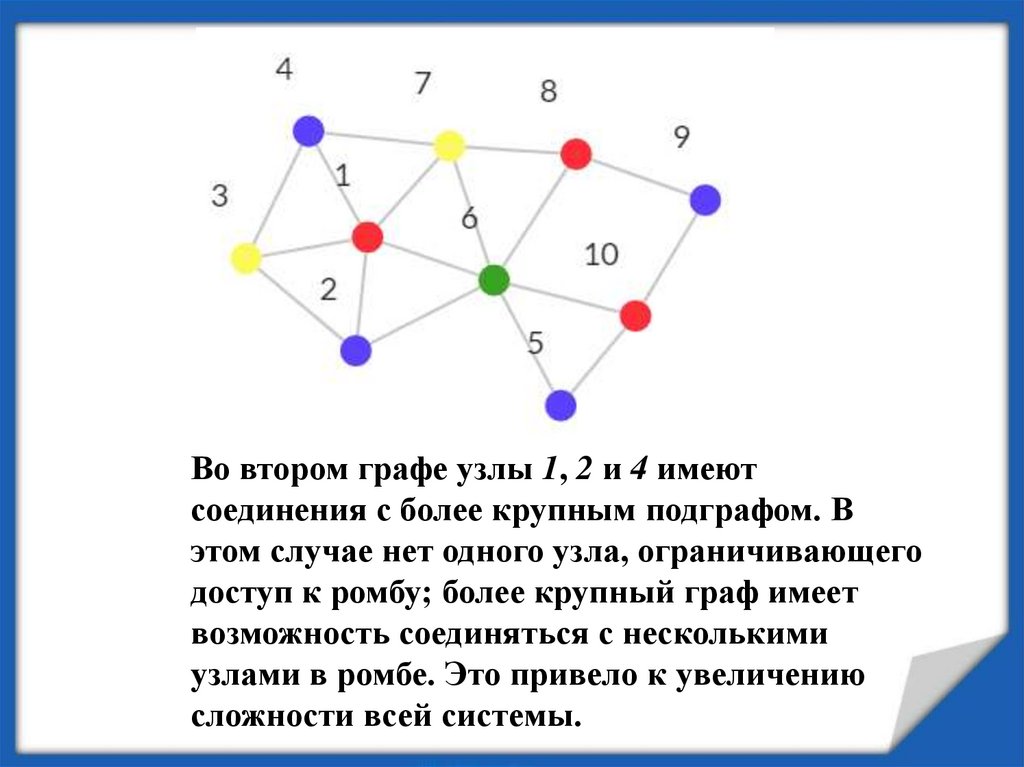
Во втором графе узлы 1, 2 и 4 имеютсоединения с более крупным подграфом. В
этом случае нет одного узла, ограничивающего
доступ к ромбу; более крупный граф имеет
возможность соединяться с несколькими
узлами в ромбе. Это привело к увеличению
сложности всей системы.
18.
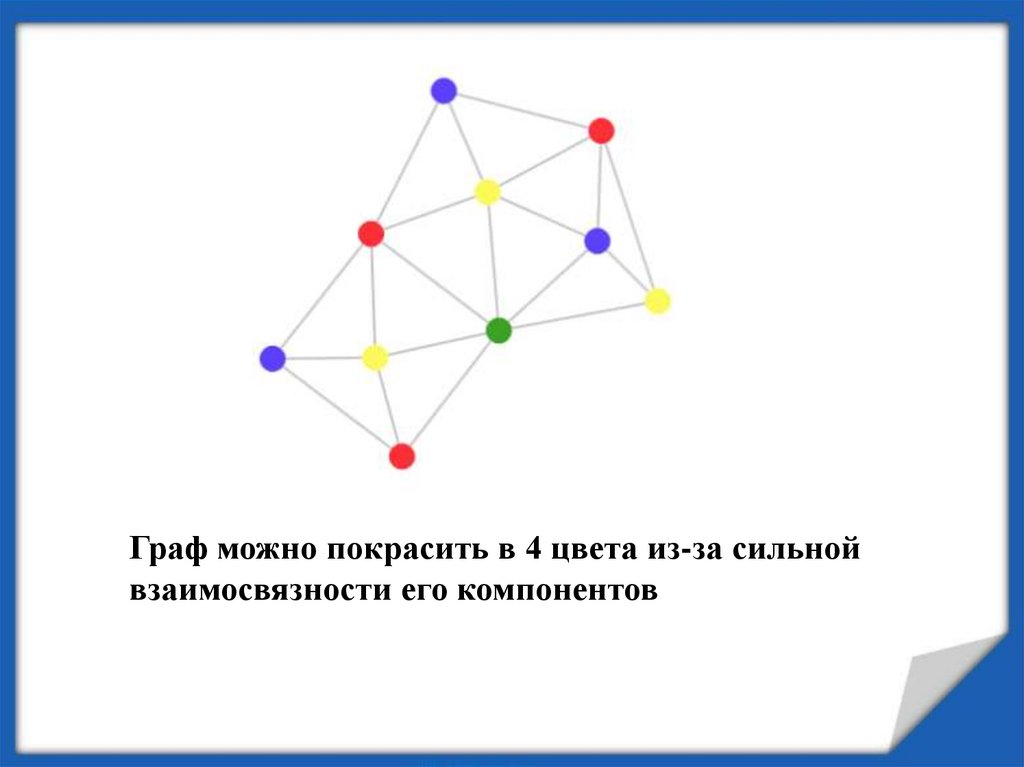
Граф можно покрасить в 4 цвета из-за сильнойвзаимосвязности его компонентов
19.
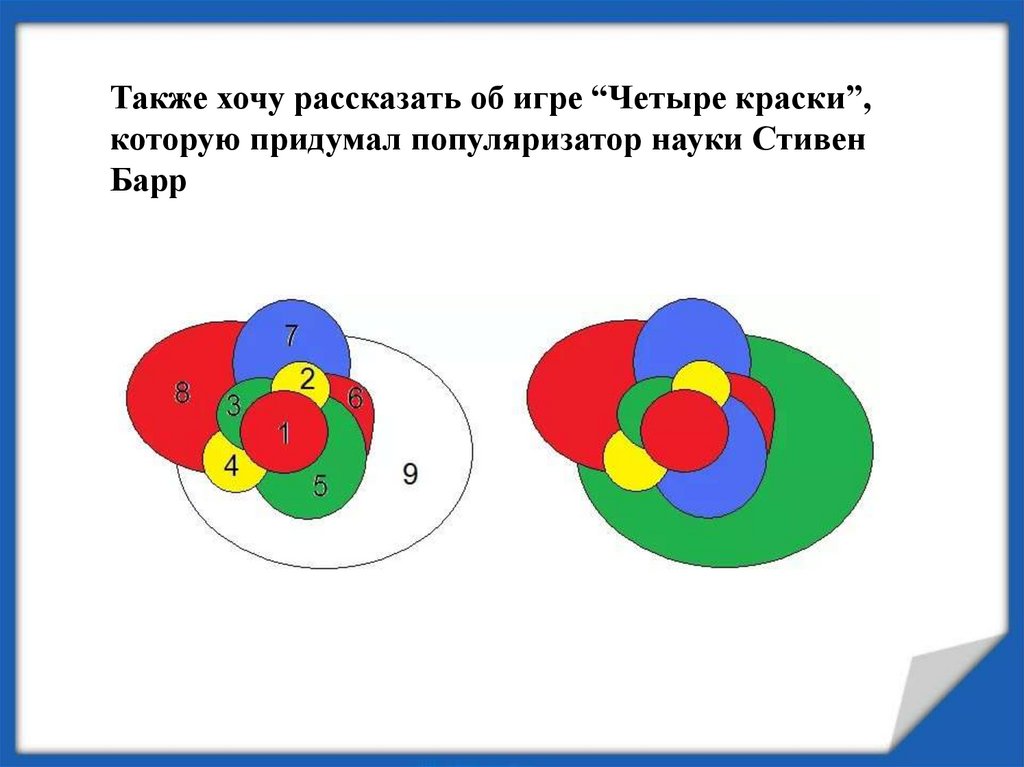
Также хочу рассказать об игре “Четыре краски”,которую придумал популяризатор науки Стивен
Барр
20.
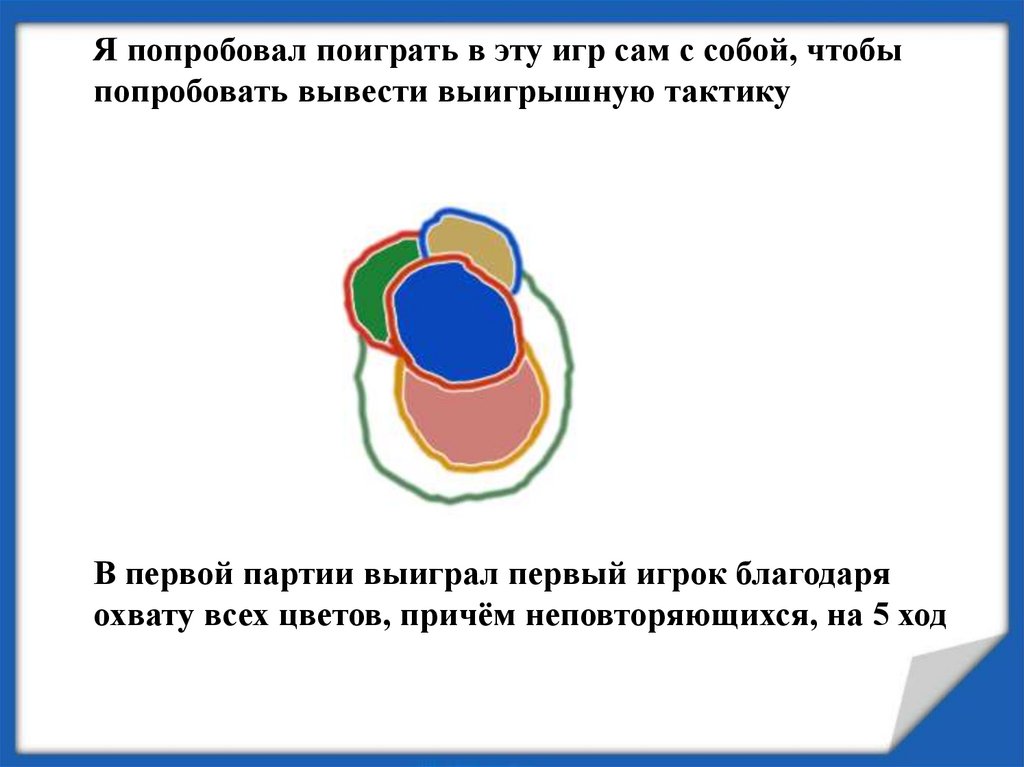
Я попробовал поиграть в эту игр сам с собой, чтобыпопробовать вывести выигрышную тактику
В первой партии выиграл первый игрок благодаря
охвату всех цветов, причём неповторяющихся, на 5 ход
21.
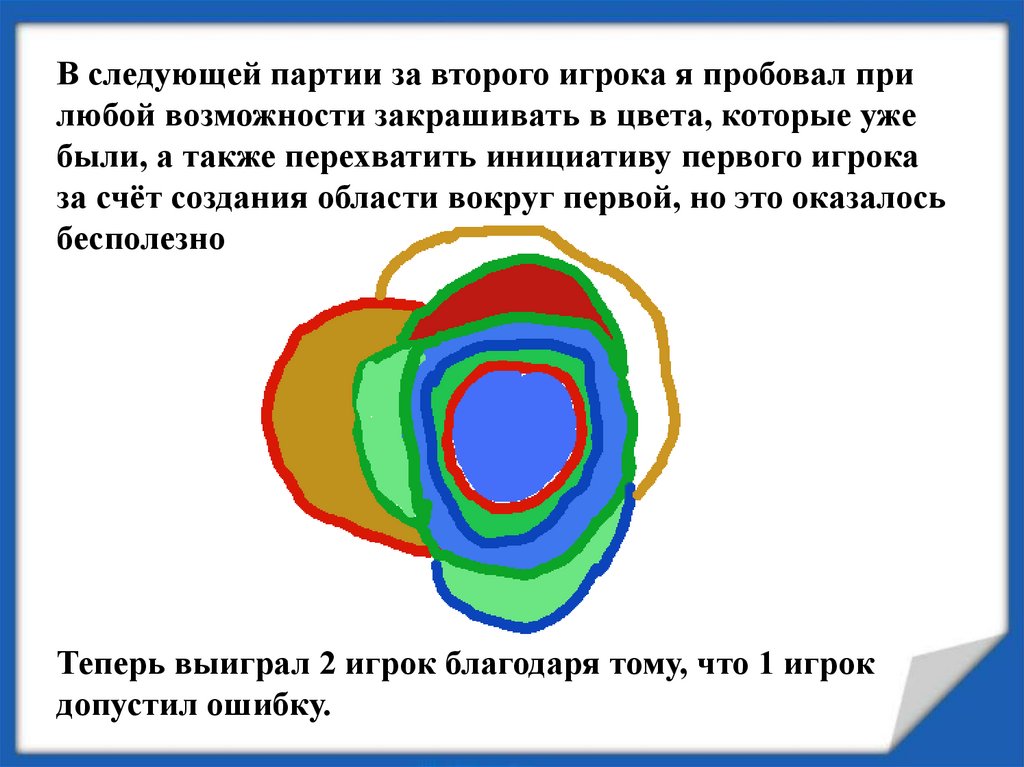
В следующей партии за второго игрока я пробовал прилюбой возможности закрашивать в цвета, которые уже
были, а также перехватить инициативу первого игрока
за счёт создания области вокруг первой, но это оказалось
бесполезно
Теперь выиграл 2 игрок благодаря тому, что 1 игрок
допустил ошибку.
22.
В третьей партии оба игрока делали так, чтобы областьмогла охватить только 3 цвета, то есть каждым ходом
закрывали своей областью другую и при возможности
окрашивали в повторяющиеся цвета:
23.
В итоге в игру ‘четыре краски’ можно игратьбесконечно при соблюдении одного условия:
Начиная со второго хода своей областью закрывать
другую.
24.
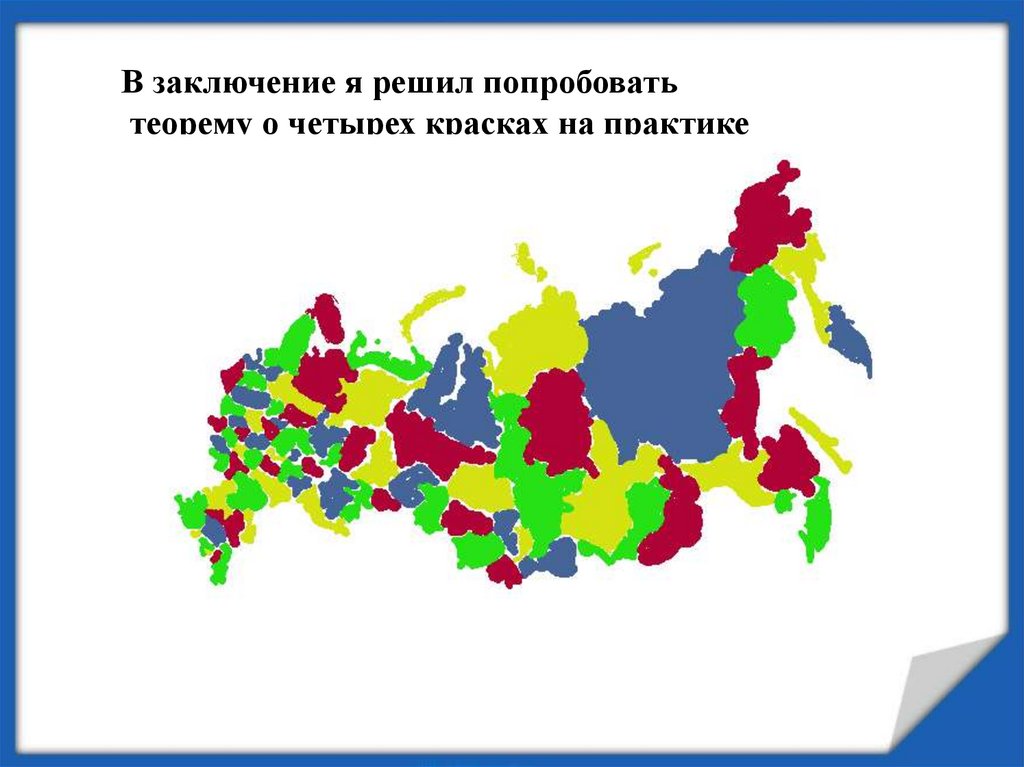
В заключение я решил попробоватьтеорему о четырех красках на практике
25.
Выводы:• Теорема о четырех красках работает.
• Игра “четыре краски” может идти бесконечно
при правильной игре обоих игроков.
• На данный момент гипотеза верна.










 Искусство
Искусство








