Правильные многогранники и элементы их симметрии

1.

Муниципальное бюджетное общеобразовательное учреждение «средняя
общеобразовательная школа №2»
Правильные многогранники
и элементы их симметрии
Выполнила: Шаповалова Виктория ученица 11 класса
Руководитель: Фоменко Ольга Анатольевна
2022

2.

Содержание
Введение
1.1.Гипотеза
1.2.Цель работы
1.3.Задачи работы
1.4.Актуальность проекта
1.5.Методы исследования
Основная часть
2.Исторические сведения
2.1 Первые упоминания
2.2. Платоновы тела
2.3. Формула Эйлера
2.4. Полуправильные многогранники Архимеда
2.5. Кеплер и его модель Солнечной системы
2.6. Икосаэдро - додекаэдровая структура Земли
2.7. Основные понятия
Многогранники вокруг нас
3.1. Многогранники в природе. Микромир
3.2. Многогранники в природе. Кристаллы
3.3. Многогранники в архитектуре
3.4. Многогранники в искусстве
Заключение
Список используемой литературы
Приложение. Развертки правильных многогранников

3.

Введение
Правильных многогранников вызывающе мало, - но этот весьма скромный
по численности отряд сумел пробраться в самые глубины различных наук.
Л. Кэрролл.

4.

1.1.Гипотеза:
Посмотрите вокруг - как разнообразен наш мир, какие разные предметы нас
окружают. И можно заметить, что все это - геометрические фигуры и тела. И
наши дома, и египетские пирамиды, и кубики, которыми играют дети, и
объекты архитектуры и дизайна, и предметы обихода состоят из правильных
многогранников.
Они встречаются в природе в виде кристаллов, и в виде вирусов. А биологи
говорят о том, что шестиугольные соты пчел, содержащие мед, тоже имеют
форму правильного многогранника. Существует гипотеза, что именно
правильная шестиугольная форма сот помогает сохранить полезные
свойства этого ценного продукта.
Так что же представляют собой эти столь совершенные тела?
И возможно ли обойтись без многогранников?
1)Цель работы:
Цель моей работы — это изучить удивительный мир многогранников.

5.

2)Задачи работы:
Познакомиться с многогранниками.
Изучить влияние правильных многогранников на возникновение философских теорий
и гипотез.
Показать связь геометрии и природы.
4. Познакомиться с примерами применения многогранников в архитектуре и искусстве.
5. Провести практическую работу «Многогранник своими руками».
6. Развить свой математический кругозор, мышление и речь, внимание и память,
интуицию, воображение и фантазию.
3)Актуальность проекта:
В течение многих веков математики проявляли живейший интерес к многогранникам.
Интерес к ним обусловлен не только их красотой и оригинальностью, но и большой
практической ценностью. Готовя этот проект я попала в удивительный мир
правильных многогранников, узнала много нового об их видах и свойствах.
4)Методы исследования:
1. теоретический: библиографический анализ литературы и материалов сети Internet;
2. эмпирический:
- анализ полученных данных.
- изготовление моделей многогранников.

6.

Исторические сведения
Первые упоминания о многогранниках
известны еще за три тысячи лет до нашей
эры в Египте и Вавилоне. Достаточно
вспомнить знаменитые египетские
пирамиды и самую известную из них –
пирамиду Хеопса. В значительной мере
правильные многогранники были изучены
древними греками (начиная с VII до н.э.)
Некоторые источники приписывают честь их
открытия Пифагору. Другие утверждают, что
ему были знакомы только тетраэдр, куб и
додекаэдр, а честь открытия октаэдра и
икосаэдра принадлежит Теэтету Афинскому,
современнику Платона. В любом случае,
Теэтет дал математическое описание всем
пяти правильным многогранникам и первое
известное доказательство того, что их ровно
пять.

7.

8.

9.

10.

В книге «Тайна мира», опубликованной в
1596 году, Кеплер изложил свою модель
Солнечной системы

11.

Многие залежи полезных
ископаемых тянутся вдоль
икосаэдро-додекаэдровой
сетки; 62 вершины и середины
рёбер многогранников,
называемых авторами узлами,
обладают рядом
специфических свойств,
позволяющих объяснить
некоторые непонятные
явления. Здесь располагаются
очаги древнейших культур и
цивилизаций. В этих точках
наблюдаются максимумы и
минимумы атмосферного
давления, гигантские
завихрения Мирового океана.
В этих узлах находятся озеро
Лох-Несс, Бермудский
треугольник.

12.

Основные понятия
• Многогранник – это геометрическое тело, ограниченное со
всех сторон плоскими многоугольниками, называемыми
гранями.
• Стороны граней – рёбра многогранника, а концы рёбер –
вершины многогранника. По числу граней различают
четырёхгранники, пятигранники и т. д.

13.

Тетраэдр -
(от греческого tetra – четыре
и hedra – грань) - правильный многогранник,
составленный из 4 равносторонних
треугольников. Из определения правильного
многогранника следует, что все ребра
тетраэдра имеют равную длину, а грани
- равную площадь.

14.

Октаэдр - (от греческого okto – восемь и
hedra – грань) - правильный многогранник,
составленный из 8 равносторонних
треугольников. Октаэдр имеет 6 вершин
и 12 ребер. Каждая вершина октаэдра
является вершиной 4 треугольников, таким
образом, сумма плоских углов при
вершине октаэдра составляет 240° .

15.

Икосаэдр – (от греческого ico —
шесть и hedra
— грань) правильный выпуклый многогранник,
составленный из 20 правильных треугольников.
Каждая из 12 вершин икосаэдра является
вершиной 5 равносторонних треугольников,
поэтому сумма углов при вершине равна
300 °.

16.

Куб или гексаэдр (от греческого hex —
шесть и hedra — грань) составлен из 6
квадратов. Каждая из 8 вершин куба
является вершиной 3
квадратов, поэтому сумма плоских углов при
каждой вершине равна 2700. У куба 12 ребер,
имеющих равную длину.

17.

Многогранники вокруг нас
зачастую не менее загадочный, чем мир
живой природы. Важность кристаллов
для геологических наук состоит в том, что
подавляющая часть земной коры
находится в кристаллическом состоянии.
В естественной среде правильные
многогранники можно встретить в виде
кристаллов Мир кристаллов - мир не
менее красивый, разнообразный,
развивающийся, (минералов).
Форму тетраэдра передает сурьменистый
сернокислый натрий.
Даже необработанный алмаз отчетливо
передает форму октаэдра. После
шлифовки камень точно соответствует
геометрической форме октаэдра.
Строение молекулы перовскита,
химическая формула - СаТiO3, точно
соответствует правильному
многограннику.

18.

Многогранники в
архитектуре
Архитектурные шедевры находятся в разных
уголках земного шара и отражают
особенности человеческой души. Тайные
людские желания воплощаются в форме
необыкновенных зданий.

19.

Многогранники в искусстве

20.

Знаменитый художник, увлекавшийся геометрией, Альбрехт Дюрер (1471- 1528), в
известной гравюре «Меланхолия» на переднем плане изобразил многогранник.

21.

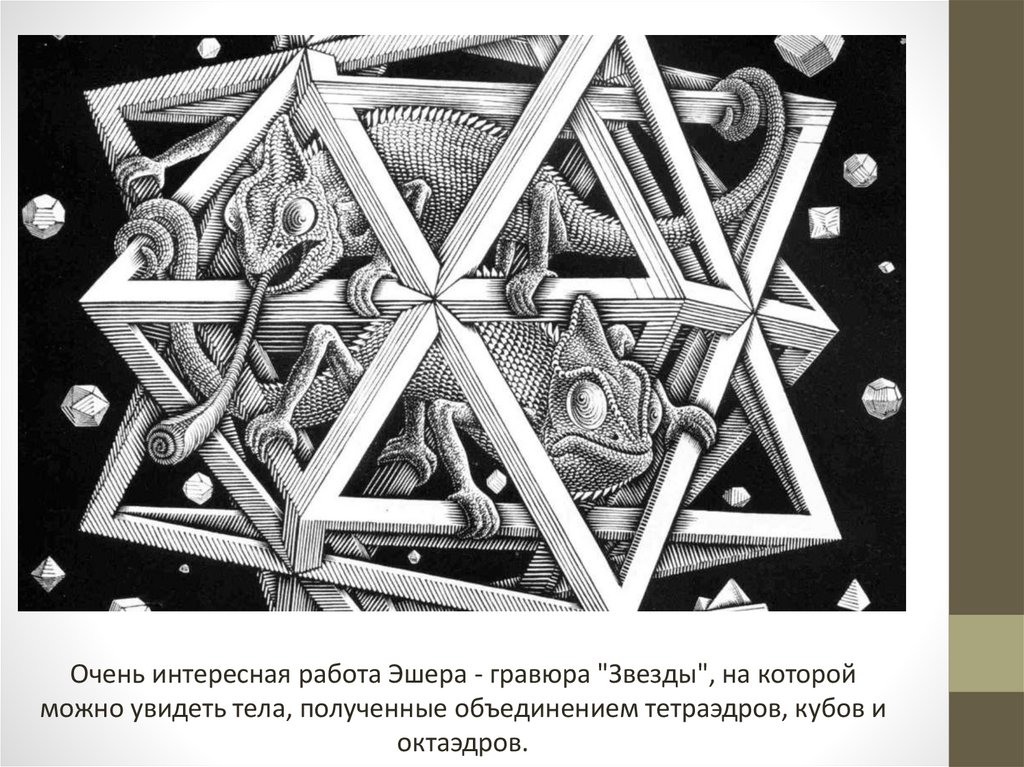
Очень интересная работа Эшера - гравюра "Звезды", на которой
можно увидеть тела, полученные объединением тетраэдров, кубов и
октаэдров.

22.

Заключение
Работая над данным проектом я сделала вывод о том . что
многогранники присутствуют в нашей жизни во всем.
Благодаря этим фигурам создаются великие архитектурные
сооружения, картины. Многие формы окружают нас но мы
даже не задумывается что все это многогранники. Выполнив
проектную деятельность я решила сама изготовить
многогранники и показать вам . цель моей работы достигнута,
я не только познала мир многогранников но и получила новые
знания

23.

Список используемой литературы
1.Шарыгин И. Ф., Ерганжиева Л.Н. Наглядная
2.геометрия.Учебное пособие для V – VI классов. –
М: Мирос 1992.(стр166)
3.Смирнова И.М., Смирнов В.А. «Правильные,
полуправильные и звездчатые
многогранники».-М.:МЦМНО,2010
4.Ж.Адамар Элементарная геометрия, часть 2
Стереометрия. Пособие для учителей средней
школы.
Интернет-ресурсы:
1.Мир многогранников
http://www.sch57.msk.ru:8101/collect/smogl.htm
2. Библиотека электронных учебных пособий
http://www.ega-math.narod.ru/
3. Статьи по математике
http://dondublon.chat.ru/math.htm
4. Популярная математика
http://www.uic.ssu.samara.ru/~nauka/index.htm
5.Многогранники.ru – сайт о создании моделей
многогранников из бумаги
https://www.mnogogranniki.ru/

24.

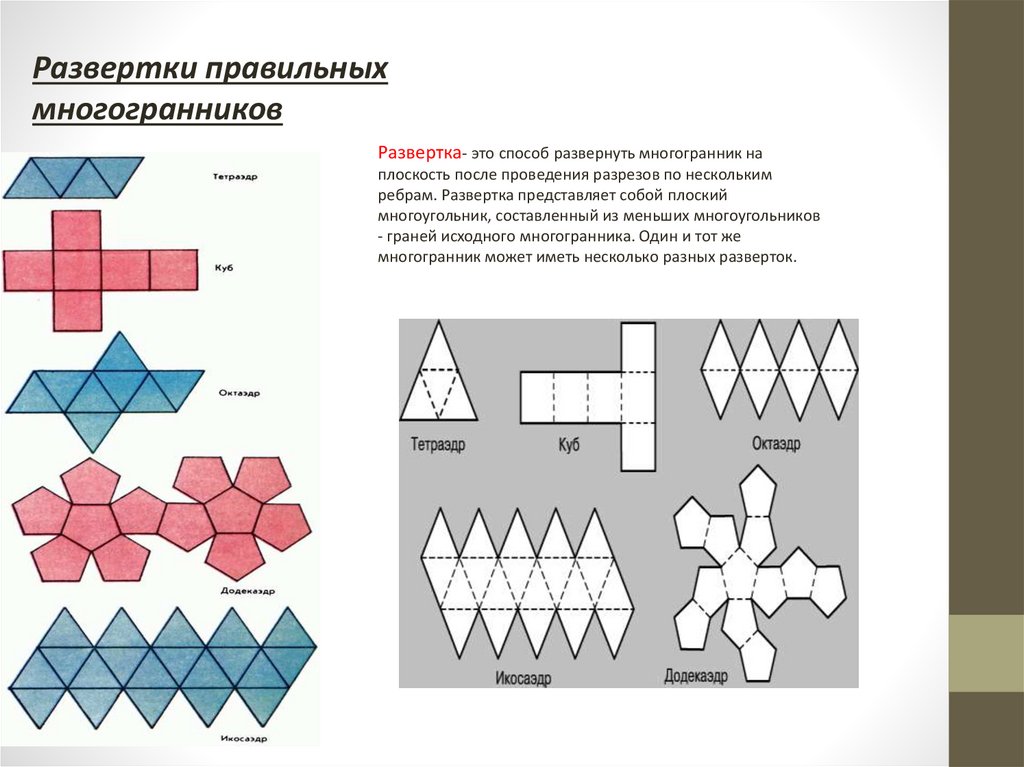
Развертки правильных
многогранников
Развертка- это способ развернуть многогранник на
плоскость после проведения разрезов по нескольким
ребрам. Развертка представляет собой плоский
многоугольник, составленный из меньших многоугольников
- граней исходного многогранника. Один и тот же
многогранник может иметь несколько разных разверток.

25.

Спасибо за внимание!