Похожие презентации:
Теоретические основы электротехники
1.
Теоретические основы электротехники2. Оглавление
Лекция № 1. ВведениеЛекция № 2. Основные законы линейных электрических цепей
постоянного тока
Лекция № 3. Методы расчета токов
Лекция № 4. Методы расчета токов
Лекция № 5. Способы изображения и параметры синусоидальных
электрических величин
Лекция № 6. Приемники в схемах замещения цепей
синусоидального тока
Лекция № 7. Анализ цепи с последовательным соединением
приемников
Лекция № 8. Анализ цепи с последовательным соединением
приемников
Лекция № 9. Расчет цепей синусоидального тока
2
3. Оглавление
Лекция № 10. Электрические цепи с взаимной индуктивностьюЛекция № 11. Трехфазные цепи
Лекция № 12. Расчет трехфазных цепей
Лекция № 13. Расчет трехфазных цепей
Лекция № 14. Электрические цепи при несинусоидальных
периодических воздействиях
Лекция № 15. Классический метод расчета переходных процессов
Лекция № 16. Переходные процессы в цепях с одним реактивным
элементом
Лекция № 17. Переходные процессы в цепях с двумя реактивными
элементами
Лекция № 18. Расчет нелинейных электрических цепей постоянного
тока графическими методами
Лекция № 19. Расчет нелинейных электрических цепей постоянного
тока графическими методами
3
4. Оглавление
Лекция № 20. Численные методы анализа нелинейных цепейЛекция № 21. Основные понятия о магнитных цепях постоянного
тока
Лекция № 22. Расчет неразветвленных магнитных цепей
Лекция № 23. Нелинейные цепи переменного тока
Лекция № 24. Расчет катушки с ферромагнитным сердечником
Лекция № 25. Явление феррорезонанса
Лекция № 26. Четырехполюсники при синусоидальных воздействиях
Лекция № 27. Характеристические параметры четырехполюсника
Лекция № 28. Цепи с распределенными параметрами
Лекция № 29. Анализ длинной однородной линии
Лекция № 30. Особые режимы работы длинной однородной линии
Лекция № 31. Введение в теорию электромагнитного поля
Лекция № 32. Уравнение Максвелла
Лекция № 33. Основные уравнения и элементы электромагнитного
поля
4
5. Лекция № 1 Основные понятия и определения
1. Общие понятия2. Интегральные величины электромагнитного
поля, применяемые в теории электрических
цепей
3. Элементы схем замещения электрических
цепей
4. Геометрические элементы схем замещения
5
6.
Общие понятияПредмет ТОЭ
Предмет ТОЭ изучает количественные и качественные стороны
электромагнитных процессов в электрических цепях и электромагнитном
поле.
Теория электрических цепей изучает электромагнитные явления
в технических системах, предназначенных для производства, передачи
и распределения электрической энергии, распространения,
преобразования и переработки информации.
В основе курса лежат знания, полученные студентами в различных
областях:
• высшей математики – алгебре;
• теории дифференциальных уравнений;
• интегральных преобразованиях Фурье и Лапласа;
• теории численного решения алгебраических и дифференциальных
уравнений.
Лекция № 1. Основные понятия и определения
6
7.
Интегральные величины электромагнитного поля, применяемые в теории электрических цепейЭлектрический ток – это явление направленного движения
заряженных частиц:
Δq dq
.
Δt 0 Δt
dt
i lim
Напряжение – количество энергии, затраченной на перемещение
единичного заряда из одной точки электромагнитного поля в другую:
ΔW dW
.
Δq 0 Δq
dq
u lim
Потенциал – количество энергии, затраченной на перемещение
единичного заряда из бесконечности в какую-либо точку электромагнитного
поля. Отсюда напряжение – это разность потенциалов.
Мощность – это скорость изменения энергии во времени:
W dW
p lim
,
t Δt
dt
dW dq
p
u i.
dq dt
Лекция № 1. Основные понятия и определения
7
8.
Элементы схем замещения электрических цепейЭлектрическая цепь – это совокупность генерирующих, приемных
и вспомогательных устройств, соединенных между собой электрическими
проводами.
Электрическая схема замещения – это графическое изображение
электрической цепи идеализированными элементами, которые учитывают
явления, происходящие в реальной цепи.
Идеальные источники ЭДС и тока
+
e
+
Реальные источники ЭДС и тока
e
j
_
j
_
Rвн
Rвн
У идеального источника ЭДС сопротивление бесконечно мало.
У идеального источника тока сопротивление бесконечно велико.
Идеальных устройств в реальной жизни нет. Реальный источник ЭДС
обладает небольшим сопротивлением. Реальный источник тока обладает
большим, но конечным сопротивлением.
Лекция № 1. Основные понятия и определения
8
9.
Элементы схем замещения электрических цепейРазличают три
идеализированных
приемных элемента.
R
L
C
Резистивный элемент, или идеальный резистор, учитывает
преобразование электрической энергии в другие виды энергии.
Обладает сопротивлением R, которое измеряют в Омах (Ом).
Индуктивный элемент, или идеальная индуктивная катушка,
учитывает энергию магнитного поля катушки, а также ЭДС самоиндукции.
Обладает индуктивностью L, которую измеряют в Генри (Гн).
Емкостный элемент, или идеальный конденсатор, учитывает энергию
электрического поля конденсатора, а также токи смещения. Обладает
емкостью С, измеряемой в Фарадах (Ф).
C
R
L
Рассмотрим схему замещения реальной
индуктивной катушки, которая греется, что учитывает
резистивный элемент, в ней наводится ЭДС
(индуктивный элемент). Емкостный элемент учитывает
энергию электрических полей между витками.
Лекция № 1. Основные понятия и определения
9
10.
Геометрические элементы схем замещенияВетвь – часть электрической схемы, состоящая из одного
или нескольких последовательно соединенных источников
и приемников энергии, ток в которых один и тот же.
Можно сформулировать короче. Ветвь – участок схемы
с одним током.
Ветви могут быть активными, содержащими источники энергии,
и пассивными, состоящими из одних приемников.
Узел – это точка в схеме, где сходятся не менее трех ветвей.
Тогда ветвь – участок схемы от одного узла до другого узла.
Контур – любой замкнутый по ветвям схемы путь. Схема может
быть одноконтурной и многоконтурной.
Лекция № 1. Основные понятия и определения
10
11. Вопросы для самопроверки
1.2.
3.
4.
5.
6.
7.
8.
9.
Какое явление называется электрическим током?
Ток какой величины опасен для жизни?
Каково определение напряжения?
Что понимают под мощностью?
Какие идеальные источники энергии вы знаете?
Чем они принципиально отличаются друг от друга?
Что учитывают приемные элементы схемы замещения?
Что назвали ветвью?
Что понимают под контуром схемы замещения?
Лекция № 1. Основные понятия и определения
11
12. Лекция № 2. Основные законы линейных электрических цепей постоянного тока
1. Закон Ома2. Первый закон Кирхгофа
3. Второй закон Кирхгофа
4. Закон Ома для активной цепи
5. Баланс мощностей
12
13. Закон Ома
Напряжение на резистивном элементе пропорционально току:U R I.
U
Геометрической интерпретацией закона
Ома является вольт-амперная
характеристика (ВАХ). Для линейного
элемента она имеет вид прямой линии.
I
Лекция № 2. Основные законы линейных электрических цепей постоянного тока
13
14. Первый закон Кирхгофа
Первый закон Кирхгофа сформулирован для узла. Узел – этоточка в схеме, где сходятся не менее трех ветвей. При использовании
ЭВМ для ввода исходных данных узлами выделяют каждый элемент
схемы замещения. Эти узлы называют ложными или устранимыми.
В дальнейшем речь будет идти о неустранимых узлах.
Алгебраическая сумма токов в узле равна нулю:
n
I
j 1
j
0.
Правило знаков: токи, одинаково направленные относительно
узла, записывают с одинаковыми знаками.
Лекция № 2. Основные законы линейных электрических цепей постоянного тока
14
15. Второй закон Кирхгофа
Второй закон Кирхгофа относится к контуру. Алгебраическая сумманапряжений на приемниках в любом контуре равна алгебраической
сумме ЭДС, действующих в этом же контуре:
p
m
U E .
k 1
k
i 1
i
С учетом закона Ома
p
m
R I E .
k 1
k k
i 1
i
Правило знаков: со знаком плюс записывают напряжения и ЭДС,
направления которых совпадают с выбранным направлением
обхода контура.
Лекция № 2. Основные законы линейных электрических цепей постоянного тока
15
16. Закон Ома для активной ветви
Активная ветвь, названная так из-за наличия источника ЭДС,изображена на рисунке:
a
I
R
c
_
Va Vb E RI ,
E
+
b
Va Vb E RI ,
U ab E RI .
U ab
Можно определить напряжение между двумя любыми точками,
рассчитав изменение потенциалов между ними. При этом нужно вести
расчет в сторону увеличения потенциала, т. е. от второго индекса
напряжения к первому.
Закон Ома для активной ветви:
I
U ab E
G U ab E
R
Лекция № 2. Основные законы линейных электрических цепей постоянного тока
16
17. Баланс мощностей
Баланс мощностей – это интерпретация закона сохранения энергиив электротехнике.
Мощность генераторов энергии в электрической цепи равна
мощности потребителей:
Pг Рн ,
n
m
i 1
j 1
Рг Ei I i U j J j ,
l
l
к 1
к 1
Рн U к I к Rк I к2
Лекция № 2. Основные законы линейных электрических цепей постоянного тока
17
18. Вопросы для самопроверки
1. Сформулируйте первый закон Кирхгофа. Назовитеправило знаков.
2. Сформулируйте второй закон Кирхгофа. Назовите
правило знаков.
3. Какие электрические величины можно вычислить
с помощью закона Ома для активной ветви?
4. Для чего используют баланс мощностей?
5. Сформулируйте баланс мощностей.
6. Как определить, в каком режиме работает источник
энергии?
Лекция № 2. Основные законы линейных электрических цепей постоянного тока
18
19. Лекция № 3. Методы расчета токов
1. Метод непосредственного использованиязаконов Кирхгофа
2. Метод узловых потенциалов
3. Метод напряжения между двумя узлами
4. Метод эквивалентных преобразований схем
с последовательно-параллельным
соединением приемников
19
20. Метод непосредственного использования законов Кирхгофа
Предварительно нужно выявить в схеме узлы и ветви.Число уравнений должно быть минимальным, но достаточным
и равным числу неизвестных токов, т.е. m mJ, где m – общее число ветвей
в схеме;
m–J число ветвей с источниками тока.
По первому закону Кирхгофа составляют n-1 уравнение,
где n – число узлов схемы.
Недостающие уравнения дописывают по второму закону Кирхгофа.
Уравнения по второму закону Кирхгофа составляют для контуров,
не содержащих источников тока.
a
R1
R2
R3
J
E1
E3
I1
I2
I3
I1 I 2 I 3 J ;
R1 I1 R2 I 2 E1 ;
R2 I 2 R3 I 3 E3 .
b
Лекция № 3. Методы расчета токов
20
21. Метод узловых потенциалов
В качестве промежуточных неизвестных принимают потенциалы узлов.Потенциал – функция многозначная, поэтому потенциал одного из узлов
принимают равным нулю. Рационально заземлять узел, в котором сходится
максимальное число ветвей.
Систему можно записать в трафаретном виде:
G11V1
G V
21 1
Gm1V1
где
G12V2
G13V3
G1mVm
J11
G22V2
G23V3
G2 mVm
J 22
Gm 2V2
Gm 3V3
GmmVm
J mm
,
Gii – собственная проводимость узла, равная сумме проводимостей
ветвей, соединяющихся в соответствующем узле;
Gij – общие проводимости между двумя узлами, равные сумме
проводимостей ветвей, соединяющих эти узлы;
Jii – узловой ток, равный алгебраической сумме произведений
проводимостей активных ветвей на ЭДС этих ветвей и токов
источников тока, соединяющихся в этом узле.
Лекция № 3. Методы расчета токов
21
22.
Метод узловых потенциаловR1
R3
1
I3
E3
2 R6
I6
I1
R2
E1
J2
R5
I2
I4
4
E6
I5
R4
3
E4
С положительным знаком берут ЭДС и токи, направленные к узлу.
Составим систему уравнений
(G1 G2 G3 )V1
G3V1
0
G3V2
0
G1 E1 J 2 G3 E3 ;
(G3 G5 G6 )V2
(G5 G6 )V3
G3 E3 G6 E6 ;
(G5 G6 )V2
(G4 G5 G6 )V3
G4 E4 G6 E6 .
Решением системы уравнений определим потенциалы узлов. Затем
рассчитаем токи ветвей по закону Ома:
I1 G1 (V4 V1 E1 ) G1 ( V1 E1 ),
I 2 G2V1 ,
I3 G3 (V1 V2 E3 ),
I 4 G4 ( V3 E4 ),
I5 G5 (V2 V3 ),
Лекция № 3. Методы расчета токов
22
23. Метод напряжения между двумя узлами
Этот метод является частным случаем метода узловыхпотенциалов, он применим для схемы с двумя узлами.
Формулу для определения напряжения между двумя узлами
в общем виде можно записать следующим образом:
n
U12
m
G E J
i 1
i
i
l
G
i 1
где
j 1
j
,
i
Gi проводимости ветвей;
n
число ветвей, содержащих источники ЭДС с отличными
от нуля проводимостями;
m число ветвей, содержащих источники тока;
l число ветвей без источников тока.
Число слагаемых в числителе равно числу активных ветвей.
С положительным знаком записывают E и J, направленные к первому
в индексе напряжения узлу. Сумма в знаменателе формулы –
арифметическая. Вычислив напряжение между двумя узлами,
по закону Ома для ветви находят токи.
Лекция № 3. Методы расчета токов
23
24. Метод эквивалентных преобразований схем с последовательно-параллельным соединением приемников
Метод эквивалентных преобразований применяют каксамостоятельный для расчета токов в схемах с одним источником
энергии и несколькими приемниками. Его можно использовать и для
упрощения частей сложной схемы при расчетах другими методами.
Все приемники заменяют одним с эквивалентным
сопротивлением. При этом токи и напряжения в частях схемы,
не затронутых преобразованием, должны оставаться неизменными.
Находят токи в свернутой схеме. Затем возвращаются
к исходной схеме с определением остальных токов.
Преобразование схемы проводят постепенно, рассматривая
участки с последовательными и параллельными соединениями
приемников. Предварительно нужно выявить узлы и ветви.
Лекция № 3. Методы расчета токов
24
25.
Метод эквивалентных преобразований схем с последовательно-параллельным соединением приемниковЭлементы, принадлежащие одной ветви, соединены между собой
последовательно. В них один ток. Эквивалентное сопротивление
последовательно соединенных резисторов равно сумме их сопротивлений:
n
Rэ Ri .
i 1
При параллельном соединении элементы схемы замещения
находятся под одним напряжением и соединены между собой двумя
выходными зажимами. Эквивалентная проводимость параллельно
соединенных резисторов равна сумме их проводимостей:
n
1
1
.
Rэ i 1 Ri
В свернутой схеме ток определяют по закону Ома: I
E
.
Rэ
Ток в одной из двух параллельно соединенных пассивных ветвей
пропорционален току в неразветвленной части схемы. В числителе
коэффициента пропорциональности записывают сопротивление другой
пассивной ветви, в знаменателе – cумму сопротивлений двух пассивных ветвей.
Лекция № 3. Методы расчета токов
25
26. Вопросы для самопроверки
1. Чему равно минимальное и достаточное число уравненийв системе, составленной по законам Кирхгофа?
2. Сколько уравнений составляют по первому закону Кирхгофа?
3. Чему равно число уравнений в системе для определения
потенциалов узлов?
4. Что назвали узловым током?
5. Для расчета каких схем метод эквивалентных преобразований
можно использовать как самостоятельный?
Лекция № 3. Методы расчета токов
26
27. Лекция № 4. Методы расчета токов
1. Метод эквивалентных преобразованийдля расчета схем с трехполюсниками
2. Метод наложения
3. Метод эквивалентного генератора
27
28. Метод эквивалентных преобразований для расчета схем с трехполюсниками
AA
R CA
RA
R AB
RC
C
R BC
B
RB
B
C
RAB
R R
RA RB A B ,
RC
RA
RAB RCA
,
RAB RBC RCA
RBC
R R
RB RC B C ,
RA
RB
RBC RAB
,
RAB RBC RCA
RCA
R R
RC RA C A ,
RB
RC
RCA RBC
.
RAB RBC RСА
Лекция № 4. Методы расчета токов
28
29. Метод наложения
Метод наложения основан на принципе независимости действияисточников энергии. Ток в любой ветви схемы равен алгебраической
сумме токов, возникающих в этой ветви под действием каждого отдельно
работающего источника.
Схему делят на столько подсхем, сколько источников энергии.
В каждой подсхеме оставляют только один источник, остальные источники
ЭДС закорачивают, источники тока – разрывают.
Приемники во всех подсхемах остаются неизменными.
Токи в подсхемах ищут методом эквивалентных преобразований.
Токи в схеме вычисляют алгебраическим суммированием токов
в подсхемах.
Метод наложения рационально применять, если в схеме не больше
трех источников энергии.
Лекция № 4. Методы расчета токов
29
30. Метод эквивалентного генератора
Этот метод дает возможность вычислить ток только одной ветви схемы.Любой активный двухполюсник можно заменить эквивалентным
ему генератором.
a In
A
Rn
b
а
In
EГ
Rn
ЭДС генератора равна напряжению между
зажимами а и b активного двухполюсника в режиме
холостого хода. Внутреннее сопротивление
генератора равно эквивалентному сопротивлению
пассивного двухполюсника относительно входных
зажимов. Пассивный двухполюсник получают
из активного, закорачивая идеальные источники
ЭДС и разрывая идеальные источники тока.
RГ
b
Eг
U хх
In
.
Rг Rn Rг Rn
Лекция № 4. Методы расчета токов
30
31. Вопросы для самопроверки
На чем основан расчет методом наложения?На сколько подсхем делят исходную схему?
Каким методом вычисляют токи в подсхемах?
Как находят токи в исходной схеме?
Чем метод эквивалентного генератора отличается от
всех остальных методов расчетов?
6. В чем суть метода эквивалентного генератора?
7. Чему равно ЭДС эквивалентного генератора?
8. Чему равно сопротивление эквивалентного генератора?
1.
2.
3.
4.
5.
Лекция № 4. Методы расчета токов
31
32. Лекция № 5. Способы изображения и параметры синусоидальных электрических величин
1. Преимущества переменного тока2. Способы представления гармонических
функций
3. Действующие и средние значения
гармонических величин
32
33. Преимущества переменного тока
Переменный ток поддается трансформации, отсюдавозможность передачи на большие расстояния.
Производство переменного тока просто и рационально.
Потребитель при переменном токе легче решает вопросы
преобразования электрической энергии в механическую.
Преимущества синусоидальной формы кривых тока
и напряжения перед другими периодическими формами.
Форма кривых после трансформации не меняется.
Величины меняются плавно, нет перенапряжений, толчков
тока, которые недопустимы в энергетике.
Лекция № 5. Способы изображения и параметры синусоидальных электрических величин
33
34. Способы представления гармонических функций
Графическое изображение – синусоидаЗначение переменной
величины в данный момент
называют мгновенным.
i
i Im
t
T
Мгновенные значения
обозначают строчными
буквами: i, u, e.
Период – время одного полного колебания.
Величину, обратную периоду, называют частотой f:
Частота – число полных колебаний в единицу времени.
f
1
.
T
1
f с 1 Гц.
с
Промышленная частота в России – 50 Гц, в США, Японии – 60 Гц.
Лекция № 5. Способы изображения и параметры синусоидальных электрических величин
34
35.
Способы представления гармонических функцийИзображение тригонометрическими функциями
Мгновенные значения электрических величин являются
синусоидальными функциями времени:
i I m sin ω t ψi ,
где
u U m sin ω t ψu ,
e Em sin ω t ψe ,
i, u, e – мгновенные значения;
I m , U m , Em – максимальные (амплитудные) значения;
(ω t ψ) – фаза колебания, характеризующая развитие процесса
во времени;
ωt – текущий угол, который отсчитывают от начала отсчета времени;
ω 2 f
ψ
2 – угловая циклическая частота, определяющая скорость
T изменения фазы;
– начальная фаза. Это угол, определяющий значение функции
в начальный момент времени.
Лекция № 5. Способы изображения и параметры синусоидальных электрических величин
35
36.
Способы представления гармонических функцийИзображение вращающимися векторами
Непосредственные математические действия с синусоидальными
величинами весьма трудоемки.
Любую синусоиду можно изобразить вектором, вращающимся против
часовой стрелки со скоростью ω .
i
y
i0
y
Im
wt
0
w
Im
y
x
Применение вращающихся
векторов позволяет заменить
тригонометрические
и графические действия над
мгновенными значениями
действий над вращающимися
векторами. Но векторные
диаграммы дают только
графическое решение задачи.
Лекция № 5. Способы изображения и параметры синусоидальных электрических величин
36
37.
Способы представления гармонических функцийИзображение комплексными числами
Так как буквой i в электротехнических
дисциплинах обозначают ток, то мнимую
единицу обозначают буквой j 1.
+j
j Im
Im
y
+1
0
Вектору на комплексной плоскости можно
сопоставить комплексное число:
I m I m e jψ .
Im
Переход от одной формы записи к другой делают по формулам:
Im
I m I m
ψ arctq
2
I m
,
I m
2
,
I m I m cos ψ,
I m I m sin ψ.
Лекция № 5. Способы изображения и параметры синусоидальных электрических величин
37
38.
Действующие и средние значения гармонических величинДействующие значения
Действующим значением тока считают такой постоянный ток, который
производит тот же тепловой эффект, что и реальный переменный ток.
Действующее значение тока:
T
Im
1 2
2
I
I
sin
ω
t
d
t
0,707 I m .
m
T0
2
Аналогично
U
Um
2
0,707 U m ;
E
Em
0,707 E m
2
Действующие значения токов и напряжений показывают амперметры
и вольтметры электромагнитной и электродинамической систем.
Лекция № 5. Способы изображения и параметры синусоидальных электрических величин
38
39.
Действующие и средние значения гармонических величинСредние значения
В общем случае среднее значение – это среднее значение за период:
T
1
I ср i d t.
T 0
Но для синусоидальной величины это выражение равно нулю.
Поэтому среднее значение определяют для половины периода:
I ср
Аналогично
T
2
T
2
2
2
2
i
d
t
I
sin
ω
t
dt
I m 0,637 I m .
m
T 0
T 0
π
2
U ср U m 0,637 U m ;
π
Eср
2
Em 0,637 Em .
π
Лекция № 5. Способы изображения и параметры синусоидальных электрических величин
39
40. Вопросы для самопроверки
1. В чем преимущества переменного тока?2. Почему выбрали синусоидальную форму изменения тока
и напряжения?
3. В какую сторону от начала координат смещена синусоида
при положительной начальной фазе?
4. Какой физический смысл имеет угловая циклическая частота?
5. Какой буквой обозначают угол сдвига фаз напряжения и тока?
6. Какие формулы записи комплексных чисел Вы знаете?
7. Что характеризуют модуль и аргумент комплекса?
8. Что понимают под действующим значением переменного тока?
9. Как связаны максимальное и действующее значения
синусоидальных электрических величин?
Лекция № 5. Способы изображения и параметры синусоидальных электрических величин
40
41. Лекция № 6. Приемники в схемах замещения цепей синусоидального тока
1. Идеальный резистор или резистивныйэлемент
2. Индуктивный элемент либо идеальная
индуктивная катушка
3. Идеальный конденсатор либо емкостный
элемент
41
42.
Идеальный резистор либо резистивный элементРезистивный элемент обладает сопротивлением R, которое измеряют
в Омах (Ом).
i
R
Закон Ома для мгновенных значений:
uR R i.
uR
uR
i
wt
Мощность для резистивного элемента:
Т
Т
1
1
1
P p dt U R I 1 cos 2 ω t ψi dt U R I T U R I R I 2 .
T 0
T 0
T
Лекция № 6. Приемники в схемах замещения цепей синусоидального тока
42
43. Индуктивный элемент либо идеальная индуктивная катушка
iL
uL
Индуктивный элемент учитывает ЭДС
самоиндукции, которая пропорциональна
скорости изменения потокосцепления
и мешает этому изменению:
eL
eL
dψ
dФ
W
.
dt
dt
.
Индуктивность – это коэффициент,
характеризующий
dψ
способность тока создавать магнитный поток:
L
Индуктивность измеряют в Гн = Ом с
di
.
di
.
dt
Закон Ома для мгновенных значений:
uL L
Закон Ома для действующих значений:
UL L ω I.
Закон Ома для комплексных значений:
UL j X L I X L I e
j
2
Лекция № 6. Приемники в схемах замещения цепей синусоидального тока
X L I e j 90 .
0
43
44. Индуктивный элемент либо идеальная индуктивная катушка
1. При синусоидальном токе напряжение на индуктивном элементеπ
тоже синусоидально.
2. Напряжение опережает по фазе ток на угол, равный 2
UL
uL
i
wt
I
XL
Индуктивное сопротивление – это расчетное
понятие, учитывающее ЭДС самоиндукции.
Мгновенная мощность индуктивного элемента:
w
p uL i U Lm I m cos ω t ψi sin ω t ψi U L I sin 2 ω t ψi .
Идеальная индуктивная катушка энергии не потребляет.
Энергия магнитного поля
индуктивного элемента:
di
L i2
WM p dt uL i dt L i dt L i d i
.
dt
2
Лекция № 6. Приемники в схемах замещения цепей синусоидального тока
44
45. Идеальный конденсатор либо емкостный элемент
iC
u
Емкостный элемент обладает емкостью С,
которую измеряют в Фарадах:
C
с
Ф
.
Ом
Закон Ома для мгновенных значений:
duC
i C
.
dt
Закон Ома для действующих значений:
I C ω UC .
Закон Ома для комплексных значений:
По аналогии с резистором для упрощения
расчетов вводят понятие емкостного
сопротивления.
UC j X C I X C I e
j
2
X C I e j 90 .
0
XC
w
Лекция № 6. Приемники в схемах замещения цепей синусоидального тока
45
46. Идеальный конденсатор либо емкостный элемент
1. При синусоидальном токе напряжение на емкостном элементе тожесинусоидально.
π
2. Напряжение на емкостном элементе отстает по фазе от тока на угол .
2
uC
I
i
wt
UC
Мгновенная мощность емкостного элемента:
p uC i UCm I m cos ω t ψu sin ω t ψu
U Cm I m
2 cos ω t ψu sin ω t ψu U C I sin 2 ω t ψu .
2
Идеальный конденсатор энергии не потребляет.
Энергия электрического поля
емкостного элемента:
duC
C uC2
Wэ pdt uC idt uC C
dt
.
dt
2
Лекция № 6. Приемники в схемах замещения цепей синусоидального тока
46
47. Вопросы для самопроверки
1. Какие явления учитывает идеальный резистор?2. Каковы фазные соотношения тока и напряжения резистора?
3. Что Вы знаете о мгновенной мощности резистивного
элемента?
4. Что назвали активной мощностью?
5. Каковы фазные соотношения тока и напряжения идеальной
индуктивной катушки?
6. Что Вы знаете о мгновенной мощности индуктивного
элемента?
7. Каковы фазные соотношения тока и напряжения идеального
конденсатора?
8. Что Вам известно о мгновенной мощности емкостного
элемента?
Лекция № 6. Приемники в схемах замещения цепей синусоидального тока
47
48. Лекция № 7. Анализ цепи с последовательным соединением приемников
1. Основные законы цепей переменного тока2. Построение векторной диаграммы
3. Треугольники сопротивлений и мощностей.
Закон Ома для активной цепи
4. Резонанс напряжений
48
49. Основные законы цепей переменного тока
В цепях переменного тока закон Ома выполняется для всехзначений, законы Кирхгофа – только для мгновенных и комплексных,
которые учитывают фазные соотношения.
n
i
Первый закон Кирхгофа:
k 1
m
i 1
i
U
XL
UR
UL
j 1
I
k 1
l
Закон Ома в комплексной форме:
R
0,
u e ,
Второй закон Кирхгофа:
I
k
n
j
k
m
0.
l
U E .
i 1
i
j 1
j
U Z I.
U U R U L UC ,
UC
XC
U R I j X L I j X C I R j X L X C I Z I ,
Z R j X L XC R j X .
Уравнения, составленные по законам Кирхгофа, называют
уравнениями электрического состояния.
Лекция № 7. Анализ цепи с последовательным соединением приемников
49
50. Построение векторной диаграммы
UCПостроение векторной диаграммы начинают
с вектора величины, общей для данной цепи.
При последовательном соединении элементов
такой величиной является ток. Вид диаграммы
зависит от характера цепи. Построение
векторной диаграммы для цепи, имеющей
активно-индуктивный характер, т. е.
UL
B
U
O
j
A
I
X L XC .
UR
B
U
U L UC
j
O
UR
A
U U R2 U L UC ,
2
U R U cos j,
Входное напряжение складывается из
напряжений на трех идеальных элементах
при учете сдвига фаз. Треугольник ОАВ дает
возможность оперировать действующими
значениями, для которых законы Кирхгофа
не выполняются:
U UC
j Arc tq L
,
UR
U L UC U sin j.
Лекция № 7. Анализ цепи с последовательным соединением приемников
50
51. Треугольники сопротивлений и мощностей
UI =Z
Если разделить все стороны
треугольника напряжений на ток I,
получим подобный ему
треугольник сопротивлений.
Z R2 X 2 R2 X L X C ,
2
j Arc tq
j
U L UC
= X L XC = X
I
UR
=R
I
X
,
R
Умножением всех сторон
треугольника напряжений на
ток, получаем треугольник
мощностей.
R Z cosj,
U I=S
X Z sinj.
U L UC I = Q
j
UR I = P
Активная мощность, Вт:
P U R I R I 2 U I cosj.
Реактивная мощность, вар:
Q U L UC I X I 2 U I sinj.
Полная (кажущаяся) мощность, ВА:
S U I P2 Q2 .
Лекция № 7. Анализ цепи с последовательным соединением приемников
51
52. Резонанс напряжений
Резонанс напряжений возникает при последовательном соединениииндуктивных катушек и конденсаторов. Условие резонанса напряжений:
входное реактивное сопротивление Х равно нулю.
I
R
XL
UR
UL
U
X X L X C 0,
UC
XC
ω0
U UR,
UL
f0
U L U C ,
1
.
2π L C
U L UC ,
UC
UR
I
U
1
,
LC
Z R 2 X 2 R,
I
U
I max ,
R
j 0.
Лекция № 7. Анализ цепи с последовательным соединением приемников
52
53.
Резонанс напряженийЗначение резонанса напряжений:
1. В электроэнергетических устройствах в большинстве случаев
явление нежелательное, связанное с неожиданным появлением
перенапряжений.
2. В электротехнике - связи (в радиотехнике, проволочной
телефонии), в автоматике явление резонанса напряжений широко
используют для настройки цепи на определенную частоту.
Лекция № 7. Анализ цепи с последовательным соединением приемников
53
54. Вопросы для самопроверки
1. Для каких значений электрических величинвыполняются законы Кирхгофа?
2. Что является модулем комплексного сопротивления?
3. Что является аргументом комплексного сопротивления?
4. Как связаны между собой активное, реактивное и
комплексное сопротивления?
5. Как вычислить полное сопротивление схемы?
6. От чего зависит угол φ между напряжением и током?
7. Какая мощность является потребляемой?
8. Какую энергию характеризует активная мощность?
9. Какую энергию характеризует реактивная мощность?
10. В каких единицах измеряют активную, реактивную и
полную мощности?
11. Каково условие резонанса напряжений?
12. Каково значение резонанса напряжений?
Лекция № 7. Анализ цепи с последовательным соединением приемников
54
55. Лекция № 8. Анализ цепи с последовательным соединением приемников
1. Основные законы2. Построение векторной диаграммы
3. Треугольники проводимостей
и мощностей
4. Резонанс токов
55
56. Основные законы
IU
IR
R
IL
XL
IC
XС
Для анализа цепи воспользуемся
уравнением по первому закону
Кирхгофа для комплексных значений:
I I R I L IC .
1 1 1
U
U
U
1
1
I
U
R jX L jX C R j X L X C
R
1
1
j
U .
X L XC
Y G j BL BC G j B.
Лекция № 8. Анализ цепи с последовательным соединением приемников
56
57. Построение векторной диаграммы
OIR
A
U
j
I
IC
B
IL
Построение векторной диаграммы
начинаем с вектора напряжения, которое
является одинаковым для всех элементов
схемы. Векторная диаграмма для случая,
когда
X L XC .
O
j
IR
A
IL IC
I
B
I I R2 I L IC ,
2
j Arc tg
I L IC
IR
,
Из свойств треугольника токов получаем
следующие соотношения, позволяющие
оперировать действующими
значениями:
I R I cos j,
I L IC I sin j.
Лекция № 8. Анализ цепи с последовательным соединением приемников
57
58. Треугольники сопротивлений и мощностей
Разделив все сторонытреугольника токов на
напряжение, получим подобный
ему треугольник проводимостей.
Y G 2 B2 ,
G Y cos j,
B Y sin j,
Умножив все стороны
треугольника токов на
напряжение, получим
треугольник мощностей.
IR
=G
U
j
IL IC
=B
U
I
=Y
U
j Arc tq
B
,
G
Y
G B B .
2
2
L
C
IR U= P
j
I U=S
I L I C U= Q
Комплексная проводимость – это величина, обратная комплексному
сопротивлению:
Y
1
1
,
Z R jX
Y
R jX
R jX
R
X
2
j
R jX R jX R X 2 R2 X 2 R2 X 2
Лекция № 8. Анализ цепи с последовательным соединением приемников
58
59. Резонанс токов
Этот режим наблюдается в цепи с параллельным соединениеминдуктивных катушек и конденсаторов. Условие резонанса токов:
входная реактивная проводимость В = 0.
I
I1
R1
U
XL
Y
I
G
GU
I2
R2
XC
wо/
BL
BC
w
wо/
w
XL
, Y G 2 B 2 G Ymin , I YU GU I min .
2
2
R1 X L
XC
, B L BC
2
2
R2 X C
Лекция № 8. Анализ цепи с последовательным соединением приемников
59
60. Резонанс токов
Построим векторную диаграмму. Величины, общей для схемы, нет.Поэтому сначала построим векторные диаграммы для отдельных
ветвей, в которых элементы соединены последовательно
U
j
UL
j
1
UR
2
UR
1
U
I1
I2
2
UC
Построим объединенную векторную диаграмму
U
j
I
1
I1
j
I2
2
Применение режима резонанса токов:
1. Фильтр-пробка для определенной частоты.
2. Для улучшения коэффициента мощности.
Лекция № 8. Анализ цепи с последовательным соединением приемников
60
61. Вопросы для самопроверки
1. Что является модулем комплексной проводимости?2. Как связаны между собой активная, реактивная
и комплексная проводимости?
3. Как вычислить полную проводимость схемы?
4. Каков порядок построения векторной диаграммы?
5. Каково условие резонанса токов?
6. Для чего применяют режим резонанса?
Лекция № 8. Анализ цепи с последовательным соединением приемников
61
62. Лекция № 9. Расчет цепей синусоидального тока
1. Цепь с одним источником энергии2. Цепь с несколькими источниками энергии
3. Мощности в цепях синусоидального тока
4. Понятие о коэффициенте мощности
и способах его улучшения
62
63. Цепь с одним источником энергии
I1a
I
R b
XL
R1
XL
c
d
XC
I2
Вычислить токи в цепи с одним
источником энергии, если
известны значения
1
U , R, R1 , X L , X L1 , X C
U
Построить векторную
диаграмму.
Решение
1. Выявим узлы (с и d), ветви, направим токи.
2. Для расчета токов в схеме с одним источником энергии
рационально использовать метод эквивалентных
преобразований.
Эквивалентное комплексное сопротивление:
Z R jX L
R jX jX .
1
L1
C
R1 jX L jX C
U
I
.
3. Комплекс тока в свернутой схеме найдем по закону Ома:
Z
4. Токи в пассивных параллельных ветвях вычислим по формулам:
I1
jX C
I,
R1 jX L1 jX C
I2
R1 jX L1
R1 jX L1 jX C
I.
5. Действующие значения токов являются модулями комплексных значений.
Лекция № 9. Расчет цепей синусоидального тока
63
64. Цепь с одним источником энергии
Векторную диаграмму строим в соответствии с алгоритмом:U
U bc
I2
j
j
I
U ab
1
U cd
I1
1. Построим вектор напряжения между двумя узлами U cd .
2. Построим векторы токов в пассивных параллельных ветвях I1 и I 2 .
3. Построим вектор тока
I.
4. Вектор входного напряжения складывается из векторов трех
напряжений:
U ab , U bc и U cd .
Лекция № 9. Расчет цепей синусоидального тока
64
65. Цепь с несколькими источниками энергии
ci1
R1
a
i3
i2
C2
L1
n
k
e1
R3
e2
m
Расчет можно выполнить методом
непосредственного
использования законов Кирхгофа
e3
b
Система уравнений электрического
состояния в дифференциальной
форме:
i1 i2 i3 0;
di1
1
R1i1
L1
i2dt e1 e2 ;
dt
C
2
1
i2 dt R3i3 e2 e3 .
С2
Для расчета токов систему
уравнений электрического
состояния нужно записать
для комплексных значений:
I1 I 2 I 3 0;
jX L1 I1 R1 I1 jX C2 I 2 E1 E2 ;
jX C2 I 2 R3 I 3 E2 E3 .
Решением системы найдем комплексные значения токов.
Лекция № 9. Расчет цепей синусоидального тока
65
66. Расчет методом напряжения между двумя узлами выполняют в два этапа:
Цепь с несколькими источниками энергииc
i1
R1
a
Расчет методом напряжения между
двумя узлами выполняют в два этапа:
i3
i2
C2
L1
R3
n
k
m
e2
e1
а) вычисление напряжения
по формуле
e3
U ab
b
U ab
J YE ,
Y
1
1
1
E1
E2 E3
R1 jX L1
jX C2
R3
U ab
;
1
1
1
R1 jX L1 jX C2 R3
б) вычисление токов:
I1
U ab E1
,
R1 jX L1
U ab E2
I2
,
jX C2
I3
U ab E3
.
R3
Лекция № 9. Расчет цепей синусоидального тока
66
67. Мощности в цепях синусоидального тока
При расчетах удобно пользоваться понятиемкомплексной мощности:
*
S U I .
Активная мощность является действительной
составляющей комплексной мощности:
*
P Re S Re U I .
Реактивная мощность является мнимой
составляющей комплексной мощности:
*
Q Im S Im U I .
Лекция № 9. Расчет цепей синусоидального тока
67
68.
Понятие о коэффициенте мощности и способах его улучшенияP S cos j.
Активная мощность
Косинус угла j называют коэффициентом мощности, потому что от
его величины зависит, какая доля полной мощности потребляется. Под
улучшением коэффициента мощности понимают увеличение cos j .
cos j
P
S
Способы улучшения
P
P Q
2
2
R
Z
R
R X
2
2
.
cos j :
Естественный путь – увеличение активной мощности, повышение
загрузки оборудования.
Искусственный путь – уменьшение реактивной мощности, которая
связана с реактивным сопротивлением.
Лекция № 9. Расчет цепей синусоидального тока
68
69. Вопросы для самопроверки
1. Чем отличается расчет цепей синусоидального токаот цепей постоянного тока?
2. Каков алгоритм построения векторной диаграммы для
схемы с двумя узлами и одним источником энергии?
3. Что назвали коэффициентом мощности?
4. От чего зависит угол φ между напряжением и током?
5. Что понимают под улучшением коэффициента
мощности?
6. Зачем нужно улучшать коэффициент мощности?
7. Какие пути улучшения коэффициента мощности
Вы знаете?
Лекция № 9. Расчет цепей синусоидального тока
69
70.
Лекция № 10. Электрические цепис взаимной индуктивностью
1. Основные понятия и определения
2. Анализ цепи с последовательным соединением
индуктивно связанных катушек
3. Расчет электрических цепей при наличии
взаимной индуктивности
70
71. Основные понятия и определения
Коэффициент, характеризующий способность тока создаватьмагнитный поток в другом контуре, называют взаимной
индуктивностью М:
М 12
dψ12
.
di1
Степень индуктивной связи характеризуют коэффициентом
связи k, под которым понимают отношение:
k
где
X M Mω
M
Mw
L1 L2
L1ω L2ω
XM
,
X L1 X L2
– сопротивление взаимной индукции.
Для решения вопроса о знаках прибегают к специальной разметке
зажимов индуктивно связанных катушек. Два зажима двух индуктивно
связанных элементов называют одноименными, если при одинаковых
направлениях токов относительно них магнитные потоки самоиндукции
и взаимоиндукции складываются. Одноименные зажимы обозначают
точками.
Лекция № 10. Электрические цепи с взаимной индуктивностью
71
72.
Анализ цепи с последовательным соединением индуктивно связанных катушекU2
Согласное включение
i
R1
uR
1
uL
u1
u
R2
L1
1
uM
uL
2
2
U
R2I
L2
uR
= jX M I
U1
=
jX L2I
jX M I
uM
u2
jX L1I
R1I
I
Уравнение электрического состояния в дифференциальной форме:
u u1 u2 R1i L1
di
di
di
di
M R2i L2 M .
dt
dt
dt
dt
Для комплексных значений:
U U1 U 2 R1I jX L I jX M I R2 I jX L2 I jX M I R1 R2 j X L1 X L2 2 X M I Z согл. I .
Комплексное сопротивление:
где
Z согл. Rсогл. jX согл. ,
Rсогл. R1 R2 , X согл. X L1 X L2 2 X M .
Лекция № 10. Электрические цепи с взаимной индуктивностью
72
73.
Анализ цепи с последовательным соединением индуктивно связанных катушекВстречное включение
i
R1
uR
1
R2
L1
uL
1
uL
2
u1
u
=
- jX M I
L2
uR
uM
jX L2I
2
uM
jX L1I - jX M I
U
u2
R1I
=
U2
I
U1
R2I
Уравнение электрического состояния в дифференциальной форме:
di
di
di
di
u u1 u2 R1i L1 M R2i L2 M .
dt
dt
dt
dt
Для комплексных значений:
U U1 U 2 R1I jX L I jX M I R2 jX L I jX M I R1 R2 j X L X L 2 X M I Z встр.I .
1
2
Комплексное сопротивление
где
1
2
Z встр. Rвстр. jX встр. ,
Rсогл. R1 R2 , X согл. X L1 X L2 2 X M .
Лекция № 10. Электрические цепи с взаимной индуктивностью
73
74. Расчет электрических цепей при наличии взаимной индуктивности
12
R1
XL
Составим систему уравнений по законам Кирхгофа:
I2
I1
R2
XM
XL
1
2
I1 I 2 I 3 0;
R1 I1 jX L1 I1 jX M I 2 U13 ;
R2 I 2 jX L2 I 2 jX M I1 U 23 .
I3
3
1
2
I1
I2
R1
R2
±
±
X L1 XM
XL 2 XM
I3
± XM
j X
I
R1 I1 j X L1
X M I1 jX M I 3 U13 ,
R2 I 2
XM
L2
2
jX M I 3 U 23 .
Правило развязки
Верхние знаки относятся к случаю,
когда в узле соединены одноименные
зажимы индуктивно связанных элементов.
3
Лекция № 10. Электрические цепи с взаимной индуктивностью
74
75. Вопросы для самопроверки
1.2.
3.
4.
5.
6.
7.
8.
9.
Что назвали явлением взаимоиндукции?
Что назвали взаимной индуктивностью?
Что понимают под коэффициентом связи k?
Чему равно сопротивление взаимной индукции?
Какое включение индуктивно связанных катушек называют
согласным, какое – встречным?
Чему равно реактивное сопротивление двух индуктивно
связанных катушек при согласном и встречном включениях?
Какие методы расчета можно применять при наличии
взаимной индуктивности?
Что назвали развязкой магнитных связей?
Каково правило развязки магнитных связей?
Лекция № 10. Электрические цепи с взаимной индуктивностью
75
76.
Лекция № 11. Трехфазные цепи1. Достоинства трехфазных цепей
2. Трехфазный генератор
3. Классификация и способы включения
в трехфазную цепь приемников
76
77. Достоинства трехфазных цепей
Наличие вращающегося магнитного поля, на основе которогопостроен асинхронный двигатель.
При передаче энергии на расстояние в трехфазных цепях
по сравнению с однофазными достигается существенная экономия
материала проводов.
Возможность иметь два эксплуатационных напряжения.
Трехфазные цепи – это частный случай многофазных систем.
Многофазной системой называют совокупность электрических
цепей, в которых действуют синусоидальные ЭДС одинаковой частоты,
отличающиеся одна от другой по фазе и индуктируемые в одном
источнике питания.
Каждую из цепей, входящих в многофазную систему, называют
фазой.
Трехфазная цепь состоит из трех основных элементов: генератора,
линии передачи и приемника.
Лекция № 11. Трехфазные цепи
77
78. Трехфазный генератор
Принцип действия и разметка зажимов фаз обмоткиПростейший трехфазный генератор состоит из неподвижной
(статора) и подвижной (ротора) частей. Статор – это полый цилиндр,
набранный из листов электротехнической стали. Ротор является
электромагнитом. Его необходимо принудительно вращать.
При пересечении магнитными силовыми линиями поля ротора
обмоток статора в последних наводятся ЭДС одинаковой величины
с фазовым сдвигом 1200. Такую систему называют симметричной.
A
eA
X
eC
C
Z
Y
eB
B
Буквами А, В, С обозначают начала фаз обмоток; X, Y, Z – их концы
Лекция № 11. Трехфазные цепи
78
79. Трехфазный генератор
Способы изображения симметричной системы ЭДСГрафический
Симметричная система ЭДС – это три синусоиды.
Тригонометрический
ЭДС можно записать
следующим образом:
eA Em sin ω t ,
как
синусоидальные
eB Em sin( ω t 120 ),
функции
времени
eС Em sin( ω t 120 ).
Вращающимися векторами в декартовой системе координат
Комплексными числами
+1
EA E, EB Ee
EA
+j
EC
EB
EC Ee
j
2
3
j
2
3
Ee
Лекция № 11. Трехфазные цепи
Ee j120 a 2 E ,
j120
Ee
j
4
3
aE.
79
80. Способы соединения фаз обмоток генератора
Трехфазный генераторСпособы соединения фаз обмоток генератора
Соединение звездой
Соединение треугольником
A(Z)
A
uA
eA
uAB
eC
N
uCA
C(Y)
eB
C
uC
uB
eC
eA
eB
B(X)
B
uBC
Получается при объединении
концов фаз обмоток X, Y, Z
в нейтральную точку N. Условное
обозначение Y.
Получается при соединении
начала одной фазы с концом
другой. Условное обозначение .
Лекция № 11. Трехфазные цепи
80
81.
Трехфазный генераторУсловные положительные направления фазных
и линейных напряжений и соотношения между ними
Обычно обмотки генератора соединяют звездой. Напряжения между началом
и концом фазы называют фазными, а напряжения между началами фаз
генератора –линейными.
Топографическая диаграмма фазных и линейных напряжений
A
U AB U A U B ,
UAB
UCA UA
0
U BC U B U C ,
0
120
N
UC
120
UB
0
120
C
UBC
B
U CA U C U A .
Лекция № 11. Трехфазные цепи
81
82.
Классификация и способы включения в трехфазную цепь приемниковТрехфазные цепи бывают четырех- и трехпроводные. Фазы
генератора и фазы приемника могут быть соединены по-разному.
Приемники, включаемые в трехфазную цепь, могут быть однофазными и трехфазными. Начала и концы фаз трехфазных приемников
обозначают соответственно буквами а, х; b, y; с, z.
Трехфазные приемники могут быть симметричными
и несимметричными. У симметричных приемников равны между собой
комплексные сопротивления фаз:
Z a Zb Z c.
У несимметричного приемника нагрузка может быть равномерной,
если сопротивления фаз равны между собой по величине (по модулю),
или однородной, если
ja jb jc .
Лекция № 11. Трехфазные цепи
82
83. Вопросы для самопроверки
1. Перечислите преимущества трехфазных цепей.2. Какие способы изображения симметричной системы ЭДС
вы знаете?
3. Как получают соединение фаз обмоток генератора
звездой и треугольником?
4. Какие напряжения называют фазными, какие –
линейными?
5. Каково соотношение фазных и линейных напряжений при
соединении фаз звездой и треугольником?
6. Какие трехфазные приемники называют симметричными?
Лекция № 11. Трехфазные цепи
83
84.
Лекция № 12. Расчет трехфазных цепей1. Соединение фаз приемника
треугольником
2. Соединение звездой трехпроводной
84
85. Соединение фаз приемника треугольником
Приемник несимметричныйIA
A
a
U ca
EA
EC
I ca
N
U ab
Z ca
Z bc
Z ab
I ab
b
c
EB
C
B
U bc
IB
I bc
IC
U ab
I ab
,
Z ab
U bc
I bc
,
Z bc
U ca
I ca
,
Z ca
I A I ab I ca ,
I B I bc I ab ,
I C I ca I bc ,
I A I B I C 0.
Лекция № 12. Трехфазные цепи
85
86. Соединение фаз приемника треугольником
Топографическая диаграмма напряжений и векторная диаграмма токовAa
jca
Ica
UAB
UCA
IA
Ica
Iab
IB
jab
Iab
Bb
Ibc
Cc
j
Ibc
bc
IC
UBC
Построение начинают
с топографической диаграммы
напряжений генератора. Далее
строят топографическую диаграмму
напряжений приемника. Затем
проводят векторы фазных токов под
соответствующими углами
к векторам фазных напряжений.
Векторы фазных токов
переносят в центр треугольника
напряжений. Векторы линейных
токов получают как геометрические
разности соответствующих фазных
токов.
Лекция № 12. Трехфазные цепи
86
87. Соединение фаз приемника треугольником
Приемник симметричныйУ симметричного приемника
комплексные сопротивления
фаз равны между собой
Aa
UAB
Z ab Z bc Z ca .
UCA
IA
Ica
I ab
IB
IC
Cc
UBC
Ibc
Iab
jab
Bb
I A 3I ab e j 30 ; I B I A e j120 ; I C I A e j120 .
Лекция № 12. Трехфазные цепи
87
88.
Соединение звездой трехпроводнойIA
A
a
Ia
EA
EC
Za
UA
UnN
N
C
UC
UB
B
n
Zc
EB
c
IB
Ic
Ua
Zb
Uc
Ub
Ib b
Cc
IC
Лекция № 12. Трехфазные цепи
88
89.
Соединение звездой трехпроводнойПриемник несимметричный
Напряжение между нейтральными точками генератора
и приемника можно вычислить по формуле
U nN
Y a U A Y b U B Y c UC
.
Y a Yb Yc
Линейные и равные им соответственно фазные токи можно
определить по закону Ома для активной ветви:
I A I a Y a U A U nN ,
I B I b Y b (U B U nN ),
I C I c Y c U C U nN .
Лекция № 12. Трехфазные цепи
89
90.
Соединение звездой трехпроводнойПриемник симметричный
Z a Zb Z c Z, Y a Y b Y c Y ,
Если приемник симметричный
напряжение между нейтральными точками генератора и приемника
не возникает.
Aa
I A Ia
UCA
UA U a
IC
Nj
j
n
j
IB
UC Uc
Cc
UA
,
Za
I B I A e j120 ,
UAB
I C I A e j120 .
IA
UB Ub
Bb
Лекция № 12. Трехфазные цепи
90
91. Вопросы для самопроверки
1. По каким законам вычисляют токи при соединении фазприемника треугольником?
2. Чему равно напряжение на фазе приемника при соединении
его треугольником?
3. Каков порядок построения векторно-топографической
диаграммы при соединении фаз приемника треугольником?
4. Каково соотношение фазного и линейного токов при
симметричном приемнике, соединенном треугольником?
5. Каким методом рассчитывают токи при соединении звездой
трехпроводной?
6. Что назвали напряжением смещения нейтрали?
7. Каков порядок построения векторно-топографической
диаграммы при несимметричном приемнике?
8. Чему равно напряжение на фазе симметричного приемника
при соединении звездой трехпроводной?
Лекция № 12. Трехфазные цепи
91
92.
Лекция № 13. Расчет трехфазных цепей(продолжение)
1. Соединение звездой четырехпроводной
с нейтральным проводом без сопротивления
2. Мощности трехфазных цепей
3. Способы измерения активной мощности
92
93. Соединение звездой четырехпроводной с нейтральным проводом без сопротивления
IAA
a
Ia
EA
EC
Za
UA
I nN
N
C
UC
B
UB
n
Zc
EB
c
IB
Ic
Ua
Zb
Uc
Ub
Ib b
IC
Приемник несимметричный
Линейные и фазные токи определяют по закону Ома:
I A Ia
U
UA
U
; I B Ib B ; IC I c C .
Za
Zb
Zc
Ток в нейтральном проводе:
I nN I a I b I c .
Лекция № 13. Расчет трехфазных цепей (продолжение)
93
94. Соединение звездой четырехпроводной с нейтральным проводом без сопротивления
Приемник симметричныйЕсли приемник симметричный, токи в фазах и линиях равны между
собой по величине и сдвинуты относительно друг друга по фазе на 120 ○
Достаточно вычислить только один ток:
UA
I A Ia
.
Za
Тогда
I B Ib I a e
j120
a IA,
2
IC I c I A e j120 a I A .
Ток в нейтральном проводе:
I nN I a I b I c 0.
Лекция № 13. Расчет трехфазных цепей (продолжение)
94
95.
Мощности трехфазных цепейМощности р, Р и Q находят как суммы мощностей трех фаз:
р рф , Р Рф ,
Q Qф .
Потребляемой является активная мощность. Активную мощность
фазы проще всего определить по формуле
Рф Uф I ф cos jф Rф Iф2 .
Реактивную мощность фазы ищут следующим образом:
Qф Uф I ф sin jф Х ф I ф2 .
Полную мощность трехфазной цепи вычисляют как гипотенузу
суммарного треугольника мощностей:
S P2 Q2
Р 3 U л I л cos jф ,
P Q .
2
ф
Q 3 U л I л sin jф ,
2
ф
S P2 Q2 3 U л I л .
Лекция № 13. Расчет трехфазных цепей (продолжение)
95
96.
Способы измерения активной мощностиДля измерения активной мощности используют
ваттметры. Число ваттметров и способ их включения зависят от
способа соединения фаз приемника и от их параметров.
Ваттметр показывает активную мощность, которую
вычисляют по формуле
^
*
PW UW IW cos UW IW Re S W Re UW IW .
Угол сдвига фаз между ними соответствует одинаковым
положительным направлениям, отмеченным звездочками.
Лекция № 13. Расчет трехфазных цепей (продолжение)
96
97.
Способы измерения активной мощностиСпособ одного ваттметра
*
W *
Z
N
n
Z
*
W *
Z
Z
Применяют
при симметричной
нагрузке
Z
Z
B
C
B
C
Если фаза приемника
следующим образом:
A
B
C
*
* W
недоступна,
можно
*
A
*
W
B
Симметричный
приемник
подключить
Симметричный
приемник
C
RД
RД
N
Лекция № 13. Расчет трехфазных цепей (продолжение)
97
98.
Способы измерения активной мощностиСпособ двух ваттметров
A
B
C
IА
*
* W1
IB
IС
Применяют в трехпроводной цепи
при несимметричной нагрузке.
*
S S W1 S W2 U AB I A U CB I C
Z
* W2
*
*
*
U A U B I A U C U B I C
*
*
*
* *
U A I A U B I A IC U C IC
S A S B SC.
*
Лекция № 13. Расчет трехфазных цепей (продолжение)
98
99.
Способы измерения активной мощностиСпособ трех ваттметров
Применяют в четырехпроводной цепи при несимметричной
нагрузке. Каждый ваттметр измеряет активную мощность одной
фазы. Мощность системы определяют как сумму показаний
ваттметров. Метод громоздкий и неудобный.
Измерение трехфазным ваттметром
Представляет из себя конструктивное сочетание трех
однофазных ваттметров. Суммирование их показаний происходит
автоматически.
Применение измерительных комплексов
Представляется
наиболее
удобным.
Измерительные
комплексы снабжены амперметром, вольтметром и ваттметром. При
переключении тумблера происходит подключение измерительных
приборов на разные фазы.
Лекция № 13. Расчет трехфазных цепей (продолжение)
99
100. Вопросы для самопроверки
1. Чему равно напряжение на фазе приемника присоединении звездой четырехпроводной с нейтральным
проводом без сопротивления?
2. Как вычислить ток в нейтральном проводе?
3. Каков алгоритм построения векторно-топографической
диаграммы при соединении звездой четырехпроводной
с нейтральным проводом без сопротивления?
4. Какие мощности различают в трехфазных цепях?
5. Какие способы измерения активной мощности Вы знаете?
6. В каких цепях для измерения активной мощности
применяют метод двух ваттметров?
Лекция № 13. Расчет трехфазных цепей (продолжение)
100
101.
Лекция № 14. Электрические цепипри несинусоидальных
периодических воздействиях
1. Причины возникновения
2. Способы изображения несинусоидальных
периодических функций
3. Действующие значения несинусоидальных
периодических токов и напряжений
4. Коэффициенты, характеризующие периодические
несинусоидальные функции
5. Мощности в цепях несинусоидального тока
6. Расчет однофазных цепей при несинусоидальных
периодических воздействиях
Лекция № 14. Электрические цепи при несинусоидальных периодических воздействиях
101
102. Причины возникновения
Несовершенство промышленных генераторовэлектрической энергии.
Существование генераторов специальных,
отличных от синусоиды, форм сигналов.
Наличие в цепях нелинейных элементов,
искажающих форму синусоидальных кривых
электрических величин.
Лекция № 14. Электрические цепи при несинусоидальных периодических воздействиях
102
103.
Способы изображения несинусоидальных периодических функцийГрафический
f(ωt)
wt
Аналитический
Если периодическая функция удовлетворяет условию Дирихле (на всяком
конечном интервале имеет конечное число разрывов первого рода
и конечное число экстремумов), то ее можно разложить в ряд Фурье:
f ω t A0 A1m sin ω t ψ1 A2m sin 2ω t ψ2 Aкm sin к ω t ψк .
Совокупность
гармонических
составляющих
несинусоидальной
периодической функции называют ее дискретным частотным спектром.
Первую гармонику ряда называют основной, остальные – высшими.
Лекция № 14. Электрические цепи при несинусоидальных периодических воздействиях
103
104.
Действующие значения несинусоидальных периодических токов и напряженийДействующее значение тока:
T
1 2
I
i d t,
T 0
I I 02 I12 I 22 I32
Действующие значения напряжения и ЭДС определяют аналогично:
U U02 U12 U 22 U32 ,
Amax
А max
wt
E E02 E12 E22 E32 .
Практической синусоидой называют
такую кривую, у которой разность
между соответствующими точками
кривой и ее первой гармоники
не превышает 5 % от максимального
значения.
Лекция № 14. Электрические цепи при несинусоидальных периодических воздействиях
104
105.
Коэффициенты, характеризующие периодические несинусоидальные функцииКоэффициент амплитуды определяют как отношение
максимального значения к действующему:
ka
Аmax
.
А
Для синусоиды
ka 2 1, 41.
Коэффициент искажения – это отношение действующего
значения основной гармоники к действующему значению всей кривой:
ku
A1
.
A
Для синусоиды
ku 1.
Коэффициент формы – это отношение действующего
к среднему по модулю значению:
А
kф
.
Аср
Для синусоиды
kф
2 2
1,11.
Лекция № 14. Электрические цепи при несинусоидальных периодических воздействиях
105
106.
Мощности в цепях несинусоидального токаАктивную мощность получают суммированием активных мощностей
всех подсхем:
P P0 P1 P2 Pк .
Реактивную мощность вычисляют суммированием
мощностей подсхем с синусоидальными токами:
реактивных
Q Q1 Q2 Qк
Полную мощность определяют как произведение действующих
значений напряжения и тока в схеме: S = UI.
Мощность искажения:
UЭ
q
IЭ
T S 2 P2 Q2 .
Отношение активной мощности к полной
называют коэффициентом мощности и иногда
приравнивают к косинусу некоторого условного
угла θ :
χ
P
cos q.
S
Лекция № 14. Электрические цепи при несинусоидальных периодических воздействиях
106
107.
Расчет однофазных цепей при несинусоидальных периодических воздействияхИсточник несинусоидальной ЭДС представим как ряд последовательно
соединенных источников ЭДС. Источник несинусоидального тока – как ряд
параллельно соединенных источников тока с разной частотой.
E0
e (t)
e1
i (t)
J0
i1
i2
e2
При расчете применяют метод наложения. Рационально разбить схему
на столько подсхем, сколько частот получается при разложении в ряд
Фурье несинусоидальных ЭДС и токов.
Действующие значения токов, напряжений и ЭДС определяют через
соответствующие действующие значения в подсхемах по формулам:
I I 02 I12 I 22 I к2 ,
Активная мощность
U U 02 U12 U 22 U к2 ,
Е Е02 Е12 Е22 Ек2 .
P P0 P1 P2 Pк .
Лекция № 14. Электрические цепи при несинусоидальных периодических воздействиях
107
108. Вопросы для самопроверки
1. Каковы причины возникновения несинусоидальныхпериодических токов и напряжений?
2. Что представляет собой ряд Фурье?
3. Что называют дискретным частотным спектром?
4. Чему равно действующее значение несинусоидальной
периодической функции?
5. Что называют практической синусоидой?
6. Что называют эквивалентной синусоидой?
7. Как вычисляют активную, реактивную и полную мощности
в цепях с несинусоидальными периодическими
воздействиями?
8. Что называют мощностью искажения?
9. Какой метод используют для расчета цепей при
несинусоидальных периодических воздействиях?
Лекция № 14. Электрические цепи при несинусоидальных периодических воздействиях
108
109.
Лекция № 15. Классический методрасчета переходных процессов
1. Основные понятия. Законы коммутации
2. Суть классического метода расчета
переходных процессов
3. Подключение реального конденсатора
к источнику постоянного напряжения
4. Определение длительности переходного
процесса
109
110. Основные понятия. Законы коммутации
Если в электрической цепи есть конденсаторы и индуктивныекатушки, то при переходе от одного установившегося режима к другому
наблюдается переходный процесс. Сам процесс изменения режима
работы цепи (включение или выключение рубильника) в электротехнике
называют коммутацией.
Последовательность событий такова: установившийся режим →
коммутация → переходный процесс → новый установившийся режим.
Переходные процессы подчиняются двум законам коммутации.
Первый закон коммутации: ток в ветви с индуктивной катушкой
не может измениться скачком:
iL (0 ) iL (0 ).
Второй закон коммутации: напряжение на конденсаторе
не может измениться скачком:
uС (0 ) uС (0 ).
Лекция № 15. Классические методы расчета переходных процессов
110
111.
Суть классического метода расчета переходных процессовСоставим систему уравнений электрического состояния
в дифференциальной форме для схемы замещения электрической цепи.
Как известно из математики, решение полученной системы линейных
дифференциальных неоднородных уравнений есть сумма двух слагаемых:
частного решения неоднородных уравнений и общего решения однородных
уравнений.
В качестве частного решения берут принужденный режим,
вызываемый внешними источниками энергии.
Общее решение однородного уравнения характеризует процессы,
происходящие в цепи при отсутствии внешних источников энергии.
Составляющие токов и напряжений, найденные в результате общего
решения однородных уравнений, называют свободными.
i iпр iсв ; u uпр uсв .
Когда свободные составляющие станут равны нулю, переходный
процесс закончится. Отсюда следует, что принужденный режим – это
новый установившийся режим после переходного процесса.
Лекция № 15. Классические методы расчета переходных процессов
111
112.
Подключение реального конденсатора к источнику постоянного напряжения1. Составим систему уравнений электрического
состояния. Так как схема одноконтурная, то можно
написать только одно уравнение по второму закону
Кирхгофа:
du
RC
С
dt
uС U .
Ищем решение этого уравнения как сумму двух слагаемых: uС uС пр uС св .
Найдем uС пр . uС пр U .
Вычислим uС св . Из математики известно, что свободные составляющие
меняются по экспоненциальному закону:
uС св Ае pt .
• Определим показатель степени р, который является корнем
характеристического уравнения.
RC
duС св
dt
uС св 0,
RCp 1 0,
p
1
.
RC
Лекция № 15. Классические методы расчета переходных процессов
112
113.
Подключение реального конденсатора к источнику постоянного напряжения• Определим постоянную интегрирования А.
Постоянные интегрирования определяют из начальных
условий с использованием законов коммутации.
Уравнение, по которому проводим решение, справедливо
для любого момента времени, следовательно, и для начального:
uС (0 ) uС пр (0 ) uС св (0 ).
uС (0 ) uС (0 ) 0,
uС пр (0 ) U ,
Тогда закон изменения напряжения:
uС св Ае рt A,
uС U Ue
A U .
1
t
RC
.
Лекция № 15. Классические методы расчета переходных процессов
113
114.
Подключение реального конденсатора к источнику постоянного напряженияЗакон изменения тока:
uC
U uС U U Ue
i
R
R
1
t
RC
1
t
U RC
e
.
R
iC
uC пр
U
U
R
uC
t
t
uC св
-U
Лекция № 15. Классические методы расчета переходных процессов
114
115.
Определение длительности переходного процессаТеоретически переходный процесс длится бесконечно долго.
Практически переходный процесс заканчивается через (3–5) t.
Постоянная времени – это время, в течение которого свободные
составляющие уменьшаются t в е раз.
i св
i св
t1
t2
t
t
t
Постоянной времени можно дать геометрическую интерпретацию:
t – это величина подкасательной к любой точке экспоненты.
Поэтому можно определить постоянную времени по известному графику
изменения свободной составляющей и неизвестным параметрам схемы.
Лекция № 15. Классические методы расчета переходных процессов
115
116. Вопросы для самопроверки
1. Какие законы коммутации Вы знаете?2. Как доказывают законы коммутации?
3. В чем суть классического метода расчета переходных процессов?
4. За счет чего возникают принужденные составляющие токов и напряжений?
5. Какие процессы характеризует общее решение однородного уравнения?
6. По какому закону меняются свободные составляющие?
7. Как составить характеристическое уравнение для неразветвленной цепи?
8. Сколько длится переходный процесс?
9. Каков физический смысл постоянной времени t ?
10. Как графически определить постоянную времени t ?
Лекция № 15. Классические методы расчета переходных процессов
116
117.
Лекция № 16. Переходные процессыв цепях с одним реактивным элементом
1. Разряд конденсатора на резистор
2. Подключение реальной катушки к источнику
постоянного напряжения
3. Короткое замыкание индуктивной катушки
4. Подключение реальной индуктивной катушки
к источнику синусоидального напряжения
5. Учет первого закона коммутации на практике
117
118. Разряд конденсатора на резистор
В положении ключа 1 происходитуже рассмотренный процесс заряда
конденсатора до напряжения источника
U с постоянной времени t зар R1C.
При положении
сопротивлением R.
ключа
2
конденсатор
разряжается
на
резистор
Напряжение на конденсаторе при его разряде меняется по закону
uС Ue
1
t
RC
.
Ток разряда конденсатора:
1
t
uС
U RC
iС e
.
R
R
Лекция № 16. Переходные процессы в цепях с одним реактивным элементом
118
119. Разряд конденсатора на резистор
uCiC
U
t
U
R
t
При периодическом переключении рубильника из положения
1 в положение 2 и обратно графики будут иметь вид:
uC
iC
t
Лекция № 16. Переходные процессы в цепях с одним реактивным элементом
119
120.
Подключение реальной катушки к источнику постоянного напряженияУравнение электрического состояния
в дифференциальной форме:
L
Закон изменения тока:
diL
RiL U .
dt
U U RL t
iL e .
R R
Закон изменения напряжения:
R
t
diL
U R RL t
uL L
L e Ue L .
dt
R L
Лекция № 16. Переходные процессы в цепях с одним реактивным элементом
120
121.
Короткое замыкание индуктивной катушкиДо замыкания ключа в индуктивной
катушке был ток от источника энергии.
После коммутации
входной ток будет
замыкаться по закоротке.
Закон изменения тока:
U
iL
e
R1 R
R
t
L
iL
U
R1+R
.
Лекция № 16. Переходные процессы в цепях с одним реактивным элементом
t
121
122.
Подключение реальной индуктивной катушки к источнику синусоидального напряженияВходное напряжение
u U m sin(ωt ψu ).
Уравнение электрического состояния в дифференциальной форме:
diL
L
RiL u.
dt
Лекция № 16. Переходные процессы в цепях с одним реактивным элементом
122
123.
Подключение реальной индуктивной катушки к источнику синусоидального напряженияЗакон изменения тока
iL I Lm пр sin(ωt ψi пр ) I Lm пр sin ψi пр e
R
t
L
.
Лекция № 16. Переходные процессы в цепях с одним реактивным элементом
123
124.
Учет первого закона коммутации на практикеВ момент, наступивший сразу после
коммутации, ток останется тем же, что и до
коммутации. На месте разрыва возникает
перенапряжение, так как сопротивление
воздушного промежутка велико. Это приводит
к пробою, появляется искрение (электрическая
дуга), портящее оборудование.
Ситуация ухудшается, если к зажимам индуктивной катушки подключен
вольтметр. Сопротивление вольтметра велико, ток в нем при нормальной
работе мал. При размыкании ключа большой ток индуктивной катушки,
который не может измениться скачком, будет замыкаться через вольтметр,
сопротивление которого все же меньше, чем у воздушного промежутка.
На вольтметре возникает перенапряжение, прибор может выйти из строя.
Такое же напряжение будет и на индуктивной катушке, что может привести
к пробою ее изоляции.
Поэтому нельзя отключать незашунтированную катушку с током. Сначала
нужно убрать напряжение либо параллельно подключить ветвь для
замыкания тока катушки.
Лекция № 16. Переходные процессы в цепях с одним реактивным элементом
124
125. Вопросы для самопроверки
1. Какова простейшая схема генератора пилообразного напряжения?2. Как необходимо учитывать первый закон коммутации на практике?
3. Какой закон коммутации выполняется в RL-цепях?
4. Какой режим работы цепи назвали принужденным?
5. Как определить постоянную интегрирования?
6. Как изменяются графики при изменении значений R и L?
7. Каково перераспределение токов после короткого замыкания
индуктивной катушки?
8. Чем принципиально отличаются законы изменения тока при
подключении индуктивной катушки к источникам постоянного
и синусоидального напряжения?
9. В каком случае при подключении индуктивной катушки к источнику
синусоидального напряжения переходный процесс не возникает?
10. Какой ток называют ударным?
Лекция № 16. Переходные процессы в цепях с одним реактивным элементом
125
126.
Лекция № 17. Переходные процессыв цепях с двумя реактивными элементами
1. Подключение цепи с последовательным
соединением реальной индуктивной катушки
и конденсатора к источнику постоянного
напряжения.
2. Апериодический переходный процесс.
3. Критический переходный процесс.
4. Колебательный переходный процесс.
Лекция № 17. Переходные процессы в цепях с двумя реактивными элементами
126
127. Подключение цепи с последовательным соединением реальной индуктивной катушки и конденсатора к источнику постоянного напряжения
Уравнение электрического состоянияв дифференциальной форме:
di
L Ri uС U .
dt
2
d uС R duС
1
U
uС
.
2
dt
L dt LC
LC
Лекция № 17. Переходные процессы в цепях с двумя реактивными элементами
127
128.
Подключение цепи с последовательным соединением реальной индуктивной катушкии конденсатора к источнику постоянного напряжения
Составим характеристическое уравнение на основе уравнения
электрического состояния:
R
1
p p
0.
L
LC
2
Его корни:
R
R2
1
p1,2
.
2
2L
4 L LC
В зависимости от параметров схемы возможны три вида корней
характеристического уравнения.
Лекция № 17. Переходные процессы в цепях с двумя реактивными элементами
128
129.
Апериодический переходный процессR2
1
2
4L
LC
Если
, корни будут действительными и разными. Такой
случай переходного процесса называют апериодическим.
При этом закон изменения свободной составляющей представляет
собой сумму двух экспонент:
p1t
p2t
uС св Ае
А
е
.
1
2
Закон изменения напряжения на конденсаторе при его заряде от
источника постоянного напряжения имеет вид:
uС U
U
p2 e p1t p1e p2t .
p1 p2
Закон изменения тока найдем по закону Ома:
duС
CU
U
p1t
p2t
i C
p2 p1e p1 p2e
e p1t e p2t .
dt
p1 p2
L( p1 p2 )
Лекция № 17. Переходные процессы в цепях с двумя реактивными элементами
129
130.
Апериодический переходный процессПроиллюстрируем процессы графиками
uC пр
U
i
Up2
p-12 p
uC
Up2 pt 1
p-12 p e
t
Up1 pt 2
e
p- p
12
Up1
p-12 p
Ток в начале переходного процесса и после его окончания равен нулю.
Лекция № 17. Переходные процессы в цепях с двумя реактивными элементами
130
131.
Критический переходный процесс2
R
1 , корни будут действительными и равными:
Если
4 L2 LC
p1 p2 p
R
.
2L
Такой случай переходного процесса называют критическим или
предельным апериодическим.
При этом свободная составляющая напряжения меняется по закону:
uC св A1 A2t e pt .
Закон изменения напряжения:
uС U ( U pUt )e pt U 1 (1 pt ) e pt .
Закон изменения тока:
duС
iС C
.
dt
Графики аналогичны приведенным на предыдущем слайде.
Лекция № 17. Переходные процессы в цепях с двумя реактивными элементами
131
132.
Колебательный переходный процессR2
1
Если 4 L2 LC , корни будут комплексными сопряженными.
Такой случай переходного процесса называют колебательным.
Введем обозначения:
R
β – коэффициент затухания;
2L
1
R2
ω0 – угловая частота собственных колебаний контура.
LC 4 L2
Тогда
p1,2 β jω0 .
Свободную составляющую удобно записать как синусоиду, затухающую
по экспоненте:
uС св Ae
βt
sin(ω0t λ).
Лекция № 17. Переходные процессы в цепях с двумя реактивными элементами
132
133.
Закон изменения напряжения:U
uС U
e βt sin(ω0t λ).
ω0 LC
Закон изменения тока:
duС
U βt
iС C
e sin ω0t.
dt
ω0 L
Лекция № 17. Переходные процессы в цепях с двумя реактивными элементами
133
134. Вопросы для самопроверки
1. Какие законы коммутации выполняются в цепи, содержащейиндуктивную катушку и конденсатор?
2. Какой режим назвали принужденным?
3. Как составить характеристическое уравнение для
неразветвленной цепи?
4. Каким образом ищут постоянные интегрирования?
5. Как получают второе уравнение для вычисления постоянных
интегрирования?
6. В каком случае переходный процесс будет апериодическим?
7. В каком случае переходный процесс будет критическим?
8. В каком случае переходный процесс будет колебательным?
9. От чего зависят корни характеристического уравнения?
Лекция № 17. Переходные процессы в цепях с двумя реактивными элементами
134
135.
Лекция № 18. Расчет нелинейныхэлектрических цепей постоянного тока
графическими методами
1. Основные понятия и определения
2. Линейные эквивалентные схемы замещения
нелинейных элементов
3. Расчет нелинейной цепи с последовательным
соединением элементов
135
136. Основные понятия и определения
Нелинейные электрические цепи содержат нелинейные элементы,параметры которых зависят от тока либо напряжения.
Все НЭ делят на две большие группы: неуправляемые
и управляемые.
К неуправляемым НЭ относятся лампа накаливания, бареттер,
диод, газотрон.
Управляемыми НЭ являются трех - и более электродные лампы,
транзисторы, тиристоры.
Вольт-амперная характеристика (ВАХ) НЭ может быть
симметричной и несимметричной.
Лекция № 18. Расчет нелинейных электрических цепей постоянного тока графическими методами 136
137. Основные понятия и определения
Статическое сопротивление Rст характеризует НЭ в неизменномрежиме. Оно равно отношению напряжения на НЭ к току через него:
Rст
U
.
I
Статическое сопротивление можно определить тангенсом угла α между
соответствующей осью координат и прямой, соединяющей рабочую точку
с нулевой. При изображении ВАХ НЭ ток и напряжение могут быть
отложены на разных координатных осях.
Дифференциальное (динамическое) сопротивление R равно отношению
д
бесконечно малого приращения напряжения на НЭ к соответствующему
бесконечно малому приращению тока:
dU
Rд
.
dI
Лекция № 18. Расчет нелинейных электрических цепей постоянного тока графическими методами 137
138.
Линейные эквивалентные схемы замещения нелинейных элементовРасчет нелинейных цепей очень сложен. Но если
рабочая точка перемещается на небольшом участке,
который можно считать практически линейным, то нелинейный резистор
можно заменить линейной эквивалентной схемой, состоящей из источника
энергии и резистора сопротивлением Rд .
U Rд I E0 .
E
U
I 0,
Rд
Rд
U
Iд ,
Rд
E0
J0 ,
Rд
Iд J0 I .
Лекция № 18. Расчет нелинейных электрических цепей постоянного тока графическими методами 138
139.
Расчет нелинейной цепи с последовательным соединением элементовОпределить ток в цепи и напряжения на НЭ
входное напряжение U и ВАХ каждого элемента.
I
U
НЭ1
U1
U 1 иU 2 ,
если заданы
НЭ2
2
Лекция № 18. Расчет нелинейных электрических цепей постоянного тока графическими методами 139
140.
Расчет нелинейной цепи с последовательным соединением элементовЗадачу можно решить двумя путями
1. Отыскание рабочей точки
на результирующей ВАХ.
Ток в цепи один. Входное напряжение на
основании второго закона Кирхгофа
складывается из напряжений на отдельных
НЭ. В рассматриваемой цепи
U U1 U 2 .
Лекция № 18. Расчет нелинейных электрических цепей постоянного тока графическими методами 140
141.
Расчет нелинейной цепи с последовательным соединением элементов2. Отыскание рабочей точки на пересечении ВАХ одного элемента
с зеркальным отображением ВАХ другого элемента.
Ток в цепи один, поэтому
I1 I 2 I .
Строим график I (U1 ).
В рабочей точке на
основании второго закона Кирхгофа
напряжение
U1 U U 2 .
Построим график
I (U U 2 ).
Очевидно, что графики пересекаются в рабочей точке А.
Находим соответствующие ей значения тока I и напряжений U1 и U 2 .
Этот метод рационально использовать для цепи с двумя
элементами, один из которых – линейный.
Лекция № 18. Расчет нелинейных электрических цепей постоянного тока графическими методами 141
142. Вопросы для самопроверки
1. Чем нелинейный элемент отличается от линейного?2. На какие группы делят нелинейные элементы?
3. Чем линейный элемент с симметричной ВАХ принципиально
отличается от нелинейного элемента с несимметричной ВАХ?
4. Как можно графически определить статическое
и дифференциальное сопротивления?
5. Каков алгоритм составления линейной схемы замещения,
эквивалентной на рабочем участке ВАХ нелинейному элементу?
6. Какие пути отыскания рабочей точки при последовательном
соединении нелинейных элементов Вы знаете?
7. Для каких цепей рационально использовать отыскание рабочей
точки на пересечении ВАХ одного элемента с зеркальным
отображением ВАХ второго элемента?
8. Как построить результирующую ВАХ цепи с последовательным
соединением элементов?
Лекция № 18. Расчет нелинейных электрических цепей постоянного тока графическими методами 142
143.
Лекция № 19. Расчет нелинейныхэлектрических цепей постоянного тока
графическими методами (продолжение)
1. Расчет нелинейной цепи с параллельным
соединением элементов
2. Расчет нелинейной цепи со смешанным
соединением элементов
3. Расчет нелинейных цепей методом напряжения
между двумя узлами
143
144. Расчет нелинейной цепи с параллельным соединением элементов
Определить все токи, если заданы входное напряжение и ВАХ каждогонелинейного элемента.
Лекция № 19. Расчет нелинейных электрических цепей постоянного тока графическими методами 144
145.
Расчет нелинейной цепи с параллельным соединением элементовНа ВАХ отдельных элементов находим токи I1 и I 2 .
Входной ток на основании первого закона Кирхгофа равен сумме
токов в пассивных ветвях:
1
2
I I I .
Если в анализируемой цепи
нужно найти токи I1 и I 2 , а также
входное напряжение при заданном
входном токе, то рабочую точку можно
найти на результирующей ВАХ.
Лекция № 19. Расчет нелинейных электрических цепей постоянного тока графическими методами 145
146.
Расчет нелинейной цепи со смешанным соединением элементовРешение методом эквивалентных преобразований
Определить все токи, если задано
входное напряжение и ВАХ отдельных
элементов: I1 (U1 ), I 2 (U 23 ), I3 (U 23 ).
Решение заключается в постепенном построении результирующих ВАХ.
Очевидно, что сначала нужно построить результирующую ВАХ для
параллельного участка.
Затем нужно построить результирующую ВАХ всей схемы.
По заданному значению входного напряжения найдем рабочую точку
и соответствующее ей значение входного тока I1.
Лекция № 19. Расчет нелинейных электрических цепей постоянного тока графическими методами 146
147.
Расчет нелинейной цепи со смешанным соединением элементовРешение с использованием
метода эквивалентного генератора
Этот метод можно использовать для схемы
с одним нелинейным элементом, ток в котором и надо
найти. Делим схему на две части: НЭ и всю остальную
часть схемы, которая является активным
двухполюсником.
Лекция № 19. Расчет нелинейных электрических цепей постоянного тока графическими методами 147
148.
Расчет нелинейной цепи со смешанным соединением элементовАктивный двухполюсник заменим эквивалентным ему генератором.
Рабочую точку рационально найти на
пересечении ВАХ НЭ и зеркального
изображения ВАХ линейного элемента.
Лекция № 19. Расчет нелинейных электрических цепей постоянного тока графическими методами 148
149.
Расчет нелинейных цепей методом напряжения между двумя узламиЦепи с двумя узлами часто
встречаются на практике.
Рассмотрим метод на конкретном
примере.
Вычислить все токи, если заданы
ЭДС и ВАХ нелинейных элементов.
Лекция № 19. Расчет нелинейных электрических цепей постоянного тока графическими методами 149
150.
Расчет нелинейных цепей методом напряжения между двумя узлами1. Запишем уравнение на основании первого закона Кирхгофа:
I1 I 2 I 3 .
2. Приведем токи к зависимости от одного аргумента.
U ab E1 U1 ,
U ab E2 U 2 ,
3. Построим графики токов I1 (U ab ),
I 2 (U ab ),
U ab E3 U3 .
I 3 (U ab ).
4. Ищем рабочую точку
на пересечении графиков
( I1 I 2 ) f (U ab )
и I3 f (U ab ).
5. Определяем токи
в ветвях и напряжение U ab .
Лекция № 19. Расчет нелинейных электрических цепей постоянного тока графическими методами 150
151. Вопросы для самопроверки
1. Какой закон используют для анализа нелинейной цепис параллельным соединением элементов?
2. Как построить результирующую ВАХ цепи с параллельным
соединением элементов?
3. Каким методом можно сделать расчет цепи с одним
источником энергии при смешанном соединении приемников?
4. В каком случае для расчета нелинейной цепи можно
применять метод эквивалентного генератора?
5. В чем суть метода эквивалентного генератора?
6. Что является условием для нахождения рабочей точки при
решении методом напряжения между двумя узлами?
Лекция № 19. Расчет нелинейных электрических цепей постоянного тока графическими методами 151
152.
Лекция № 20. Численные методыанализа нелинейных цепей
1. Расчет нелинейных цепей
методом итераций
2. Расчет нелинейных цепей
методом Ньютона - Рафсона
152
153. Расчет нелинейных цепей методом итераций
Точность расчетов графическими методами мала и существеннозависит от субъективных факторов.
Сущность метода итерации (последовательных приближений)
заключается в аналитическом решении системы алгебраических
нелинейных уравнений. Статическое сопротивление нелинейного
элемента должно быть задано в функции от тока или напряжения.
Пусть в схеме один нелинейный элемент (НЭ), ток в котором
и надо найти. Остальную часть схемы (активный двухполюсник) заменим
эквивалентным ему генератором.
Лекция № 20. Численные методы анализа нелинейных цепей
153
154. Расчет нелинейных цепей методом итераций
Ток в схеме по закону ОмаI k 1
Ег
.
Rг Rст ( I k )
Ег 10 В Rг 5 Ом, ВАХ НЭ задана уравнением
k
.
Ik , А
Rст ( I k ) , Ом
U 3I I 2 .
I k 1 , А
0
1
2
1,428
1
1,428
1,572
1,522
2
1,522
1,478
1,544
3
1,544
1,456
1,548
4
1,548
1,452
1,549
5
1,549
1,451
1,550
6
1,550
1,450
1,550
Следовательно, ток
I 1,55 А.
Лекция № 20. Численные методы анализа нелинейных цепей
154
155. Расчет нелинейных цепей методом Ньютона – Рафсона
Итерационный процесс может быть организован различнымиметодами. Наиболее эффективным считается метод Ньютона – Рафсона.
Рассмотрим его применительно к решению одного уравнения. Пусть
нелинейное уравнение f ( x) 0 имеет единственный корень x xk 1.
В окрестности этого корня функция f ( xk 1 ) 0 разлагается в ряд Тейлора:
f ( xk 1 ) f ( xk xk ) f ( xk ) xk f ( xk ) 0,
xk 1 xk xk xk
где
xk h
f ( xk )
f ( xk )
f ( xk )
.
f ( xk )
– поправка к предыдущему решению.
Лекция № 20. Численные методы анализа нелинейных цепей
155
156. Расчет нелинейных цепей методом Ньютона – Рафсона
Алгоритм итерационного метода Ньютона – Рафсона, которыйреализуется следующим образом:
1. Задаем начальное приближенное значение искомого решения
x0 (k 0)
2. Определяем поправку h0 . Для ее вычисления по выражению
функции находим производную.
3. Определяем уточненное значение корня
х1 х0 h0
4. Повторяем процесс на следующем шаге и уточняем предыдущее
решение до необходимой точности.
f ( xk ) tg k
f ( xk )
hk
или
hk
f ( xk ) f ( xk )
f ( xk ) tg k
Лекция № 20. Численные методы анализа нелинейных цепей
156
157. Расчет нелинейных цепей методом Ньютона – Рафсона
Геометрическая интерпретация методаЛекция № 20. Численные методы анализа нелинейных цепей
157
158. Вопросы для самопроверки
1. В чем суть метода итераций?2. Какова графическая иллюстрация метода простых итераций?
3. Каково условие сходимости простого итерационного процесса?
4. Каков алгоритм итерационного метода Ньютона – Рафсона?
5. Какова графическая иллюстрация метода Ньютона – Рафсона?
6. От чего зависит сходимость метода Ньютона – Рафсона?
Лекция № 20. Численные методы анализа нелинейных цепей
158
159.
Лекция № 21. Основные понятияо магнитных цепях постоянного тока
1. Основные величины, характеризующие
магнитные цепи
2. Основные законы магнитных цепей
3. Формальная аналогия между магнитными
и электрическими цепями
159
160.
Основные величины, характеризующие магнитные цепи1. Основные величины, характеризующие магнитные цепи.
Магнитная цепь – это совокупность тел для замыкания магнитного
потока.
Все вещества по магнитным свойствам делят на три группы:
1. Диамагнитные, у которых относительная магнитная проницаемость
1.
2. Парамагнитные, у которых 1.
3. Ферромагнитные, у которых 1.
Лекция № 21. Основные понятия о магнитных цепях постоянного тока
160
161.
Основные величины, характеризующие магнитные цепиВокруг каждого проводника с током возникает магнитное поле.
Интенсивность магнитного поля в каждой его точке определяют вектором
магнитной индукции В.
Единицей измерения магнитной индукции является Тесла (Тл).
Магнитное поле
магнитного поля Н .
характеризуют
также
Величины В и Н связаны зависимостью:
вектором
напряженности
В μа Н μ0μ Н .
В общем случае эта зависимость сложна. Ее устанавливают
экспериментально и представляют графически в виде кривой
намагничивания, называемой циклом (петлей) магнитного гистерезиса.
Лекция № 21. Основные понятия о магнитных цепях постоянного тока
161
162.
Основные величины, характеризующие магнитные цепиМатериалы
с
широким
циклом
магнитного
магнитотвердыми, с узким – магнитомягкими.
B
называют
B
B
H
гистерезиса
H
H
При расчетах, если позволяет требуемая точность, пользуются основной
кривой намагничивания.
Магнитный поток – поток магнитной индукции через площадь S: Ф В S.
Магнитный поток измеряют в Веберах (Вб).
Магнитодвижущая сила F WI .
Очевидно, что единицей измерения магнитодвижущей силы является
Ампер (А).
Лекция № 21. Основные понятия о магнитных цепях постоянного тока
162
163.
Основные законы магнитных цепейПринцип непрерывности магнитного потока. Линии магнитной
индукции непрерывны и замкнуты. Поэтому магнитный поток через
замкнутую поверхность Ф В dS 0. Отсюда следует, что
в неразветвленных цепях магнитный поток на всех участках одинаков,
а в разветвленных цепях алгебраическая сумма магнитных потоков в точке
разветвления равна нулю:
Ф 0.
Закон полного тока. Линейный интеграл напряженности магнитного
поля вдоль замкнутого контура равен алгебраической сумме токов,
пронизывающих этот контур:
Нdl
I.
Правило знаков: со знаком плюс записывают токи, связанные
с выбранным направлением обхода контура интегрирования правилом
правоходового винта (правой руки).
Напряженность магнитного поля принимают для средней силовой линии.
Лекция № 21. Основные понятия о магнитных цепях постоянного тока
163
164.
Формальная аналогия между магнитными и электрическими цепямиВоспользуемся законом полного тока для анализа неразветвленной
неоднородной магнитной цепи. Эта цепь представляет собой индуктивную
катушку с сердечником из ферромагнитного материала, который
усиливает магнитный поток и придает ему требуемую форму.
Сердечник изготавливают разборным, чтобы на стержень можно было
надеть катушку. В местах стыков возникают зазоры, которые учтены одним
с суммарной длиной.
Лекция № 21. Основные понятия о магнитных цепях постоянного тока
164
165.
Формальная аналогия между магнитными и электрическими цепямиДля приближенного решения делают следующие допущения:
1. Пренебрегают магнитным потоком рассеяния (Фs 0).
2. Площадь, которую пронизывает поток Ф в зазоре, считают равной
площади поперечного сечения S сердечника магнитопровода,
т. е. пренебрегают выпучиванием магнитных линий в зазоре.
3. При расчете пользуются основной кривой намагничивания.
Если сечение магнитопровода одинаково, то магнитную цепь делим на два
участка: сердечник и воздушный зазор. По закону полного тока
Hl H вlв F ,
l
lв
Ф
F.
μ×μ 0 S μ 0 S
Лекция № 21. Основные понятия о магнитных цепях постоянного тока
165
166. Вопросы для самопроверки
1.2.
3.
4.
5.
6.
7.
8.
9.
Что называют магнитной цепью?
Что называют магнитной постоянной?
В каких единицах измеряют магнитную индукцию?
Какая зависимость связывает магнитную индукцию
и напряженность магнитного поля?
Что называют основной кривой намагничивания?
Что назвали магнитным потоком и в каких единицах его
измеряют?
Что называют магнитодвижущей силой и в каких единицах
ее измеряют?
Какие основные законы магнитных цепей Вы знаете?
Назовите величины – аналоги в электрических и магнитных
цепях.
Лекция № 21. Основные понятия о магнитных цепях постоянного тока
166
167.
Лекция № 22. Расчетнеразветвленных магнитных цепей
1. Прямая задача
2. Обратная задача
3. Расчет магнитной цепи постоянного магнита
167
168. Прямая задача
При расчете магнитных цепей различают два типа задач:прямую и обратную.
В прямой задаче по заданному магнитному потоку нужно
определить магнитодвижущую силу катушки, необходимую для его
создания. Заданы геометрические размеры магнитопровода и кривая
намагничивания ферромагнетика.
Порядок решения
1. Нанесем среднюю силовую линию и определим направление МДС.
2. Разобьем магнитную цепь на участки, отличающиеся друг от друга
площадью поперечного сечения и материалом. Длины участков берем
по средней силовой линии.
3. Для каждого участка находим значения магнитной индукции,
исходя из постоянства потока вдоль всей цепи.
Ф
Так как S1 Sв , то B1 Bв
S1
Лекция № 22. Расчет неразветвленных магнитных цепей
168
169. Прямая задача
Магнитную цепь, представленную на рисунке, разбиваем на триучастка: два
из ферромагнитного материала, отличающиеся
площадью поперечного сечения, и воздушный зазор.
4. По основной кривой намагничивания,
зная индукции В1 и В2 ,
определим напряженности поля на
ферромагнитных участках Н1 и Н 2 .
Напряженность поля в воздушном
зазоре вычислим по формуле
Нв
Bв
0,8 106 Bв .
μ0
5. По закону полного тока находим МДС:
F H1l1 H 2l2 H вlв .
Лекция № 22. Расчет неразветвленных магнитных цепей
169
170.
Обратная задачаПо заданной МДС находим созданный ею магнитный поток. Для
решения обратной задачи используют формальную аналогию между
магнитными
и
электрическими
цепями.
Схема
замещения
неразветвленной неоднородной магнитной цепи аналогична схеме
замещения нелинейной электрической цепи с одним источником энергии
и последовательным соединением элементов. При расчете электрических
нелинейных цепей используют вольт-амперные характеристики (ВАХ).
Аналогом ВАХ в
магнитной
цепи является вебер-амперная
характеристика, т. е. зависимость Ф(U м ).
Для построения вебер-амперной характеристики выбирают ряд значений
Ф k и вычисляют для них магнитное напряжение U м , как в прямой задаче.
k
Лекция № 22. Расчет неразветвленных магнитных цепей
170
171.
Обратная задачаРешение обратной задачи возможно двумя способами
1. Отыскание рабочей точки на результирующей вебер-амперной
характеристике по заданному значению МДС
В неразветвленной магнитной цепи поток один, а МДС F равна
сумме магнитных напряжений отдельных участков. Поэтому для
построения результирующей вебер-амперной характеристики
складывают значения магнитных напряжений при одном потоке. Можно
построить вебер-амперные характеристики для каждого участка цепи,
а затем их сложить. Но такое решение является нерациональным.
Лучше сразу строить результирующую характеристику, вычислив U м
для выбранного ряда значений Ф k .
k
Лекция № 22. Расчет неразветвленных магнитных цепей
171
172.
Обратная задача2. Отыскание рабочей точки на пересечении вебер-амперной
характеристики сердечника с зеркальным изображением веберамперной характеристики воздушного зазора
Этот способ рационально использовать при одинаковой площади
поперечного сечения магнитопровода.
Лекция № 22. Расчет неразветвленных магнитных цепей
172
173. Расчет магнитной цепи постоянного тока
В настоящее время постоянные магниты имеютограниченное применение (в магнето, запальных
машинах).
Рассмотрим магнитопровод, имеющий вид кольца
без зазора.
Лекция № 22. Расчет неразветвленных магнитных цепей
173
174. Вопросы для самопроверки
1. Какую задачу называют прямой?2. Чем отличаются друг от друга участки, на которые делят магнитную
цепь?
3. Приведите алгоритм решения прямой задачи.
4. Как определить напряженность магнитного поля для ферромагнитных
участков?
5. Как определить напряженность магнитного поля в воздушном зазоре?
6. Какую задачу называют обратной?
7. Что является аналогом вольт-амперной характеристики в магнитных
цепях?
8. Какие способы решения обратной задачи Вы знаете? Для каких
магнитных цепей рационально применять каждый из способов?
9. В каких магнитных цепях направления Н и В противоположны?
10. Каким способом рационально делать расчет цепи постоянного
магнита?
Лекция № 22. Расчет неразветвленных магнитных цепей
174
175.
Лекция № 23. Нелинейные цепипеременного тока
1. Магнитный поток и ЭДС катушки
с ферромагнитным сердечником
2. Потери в катушке с ферромагнитным
сердечником
3. Ток катушки с ферромагнитным сердечником
175
176. Магнитный поток и ЭДС катушки с ферромагнитным сердечником
В электротехнических устройствах в основном используютиндуктивные катушки с ферромагнитным сердечником.
При наличии в индуктивной катушке переменного тока созданный
им магнитный поток будет тоже переменным, поэтому в катушке
наводится ЭДС самоиндукции. Основная часть магнитного потока Ф о
замыкается по сердечнику. Этот поток наводит ЭДС
dФ о
eо W
.
dt
Ферромагнитные цепи являются нелинейными.
Ф Фm sin ωt ,
e W
dФ
π
WФ m ω cos ωt WФ m ωsin(ωt ),
dt
2
Em WФm 2πf ,
E
Em
2
2π
WfФ m 4, 44WfФ m .
2
Лекция № 23. Нелинейные цепи переменного тока
176
177. Магнитный поток и ЭДС катушки с ферромагнитным сердечником
Расчет магнитных цепей аналогичен расчету нелинейныхэлектрических цепей с сосредоточенными параметрами, причем МДС F
соответствует ЭДС Е, поток Ф – току I, магнитное сопротивление Rм –
электрическому сопротивлению.
Лекция № 23. Нелинейные цепи переменного тока
177
178.
Потери в катушке с ферромагнитным сердечникомОдна из особенностей катушки с ферромагнитным сердечником состоит
в том, что кроме активной мощности, потребляемой на нагрев самой
катушки, активная мощность расходуется в сердечнике.
Р Рм Рст .
Рст Рг Рвт .
Потери на гистерезис вычисляют по формуле
Рг σ г fBmn G.
Потери от вихревых токов вычисляют по формуле
Рвт σ в f 2 Вт2 G.
Лекция № 23. Нелинейные цепи переменного тока
178
179.
Ток катушки с ферромагнитным сердечникомПренебрегаем потерями на гистерезис ( Рг ) 0.
Лекция № 23. Нелинейные цепи переменного тока
179
180.
Ток катушки с ферромагнитным сердечникомУчитываем потери на гистерезис ( Рг 0).
Лекция № 23. Нелинейные цепи переменного тока
180
181. Вопросы для самопроверки
1. Чем катушка с ферромагнитным сердечником принципиальноотличается от катушки без сердечника?
2. Каково фазное соотношение между ЭДС и создавшим ее
магнитным потоком?
3. Приведите формулу трансформаторной ЭДС.
4. Что называют потерями в меди и потерями в стали?
5. По каким причинам сердечник греется?
6. Как уменьшают потери от вихревых токов?
7. Как меняется ток в катушке с ферромагнитным сердечником?
8. Какие особенности имеет ряд Фурье, полученный при
разложении кривой тока?
9. Чем отличаются кривые тока при учете потерь на гистерезис
и при пренебрежении ими?
Лекция № 23. Нелинейные цепи переменного тока
181
182.
Лекция № 24. Расчет катушкис ферромагнитным сердечником
1. Схема замещения и векторная диаграмма
катушки с ферромагнитным сердечником
2. Расчет параметров схемы замещения
катушки с ферромагнитным сердечником
3. Расчет катушки с ферромагнитным
сердечником методом кусочно-линейной
аппроксимации
182
183.
Схема замещения и векторная диаграмма катушки с ферромагнитным сердечникомВ схеме замещения идеальными элементами учитывают явления,
происходящие в реальной катушке.
Gо
Rо 2 ;
Yо
Bо
Rо
Xо
X о 2 ; Gо 2 ; Bо 2 .
Yо
Zо
Zо
Лекция № 24. Расчет катушки с ферромагнитным сердечником
183
184.
Схема замещения и векторная диаграмма катушки с ферромагнитным сердечникомU Eо Es RI .
ЭДС можно учесть соответствующими напряжениями:
Eо Uо и Es Us jXsI.
Тогда уравнение электрического
состояния примет вид
U U о RI jX s I .
Лекция № 24. Расчет катушки с ферромагнитным сердечником
184
185.
Расчет параметров схемы замещения катушки с ферромагнитным сердечникомКатушку рассматриваем как условно-нелинейный элемент, заменяя
несинусоидальный режим для мгновенных значений синусоидальным.
В этом случае применимы все методы расчетов для линейных цепей.
Расчет параметров схемы
замещения по результатам опытов
Используя показания таких приборов, как амперметр, вольтметр,
ваттметр, фазометр, на основании законов Кирхгофа с помощью
векторных диаграмм и основных формул электротехники.
Лекция № 24. Расчет катушки с ферромагнитным сердечником
185
186.
Расчет параметров схемы замещения катушки с ферромагнитным сердечникомРасчет параметров схемы
замещения по кривым удельных потерь
В качестве характеристик стали принимают кривые удельных
потерь, которые приведены в справочной литературе.
Лекция № 24. Расчет катушки с ферромагнитным сердечником
186
187.
Расчет параметров схемы замещения катушки с ферромагнитным сердечникомПод удельными потерями понимают отношения активной
и реактивной мощностей сердечника к единице массы стального
магнитопровода:
Рст.уд
Рст
Qст
; Gст.уд
.
G
G
Активная мощность сердечника:
Рст U о I cos φо ,
2
I
Рст U о I sin δ U о I с U оGоU о GоU о2 с .
Gо
Реактивная мощность сердечника:
Qст U о I sin φо U о I cos δ U о I μ BоU о2
I μ2
Bо
Лекция № 24. Расчет катушки с ферромагнитным сердечником
.
187
188.
Расчет катушки с ферромагнитным сердечником методом кусочно-линейной аппроксимацииМетод кусочно-линейной аппроксимации можно применять в случае,
если материал сердечника имеет почти прямоугольную кривую
намагничивания. Такой формой кривой намагничивания обладают
некоторые высококачественные магнитомягкие материалы.
Уравнение электрического состояния катушки с ферромагнитным
сердечником в самом общем виде можно записать следующим образом:
dψ
Ri
U m sin ωt.
dt
Закон изменения потокосцепления в более полном виде:
Um
Um
Um
ψ=cosωt+
-ψн =
(1-cosωt)-ψ н .
ω
ω
ω
Лекция № 24. Расчет катушки с ферромагнитным сердечником
188
189.
Расчет катушки с ферромагнитным сердечником методом кусочно-линейной аппроксимацииЛекция № 24. Расчет катушки с ферромагнитным сердечником
189
190. Вопросы для самопроверки
1. Какое явление учитывает линейный резистивный элементсхемы замещения?
2. Какое явление учитывает нелинейный резистивный элемент
схемы замещения?
3. Какое явление учитывает линейный индуктивный элемент
схемы замещения?
4. Какое явление учитывает нелинейный индуктивный элемент
схемы замещения?
5. По каким формулам делают переход от последовательной
схемы замещения к параллельной и обратно?
6. Каков порядок построения векторной диаграммы катушки
с ферромагнитным сердечником?
7. Какие методы расчета параметров схемы замещения катушки
с ферромагнитным сердечником Вы знаете?
8. Что назвали кривыми удельных потерь?
9. В чем суть расчета методом кусочно-линейной аппроксимации?
Лекция № 24. Расчет катушки с ферромагнитным сердечником
190
191.
Лекция № 25. Явление феррорезонанса1. Феррорезонанс напряжений
2. Феррорезонанс токов
191
192.
Явление феррорезонанса возникает в цепях с нелинейнымииндуктивными катушками и конденсаторами, когда они
компенсируют действие друг друга. Цепь имеет чисто активный
характер.
Для достижения резонанса в линейных цепях нужно изменить
параметры или частоту. Феррорезонанс возникает за счет изменения
индуктивности при изменении величины тока и напряжения.
При анализе феррорезонансных явлений делаем
допущения:
1. Считаем индуктивную катушку условно-нелинейным
элементом, заменяя кривую тока ее первой гармоникой, полученной
при разложении в ряд Фурье.
2. Пренебрегаем потерями на гистерезис, т. е. при анализе
используем основную кривую намагничивания.
Лекция № 25. Явление феррорезонанса
192
193.
Феррорезонанс напряженийНаблюдается в цепи с последовательным соединением нелинейной
индуктивной катушки и конденсатора.
Пренебрегаем активным сопротивлением
Входное напряжение:
U U L UC .
Лекция № 25. Явление феррорезонанса
193
194.
Феррорезонанс напряженийРезультирующая вольт-амперная характеристика
Лекция № 25. Явление феррорезонанса
194
195.
Феррорезонанс напряженийУчитываем активное сопротивление цепи.
Как видно из векторной диаграммы, входное напряжение:
U U R2 (UС U L )2 .
Лекция № 25. Явление феррорезонанса
195
196.
Феррорезонанс напряженийРезультирующая вольт-амперная характеристика
Лекция № 25. Явление феррорезонанса
196
197.
Феррорезонанс напряженийПусть цепь с последовательным соединением нелинейной
индуктивной катушки и конденсатора подключена к источнику
напряжения, действующее значение которого с помощью
автотрансформатора будем плавно увеличивать, начиная с нуля.
Рабочая точка при этом будет перемещаться по вольт-амперной
характеристике.
Лекция № 25. Явление феррорезонанса
197
198.
Феррорезонанс токовНаблюдается в цепи с параллельным
соединением нелинейной индуктивной
катушки и конденсатора.
Лекция № 25. Явление феррорезонанса
198
199.
Феррорезонанс токовПо первому закону Кирхгофа входной ток
I I L IC .
Лекция № 25. Явление феррорезонанса
199
200.
Феррорезонанс токовВольт-амперная характеристика.
При питании от источника тока будут наблюдаться
скачки напряжения.
Лекция № 25. Явление феррорезонанса
200
201. Вопросы для самопроверки
1. Чем феррорезонансные явления принципиально отличаютсяот резонансных?
2. В каких цепях бывает резонанс напряжений?
3. Какой характер имеет цепь при резонансе?
4. Какой вид имеет ВАХ цепи с последовательным соединением
нелинейной индуктивной катушки и конденсатора?
5. Какое явление называют триггерным эффектом?
6. Как экспериментально выявить участок неустойчивой работы ВАХ
цепи с последовательным соединением нелинейной катушки
и конденсатора?
7. В какой цепи наблюдается явление феррорезонанса токов?
8. Какой вид имеет ВАХ цепи с параллельным соединением нелинейной
катушки и конденсатора?
9. В каком случае будет наблюдаться триггерный эффект в цепи
с параллельным соединением нелинейной индуктивной катушки
и конденсатора?
Лекция № 25. Явление феррорезонанса
201
202.
Лекция № 26. Четырехполюсникипри синусоидальных воздействиях
1. Четырехполюсники и их основные
уравнения
2. Определение коэффициентов уравнений
связи четырехполюсника
202
203.
Четырехполюсники и их основные уравненияЧетырехполюсники могут быть пассивными и активными.
Рассмотрим пассивный четырехполюсник.
1
I1
U1
I2
П
2
U
2
´
´
2
1
Разработаны 6 форм уравнений связи четырехполюсников.
Уравнения в Z-форме связывают входное и выходное напряжения
с входным и выходным токами:
U1 Z 11 I1 Z 12 I 2 ;
U 2 Z 21 I1 Z 22 I 2 .
Лекция № 26. Четырехполюсники при синусоидальных воздействиях
203
204.
Четырехполюсники и их основные уравненияБолее компактной является запись уравнений связи в матричной форме:
U1 Z 11
U 2 Z 21
Z 12 I1
.
Z 22 I 2
Если токи выразить через напряжения, получим уравнения
связи в Y-форме:
I1 Y 11U1 Y 12U 2 ;
I 2 Y 21U1 Y 22U 2 .
Уравнения в А-форме:
U1 AU 2 BI 2 ;
I1 C U 2 DI 2 ,
Лекция № 26. Четырехполюсники при синусоидальных воздействиях
204
205.
Четырехполюсники и их основные уравненияАналогично можно получить систему уравнений связи
относительно выходных величин:
U 2 DU1 B I1 ;
I 2 CU1 A I1.
Уравнения связи в Н-форме записывают следующим образом:
U1 H 11 I1 Н 12U 2 ;
I 2 H 21 I1 H 22U 2 .
Уравнения связи в G-форме имеют вид:
I1 G11 U1 G12 I 2 ;
U 2 G 21 U1 G 22 I 2 .
Лекция № 26. Четырехполюсники при синусоидальных воздействиях
205
206.
Определение коэффициентов уравнений связи четырехполюсникаДля опытного определения проводят опыты холостого хода
и короткого замыкания. При этом нужно измерять не только модули
комплексных величин, но и их аргументы.
Рассмотрим нахождение коэффициентов в А-форме уравнений связи.
В режиме холостого хода вторичных зажимов ток I 2 0
U1х AU 2 ;
I1х CU 2 .
Отсюда сопротивление
Z 1х
U1х A
.
I1х С
В режиме короткого замыкания вторичных зажимов напряжение
U1k B I 2 ;
I1k D I 2 .
Сопротивление
U2 0
U1k B
Z 1k
.
I1k D
Лекция № 26. Четырехполюсники при синусоидальных воздействиях
206
207. Вопросы для самопроверки
1. Что называют многополюсником?2. Какие формы уравнений связи Вы знаете?
3. В каких цепях используют уравнения связи
в А-форме?
4. В каких цепях используют уравнения связи в Ни G-формах?
5. Какой четырехполюсник называют симметричным?
6. Какие опыты проводят для определения
коэффициентов уравнений связи
четырехполюсника?
Лекция № 26. Четырехполюсники при синусоидальных воздействиях
207
208.
Лекция № 27. Характеристическиепараметры четырехполюсника
1. Режим четырехполюсника под нагрузкой
2. Характеристические сопротивления
3. Постоянная передачи четырехполюсника
4. Уравнения четырехполюсника
в гиперболических функциях
5. Основные понятия о цепях
с распределенными параметрами
208
209.
Режим четырехполюсника под нагрузкой1
I1
I2
П
U1
Z1вх
2
U
2
´
1
Z
2
´
2
а
1
Z1
I1
U1
I2
П
2
Z
U
2
2 вх
´
2
´
1
б
Лекция № 27. Характеристические параметры четырехполюсника
209
210. Интегральные величины электромагнитного поля, применяемые в теории электрических цепей
Электрический ток – это явление направленногодвижения заряженных частиц.
Входное сопротивление четырехполюсника со стороны
зажимов 1–1’, когда к зажимам 2–2’ подсоединена нагрузка.
Z 1вх
U1
,
I1
Z 1вх
АU 2 ВI 2
CU 2 D I 2
.
Лекция № 27. Характеристические параметры четырехполюсника
210
211. Интегральные величины электромагнитного поля, применяемые в теории электрических цепей
НапряжениеU 2 Z 2I2
Z 1вх
, тогда
А Z 2 I 2 ВI 2
AZ 2 B
.
C Z 2 I 2 D I 2 CZ 2 D
Входное сопротивление четырехполюсника со стороны
зажимов 1–1’, когда к зажимам 2–2’ подсоединена нагрузка
Z 2вх
U2
,
I2
Z 2вх
Z 2вх
DU1 B I1
,
CU1 A I1
D Z 1I1 ВI1 DZ 1 B
.
C Z 1 I1 A I1 CZ 1 A
Лекция № 27. Характеристические параметры четырехполюсника
211
212.
Характеристические сопротивленияВходные сопротивления в согласованном режиме
называют характеристическими и обозначают Z 1с и Z 2с
A Z 2c B
Z 1с
C Z 2c D
;
Z 2с
D Z 1c B
.
C Z 1c A
Из совместного решения этих уравнений получим:
Z 1с
A B
Z 1x Z 1k
C D
;
Z 2с
У симметричного четырехполюсника
Z 1с Z 2c Z c
D B
Z 2x Z 2 k .
C A
A D
;
B
.
C
Лекция № 27. Характеристические параметры четырехполюсника
212
213.
Постоянная передачи четырехполюсникаПостоянная передачи четырехполюсника:
1 U1 I1
g ln
.
2 U2 I2
Коэффициент затухания:
1 U1 I1 1 S1
a ln
ln .
2 U 2 I 2 2 S2
Коэффициент фазы:
1
b= ψ u1 -ψ u 2 + ψi1 -ψi2 .
2
Лекция № 27. Характеристические параметры четырехполюсника
213
214.
Уравнения четырехполюсника в гиперболических функцияхZ 1c
ch g A,
Z 2c
Z 2c
ch g D,
Z 1c
Z 1c Z 2c sh g B,
1
sh g C.
Z 1c Z 2c
Подставив коэффициенты в уравнения связи четырехполюсника,
получим уравнения в гиперболических функциях:
Z 1c
U
ch g U 2 Z 1c Z 2c sh g I 2 ;
1
Z
2c
1
Z 2c
I
sh
g
U
ch g I 2 .
2
1
Z
Z 1c Z 2c
1c
U1 ch g U 2 Z c sh g I 2 ;
1
I
1 Z sh g U 2 ch g I 2 .
c
Лекция № 27. Характеристические параметры четырехполюсника
214
215. Вопросы для самопроверки
1. Что называют входным сопротивлениемчетырехполюсника?
2. Какое сопротивление называют характеристическим?
3. Чему равно характеристическое сопротивление
симметричного четырехполюсника?
4. Чему равна постоянная передачи четырехполюсника?
5. Что характеризует коэффициент затухания?
6. Чему равен коэффициент фазы?
7. Чему равны ch g и sh g?
Лекция № 27. Характеристические параметры четырехполюсника
215
216.
Лекция № 28. Цепис распределенными параметрами
1. Основные понятия
2. Уравнения однородной линии
3. Синусоидальные напряжения и токи
216
217. Основные понятия
Ранее в курсе ТОЭ рассматривали цепи с сосредоточеннымипараметрами. В них можно выделить элементы, в которых запасается энергия
магнитного
поля,
электрического
поля,
происходят
необратимые
преобразования электромагнитной энергии в другие виды энергии. Эти
явления учитывают резистивный, индуктивный, емкостный элементы.
Под цепями с распределенными параметрами понимают такие цепи,
в которых энергии электрического и магнитного полей, а также необратимые
преобразования энергии (потери в виде тепла) распределены равномерно или
неравномерно вдоль цепи (ее длины).
К цепям с распределенными параметрами относят ЛЭП, линии
телефонной связи, антенны приемно-передающих устройств. Обмотки
электрических машин и трансформаторов тоже можно считать цепями
с распределенными параметрами.
Лекция № 28. Цепи с распределенными параметрами
217
218. Основные понятия
Рассмотрим двухпроводную однородную линию электропередачи.Однородной называют линию, параметры которой равномерно
распределены вдоль ее длины. Это идеализированная линия, так как
учитывают изменение параметров от влияния провиса проводов
и неравномерности поверхности земли.
di
i + dx dx
i
du
u + dx dx
u
x
dx
Элементарный участок с учетом и первичных параметров
L0 dx r0 dx
i
u C0
dx
g0 dx
dx
Лекция № 28. Цепи с распределенными параметрами
218
219.
Уравнения однородной линииОпределим изменение напряжения на участке dx, которое равно сумме
падений напряжений на элементах этого участка:
du
du
u u
dx dx,
dx
dx
du
di
dx R0 dx i L0 dx ,
dx
dt
du
di
R 0 i L0 .
dx
dt
Изменение тока в пределах этого участка равно сумме токов утечки
в элементах этого участка:
Отсюда
di
du
dx G0 dx u C0 dx .
dx
dt
di
du
G0u C0
.
dx
dt
Лекция № 28. Цепи с распределенными параметрами
219
220.
Уравнения однородной линииПолучим систему уравнений, которую называют телеграфными
уравнениями однородной линии.
di
du
dx R0i L0 dt ,
di
du
G0u C0
,
dt
dx
di
du
dx R0i L0 dt ,
di
du
G0u C0
.
dt
dx
Начальные условия – это значения токов и напряжений в начале
или конце линии для момента времени t 0.
Граничные условия устанавливают связь между напряжением и током
в начале или конце линии в зависимости от режима работы линии.
Лекция № 28. Цепи с распределенными параметрами
220
221.
Синусоидальные напряжения и токи в линииЕсли линия подключена к источнику синусоидального напряжения
с частотой f, то напряжение и ток установившегося режима
изменяются по синусоидальному закону с той же частотой.
dU
R0 I jωL0 I R0 jωL0 I Z 0 I ;
dx
dI
G0U jωC0U G0 jωC0 U Y 0U .
dx
Более краткая запись:
dU
Z 0I
dx
.
dI
Y 0U
dx
Лекция № 28. Цепи с распределенными параметрами
221
222.
Синусоидальные напряжения и токи в линииt1 и t2 .
Волны напряжения для двух моментов времени
u
t1
А1m e - x
t2
x
-А1m e - x
Волна перемещается от начала линии к концу с постоянной скоростью
.
Вторая составляющая напряжения перемещается с той же
скоростью, что и первая, но от конца линии к началу.
А2m e x
u
-
t1
x
t2
-А2m e x
Лекция № 28. Цепи с распределенными параметрами
222
223. Вопросы для самопроверки
1. Чем цепи с распределенными параметрами отличаютсяот цепей с сосредоточенными параметрами?
2. Какие уравнения используют при анализе процессов
в линиях?
3. Чем частные производные отличаются от полных?
4. Каков физический смысл слагаемых напряжения
в уравнении однородной линии?
5. Как вычислить активную мощность?
Лекция № 28. Цепи с распределенными параметрами
223
224.
Лекция № 29. Анализдлинной однородной линии
1.
2.
3.
Основные характеристики бегущей волны
Вторичные параметры однородной линии
Зависимость режима работы линии от
нагрузки
224
225.
Основные характеристики бегущей волныЛюбое колебательное движение характеризуют фазовой скоростью
и длиной волны.
Фазовая скорость – это скорость изменения фазы колебания, которая
с течением времени и ростом координаты х остается неизменной:
ωt βx ψ1 const,
ν=
ω
,
β
с 3 105
км
.
с
Длина волны – это кратчайшее расстояние между двумя точками,
взятое в направлении распространения волны, фаза колебания которых
отличается на 2
2π
λ=
β
υ=
ω 2πf
λ
=
=λf = .
β
β
T
Лекция № 29. Анализ длинной однородной линии
225
226.
Вторичные параметры однородной линииОднородную линию можно характеризовать с помощью двух параметров:
коэффициента распространения:
γ Z 0Y 0
R0 jL0ω G0 jC0ω α jβ,
и волнового (характеристического) сопротивления:
Z0
Zc
Y0
R0 jL0ω Z e jθ .
G0 jC0ω c
Коэффициент распространения:
α Jβ
R0 jL0ω G0 jC0ω
R0G0 ω2 L0C0 jω G0 L0 R0C0 ,
α
1
R0G0 ω2 L0C0
2
R
ω2 L20 G02 ω2C02 ,
β
1 2
ω L0C0 R0G0
2
R
ω2 L20 G02 ω2C02 .
2
0
2
0
Лекция № 29. Анализ длинной однородной линии
226
227.
Вторичные параметры однородной линииГрафики зависимостей
(w ) и (w )
0
3
2
arctg L0C0 m
w
Фазовая скорость зависит
от материала.
Графики зависимости ( f
Медные
1
)
Стальные
f
20 40 80 160 370 640
1280
Гц
Лекция № 29. Анализ длинной однородной линии
227
228.
Зависимость режима работы линии от нагрузкиI1
Rг
Ег
2 I2
1
U2
U1
1
х
х
_Z н
2
l
По закону Ома ток
U2
I2
.
Zн
Напряжение
и
ток
на
расстоянии х от начала
линии:
U A e γ x A e γ x ;
1
2
I A1 e γ x A2 e γ x .
Zc
Zc
Лекция № 29. Анализ длинной однородной линии
228
229.
Зависимость режима работы линии от нагрузкиНапряжение в линии:
U
U 2 Z c I 2 γx U 2 Z c I 2 γx
e
e
2
2
e γx e γx
e γx e γx
U2
Z c I2
U 2 сh x Z c I 2sh x
2
2
Уравнения линии в гиперболической форме, выражающие
напряжение и ток в начале линии через напряжение и ток в конце линии:
U1 U 2 сh γ l Z c I 2 sh γl ;
U2
sh γ l.
I1 I 2 ch γ l
Zc
U U1 ch γ x Z c I1 sh γ x;
U1
sh γ x.
I I1 ch γ x
Zc
Лекция № 29. Анализ длинной однородной линии
229
230. Вопросы для самопроверки
1.2.
3.
4.
5.
6.
7.
Что назвали первичными параметрами длинной волны?
Что назвали вторичными параметрами длинной волны?
Чему равен коэффициент распространения?
Чему равно характеристическое уравнение?
Что называют фазовой скоростью волны?
Что называют длиной волны?
Какова связь между длиной волны и фазовой скоростью?
Лекция № 29. Анализ длинной однородной линии
230
231.
Лекция № 30. Особые режимы работыдлинной однородной линии
1. Режим согласованной нагрузки
2. Линия без потерь
3. Согласованная нагрузка линии без потерь
4. Входное сопротивление линии
231
232.
Режим согласованной нагрузкиВ однородной линии обратная волна существует в случае, если
нагрузка линии не согласована с ее характеристическим
сопротивлением: Z н Z c
При передаче сигналов и информации, как правило, подбирают
согласованный режим. В этом случае
U 2 Z c I 2 γx
γx
γx
U
U
B
e
e
U
e
;
пр
1
2
2
I I B1 e γx U 2 Z c I 2 e γx I e γx .
пр
2
Zc
2Z c
Действующие значения
напряжения и тока вдоль линии
при согласованной нагрузке
изменяются по экспоненте.
U;I
U2 e x
I2 e x
x
Лекция № 30. Особые режимы работы длинной однородной линии
U2
I2
0
232
233.
Линии без потерьВ линиях, соединяющих приемно-передающую аппаратуру с антеннами,
потери много меньше мощности, потребляемой нагрузкой. Этими потерями
пренебрегают и такую линию считают линией без потерь, принимают
R0 0 и G0 0.
У линии без потерь волновое сопротивление чисто активное
и не зависит от частоты:
Zc
R0 jωL0
L0
Zc .
G0 jC0ω
C0
Коэффициент распространения
γ α jβ ( R0 jl0ω)(G0 jC0w jω L0C0 .
Коэффициент фазы
β=ω L0C0 .
Лекция № 30. Особые режимы работы длинной однородной линии
233
234.
Линии без потерьУравнения однородной линии с гиперболическими функциями от
комплексного аргумента заменяют для линии без потерь уравнениями
с круговыми функциями от вещественного аргумента.
U U 2 cosβ x jZ с I 2 sin β x;
U2
I I 2 cosβ x j Z sin β x.
c
В случае несогласованной нагрузки есть прямая и обратная
составляющие напряжения и тока. Амплитуда каждой составляющей
вдоль линии остается постоянной ( 0) .
Результирующие действующие значения напряжения и тока вдоль
линии распределены неравномерно.
Лекция № 30. Особые режимы работы длинной однородной линии
234
235.
Согласованная нагрузка линии без потерьПри согласованной активной нагрузке
Z н Z с Zc
L0
,
C0
U 2 Zc I2 ,
U U 2 cosβ x jU 2 sin β x U 2e j β x ;
jβ x
I
I
cosβ
x
j
I
sin
β
x
I
e
.
2
2
2
Примем, что начальная фаза напряжения в конце линии равна
нулю. Тогда мгновенные значения напряжения и тока
u( x, t ) U 2 msin(ω t βx),
i( x, t ) I 2 msin(ω t βx).
Лекция № 30. Особые режимы работы длинной однородной линии
235
236.
Согласованная нагрузка линии без потерьНапряжение и ток вдоль
линии изменяются
по синусоидальному закону
с постоянной амплитудой
и совпадают по фазе.
Отраженной волны нет.
Действующие значения
напряжения и тока не зависят
от координаты х.
u; i
U; I
U2m
I2m
х
х2 х1
U
I
х
Лекция № 30. Особые режимы работы длинной однородной линии
236
237.
Входное сопротивление линииВходное сопротивление линии – это входное сопротивление
двухполюсника, который необходимо подключить к зажимам генератора
вместо линии, чтобы режим работы генератора остался без изменения.
При известных напряжении и токе генератора система уравнений
линии:
Zc
U
U
ch
γ
l
Z
I
sh
γ
l
U
(ch
γ
l
sh γ l );
c 2
2
2
1
Zн
I I ch γ l U 2 shγ l U 1 sh γ l 1 sh γ l .
2
2
1
Zc
Z
Z
н
н
Z вх Z с
th M th γ l
1 th M th γl
Z c th (γ l M ) Z c th (α l m1 ) (β l m2 ) .
Входное сопротивление линии без потерь при согласованном режиме:
Z вх
Z н jZ c tg β l
1 n e j 2β l
Zс
Zc
.
j 2β l
Z c jZ н tg β l
1 n e
Лекция № 30. Особые режимы работы длинной однородной линии
237
238. Вопросы для самопроверки
1. Какой режим называют согласованным?2. Для чего и по какой причине используют
согласованный режим?
3. В какой линии отсутствуют потери?
4. Чему равно характеристическое сопротивление линии
без потерь?
5. Чему равен коэффициент затухания линии без потерь?
6. Чему равен коэффициент фазы линии без потерь?
7. Чему равна фазовая скорость линии без потерь?
8. По какому закону распределены ток, напряжение вдоль
линии без потерь при согласованной нагрузке?
Лекция № 30. Особые режимы работы длинной однородной линии
238
239.
Лекция № 31. Введение в теориюэлектромагнитного поля
1. Общие сведения
2. Основные векторные величины,
характеризующие электромагнитное поле
239
240.
Общие сведенияТеория электромагнитного поля изучает физические явления
и процессы, происходящие в электромагнитном поле, и инженерные
методы расчета этих процессов. Эти явления и процессы лежат в основе
действия большого числа различных электромагнитных и электронных
приборов и устройств, широко применяемых на практике. К ним могут
быть отнесены электрические машины и аппараты, электроэнергетические
установки для передачи электрической энергии, электромагнитные
и электронные элементы автоматики, средства передачи информации,
устройства электрометаллургии, а также оборудование, предназначенное
для исследования электромагнитных полей биологических объектов,
искусственного интеллекта и многие др.
Изучение теории электромагнитного поля не только расширяет
физические представления о поле, дает возможность проектировать
различные практические устройства, но и способствует формированию
у студентов современного мировоззрения.
Теория электромагнитного поля – теоретическая дисциплина,
т. е. базисная для целого ряда других дисциплин радиотехники,
радиолокации, электрических машин и др.
Лекция № 30. Особые режимы работы длинной однородной линии
240
241.
Общие сведенияЭлектрические и магнитные поля – различные проявления единого
электромагнитного поля.
Все электромагнитные процессы есть процессы преобразования
и распространения электромагнитного поля. В теории цепей исследование
процессов преобразования энергии осуществляют при помощи уравнений
в интегральной форме и интегральных понятий: тока I, напряжения U,
мощности P, магнитного потока Ф, которые характеризуют, как правило,
целые участки или области электромагнитного поля. Теория
электромагнитного
поля
позволяет
рассматривать
процессы
в электромагнитном поле в каждой точке пространства.
С помощью теории электромагнитного поля
определяют
параметры элементов электрических цепей (емкости, индуктивности,
взаимные
индуктивности,
параметры
электрических
машин
и многочисленных электромагнитных механизмов для цепей автоматики,
телемеханики, электрической связи и т. д.), объясняют процессы
распространения электромагнитных волн, электрические и магнитные
поверхностные эффекты, эффекты близости и экранирования.
Лекция № 30. Особые режимы работы длинной однородной линии
241
242.
Основные векторные величины, характеризующие электромагнитное полеВектор напряженности электрического поля –
E
Напряженность электрического поля равна пределу отношения силы,
действующей со стороны поля на внесенный в него точечный заряд,
к величине заряда, когда последний стремится к нулю:
F
.
q 0 q
E lim
Электростатическое поле
E
E
E
E
E
q
q
q
q
q
q
+q
E
-q
Лекция № 30. Особые режимы работы длинной однородной линии
242
243.
Основные векторные величины, характеризующие электромагнитное полеВектор магнитной индукции
В
Его определяют из силового воздействия магнитного поля
на движущийся заряд или проводник с током. Опытным путем
установлено, что
F I lB sin90 I lB.
Размерность
F
H
Дж/м ВАс Вб
2 Тл.
В
2
I l A м А м А м м
Вектор электрического смещения D
Вектор напряженности магнитного поля H
D0 ε0 E.
B0 μ 0 H .
Лекция № 30. Особые режимы работы длинной однородной линии
243
244. Вопросы для самопроверки
1. Что изучает теория электромагнитного поля?2. Назовите свойства и особенности электромагнитного поля.
3. Какие величины характеризуют электромагнитное поле?
4. Как можно графически представить электрическое поле двух
зарядов?
5. Что называют точечным зарядом?
6. Как определяется напряженность поля, созданного
несколькими зарядами?
7. Укажите размерности величин, характеризующих
электромагнитное поле.
8. Назовите условия, при которых можно говорить отдельно об
электрическом и магнитном поле.
9. Какие отличия силовых линий магнитного поля от силовых
линий поля электрического?
10. Запишите уравнение силовой линии поля в декартовой системе
координат.
Лекция № 30. Особые режимы работы длинной однородной линии
244
245.
Лекция № 32. Уравнения Максвелла1. Две теории электричества
2. Рождение великих уравнений
245
246.
Две теории электричестваДо того как Максвелл записал свои великие уравнения, существовало
две теории электричества: теория «силовых линий» Фарадея и теория,
разработанная французами Кулоном, Ампером, Био, Саваром, Араго
и Лапласом. Исходная точка французов – представление о так
называемом «дальнодействии», мгновенном действии одного тела на
другое на расстоянии без помощи какой-либо промежуточной среды.
Теории великих французов были прекрасно математически
обработаны, и, в общем, выстраивались в довольно изящную и цельную
теорию.
Воззрения Фарадея в корне расходились с такими
представлениями. Он не был силен в математике. По словам Эйнштейна,
это был «ум, который никогда не погрязал в формулах».
Фарадей считал, что материя не может действовать там, где ее
нет. Следовательно, область действия зарядов должна быть заполнена
материей. Среду, через которую передается воздействие, Фарадей
назвал «полем». Поле, считал он, пронизано магнитными
и электрическими «силовыми линиями».
Лекция № 32. Уравнения Максвелла
246
247.
Рождение великих уравненийМаксвелл присоединился к Фарадеевской концепции поля.
Он видел, что Фарадей постепенно отходит от силовых линий как
геометрических символов к вполне реальным силовым линиям,
обладающим, например, упругостью, стремящимся пойти по кратчайшему
пути, отталкивающимся друг от друга.
Максвеллу нравилось, что Фарадей признавал рациональное зерно,
имеющееся в работах чуждых ему по духу и манере исследователей,
например, Ампера. Так, он целиком принимал идею кругового магнитного
поля, окружающего провод с электрическим током. Максвелл записал этот
тезис в форме уравнения:
4π
rotH
j
c
где
,
H – вектор напряженности магнитного поля,
j – вектор плотности электрического тока,
с – некоторая постоянная.
Лекция № 32. Уравнения Максвелла
247
248.
Рождение великих уравненийДругой сразу же завоевавшей признание Максвелла идеей стало
представление Фарадея о природе электромагнитной индукции – то
есть возникновении электричества в контуре, число магнитных силовых
линий в котором изменяется то ли вследствие относительного
движения контура и магнита, то ли вследствие изменения магнитного
поля. Эта зависимость также вполне укладывалась во внешне
формальные математические операции. После многолетних трудов
Максвелл записал строку:
1 B
rotE
.
c t
Максвелл дописал к двум имеющимся уравнениям еще два:
divD 4πρ,
divB 0.
Эти четыре уравнения и составляют «великие уравнения
Максвелла», а система взглядов, которая легла в основу уравнений,
получила название «максвелловой теории электромагнитного поля».
Лекция № 32. Уравнения Максвелла
248
249. Вопросы для самопроверки
1. В чем принципиальное отличие теории«дальнодействия» от теории силовых линий Фарадея?
2. Какие идеи Фарадея Максвелл использовал для
написания своих уравнений?
3. Объясните физический смысл уравнений Максвелла.
4. Каким образом Максвеллу удалось обнаружить
волновую природу света?
Лекция № 32. Уравнения Максвелла
249
250.
Лекция № 33. Основные уравненияи эффекты электромагнитного поля
1. Основные уравнения
2. Поверхностный эффект
3. Поверхностный эффект в массивных
проводах из ферромагнитного материала
4. Эффект близости
5. Графическое изображение
электростатического поля
6. Электростатическое экранирование
250
251.
Основные уравненияВ общем случае изменяющихся во времени зарядов,
изменяющихся во времени токов, движущихся заряженных или
намагниченных тел или движущихся контуров с токами в окружающем
их пространстве существует переменное электромагнитное поле.
Для исследования такого поля необходимо обратиться
к полной системе уравнений ЭМП:
D
rotH δ γE
;
t
B
rotE ;
t
divD ρ;
divB 0;
divδ 0;
D ε a E;
B μa H ;
δ γE.
Лекция № 33. Основные уравнения и эффекты электромагнитного поля
251
252.
Поверхностный эффект (ПЭ)Проникая извне в проводящую среду, ЭМВ очень быстро затухает.
Наружные слои экранируют глубинные слои от проникновения поля. Это
явление называют поверхностным эффектом или скинн-эффектом.
Кроме того, из теории переменных токов известно, что ток
в цилиндрическом проводнике распределяется по сечению проводника
неравномерно, причем плотность тока в центральных частях сечения имеет
меньшее значение, чем на поверхности проводника и вблизи от нее.
С возрастанием частоты степень неравномерности увеличивается. Наличие
поверхностного эффекта приводит к тому, что значительная часть провода
оказывается слабо использованной для протекания тока, а при резко
выраженном ПЭ и вообще не использованной. При этом уменьшается
эффективное сечение провода и его активное сопротивление возрастает.
Наличие ПЭ приводит к увеличению активного и уменьшению
индуктивного сопротивлений проводов. Первое – результат не полного
использования током сечения проводов. Второе связано с ослаблением
магнитного поля в теле проводов и уменьшением внутренней
индуктивности Lвнутр .
Лекция № 33. Основные уравнения и эффекты электромагнитного поля
252
253.
Поверхностный эффект в массивных проводах из ферромагнитного материалаВсе полученные ранее соотношения предполагают, что
магнитная проницаемость среды постоянна. Для проводов
из ферромагнитного материала это условие
не выполняется. Магнитная проницаемость ферромагнитных
веществ зависит от напряженности магнитного поля.
μ
δ
δm
Ha
а
Ha
B
μ const
μ const
б
μ const
Hm
μ const
μ const
δm
μ const
Лекция № 33. Основные уравнения и эффекты электромагнитного поля
253
254.
Эффект близостиЕсли в непосредственной близости друг от друга
расположены несколько проводников с переменным
током, то каждый из проводников находится не только
в собственном переменном магнитном поле,
но и в магнитном поле других проводников. Это
приводит к тому, что распределение переменного тока
в каждом проводнике будет отличным от случая, если
бы этот проводник был уединенным. Этот эффект
называют эффектом близости. Он приводит
к дополнительному увеличению активного
сопротивления проводников.
Лекция № 33. Основные уравнения и эффекты электромагнитного поля
254
255.
Электростатическое экранированиеПредставим себе полость А, окруженную со всех сторон проводником.
E
Eвн 0
E вн
а
б
Как бы ни был заряжен проводник и в каком бы внешнем
электростатическом поле он ни находился, электростатическое поле в полости
А существовать не может, так как поверхность проводника всегда
эквипотенциальна.
Поэтому возможно электростатическое экранирование приборов
в электростатических полях. Практически достаточно окружить защищаемый
объем металлической сеткой.
Лекция № 33. Основные уравнения и эффекты электромагнитного поля
256
256.
Вопросы для самопроверки1. На чем основан эффект экранирования в переменном
электромагнитном поле?
3. Сформулируйте понятие электрического поверхностного
эффекта.
4. Каково соотношение активных сопротивлений с учетом
и без учета поверхностного эффекта?
5. Что такое эффект близости?
6. Объясните физическую сущность поверхностного
эффекта.
7. Объясните принцип экранирования в электростатическом
поле.
Лекция № 33. Основные уравнения и эффекты электромагнитного поля
257








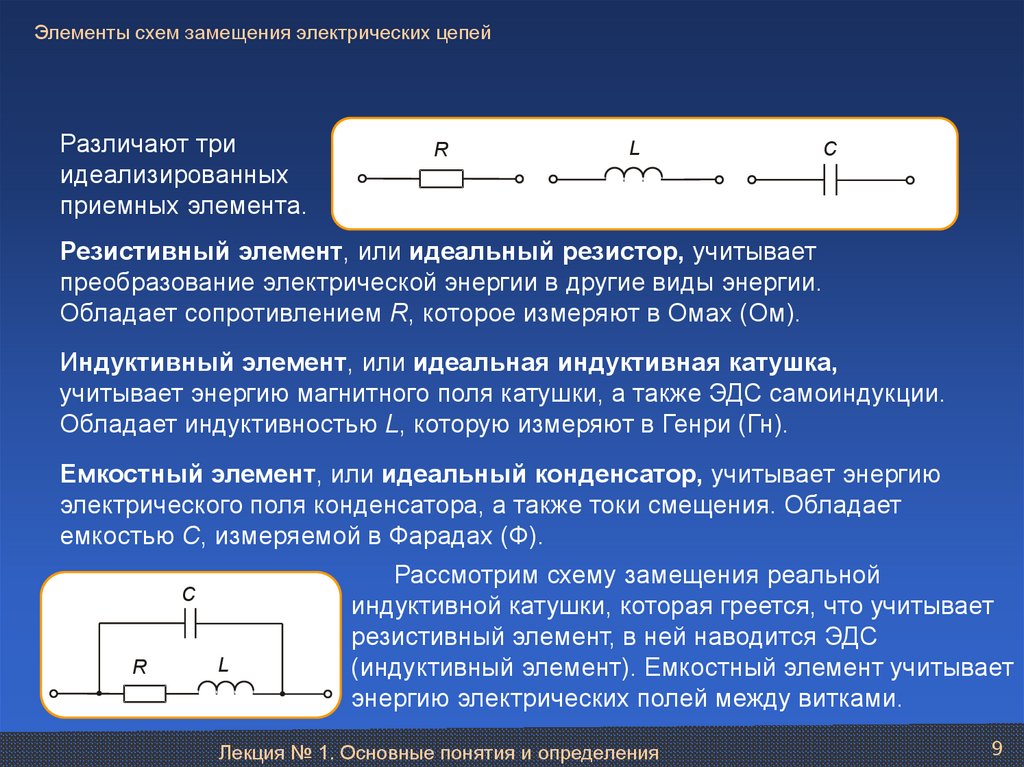


















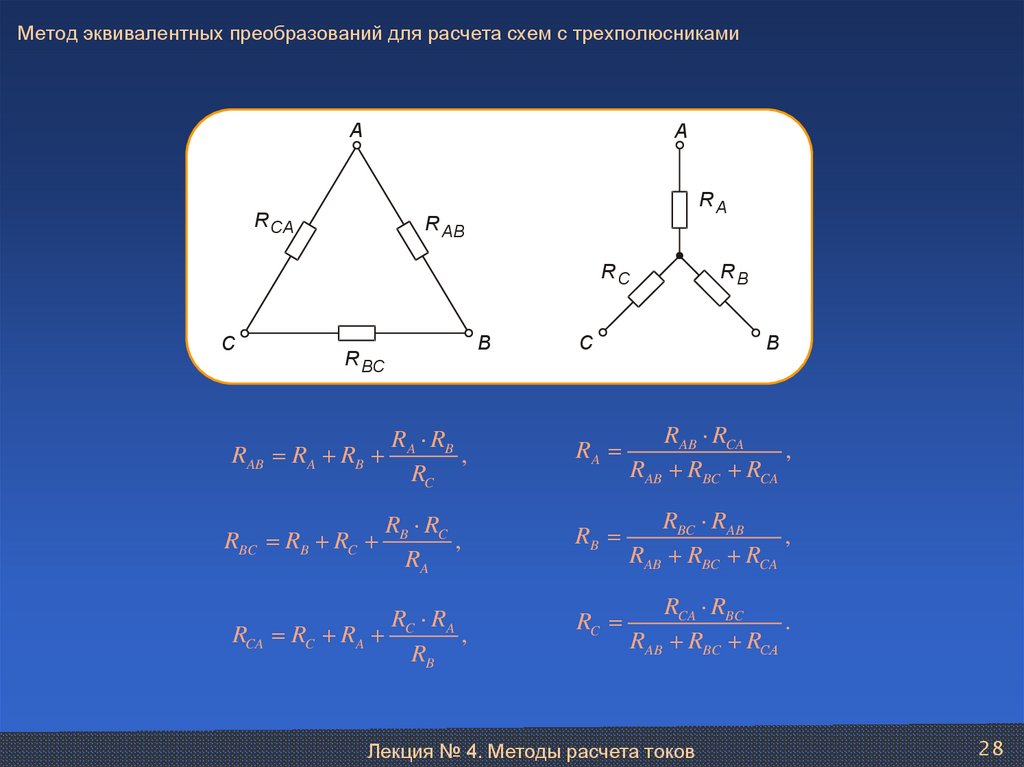





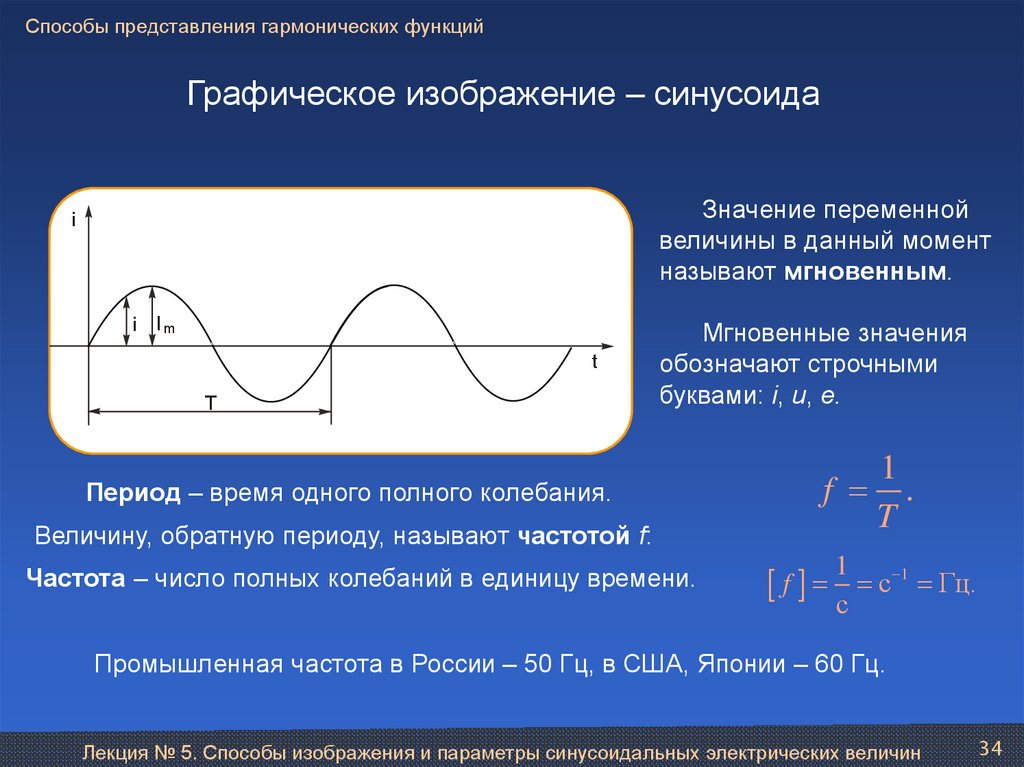







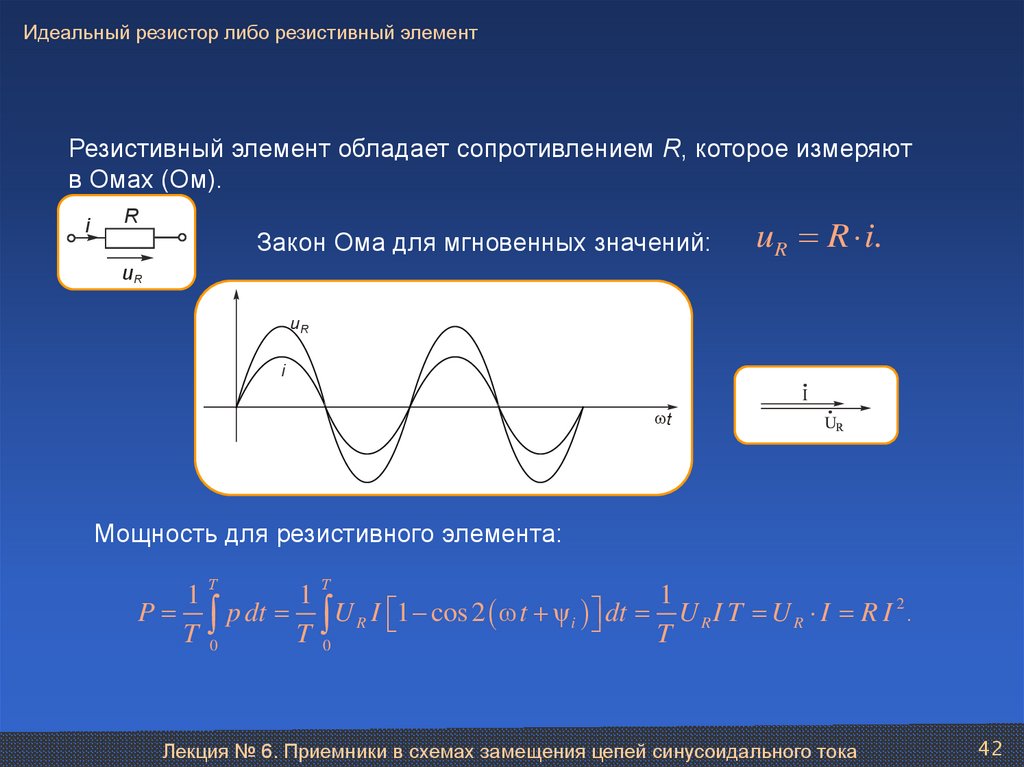

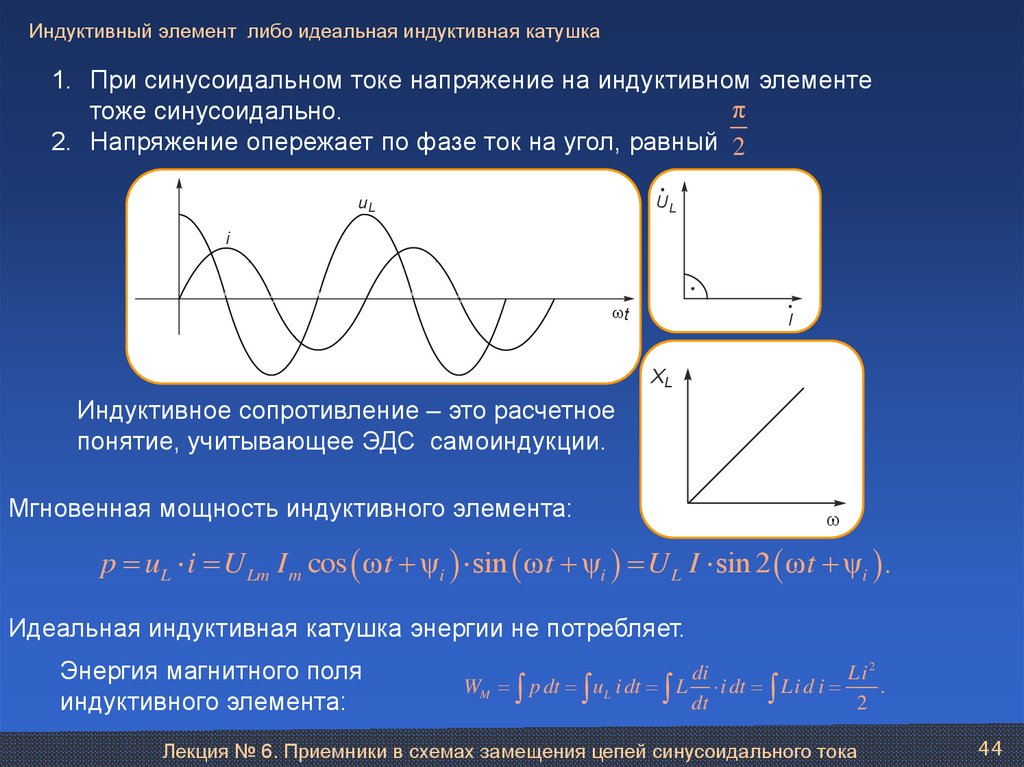













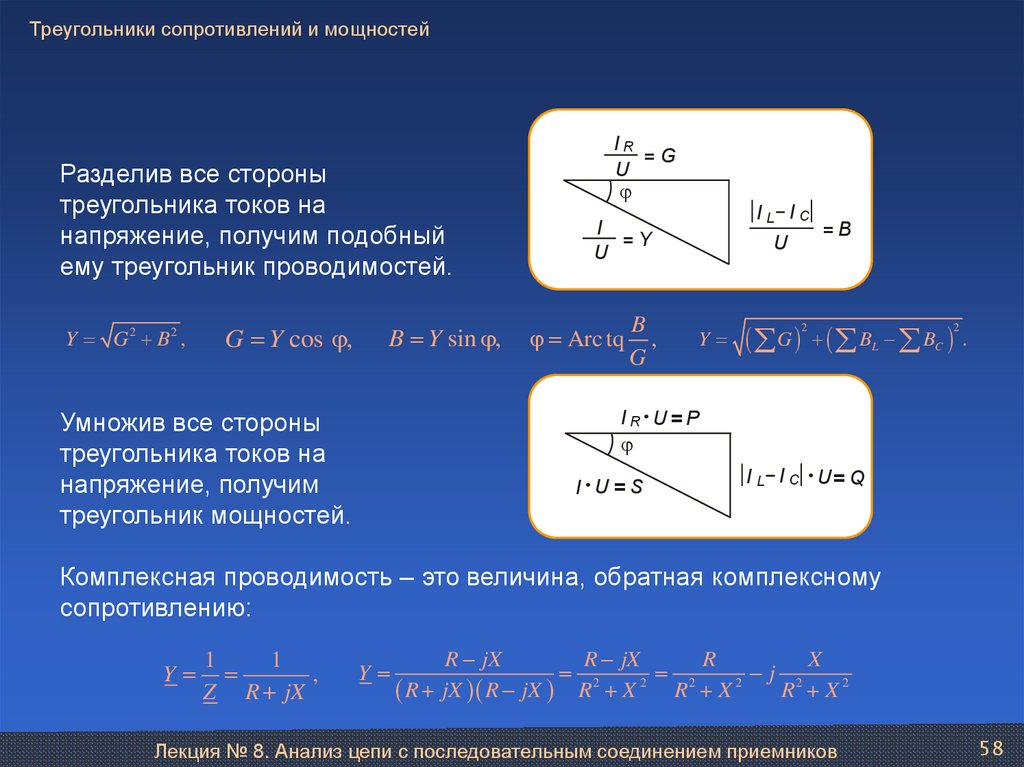
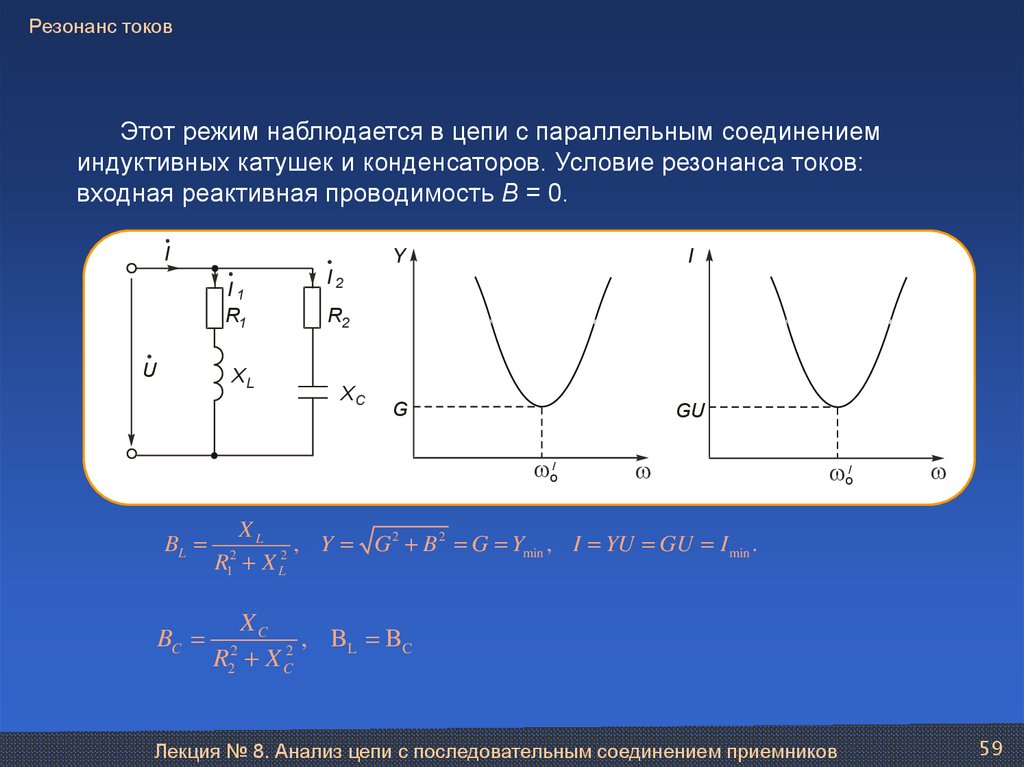
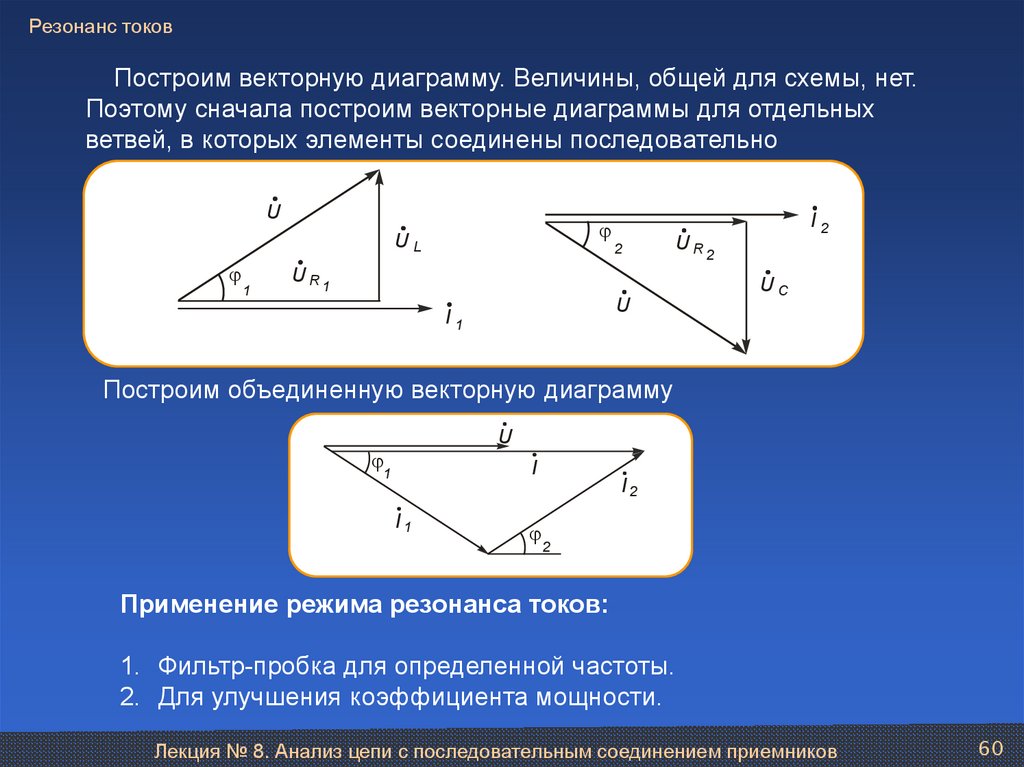



















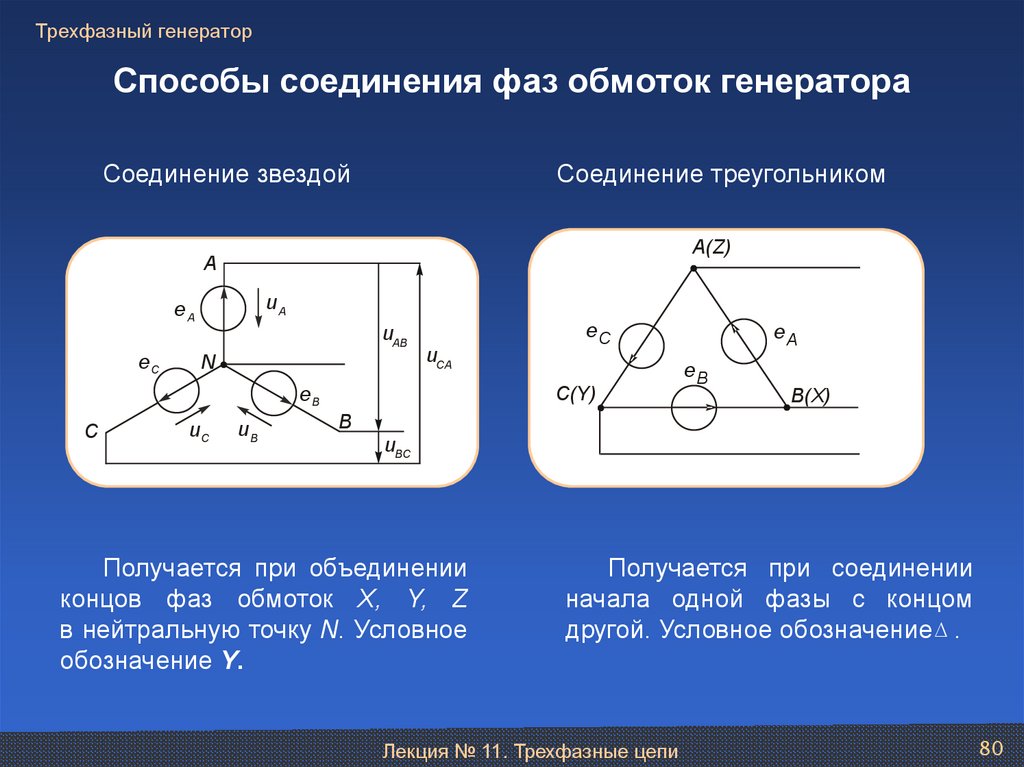




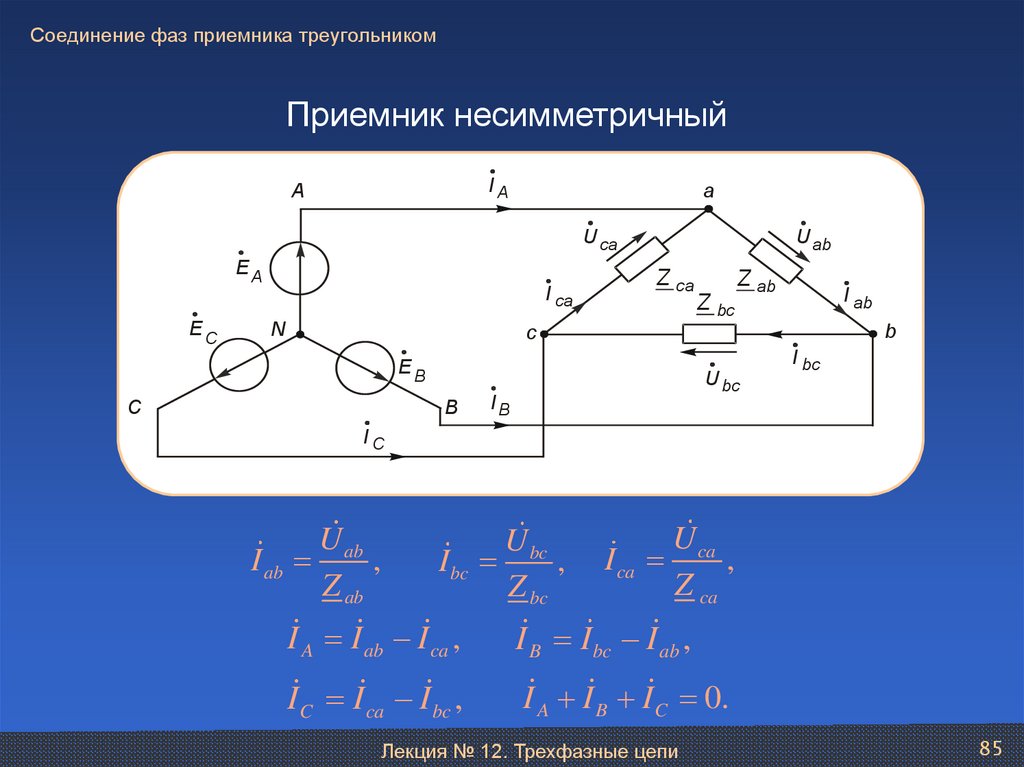
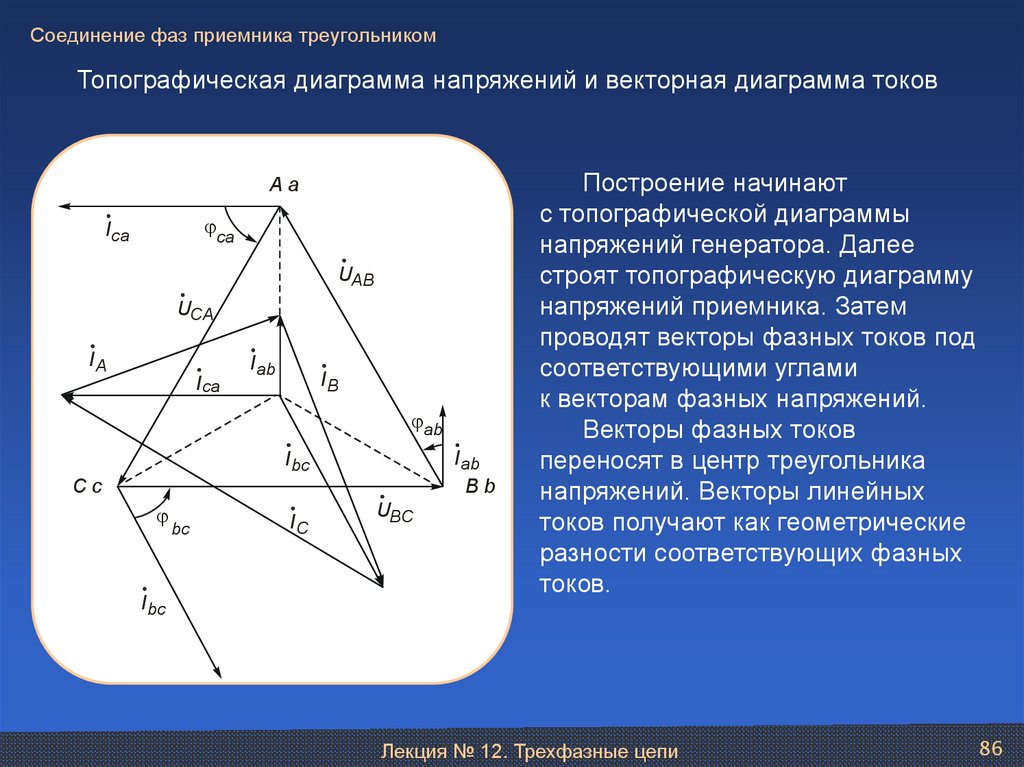

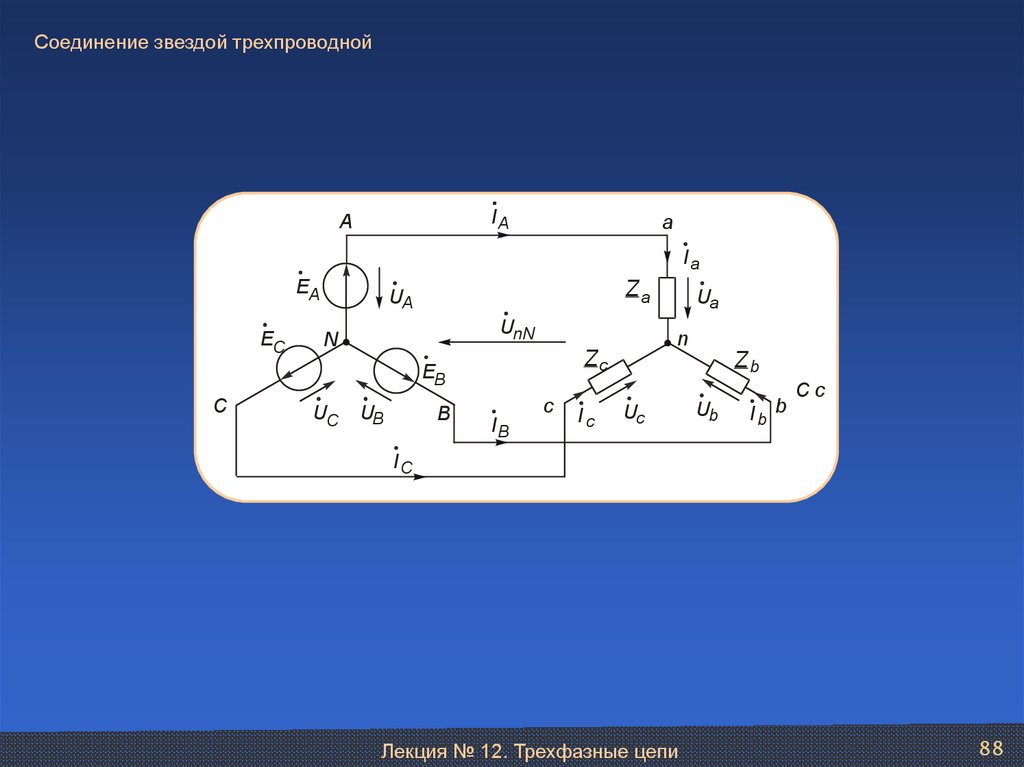




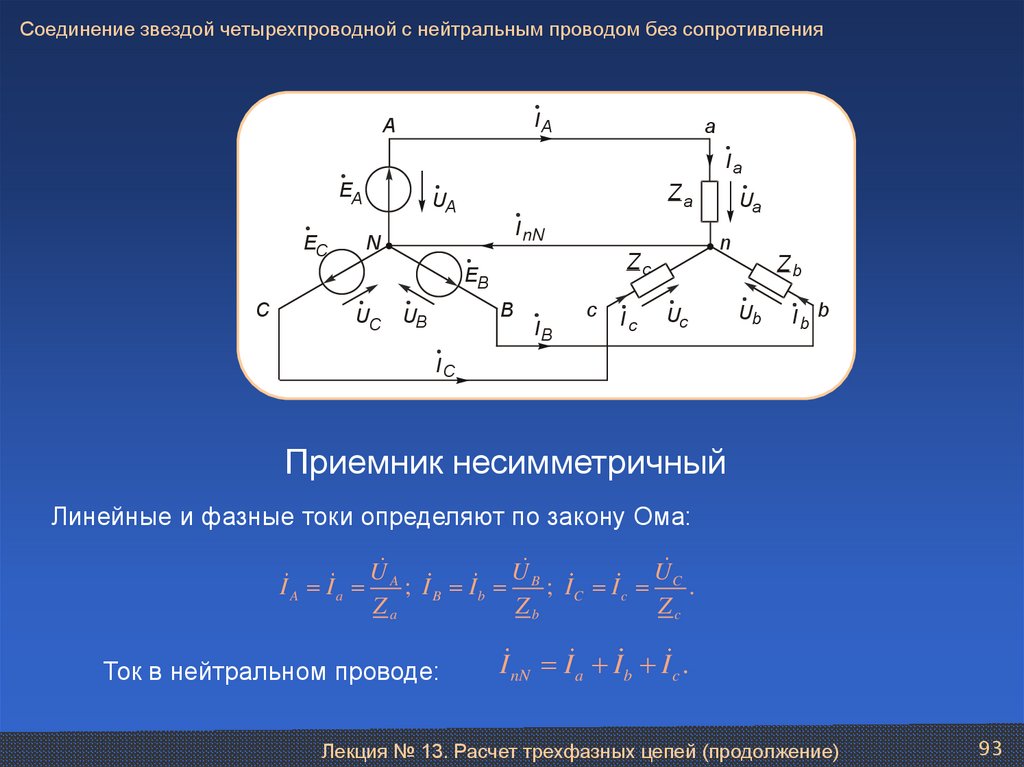



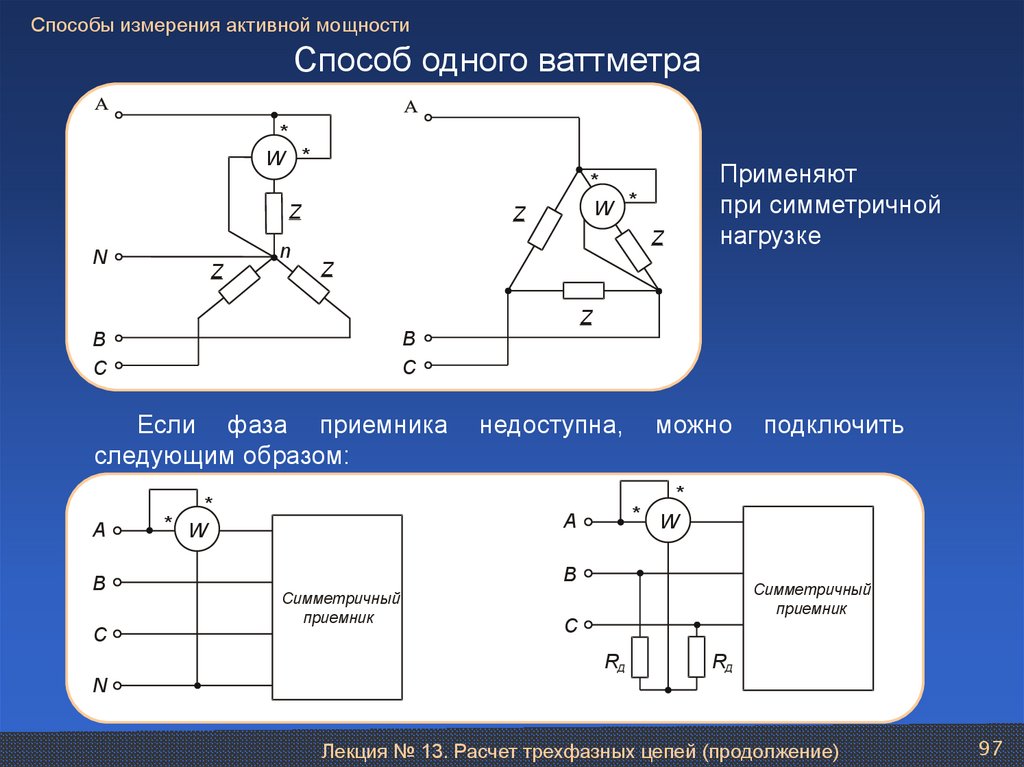





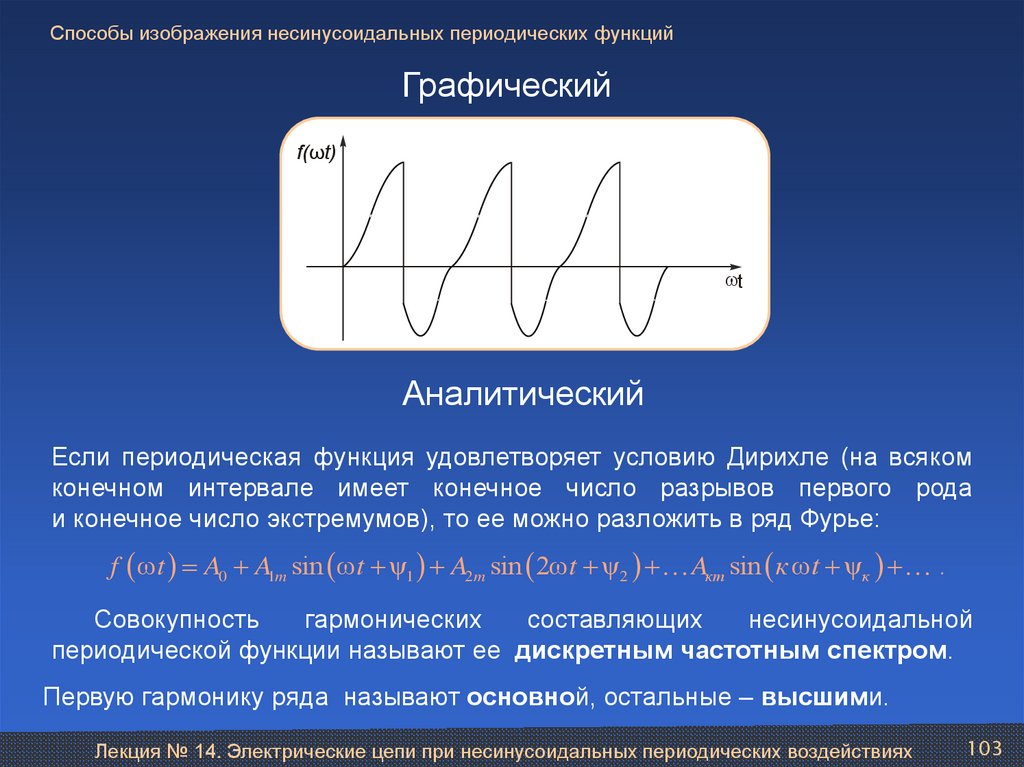










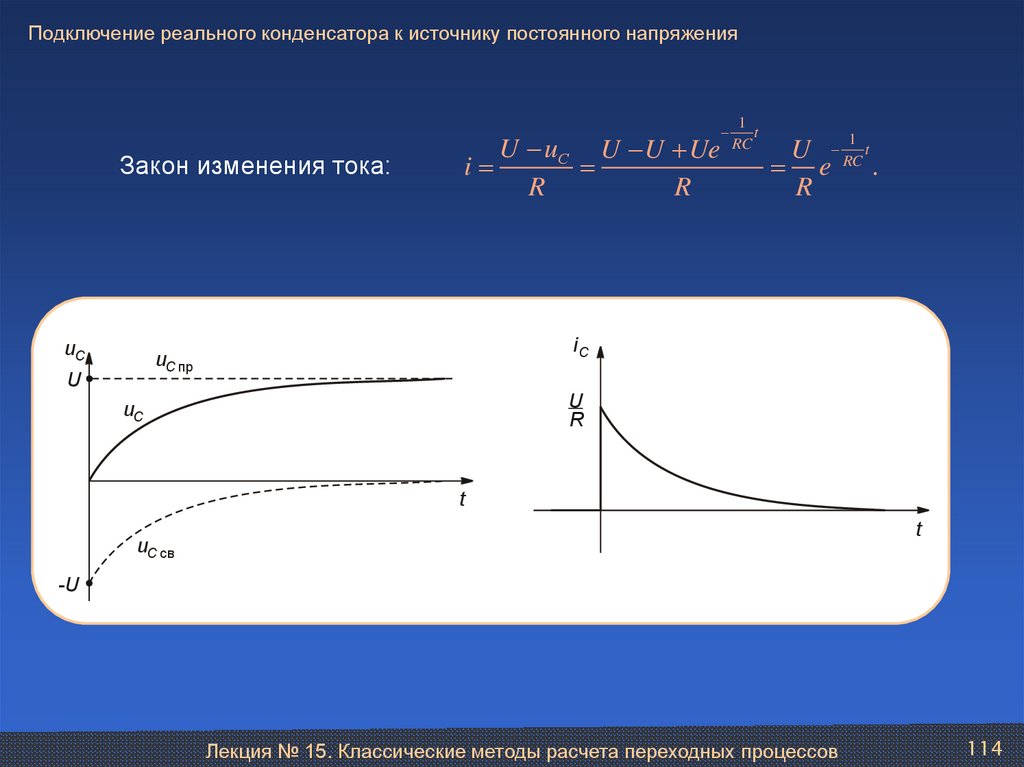
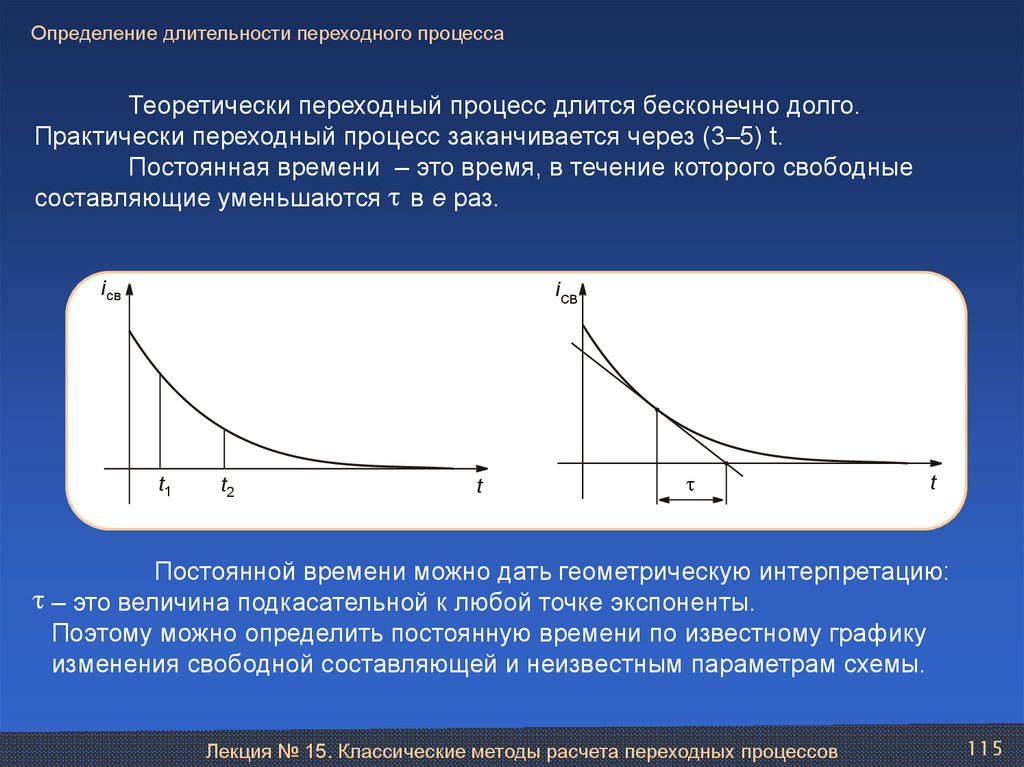


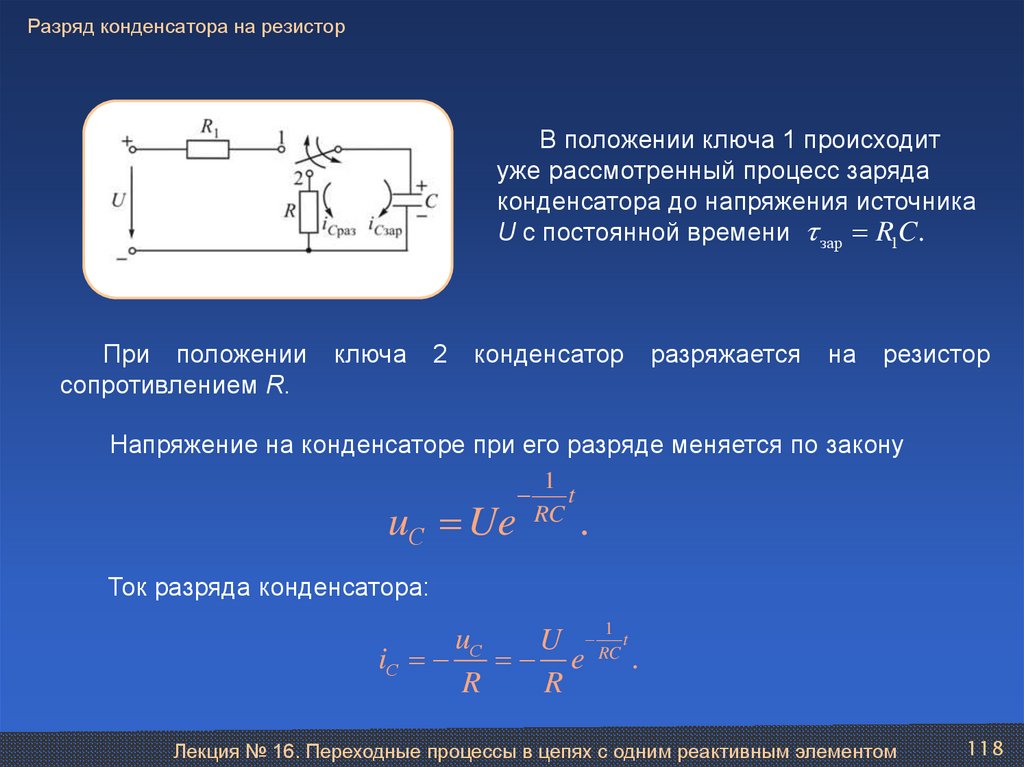

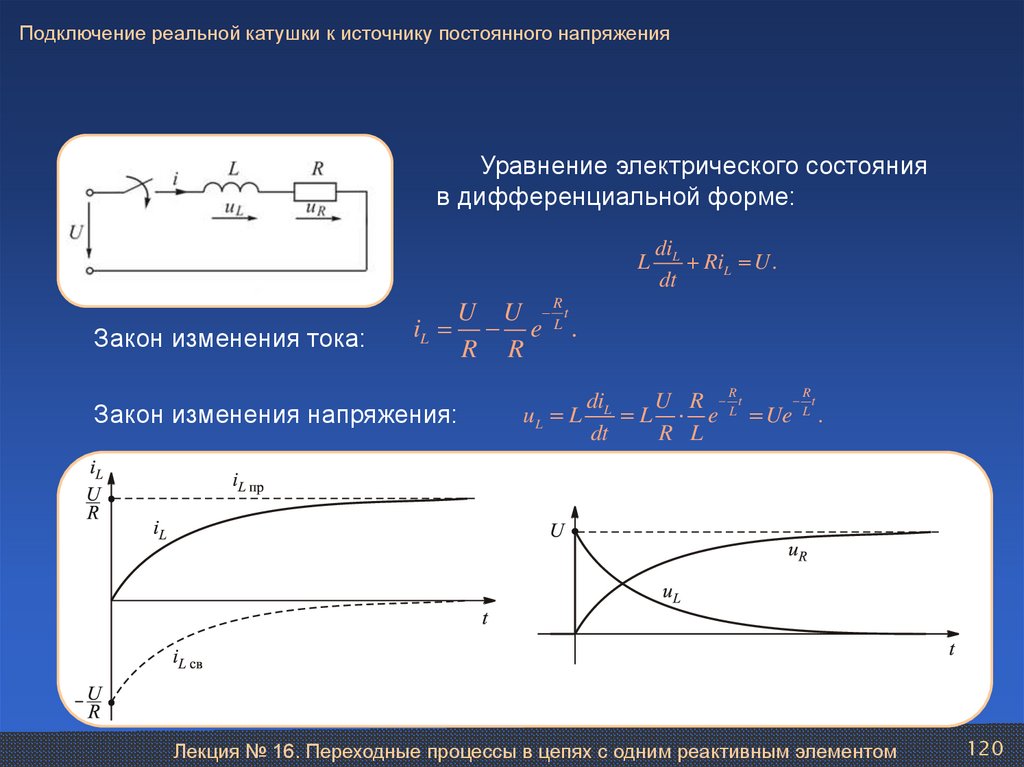


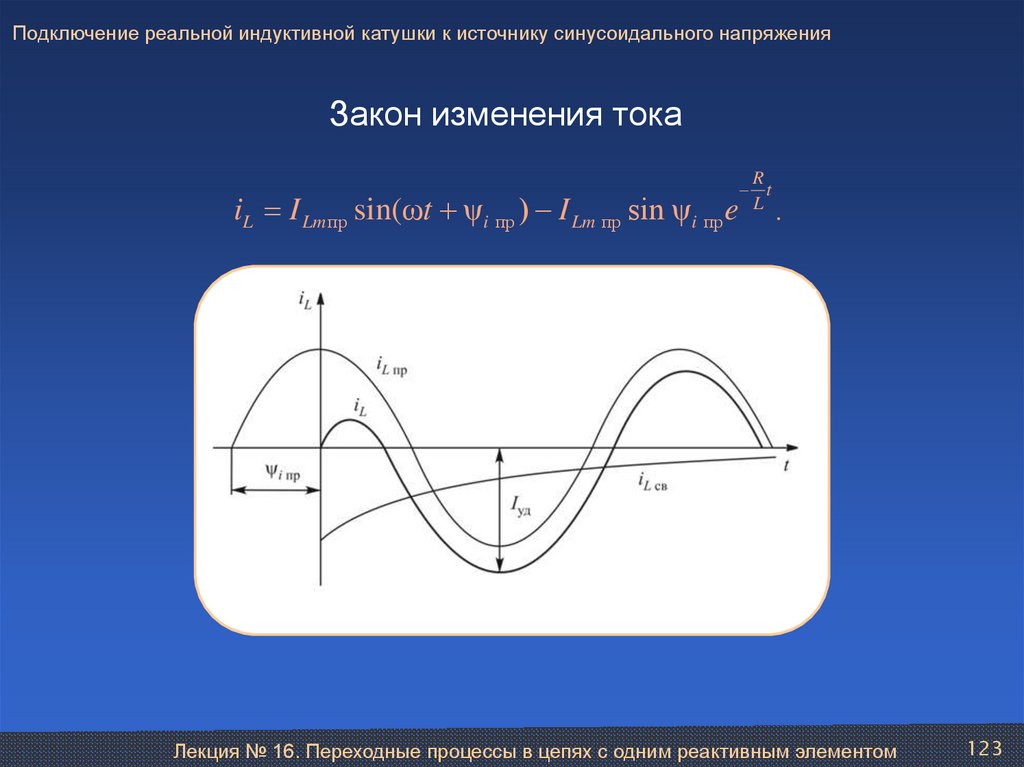



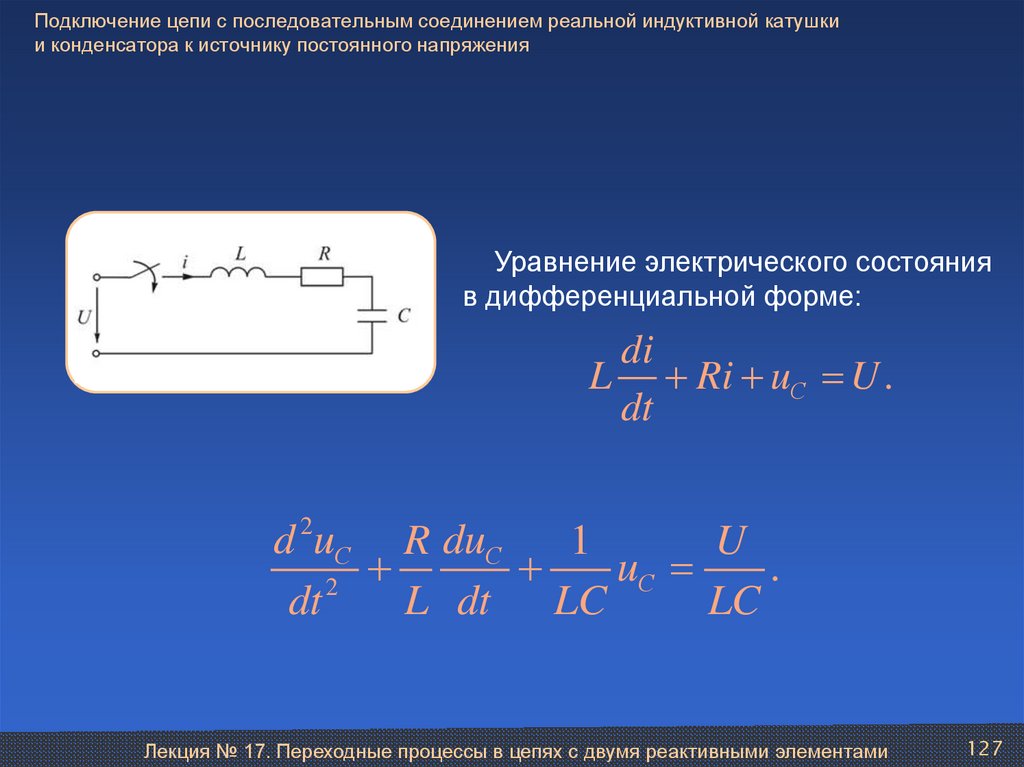


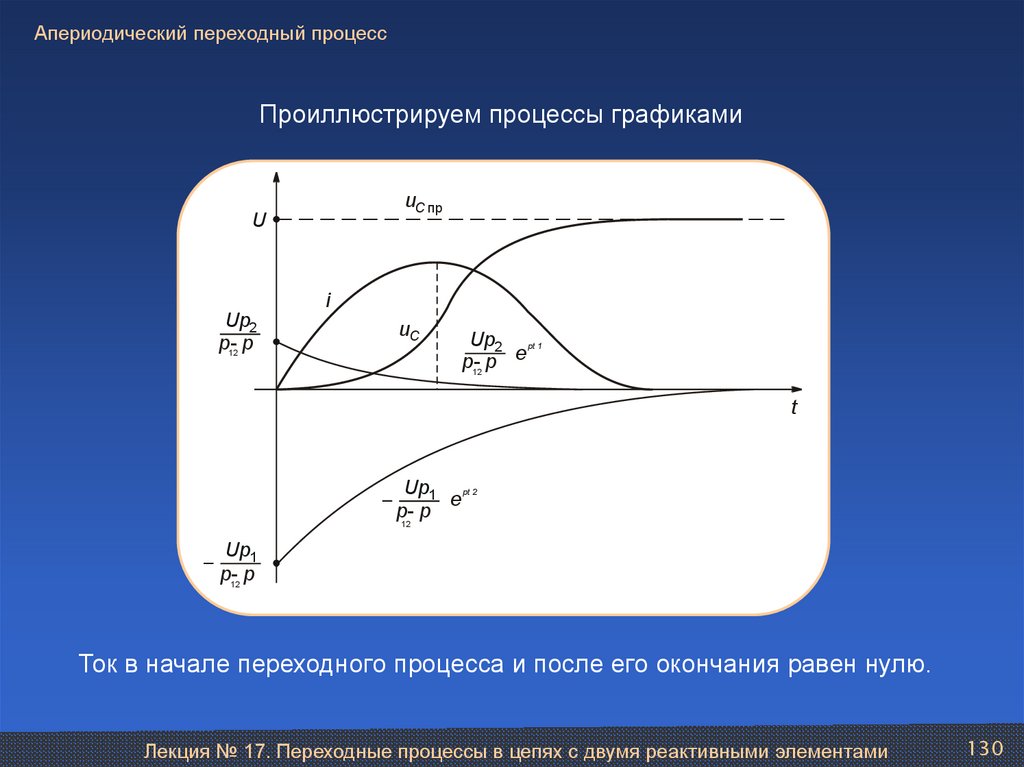






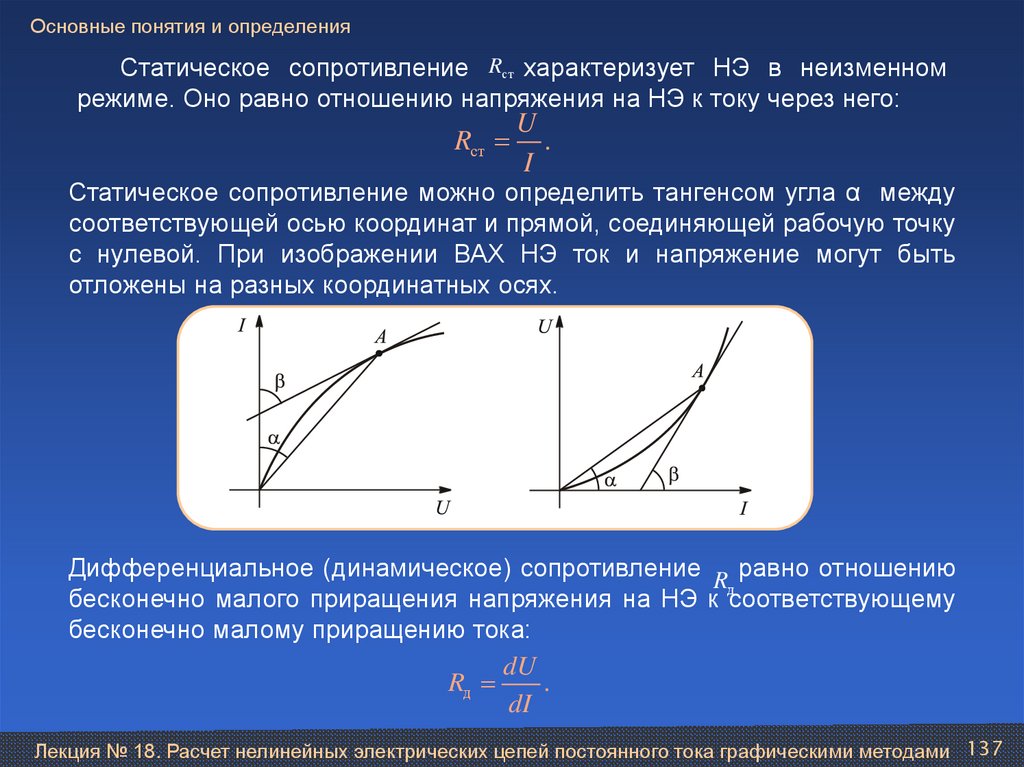

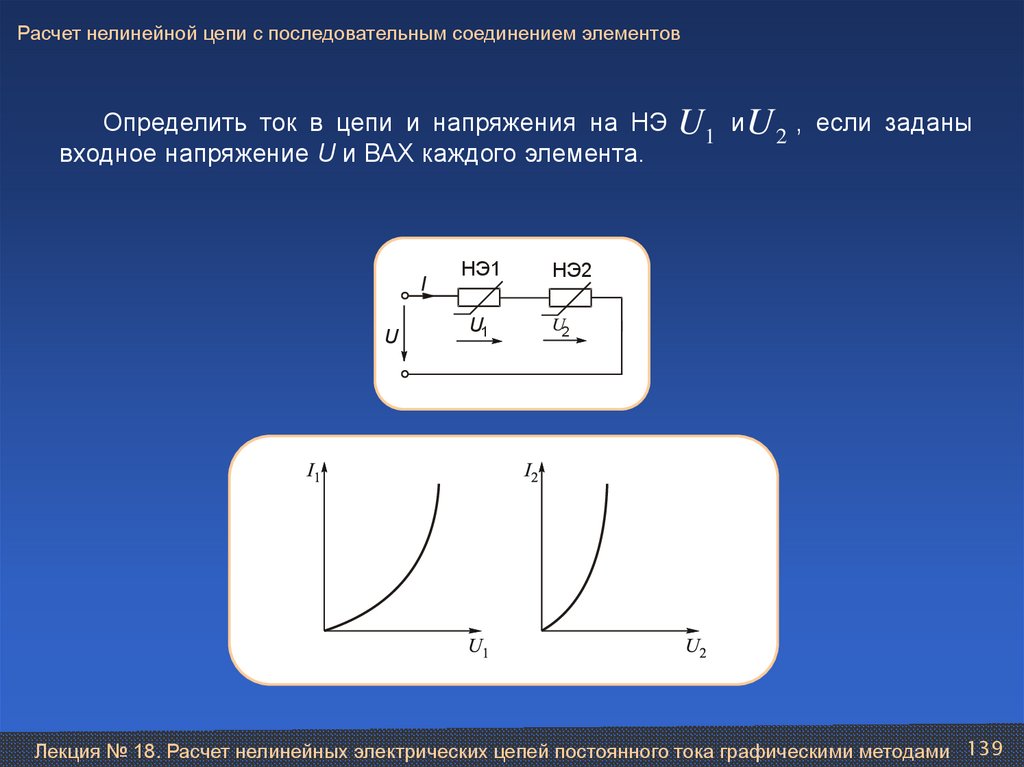




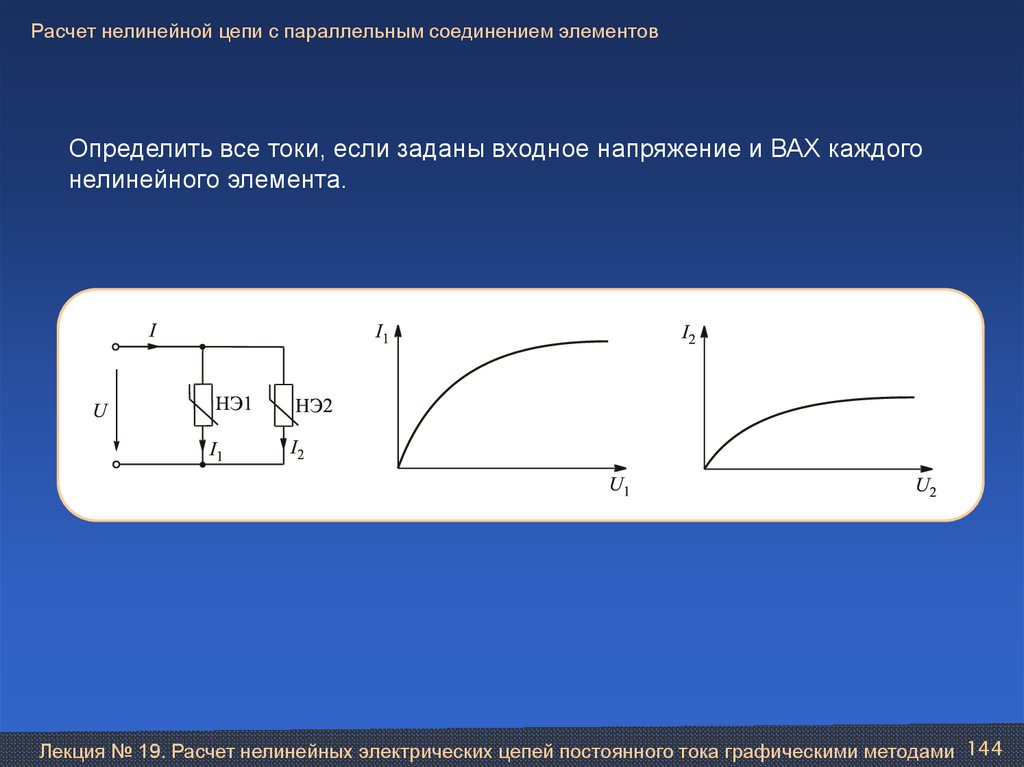



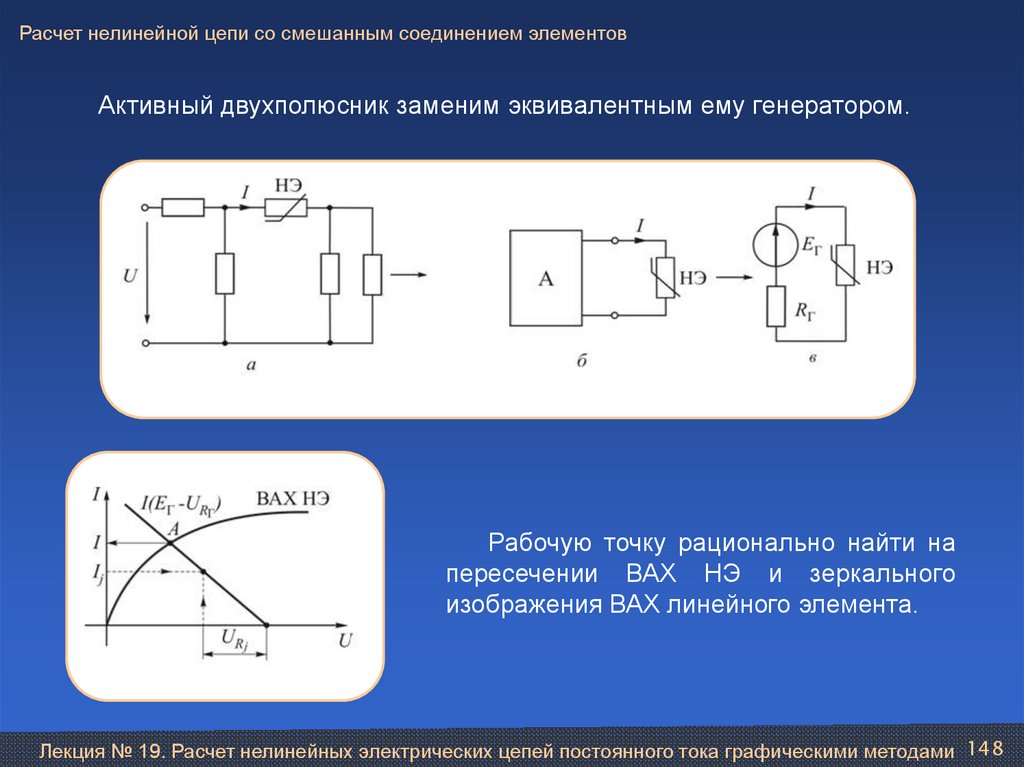






















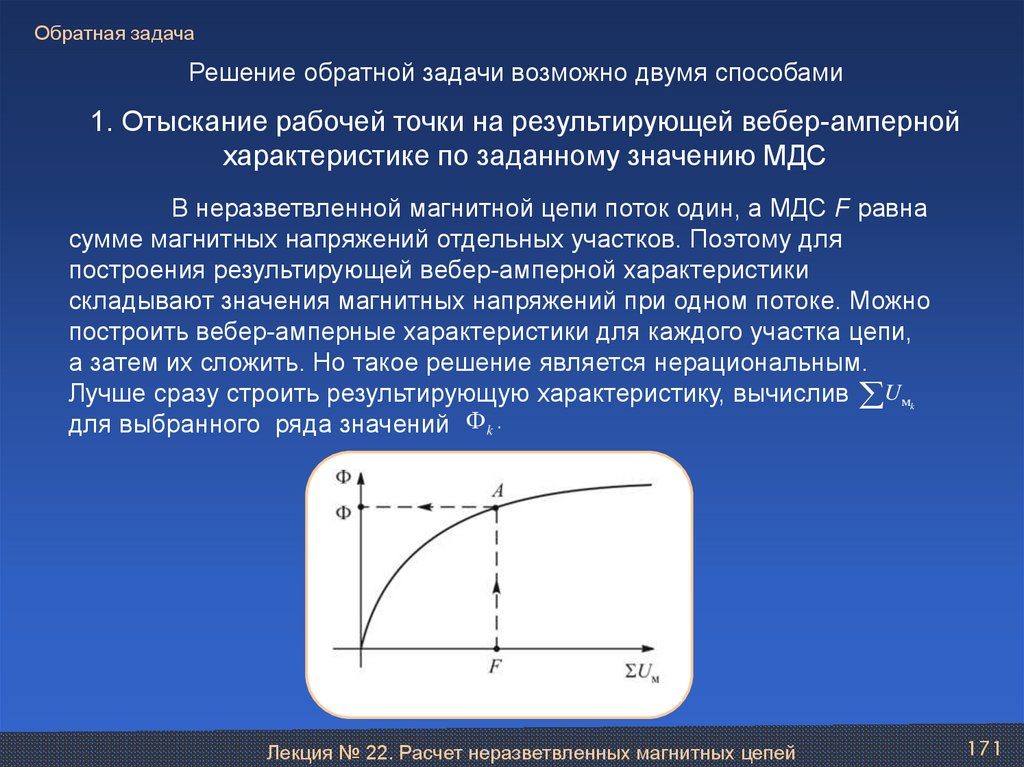











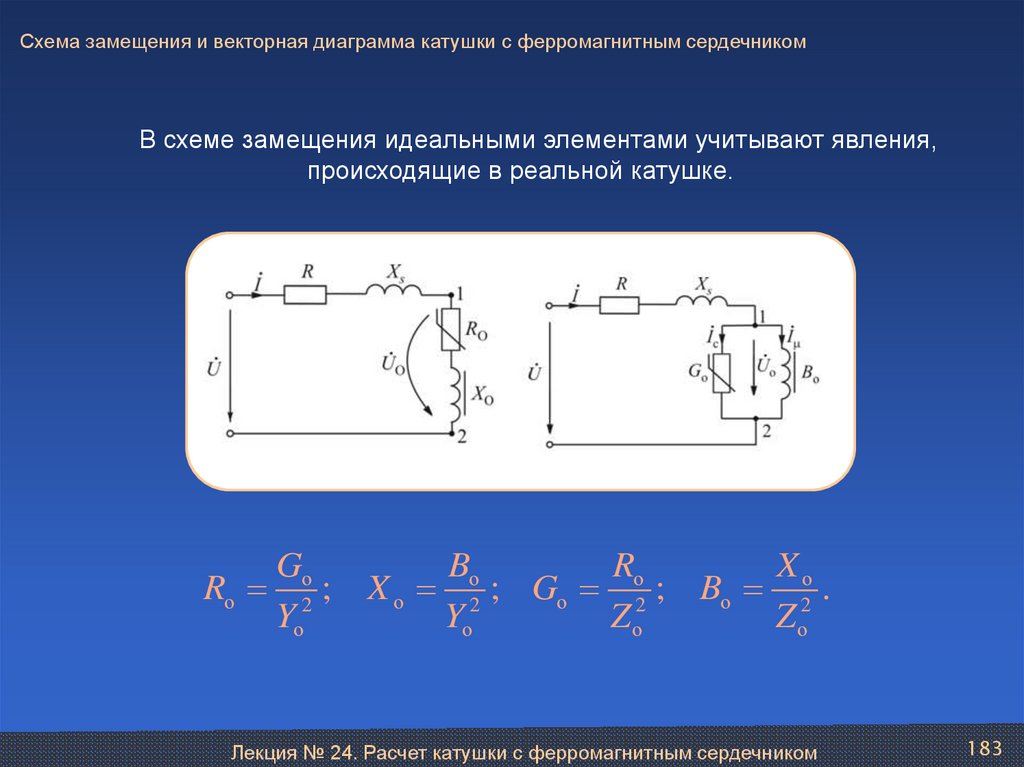





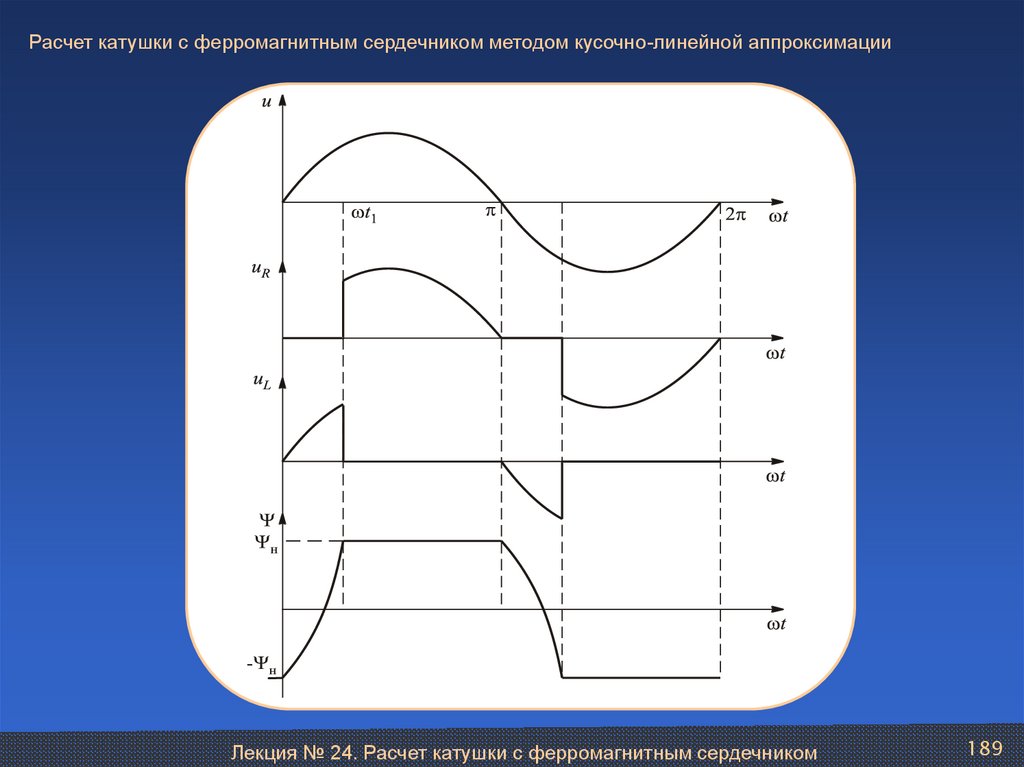




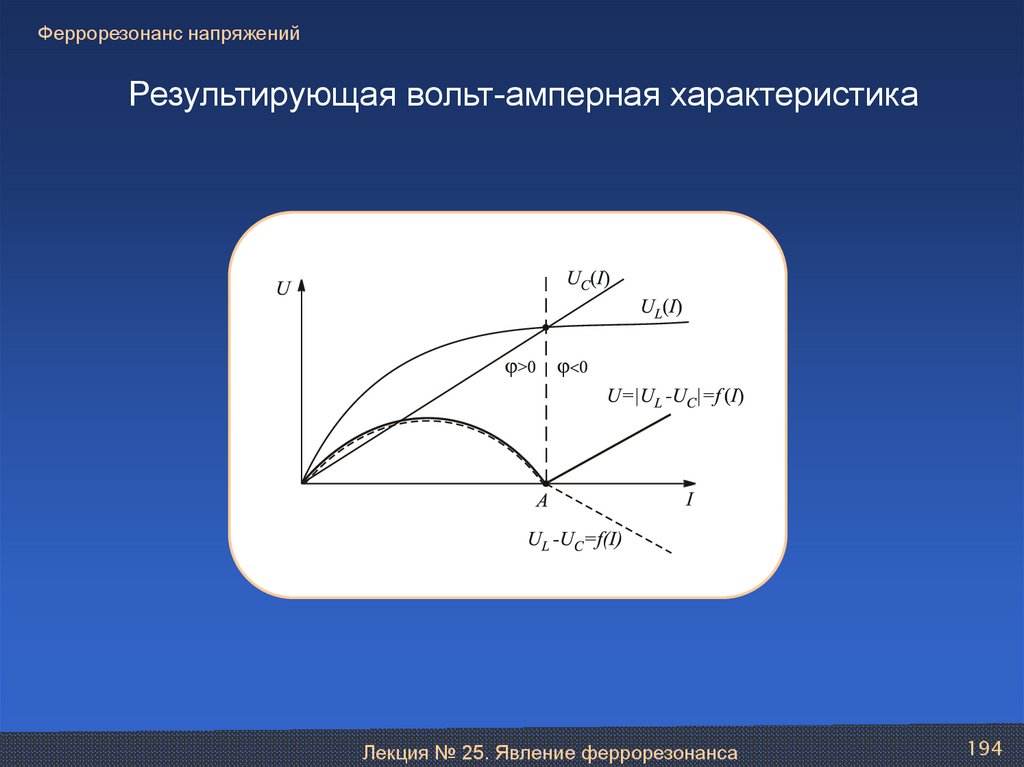


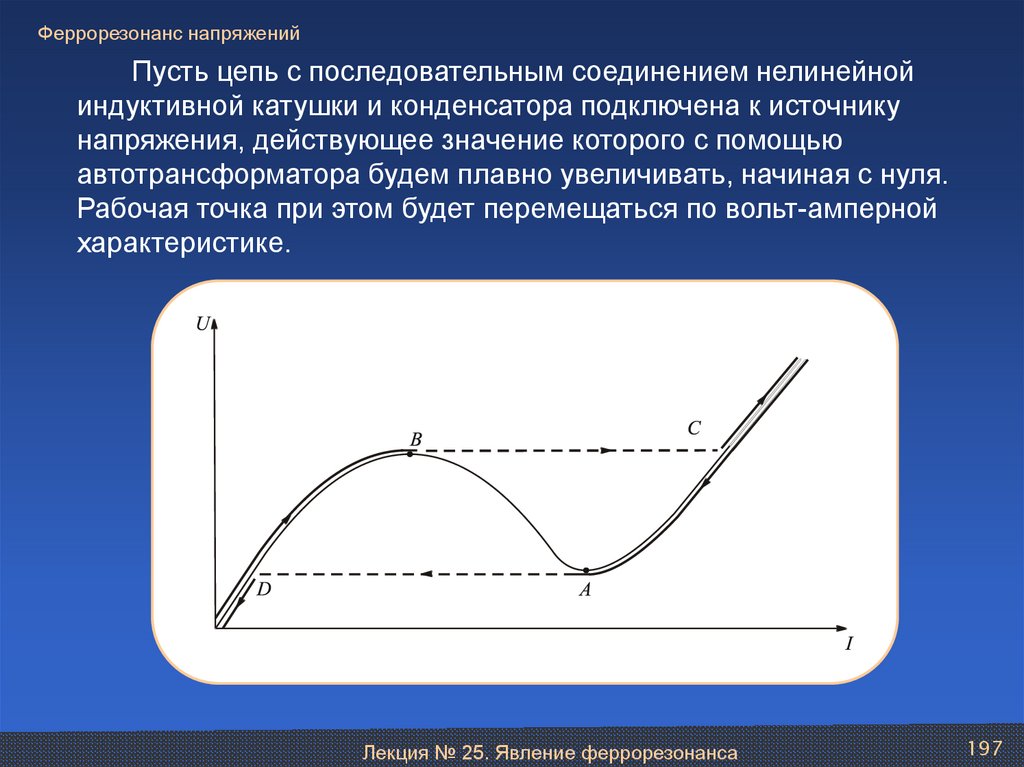











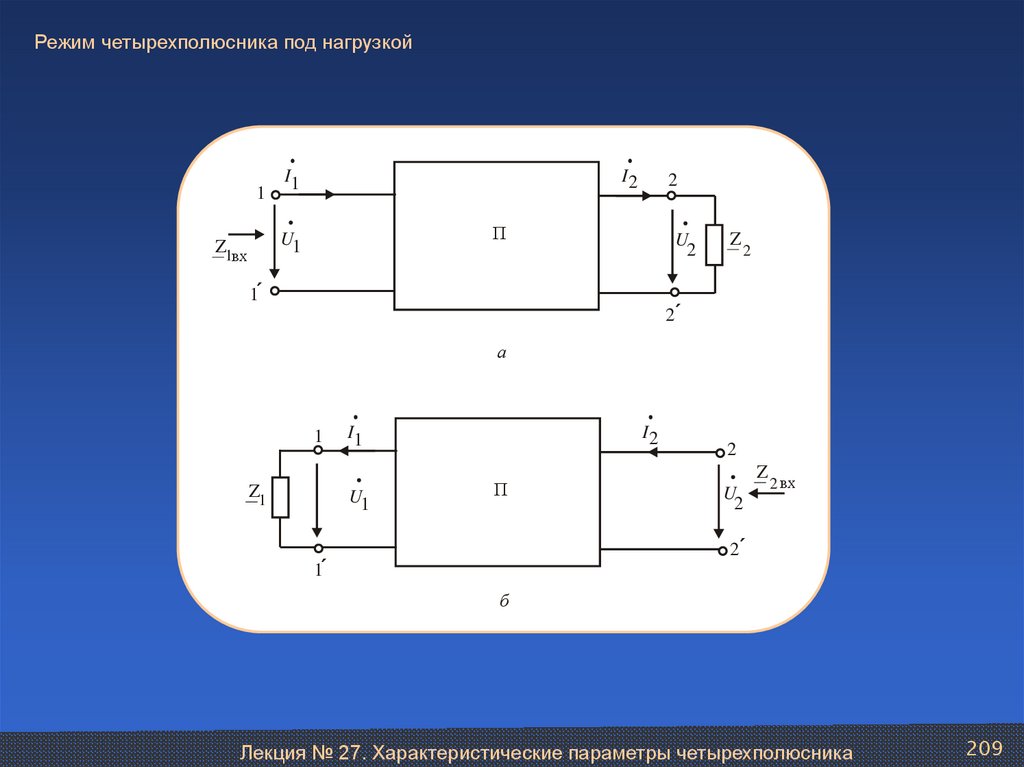

















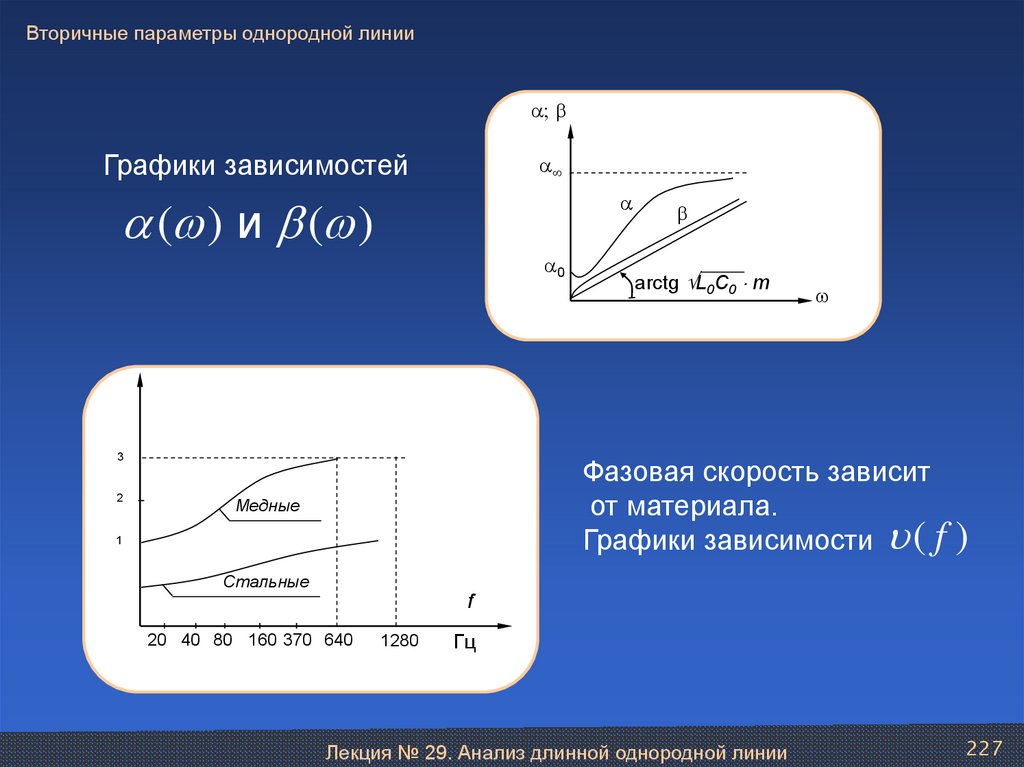
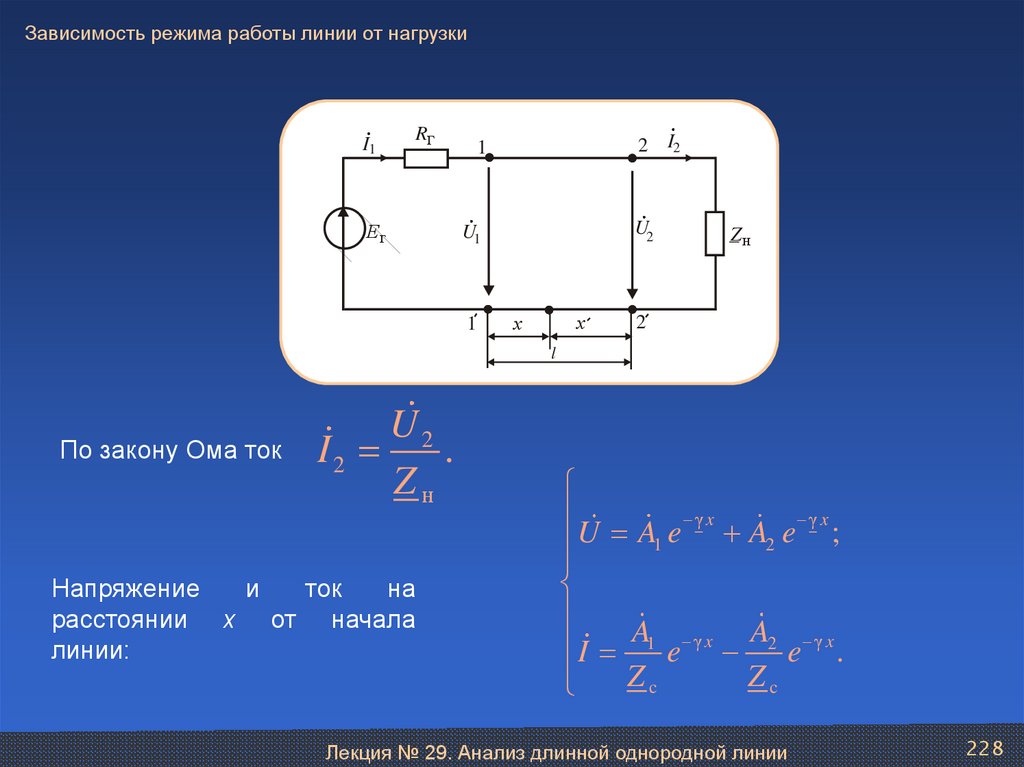







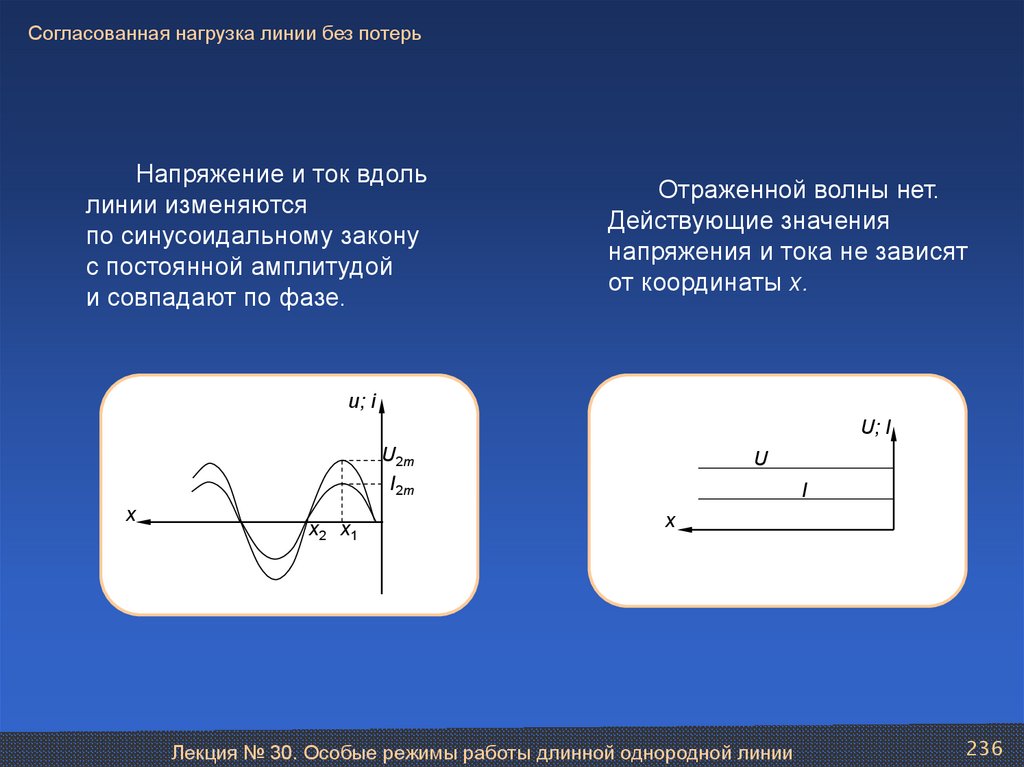





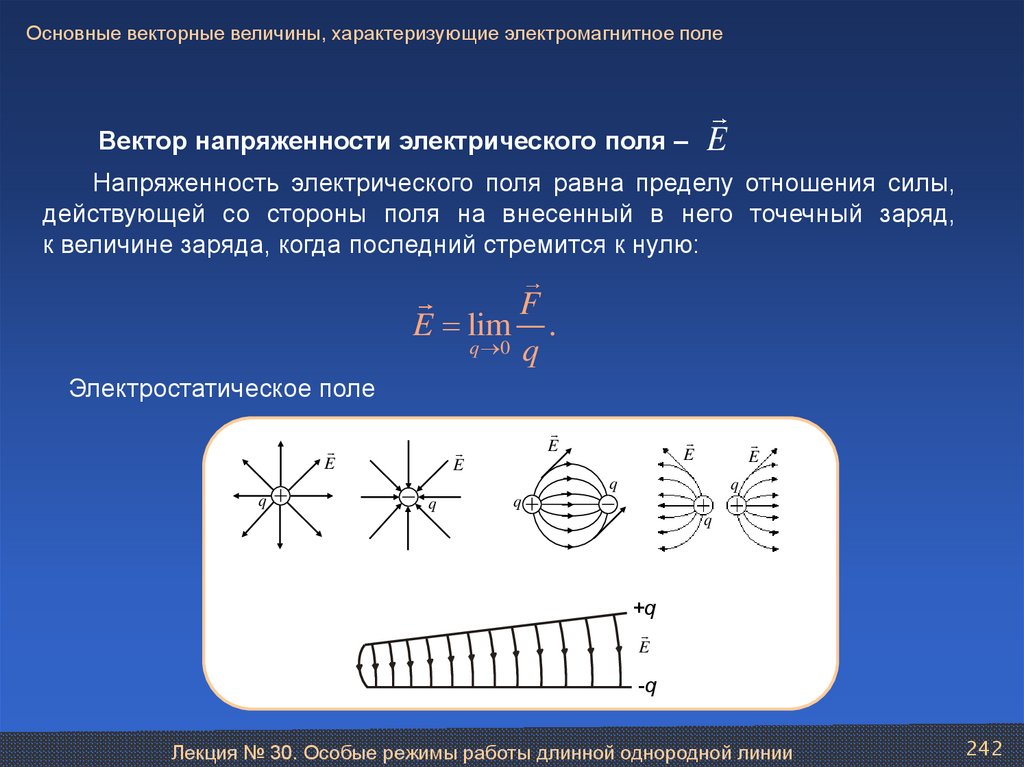










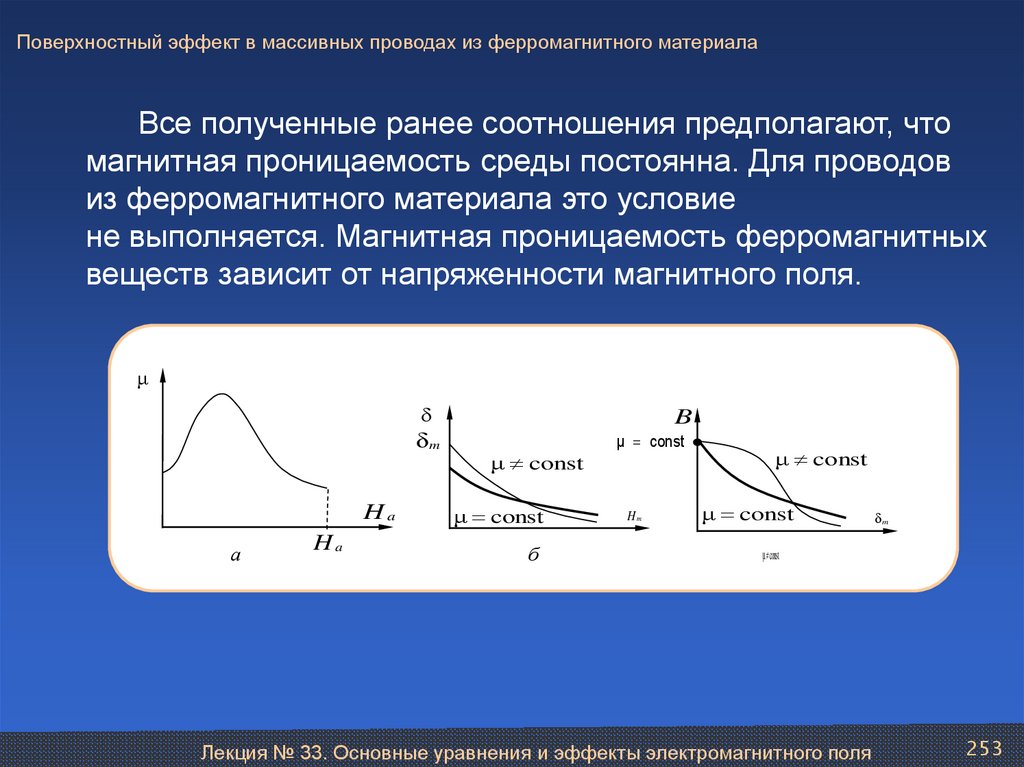



 Электроника
Электроника








