Похожие презентации:
Электротехника и электроника. Электрические цепи синусоидального тока
1. Электротехника и электроника
Электрические цеписинусоидального тока
Токи, напряжения и ЭДС, значения которых периодически изменяются во времени по
синусоидальному закону, называют синусоидальными (гармоническими). По сравнению с
постоянным током синусоидальный имеет ряд преимуществ. В частности, производство,
передача и использование электрической энергии наиболее экономичны при
синусоидальном токе, в цепях синусоидального тока относительно просто
преобразовывать форму напряжения, а также создавать трехфазные системы напряжения.
Синусоидальные токи широко используют в радио-, связной и контрольно-измерительной
технике и других областях.
В зависимости от типа решаемой задачи синусоидальные функции представляют:
• в виде аналитических выражений;
• графически, посредством временной или векторной диаграмм;
• в виде комплексных функций (комплексных чисел).
2.
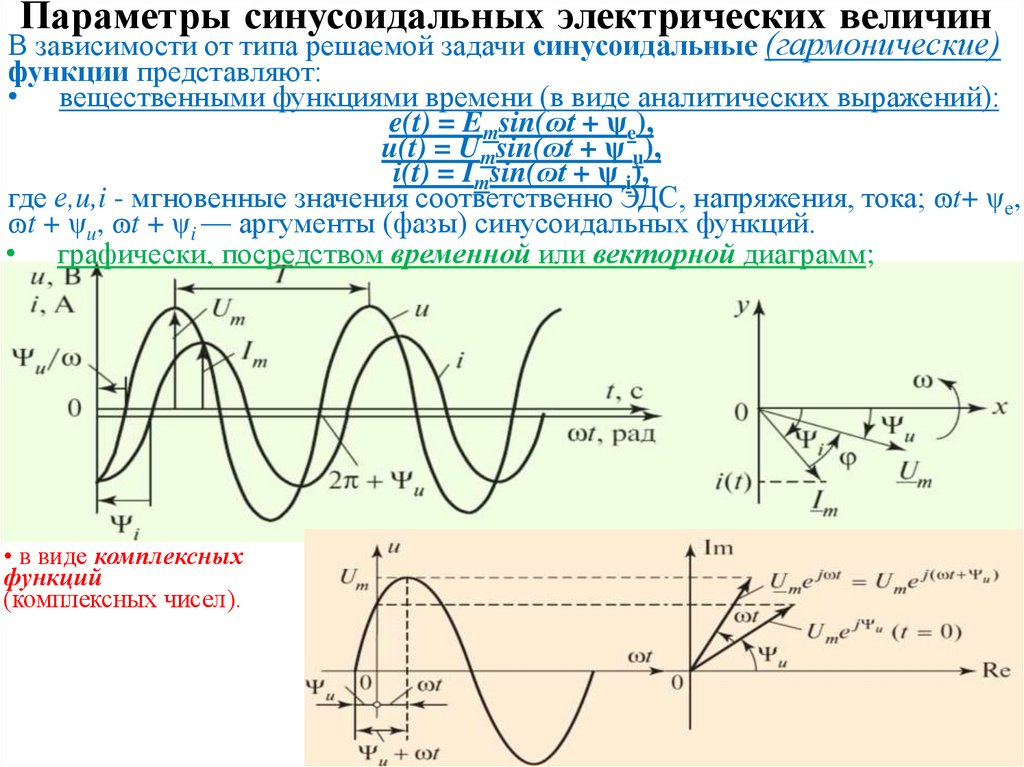
Параметры синусоидальных электрических величинВ зависимости от типа решаемой задачи синусоидальные (гармонические)
функции представляют:
• вещественными функциями времени (в виде аналитических выражений):
e(t) = Emsin(ɷt + ψe),
u(t) = Umsin(ɷt + ψ u),
i(t) = Imsin(ɷt + ψ i),
где е,u,i - мгновенные значения соответственно ЭДС, напряжения, тока; ɷt+ ψe,
ɷt + ψu, ɷt + ψi — аргументы (фазы) синусоидальных функций.
• графически, посредством временной или векторной диаграмм;
• в виде комплексных
функций
(комплексных чисел).
3.
Синусоидальная функция - периодическая функция времени (черезравный промежуток времени, наз. периодом T, цикл колебаний
повторяется). Периоду Т соответствует фазовый угол 2π или 360°
При построении временной диаграммы за аргумент
синусоидальной функции, например напряжения u(t),
принимают время t (чему соответствуют период T и
начальное время t0 = ψu/ɷ) или угол ɷt (чему
соответствуют период ɷT = 2p и начальная фаза ψu в
радианах). Угол ψu часто выражают в градусах. Тогда
аргумент ɷt также переводят в градусы (1 рад ≈ 57,3°).
В этом случае период ɷT составляет 360°.
Величину,
обратную периоду Т,
наз. циклической частотой:
1
f
T
(Гц)
Фаза (мгновенный фазовый угол) гармонической функции в радианах (рад) или градусах
— аргумент синусоидальной функции, отсчитываемый от нулевого значения функции в
положительном направлении, например, фаза напряжения.
Начальная фаза (начальный фазовый угол) — значение фазы при t = 0;
Сдвиг фаз между двумя синусоидальными функциями — разность начальных фаз этих
двух функций.
Угловая частота ɷ [рад/с] — скорость изменения фазы
Угловая частота показывает насколько фазовый угол синусоиды изменился за
период Она определяет число периодов в интервале времени, равном
2 f
4.
Среднее значение гармонического тока i(t) = Imsinwt запериод T равно нулю, то под средним значением тока i(t)
понимают среднее в интервале времени T/2
Действующий ток (напряжение) - основной эксплуатационный
параметр цепей синусоидального тока, т.к. тепловое действие
тока и механическая сила взаимодействия проводников с
токами пропорциональны квадрату тока (произведению токов).
Шкалы большинства измерительных приборов (амперметров,
вольтметров) проградуированы на эти значения.
5. Аналитические выражения синусоидальных величин
e(t ) Em sin( t e )Мгновенное значение ЭДС
u(t ) U m sin( t u )
Мгновенное значение напряжения
i(t ) I m sin( t i )
Мгновенное значение тока
Im, Um, Em - амплитудные значения тока, напряжения и ЭДС
(ωt+ψ)- аргумент синуса, который определяют фазовый угол
синусоидальной функции в данный момент времени t (фаза)
Ψ – начальная фаза
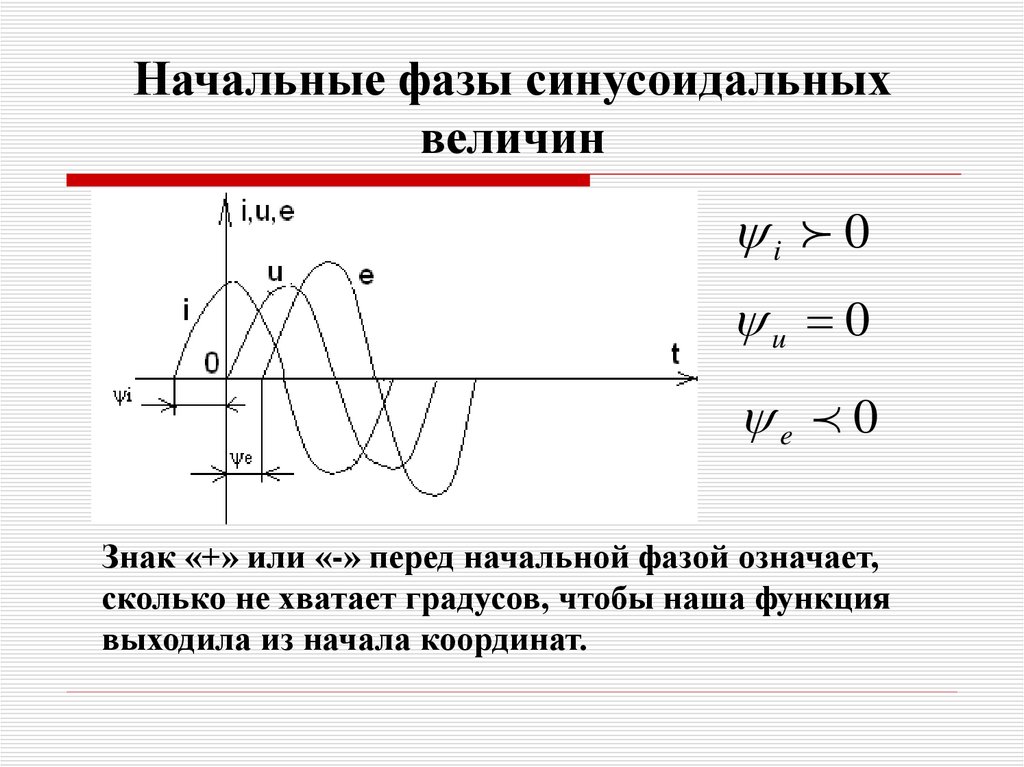
6. Начальные фазы синусоидальных величин
i 0u 0
e 0
Знак «+» или «-» перед начальной фазой означает,
сколько не хватает градусов, чтобы наша функция
выходила из начала координат.
7. Сдвиг фаз между напряжением и током
u i8. Действующие и средние значения
Расчет действующих значенийT
1 2
I
dt
i
T 0
Im
I
2
0,707 I m
U
Um
2
0,707 U m
Расчет среднего значения
Т
1
I ср
Т
2
2
I
0
m
sin tdt
2
I m 0,638I m
9.
10. Применение комплексных чисел для расчета электрических цепей
A(t ) Am sin( t a ) A m Am ej a
A a1 ja2
a1 A cos a a2 A sin a
A Ae
j a
A A cos a jAsin a
11.
12. Правила перехода из одной формы в другую Из показательной в алгебраическую
A Aej a
Формула Эйлера:
e
j a
cos a j sin a
Результат:
A A(cos a j sin a ) A cos a jA sin a
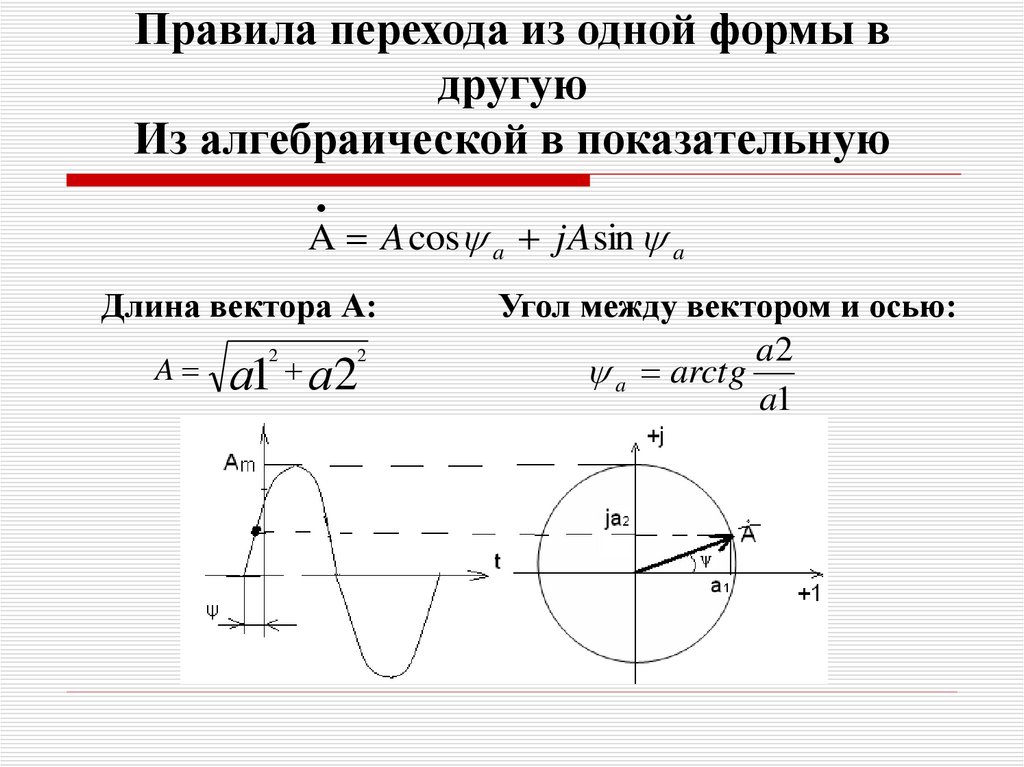
13. Правила перехода из одной формы в другую Из алгебраической в показательную
A A cos a jA sin aДлина вектора А:
A
а1
2
а2
2
Угол между вектором и осью:
a2
a arctg
a1
14. Простейшие математические операции с комплексными числами
A A cos jAsinAe
j
B B cos jB sin Be
Сложение и вычитание:
A B A cos B cos j ( A sin B sin )
Умножение и деление:
AB
j
Ae Be
j
AB
j
A
B
A j
Be
j
15. Простейшие математические операции с комплексными числами
Единичные комплексыe
e
e
j0
j180
j 90
e
j 90
Действия с j
1
jj 1
1
j ( j ) 1
j
j
1
j
j
1
j
j
16. Комплексное сопротивление
Комплексное сопротивление:Um
Um j ( u i ) Um j
j
Z
Ze
e
e
Im
Im
Im
Модуль комплексного
Комплексное сопротивление
сопротивления:
через действующие значения:
Um
Z
Im
U
Z
I
Закон Ома для амплитудных значений:
Um Im Z
Закон Ома для действующих значений:
U I Z
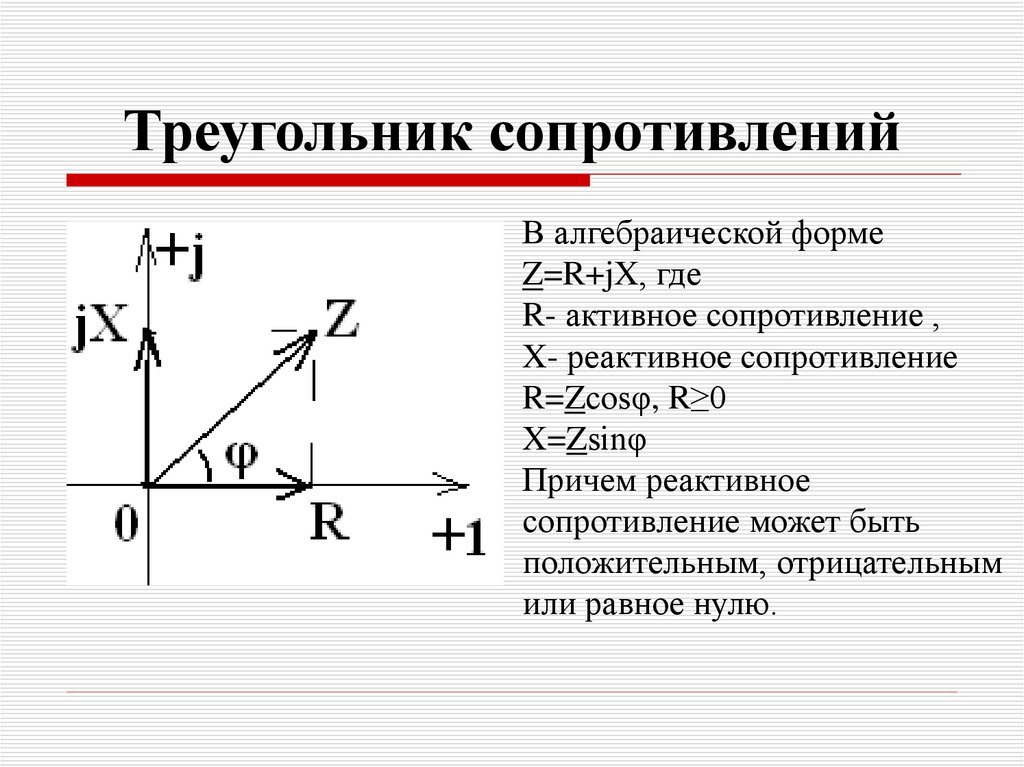
17. Треугольник сопротивлений
В алгебраической формеZ=R+jX, где
R- активное сопротивление ,
X- реактивное сопротивление
R=Zcosφ, R≥0
X=Zsinφ
Причем реактивное
сопротивление может быть
положительным, отрицательным
или равное нулю.
18. Мощности в цепях переменного тока
Полная мощность:S UI
Комплексное действующее
значение напряжения:
Сопряженный
I I
комплекс тока:
U U e
j i
e
S U e
S UI e
j u i
j u
j u
Ie
j i
j
UI e S e
S UI
j
19. Мощности в цепях переменного тока в алгебраической форме
S UI cos jUI sin(ВА –вольт-ампер)
Активная мощность:
P UI cos
(Вт – ватт)
Реактивная мощность:
Q UI sin
(ВАр – вольт-ампер реактивный)
20. Электрическая цепь с R,L,C-элементами
Для каждого элемента необходимо определить:Угол сдвига фаз между напряжением и током
(угол φ), построить векторную диаграмму
Полное комплексное сопротивление (Z)
Энергетическую характеристику цепи (P, Q, S)
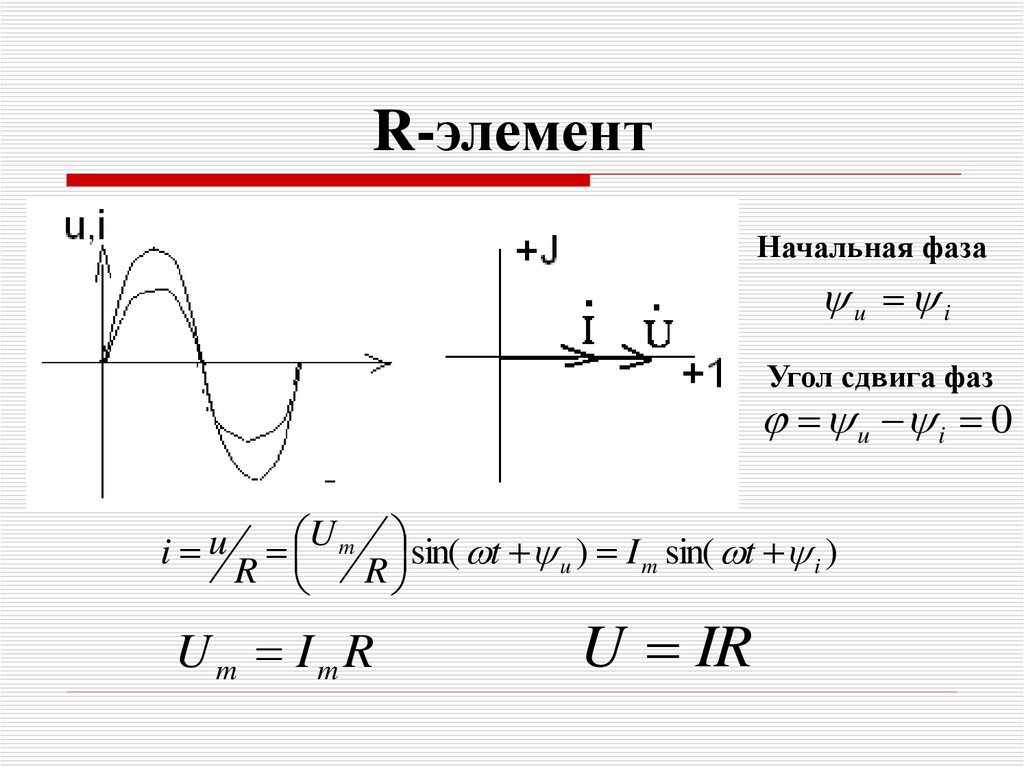
21. R-элемент
Начальная фазаu i
Угол сдвига фаз
u i 0
i u
Um
sin( t u ) I m sin( t i )
R
R
Um ImR
U IR
22. Полное комплексное сопротивление R-элемента
Комплексное сопротивлениерезистивного элемента всегда
является действительным
положительным числом,
которое равно значению
активного сопротивления R.
Закон Ома: U IR
Z
U
I
Z R
23. Мощность на R-элементе
На резистивном элементеполная мощность равна
активной мощности. Это
означает, что на резисторе
совершается работа по
преобразованию
электрической энергии в
другие виды энергии.
S R P jQ
P UI cos UI
Q UI sin 0
SR P
24. L-элемент
Начальная фазаu i 90
Угол сдвига фаз
u i 90
i(t ) I m sin( t i )
di
u L L L I m sin( t i 90 ) U m sin( t u )
dt
u(t ) U m sin( t u )
25. Полное комплексное сопротивление L-элемента
Комплексное сопротивление Lэлемента всегда является мнимымположительным числом, модуль
которого равен ХL.
Реальная катушка имеет активное
сопротивление, определяемое
сопротивлением проводов, поэтому
полное комплексное сопротивление
равно:
Z
U
jX L
I
Z X L L
Z L RL jX L
Закон Ома: U IX L
26. Мощность на L-элементе
S L P jQНа L–элементе происходит
обмен энергией между
источником электрической
энергии и магнитным полем
катушки, что определяет
реактивную мощность Q.
P UI cos 0
Q UI sin UI
S L jQ
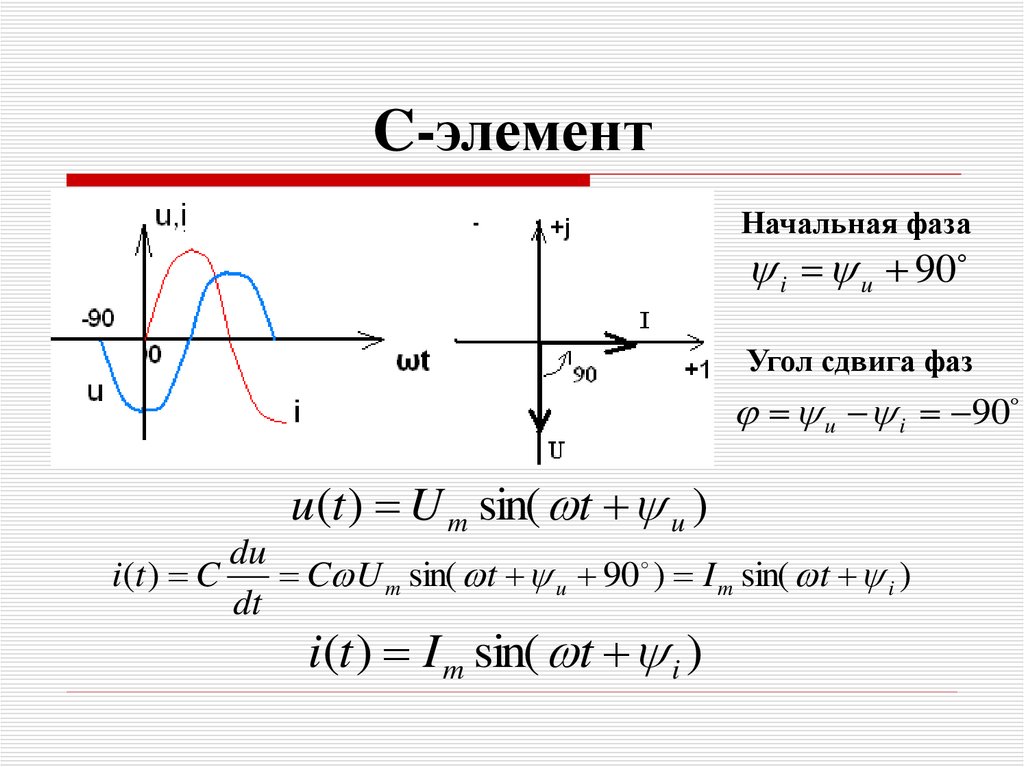
27. C-элемент
Начальная фазаi u 90
Угол сдвига фаз
u i 90
u(t ) U m sin( t u )
i (t ) C
du
C U m sin( t u 90 ) I m sin( t i )
dt
i(t ) I m sin( t i )
28. Полное комплексное сопротивление C-элемента
Комплексное сопротивление C-элемента всегдаявляется мнимым отрицательным числом,
модуль которого равен ХС.
Z
U
jX C
I
1
Z XC
C
Следовательно сопротивление конденсатора
чисто реактивное и равно:
Z C jZ
Закон Ома: U IX C
29. Мощность на C-элементе
S C P jQНа C–элементе происходит обмен
энергией между источником
электрической энергии и
электрическим полем конденсатора,
что определяет реактивную
мощность Q. С-элемент работы не
совершает, поэтому активная
мощность равна 0.
P UI cos 0
Q UI sin UI
S C jQ
30. Анализ цепей синусоидального тока
Анализ цепей синусоидального тока происходит при условии, что все элементыцепи идеальны, т.е. R, L, C идеальны.
Электрическое состояние цепей синусоидального тока описывается теми же
законами, что и в цепях постоянного тока.
U
I
z экв
Закон Ома:
Законы Кирхгофа
Первый закон:
Тригонометрический
вид
n
n
k 1
j ik
I
I
e
0
k k
k 1
k 1
m
m
m
m
k 1
k 1
k 1
k 1
i
k 1
Второй закон:
n
Комплексный вид
k
I km sin( ik t ) 0
u k U km sin( t n ) 0
U e j nk 0
U
k k
31. Правила построения векторных диаграмм
Если электрическаяцепь содержит
идеализированный R
элемент, то угол φ=0 и
векторная диаграмма
имеет вид
Если электрическая
цепь содержит
идеализированный L
элемент, то угол φ=90
и векторная
диаграмма имеет вид
Если электрическая
цепь содержит
идеализированный C
элемент, то угол φ=-90
и векторная
диаграмма имеет вид
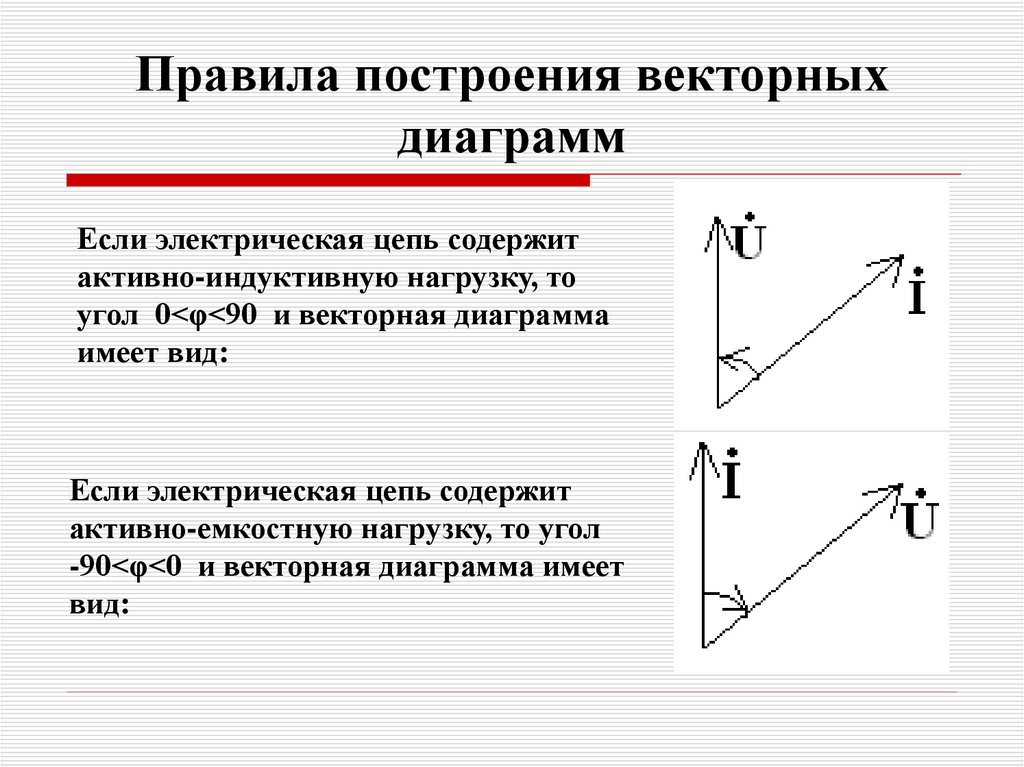
32. Правила построения векторных диаграмм
Если электрическая цепь содержитактивно-индуктивную нагрузку, то
угол 0<φ<90 и векторная диаграмма
имеет вид:
Если электрическая цепь содержит
активно-емкостную нагрузку, то угол
-90<φ<0 и векторная диаграмма имеет
вид:
33. Правила построения векторных диаграмм
Если электрическая цепь содержитпоследовательное соединение элементов, то за
основу векторной диаграммы принимается
вектор тока, относительно которого строятся
вектора напряжений.
Если электрическая цепь содержит
параллельное соединение элементов, то за
основу векторной диаграммы принимается
вектор напряжения, относительно которого
строятся вектора токов.
34. Последовательное соединение элементов в цепи синусоидального тока.
iU U R U L U C RI jX L I ( jX C ) I
R
U ( R jX L jX C ) I ( R j ( X L X C )) I
U
z экв
UR
UL
C
L
Закон Ома:
Z Экв
UC
U Z экв I
U
R jX L jX C Z экв e j экв
I
35. Треугольник сопротивлений
Z R j ( X L X C ) R jX+j
X XL XC
Z
jX
jX
+1
R
z R X
2
X L L
2
R Z cos
1
XC
c
2 f
X Z sin
arctg
X
R
36. Треугольники напряжений
+jЕсли XL>XC то отсюда
следует что U опережает I,
значит цепь имеет
индуктивный характер.
UC=-jXCI
UL=jXLI
0
UR=IR
I
+1
37. Треугольники напряжений
+jUL=jXLI
UR=IR
I
+1
UC=-jXCI
Если XL<XC то отсюда
следует что I опережает U,
значит цепь имеет
емкостной характер.
0
38. Резонанс напряжений
Режим работы RLC цепи, приусловии равенства реактивных
сопротивлений XC=XL, когда
общее напряжение цепи
совпадает по фазе с её током φ=0
- называется резонансом
напряжений.
Цепь имеет активный характер:
0
39. Признаки резонанса напряжений
1. Напряжение на входе совпадает по фазе с током,т.е. сдвиг фаз между I и U φ=0, cos(φ)=1
2. Ток в цепи будет наибольшим и как следствие
Pmax=I2maxR тоже максимальна, а реактивная
мощность равна нулю.
3. Напряжения на элементах цепи могут в несколько
раз превышать напряжение на входе
4. U C U L U C U L 0 U U L U C U R U R .
40. Параллельное соединение элементов в цепях синусоидального тока
II I1 I 2
A
U
I2
I1
R1
I 1
-jXC
jXL
B
R2
I 2
U
Z ЭКВ1
U
Z ЭКВ 2
Z ЭКВ1 R1 jX L Z ЭКВ 2 R2 jX C
41. Треугольники проводимостей
1Y G jB
Z
B
G – действительная часть, активная составляющая
B – мнимая часть, реактивная составляющая
Y
jB
G Y cos
B Y sin
Y G B
2
G
R
G 2
R X2
R
G 2
Z
X
B 2
R X2
2
X
B 2
Z
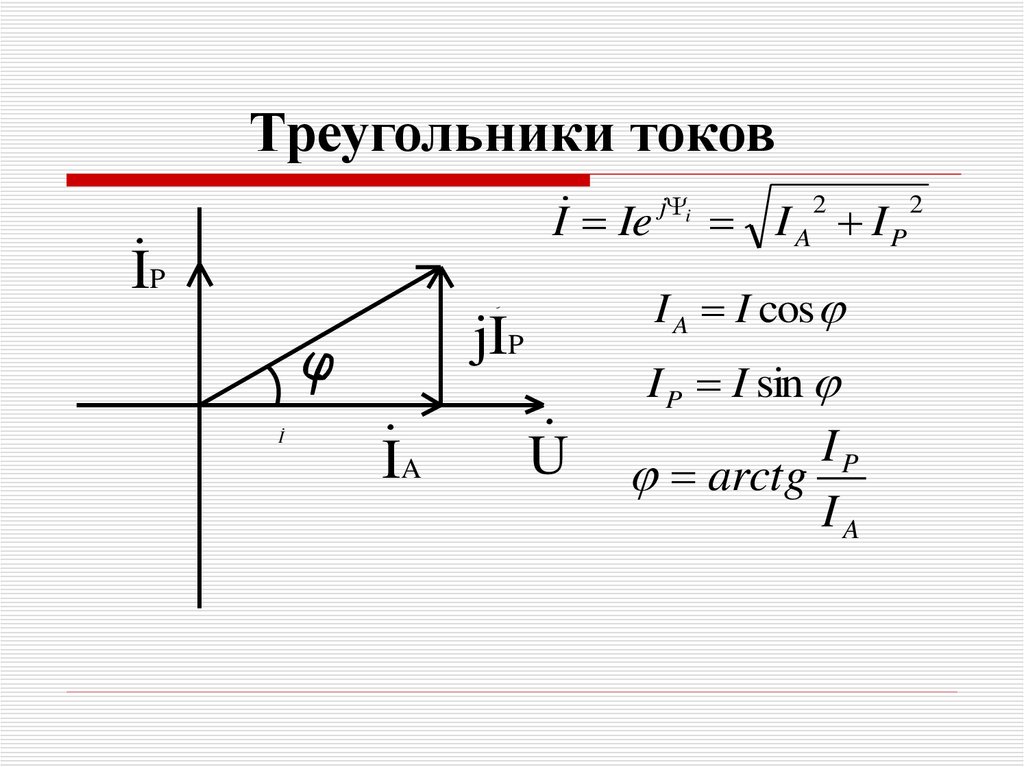
42. Треугольники токов
I Ie j i I 2 I 2A
P
IP
I A I cos
jIP
I
IA
I P I sin
U
IP
arctg
IA
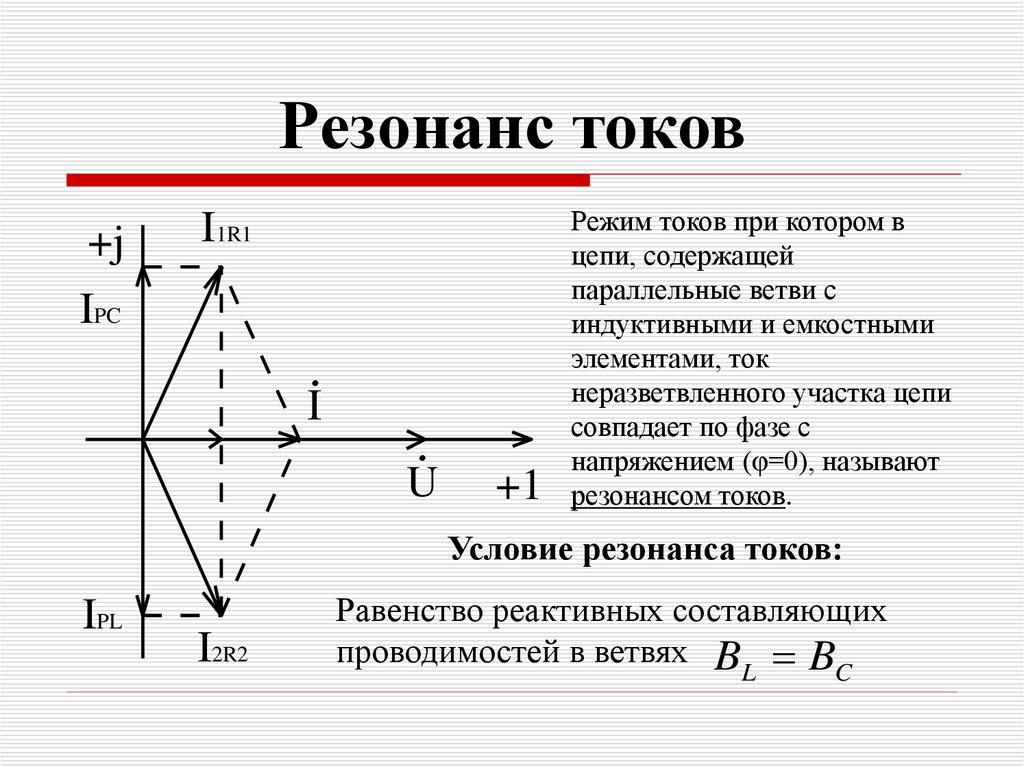
43. Резонанс токов
+jI1R1
IPC
I
U
+1
Режим токов при котором в
цепи, содержащей
параллельные ветви с
индуктивными и емкостными
элементами, ток
неразветвленного участка цепи
совпадает по фазе с
напряжением (φ=0), называют
резонансом токов.
Условие резонанса токов:
IPL
I2R2
Равенство реактивных составляющих
проводимостей в ветвях B B
L
C
44. Признаки резонанса токов
1. Токи ветвей равны IPC=IPL и находятся впротивофазе.
2. Токи ветвей превышают полный ток цепи,
который имеет минимальное значение.
3.
I и U совпадают по фазе, φ= 0
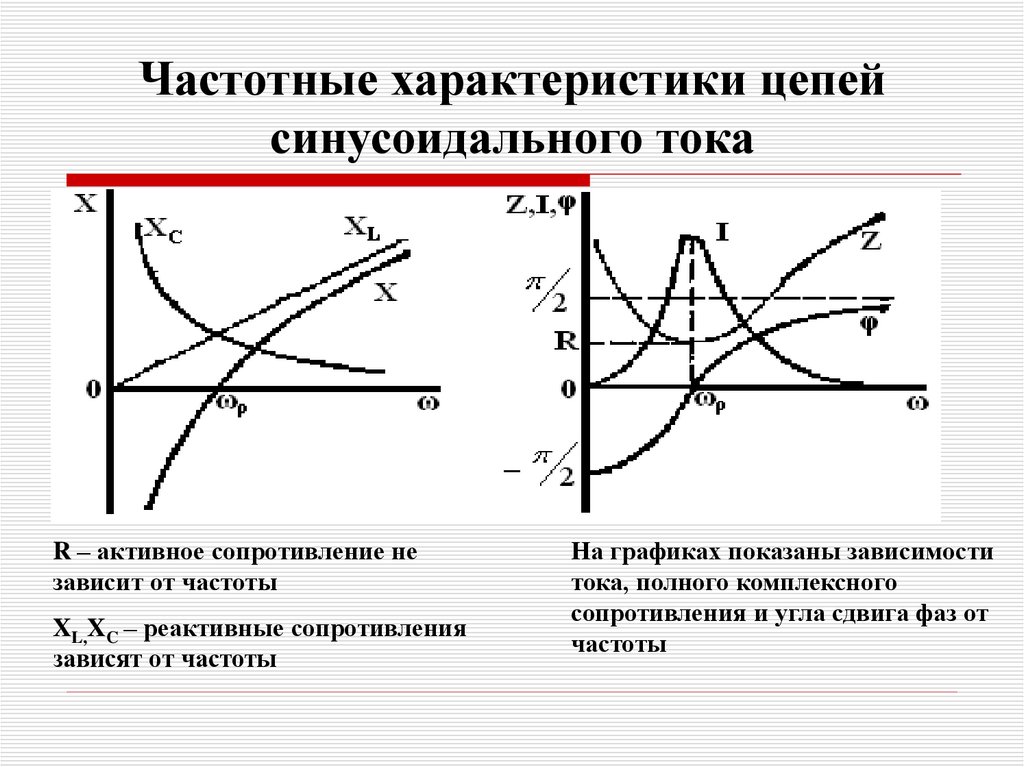
45. Частотные характеристики цепей синусоидального тока
R – активное сопротивление независит от частоты
XL,XC – реактивные сопротивления
зависят от частоты
На графиках показаны зависимости
тока, полного комплексного
сопротивления и угла сдвига фаз от
частоты
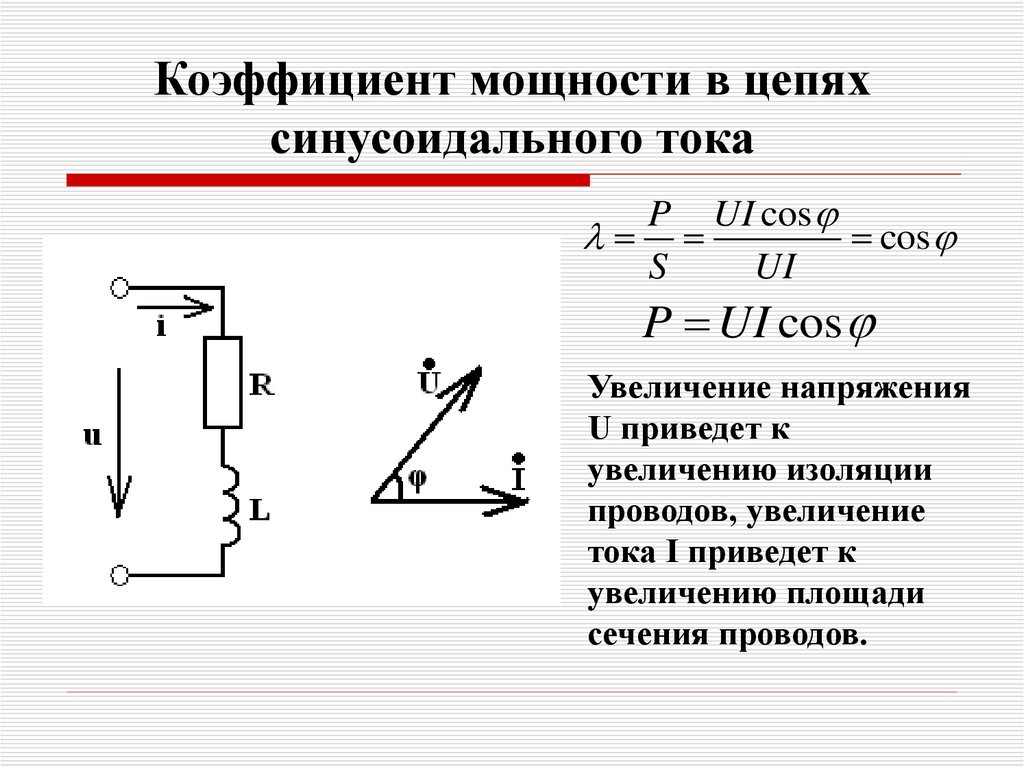
46. Коэффициент мощности в цепях синусоидального тока
P UI coscos
S
UI
P UI cos
Увеличение напряжения
U приведет к
увеличению изоляции
проводов, увеличение
тока I приведет к
увеличению площади
сечения проводов.
47. Электротехника и электроника
Трёхфазные электрическиецепи синусоидального тока
48.
Трёхфазная система электроснабженияТрехфазная цепь — это совокупность трёхфазной системы ЭДС, трехфазной
нагрузки (нагрузок) и соединительных проводов.
Трёхфазной системой ЭДС (напряжений) наз. систему из трёх однофазных
электрических цепей, в которых действуют три синусоидальные ЭДС одной и той
же частоты, равные по амплитуде и сдвинутые по фазе относительно друг друга на
угол 2π/3 (120°).
Преимущества генерирования, передачи и преобразования электрической энергии в
трёхфазных цепях по сравнению с однофазными цепями заключаются в следующем:
1. меньший расход меди в проводах и стали в одном трёхфазном трансформаторе по
сравнению с расходом материалов в трёх однофазных трансформаторах;
2. простота получения вращающегося магнитного поля в электродвигателях переменного
тока и меньшие пульсации момента на валу трёхфазных генераторов и двигателей;
3. элементы системы — трёхфазный синхронный генератор, трехфазный асинхронный
двигатель и трёхфазный трансформатор — просты в производстве, экономичны и
надёжны в работе.
4. Напряжение двум номиналов.
Под фазой трёхфазной цепи понимают участок цепи, по которой протекает одинаковый
ток. Под фазой будем также понимать аргумент (wt - Y) синусоидальной функции. Т.е., в
зависимости от рассматриваемого вопроса фаза — это либо участок трёхфазной цепи, либо
аргумент синусоидальной функции.
В трёхфазной цепи различают фазы А, B и С генератора — источника напряжения (ИН) и
фазы а, b и с приёмника. Обозначают (окрашивают) их соответственно в жёлтый (фаза А),
зелёный (фаза B) и красный (фаза С) цвета. Концы обмоток фаз ИН Х, Y и Z соединяют в
общую точку N (реже обозначают эту точку символом 0 (ноль)) и называют ее нейтралью
трёхфазного генератора.
49. Получение трехфазной системы ЭДС
Основные элементытрехфазной цепи:
1. Трёхфазный
генератор
2. Линии передачи
3. Приёмники
Основные элементы
генератора:
1. Неподвижный статор
(состоит из трёх
обмоток).
2. Вращающийся ротор
(электромагнит)
A,B,C – начала фаз
X,Y,Z – концы фаз
50.
Схемы соединения фаз генератора и трёхфазной нагрузки. Обмоткистатора трёхфазного генератора соединяют по схеме звезда (Y) (см.
рис. слева) или треугольник (D) (см. рис. справа). Трёхфазная нагрузка
(приёмник) также может быть соединена по схеме звезда или треугольник.
Электрические величины, относящиеся к генератору, будем снабжать
индексами из прописных букв А, B и C, а величины, относящиеся к
трёхфазному приёмнику, — индексами из строчных букв а, b и c.
Провода, соединяющие точки А и а, B и b, С и с, называют линейными (провод
А, провод B и провод С ), соответственно и токи в них IA, IB, IC называют
линейными. Провод, соединяющий точку N (нейтраль генератора) с точкой n
(нейтралью приёмника), называют нейтральным (иногда, нулевым), а ток IN в
нем — током в нейтральном проводе.
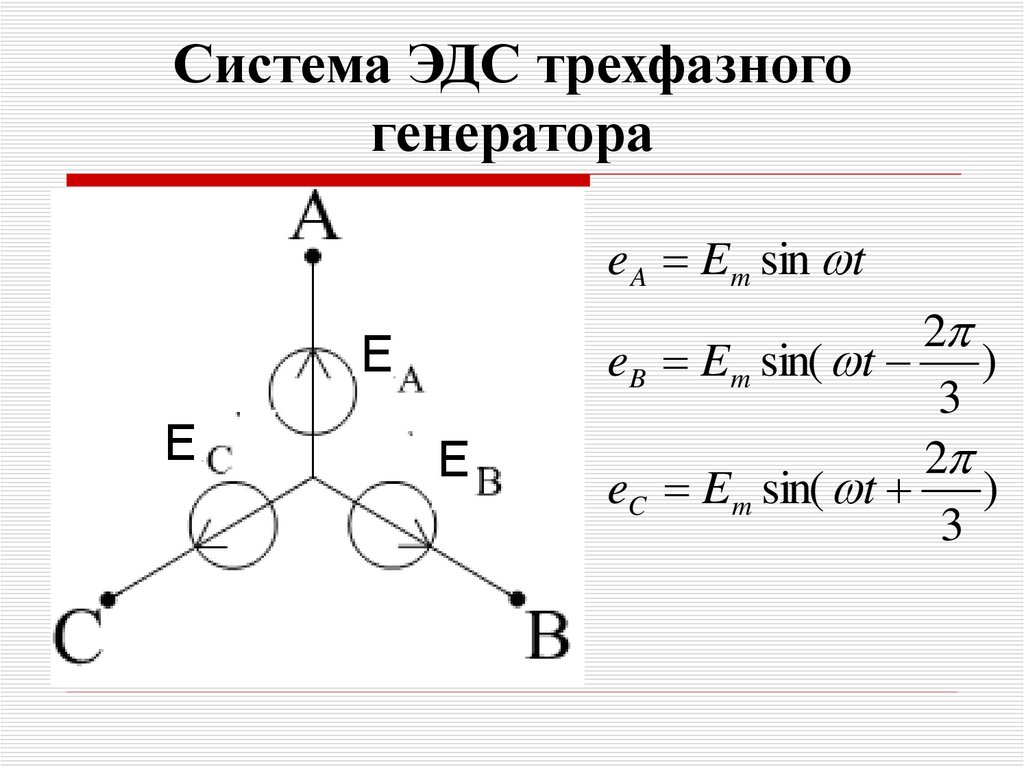
51. Система ЭДС трехфазного генератора
e A Em sin t2
eB Em sin( t )
3
2
eC Em sin( t )
3
52. Векторная диаграмма линейных и фазных напряжений
OA UЛ
2
U Ф cos
U
Л
6
U Ф
3U Ф
U Л 660 В U Ф 660
U Л 380 В U Ф 380
U Л 220 В U Ф 220
I
3
2
л
IФ
3
3
3
380 В
220 В
127 В
53. Способы соединения фаз источников питания Соединение треугольником
Алгоритмсоединения:
A-Y
B-Z
C-X
U Л UФ
I Л 3I Ф
54. Соединение обмоток источника и фаз приёмника звездой
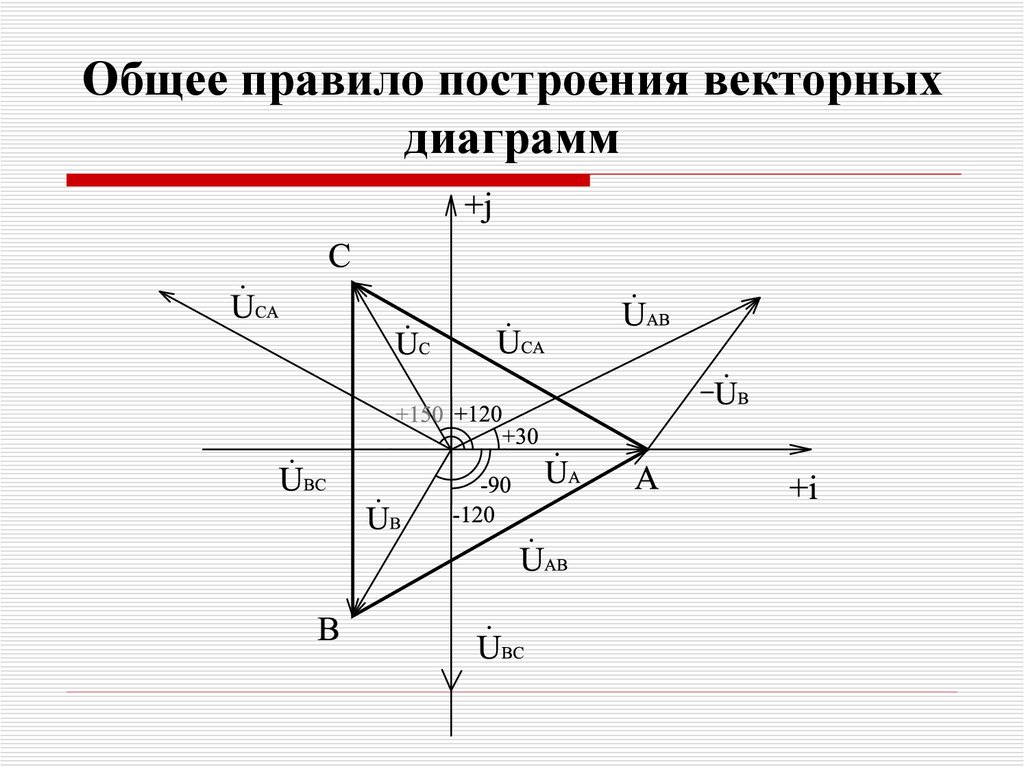
55. Общее правило построения векторных диаграмм
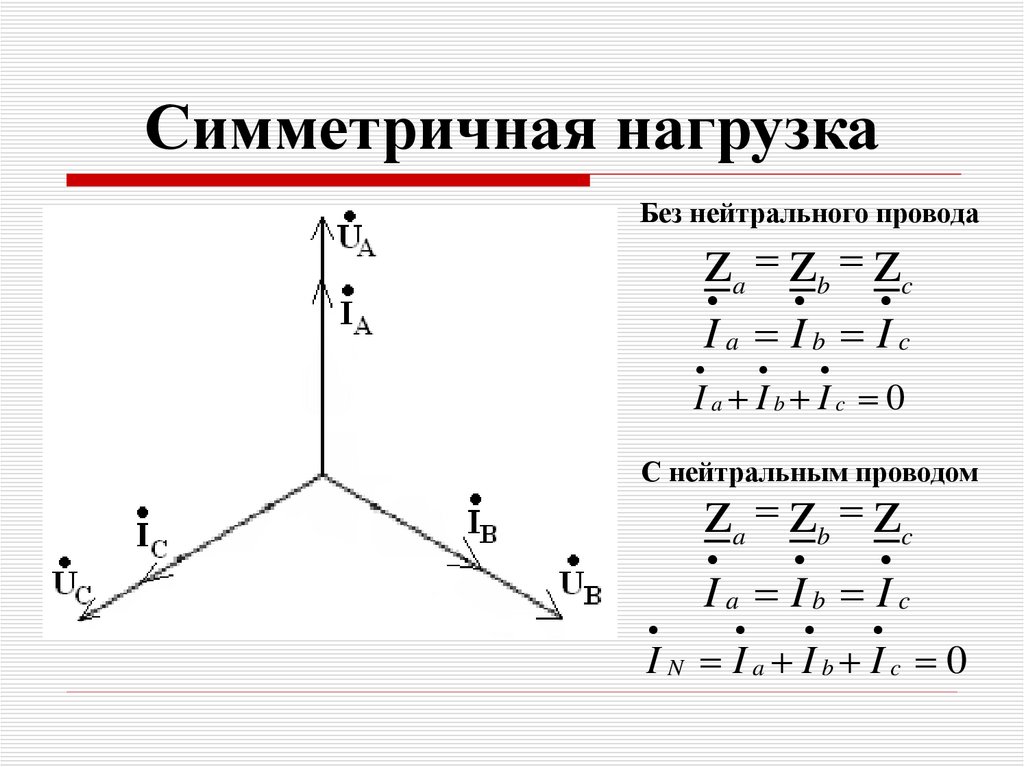
56. Симметричная нагрузка
Без нейтрального проводаz z z
a
b
c
Ia Ib Ic
Ia Ib Ic 0
С нейтральным проводом
z z z
a
b
c
Ia Ib Ic
I N Ia Ib Ic 0
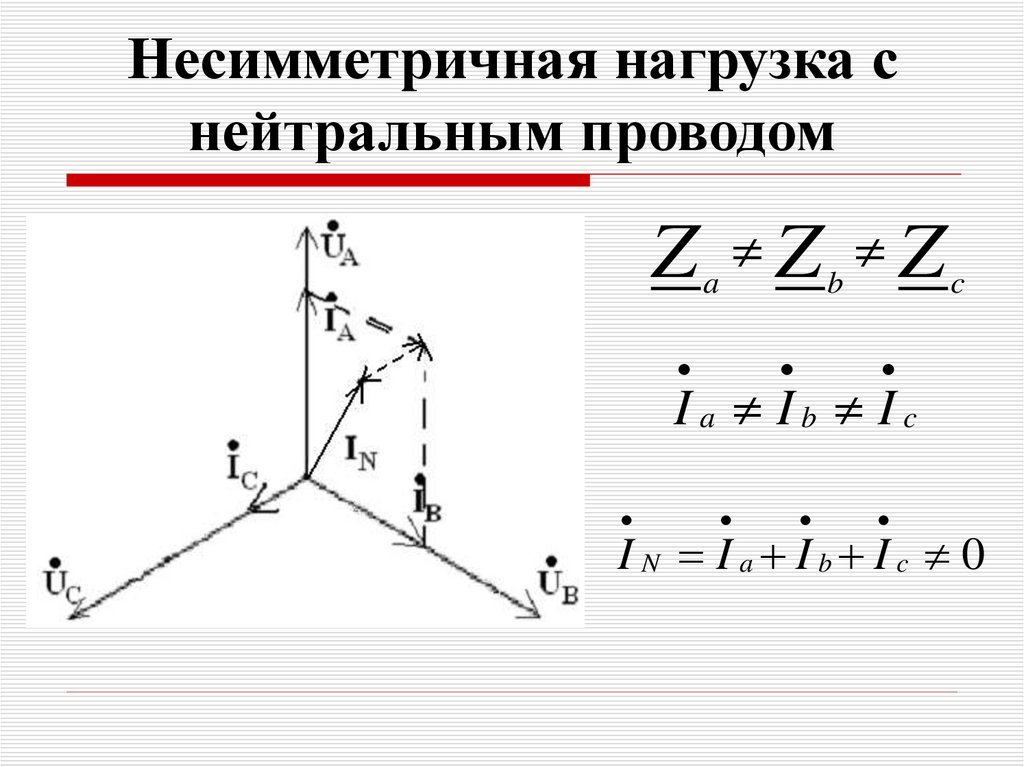
57. Несимметричная нагрузка с нейтральным проводом
Z Z Za
b
c
Ia Ib Ic
I N Ia Ib Ic 0
58. Несимметричная нагрузка без нейтрального провода
Z Z Za
b
c
Ia Ib Ic
Получаем
несимметричную систему
фазных напряжений.
Определяем напряжение
смещения нейтрали Unn0.
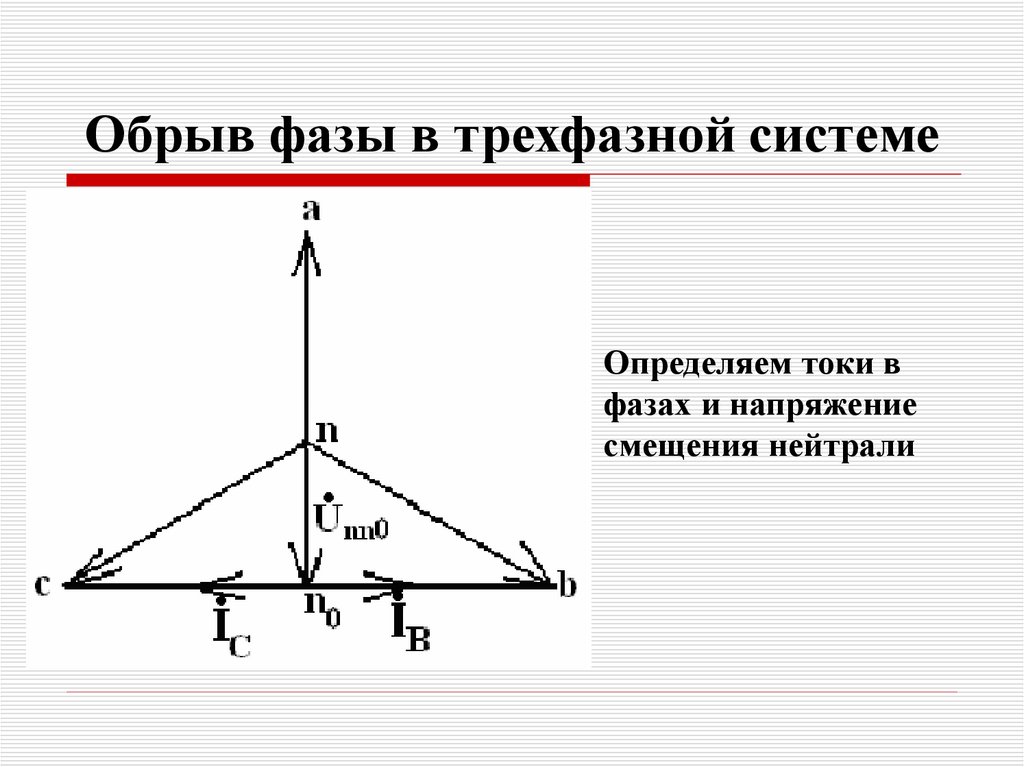
59. Обрыв фазы в трехфазной системе
Исходная схема превращается вдва последовательно
соединенных элемента
попадающих под линейное
напряжение
60. Обрыв фазы в трехфазной системе
Определяем токи вфазах и напряжение
смещения нейтрали
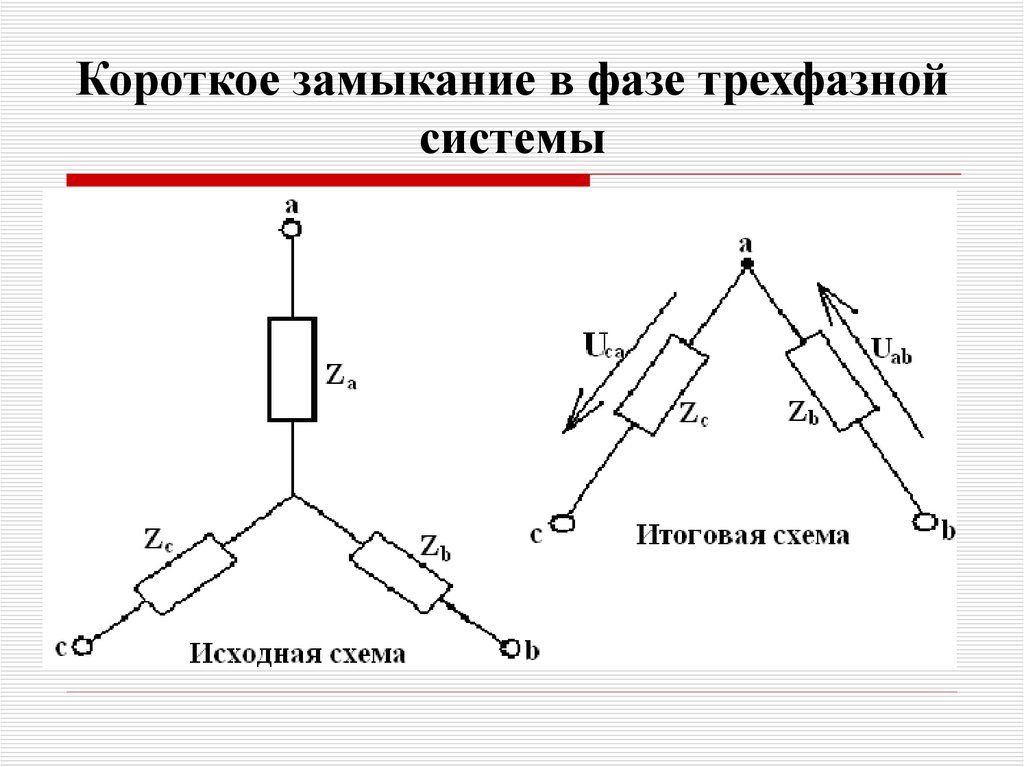
61. Короткое замыкание в фазе трехфазной системы
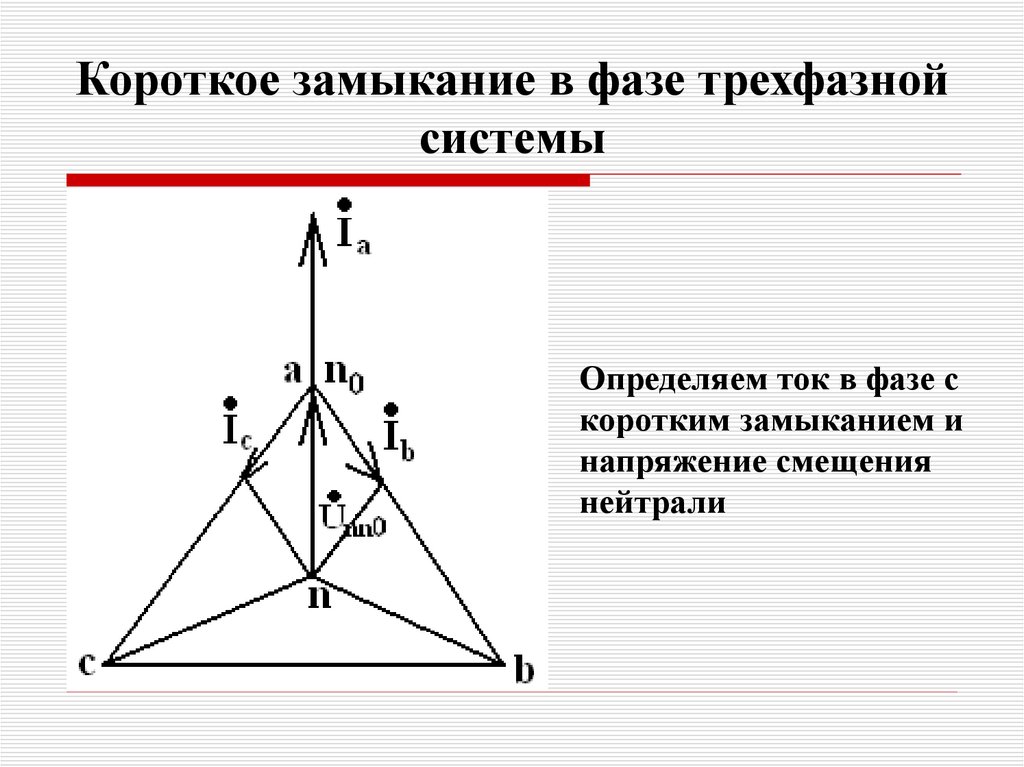
62. Короткое замыкание в фазе трехфазной системы
Определяем ток в фазе скоротким замыканием и
напряжение смещения
нейтрали
63. Соединение фаз приемника треугольником
64. Соединение фаз приемника треугольником
Фазные напряженияприемника равны
соответствующим
линейным напряжениям
источника питания
U ab U
U bc U
U ca U
AB
BC
CA
U Л UФ
Линейные токи определяются
по фазным токам по первому
закону Кирхгофа
I
I
I
A
B
C
I ab I ca
I bc I ab
I ca I bc
I Л 3IФ
I A I B I C 0
65. Мощность трехфазных цепей Мощность источника
Мгновенная мощность трехфазного источникаэлектрической энергии:
p p A pB pC u Ai A u B iB uC iC
Среднее за период значение мощности:
T
1
P pdt PA PB PC U A I A cos A U BI Bcos B U C ICcos C
T0
66. Мощность трехфазной цепи при несимметричной нагрузке
Активная мощность:Реактивная мощность:
P Pa Pb Pc
Q Qa Qb Qc
P Pab Pbc Pca
Q Qab Qbc Qca
Pф U ф I ф cos ф R I
2
ф ф
Q
ф
Uф Iф sin Хф Iф
2
ф
Модуль полной мощности трехфазной цепи:
S P 2 Q2
67. Мощность трехфазной цепи при симметричной нагрузке
P 3Pф 3U ф I ф cos фQ 3Qф 3U ф I ф sin ф
S 3S ф 3U ф I ф
68. Мощность трехфазной цепи при симметричной нагрузке
Соединение по схеме звезда:Uф
Uл
3
Iф I Л
Uл
I cos
P 3
л
ф
3
3 U л I л cos ф
Соединение по схеме треугольник:
Uф U Л
I л Iф 3
Iл
Р 3 U л cos
ф
3
3 U л I л cos ф
При симметричной нагрузке формулы мощности независимо
от схемы соединения приемников одинаковы.


















































 Электроника
Электроника








