СКНФ и СДНФ. Алгоритм получения по таблице истинности

1.

СКНФ и СДНФ. Алгоритм
получения по таблице
истинности
Дискретная математика, группа
2ИС 26.03.2022

2.

3.

СДНФ и СКНФ (определения)
Элементарной конъюнкцией называется конъюнкция нескольких
переменных, взятых с отрицанием или без отрицания, причем среди
переменных могут быть одинаковые
X Y X Z
Элементарной дизъюнкцией называется дизъюнкция нескольких
переменных, взятых с отрицанием или без отрицания, причем среди
переменных могут быть одинаковые
X Y X Z
Всякую дизъюнкцию элементарных конъюнкций назовем дизъюнктивной
нормальной формой (ДНФ)
X Y X Z
Всякую конъюнкцию элементарных дизъюнкций назовем конъюнктивной
нормальной формой (ДНФ)
(X Y) (X Z)

4.

СДНФ и СКНФ (определения)
Совершенной дизъюнктивной нормальной формой (СДНФ),
называется ДНФ, в которой нет одинаковых элементарных конъюнкций и
все конъюнкции состоят из одного и того же набора переменных, в
который каждая переменная входит только один раз (возможно с
отрицанием).
X Y Z X Y Z X Y Z
Совершенной конъюнктивной нормальной формой (СКНФ),
называется КНФ, в которой нет одинаковых элементарных дизъюнкций и
все дизъюнкции состоят из одного и того же набора переменных, в
который каждая переменная входит только один раз (возможно с
отрицанием).
(X Y Z) (X Y Z) (X Y Z)

5.

Алгоритм получения СДНФ
по таблице истинности
1. Отметить строки таблицы истинности в
последнем столбце которых стоят 1.
2. Выписать для каждой отмеченной строки
конъюнкцию всех переменных следующим
образом: если значение переменной в
данной строке равно 1, то в конъюнкцию
включать саму эту переменную, если
равно 0, то ее отрицание.
3. Все полученные конъюнкции связать в
дизъюнкцию.

6.

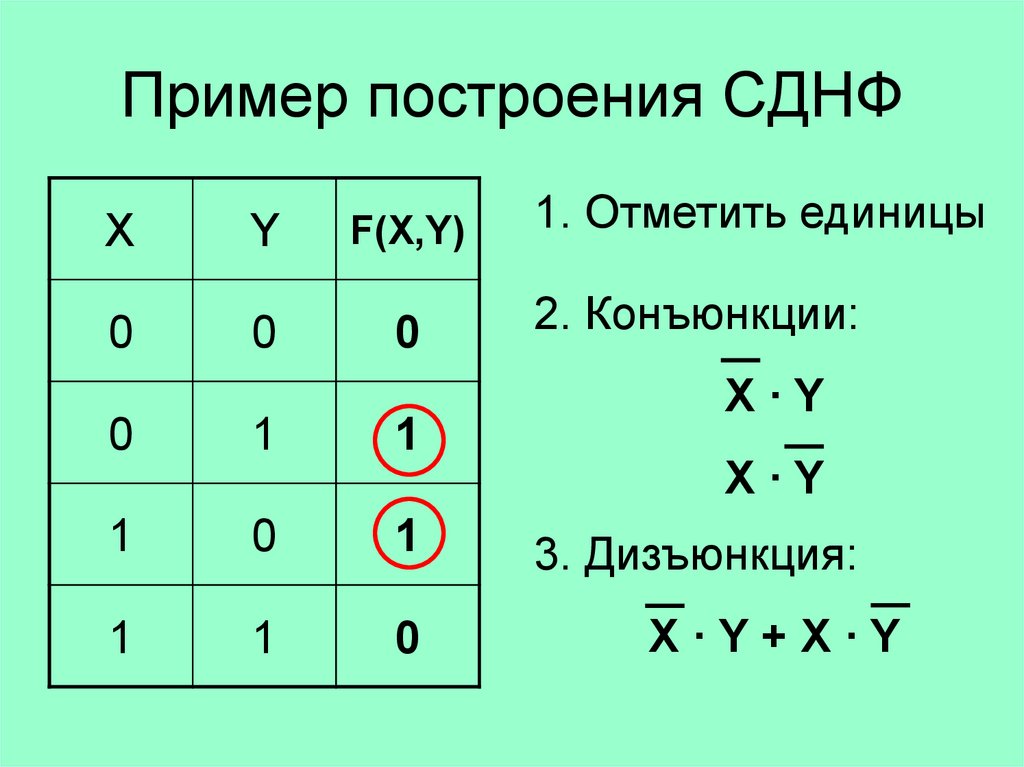
Пример построения СДНФ
X
0
Y
0
F(X,Y)
0
0
1
1
1
0
1
1
1
0
1. Отметить единицы
2. Конъюнкции:
X·Y
X·Y
3. Дизъюнкция:
X·Y+X·Y

7.

Алгоритм получения СКНФ
по таблице истинности
1. Отметить строки таблицы истинности в
последнем столбце которых стоят 0.
2. Выписать для каждой отмеченной строки
дизъюнкцию всех переменных следующим
образом: если значение переменной в
данной строке равно 0, то в конъюнкцию
включать саму эту переменную, если
равно 1, то ее отрицание.
3. Все полученные дизъюнкции связать в
конъюнкцию.

8.

Пример построения СKНФ
X
0
0
Y
0
1
F(X,Y)
0
1
1. Отметить нули
2. Дизъюнкции:
X+Y
X+Y
1
0
1
1
1
0
3. Конъюнкция:
(X + Y) · (X + Y)