Похожие презентации:
Булевые функции
1.
Булевой функцией y=f(x1, x2 ... xn) от n переменныхx1, x2 ... xn называется любая функция, в которой
аргументы и функция могут принимать значение либо
0 либо 1
0 - ложь
1 – истина
булевы функции называют логическими
1
2.
Область определения булевой функции конечна ->можно задать значения во всех точках (таблица
истинности)
2
3.
Наиболее важные функции- Отрицание
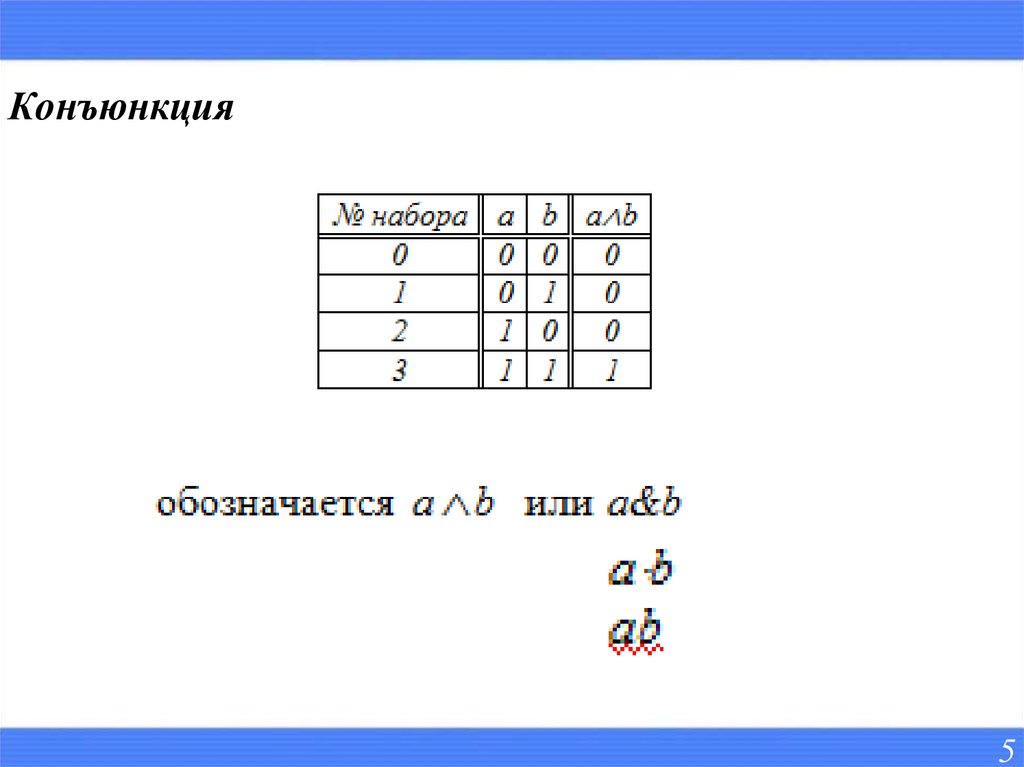
- Конъюнкция
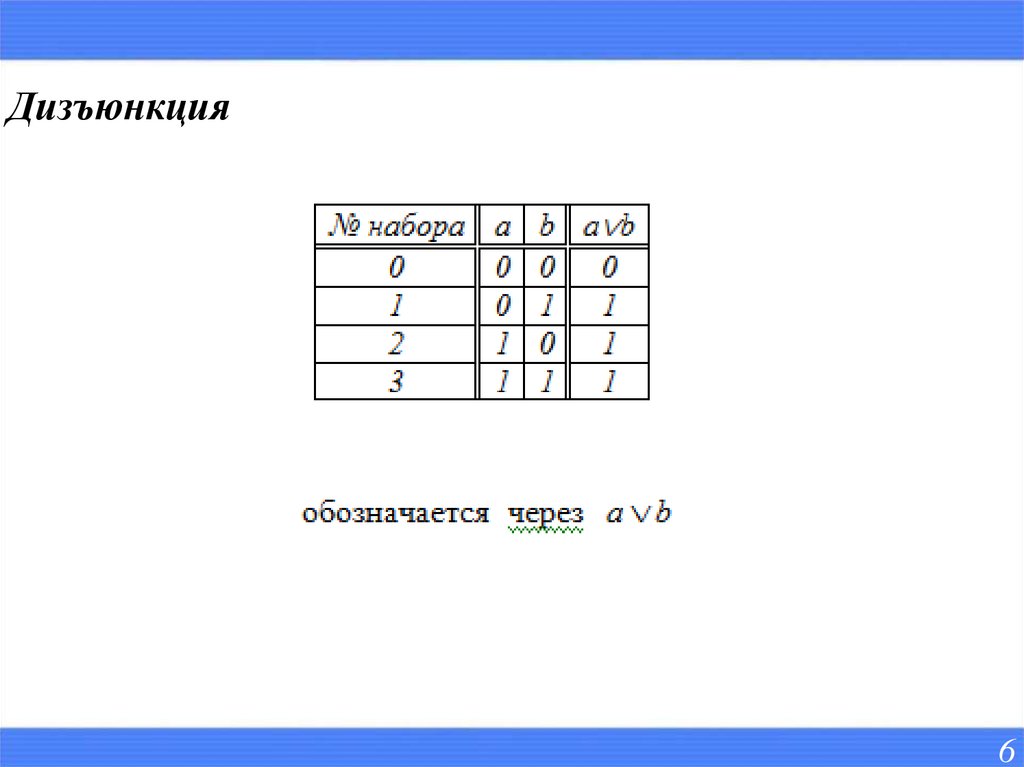
- Дизъюнкция
- Импликация
- Эквиваленция (или эквивалентность)
3
4.
Отрицание4
5.
Конъюнкция5
6.
Дизъюнкция6
7.
Импликация7
8.
Эквиваленция8
9.
Способы задания булевых функцийЗадание булевой функции таблицей истинности
9
10.
Задание булевой функции вектором значенийf(0,0,...,0,0), f(0,0,...,0,1), f(0,0,...,1,0),
f(0,0,...,1,1),..., f(1,1,...,0,0), f(1,1,...,0,1), f(1,1,...,1,0),
f(1,1,...,1,1)
φf=00010111
10
11.
Задание булевой функции номеромКаждой функции присваивается порядковый номер в
виде натурального числа, двоичный код которого
представляет собой столбец значений функции в
таблице истинности.
11
12. Пример
Найтипорядковый
номер
функции
f(x,y),
принимающей следующие значения: f(0,0)=1, f(0,1)=1,
f(1,0)=0, f(1,1)=1.
x y f(x,y)
0 0 1
0 1 1
1 0 0
1 1 1
Двоичный код, соответствующий
значению этой функции – 1101.
11012 = 1 23 + 1 22 + 0 21 + 1 20 =
=8+4+0+1=1310
Таким образом
f13(x,y) = (1101)2
12
13. Пример
Построить таблицу истинности для функции f198198 | 2
0 | 99 | 2
1 | 49 | 2
1 | 24 | 2
0 | 12 | 2
0 |6 | 2
0 |3 | 2
1 |1
x
0
0
0
0
1
1
1
1
y
0
0
1
1
0
0
1
1
z f (x,y,z)
0
1
1
1
0
0
1
0
0
0
1
1
0
1
1
0
13
14.
Формулами14
15. Приоритет выполнения операций
Если в формуле отсутствуют скобки, тооперации
выполняются
в
следующей
последовательности:
1. Отрицание.
2. Конъюнкция.
3. Дизъюнкция.
4. Импликация.
5. Эквивалентность
Пример
Убрать все возможные скобки
–
~
(( x y ) z ) ( x y ) x y z x y
Расставить скобки с учетом приоритета операций
((
(xx x yy
y))
y (y(yz y ~
z zx~z)
))x~ ~
xy(x
xy
y yy )
15
16.
Формула называется выполнимой (опровержимой),если существует такой набор значений переменных,
при которых эта формула принимает значение 1 (0).
Формула называется тождественно-истинной, или
тавтологией (тождественно-ложной или
противоречием), если эта формула принимает
значение 1 (0) при всех наборах значений переменных.
16
17.
Пусть А и В – две формулы, зависящие от одного итого же списка переменных. Будем называть их
равносильными, если для любого набора значений
переменных они принимают одинаковые значения
17
18.
свойства логических операций18
19.
1920.
2021.
Любая из равносильностей легко может быть доказана спомощью таблицы истинности
21
22.
2223.
Однако часто равносильность экономнее доказывать безсоставления полной таблицы истинности, а с
помощью приведенных равносильностей
Доказать равносильность формулы, используя
логические законы
23
24.
2425.
2526.
Нормальные формыЭлементарной конъюнкцией называется конъюнкция,
составленная из попарно различных переменных или
отрицаний переменных.
Дизъюнктивной нормальной формой (ДНФ)
называется дизъюнкция попарно различных
элементарных конъюнкций.
26
27.
Элементарной дизъюнкцией называется дизъюнкция,составленная из попарно различных переменных или
отрицаний переменных.
Конъюнктивной нормальной формой (КНФ)
называется конъюнкция попарно различных
элементарных дизъюнкций.
27
28.
Совершенные нормальные формыCовершенной ДНФ называется ДНФ, в которой
- нет одинаковых элементарных конъюнкций и
- все конъюнкции состоят из одного и того же набора
переменных, в который каждая переменная входит только
один раз ( возможно с отрицанием) X&Y&¬Z V X&Y& Z
F x1 , x2 , ..., xn
F c1 , ..., cn 1
c1
1
x ...x
cn
n
по всем наборам с=(с1, с2, …, сn) из 0 и 1
28
29.
Совершенные нормальные формыCовершенной КНФ называется КНФ, в которой
- нет одинаковых элементарных дизъюнкций и
- все дизъюнкции состоят из одного и того же набора
переменных, в который каждая переменная входит только
один раз ( возможно с отрицанием)
(¬ X VY V Z) & (X V¬Y V Z).
F x1, x2 , ..., xn
F c1 , ..., c n 0
( x ... x )
ñ1
1
cn
n
по всем наборам с=(с1, с2, …, сn) из 0 и 1
29
30.
Алгоритм получения СДНФ по таблице истинностиОтметить те строки ТИ, в последнем столбце
которых стоят 1:
Выписать для каждой отмеченной строки
конъюнкцию всех переменных следующим образом:
- если значение некоторой переменной в данной
строке =1, то в конъюнкцию включают саму эту
переменную,
- если =0, то ее отрицание:
Все полученные конъюнкции связать в дизъюнкцию:
30
31.
Алгоритм получения СДНФ по таблице истинностиF x y z
F x y z x yz xyz.
31
32.
Алгоритм получения СКНФ по таблице истинностиОтметить те строки ТИ, в последнем столбце
которых стоят 0:
Выписать для каждой отмеченной строки
дизъюнкцию всех переменных следующим образом:
- если значение некоторой переменной в данной
строке =0, то в дизъюнкцию включают саму эту
переменную,
- если =1, то ее отрицание:
Все полученные дизъюнкции связать в конъюнкцию:
32
33.
Алгоритм получения СКНФ по таблице истинностиF x y z
F x y z x y z x y z x y z x y z .
33
































 Математика
Математика








