Процесс в химическом реакторе

1.

ЛЕКЦИЯ 6
Процесс в химическом
реакторе

2.

Химический реактор - устройство,
предназначенное для проведения химических
превращений
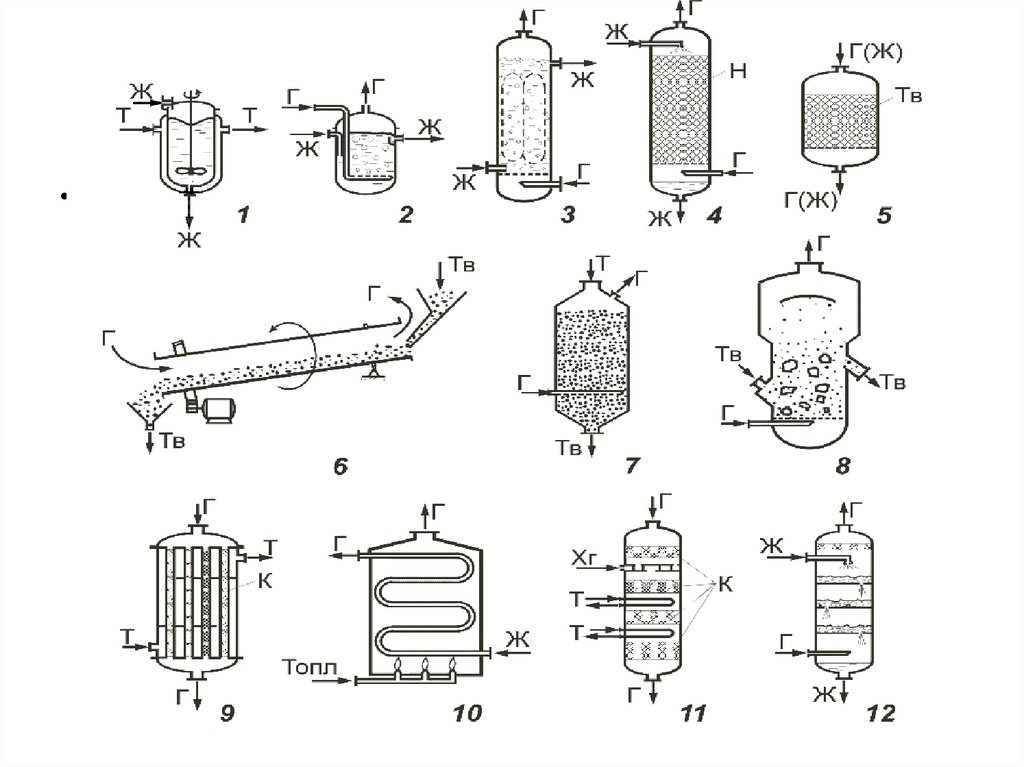
• Схемы химических реакторов

3.

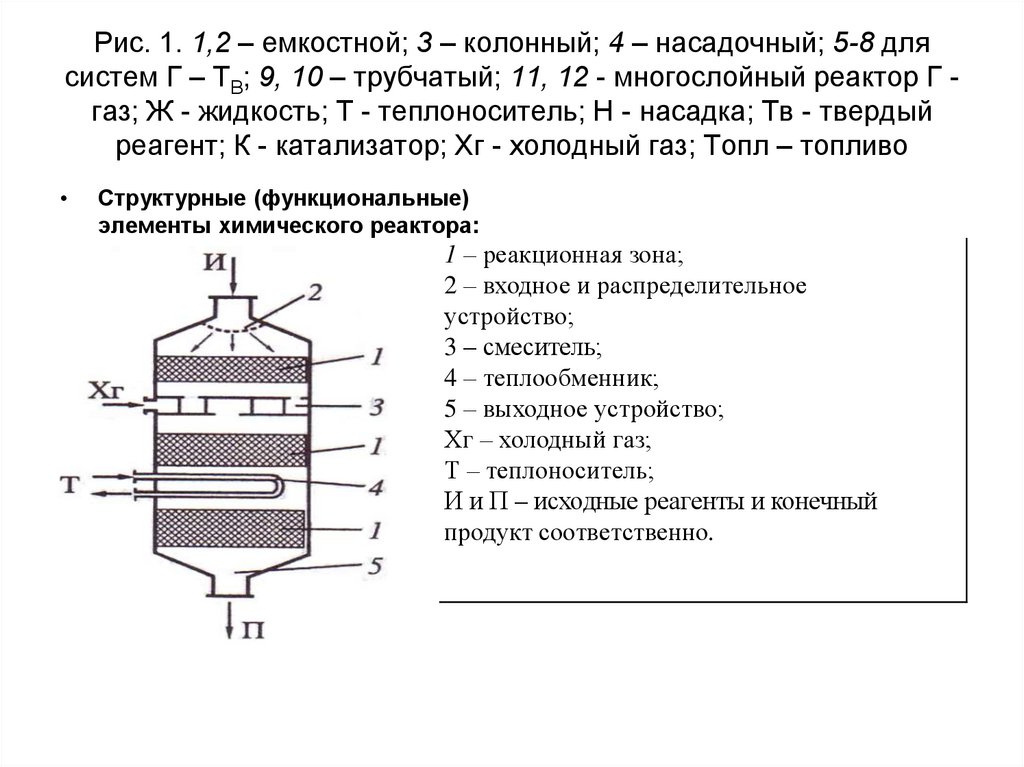
Рис. 1. 1,2 – емкостной; 3 – колонный; 4 – насадочный; 5-8 для
систем Г – ТВ; 9, 10 – трубчатый; 11, 12 - многослойный реактор Г газ; Ж - жидкость; Т - теплоноситель; Н - насадка; Тв - твердый
реагент; К - катализатор; Хг - холодный газ; Топл – топливо
Структурные (функциональные)
элементы химического реактора:
1 – реакционная зона;
2 – входное и распределительное
устройство;
3 – смеситель;
4 – теплообменник;
5 – выходное устройство;
Хг – холодный газ;
Т – теплоноситель;
И и П – исходные реагенты и конечный
продукт соответственно.

4.

КЛАССИФИКАЦИЯ РЕАКТОРОВ
• организация материальных потоков (вытеснения,
смешения, промежуточный тип);
• организация тепловых потоков (изотермический,
адиабатический, с теплообменом);
• по назначению (гомогенный, гетерогенный,
каталитический);
• принцип действия (периодический или непроточный,
непрерывный или проточный, полупериодический);

5.

ПОСТРОЕНИЕ МАТЕМАТИЧЕСКОЙ МОДЕЛИ
ПРОЦЕССА В ХИМИЧЕСКОМ РЕАКТОРЕ
• Процедура построения:
• 1) Выяснить схему организации материальных и тепловых
потоков в реакционной зоне: характер движения потоков, режим
вытеснения, смешения, с циркуляцией, проточный,
периодический, изо- или неизотермический и т.д.
• 2) Выделить элементарный объем dVр , в котором протекает
процесс и для которого ранее была получена кинетическая
модель Wн(с,Т).
• 3) Рассмотреть явления переноса, оказывающие влияние на
протекание химического процесса в элементарном объеме.
• 4) Составить математическую модель процесса для dVр и
определить начальные и граничные условия.

6.

ОБЩИЙ ВИД МАТЕМАТИЧЕСКОЙ МОДЕЛИ
ПРОЦЕССА В ХИМИЧЕСКОМ РЕАКТОРЕ
уравнение материального баланса:
dNi /dt = Ni вх/вых + Ni ист
(1)
уравнение теплового баланса
dq/dt = Qвх/вых + Qист.
(2)
• Здесь dNi/dt и dq/dt – накопление (расход) вещества
и тепла в выделенном элементарном объеме;
Niвх/вых, Qвх/вых - материальные и тепловые
потоки, входящие в выделенный объем и выходящие
из него (покидающие объем потоки имеют
отрицательное значение); Niист, Q ист - источники
вещества и тепла внутри выделенного объема.
Источником вещества является химическая реакция,
источником тепла - химическая реакция и фазовые
превращения.

7.

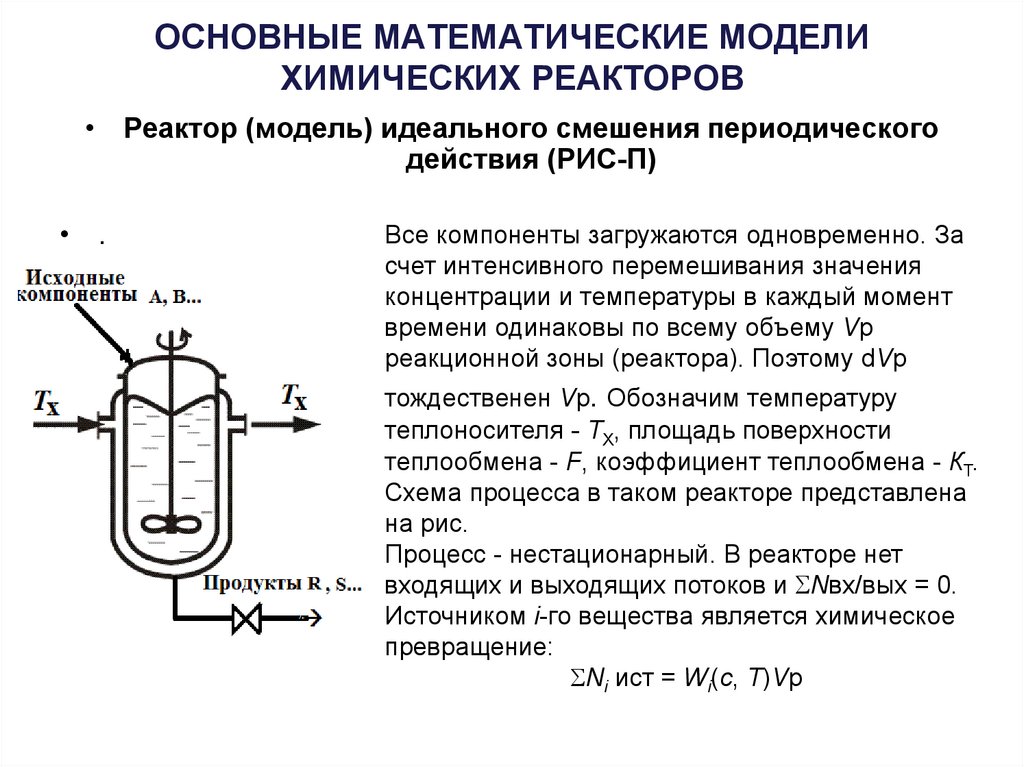
ОСНОВНЫЕ МАТЕМАТИЧЕСКИЕ МОДЕЛИ
ХИМИЧЕСКИХ РЕАКТОРОВ
• Реактор (модель) идеального смешения периодического
действия (РИС-П)
• .
Все компоненты загружаются одновременно. За
счет интенсивного перемешивания значения
концентрации и температуры в каждый момент
времени одинаковы по всему объему Vp
реакционной зоны (реактора). Поэтому dVp
тождественен Vp. Обозначим температуру
теплоносителя - ТX, площадь поверхности
теплообмена - F, коэффициент теплообмена - КT.
Схема процесса в таком реакторе представлена
на рис.
Процесс - нестационарный. В реакторе нет
входящих и выходящих потоков и Nвх/вых = 0.
Источником i-го вещества является химическое
превращение:
Ni ист = Wi(с, Т)Vp

8.

Уравнение dNi /dt = Niвх/вых + Niист преобразуется в :
dNi /dt = 0 +Wi(с, Т)Vp
Количество i-вещества в реакторе Ni = Vp сi, тогда уравнение
принимает вид:
dсi/dt = Wi(с, Т); с = сi,0 при t = 0.
(3)
например, для вещества А: dсА/dt = WА=-r.
При замене сА на степень превращения, получим:
Источник тепла – тепловой эффект химического превращения (для
единственной реакции Qист = QPr(С, Т)Vp и теплообмен с
теплоносителем КTF(ТX - Т).
dq/dt = 0 + QPr(с, Т)Vp + КTF (ТX - Т).
dxА
r
dt
с0

9.

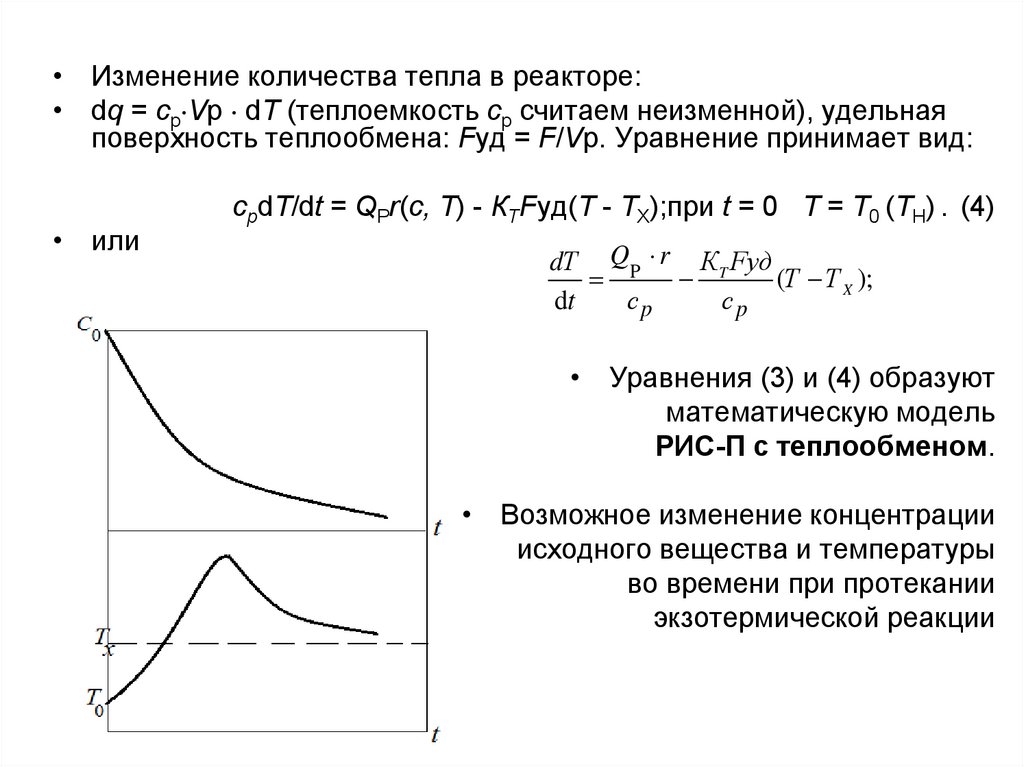
• Изменение количества тепла в реакторе:
• dq = сp Vp dТ (теплоемкость сp считаем неизменной), удельная
поверхность теплообмена: Fуд = F/Vp. Уравнение принимает вид:
• или
сpdТ/dt = QPr(с, Т) - КTFуд(Т - ТX);при t = 0 Т = Т0 (ТН) . (4)
dТ QP r КT Fуд
(Т Т X );
dt
сp
сp
• Уравнения (3) и (4) образуют
математическую модель
РИС-П с теплообменом.
• Возможное изменение концентрации
исходного вещества и температуры
во времени при протекании
экзотермической реакции

10.

РЕЖИМЫ РАБОТЫ РИС-П
Рассмотрим частные случаи
1) РИС-П изотермический (Т =const)
В реакторе QP 0 и отсутствует теплообмен с внешней средой
КTFуд(Т - ТX)=0; Тогда математическая модель РИС-П состоит
только из уравнения материального баланса (3):
dсi/dt = Wi , с = сi,0 при t = 0, например, для вещества А:
dсА/dt = WА=-r.
• При замене сА на степень превращения, получим:
dxА
r
при t 0 xА x0 ( xН ),
dt
с0
Для необратимой реакции 1-го порядка dсА/dt = WА = -ксА= -ксА,0(1-хА);
После интегрирования:
1 c
t ln 0 и cA c0 e kt ;
k cA
или
1
1
t ln
; xA 1 e kt ;
k 1 xA

11.

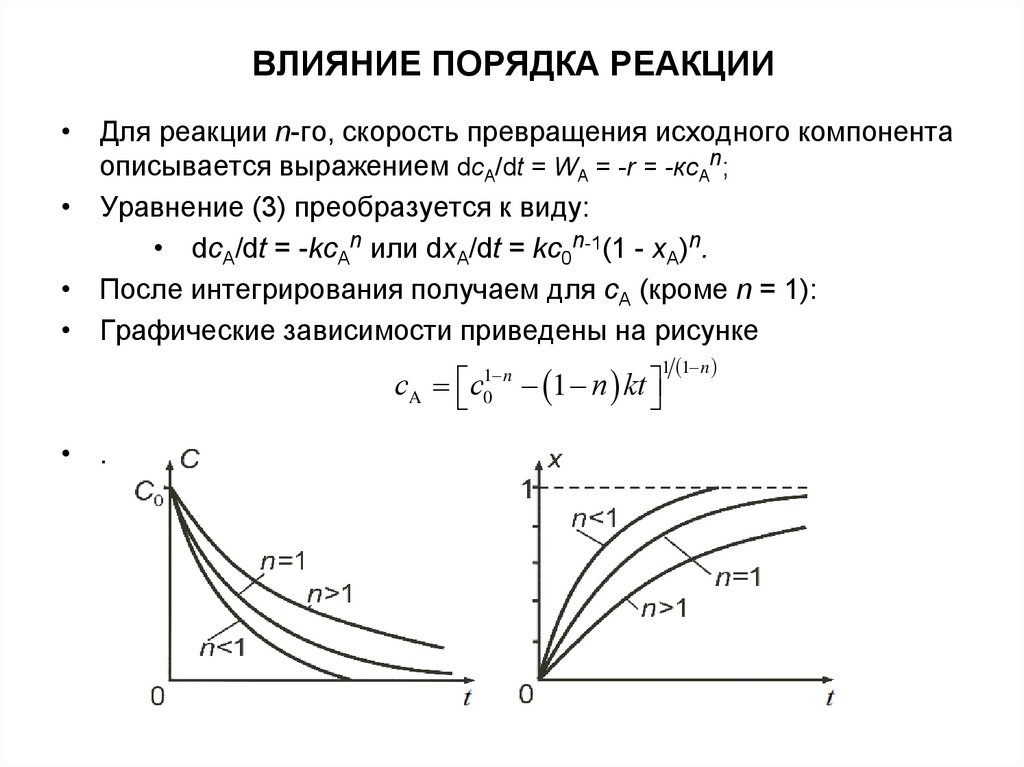
ВЛИЯНИЕ ПОРЯДКА РЕАКЦИИ
• Для реакции n-го, скорость превращения исходного компонента
описывается выражением dсА/dt = WА = -r = -ксАn;
• Уравнение (3) преобразуется к виду:
• dсA/dt = -kсAn или dхA/dt = kс0n-1(1 - хA)n.
• После интегрирования получаем для сA (кроме n = 1):
• Графические зависимости приведены на рисунке
сA с
1 n
0
• .
1 1 n
1 n kt

12.

2) РИС-П АДИАБАТИЧЕСКИЙ
При адиабатическом режиме теплообмен с окружающей
средой (теплоносителем) отсутствует: КTFуд(Т - ТX)=0;
Система уравнений материального и теплового балансов
(математическая модель) РИС-П приобретает вид:
• Найдем общее решение системы
dxА r
• уравнений, поделив одно на другое:
dt
с0
с p dТ / dt QP r или
dT Qр r
dt
cp
при t 0
xА xн , T Tн
dT Qр c0
Tад
dxА
сp
при t 0
xА xн , T Tн
• После интегрирования
• получаем уравнение адиабаты:
• Т= Тн + ∆Тад(xА – xн)

13.

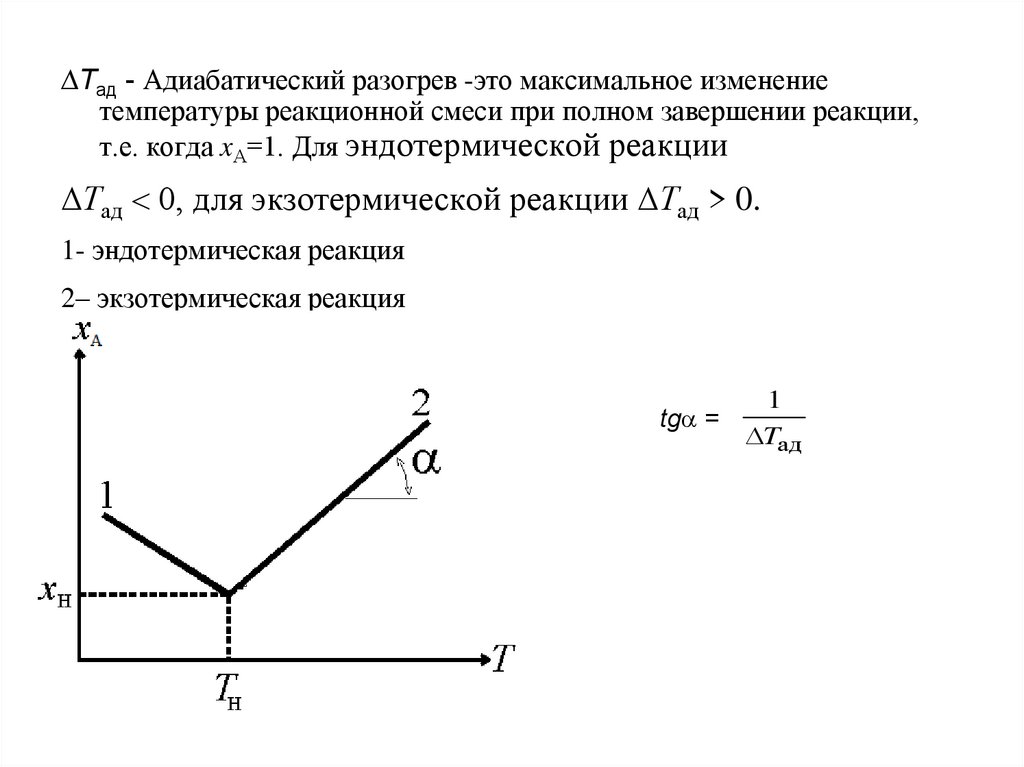
∆Тад - Адиабатический разогрев -это максимальное изменение
температуры реакционной смеси при полном завершении реакции,
т.е. когда xА=1. Для эндотермической реакции
∆Тад 0, для экзотермической реакции ∆Тад > 0.
1- эндотермическая реакция
2– экзотермическая реакция
1
tg =
Tад

14.

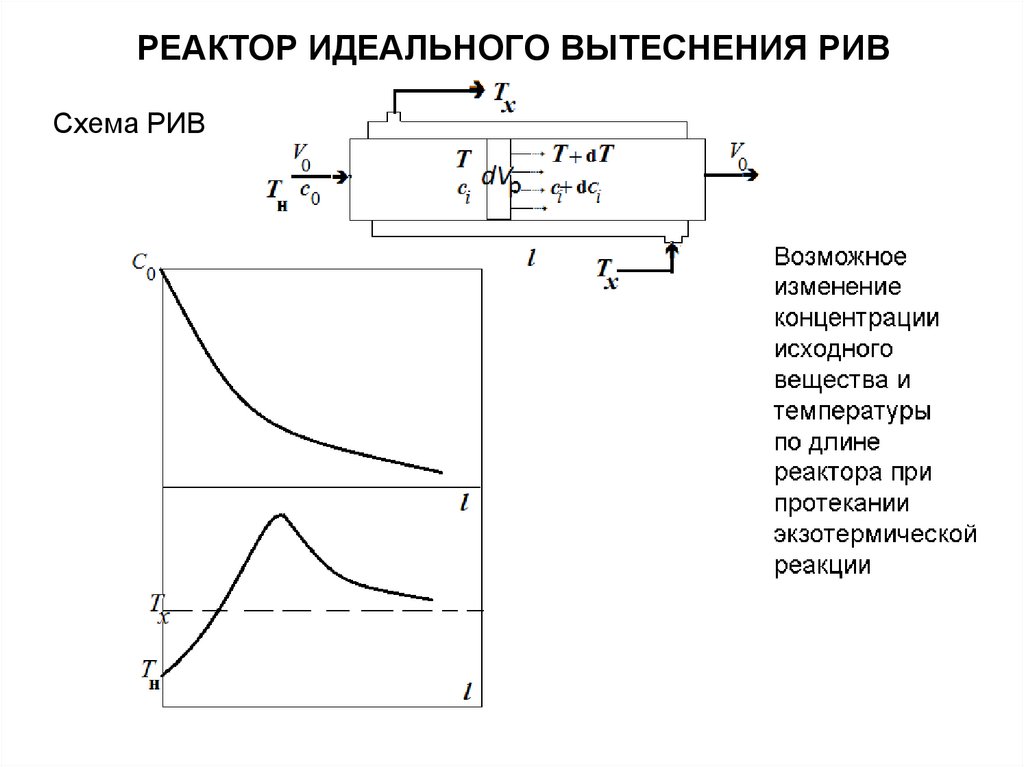
РЕАКТОР ИДЕАЛЬНОГО ВЫТЕСНЕНИЯ РИВ
Схема РИВ

15.

Допущения:
ХАРАКТЕРИСТИКА МОДЕЛИ РИВ
процесс в реакторе непрерывный и
стационарный;
перемешивание отсутствует;
профиль скорости по сечению – плоский
(поршневой режим).
общая химическая технология
15

16.

МАТЕМАТИЧЕСКОЕ ОПИСАНИЕ
Материальный и тепловой балансы составляем для элементарного
объема dVp. Процесс стационарный, поэтому
dNi /dt = 0
и dq/dt = 0
Мат. Баланс по i-му компоненту:0= V0 сi –V0 (ci + dci) + WidVp
Введем понятие условного времени пребывания (реакции):
τ = Vp / V0 и dτ =dVp / V0
Из мат.баланса получаем: dсi/dτ = Wi , с = сi,0 при τ = 0,
например, для вещества А:
dсА/dτ = WА= -r. При замене сА на степень превращения, получим:
dxА
r
dτ
с0
при τ 0
xА xн , cA c0
(5)

17.

Тепловой баланс:
0=V0 ср Т - V0 ср (Т + dT) - КTFуд(Т - ТX) + QPr(с, Т) dVp ;
Раскрыв скобки и поделив на dVp и ср, получим:
dТ Q P r КT Fуд
(Т Т X ); при τ = 0 Т = Т0(ТН). (6)
dτ
сp
сp
• Уравнения (5) и (6) образуют математическую модель
• РИВ с теплообменом

18.

РЕЖИМЫ РАБОТЫ РИВ
при τ = 0, например, для вещества А:
Рассмотрим частные случаи
1) РИВ изотермический (Т =const)
В реакторе QP 0 и отсутствует теплообмен с внешней средой
КTFуд(Т - ТX)=0; Тогда математическая модель РИВ состоит только
из уравнения материального баланса (5):
dсi/dτ = Wi , с = сi,0 dсА/dτ = WА=-r.
dxА
r
• При замене сА на степень превращения, получим:
dτ
при t 0
с0
xА xн ,
Для необратимой реакции 1-го порядка
dсА/dτ = WА = -ксА= -ксА0(1-хА);
После интегрирования:
1 c
τ ln 0 и cA c0 e kτ ;
k cA
или
1
1
τ ln
; xA 1 e kτ ;
k 1 xA

19.

2) РИВ АДИАБАТИЧЕСКИЙ
При адиабатическом режиме теплообмен с окружающей средой
(теплоносителем) отсутствует: КTFуд(Т - ТX)=0;
Система уравнений материального и теплового балансов
(математическая модель) РИВ приобретает вид:
Найдем общее решение системы
уравнений, поделив одно на другое:
dxА r
dτ с0
с p dТ / dτ QP r или
dT Q r
dτ
cp
при τ 0
xА xн , T Tн
dT Q c0
Tад
dxА
сp
при τ 0
xА xн , T Tн
После интегрирования
получаем уравнение адиабаты:
Т= Тн + ∆Тад(xА – xн)

20.

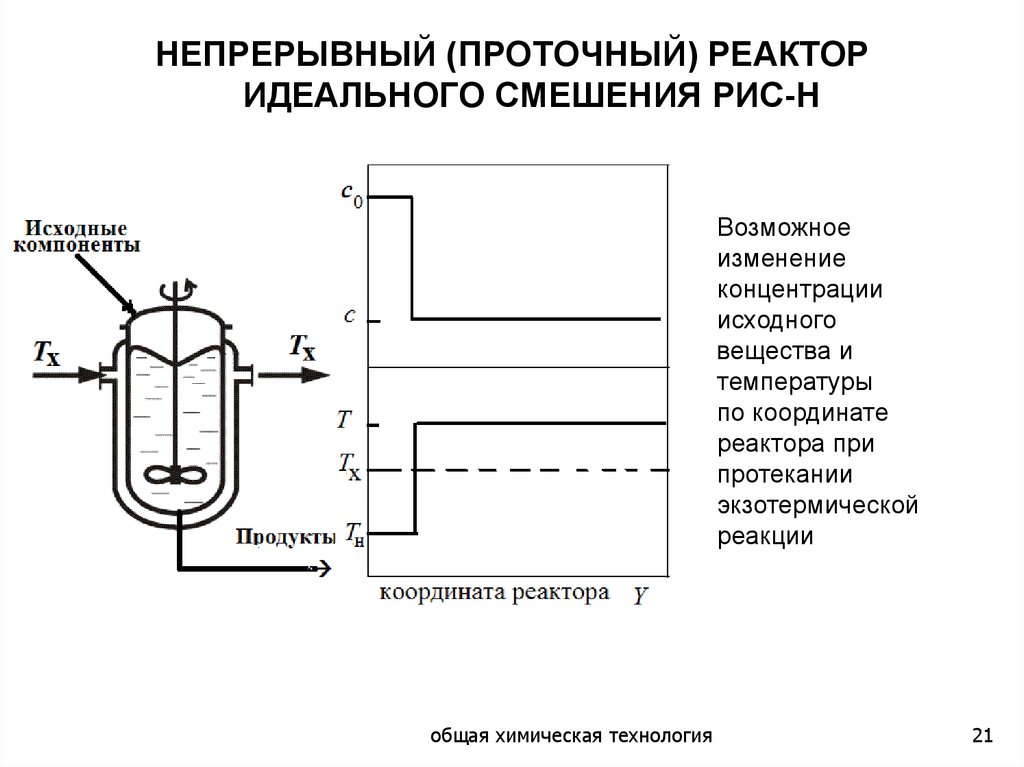
РЕАКТОР ИДЕАЛЬНОГО СМЕШЕНИЯ
НЕПРЕРЫВНОГО ДЕЙСТВИЯ (РИС-Н)
• ХАРАКТЕРИСТИКА МОДЕЛИ РИС-Н
идеальное перемешивание реакционной смеси по всему объему
реактора;
благодаря идеальному перемешиванию изменение
концентраций, степени превращения, температуры в реакторе
происходит мгновенно (скачкообразно);
в любой точке реакционного объема устанавливаются
абсолютно одинаковые значения концентрации, температуры,
степени превращения, скорости реакции;
Показатели выходного потока (состав, температура и др.) в
выходном потоке и в реакционном объеме одинаковые.
общая химическая технология
20

21.

НЕПРЕРЫВНЫЙ (ПРОТОЧНЫЙ) РЕАКТОР
ИДЕАЛЬНОГО СМЕШЕНИЯ РИС-Н
Возможное
изменение
концентрации
исходного
вещества и
температуры
по координате
реактора при
протекании
экзотермической
реакции
общая химическая технология
21

22.

МАТЕМАТИЧЕСКОЕ ОПИСАНИЕ
Поскольку свойства элементарного объема идентичны свойствам всего
реакционного объема, составим мат.описание для Vр.
• Процесс стационарный, поэтому
dNi /dt = 0
dq/dt = 0
Материальный баланс по i-му компоненту:
0 = V0 ci,0 –V0 ci + Wi Vp
Используем понятие условного времени пребывания (реакции): = Vp / V0
Из мат.баланса получаем:
сi сi ,0
τ
Wi
сА с0
WА
например, для вещества А:
τ
xА
r
Заменив сА на степень превращения, получим:
τ
с0
сi сi 0
Wi
τ
(1)

23.

• Тепловой баланс:
0=V0 ср ТН - V0 ср Т - КTFуд(Т - ТX) + QPr(с, Т) Vp ;
поделив на Vp и ср, получим:
Т TН Q P r КT Fуд
(Т Т X );
τ
сp
сp
Уравнения (1) и (2) образуют математическую модель
РИС-Н с теплообменом
(2)

24.

Частные случаи:
1) РИС-Н изотермический (Т 0=Т =const)
В реакторе QP 0 и отсутствует теплообмен с внешней средой
КTFуд(Т - ТX)=0; Тогда математическая модель РИС-Н состоит
только из уравнения материального баланса (3), например для А:
сА с0
WА
τ
или
xА
r
τ
с0
2) РИС-Н адиабатический
При адиабатическом режиме теплообмен с окружающей средой
(теплоносителем) отсутствует: КTFуд(Т - ТX)=0; Система уравнений
материального и теплового балансов (математическая модель)
приобретает вид:
xА
r
Т TН Q P r
;
τ
сp
τ
с
0
Поделив одно уравнение на другое, получим уравнение адиабаты:
Т= ТН + ∆ТадxА

25.

СРАВНЕНИЕ И ВЫБОР ЭФФЕКТИВНОГО РЕАКТОРА
• Общие критерии сравнения и выбора:
• 1 – максимальная скорость реакции или интенсивность
процесса; используется для простых реакций;
• 2 – максимальная селективность или выход целевого продукта;
• используется для сложных реакций.
• Условия сравнения: входные и выходные параметры (состав ,
температура, объемный расход…) для сравниваемых реакторов
- одинаковые.
• I. Изотермические реакторы РИВ и РИС-Н
• А) Простые реакции. Чем выше скорость реакции, тем потребуется
меньший объем реактора и будет больше интенсивность. Скорость
процесса тем выше, чем больше концентрации реагирующих веществ.
Очевидно, что в РИВ на всем протяжении процесса сА выше
концентрации в РИС-Н, где она мгновенно принимает минимальное
значение. Количественно эффективность РИВ можно оценить по
отношению объемов реакторов Vсм и VВ при прочих равных условиях..

26.

Пусть в реакторе протекает реакция n-го порядка
dсА/d = WА = -ксАn = -ксА0(1-хА)n;
xA
xA
Vсм V0 τсм
(1 xA )n
(1 xA ) n
n≠1
dx
1
VВ
V0 τ В
1 n
A
(1 xA )n n 1 (1 xA ) 1
xA
Vсм V0 τсм
(1 xA )
n=1
1
VВ
V0 τ В
ln
1 xA
C увеличением порядка реакции
и степени превращения
эффективность РИВ возрастает
по сравнению с РИС-Н; При n=0
реакторы имеют одинаковый
объем независимо от xA.

27.

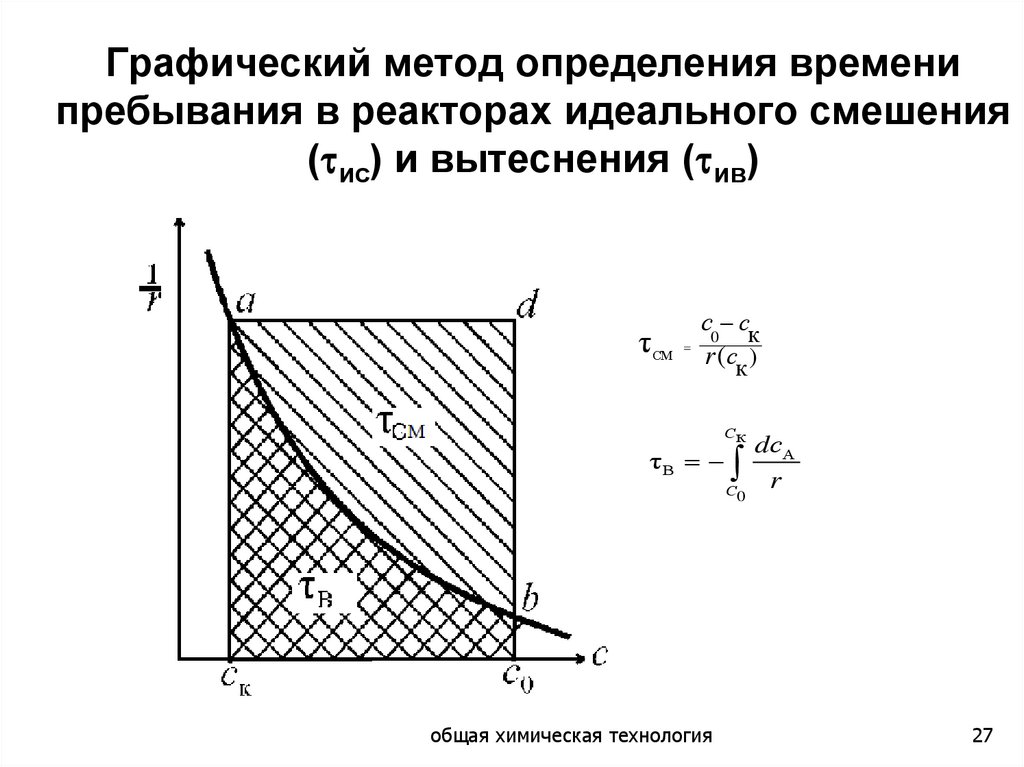
Графический метод определения времени
пребывания в реакторах идеального смешения
( ис) и вытеснения ( ив)
τСМ
с0 ск
r (ск )
Ск
τВ
С0
общая химическая технология
dсА
r
27

28.

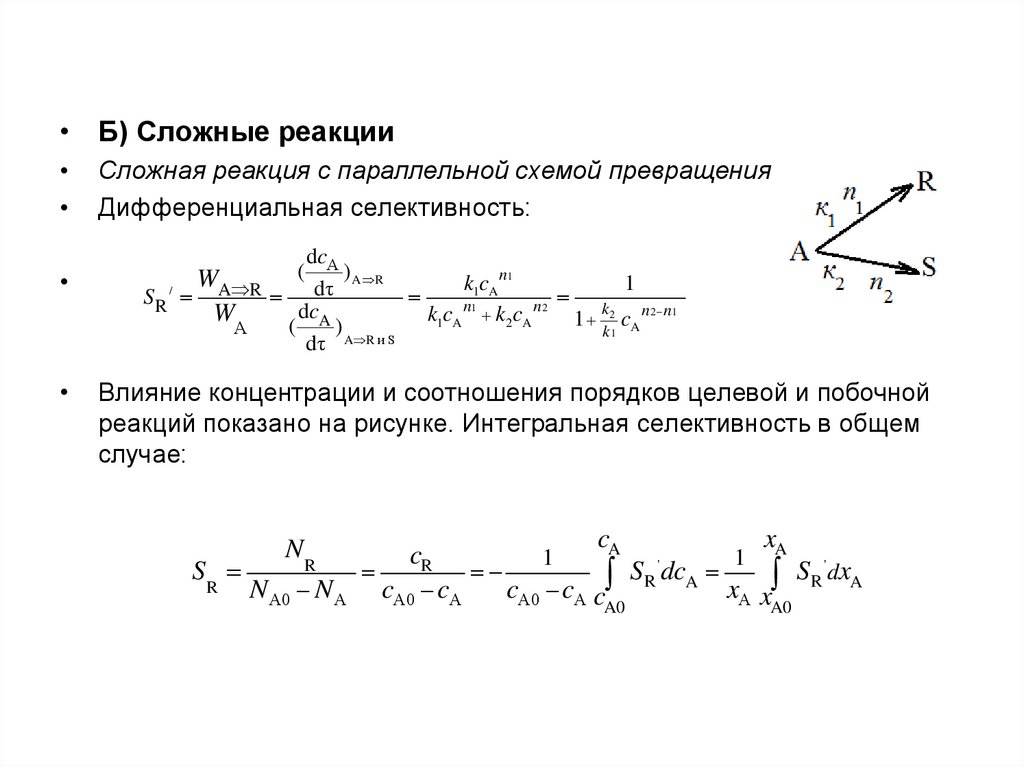
• Б) Сложные реакции
Сложная реакция с параллельной схемой превращения
Дифференциальная селективность:
dcА
) A R
WA R
k1cA n1
1
/
dτ
SR
k
n
1
n
2
dc
W
k1cA k2 cA
1 2 cA n 2 n1
( A ) A R и S
А
k1
dτ
(
Влияние концентрации и соотношения порядков целевой и побочной
реакций показано на рисунке. Интегральная селективность в общем
случае:
S
R
N
R
N А0 N А
c
x
A
1
1 A
'
'
S
dc
S
dx
cA0 cA
cA0 cA c R A xA x R A
A0
A0
cR

29.

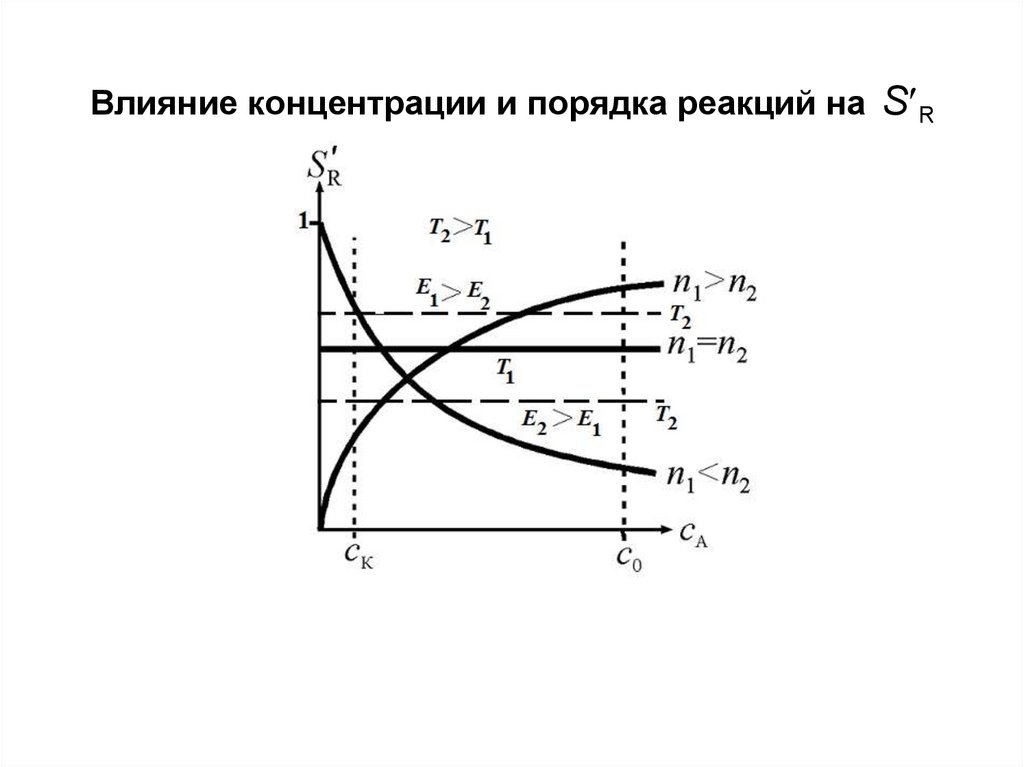
Влияние концентрации и порядка реакций на S R

30.

ВЫВОДЫ
для параллельной схемы превращения
• В РИС-Н интегральная селективность равна
дифференциальной при конечной концентрации вещества А
• SR см = S R(сК).
• В РИВ интегральная селективность равна среднеинтегральной
величине между S R(с0) и S R(сК).
• Из рис. следует:
при n1 = n2 SRВ = SR см;
при n1 > n2 с ростом концентрации сА растет S R. Концентрация в
РИВ всегда выше, чем в РИС-Н, поэтому SRВ > SR см;
при n1 < n2 с ростом концентрации сА падает S R.
Минимальная концентрация сК в РИС-Н на всем протяжении
процесса, поэтому SRВ < SR см.

31.

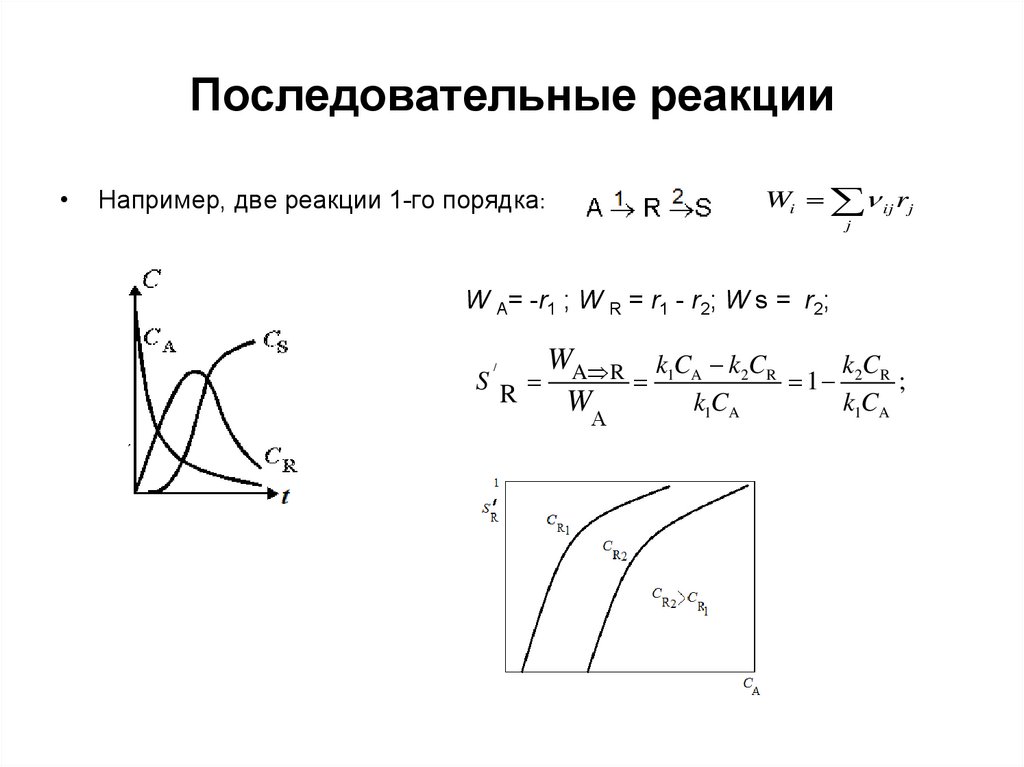
Последовательные реакции
Wi ij rj
Например, две реакции 1-го порядка:
j
W А= -r1 ; W R = r1 - r2; W s = r2;
WA R k1CA k2CR
kC
S R
1 2 R ;
W
k1CA
k1CA
/
А

32.

Выводы
для последовательной схемы превращения
Высокую селективность процесса по
промежуточному веществу R можно получить при
больших концентрациях А и малом содержании
промежуточного R, т.е. при небольшой степени
превращения исходного вещества.
Влияние температуры на селективность в
последовательной реакции аналогично
параллельной схеме превращения.