Материальный баланс химического реактора. Лекция № 3

1.

ЛЕКЦИЯ № 3
МАТЕРИАЛЬНЫЙ БАЛАНС
ХИМИЧЕСКОГО РЕАКТОРА
1

2.

Характеристическое уравнение
(математическая модель) – это
уравнение, которое связывает четыре
переменных реактора: время
пребывания, конверсию, начальную
концентрацию реагента, скорость хим.
реакции;
= f( A , CA0 , rA).
2

3.

Математическая модель – это упрощённое
изображение процессов, протекающих в реакторе,
которое сохраняет наиболее существенные свойства
реального объекта и передаёт их в математической
форме.
Математическая модель химического реактора
включает два уравнения:
– уравнение материального баланса;
– уравнение теплового баланса.
Количество вещества или количество тепла должно
быть одинаковым на входе и выходе из системы.
3

4.

Варианты составления уравнения
материального баланса:
Общий (брутто-баланс) составляется по всем
компонентам системы;
Частный материальный баланс реактора
составляется по компоненту реакционной
системы (реагенту или продукту);
Элементный баланс может быть составлен по
любому элементу, например:
- по углероду для органических смесей;
- по азоту;
- по сере;
- по кислороду.
4

5. Материальный баланс химического реактора

Основанием для получения исходного
уравнения реактора любого типа
является уравнение материального
баланса, составленное по одному из
компонентов реакционной смеси.
Составим баланс по исходному
реагенту А при проведении простой
необратимой реакции А R.
5

6.

В общем виде уравнение материального
баланса записывается так:
GA ПРИХ. = GА РАСХ.
(1)
Количество реагента А, поступающего в
единицу времени в единицу объёма
реактора, равно количеству реагента А,
расходуемого в единицу времени в
единице реакционного объёма.
6

7.

Поступающий в реактор реагент А расходуется в
трёх направлениях:
GА РАСХ. = GА Х.Р. + GА СТОК + GА НАКОП.
(2)
GА Х.Р. – количество реагента А, которое вступает в
химическую реакцию в единицу времени;
GА СТОК – количество реагента А, которое выходит
из реактора в единицу времени;
GА НАКОП. – количество реагента А, находящееся в
реакторе в неизменном виде в единицу времени.
7

8.

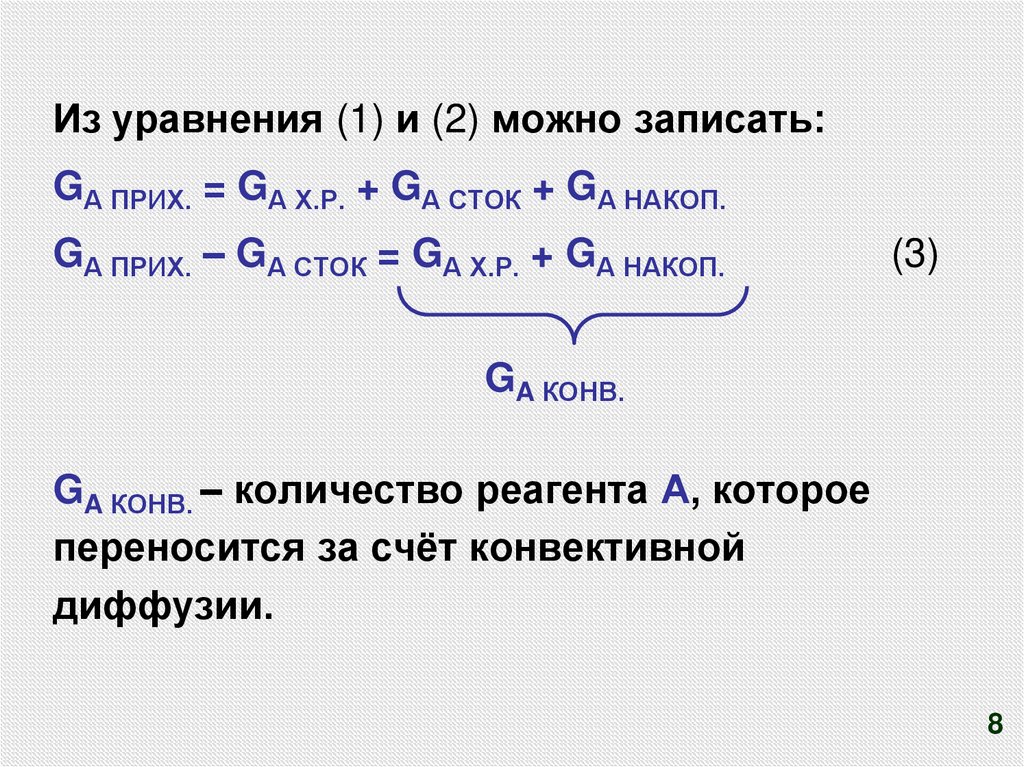
Из уравнения (1) и (2) можно записать:
GА ПРИХ. = GА Х.Р. + GА СТОК + GА НАКОП.
GА ПРИХ. – GА СТОК = GА Х.Р. + GА НАКОП.
(3)
GA КОНВ.
GA КОНВ. – количество реагента А, которое
переносится за счёт конвективной
диффузии.
8

9.

Химическая реакция протекает в потоке
движущегося через аппарат вещества.
Конвективный поток – движение массы
вещества от входа к выходу под действием
какой-либо силы. Обычно для такого
перемещения движущей силой служит
разность давлений.
Общий вид материального баланса реактора:
GА НАКОП. = GА КОНВ. GА Х.Р.
(4)
9

10.

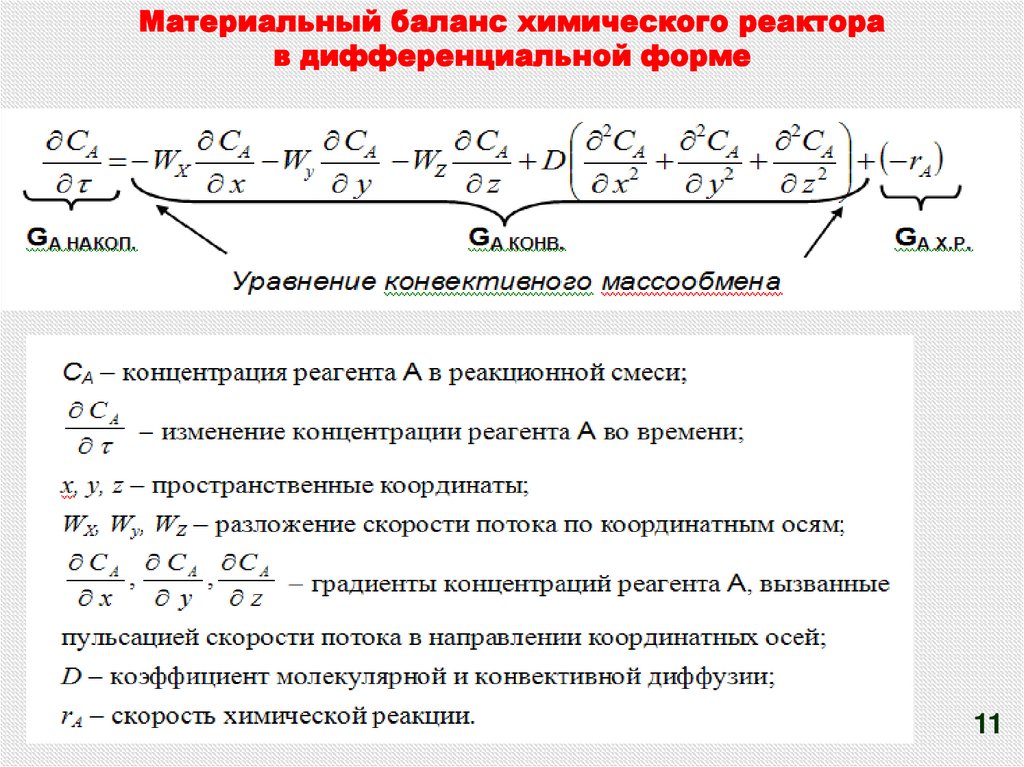
Так как концентрация реагента непостоянна в
различных точках реактора, а также
непостоянна во времени, материальный
баланс составляют в дифференциальной
форме для элементарного объёма реактора.
При этом исходят из уравнения конвективного
массообмена, в которое вводят
дополнительный член rА, учитывающий
протекание химической реакции.
10

11. Материальный баланс химического реактора в дифференциальной форме

11

12.

Сложность задачи расчёта реакторов
зависит от типа хим. реакции,
термодинамических характеристик
распределения вещества и тепла по всему
объёму реактора, скорости теплообмена с
окружающей средой.
Мы проведём расчёт при изотермическом
режиме. Это означает, что константа
скорости хим. реакции будет постоянна при
протекании хим. реакции.
12

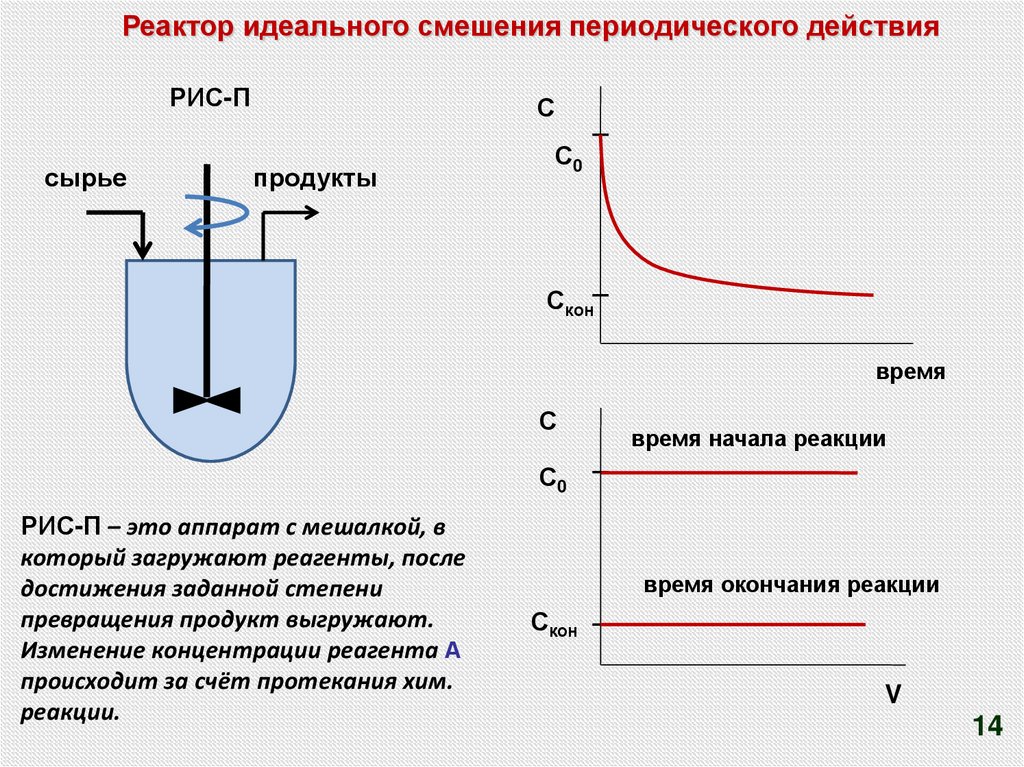
13. Реактор идеального смешения периодического действия РИС-П

При расчёте реактора периодического
действия РИС-П по характеристическому
уравнению рассчитывают рабочее время,
которое обеспечивает заданную степень
превращения.
Для периодического реактора:
ПОЛНОЕ = РАБОЧЕЕ + ВСПОМОГАТЕЛЬНОЕ
13

14.

Реактор идеального смешения периодического действия
РИС-П
сырье
С
продукты
С0
Скон
время
С
время начала реакции
С0
РИС-П – это аппарат с мешалкой, в
который загружают реагенты, после
достижения заданной степени
превращения продукт выгружают.
Изменение концентрации реагента А
происходит за счёт протекания хим.
реакции.
время окончания реакции
Скон
V
14

15.

В реакторе РИС-П не происходит перемешивание реагентов за счёт
конвективной диффузии, тогда первая и вторая производные в уравнении
материального баланса равны 0:
2CA 2CA 2CA
CA
CA
CA
CA
rA
WX
Wy
WZ
D
2
2
2
x
y
z
y
z
x
CA
CA
CA
WX
Wy
WZ
0
x
y
z
dy
dz
dx
2 CA 2 CA 2 CA
0
D
2
2
2
y
z
x
концентрация
реагента
одинакова во
всех точках
реактора
CA
rA
15

16.

Вспомним, что конверсия А – отношение количества
превращённого реагента (NA0) к его первоначальному количеству
(NA).
NAo NA
A
100 %
NAo
N A N Ao ( 1 A )
Текущую концентрацию можно определить исходя из текущего
количества:
NA NAo ( 1 A )
CA
CAo ( 1 A )
V
V
V – объём реактора (const).
16

17.

d CAo ( 1 A )
rA
d
CA
rA
Интегрируя данное выражение, получим:
A
0
0
d
d CAo ( 1 A )
rA
Математическая модель (характеристическое уравнение) РИС-П:
CAo
A
0
d A
rA
рабочее время пребывания сырья в реакторе
17

18.

Характеристическое уравнение РИС-П если n = 0
rA k
n
CA
CAo
A
0
k
n
CAo
(1 A )
n
d A
k CAno ( 1 A )n
k – константа скорости реакции
если n = 0
CAo A
k
CAo CA
k
CAo A CAo CA
18

19.

Характеристическое уравнение РИС-П если n = 1
если n = 1
CAo
A
0
d A
k C1Ao ( 1 A )1
1
1
ln
k
1 A
19

20.

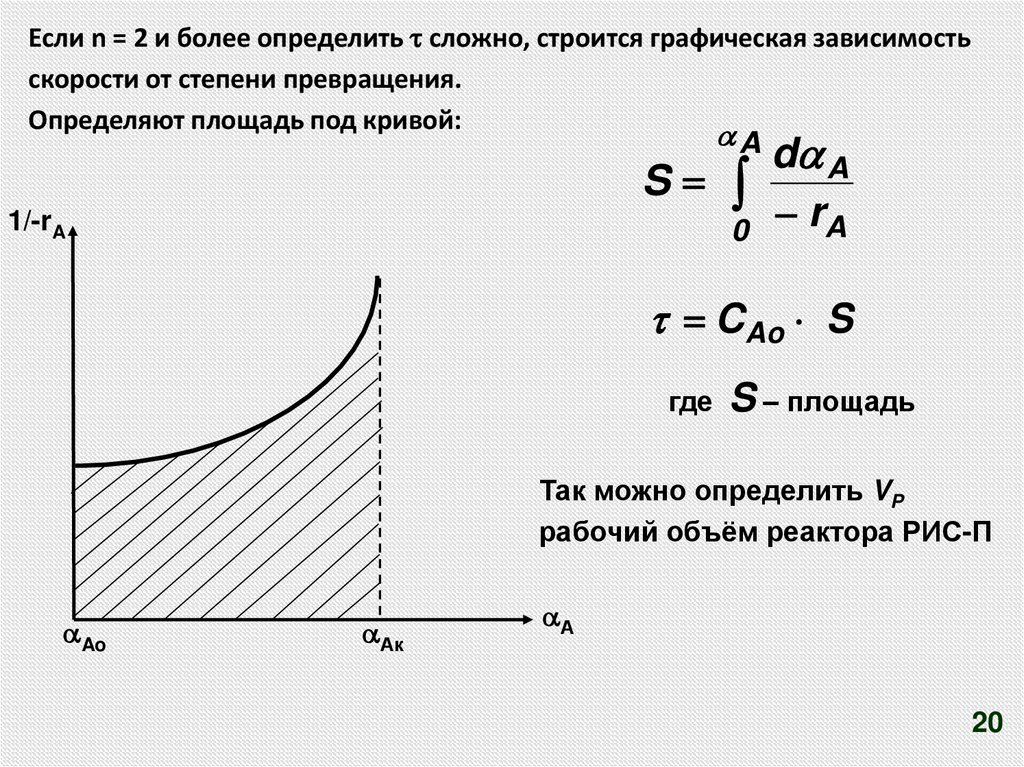
Если n = 2 и более определить сложно, строится графическая зависимость
скорости от степени превращения.
Определяют площадь под кривой:
A
d A
S
1/-rA
0
rA
CAo S
где
S – площадь
Так можно определить VP
рабочий объём реактора РИС-П
Ao
Aк
А
20

21.

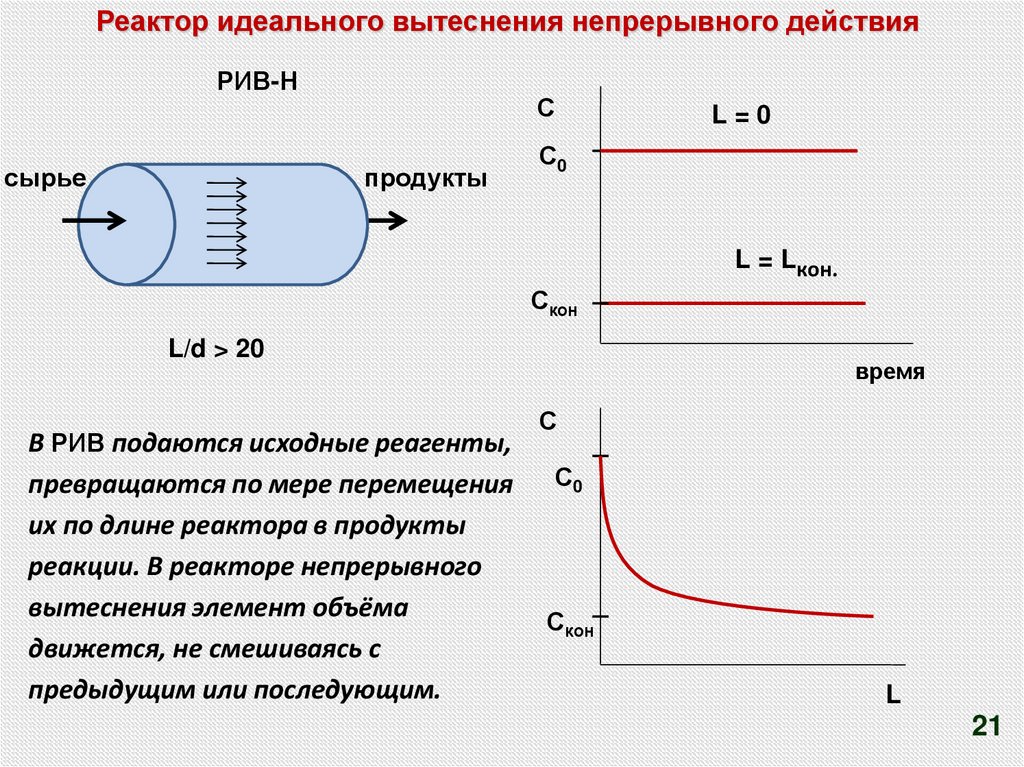
Реактор идеального вытеснения непрерывного действия
РИВ-Н
сырье
С
продукты
L=0
С0
L = Lкон.
Скон
L/d > 20
В РИВ подаются исходные реагенты,
превращаются по мере перемещения
их по длине реактора в продукты
реакции. В реакторе непрерывного
вытеснения элемент объёма
движется, не смешиваясь с
предыдущим или последующим.
время
С
С0
Скон
L
21

22.

Расчёты РИВ также сводятся к определению времени пребывания.
Для расчёта времени пребывания можно воспользоваться
уравнением мат. баланса реактора.
CA
CA
CA
CA
WX
Wy
WZ
x
y
z
2CA 2CA 2CA
rA
D
2
2
2
y
z
x
Поскольку в РИВ реакционная смесь движется только в одном
направлении и только по длине реактора – по оси Х:
CA
Wy
0
y
CA
WZ
0
z
22

23.

Так как в идеальном реакторе нет ни продольной, ни радиальной
диффузии, тогда:
2CA 2CA 2CA
0
D
2
2
2
x
y
z
движется в одном направлении потока
CA
CA
WX
W
x
l
23

24.

Уравнение РИВ при нестационарном режиме, когда
параметры процесса меняются по длине реактора и не
постоянны во времени (в период пуска и остановки):
CA
CA
W
rA
l
24

25.

Когда реактор работает в стационарном режиме, когда
параметры в каждой точке реакционного объёма не меняются во
времени,
CA
CA
W
rA
l
CA
0
CA
W
rA
l
dl W d
dl – путь, длина, расстояние
CA
W
rA
W
CA
rA
CA
rA
25

26.

Если вместо текущей концентрации подставить начальную концентрацию:
d CAo ( 1 A )
d
rA
A
d
0
0
d CAo ( 1 A )
rA
Математическая модель (характеристическое уравнение) РИВ:
CAo
A
0
d A
rA
время, в течение которого реакционная смесь проходит через РИВ от
входа в реактор до выхода из него
Уравнение одинаково для РИС-П
26

27.

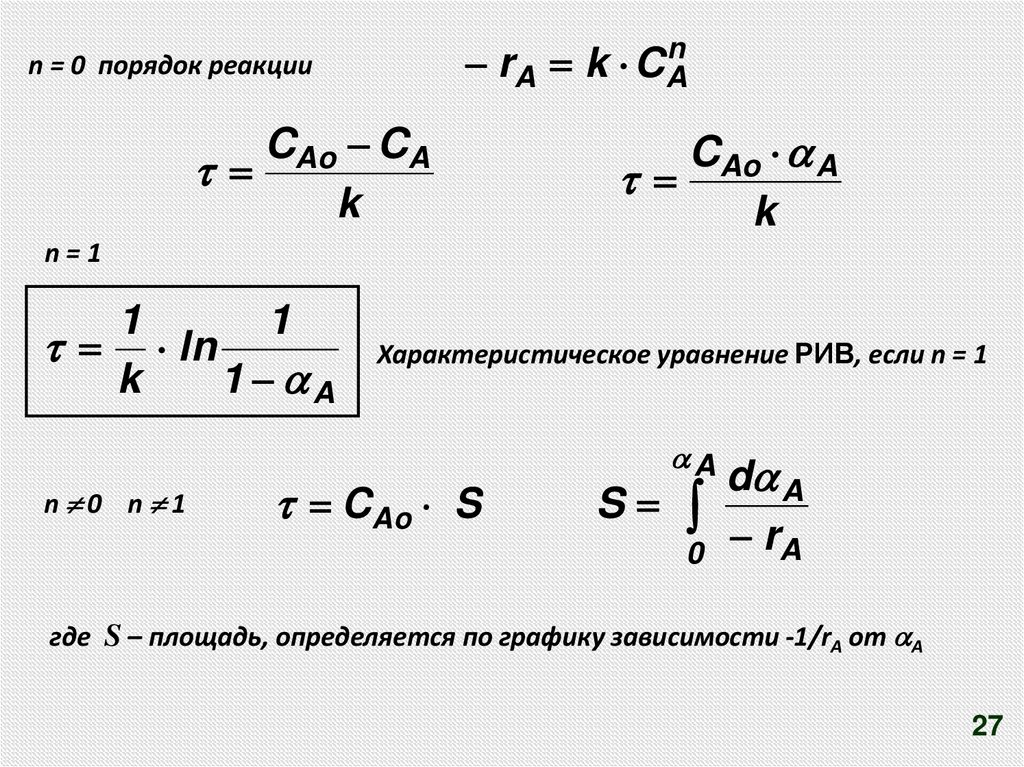
rA k CAn
n = 0 порядок реакции
CAo CA
k
CAo A
k
n=1
1
1
ln
k
1 A
n 0 n 1
Характеристическое уравнение РИВ, если n = 1
CAo S
S
A
0
d A
rA
где S – площадь, определяется по графику зависимости -1/rA от А
27

28.

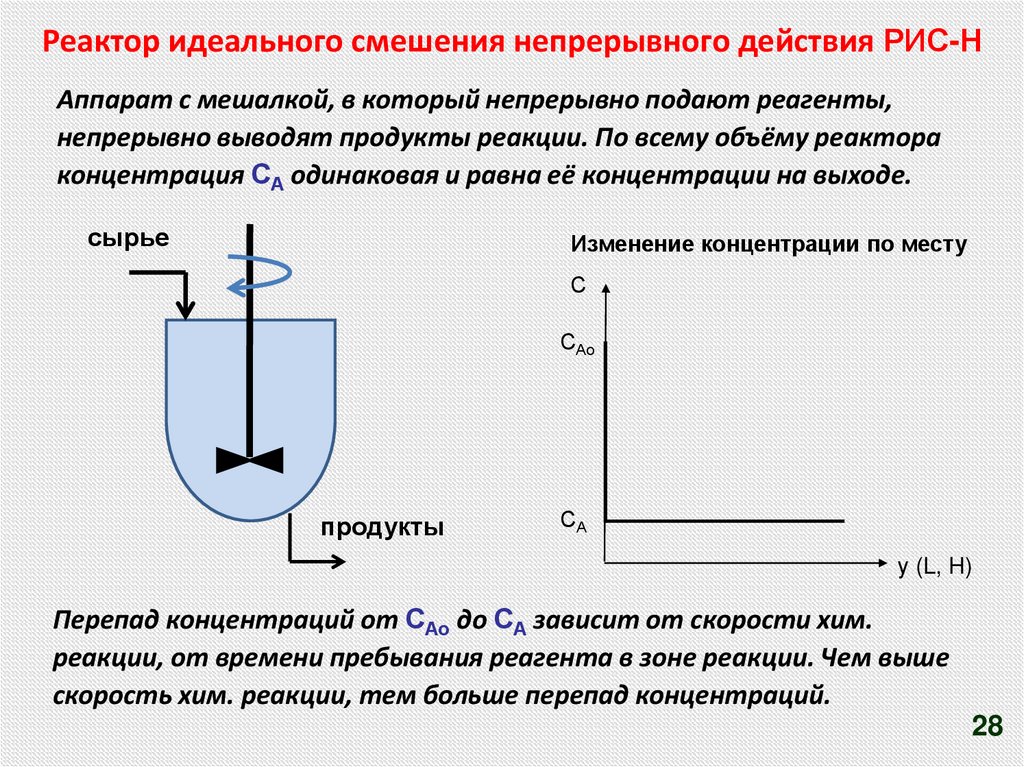
Реактор идеального смешения непрерывного действия РИС-Н
Аппарат с мешалкой, в который непрерывно подают реагенты,
непрерывно выводят продукты реакции. По всему объёму реактора
концентрация СА одинаковая и равна её концентрации на выходе.
сырье
Изменение концентрации по месту
С
САо
продукты
СА
у (L, H)
Перепад концентраций от САо до СА зависит от скорости хим.
реакции, от времени пребывания реагента в зоне реакции. Чем выше
скорость хим. реакции, тем больше перепад концентраций.
28

29.

Для реактора РИС-Н характерным является отсутствие
градиента параметров, как во времени, так и в объёме реактора,
поэтому уравнение материального баланса составляют сразу
для реактора в целом.
GА НАКОП. = GА КОНВ. GА Х.Р.
(4)
GА НАКОП. – количество реагента А, находящееся в реакторе
в неизменном виде в единицу времени;
GA КОНВ. – количество реагента А, которое переносится за счёт
конвективной диффузии;
GА Х.Р. – количество реагента А, которое вступает в химическую
реакцию в единицу времени.
29

30.

GА НАКОП. = GА КОНВ. GА Х.Р.
т.к. реактор проточный
GА НАКОП. = 0,
GА КОНВ. = GА Х.Р.,
Из вывода уравнения материального баланса (слайд 7):
GА ПРИХ. – GА СТОК = GА Х.Р. + GА НАКОП.
GA КОНВ.
GА КОНВ. = GА ПРИХ. – GА СТОК
(3)
GА ПРИХ. – количество реагента А, поступающего в единицу
времени в единицу объёма реактора;
GА СТОК – количество реагента А, которое выходит из
реактора в единицу времени.
30

31.

GА КОНВ. = GА ПРИХ. – GА СТОК
GА ПРИХ. = GАо = САо · V0
GА СТОК = GА = GАо (1 – А) = САо · V0 · (1 – А)
V0 – объёмная скорость подачи сырья
Для проточного реактора GА КОНВ. = GА Х.Р.
GА КОНВ. = САо · V0 – САо · V0 · (1 – А) = САо · V0 · А
САо · V0 · А = GА Х.Р.
GА Х.Р. = (-rA) · VP = САо · V0 · А
Vp = V0 ·
Нужно определить объём реактора, объёмная скорость всегда задаётся
САо · V0 · А = (-rA) · V0 ·
САо · А = (-rA) ·
Математическая модель
(характеристическое уравнение) РИС-Н:
CAo A
rA
31

32.

Математическая модель (характеристическое уравнение) РИС-Н:
CAo A
rA
n
n
n
r
k
C
k
C
(
1
)
n=0
A
A
Ao
A
CAo CA
CAo A
k
k
1
CAo A
1
A
n=1
k CAo ( 1 A ) k ( 1 A )
1
A
k (1 A )
n 0 n 1
Характеристическое уравнение РИС-Н если n = 1
CAo S
S
A
0
d A
rA
где S – площадь, определяется по графику зависимости -1/rA от А
32

33.

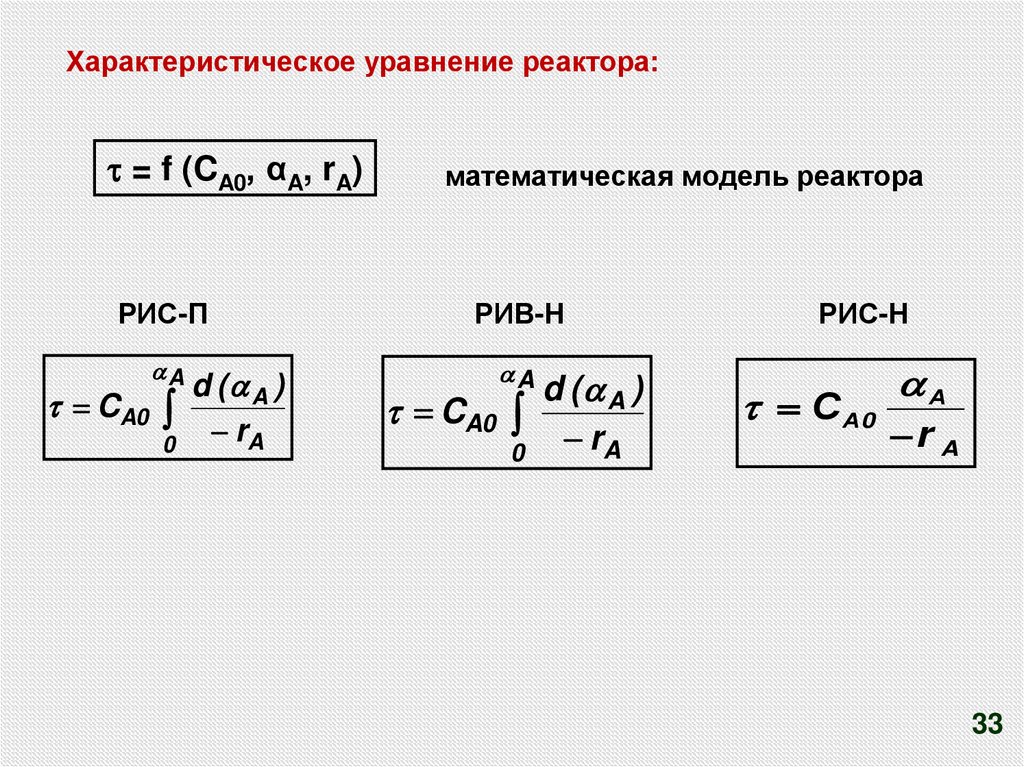
Характеристическое уравнение реактора:
= f (CA0, αA, rA)
математическая модель реактора
РИС-П
РИВ-Н
A
A
CA0
0
d ( A )
rA
CA0
0
d ( A )
rA
РИС-Н
С А0
А
r A
33

34.

СПАСИБО ЗА ВНИМАНИЕ!
34