Похожие презентации:
Движение
1.
2.
3.
4. Задачи урока.
Ввести понятие движения, видыдвижения.
Отработать навыки построения
симметрии, параллельного
переноса, поворота.
Закрепить умение определять вид
движения.
Выполнить самостоятельную
работу.
5.
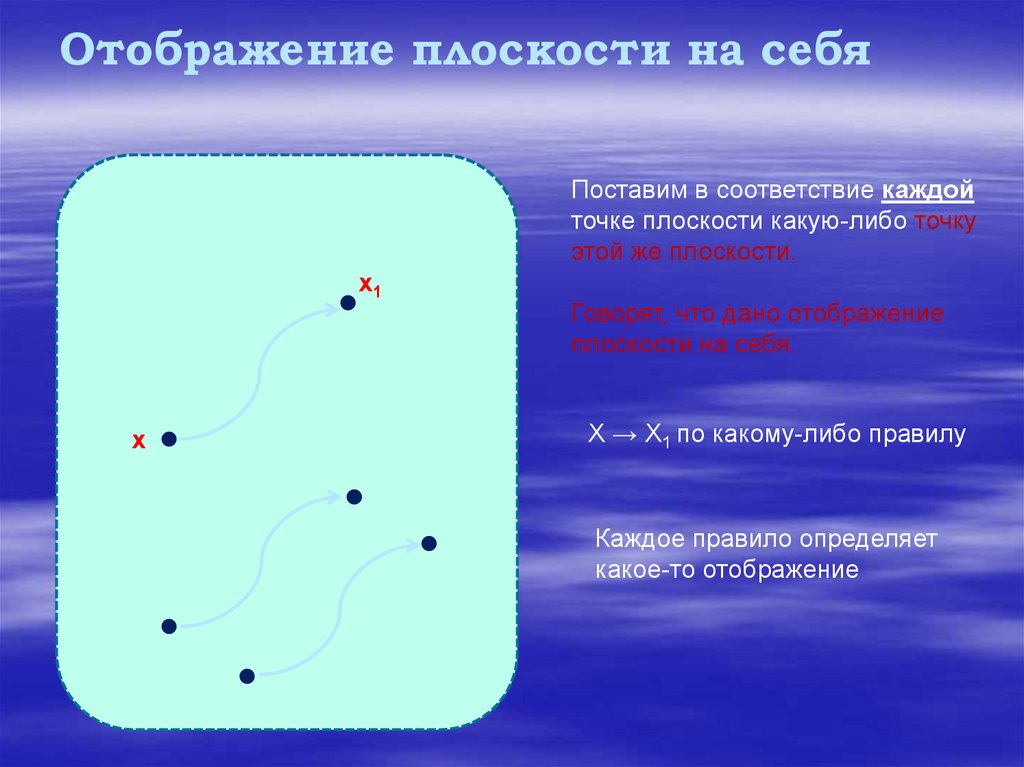
Отображение плоскости на себяПоставим в соответствие каждой
точке плоскости какую-либо точку
этой же плоскости.
х1
х
Говорят, что дано отображение
плоскости на себя.
Х → Х1 по какому-либо правилу
Каждое правило определяет
какое-то отображение
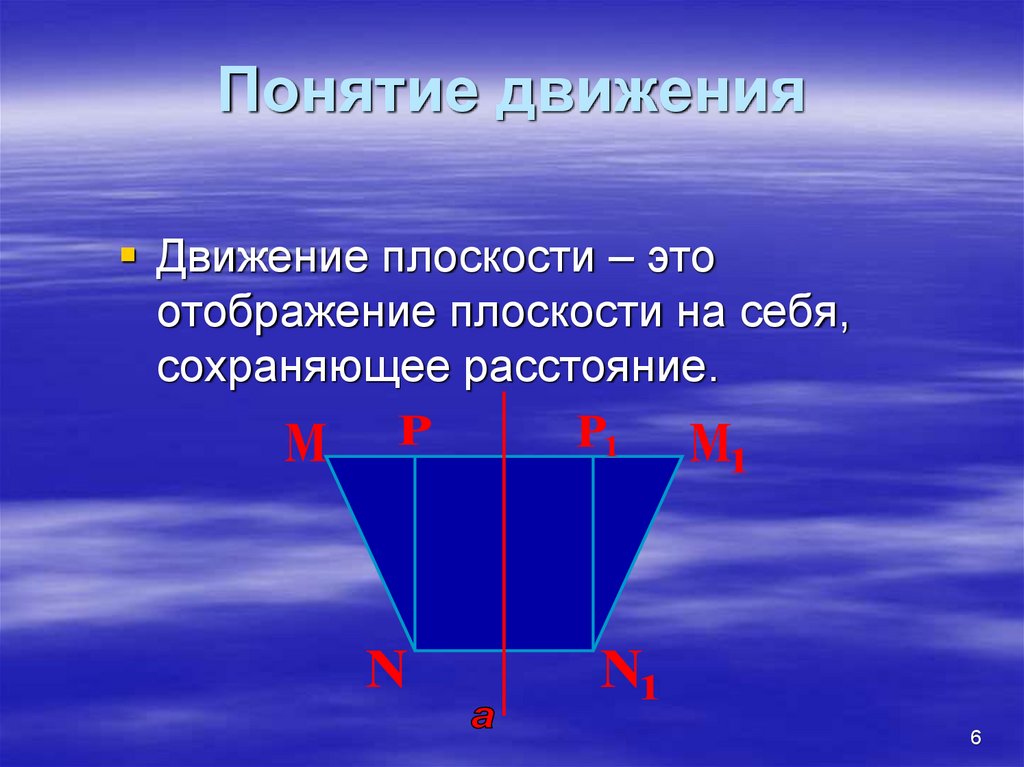
6. Понятие движения
Движение плоскости – этоотображение плоскости на себя,
сохраняющее расстояние.
6
7. Теорема. При движении отрезок отображается на отрезок.
Следствие:При движении
треугольник
отображается на
равный ему
треугольник.
7
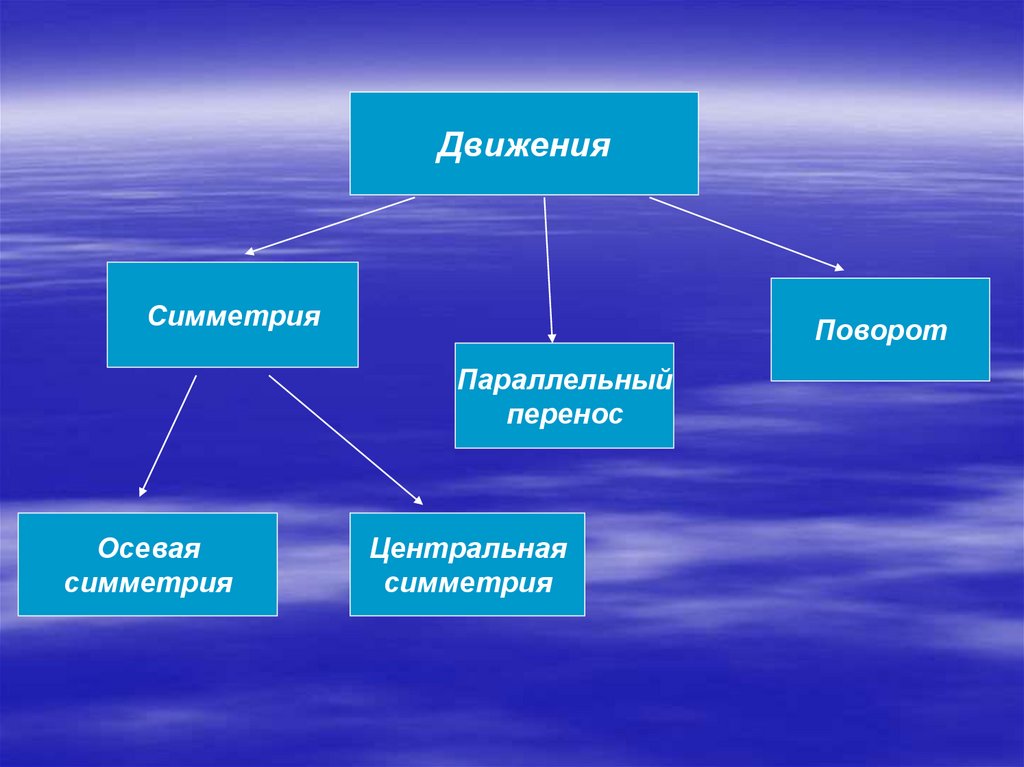
8.
ДвиженияСимметрия
Поворот
Параллельный
перенос
Осевая
симметрия
Центральная
симметрия
9. Осевая симметрия
ОпределениеОсевая симметрия –это
отображение плоскости на
себя, при котором каждая
точка М отображается в
такую точку М1, что отрезок
ММ1 перпендикулярен прямой
а (оси симметрии ) и отрезок
МР равен отрезку РМ1.
10. Построение
Пусть а – ось симметрии.∆АВС – произвольный. Проведем
перпендикуляр ВР к прямой а.
Отложим на прямой ВР отрезок
РВ1 , равный по длине отрезку
ВР. Точка В1 искомая.
Аналогично строим точки А1 и
С1. ∆А1В1С 1 симметричен
∆АВС относительно прямой а.
11.
12.
13. Задача
Сколько осей симметрии имеетравносторонний треугольник?
(1 ряд)
Сколько осей симметрии имеет
квадрат?
(2 ряд)
Сколько осей симметрии имеет
ромб, не являющийся квадратом?
(вместе)
Начертите и убедитесь в
правильности своего ответа
14. Центральная симметрия
ОпределениеЦентральная симметрия
–это отображение
плоскости на себя , при
котором каждая точка М
отображается в такую
точку М1,что отрезок ОМ
равен отрезку ОМ 1
(точка О - центр
симметрии).
15. Построение
Пусть точка О – центрсимметрии. ∆АВС произвольный. Проведём луч
ВО. Отложим отрезок ОВ1 ,
равный отрезку ОВ. Точка В1
искомая. Аналогично строим
точки А 1 и С1 . ∆А1В1С1
симметричен ∆АВС
относительно точки О.
16.
17.
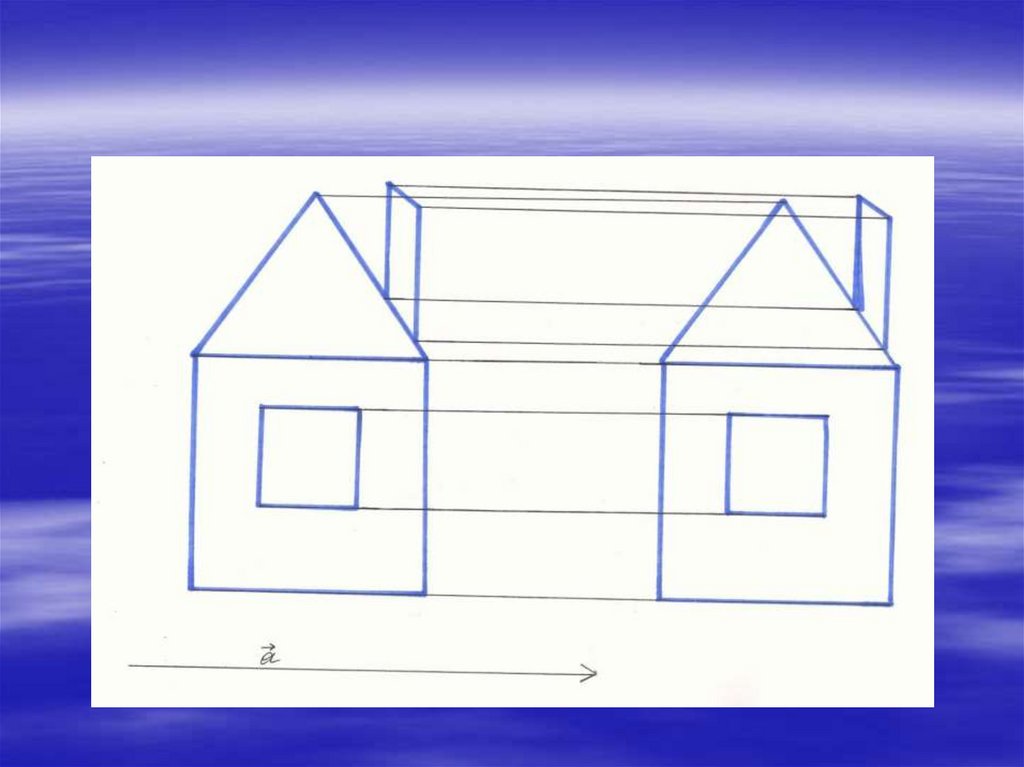
18. Параллельный перенос
Определение.Параллельный перенос –
это отображение
плоскости на себя, при
котором каждая точка
М отображается в
такую точку М1, что
вектор ММ1 равен
вектору а.
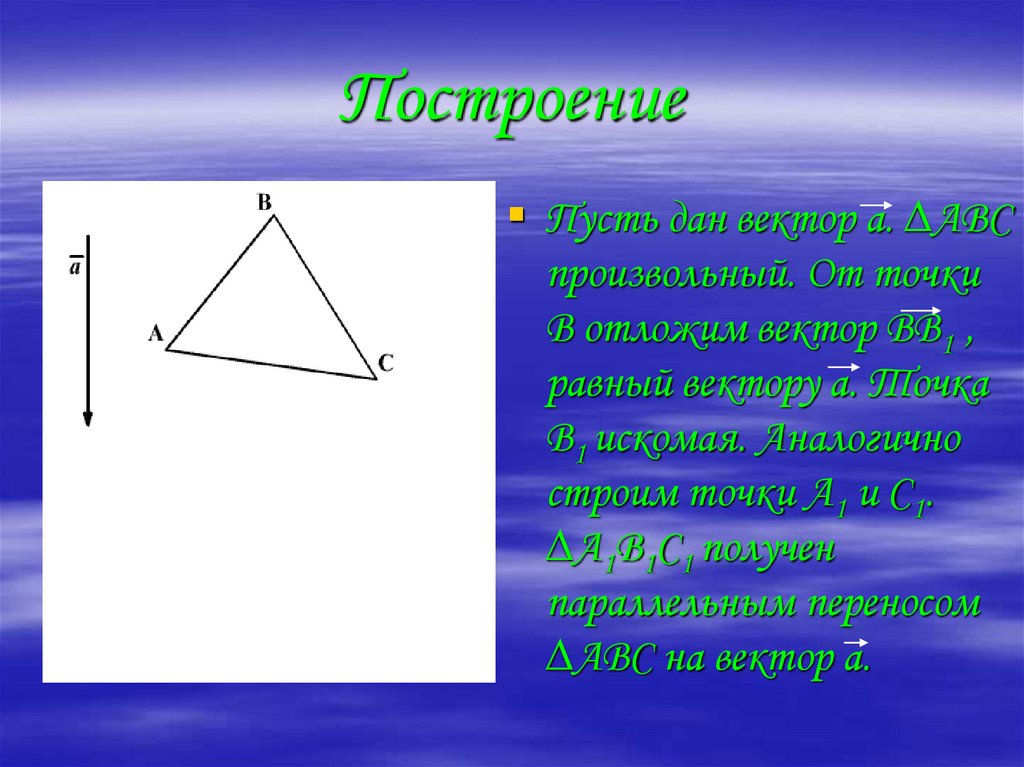
19. Построение
Пусть дан вектор а. ∆АВСпроизвольный. От точки
В отложим вектор ВВ1 ,
равный вектору а. Точка
В1 искомая. Аналогично
строим точки А1 и С1.
∆А1В1С1 получен
параллельным переносом
∆АВС на вектор а.
20.
21.
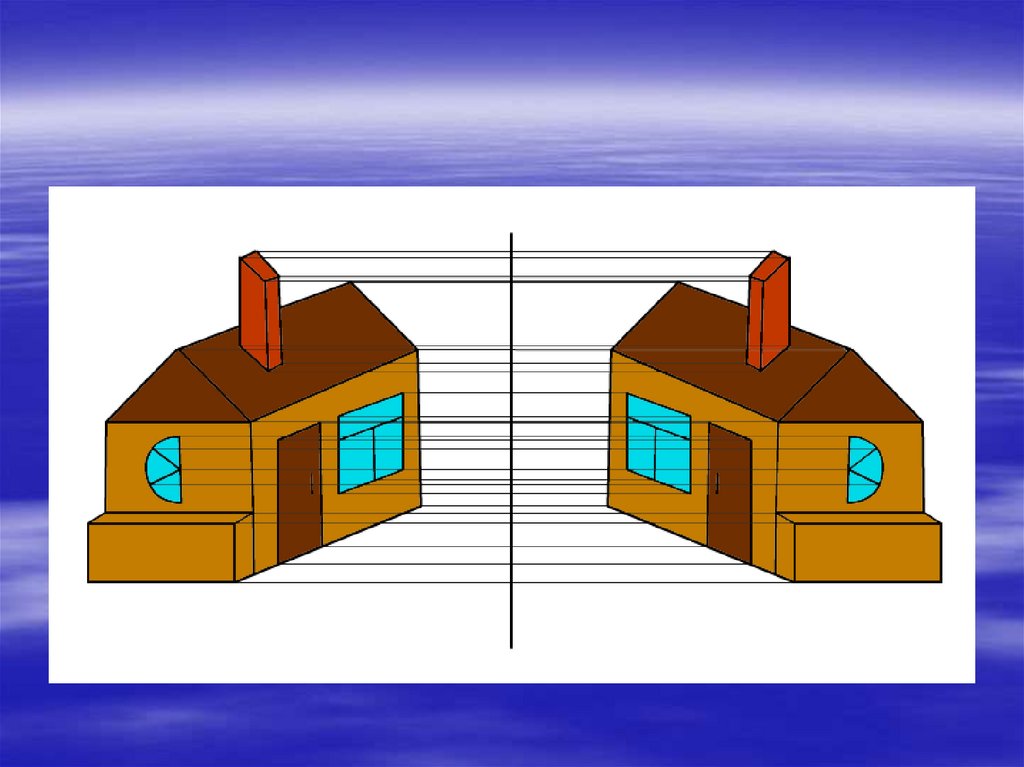
22. Движение в архитектуре. Определить вид движения.
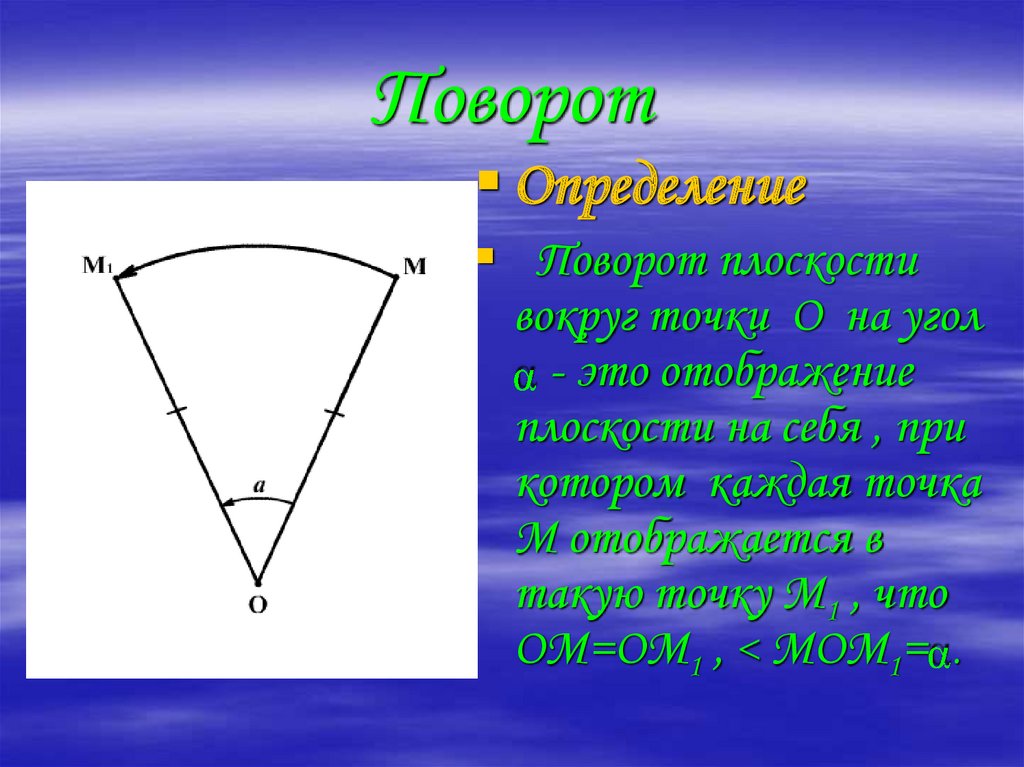
АКВИДУК23. Поворот
ОпределениеПоворот плоскости
вокруг точки О на угол
- это отображение
плоскости на себя , при
котором каждая точка
М отображается в
такую точку М1 , что
ОМ=ОМ1 , < МОМ1= .
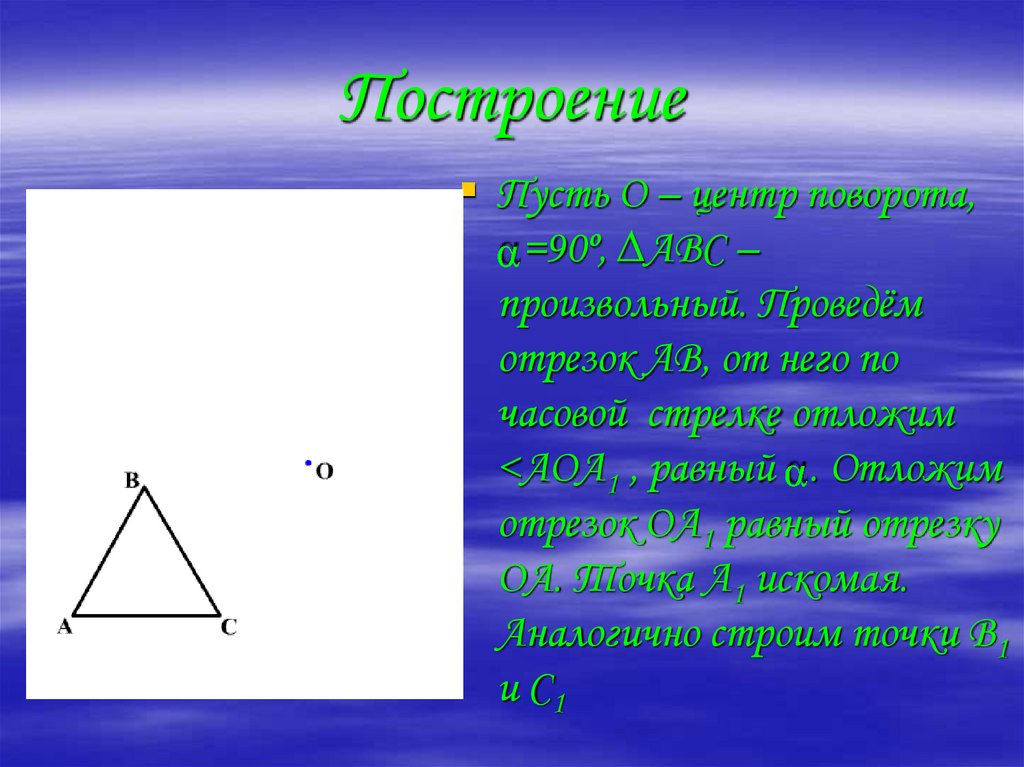
24. Построение
Пусть О – центр поворота,=90º, ∆АВС –
произвольный. Проведём
отрезок АВ, от него по
часовой стрелке отложим
<АОА1 , равный . Отложим
отрезок ОА1 равный отрезку
ОА. Точка А1 искомая.
Аналогично строим точки В1
и С1
25.
26.
27. Вопросы
Определить видсимметрии.
Что вам приходилось
встречать в природе
из известных видов
симметрии?
28. Симметрия в природе
29.
30.
31. Симметрия в архитектуре
32.
33. Что происходит в алгебре?
34. Какие из данных графиков можно отнести к движению?
А)Г)
Б)
В)
Д)
35. Наложение
Наложение- этоотображение
плоскости н себя.
35
36. Теорема. Любое движение является наложением.
Следствие:При движении любая
фигура отображается
на равную ей фигуру.
Фигуры называются равными,
если существует движение,
отображающее одну из них на другую.
36
37. Подобие фигур
Преобразование фигуры F в фигуру F' называетсяпреобразованием подобия, если при этом
преобразовании расстояния между точками
изменяются в одно и то же число раз.
число k называется коэффициентом подобия.
Х Х'
Х'Y' = k ХY
Y Y'
Y
Две фигуры F и F'
называются
Х
подобными, если одна
из них переводится
в другую подобием.
Х'
F'
F
Y'
38.
Подобие в жизни(карты местности)
39. Гомотетия
OХ
Фигуры F и F´ называются
гомотетичными.
Х'
Преобразование фигуры F, при котором каждая ее
Зафиксируем
точкув точку
O и положительное
точка Х переходит
Х' , построеннуючисло k.
Каждой
точке
Х плоскости,
от O
указанным
способом,
называется отличной
гомотетией
сопоставим
точку
Х' наO.
луче OХ так, что OХ' = k OХ.
относительно
центра
Точке O сопоставим ее саму.
Число k называется коэффициентом гомотетии.
40.
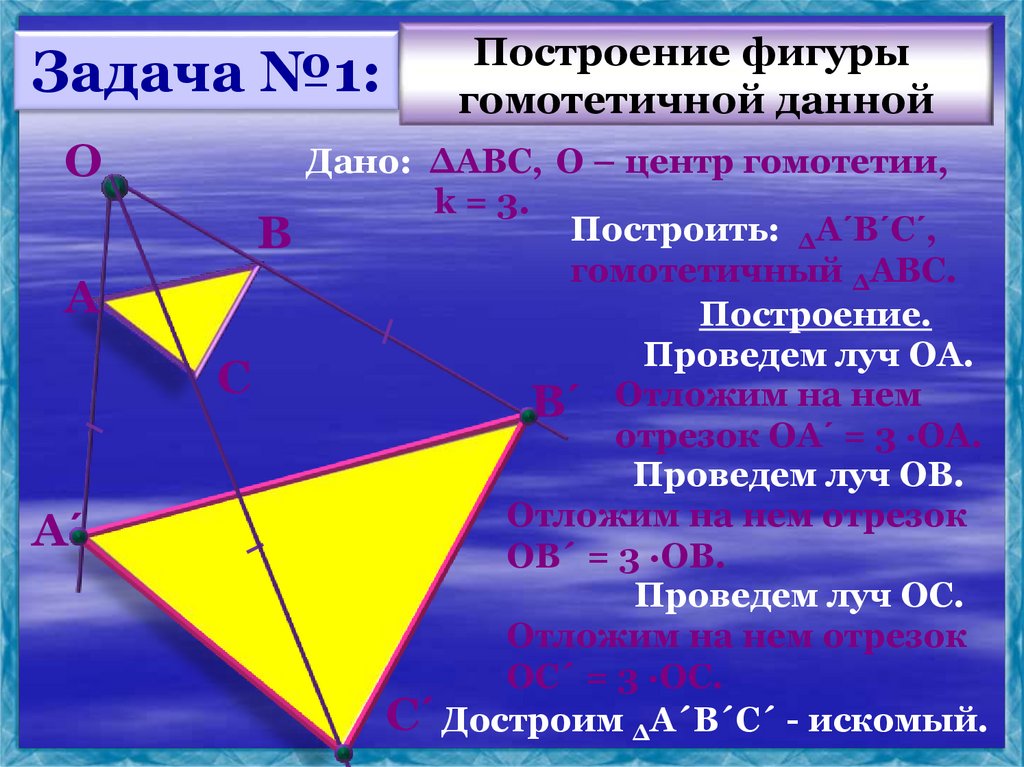
Задача №1:О
В
А
С
А´
Построение фигуры
гомотетичной данной
Дано: ∆АВС, О – центр гомотетии,
k = 3.
Построить: ∆А´В´С´,
гомотетичный ∆АВС.
Построение.
Проведем луч ОА.
В´ Отложим на нем
отрезок ОА´ = 3 ∙ОА.
Проведем луч ОВ.
Отложим на нем отрезок
ОВ´ = 3 ∙ОВ.
Проведем луч ОС.
Отложим на нем отрезок
ОС´ = 3 ∙ОС.
С´ Достроим ∆А´В´С´ - искомый.
41. Выполнение практической работы
Выполни работу на каждый видотображения.
42.
Какие виды движения мывстречаем с вами в нашей
повседневной жизни?
Привлекла ли вас красота
симметрии, поворота и движения в
архитектуре?






























 Математика
Математика








