Методы обработки экспертных оценок

1. Методы обработки экспертных оценок

Лектор: Цехан Ольга Борисовна

2. Следует повторить

Понятие и виды экспертных оценок
Шкалы и допустимые преобразования
Проверка статистических гипотез
Критическая точка распределения Пирсона

3. Входной контроль

Укажите допустимые преобразования для заданных типов шкал

4. Самопроверка

5. План лекции

• Математические методы обработки и анализа
экспертных оценок
– Стандартизация рангов
– Метод согласования кластеризованных
ранжировок
– Оценка согласованности мнений экспертов на
основе коэффициента конкордации
– Поиск результирующего ранжирования
(выработка итогового мнения комиссии)
• метод средних арифметических рангов
• метод медианных рангов
• алгоритм Кемени-Снелла (медиана Кемени)
• Автоматизация ЭО

6.

Методы обработки экспертных оценок
Обработка результатов коллективной
экспертизы направлена на согласование
позиций специалистов с целью выработки
итоговой экспертной оценки.
Может оказаться, что мнение какого-либо
эксперта или экспертов, плохо сочетающиеся
со среднеарифметическим мнением, окажется
истинным. Поэтому важнейшую роль здесь и
приобретают процедуры качественной
обработки оценок экспертов.

7.

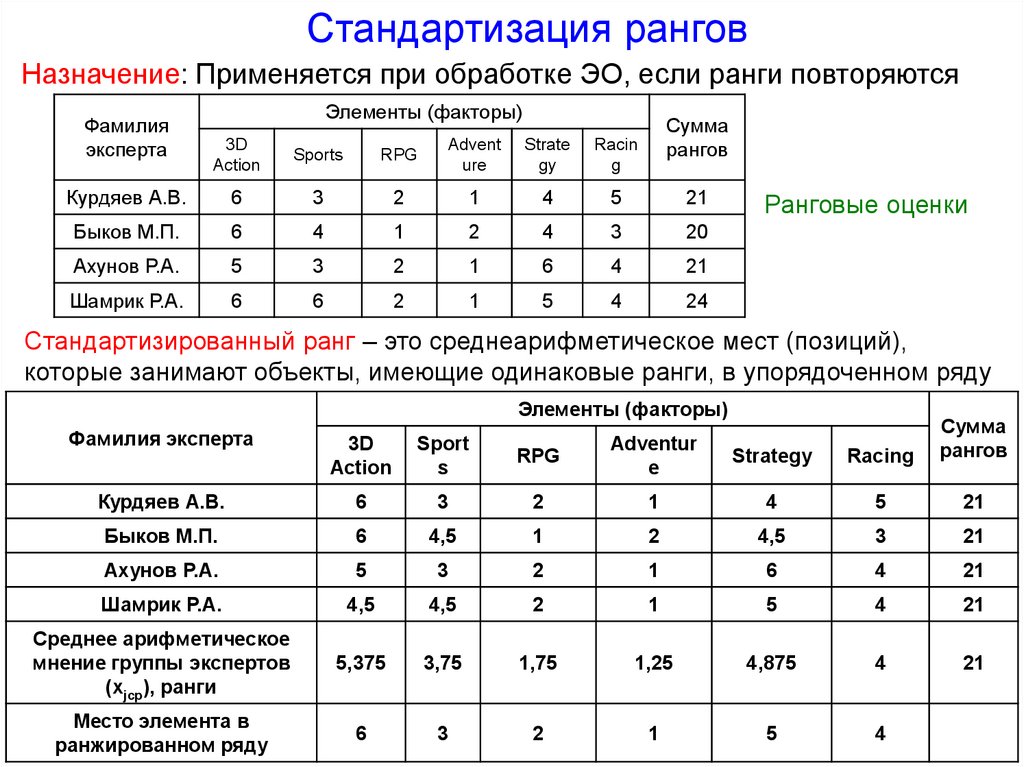
Стандартизация рангов
Назначение: Применяется при обработке ЭО, если ранги повторяются
Фамилия
эксперта
Элементы (факторы)
3D
Action
Sports
Курдяев А.В.
6
Быков М.П.
Сумма
рангов
RPG
Advent
ure
Strate
gy
Racin
g
3
2
1
4
5
21
6
4
1
2
4
3
20
Ахунов Р.А.
5
3
2
1
6
4
21
Шамрик Р.А.
6
6
2
1
5
4
24
Ранговые оценки
Стандартизированный ранг – это среднеарифметическое мест (позиций),
которые занимают объекты, имеющие одинаковые ранги, в упорядоченном ряду
Элементы (факторы)
RPG
Adventur
e
Strategy
Racing
Сумма
рангов
3
2
1
4
5
21
6
4,5
1
2
4,5
3
21
Ахунов Р.А.
5
3
2
1
6
4
21
Шамрик Р.А.
4,5
4,5
2
1
5
4
21
Среднее арифметическое
мнение группы экспертов
(хjср), ранги
5,375
3,75
1,75
1,25
4,875
4
21
Место элемента в
ранжированном ряду
6
3
2
1
5
4
Фамилия эксперта
3D
Action
Sport
s
Курдяев А.В.
6
Быков М.П.

8.

Метод согласования кластеризованных ранжировок

9.

Кластеризованная ранжировка
Ранжирование - расположение исследуемых объектов в порядке
возрастания (или убывания) какого-либо присущего им свойства
Результатом ранжирования является ранжировка объектов экспертизы.
Равнозначные по интенсивности свойства объекты образуют кластеры,
внутри которых ранги объектов равны.
Ранжировка с повторяющимися рангами объектов называется
кластеризованной ранжировкой
B 1
2,3
4
5,6,7
8
9
10
Введенная кластеризованная ранжировка является бинарным
отношением на носителе – множестве {1,2,3,...,10} .
Его структура:
задано отношение эквивалентности с 7-ю классами эквивалентности,
а именно, {2,3}, {5,6,7}, а остальные 5 классов состоят из оставшихся 5
отдельных элементов;
затем введен строгий линейный порядок между классами
эквивалентности.

10.

Кластеризованная ранжировка в виде матрицы
бинарного отношения
Кластеризованную ранжировку, (как и любое бинарное
отношение), можно задать матрицей || x(a, b) || из 0 и 1
порядка k x k.
x(a, b) = 1 тогда и только тогда, когда либо a > b, либо a =
b.
В первом случае x(b, a) = 0, а во втором x(b, a) = 1.
При этом хотя бы одно из чисел x(a, b) и x(b, a) равно 1.
A 1
2
3
4 5
B ???
A1 2 3 4 5
B 1 2 3 4 5
1 - 1 1 1 1
1 - 0 0 1 0
2 0 - 1 1 1
2 1 - 1 1 1
3 0 0 - 1 1
3 1 0 - 1 0
4 0 0 0 - 1
4 0 0 0 - 0

11.

Пусть А и В – две кластеризованные ранжировки. Пару объектов (a,b)
назовем «противоречивой» относительно кластеризованных
ранжировок А и В, если эти два элемента по-разному упорядочены в А
и В, т.е. a < b в А и a > b в В (первый вариант противоречивости) либо
a >b в А и a < b в В (второй вариант противоречивости).
Пара объектов (a,b), эквивалентная хотя бы в одной кластеризованной
ранжировке, не может быть противоречивой: эквивалентность a = b не
образует "противоречия" ни с a < b, ни с a > b.
A 1
B 1,2
C 3
2,3
4
3,4, 5
1, 4
2
5,6,7
8
6
7
9
6
5, 7, 8
9
10
8, 10 ,
9, 10
Совокупность противоречивых пар объектов для двух
кластеризованных ранжировок А и В - «ядро противоречий»: S(A,B).
S(A,B) = (8, 9)
S(A,C) =
S(B,C) =

12.

Пусть А и В – две кластеризованные ранжировки. Пару объектов (a,b)
назовем «противоречивой» относительно кластеризованных
ранжировок А и В, если эти два элемента по-разному упорядочены в А
и В, т.е. a < b в А и a > b в В (первый вариант противоречивости) либо
a >b в А и a < b в В (второй вариант противоречивости).
Пара объектов (a,b), эквивалентная хотя бы в одной кластеризованной
ранжировке, не может быть противоречивой: эквивалентность a = b не
образует "противоречия" ни с a < b, ни с a > b.
A 1
2,3
B 1,2
C 3
4
3,4, 5
1, 4
2
5,6,7
8
6
7
9
6
5, 7, 8
9
10
8, 10 ,
9, 10
Совокупность противоречивых пар объектов для двух
кластеризованных ранжировок А и В - «ядро противоречий»:
S(A,B) = (8, 9)
S(A,C) = (1,3), (2,4)
S(B,C) =

13.

Пусть А и В – две кластеризованные ранжировки. Пару объектов (a,b)
назовем «противоречивой» относительно кластеризованных
ранжировок А и В, если эти два элемента по-разному упорядочены в А
и В, т.е. a < b в А и a > b в В (первый вариант противоречивости) либо
a >b в А и a < b в В (второй вариант противоречивости).
Пара объектов (a,b), эквивалентная хотя бы в одной кластеризованной
ранжировке, не может быть противоречивой: эквивалентность a = b не
образует "противоречия" ни с a < b, ни с a > b.
A 1
2,3
B 1,2
C 3
4
3,4, 5
1, 4
2
5,6,7
8
6
7
9
6
5, 7, 8
9
10
8, 10 ,
9, 10
Совокупность противоречивых пар объектов для двух
кластеризованных ранжировок А и В - «ядро противоречий»:
S(A,B) = (8, 9)
S(A,C) = (1,3), (2,4)
S(B,C) = (1, 3), (2, 3), (2, 4), (5, 6), (8,9)

14.

Пример. Ядро противоречий ранжировок В и С
B 1,2
C 3
3,4, 5
1, 4
6
2
7
9
5, 7, 8
6
8, 10 ,
9, 10
S(B,C) = (1, 3), (2, 3), (2, 4), (5, 6), (8,9)
Представление ядра противоречий в виде графа
3
2
1
4
7
9
5
8
6
10

15.

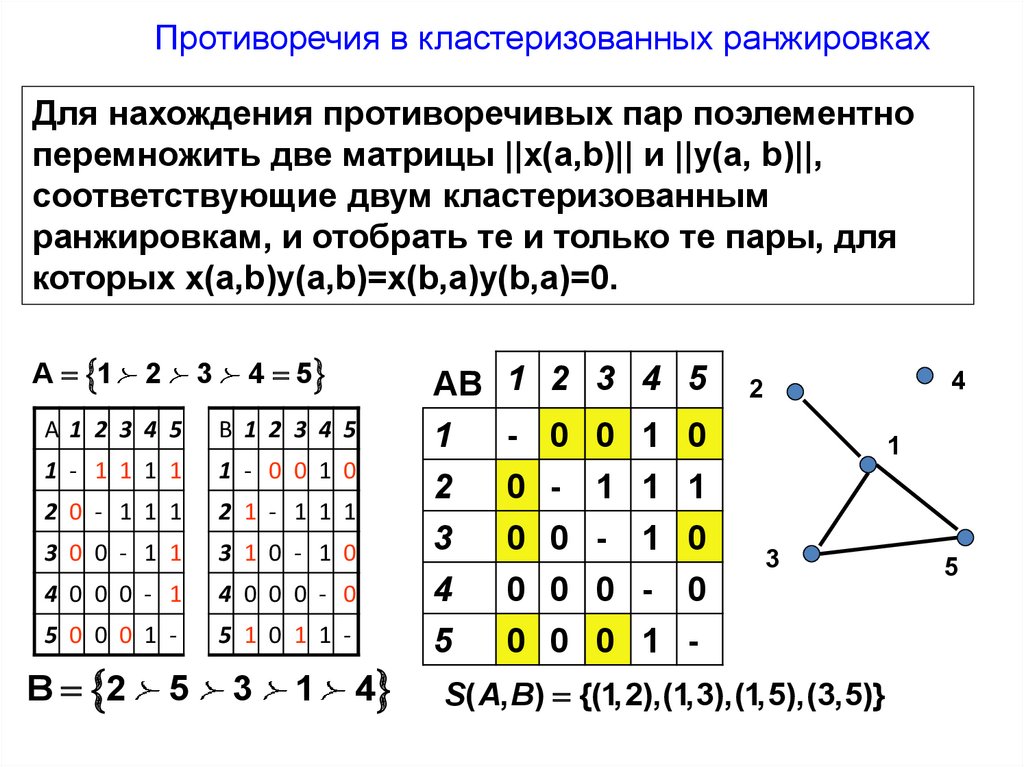
Противоречия в кластеризованных ранжировках
Для нахождения противоречивых пар поэлементно
перемножить две матрицы ||x(a,b)|| и ||y(a, b)||,
соответствующие двум кластеризованным
ранжировкам, и отобрать те и только те пары, для
которых x(a,b)y(a,b)=x(b,a)y(b,a)=0.
A 1
2
3
4 5
AB 1 2 3 4 5
A1 2 3 4 5
B 1 2 3 4 5
1 - 1 1 1 1
1 - 0 0 1 0
2 0 - 1 1 1
2 1 - 1 1 1
3 0 0 - 1 1
3 1 0 - 1 0
1
2
3
4 0 0 0 - 1
4 0 0 0 - 0
4
0 0 0 -
5 0 0 0 1 -
5 1 0 1 1 -
5
0 0 0 1 -
B 2
5
3
1
4
- 0 0 1 0
0 - 1 1 1
0 0 - 1 0
4
2
1
3
0
S( A, B) {(1,2),(1,3),(1,5),(3,5)}
5

16.

Алгоритм согласования кластеризованных ранжировок
A 1
2
3
4 5
B 2
5
3
1
4
Выделяются противоречивые пары объектов во всех парах
кластеризованных ранжировок. S( A, B) {(1,2),(1,3),(1,5),(3,5)}
Формируются кластеры итоговой кластеризованной ранжировки
(т.е. классы эквивалентности - связные компоненты графов,
соответствующих объединению попарных ядер противоречий).
{(1,2,3,5),4}
Кластеры упорядочиваются. Для этого произвольно выбирается
один объект из первого кластера и второй - из второго, порядок
между кластерами устанавливается такой же, какой имеет быть
между выбранными объектами в любой из рассматриваемых
кластеризованных ранжировок.
(1,2,3,5)
4
Если в исходных кластеризованных ранжировках два
рассматриваемых объекта находились в одном кластере, то они
находятся в одном кластере и в согласующей кластеризованной
ранжировке.

17.

Пример

18.

Оценка согласованности мнений экспертов на
основе коэффициента конкордации
1. Определяем сумму рангов по каждому из элементов
2. Вычисляем среднее значение суммы рангов
xср
xj
n
m
x j x ij
i 1
1/ 2 m n (n 1) 1
m (n 1)
n
2
3 Вычисляем фактические отклонения сумм рангов по п.1 от
среднего значения суммы рангов и их квадраты: j ( x j x ср )
4. Определяем сумму квадратов отклонений
n
Sфакт 2j
j 1
5. Вычисляем значение коэффициента конкордации Кендела
n
Wвыбор
Sфакт
Smax
12 2j
j 1
2
3
m (n n )
2
выбор W m(n 1)
6. Вычисляем значение величины:
2
2
Если выбор
то гипотеза о согласованности показаний
крит
экспертов не отвергается; иначе - отвергается
2
-критическая точка распределения Пирсона
крит

19.

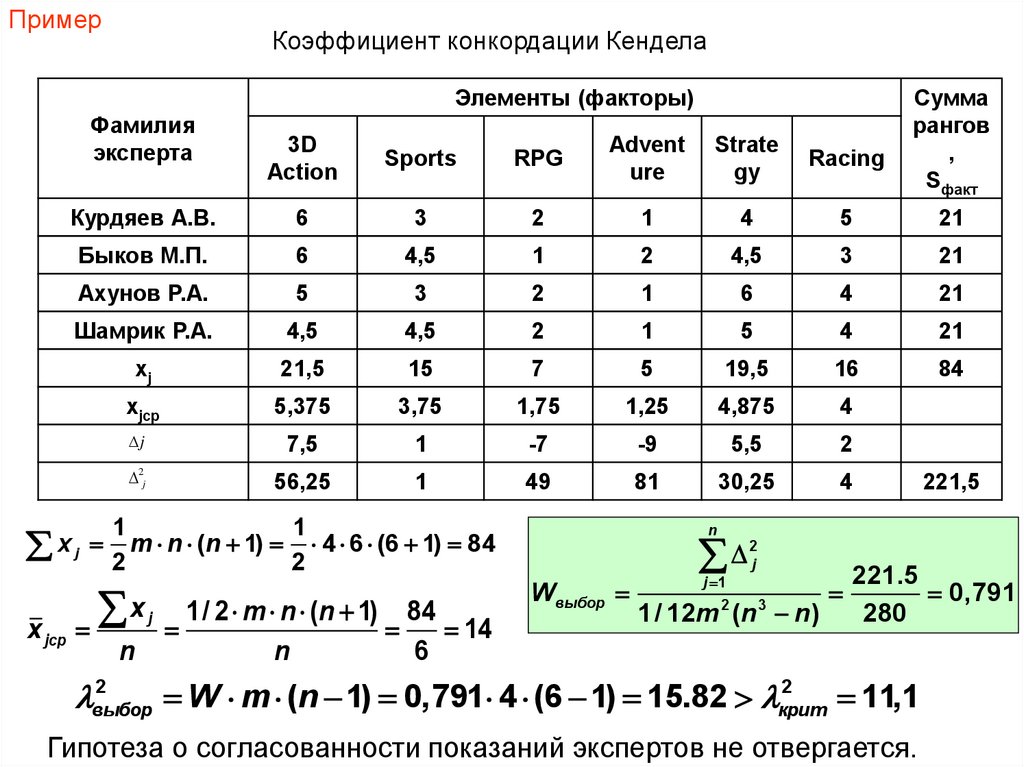
Пример
Коэффициент конкордации Кендела
Элементы (факторы)
Фамилия
эксперта
3D
Action
Sports
RPG
Advent
ure
Strate
gy
Racing
Курдяев А.В.
6
3
2
1
4
5
21
Быков М.П.
6
4,5
1
2
4,5
3
21
Ахунов Р.А.
5
3
2
1
6
4
21
Шамрик Р.А.
4,5
4,5
2
1
5
4
21
xj
21,5
15
7
5
19,5
16
84
xjср
5,375
3,75
1,75
1,25
4,875
4
j
7,5
1
-7
-9
5,5
2
2j
56,25
1
49
81
30,25
4
x
x jср
Сумма
рангов
,
Sфакт
j
1
1
m n (n 1) 4 6 (6 1) 84
2
2
x
n
j
1/ 2 m n (n 1) 84
14
n
6
221,5
n
Wвыбор
j 1
2
2
j
1/ 12m (n 3 n)
221.5
0,791
280
2
2
выбор
W m (n 1) 0,791 4 (6 1) 15.82 крит
11,1
Гипотеза о согласованности показаний экспертов не отвергается.

20.

Поиск результирующего ранжирования
Если оценки экспертов согласованы, то для
поиска результирующего ранжирования можно
использовать
•метод средних арифметических рангов
•метод медианных рангов
•алгоритм Кемени-Снелла

21.

Метод медианных рангов
1. Взять ответы экспертов, соответствующие одному из
объектов,
2. Расположить их в порядке неубывания (если нет
повторяющихся рангов, то получится в порядке возрастания).
3. Взять ранг, стоящий на центральном месте. Это - медиана.
Пример.
1. Ранги для некоторого объекта 5, 5, 1, 6, 8, 5, 6, 5, 6, 5, 7, 1.
2. Располагая в порядке неубывания, получим
последовательность: 1, 1, 5, 5, 5, 5, 5, 6, 6, 6, 7, 8.
3.На центральных местах - шестом и седьмом - стоят 5 и 5.
Следовательно, медиана равна 5.
4. Результирующая ранжировка образуется из медиан,
рассчитанных для всех объектов.

22.

Расстояние Кемени
Определение. Расстоянием Кемени между ранжировками
А и В, описываемыми матрицами || a(i,j) || и || b(i,j) ||
соответственно, называется число
k
D ( A, B) │a i , j b(i , j )│
i , j 1
т.е. расстояние Кемени между ранжировками равно сумме
модулей разностей элементов, стоящих на одних и тех же
местах в соответствующих им матрицах парных сравнений.
Расстояние Кемени - это число несовпадающих
элементов в матрицах || a(i,j) || и || b(i,j) ||
Пример
A1 2 3 4 5
B 1 2 3 4 5
A={1>2>3>4=5}
1 - 1 1 1 1
1 - 0 0 1 0
2 0 - 1 1 1
2 1 - 1 1 1
3 0 0 - 1 1
3 1 0 - 1 0
4 0 0 0 - 1
4 0 0 0 - 0
5 0 0 0 1 -
5 1 0 1 1 -
B={2>5>3>1>4}
d(A,B)=9

23.

Алгоритм Кемени-Снелла
Пусть
А1 , А2 , А3 ,…, Ар - ответы р экспертов, представленные в
виде бинарных отношений.
D (A ,В) – расстояние Кемени между ранжировками А и В
Медиана Кемени
Arg min D (Ai ,A) ,
где Arg min – та ранжировка А, при которой достигает
минимума сумма расстояний Кемени от ответов экспертов
до текущей ранжировки А

24.

Пример вычисления расстояния Кемени между ранжировками
A 1
A1
120
30
40
50
2
1
0
0
0
dA
A0
B9
C6
2
3
4 5
3
1
1
0
0
4
1
1
1
1
5
1
1
1
1
-
B
9
0
13
C
6
13
0
B 2 5 3 1 4
d A,B 9
сумма
15
22
19
B
1
2
3
4
5
C 1 3 4 2 5
12345
- 0010
1 - 1 1 1 d B,C 13
10- 10
000- 0
1011d A,C 6
C
1
2
3
4
5
1
0
0
0
0
2
1
1
1
0
3
1
0
1
0
4
1
0
1
0
5
1
1
1
1
-
Медиана Кемени:
Ранжировка
A 1
2
3
4 5

25. Автоматизация ЭО *

Вычисление результирующей экспертной оценки, а также классификация
мнений экспертов реализованы в пакете STATISTICA 6.0 на языке
STATISTICS Visual Basic в виде модуля анализа экспертных ранжировок,
который позволяет совершать следующие операции.
1. Находить точную медиану Кемени, как в классе строгих, так и в классе
нестрогих ранжировок.
2. Вычислять результирующую ранжировку на основе медианы, суммы,
среднего арифметического рангов альтернатив.
3. Классифицировать мнения экспертов иерархическими агломеративными
методами (метод Уорда, метод «ближнего соседа», метод «дальнего соседа»
и др.), вычислять для каждой из подгрупп экспертов результирующую оценку.
Классификация производится с учетом нечисловой природы ранжировок.
4. Использовать методы многомерного шкалирования для снижения
размерности задачи и представления мнений экспертов в двух- и
трехмерном пространстве. Шкалирование производится с учетом нечисловой
природы ранжировок.
5. Рассчитывать коэффициент конкордации как меру согласованности
группы экспертов и ранговые корреляции.

26. Резюме лекции

назначение, условия применения и суть метода экспертных оценок
эксперт
экспертная оценка
ранжировка
расстояние Кемени
Коэффициент конкордации
медиана Кемени
основные этапы проведения экспертизы, их назначение
классы методов экспертного анализа
шкалы для измерения экспертной информации
Метод рангов
Метод непосредственного оценивания
Метод парных сравнений
Метод последовательных сравнений
назначение и основные приемы этапа обработки экспертных оценок
стандартизация рангов
согласование кластеризованных ранжировок
согласованность мнений экспертов на основе коэффициента
конкордации
результирующая ранжировка методами
медианных рангов
Кемени-Снелла