Локальные преобразования

1. Локальные преобразования

1
of
19
Локальные преобразования
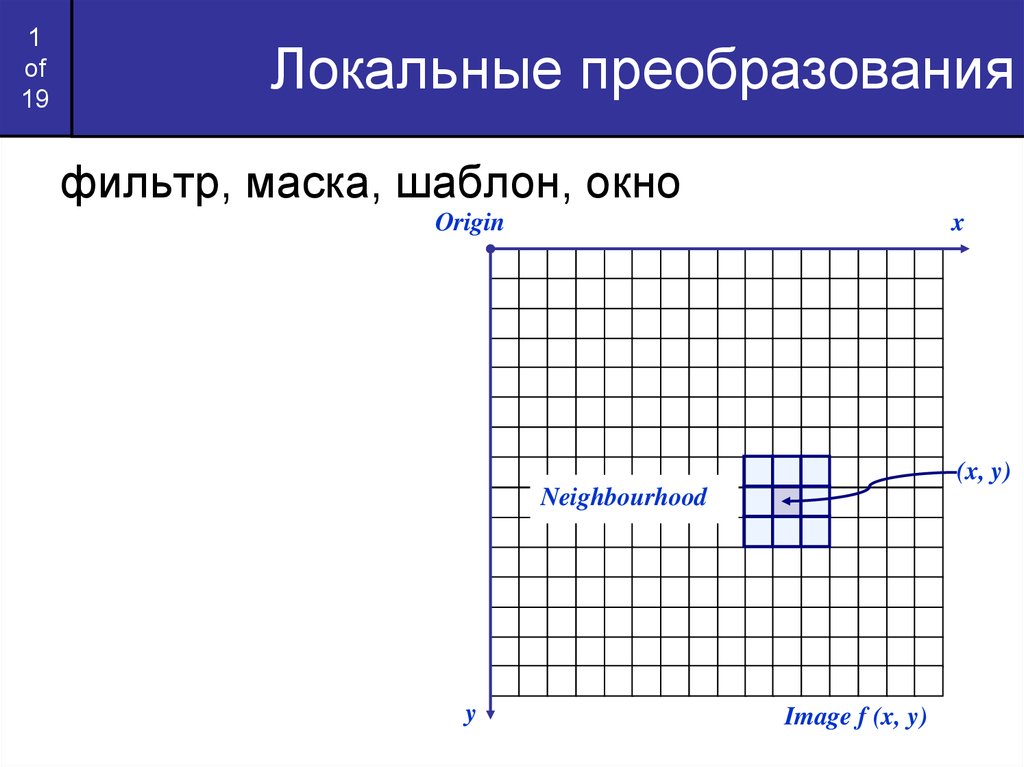
фильтр, маска, шаблон, окно
Origin
x
(x, y)
Neighbourhood
y
Image f (x, y)

2. Пространственная фильтрация

2
of
19
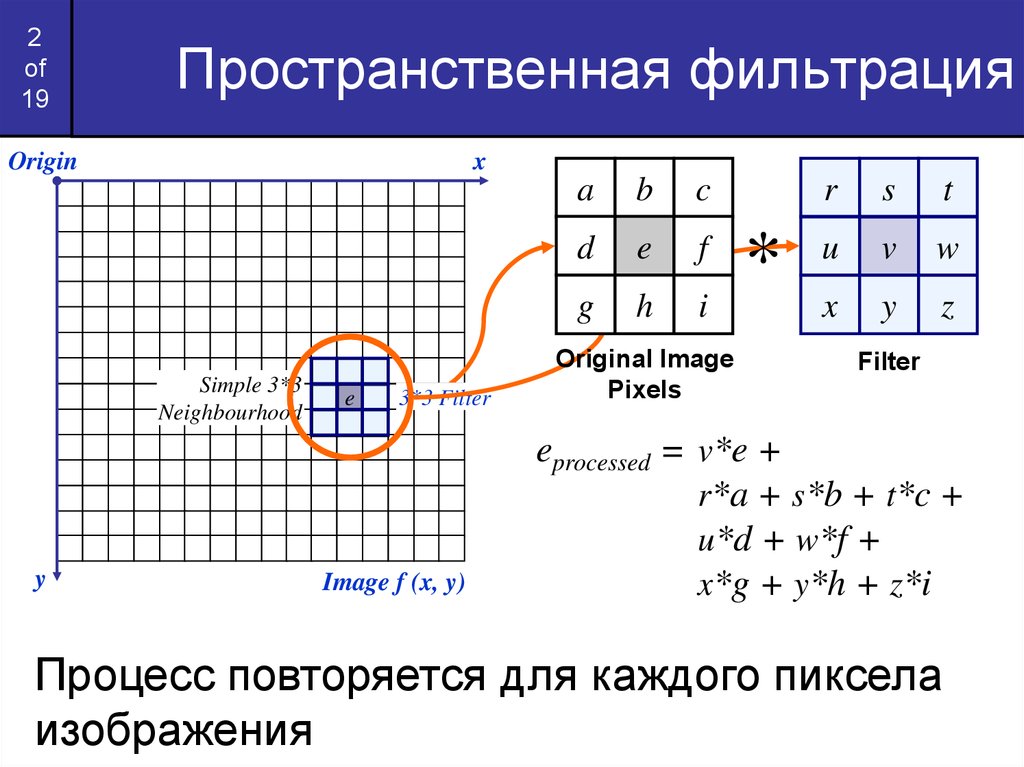
Пространственная фильтрация
Origin
x
Simple 3*3
Neighbourhood
y
e
3*3 Filter
Image f (x, y)
a
b
c
d
e
f
g
h
i
Original Image
Pixels
*
r
s
t
u
v
w
x
y
z
Filter
eprocessed = v*e +
r*a + s*b + t*c +
u*d + w*f +
x*g + y*h + z*i
Процесс повторяется для каждого пиксела
изображения

3. Пространственная фильтрация

3
of
19
Пространственная фильтрация

4. Линейная пространственная фильтрация общего вида

Images taken from Gonzalez & Woods, Digital Image Processing (2002)
4
of
19
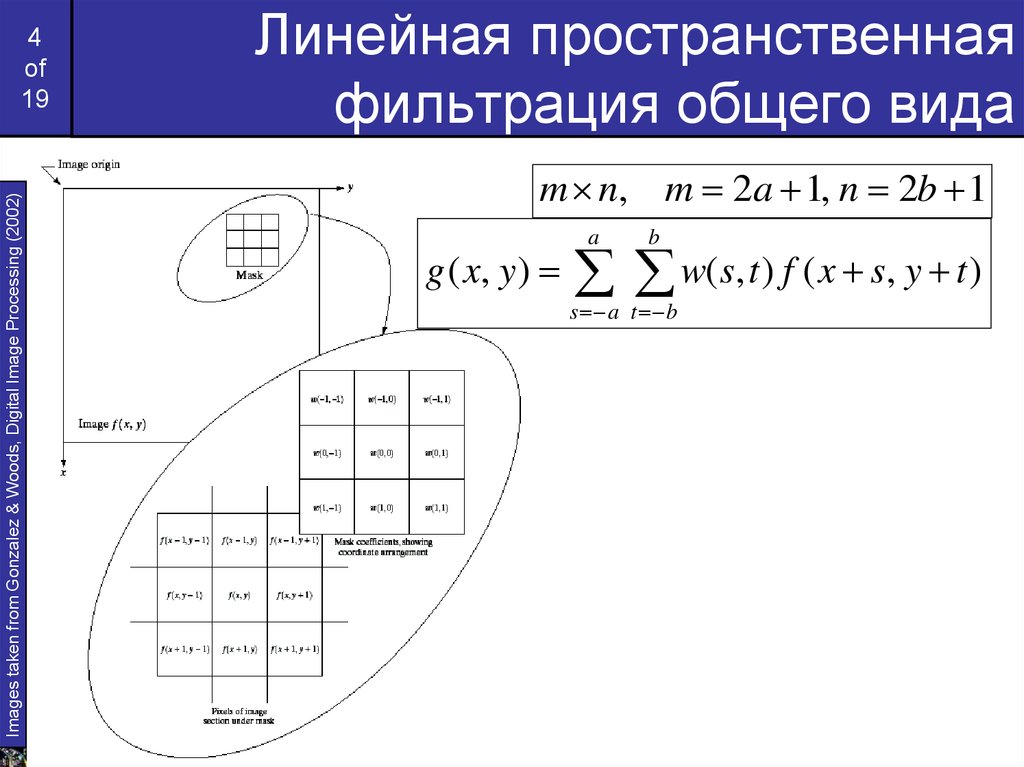
Линейная пространственная
фильтрация общего вида
m n, m 2a 1, n 2b 1
g ( x, y )
a
b
w(s, t ) f ( x s, y t )
s a t b

5. Обработка краев изображения

5
of
19
Обработка краев изображения
Origin
x
e
e
e
e
e
y
e
e
Image f (x, y)

6. Strange Things Happen At The Edges! (cont…)

Images taken from Gonzalez & Woods, Digital Image Processing (2002)
7
of
19
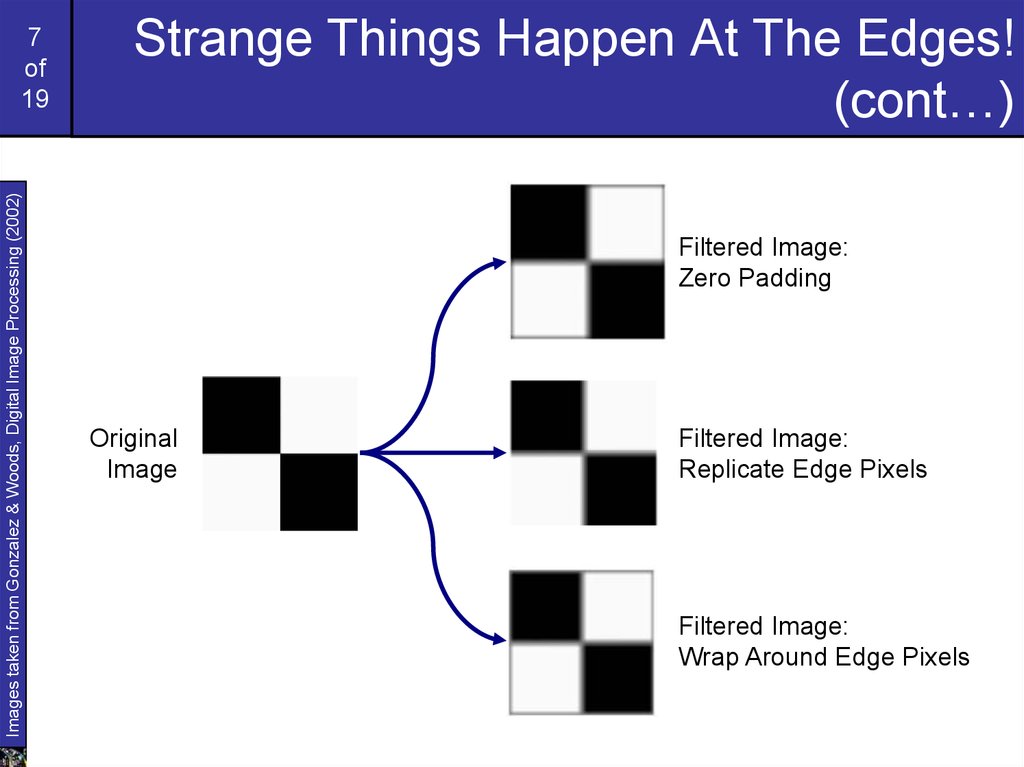
Strange Things Happen At The Edges!
(cont…)
Filtered Image:
Zero Padding
Original
Image
Filtered Image:
Replicate Edge Pixels
Filtered Image:
Wrap Around Edge Pixels

7. Strange Things Happen At The Edges! (cont…)

8
of
19
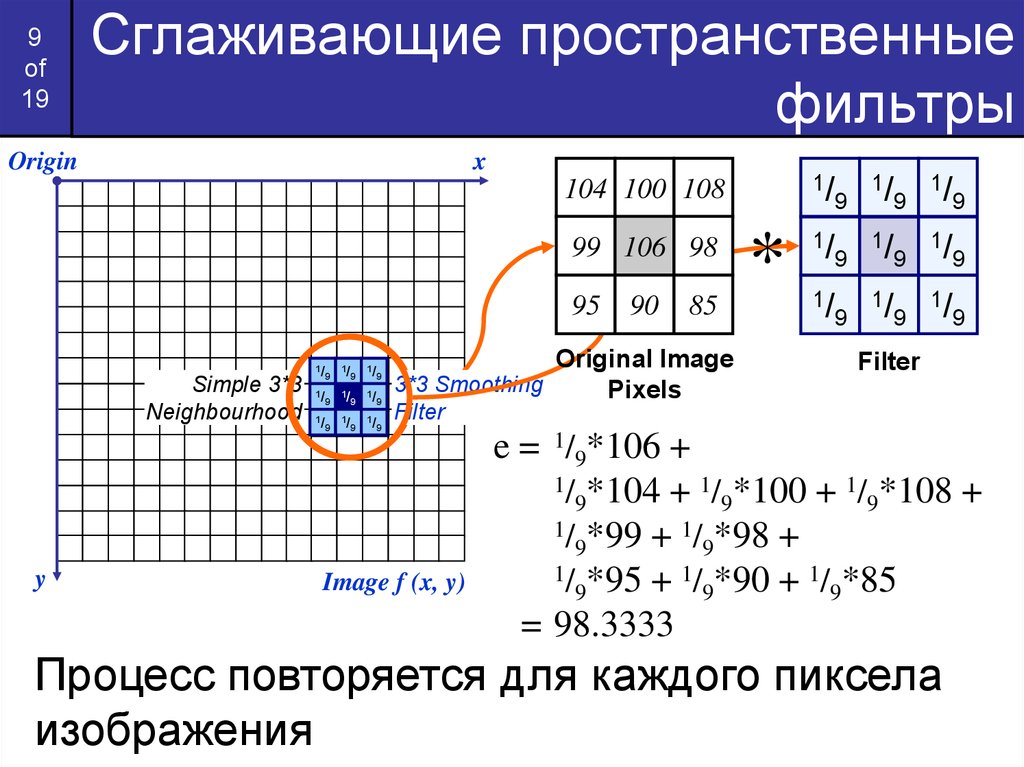
Сглаживающие пространственные
фильтры
– Удаление шума
– Расфокусировка изображения
1/
9
1/
9
1/
9
1/
9
1/
9
1/
9
1/
9
1/
9
1/
9

8. Сглаживающие пространственные фильтры

9
of
19
Сглаживающие пространственные
фильтры
Origin
x
1/
104 100 108
99 106 98
95
Simple 3*3
Neighbourhood
y
1/ 100
1/ 108
1/
104
9
9
9
1/
1/
1/
99
9 106
9 98
9
195
/9 190
/9
185
/9
90
85
Original Image
3*3 Smoothing
Pixels
*
9
1/
9
1/
9
1/
9
1/
9
1/
9
1/
9
1/
9
1/
9
Filter
Filter
Image f (x, y)
e = 1/9*106 +
1/ *104 + 1/ *100 + 1/ *108 +
9
9
9
1/ *99 + 1/ *98 +
9
9
1/ *95 + 1/ *90 + 1/ *85
9
9
9
= 98.3333
Процесс повторяется для каждого пиксела
изображения

9. Сглаживающие пространственные фильтры

Images taken from Gonzalez & Woods, Digital Image Processing (2002)
10
of
19
Пример сглаживания
Исходное изображение
500*500 пикселов
Размер фильтра
– 3, 5, 9, 15 and 35
Исчезание деталей

10. Пример сглаживания

Images taken from Gonzalez & Woods, Digital Image Processing (2002)
11
of
19
Пример сглаживания

11. Пример сглаживания

Images taken from Gonzalez & Woods, Digital Image Processing (2002)
12
of
19
Пример сглаживания

12. Пример сглаживания

Images taken from Gonzalez & Woods, Digital Image Processing (2002)
13
of
19
Пример сглаживания

13. Пример сглаживания

Images taken from Gonzalez & Woods, Digital Image Processing (2002)
14
of
19
Пример сглаживания

14. Пример сглаживания

Images taken from Gonzalez & Woods, Digital Image Processing (2002)
15
of
19
Пример сглаживания

15. Пример сглаживания

Images taken from Gonzalez & Woods, Digital Image Processing (2002)
16
of
19
Пример сглаживания

16. Пример сглаживания

17
of
19
Фильтр взвешенного среднего
1/
16
2/
16
1/
16
2/
16
4/
16
2/
16
1/
16
2/
16
1/
16

17. Фильтр взвешенного среднего

18
of
19
Пример сглаживания
Original Image
Smoothed Image
Thresholded Image

18. Пример сглаживания

19
of
19
Нелинейные фильтры
Важные локальные операции:
– Min: Set the pixel value to the minimum in
the neighbourhood
– Max: Set the pixel value to the maximum in
the neighbourhood
– Median: The median value of a set of
numbers is the midpoint value in that set (e.g.
from the set [1, 7, 15, 18, 24] 15 is the
median). Sometimes the median works better
than the average

19. Нелинейные фильтры

20
of
19
Медианный фильтр

20. Медианный фильтр

21
of
19
Сглаживающий против медианного
Original Image
With Noise
Image After
Averaging Filter
Image After
Median Filter

21. Сглаживающий против медианного

Images taken from Gonzalez & Woods, Digital Image Processing (2002)
22
of
19
Сглаживающий против медианного

22. Сглаживающий против медианного

Images taken from Gonzalez & Woods, Digital Image Processing (2002)
23
of
19
Сглаживающий против медианного

23. Сглаживающий против медианного

Images taken from Gonzalez & Woods, Digital Image Processing (2002)
24
of
19
Сглаживающий против медианного

24. Сглаживающий против медианного

25
of
19
Correlation & Convolution
The filtering we have been talking about so
far is referred to as correlation with the filter
itself referred to as the correlation kernel
Convolution is a similar operation, with just
one subtle difference
a
b
c
d
e
e
f
g
h
Original Image
Pixels
*
r
s
t
u
v
w
x
y
z
eprocessed = v*e +
z*a + y*b + x*c +
w*d + u*e +
t*f + s*g + r*h
Filter
For symmetric filters it makes no difference