Похожие презентации:
Методы адаптации в СТЗИ (лекция № 4)
1.
Методы адаптации в СТЗИОбзор первых трёх лекций
И лекция №4
Ведущий лектор - Антипов Иван Евгеньевич
2.
3.
4.
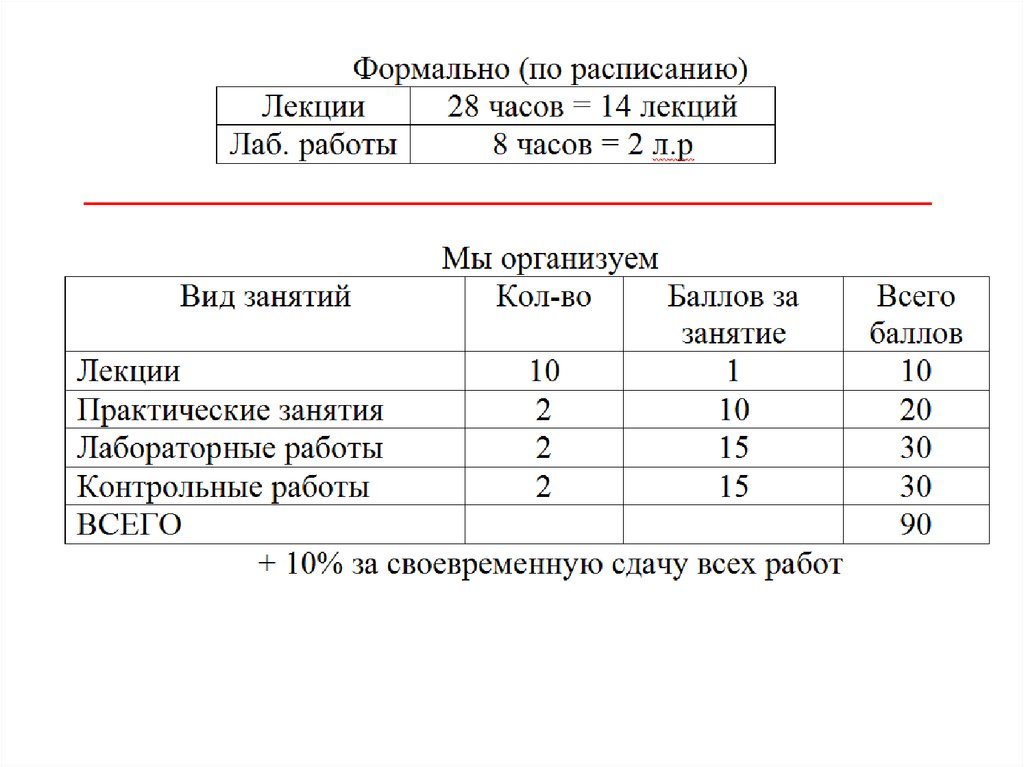
СОДЕРЖАНИЕ КУРСА. Лекции1. Вводная лекция. Краткие математические сведения.
2. Принцип весовой обработки сигнала. Метод непосредственного
обращения матрицы. Формула Винера-Хопфа.
3. Градиентный метод. Практическая реализация метода НОМ и
градиентного метода. Алгоритмы. Структурные схемы устройств.
4. Опорный сигнал, способы его формирования. Области
применимости и сравнительная характеристика методов. Факторы,
влияющие на эффективность работы адаптивных устройств.
5. Контрольная работа
5.
СОДЕРЖАНИЕ КУРСА. Практические занятия1. Расчёт весовых коэффициентов по формуле Винера-Хопфа.
2. Расчёт адаптивного фильтра
СОДЕРЖАНИЕ КУРСА. Лабораторные работы
1a. Расчёт адаптивной антенной решётки методом
непосредственного обращения корреляционной матрицы
1б. Расчёт адаптивной антенной решётки градиентным методом
2. Расчёт адаптивного фильтра для компенсации
интерференционных искажений
6.
Применение адаптивных методов в сетях связи ив радиотехнических системах
- радиолокация и радиосвязь (адаптивные антенные решётки,
поляризационное подавление помех, борьба с замираниями);
- особенно в системах связи с подвижными объектами (мощность,
частота, вид модуляции, скорость передачи);
- в телефонной (модемной) связи (электрическое эхо, местный эффект
для максимального использования для максимального использования
частотного и динамического диапазона ТФ канала);
- при подавлении помех в частотной области (адаптивные фильтры);
- в системах цифровой передачи речи (адаптивные цифровые фильтры,
фильтры с предсказанием).
7.
Применение адаптивных методов в СТЗИПрямые
Устранение искусственно добавленного шума или помех, а также
естественных помех:
- в системах MIMO;
- при зашумлении помещений;
- при зашумлении телефонных линий.
Косвенные
- для «очистки» речевого сигнала от шума и помех для задач голосовой
идентификации;
- для «очистки» и восстановления искажённых изображений для задач
идентификации по лицу, распознавании номеров и др.
8.
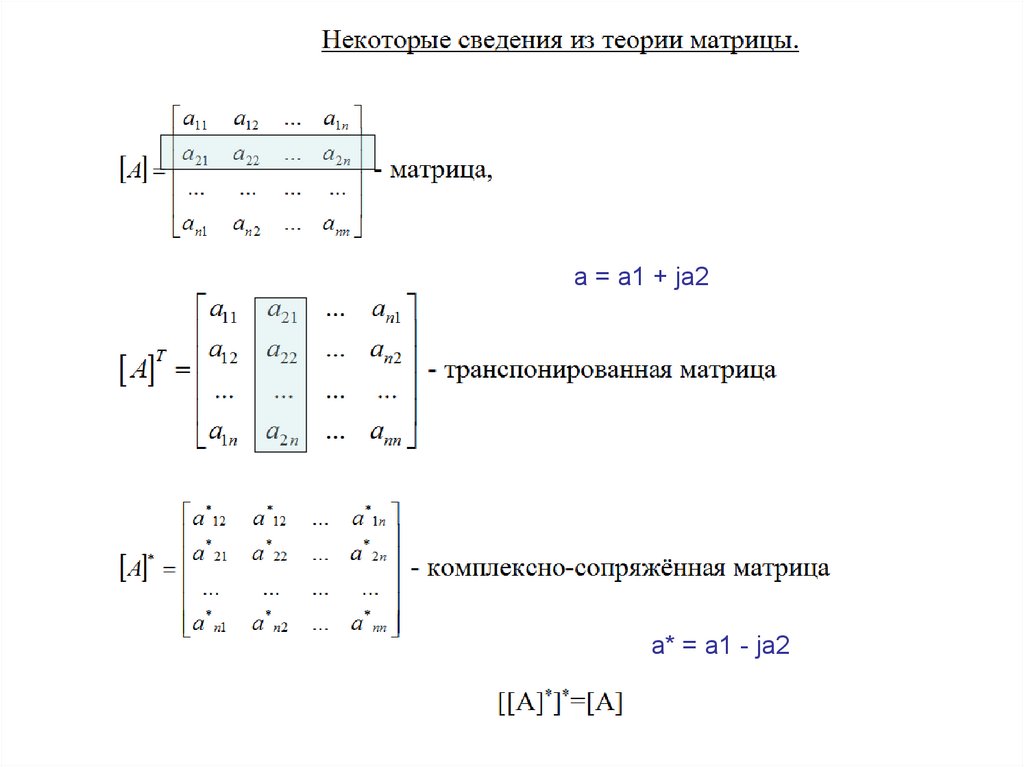
a = a1 + ja2a* = a1 - ja2
9.
Некоторые сведения из теории матриц10.
Некоторые сведения из теории матриц11.
Некоторые сведения из теории матриц12.
Некоторые сведения из теории матрицстрок
е f
13.
Некоторые сведения из теории матриц14.
Некоторые сведения из теории матриц15.
Некоторые сведения из теории матриц16.
x1(t)x2(t)
xn(t)
Формулу Винера-Хопфа желательно запомнить
w1
w2
wn
+
y(t)
17.
Принцип весовой обработкиx1(t)
x2(t)
xn(t)
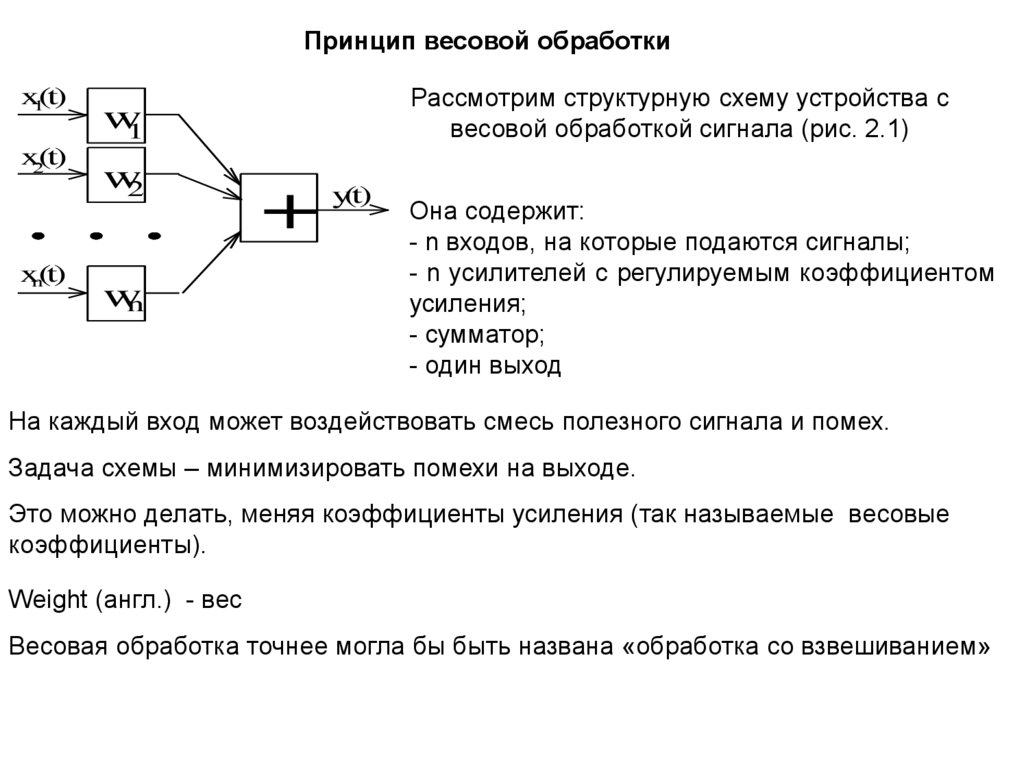
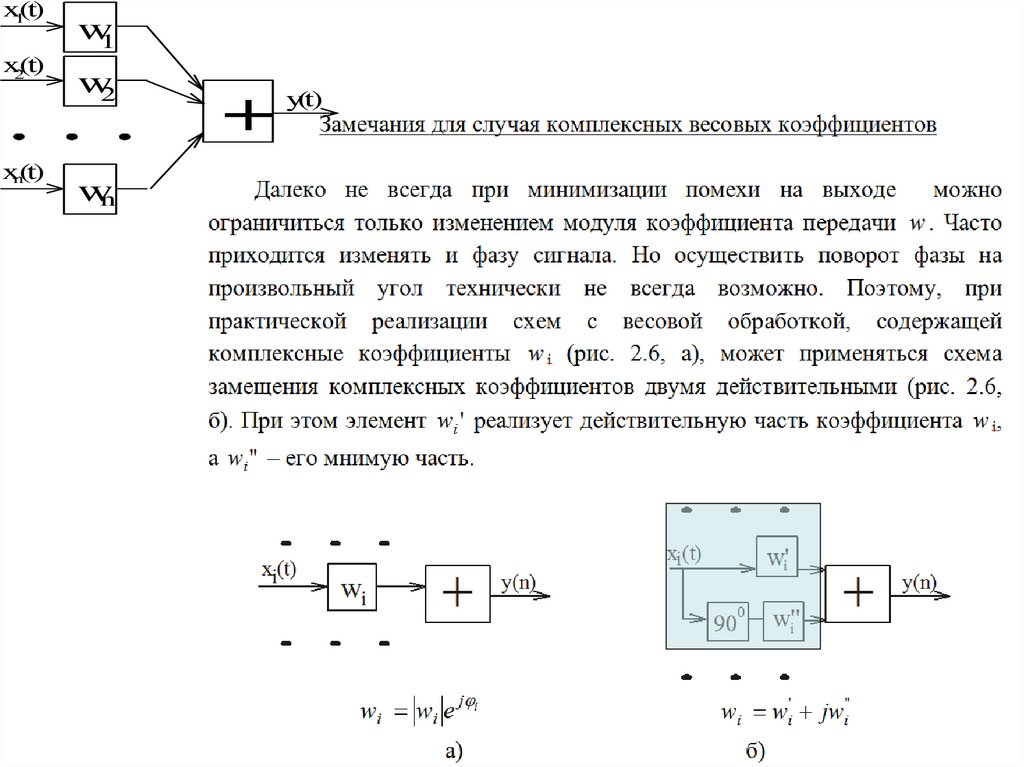
Рассмотрим структурную схему устройства с
весовой обработкой сигнала (рис. 2.1)
w1
w2
wn
+
y(t)
Она содержит:
- n входов, на которые подаются сигналы;
- n усилителей с регулируемым коэффициентом
усиления;
- сумматор;
- один выход
На каждый вход может воздействовать смесь полезного сигнала и помех.
Задача схемы – минимизировать помехи на выходе.
Это можно делать, меняя коэффициенты усиления (так называемые весовые
коэффициенты).
Weight (англ.) - вес
Весовая обработка точнее могла бы быть названа «обработка со взвешиванием»
18.
Возможная интерпретация схемы - Антенная решёткаA1
A2
An
w1
w2
wn
+
y(t)
19.
Возможная интерпретация схемы- микрофонная решётка
M1
M2
w1
w2
. . .
Mn
wn
+
y(t)
20.
21.
x1(t)x2(t)
xn(t)
w1
w2
wn
+
y(t)
22.
x1(t)x2(t)
xn(t)
w1
w2
+
y(t)
wn
х
23.
x1(t)x2(t)
xn(t)
w1
w2
wn
+
y(t)
24.
x1(t)x2(t)
xn(t)
w1
w2
wn
+
y(t)
25.
x1(t)x2(t)
xn(t)
x1(t)
w1
w2
0
+
y(t)
x2(t)
90
0
90
wn
xn(t)
w1
w2
w3
w4
. . .
0
90
w2n-1
w2n
+
y(t)
26.
x1(t)x2(t)
xn(t)
w1
w2
wn
+
y(t)
27.
28.
29.
30.
Формулу Винера-Хопфа желательно запомнить31.
32.
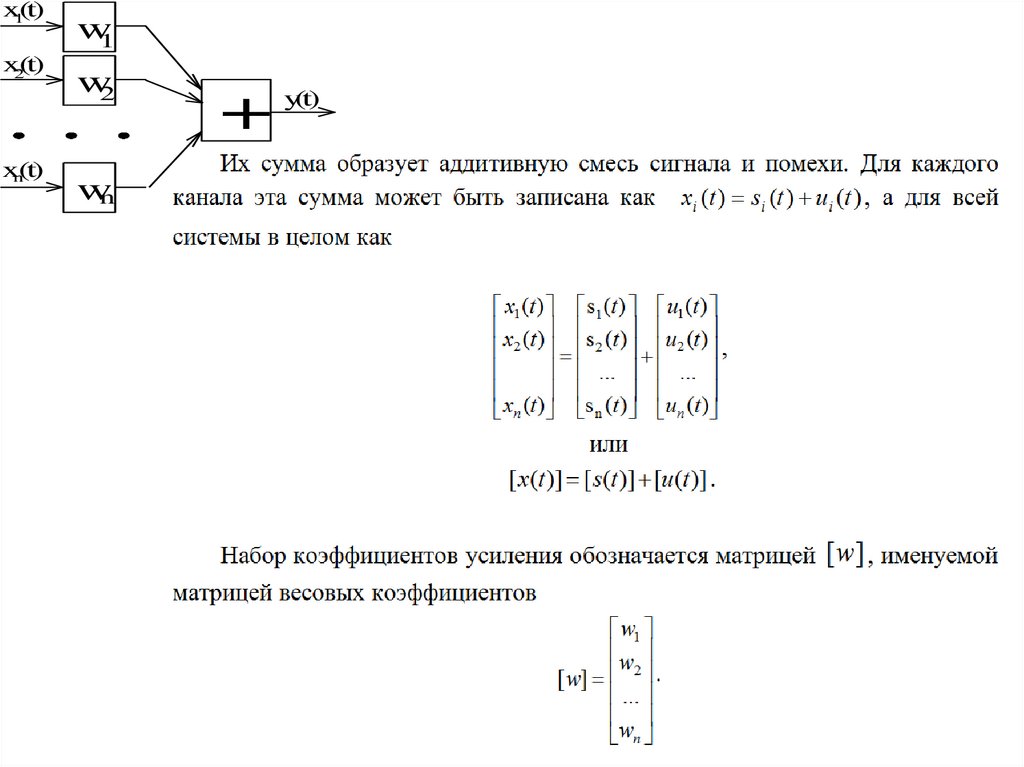
Сигналы на входах адаптивной системыx2 (t ) 2 cos( ct ) 1 cos( пt )
x1 (t ) 1 cos( ct ) 1 cos( пt )
X1
X2
33.
34.
35.
36.
37.
cos( ) cos( )1
1
cos( ) cos( )
2
2
38.
39.
40.
241.
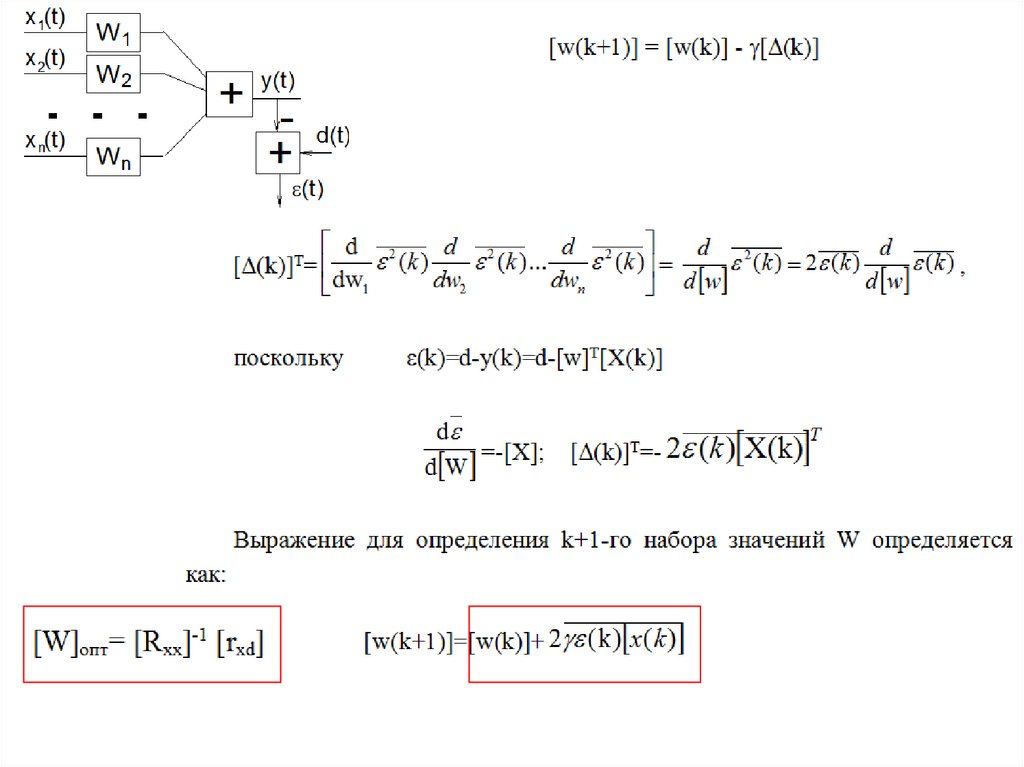
На предыдущем занятии была получена формула Винера-ХопфаСуществует два различных метода отыскания решения уравнения
Винера-Хопфа
1. Метод непосредственного обращения корреляционной матрицы (НОМ).
2. Градиентный метод.
Каждый из них имеет свои достоинства и недостатки, а также
ограничений по области применения.
42.
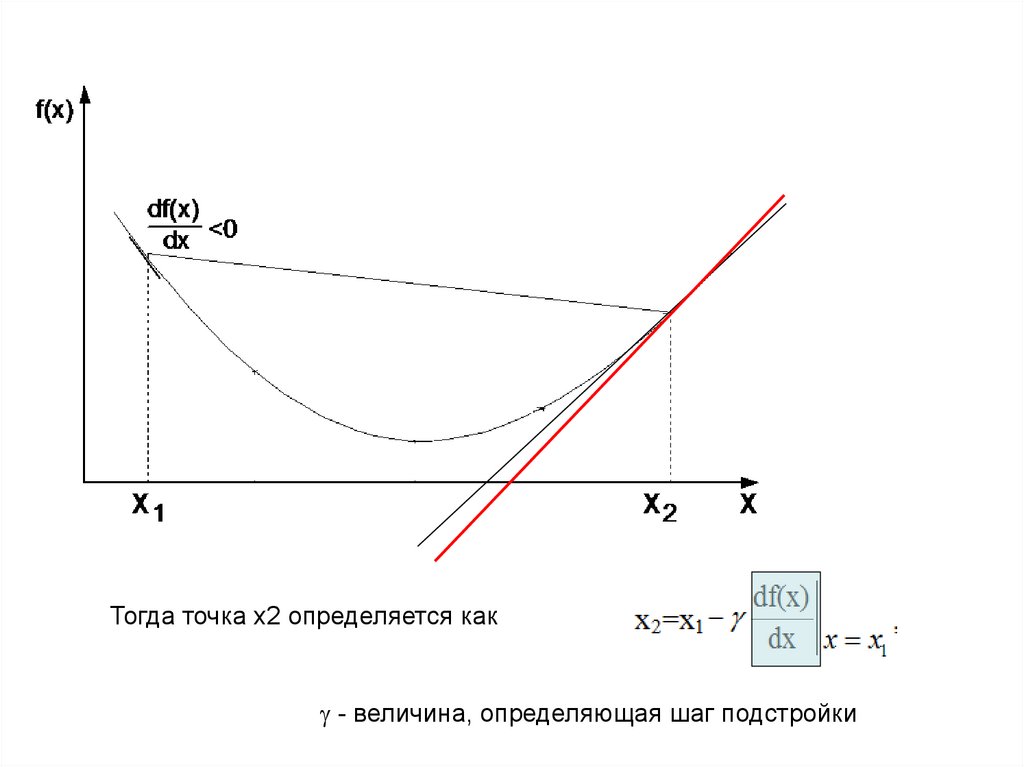
Градиентный метод (с математической точки зрения)Допустим, есть функция f(x), и у неё имеется экстремум (минимум). Его нужно
найти.
Выбирается произвольная точка x1 и в ней определяется производная (градиент)
43.
Тогда точка x2 определяется как- величина, определяющая шаг подстройки
44.
f(x)df(x)
dx <0
x1
x3
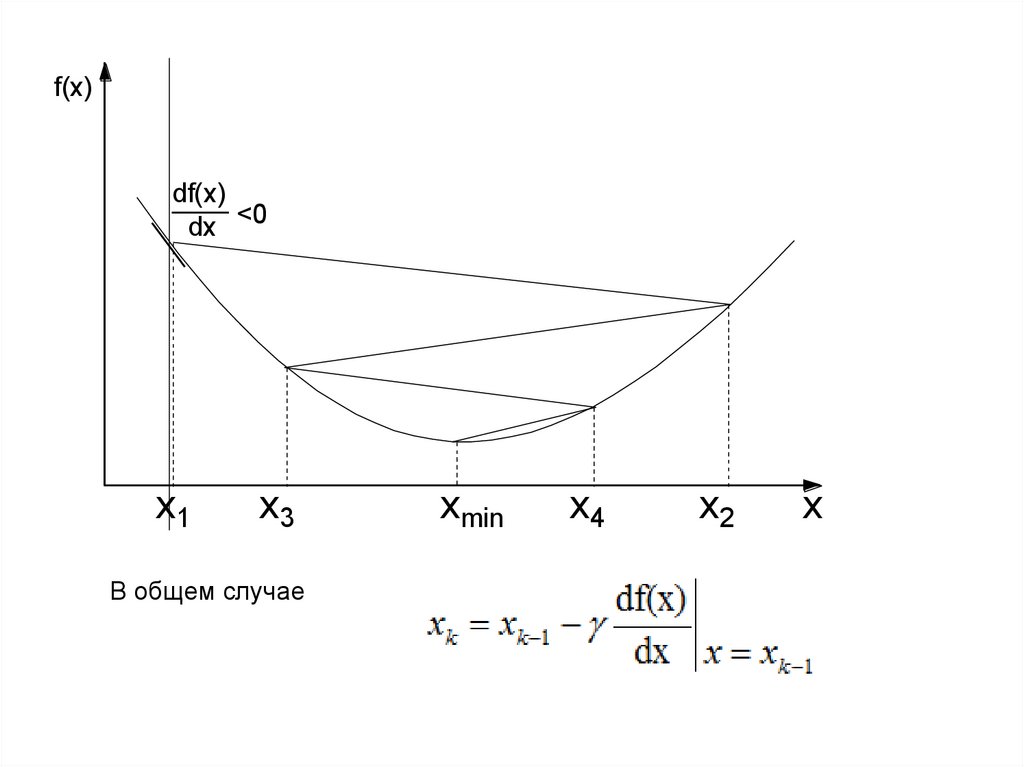
В общем случае
xmin
x4
x2
x
45.
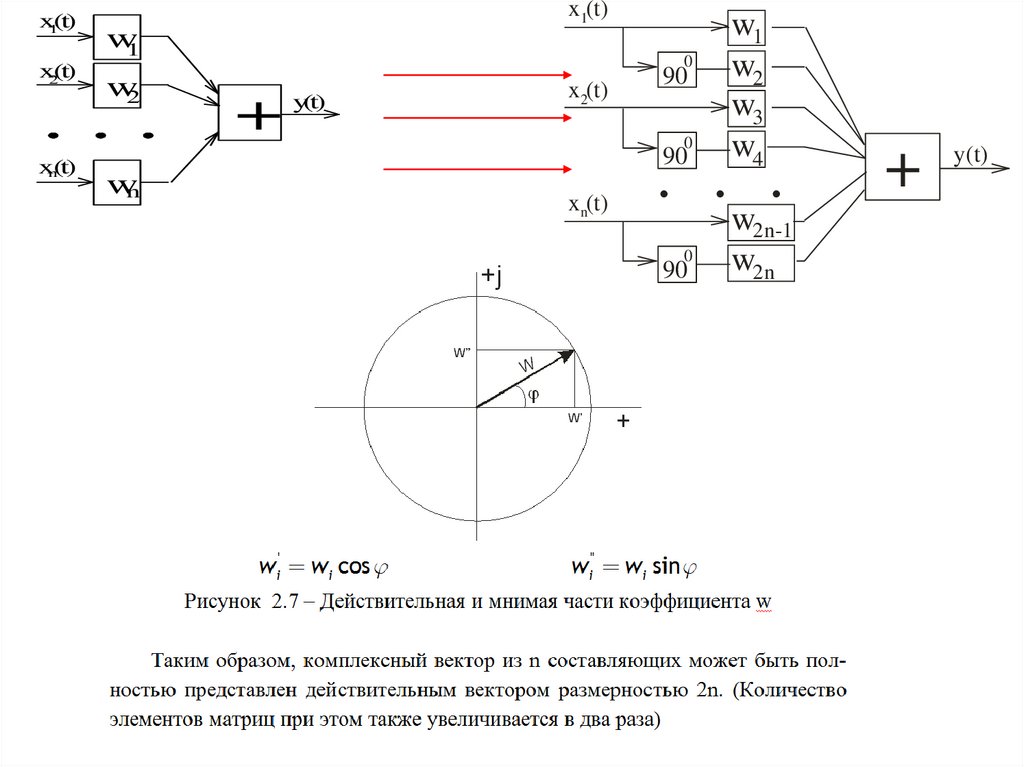
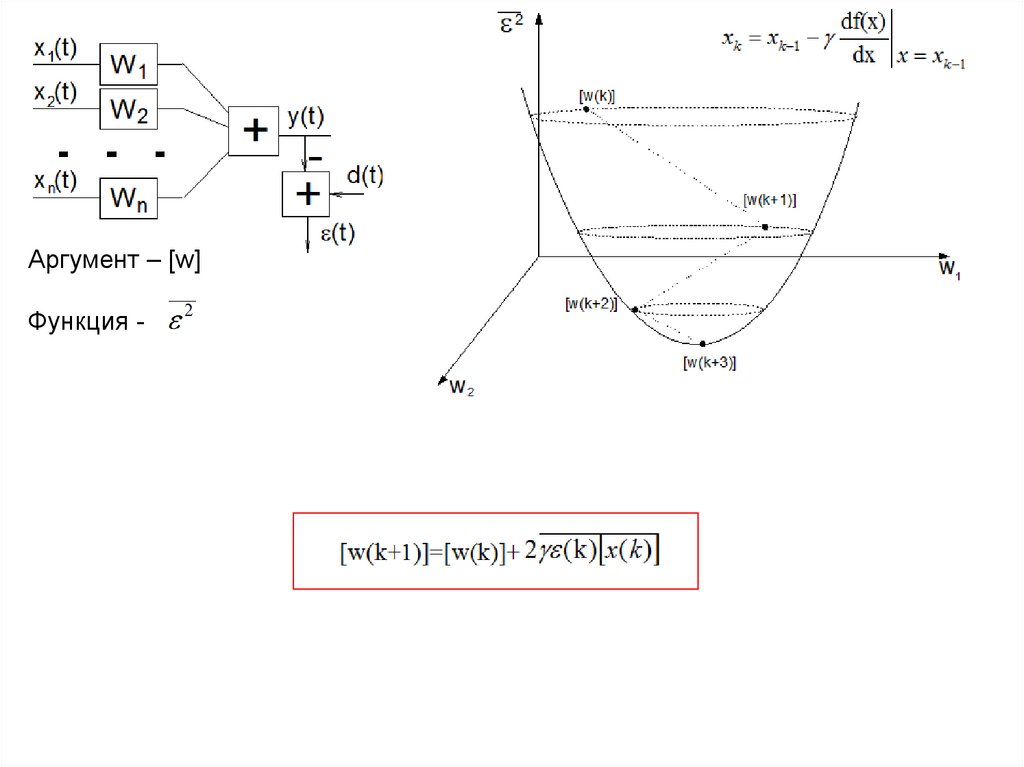
Аргумент – [w]Функция -
46.
47.
48.
49.
50.
51.
52.
Лекции 4.Практическая реализация методов.
Опорный сигнал
План лекции
1.
2.
3.
4.
Практическая реализация расчёта методом НОМ
Практическая реализация расчёта градиентным методом
Сравнительная характеристика методов
Опорный сигнал и способы его получения
53.
Аргумент – [w]Функция -
54.
55.
56.
57.
58.
59.
60.
61.
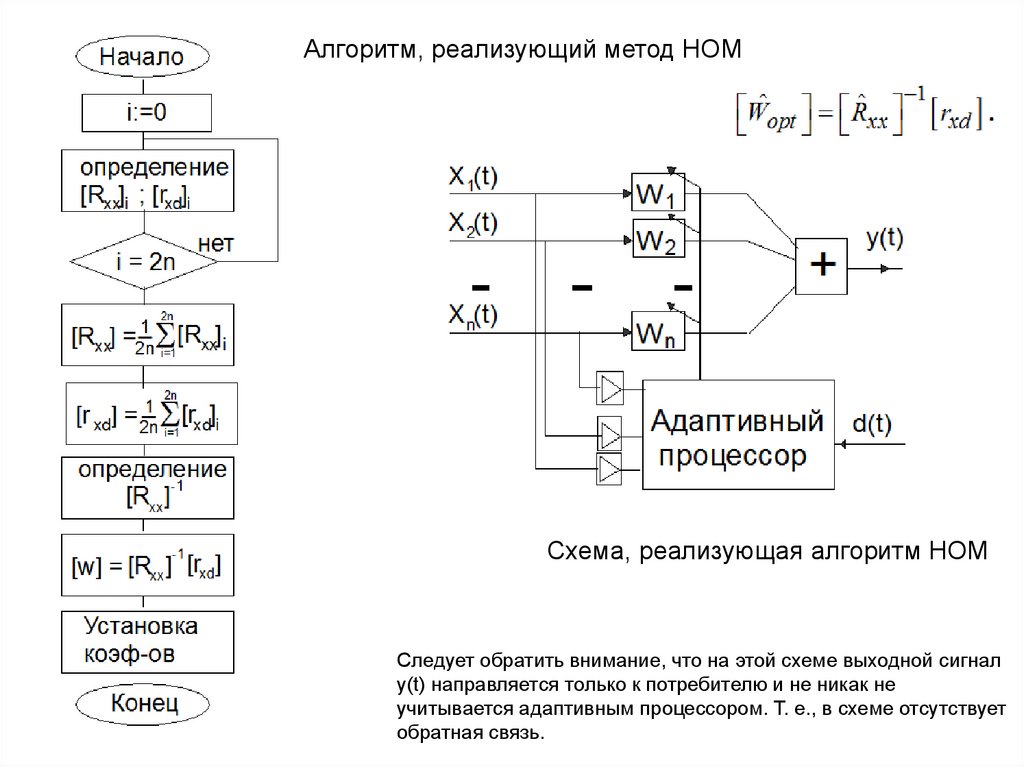
Алгоритм, реализующий метод НОМСхема, реализующая алгоритм НОМ
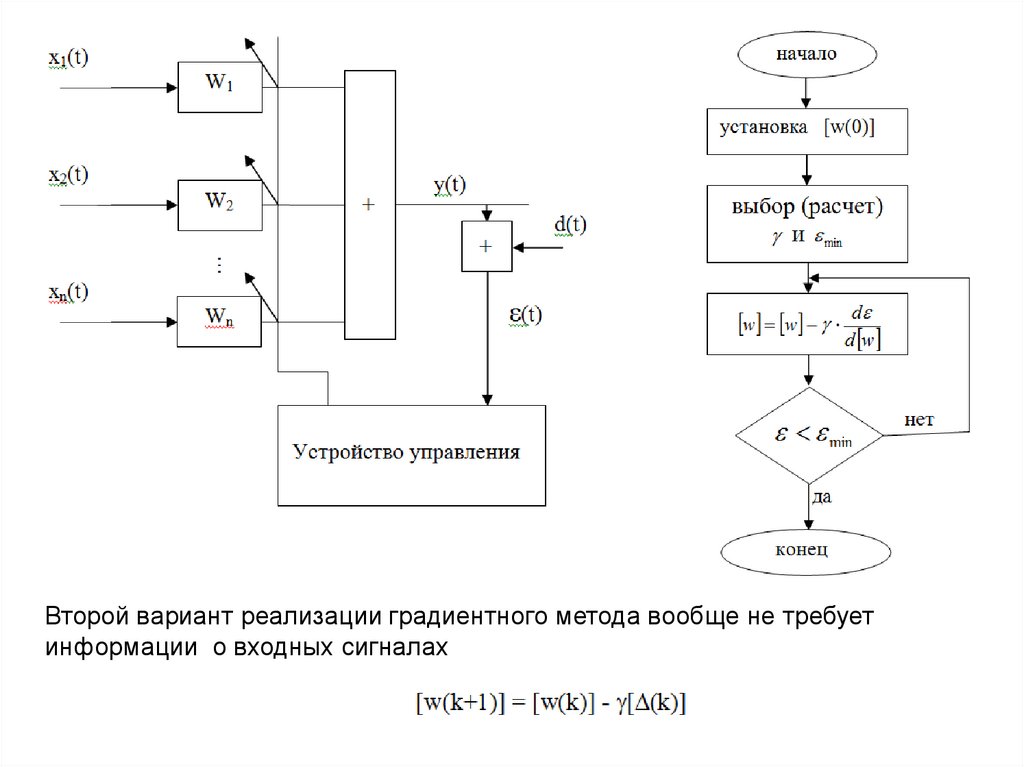
Следует обратить внимание, что на этой схеме выходной сигнал
y(t) направляется только к потребителю и не никак не
учитывается адаптивным процессором. Т. е., в схеме отсутствует
обратная связь.
62.
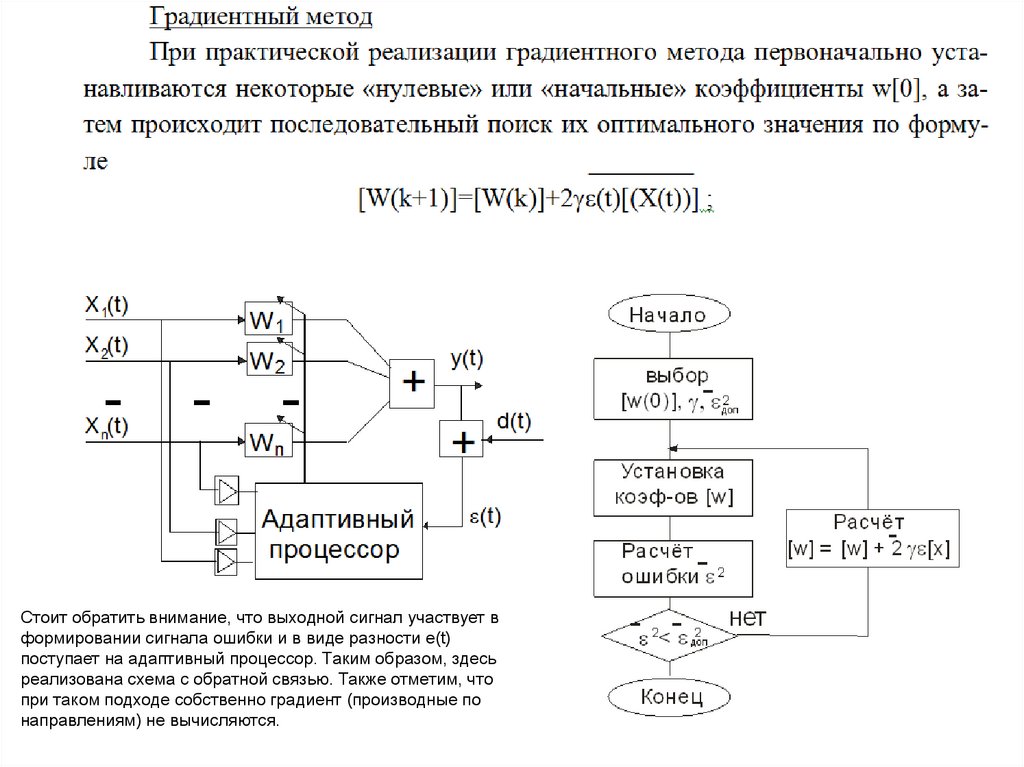
Стоит обратить внимание, что выходной сигнал участвует вформировании сигнала ошибки и в виде разности e(t)
поступает на адаптивный процессор. Таким образом, здесь
реализована схема с обратной связью. Также отметим, что
при таком подходе собственно градиент (производные по
направлениям) не вычисляются.
63.
Второй вариант реализации градиентного метода вообще не требуетинформации о входных сигналах
64.
65.
66.
d(t)? ? ?
t
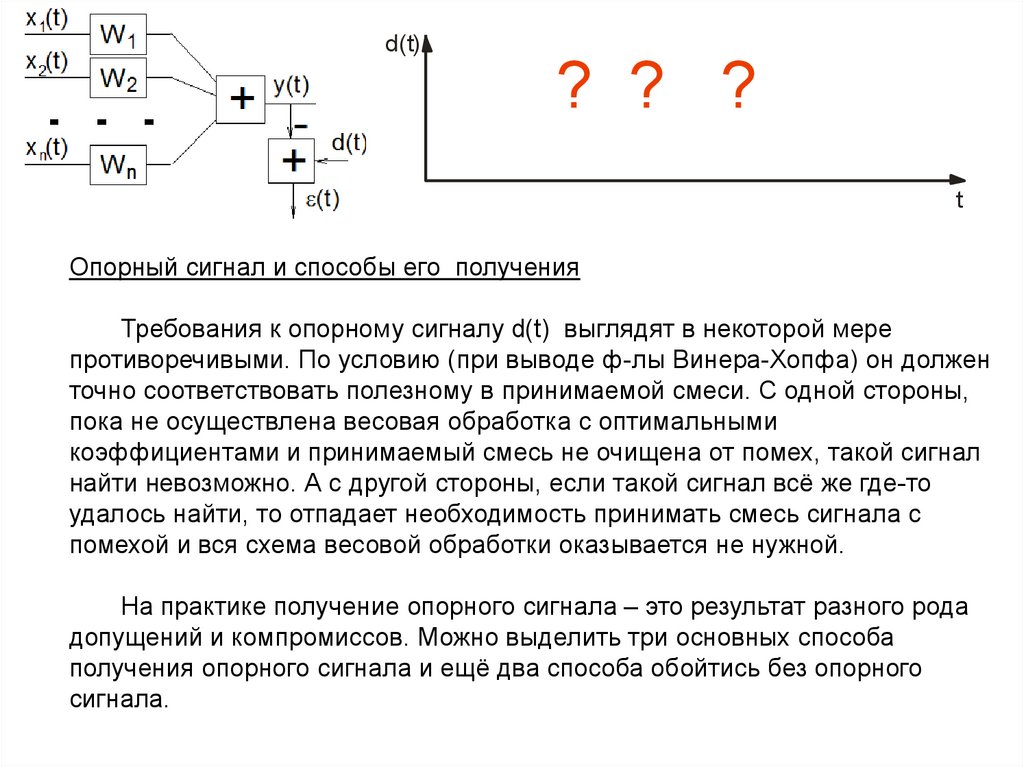
Опорный сигнал и способы его получения
Требования к опорному сигналу d(t) выглядят в некоторой мере
противоречивыми. По условию (при выводе ф-лы Винера-Хопфа) он должен
точно соответствовать полезному в принимаемой смеси. С одной стороны,
пока не осуществлена весовая обработка с оптимальными
коэффициентами и принимаемый смесь не очищена от помех, такой сигнал
найти невозможно. А с другой стороны, если такой сигнал всё же где-то
удалось найти, то отпадает необходимость принимать смесь сигнала с
помехой и вся схема весовой обработки оказывается не нужной.
На практике получение опорного сигнала – это результат разного рода
допущений и компромиссов. Можно выделить три основных способа
получения опорного сигнала и ещё два способа обойтись без опорного
сигнала.
67.
Опорный сигнал и способы его получения68.
69.
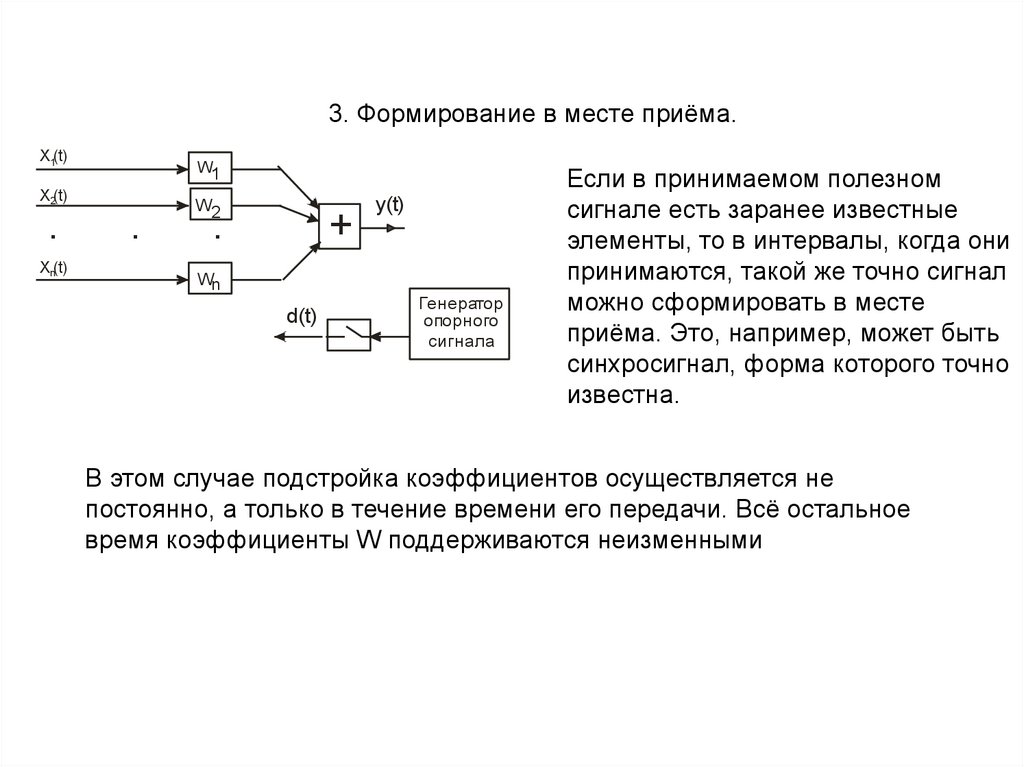
3. Формирование в месте приёма.X1(t)
W1
X2(t)
.
Xn(t)
.
W2
.
+
Wn
d(t)
y(t)
Генератор
опорного
сигнала
Если в принимаемом полезном
сигнале есть заранее известные
элементы, то в интервалы, когда они
принимаются, такой же точно сигнал
можно сформировать в месте
приёма. Это, например, может быть
синхросигнал, форма которого точно
известна.
В этом случае подстройка коэффициентов осуществляется не
постоянно, а только в течение времени его передачи. Всё остальное
время коэффициенты W поддерживаются неизменными
70.
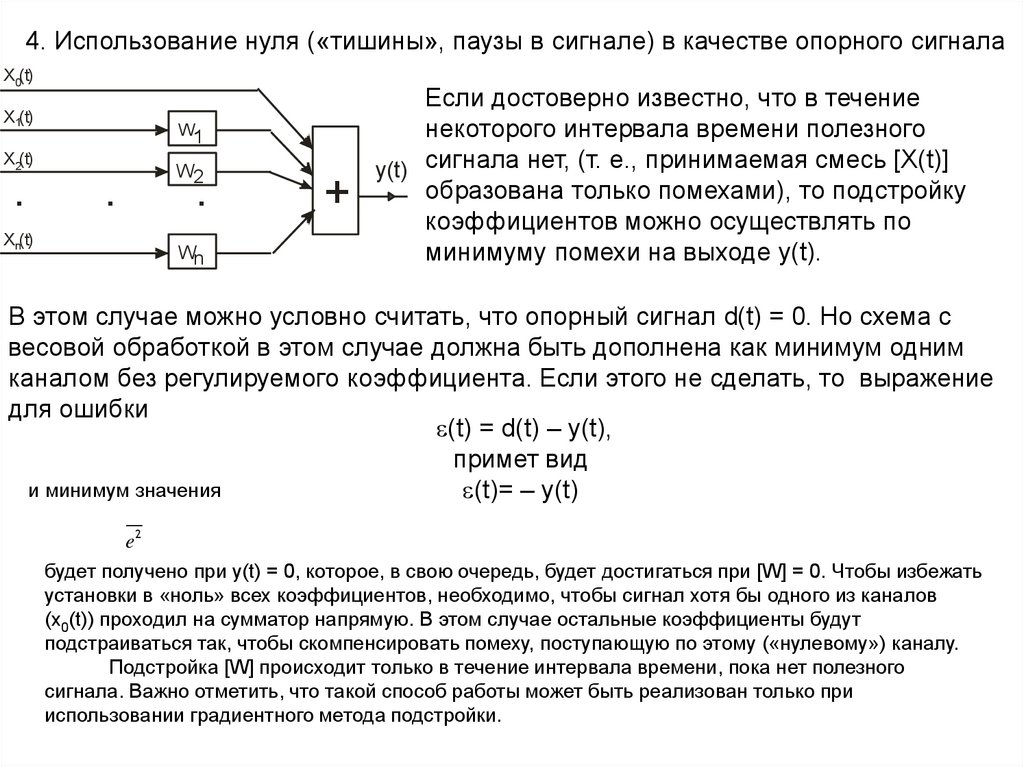
4. Использование нуля («тишины», паузы в сигнале) в качестве опорного сигналаX0(t)
X1(t)
W1
X2(t)
.
Xn(t)
.
W2
.
Wn
+
Если достоверно известно, что в течение
некоторого интервала времени полезного
y(t) сигнала нет, (т. е., принимаемая смесь [X(t)]
образована только помехами), то подстройку
коэффициентов можно осуществлять по
минимуму помехи на выходе y(t).
В этом случае можно условно считать, что опорный сигнал d(t) = 0. Но схема с
весовой обработкой в этом случае должна быть дополнена как минимум одним
каналом без регулируемого коэффициента. Если этого не сделать, то выражение
для ошибки
(t) = d(t) – y(t),
примет вид
и минимум значения
(t)= – y(t)
e2
будет получено при y(t) = 0, которое, в свою очередь, будет достигаться при [W] = 0. Чтобы избежать
установки в «ноль» всех коэффициентов, необходимо, чтобы сигнал хотя бы одного из каналов
(x0(t)) проходил на сумматор напрямую. В этом случае остальные коэффициенты будут
подстраиваться так, чтобы скомпенсировать помеху, поступающую по этому («нулевому») каналу.
Подстройка [W] происходит только в течение интервала времени, пока нет полезного
сигнала. Важно отметить, что такой способ работы может быть реализован только при
использовании градиентного метода подстройки.
71.
72.
X (t)+ х
W
Uп(t)
y (t)
73.
X (t)+ х
W
Uп(t)
y (t)
74.
Основное в лекции1. Сравнительная характеристика метода НОМ и градиентного
2. Опорный сигнал и способы его получения


























































 Информатика
Информатика








