Похожие презентации:
Теория возмущений. Плоский ротатор (основное состояние)
1.
Теория возмущений. Плоский ротатор (основное состояние)Уравнение Шрёдингера для заряженного 2D ротатора в однородном электрическом поле
Hˆ
z
E0
x
0
V ( ) E ( )
Невозмущённый гамильтониан
,q y
ˆ
l
Hˆ 0
, Hˆ 0 m(0) ( ) Em(0) m(0) ( )
2I
2 2
m
1
Em(0)
, I r 2 , m(0) ( )
eim
2I
2
2 2
z
«Возмущающий» потенциал
V ( ) q e qE0 r cos dE0 cos
2.
Основное (невырожденное) состояниеОбщие соотношения
Уравнение Шрёдингера
Hˆ
0
V l El l
«Невозмущённое» уравнение Шрёдингера
Hˆ 0 n(0) En(0) n(0)
Решение уравнения Шрёдингера
l cnl n(0)
n
Получить уравнение на коэффициенты разложения?
3.
1 шаг(0)
(0)
(0)
c
E
E
c
V
nl l n n nl n
n
n
2 шаг
dq
(0)
m
(q )
*
Уравнение Шрёдингера в представлении с.ф. невозмущённого гамильтониана
cml El Em(0) Vmn cnl ,
n
Vmn m V n dq
(0)
m
(q ) V (q ) n(0) (q )
*
4.
«Поправка» к l-ому уровню (возмущение «мало»)El El(0) El(1) El(2)
(1)
, cml ml cml
(0)
(cml
ml )
Нулевое приближение
(0)
El El(0) , cml cml
ml
Первое приближение (m=l)
cll(0)
E
(0)
l
El(1) El(0) Vln cnl(0) Vll
n
Поправка первого порядка к энергии l-ого уровня
El(1) Vll
5.
Основное состояние плоского ротатораEl(1)
0 V00 ?
6.
Второе приближение (m=l)c
(0)
ll
cll(1) El(0) El(1) El(2) El(0) Vln cnl(0) cnl(1) Vll Vln cnl(0) cnl(1)
n
n l
Или
cll(1) El(1) cll(0) El(2) Vln cnl(0) cnl(1)
n l
Надо знать коэффициенты разложения при несовпадающих индексах?
7.
Уравнение для коэффициентов разложения при несовпадающих индексах(1)
cml
El(0) Em(0) Vmncnl(0) Vml , m l
n
Или
(1)
cml
Vml
, m l
(0)
(0)
El Em
Условие применимости теории возмущений?
Коэффициент при m=l?
8.
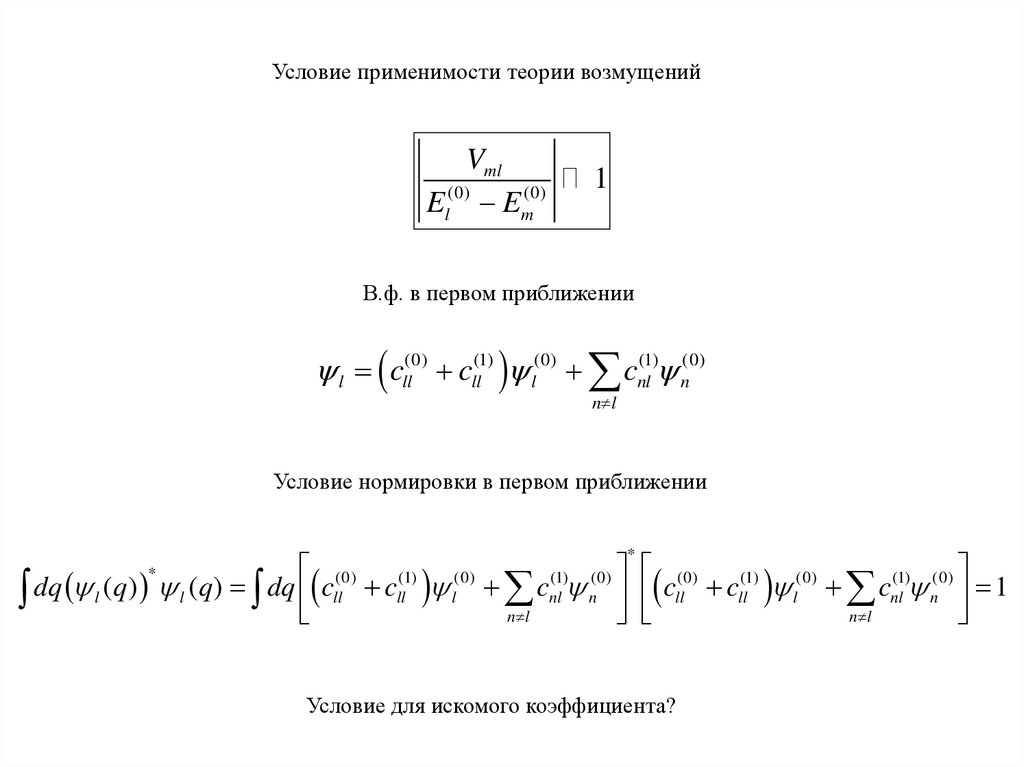
Условие применимости теории возмущенийVml
El(0) Em(0)
1
В.ф. в первом приближении
l cll(0) cll(1) l(0) cnl(1) n(0)
n l
Условие нормировки в первом приближении
*
(0)
(1)
(0)
(1) (0)
(0)
(1)
(0)
(1) (0)
dq
(
q
)
(
q
)
dq
c
c
c
c
c
c
l
l
nl
n ll
ll l
nl n 1
ll ll l
n l
n l
*
Условие для искомого коэффициента?
9.
Условие для искомого коэффициентаRe cll(1) 0 cll(0) cll(1) 1 i ei
В.ф. в первом приближении
l ei l(0) cnl(1) n(0)
n l
Выбираем фазовый множитель равным единице, т.е.
cll(1) 0
10.
Уравнение для поправки второго порядка к энергииcll(1) El(1) cll(0) El(2) Vln cnl(0) cnl(1)
n l
Или
El(2)
n l
VlnVnl
El(0) En(0)
11.
Основное состояние плоского ротатора. Поправка второго порядка к энергииE0(2)
n l
V0 nVn 0
E0(0) En(0)
2
(0)
m
E
m2
1
(0)
, m ( )
eim , V ( ) dE0 cos
2I
2
Вычислить матричные элементы?
2
Vmn
d
0
(0)
m
( ) V ( ) n(0) ( )
*
12.
Вспомогательные формулыdE0 i i
V ( ) dE0 cos
e e
2
2
Vmn
dE0
d e im ei e i ein
4 0
Vmn
dE0
m,n 1 m,n 1
2
Поправка второго порядка к энергии?
13.
Поправка второго порядка к энергииE0(2)
n l
V10
2
V0 nVn 0
V01V10 V0 1V 10
(0)
(0)
(0)
(0)
(0)
E0 En
E1
E 1
E1
Или
E0(2)
V10
2
(0)
1
E
d 2 E02 I
2


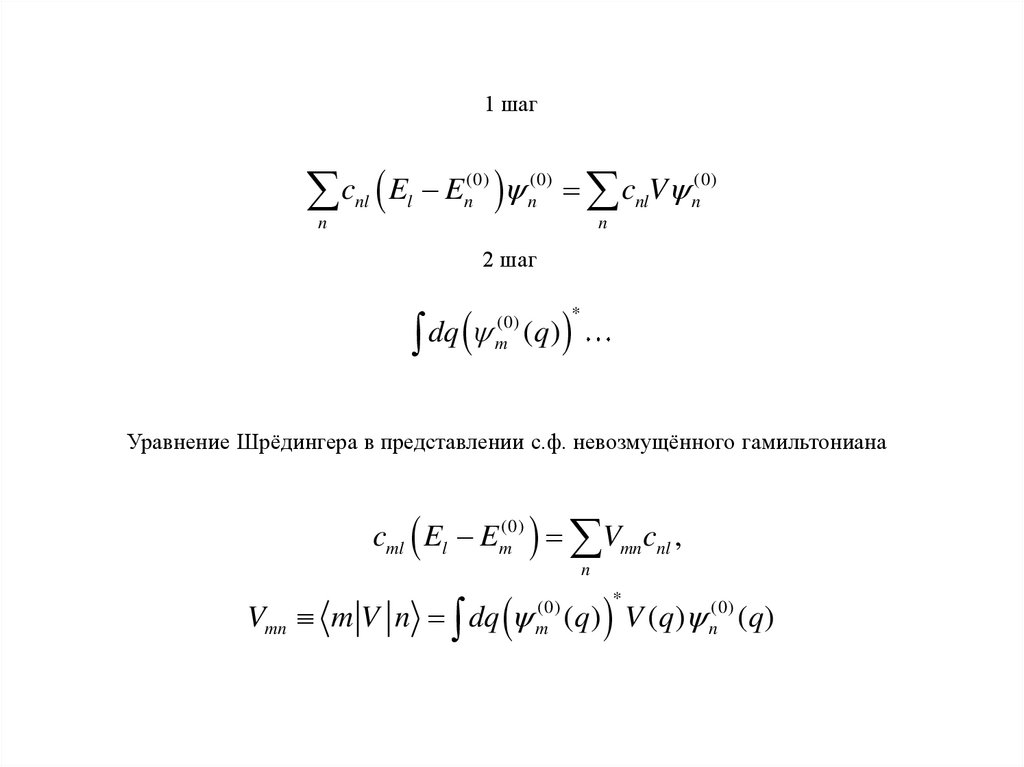









 Электроника
Электроника








