Похожие презентации:
Основные виды дискретной модуляции сигналов в телекоммуникациях (Общая теория связи, Лекция № 8)
1. Санкт- Петербургский государственный университет телекоммуникаций им. профессора М. А. Бонч-Бруевича Кафедра «Теории электрических цепе
Санкт- Петербургский государственный университет телекоммуникаций им. профессора М. А. Бонч-БруевичаКафедра «Теории электрических цепей и связи»
Факультет фундаментальной подготовки
Кафедра теории электрических цепей исвязи
(ТЭЦ и С)
Дисциплина
Общая теория связи
Лектор:
Заведующий кафедрой
Шумаков Павел Петрович
ОТС Лекция #8
1
2.
Санкт- Петербургский государственный университет телекоммуникаций им. профессора М. А. Бонч-БруевичаКафедра «Теории электрических цепей и связи»
Лекция № 8
Основные виды дискретной модуляции сигналов в
телекоммуникациях.
1.
2.
3.
4.
5.
Учебные вопросы:
Цифровая модуляция сигналов.
Сигналы с дискретной амплитудной модуляцией (АМн)
Дискретная частотная модуляция сигналов ЧМн
Дискретная фазовая модуляция сигналов ФМн.
Дискретная Квадратурная модуляция сигналов.
ОТС Лекция #7
2
3. Санкт- Петербургский государственный университет телекоммуникаций им. профессора М. А. Бонч-Бруевича Кафедра «Теоретических основ связи
и радиотехники»Литература:
Стр.
125..128, 129..136, 137..152;.
Используя MathCAD , создать временную
модель сигнала КАМ16:
Построить созвездие , изобразить
временную диаграмму при кодировании
двух байта, полученных от ДСЧ с порогом
0.5.
Рассчитать спектр используя функцию
быстрого преобразования Фурье (fft ) для
1024 отсчетов сигнала.
ОТС Лекция #8
3
4.
ОТС Лекция #84
5.
Стандартизованные аббревиатуры типов модуляцииКодовое обозначение
рус. Тип модуляции
сигнала
англ. Type of signal
modulation
quadrature phase shift
keying
CDM
компрессированная
дельта модуляция
companded delta
modulation
DQPSK
дифференциальная
QPSK (см. QPSK)
differential QPSK
adaptive delta
modulation
CFM
компрессированная
частотная модуляция
companded frequency
modulation
FFSK
фильтруемая частотная
манипуляция
filtred FSK
CFSK
M=2, 4
когерентная
частотная
манипуляция
coherent frequency
shift keying
FM
частотная модуляция
frequency modulation
CIM
частотная модуляция с
обратной связью
frequency modulation
feedback
импульсно-кодовая
модуляция
coded impulse
modulation
FMFB
частотная
манипуляция с
непрерывной фазой
FM-PM
частотно-фазовая
модуляция
frequency modulationphase modulation
FSK
частотная манипуляция
frequency shift keying
GFPM
частотно-позиционная
модуляция со
стробированием
gated frequency position
modulation
GMSK
минимальная
манипуляция с
гауссовым фильтром
или гауссовская
минимальная
манипуляция
gaussian filtered
minimum shift keying or
gaussian minimum shift
keying
GTFM
«прирученная»
частотная модуляция
generalized tamed
frequency modulation
HADM
гибридная аналоговоцифровая модуляция
hibrid analog and digital
modulation
HM
гибридная модуляция
или фоновая
модуляция
hibrid modulation or
hum modulation
QPSK
квадратурная фазовая
манипуляция
ADM
адаптивная
дельта-модуляция
ADPCM
адаптивная дифференц adaptive differntial
иальная импульсно-ко pulse code modulation
довая модуляция
ADSM
асинхронная
сигма-дельта-модуляц
ия
asynchronous delta
sigma modulation
AFM
амплитудно-частотная amplitude-frequency
модуляция
modulation
CPFSK
APCM
адаптивная
adaptive pulse-code
импульсно-кодовая мо modulation
дуляция
CPM
APK
амплитудно-фазовая amplitude phase keying
манипуляция (система
(keyed-system)
манипуляции)
APM
амплитудно-фазовая
модуляция
amplitude phase
modulation
APSK
амплитудно-фазовая
манипуляция
amplitude phase shift
keying
BCFSK
частотная
манипуляция
двоичным кодом
binary code frequency
shift keying
BDM
двоичная дельта
модуляция
BDPSK
двоичная
дифференциальная
фазовая манипуляия
binary differential phase
shift keying
BFSK
двоичная частотная
манипуляция
binary frequency shift
keying
BPSK
двоичная фазовая
манипуляция
binary phase shift
keying
CPSK
C4FM
CAP
амплитудно-фазовая
модуляция без
несущей
Carrierless AM-PM
CASK
M=16
когерентая
амплитудная
манипуляция
coherent amplitude
shift keying BIPOLAR
CASK M=2
когерентая
амплитудная
манипуляция
однополярная
coherent amplitude
shift keying UNIPOLAR
когерентная фазовая coherent phase shift
манипуляция
keying
CQPSK
coherent quadriphase
shift keying
DDM
относительная
дискретная
модуляция
difference discrete
modulation
DECPSK
дифференциальноdifferentially encoded
кодированная
coherent phase shift
когерентная фазовая keying
манипуляция
дифференциальнокодированная
фазовая
манипуляция
differential encoded
phase shift keying
DFSK
двойная частотная
манипуляция
double frequency shift
keying
DM
дельта модуляция
delta modulation
LDM
линейная дельтамодуляция
linear delta modulation
DMT
многотоновая
модуляция
(Дискретный
мультитон)
Multitone modulation
(discrete Multitone)
LPCM
линейная импульснокодовая модуляция
linear pulse code
modulation
DPCM
дифференциальная
импульсно-кодовая
модуляция
differential pulse-code
modulation
MFKP
многочастотная
манипуляция
multi-frequency key
pulsing
MFSK
многократная или
многоуровневая
частотная манипуляция
DEPSK
continuous 4-level
frequency modulation
фазовая модуляция с continuous phase
непрерывной фазой modulation
когерентная
четвертичная
фазовая
манипуляция
binary delta modulation
непрерывная
четырёхуровневая
частотная модуляция
continuous phase
frequency shift keying
DPCM
дельта импульснокодовая модуляция
delta pulse-code
modulation
DPM
дифференциальная
фазовая модуляция
differential phase
modulation
DPPM
дифференциальная
импульснопозиционвая
модуляция
differential pulse
position modulation
DPSK
M=2(4,8,
16)
дифференциальная
фазовая
манипуляция
differential phase shift
keying
multiple or multilevel FSK
MPSK
многократная фазовая
манипуляция
multiple PSK
MSK
минимальная
манипуляция
minimum shift keying
NBFM
узкополосная частотная narrow-band frequency
модуляция
modulation
NCASK
M=2
некогерентая
амплитудная
манипуляция
PSK
фазовая
манипуляция
phase shift keying
NCFSK
M=2 (4,
8)
PTM
ШИМ и фазовременная
модуляция
pulse time
modulation and
phase time
modulation
некогерентная
частотная
манипуляция
QAM m=4
(16)
квадратурноамплитудная
модуляция
quadrature
amplitude
modulation
OQPSK
квадратурно-фазовая
манипуляция со
offset QPSK
сдвигом (частоты)
QM
квадратурная
модуляция
quadrature
modulation
PACM
амплитудная
импульсно-кодовая
модуляция
QPAM
АИМ с
квантованием
quantized pulse
amplitude
modulation
PAM
амплитудно-фазовая
модуляция,
phase amplitude
амплитудноmodulation, pulseимпульсная
amplitude modulation
модуляция АИМ
QPSK
квадратурнофазовая
манипуляция
quadrature phase
shift keying
QPSK
четвертичнофазовая
манипуляция
quaternary phase
shift keying
PBM
пакетно-импульсная
модуляция
RPSK
относительная
фазовая
манипуляция
relative phase shift
keying
PCM-FM
ИКМ-ЧМ (импульсно- pulse-code frequency
кодовая модуляция)
modulation
SDM
статистическая
дельта модуляция
statistic delta
modulation
PDBM
двоичная фазоимпульсная
модуляция
pulse delay binary
modulation
SFM
ЛЧМ и
swept frequency or
пространственная space frequency
частотная
modulation
модуляция
PDM-FM
ШИМ-ЧМ (широтноимпульсная
модуляция)
pulse-frequency
modulation
SIDM
дельта модуляция
single integration
с единичной
delta modulation
интеграцией
PFM
ЧИМ (частотноимпульсная
модуляция)
pulse frequency
modulation
SQFM
симметричная
квадратичная
частотная
модуляция
symmetric
quadratic
frequency
modulation
PFSK
PHDM
частотно-фазовая
манипуляция
phase frequency shift
keying
фазо-разностная
модуляция
phase difference
modulation
SQPS
ступенчатая
квадратурнофазовая
манипуляция
PIM
ФИМ (фазоимпульсная
модуляция)
pulse interval
modulation
staggered QPSK
SSM
модуляция с
расширенным
спектром
PM
фазовая модуляция
phase modulation
spread spectrum
modulation
PNM
импульсно-числовая
модуляция
pulse number
modulation
SSPSK
фазовая
манипуляция с
расширенным
спектром
spread spectrum
phase shift keying
PPBM
двоичная
поляризационноимпульсная
модуляция
pulse polarization
binary modulation
TFM
управляемая
частотная
модуляция
tamed frequncy
modulation
PPM
фазо-импульсная
модуляция
pulse phase
modulation
WBFM
широкополосная
частотная
модуляция
wideband
frequency
modulation
PRM
ЧИМ (частотноимпульсная
модуляция)
pulse rate modulation
ОТС Лекция #8
nocoherent amplitude
shift keying
nocoherent frequency
shift keying
pulse amplitude code
modulation
pulse burst modulation
5
6.
Цифровая модуляцияДискретная модуляция – сигнал на выходе модулятора дискретный.
Если на входе дискретного модулятора сигнал дискретный, то производится манипуляция параметров
несущего колебания конечным числом значений модулирующего сигнала m=1,2,3…M и модуляция
называется цифровой.
В частном случае, когда модулирующим является двоичный сигнал (значения 0 и 1) цифровая модуляция
называется манипуляцией.
ОТС Лекция #8
6
7.
Критерии сравнения эффективности различных видов модуляцииТеоретически, величиной, характеризующей эффективность цифровой системы связи, является пропускная
способность C[бит/с]. Пропускная способность характеризует количество информации, которое может быть
передано в системе связи в единицу времени (со 100% достоверностью).
Верхняя граница пропускной способности в системе при заданном отношении сигнал/шум и доступной
полосе передачи устанавливается теоремой Шеннона:
C =ΔF log2 (1+S/N),
где C – пропускная способность (бит/с), ΔF – доступная ширина полосы пропускания системы (Гц),
S – средняя мощность принятого сигнала,
N – средняя мощность шума.
Однако,средняя мощность шума зависит от ширины полосы: N= N0ΔF ,
где N0 – спектральная плотность мощности шума.
При исследовании систем связи обычно оперируют не отношением сигнал/шум, а величиной
Eb / N 0
– отношением энергии бита к плотности мощности шума, т.к. получаемые при этом соотношения содержат
минимальное количество вторичных величин. Энергия бита – энергия, необходимая для передачи одного бита
информации, равная произведению мощности передатчика на длительность бита Eb=PTb =U2Tb .
Чем больше Eb / N 0 , тем больше информации можно передавать в одной и
той же полосе.
Чем меньше Eb / N 0 , тем большая полоса потребуется для передачи
одинакового количества информации в единицу времени.
ö
Eb D F æ DCF
=
2
1
ç
÷
N0
C è
ø
ОТС Лекция #8
7
8.
Существует два основных критерия сравнения эффективности различных видов модуляции:критерий спектральной эффективности
критерий энергетической эффективности.
Спектральная эффективность характеризует полосу частот, необходимую для передачи информации с
определенной скоростью.
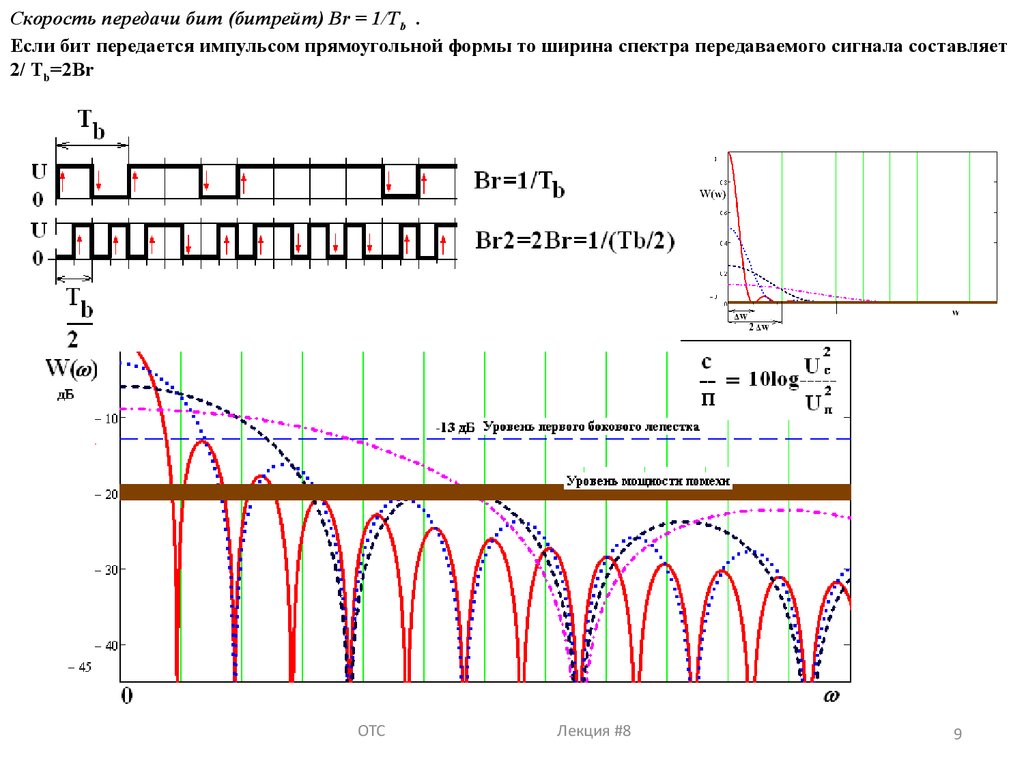
Скорость передачи бит (битрейт) Br = 1/Tb .
Если бит передается импульсом прямоугольной формы то ширина спектра передаваемого сигнала составляет
2/ Тb=2Br
Энергетическая эффективность описывает мощность, необходимую
для передачи информации с заданной достоверностью (вероятностью ошибки).
ОТС Лекция #8
8
9.
Скорость передачи бит (битрейт) Br = 1/Tb .Если бит передается импульсом прямоугольной формы то ширина спектра передаваемого сигнала составляет
2/ Тb=2Br
ОТС Лекция #8
9
10.
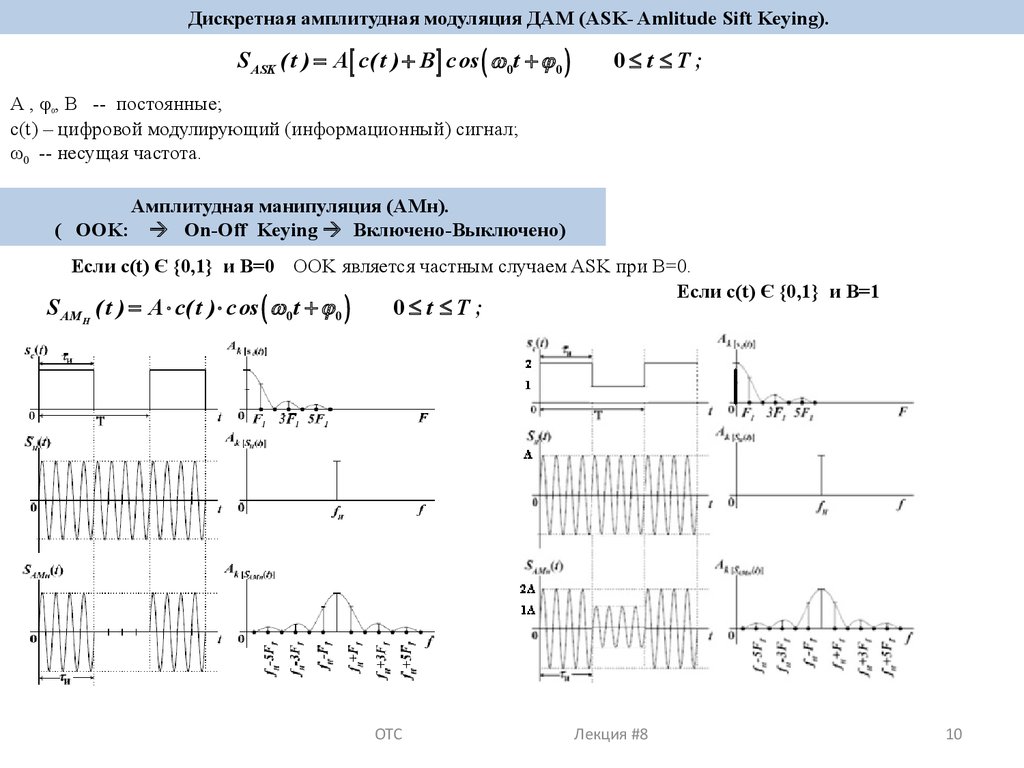
Дискретная амплитудная модуляция ДАМ (ASK- Amlitude Sift Keying).S ASK ( t ) = A [ c( t ) + B ] c os ( w 0 t + j 0 )
0£ t £T ;
А , φ , B -- постоянные;
c(t) – цифровой модулирующий (информационный) сигнал;
ω0 -- несущая частота.
0
Амплитудная манипуляция (АМн).
( OOK: On-Off Keying Включено-Выключено)
Если с(t) Є {0,1} и B=0 OOK является частным случаем ASK при B=0.
Если с(t) Є {0,1} и B=1
S AM H ( t ) = A × c( t ) × c os ( w 0 t + j 0 )
0£ t £T ;
ОТС Лекция #8
10
11.
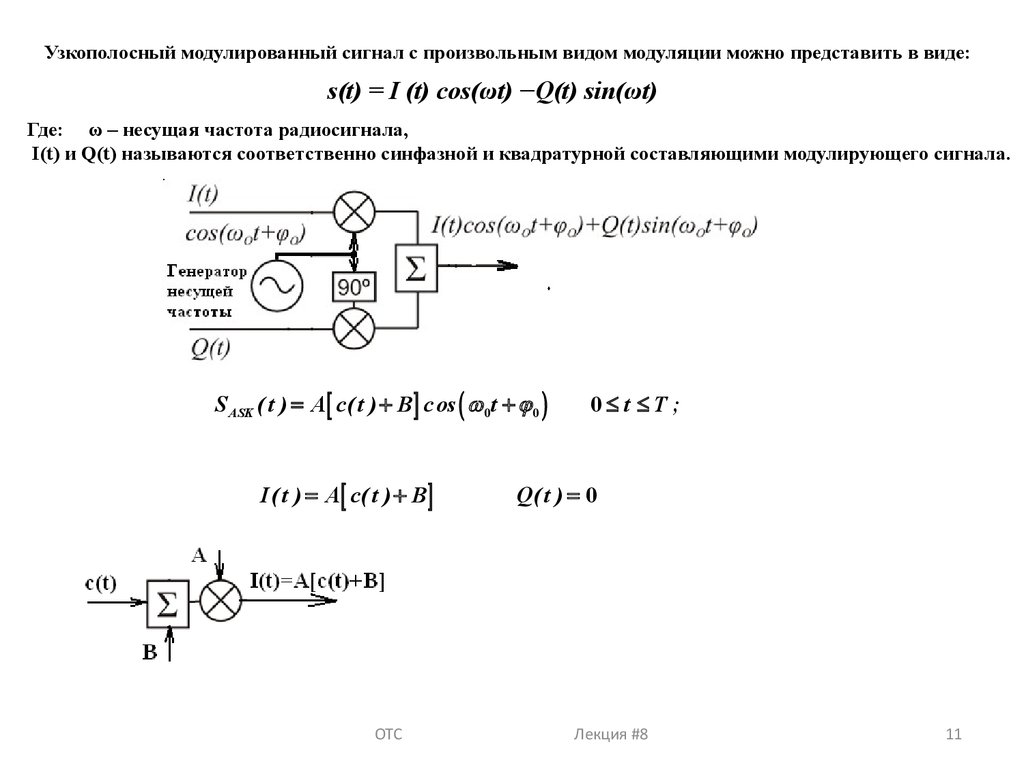
Узкополосный модулированный сигнал с произвольным видом модуляции можно представить в виде:s(t) = I (t) cos(ωt) −Q(t) sin(ωt)
Где: ω – несущая частота радиосигнала,
I(t) и Q(t) называются соответственно синфазной и квадратурной составляющими модулирующего сигнала.
S ASK ( t ) = A [ c( t ) + B ] c os ( w 0t + j 0 )
I( t ) = A [ c( t ) + B ]
0£ t £T ;
Q( t ) = 0
ОТС Лекция #8
11
12.
Cигнальное созвездие(constellation)
Множество возможных значений квадратурных компонент I(t) и Q(t) называется сигнальным созвездием.
Данное множество отображают на декартовой плоскости.
По оси абсцисс отложены значения синфазной составляющей I(t), а по оси ординат – квадратурной Q(t).
Точка на плоскости с координатами (x,y) соответствует состоянию сигнала, в котором синфазная составляющая
равна x, квадратурная равна y.
Таким образом, сигнальное созвездие – это диаграмма возможных состояний сигнала.
Амплитуда модулированного радиосигнала в текущем состоянии равна: A2(t) = I 2 (t) +Q2 (t) ,
а фаза равна углу вектора, указывающего в точку (I,Q), отсчитываемого от оси абсцисс в положительном
направлении (против часовой стрелки).
сигнальное созвездие модуляции OOK
сигнальное созвездие модуляции ASK
ОТС Лекция #8
12
13.
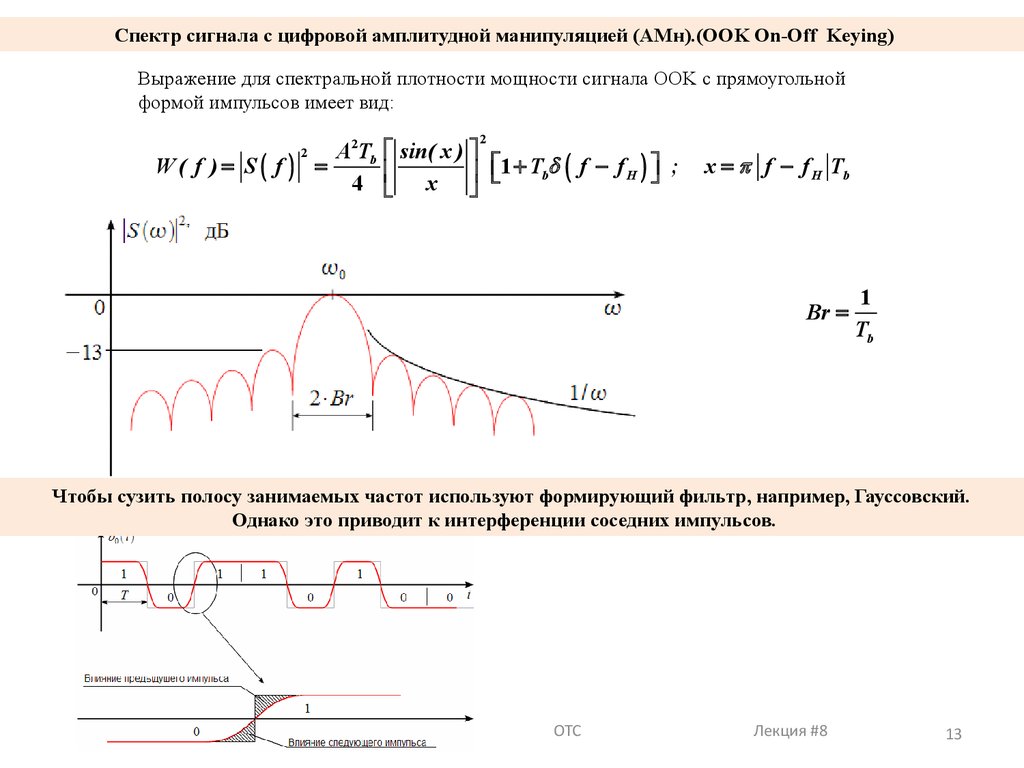
Спектр сигнала с цифровой амплитудной манипуляцией (АМн).(OOK On-Off Keying)Выражение для спектральной плотности мощности сигнала OOK с прямоугольной
формой импульсов имеет вид:
W( f )= S( f )
2
2
A2Tb é sin( x ) ù
é1 + Tbd ( f - f H ) ùû ;
=
4 êë x úû ë
x = p f - f H Tb
Br =
1
Tb
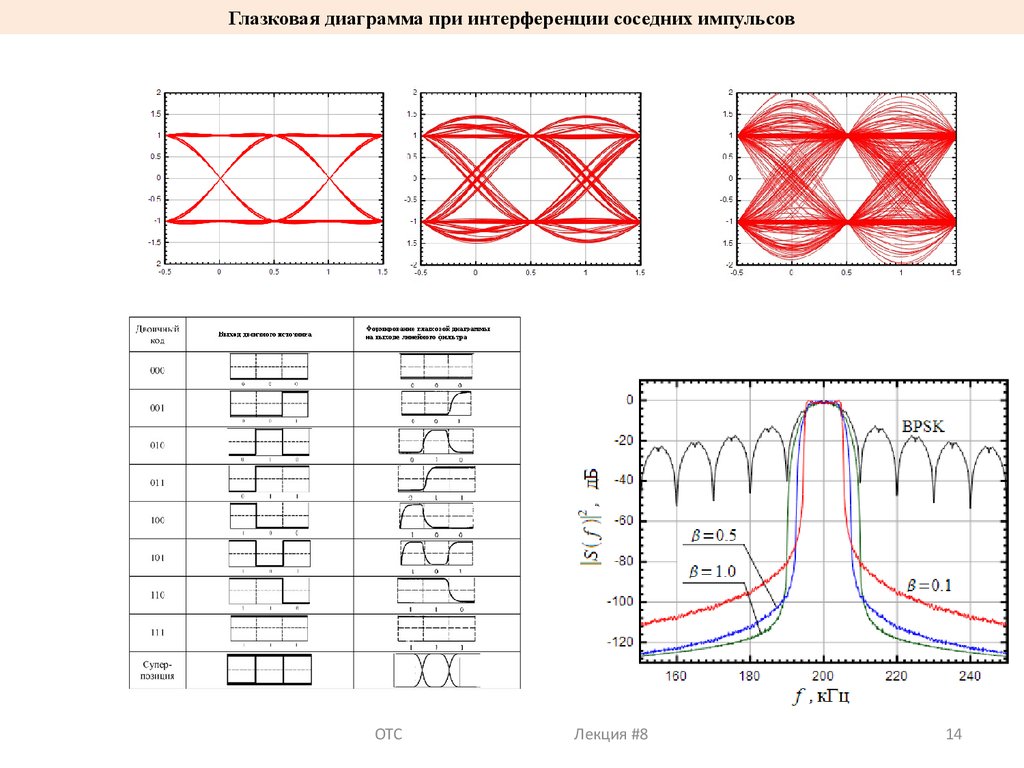
Чтобы сузить полосу занимаемых частот используют формирующий фильтр, например, Гауссовский.
Однако это приводит к интерференции соседних импульсов.
ОТС Лекция #8
13
14.
Глазковая диаграмма при интерференции соседних импульсовОТС Лекция #8
14
15.
ОТС Лекция #815
16.
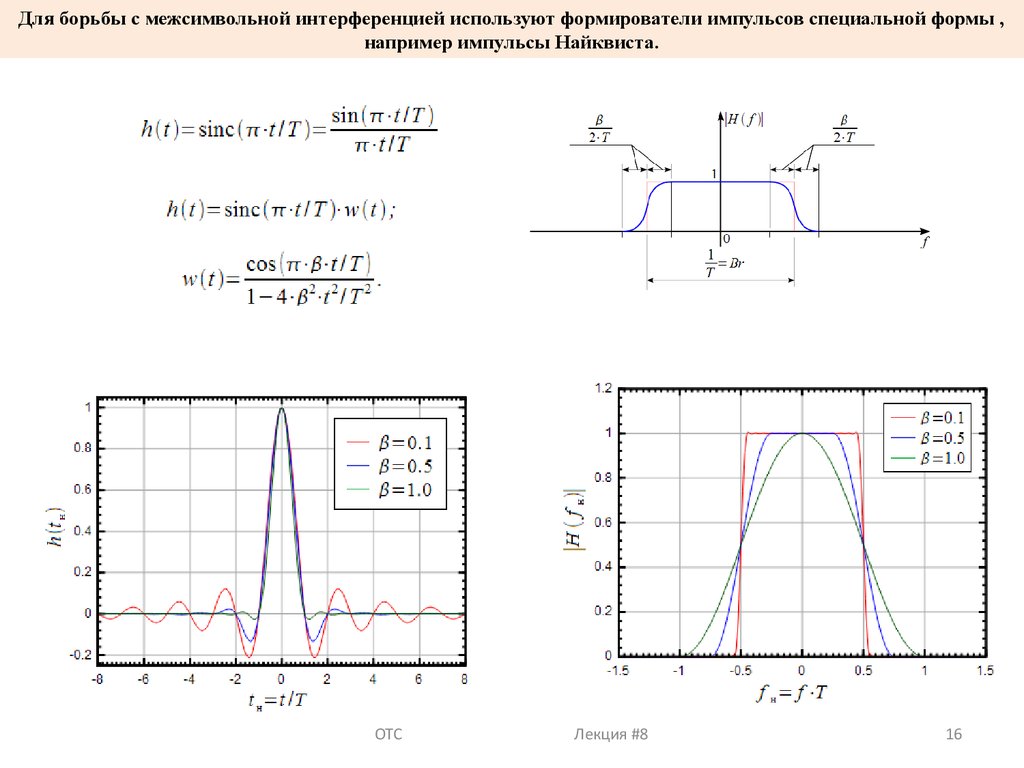
Для борьбы с межсимвольной интерференцией используют формирователи импульсов специальной формы ,например импульсы Найквиста.
ОТС Лекция #8
16
17.
Многосимвольная Амплитудная манипуляция (M-ASK)Математическая модель ДАМ сигнала
S DAÌ ( t ) = Re é Am × b( t ) × e
ë
j éëw0 t +j 0 ùû
ù = Am × b( t ) × cos ( w0t + j 0 )
û
0 £ t £ T ; m = 1..M
Am = (2m-1-M)d амплитуда сигнала , принимает M=2k вещественных положительных и отрицательных значений k=1,2,3,…;
2d - минимальное расстояние между двумя соседними амплитудами.
b(t) - управляющий вещественный сигнал в виде прямоугольного импульса либо импульса Найквиста.
–комплексное несущее колебание
j éëw0 t +j 0 ùû
e
При модуляции ASK множество возможных значений амплитуды радиосигнала ограничивается двумя
значениями. Для повышения спектральной эффективности можно использовать большее количество значений
амплитуды радиосигнала.
Сгруппируем биты исходного информационного сообщения в пары. Каждая такая пара называется символом.
Если каждый бит имеет множество значений {0,1}, то каждый символ имеет четыре возможных значения из
множества {00, 01, 10, 11}.
Сопоставим каждому из возможных значений символа значение амплитуды радиосигнала из множества
{0, A, 2A, 3A}.
Аналогичным образом можно группировать тройки, четверки и большее количество бит в одном символе.
Получится многоуровневый (многопозиционный) сигнал M-ASK с размерностью множества возможных значений
амплитуды сигнала M =2k , где k – число бит в одном символе.
Например, сигнал с модуляцией 8-ASK имеет 8 возможных значений амплитуды сигнала и 3 бит в одном символе.
сигнал с модуляцией 256-ASK имеет 256 возможных значений амплитуды сигнала и 8 бит в одном символе.
Спектральная плотность мощности
сигнала M-ASK вычисляется по
формуле аналогичной АМн с заменой
битового интервала Tb символьным
интервалом Ts
ОТС Лекция #8
=Tb log 2M
17
18.
Частотная манипуляция (ЧМн)(FSK)
Частотный модулятор без памяти
Недостатки
1. Требуется «мгновенный» ключ
2. При произвольной фазе генераторов – скачки фазы расширяют спектр
ОТС Лекция #8
18
19.
Частотная манипуляция с непрерывной фазой(CPFSK)
ЧМн (FSK) сигналы являются частным случаем сигналов с частотной модуляцией ЧМ ( FM ) при модулирующем сигнале в виде
двоичной битовой последовательности .
Квадратурный ЧМ модулятор
Частота девиации задает полосу сигнала (ширину спектра) на выходе модулятора
wd = 2 × p
Br
× m = p × Br × m
2
(t )=
2×p
Br
= W b = 2 × p × Fb
2
m=
wd
Wb
•m
индекс ЧМн (FSK)
t
ò w ( t )dt + j
-¥
0
w(t)=d /dt
Так как фаза непрерывна то и частота не будет иметь разрывов
ОТС Лекция #8
19
20.
Cпектр ЧМн (FSK) сигналаb0 ( t ) = bH ( t ) + bH ( t )
s( t ) = s H ( t ) + s L ( t )
sH ( t ) = bH ( t ) × cos éë( w0 + wd )t ùû
sL ( t ) = bL ( t ) × cos éë( w0 - w d )t ùû
S( w ) = S H ( w ) + S L ( w )
ОТС Лекция #8
20
21.
Cпектр ЧМн (FSK) сигналаb0 ( t ) = bH ( t ) + bH ( t )
S( w ) = S H ( w ) + S L ( w )
ОТС Лекция #8
21
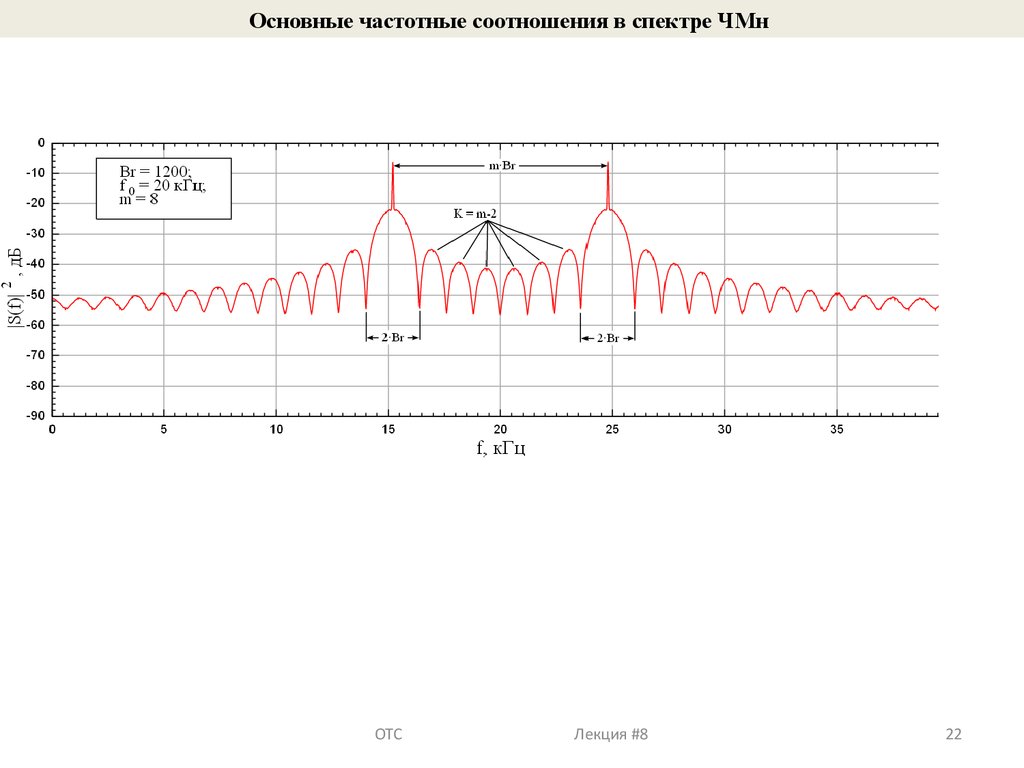
22.
Основные частотные соотношения в спектре ЧМнОТС Лекция #8
22
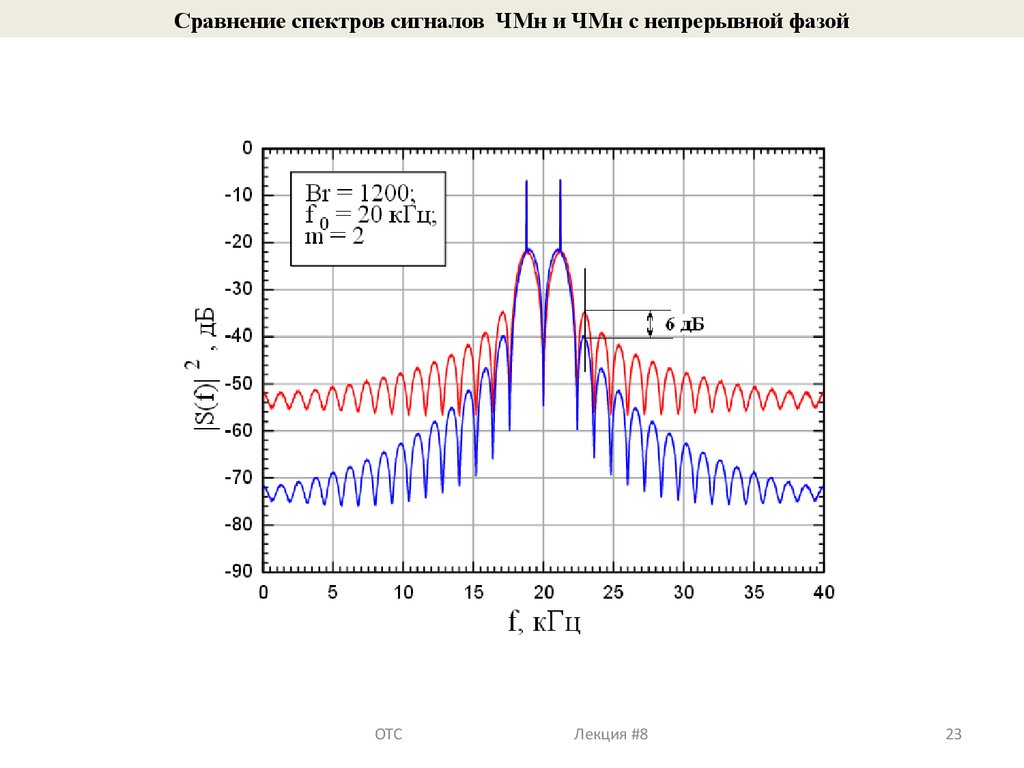
23.
Сравнение спектров сигналов ЧМн и ЧМн с непрерывной фазойОТС Лекция #8
23
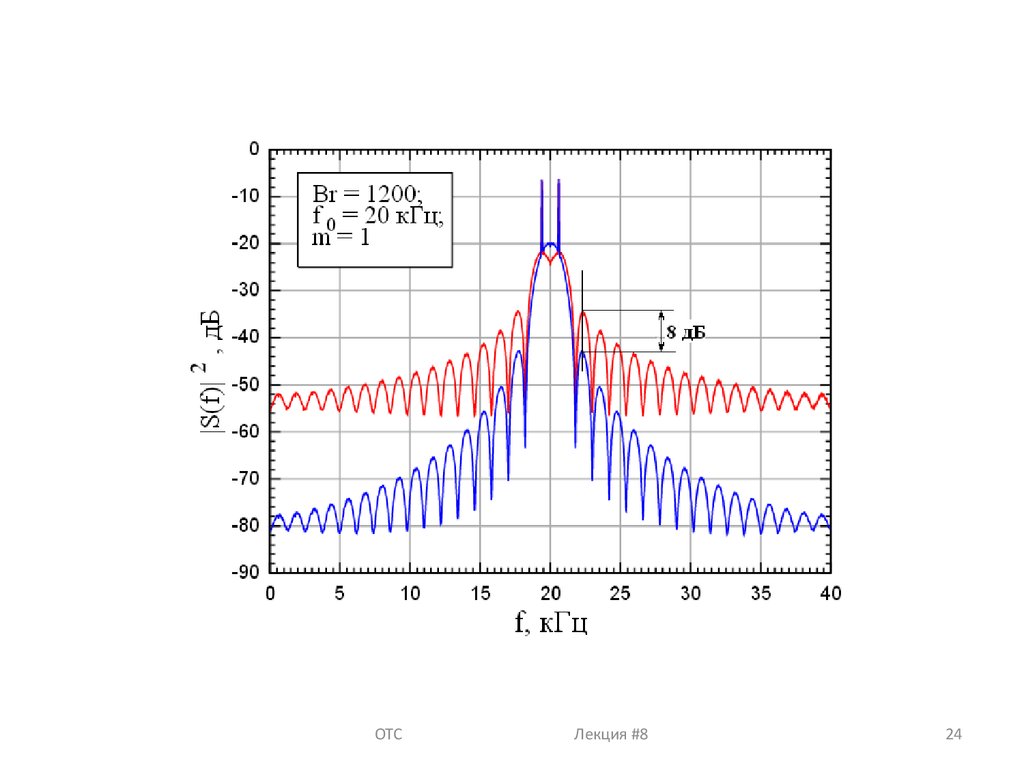
24.
ОТС Лекция #824
25.
Векторная диаграмма ЧМн сигнала с непрерывной фазой (CPFSK)ЧМн сигнал с непрерывной фазой является частным случаем ЧМ сигнала при цифровом входном сигнале, поэтому его векторная
диаграмма не отличается от векторной диаграммы ЧМ сигнала.
Но рассмотрим девиацию фазы Δφ за время длительности Т модулирующего сигнала:
T
Dj = w d × ò 1 ×dt = w d × T
0
mW b = w d
W b = Br × p
D j = m × p × Br × T = m × p
При одном информационном символе набег фазы Δφ за время длительности Т модулирующего сигнала при m=1 равен π
Если информационных символов несколько например L, то набег фазы Δφ за время длительности Т модулирующего
сигнала ,будет принимать любое значение от 0 до L m
π с шагом m π .
ОТС Лекция #8
25
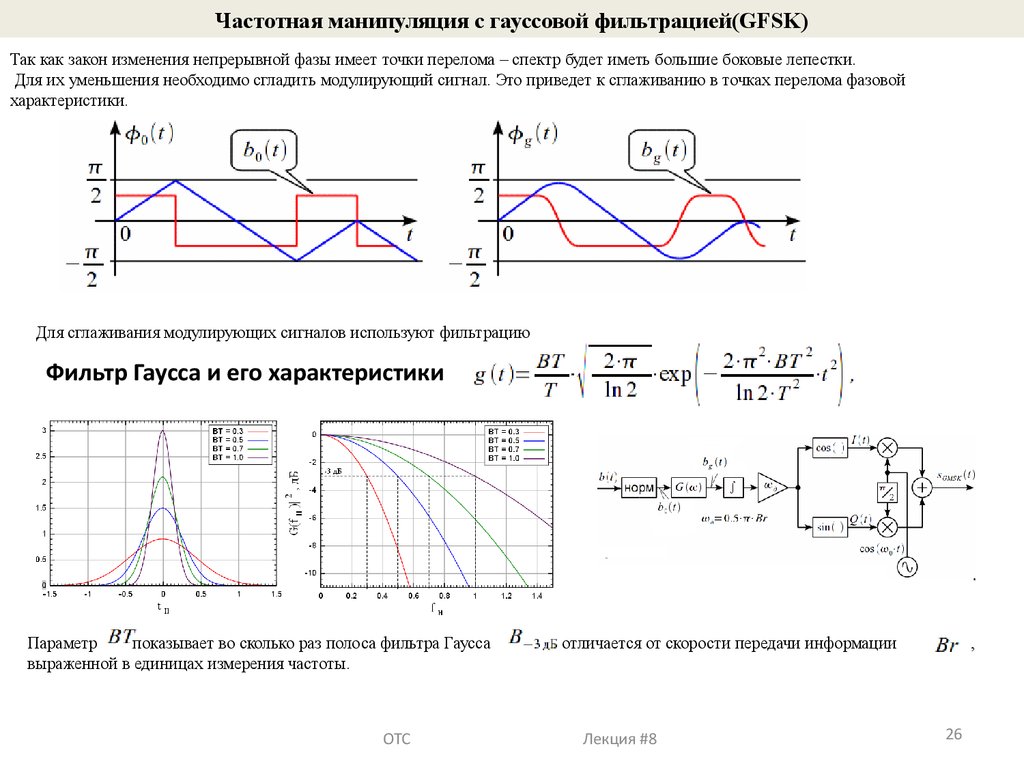
26.
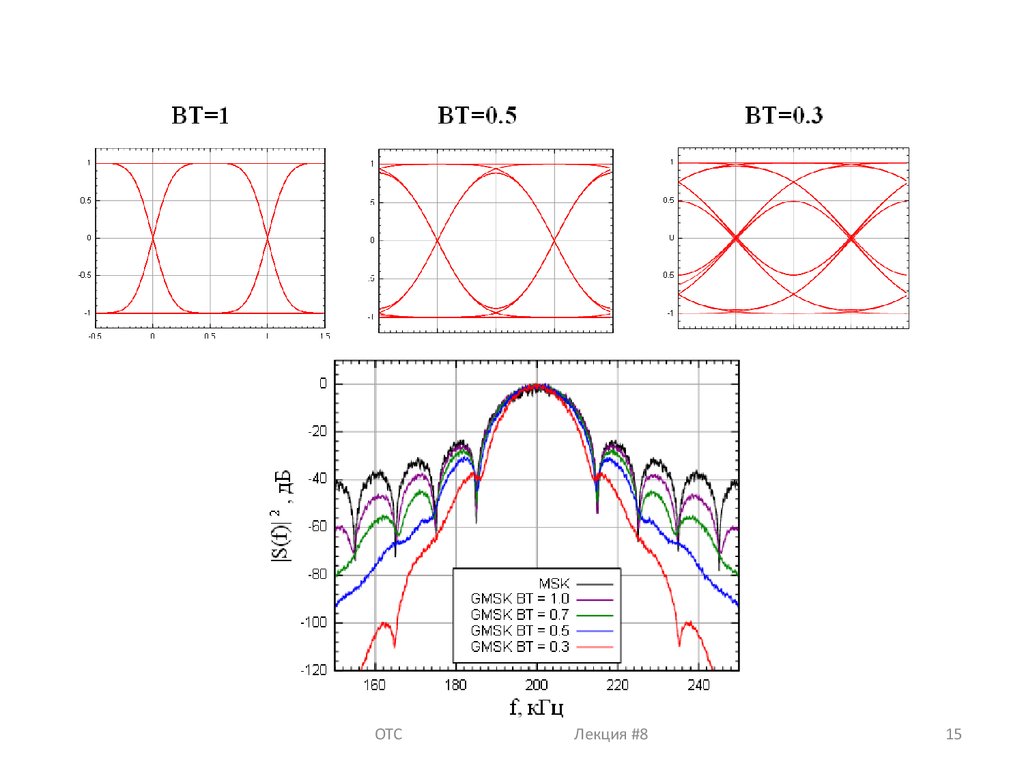
Частотная манипуляция с гауссовой фильтрацией(GFSK)Так как закон изменения непрерывной фазы имеет точки перелома – спектр будет иметь большие боковые лепестки.
Для их уменьшения необходимо сгладить модулирующий сигнал. Это приведет к сглаживанию в точках перелома фазовой
характеристики.
Для сглаживания модулирующих сигналов используют фильтрацию
Фильтр Гаусса и его характеристики
Параметр
показывает во сколько раз полоса фильтра Гаусса
выраженной в единицах измерения частоты.
отличается от скорости передачи информации
ОТС Лекция #8
,
26
27.
ОТС Лекция #827
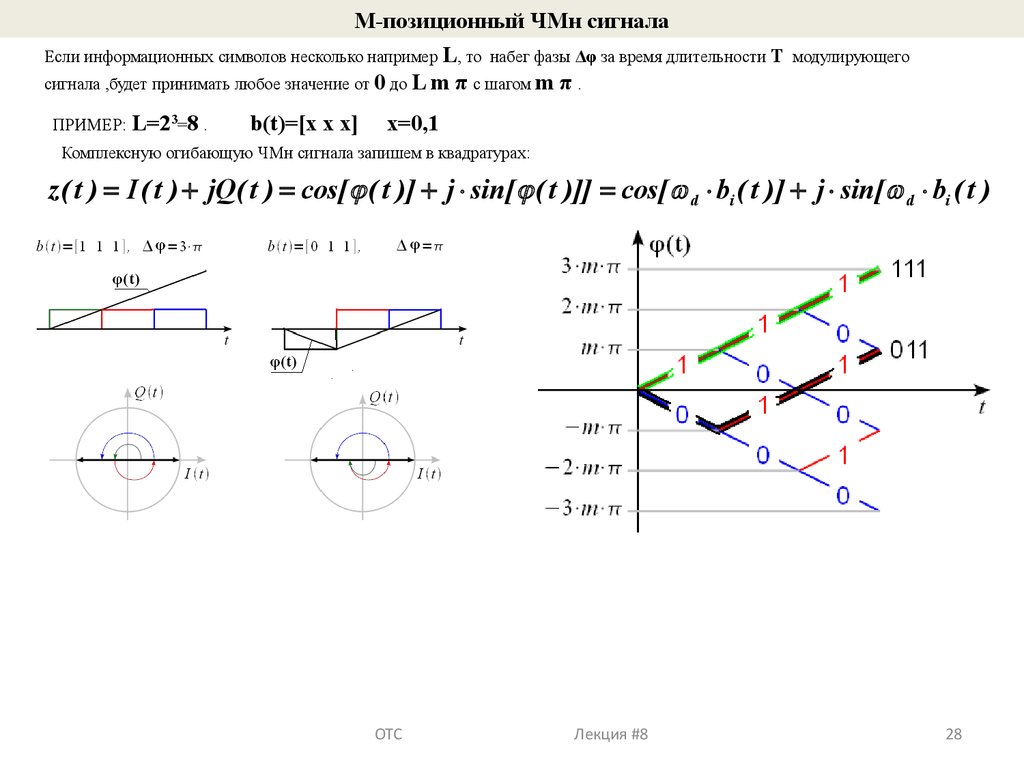
28.
М-позиционный ЧМн сигналаЕсли информационных символов несколько например L, то набег фазы Δφ за время длительности Т
сигнала ,будет принимать любое значение от 0 до L m π с шагом m π .
ПРИМЕР: L=23=8 .
b(t)=[x x x]
модулирующего
x=0,1
Комплексную огибающую ЧМн сигнала запишем в квадратурах:
z( t ) = I( t ) + jQ( t ) = cos[ j ( t )] + j × sin[ j ( t )]] = cos[ w d × bi ( t )] + j × sin[ wd × bi ( t )
ОТС Лекция #8
28
29.
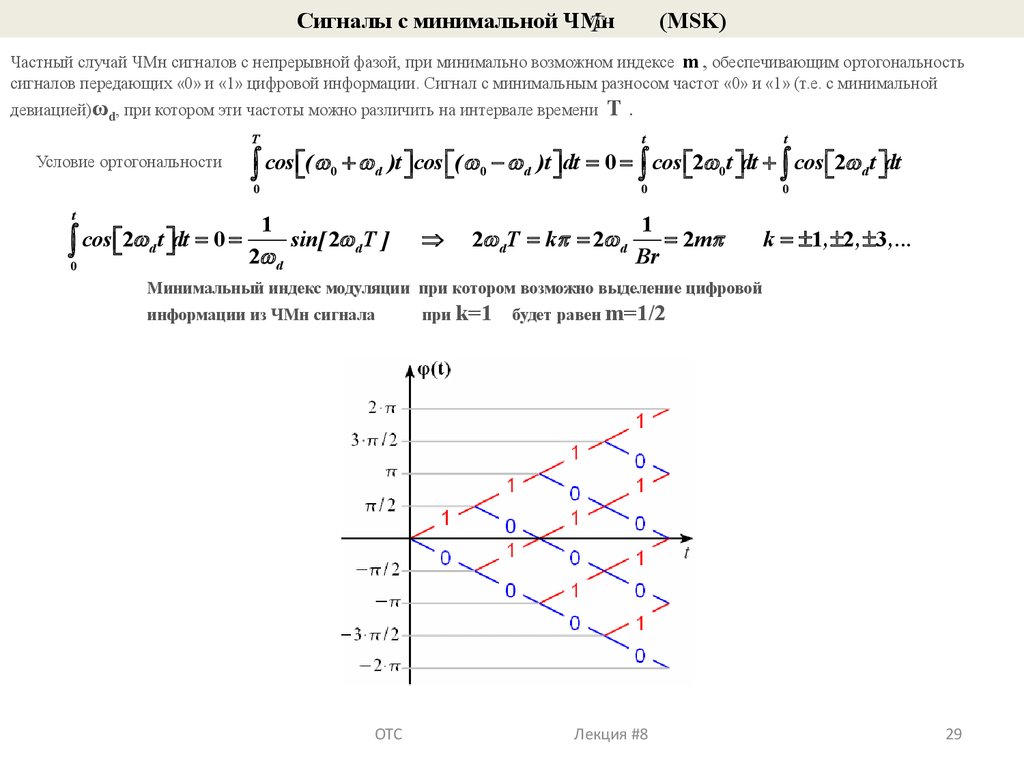
Сигналы с минимальной ЧМн(MSK)
Частный случай ЧМн сигналов с непрерывной фазой, при минимально возможном индексе m , обеспечивающим ортогональность
сигналов передающих «0» и «1» цифровой информации. Cигнал с минимальным разносом частот «0» и «1» (т.е. с минимальной
девиацией)ωd, при котором эти частоты можно различить на интервале времени
T
Условие ортогональности
ò cos éë( w
0
t
ò cos éë2wd t ùûdt = 0 =
0
0
T.
t
t
0
0
+ w d )t ùû cos éë( w 0 - w d )t ùû dt = 0 = ò cos éë 2w0 t ùûdt + ò cos éë 2w d t ùûdt
1
sin[ 2w d T ]
2wd
Þ
2w d T = kp = 2wd
1
= 2mp
Br
k = ±1, ±2 , ±3 , ...
Минимальный индекс модуляции при котором возможно выделение цифровой
информации из ЧМн сигнала
при k=1
будет равен m=1/2
ОТС Лекция #8
29
30.
Сигналы с фазовой манипуляцией ФМн2(BPSK)
Униполярный и биполярный цифровые сигналы
z( t ) = I( t ) + jQ( t ) = cos[ p b( t )] + j × sin[ p b( t )]] = cos[ p × b( t )] = m1 = b0 ( t )
sBPSK ( t ) = b0 ( t )cos( w 0 t + j 0 )
ОТС Лекция #8
30
31.
Временная диаграмма сигнала с фазовой манипуляцией ФМн2(BPSK)
ФМн2 (BPSK) модуляция – вырожденный тип фазовой манипуляции, который совпадает с балансной амплитудной модуляцией
при биполярном цифровом модулирующем сигнале
ОТС Лекция #8
31
32.
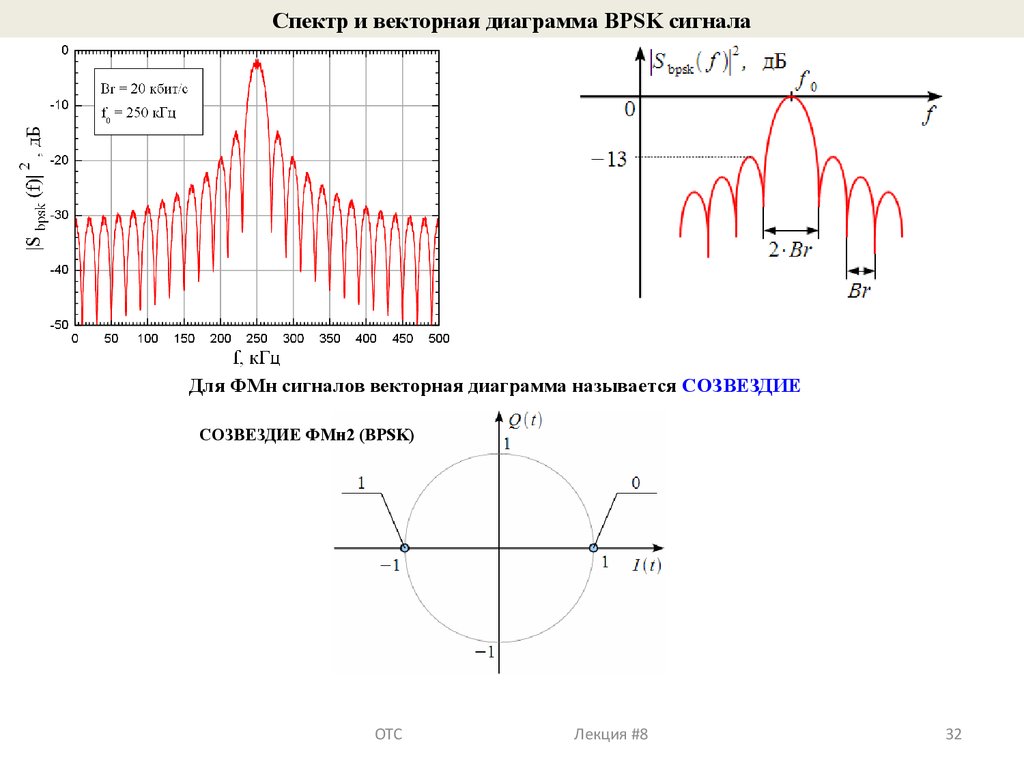
Спектр и векторная диаграмма BPSK сигналаДля ФМн сигналов векторная диаграмма называется СОЗВЕЗДИЕ
СОЗВЕЗДИЕ ФМн2 (BPSK)
ОТС Лекция #8
32
33.
Дифференциальная (относительная) ФМн2Дифференциальный кодер и декодер
XOR (исключающее ИЛИ)
Декодирование
Исправление обратной работы
Размножение ошибок при декодировании
ОТС Лекция #8
33
34.
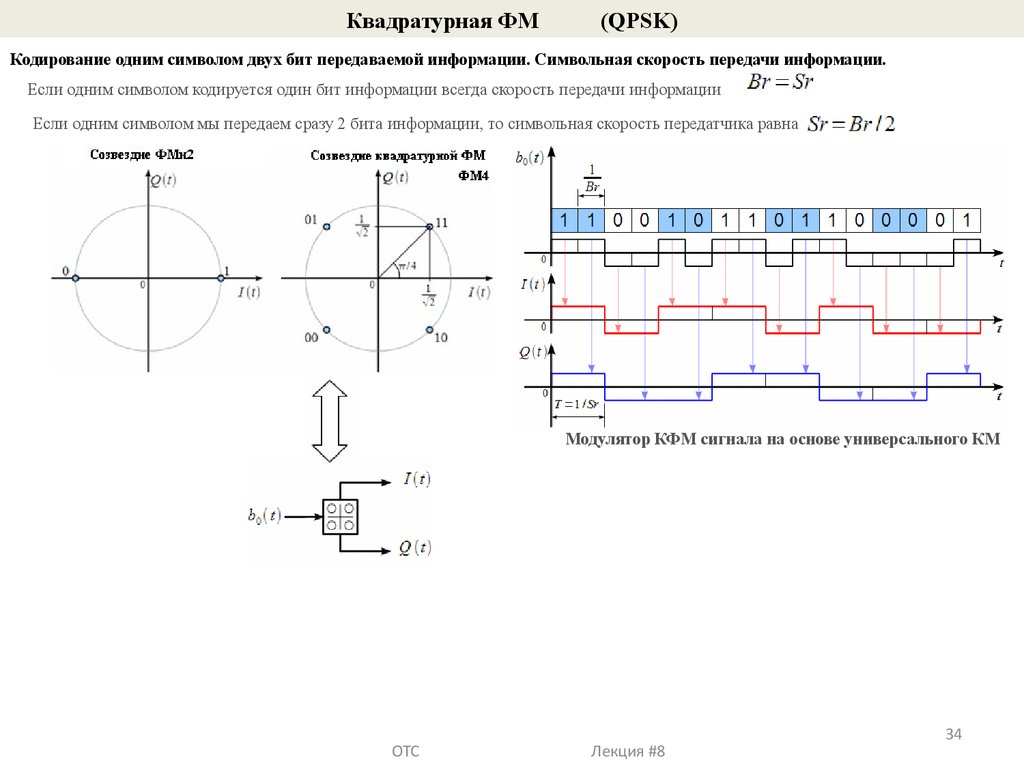
Квадратурная ФМ(QPSK)
Кодирование одним символом двух бит передаваемой информации. Символьная скорость передачи информации.
Если одним символом кодируется один бит информации всегда скорость передачи информации
Eсли одним символом мы передаем сразу 2 бита информации, то символьная скорость передатчика равна
Модулятор КФМ сигнала на основе универсального КМ
ОТС Лекция #8
34
35.
Квадратурная ФМ(QPSK)
{
sQPSK ( t ) = I( t )cos éëw 0 t + j 0 ùû - Q( t ) sin éëw 0t + j 0 ùû = Re z( t )e jw0 t
z( t ) = I( t ) + jQ( t )
æ Q( t ) ö
j ( t ) = arctg 2 ç
÷
è I( t ) ø
A( t ) = Q 2 ( t ) + I 2 ( t )
}
Комплексная огибающая
Фаза комплексной огибающей (с учетом квадранта)
Физическая огибающая (везде постоянна кроме моментов времени смены символов
ОТС Лекция #8
35
36.
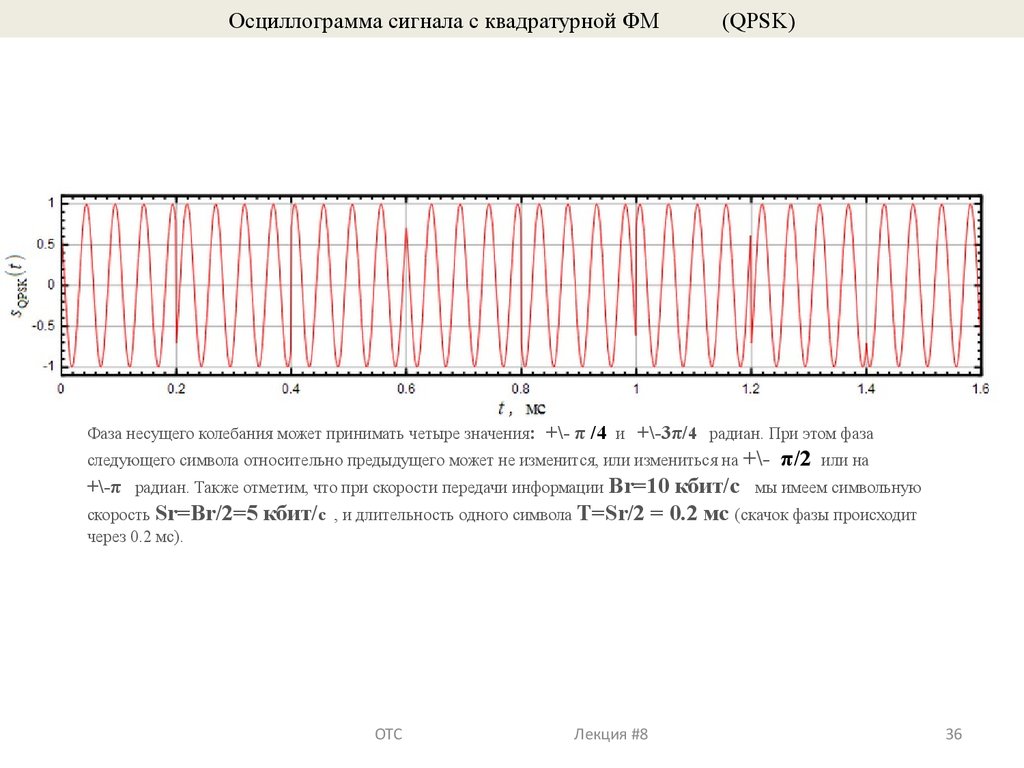
Осциллограмма сигнала с квадратурной ФМ(QPSK)
Фаза несущего колебания может принимать четыре значения: +\- π /4 и +\-3π/4 радиан. При этом фаза
следующего символа относительно предыдущего может не изменится, или измениться на +\-
π/2
или на
+\-π радиан. Также отметим, что при скорости передачи информации Br=10 кбит/с мы имеем символьную
скорость Sr=Br/2=5
через 0.2 мс).
кбит/с
, и длительность одного символа T=Sr/2
ОТС Лекция #8
= 0.2 мс (скачок фазы происходит
36
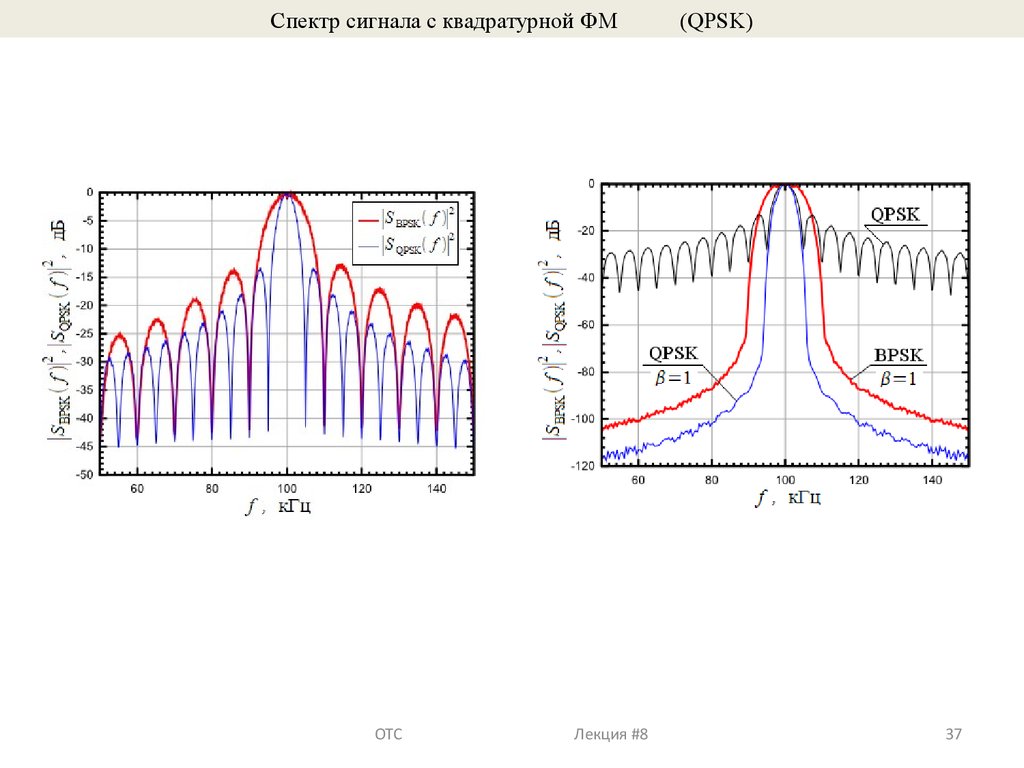
37.
Спектр сигнала с квадратурной ФМОТС Лекция #8
(QPSK)
37
38.
ОТС Лекция #838





















 Электроника
Электроника








