Линейная механика разрушения. Тема 3. Семинар 3.2. Оценка КИН методом сечений, экспериментально и с помощью МКЭ

1. МИНИСТЕРСТВО НАУКИ И ВЫСШЕГО ОБРАЗОВАНИЯ РОССИЙСКОЙ ФЕДЕРАЦИИ МОСКОВСКИЙ ПОЛИТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ Кафедра «Динамика,

прочность машин и сопротивление материалов»
Дисциплина «Основы физики прочности и механики разрушения»
Тема 3. Линейная механика разрушения
Семинар 3.2. Оценка КИН методом сечений,
экспериментально и с помощью МКЭ. Решение
практических задач по анализу хрупкой прочности.
Лектор:
д.т.н., профессор
Полилов А.Н.
Москва, 2020

2. Аннотация

Рассмотрены вывод формулы Гриффитса и
оценка допустимых напряжений. Изучен метод
податливости для определения критической
скорости высвобождения энергии, а также
метод экспериментального определения КИН.
Доказана
эквивалентность
энергетического
(Гриффитса) и силового (Ирвина) критериев
роста трещины – в линейно упругой постановке
задачи.

3. Разделы:

С3.2.1. Метод экспериментального определения
КИН и анализ требований к линейности
диаграммы и к размерам образцов.
С3.2.2. Решение практических задач по анализу
хрупкой прочности различных конструктивных
элементов.
С3.2.3. Инженерный метод сечений для оценки
КИН.
С3.2.4. Доказательство и численное сравнение
эквивалентности энергетического (Гриффитса) и
силового (Ирвина) критериев роста трещины.

4. С3.2.1. Метод экспериментального определения КИН и анализ требований к линейности диаграммы и к размерам образцов

Трещина получает возможность
распространяться тогда, когда:
1. Интенсивность освобождающей энергии G
достигает критического значения.
2. Коэффициент интенсивности К достигает
критического значения.

5. Модель трещины и асимптотика напряжений

F k l 2 z 2 - функция напряжений
yy xy 0 при x l ;
u y = 0 при x l.
Производная от функции
напряжений:
dF
kz
dz
l2 z2
Напряжения вблизи вершины
трещины:
Модель трещины в виде
«математического» разреза
Коэффициентом интенсивности
напряжений (КИН):
dF
k (l +r )
k (1+r / l )
k l
yy ( x) Im
.
r / l 0
2
2
2
dz
2 r
(l r ) l
2r / l ( r / l )
yy
KI
3
yy ( x)
(1 O( 2 ))
4
2 r
yy
KI k l
КИН при одноосном
равномерном растяжении:
K I yy l Y (l / w)
Y (l / w) К-тарировка.

6.

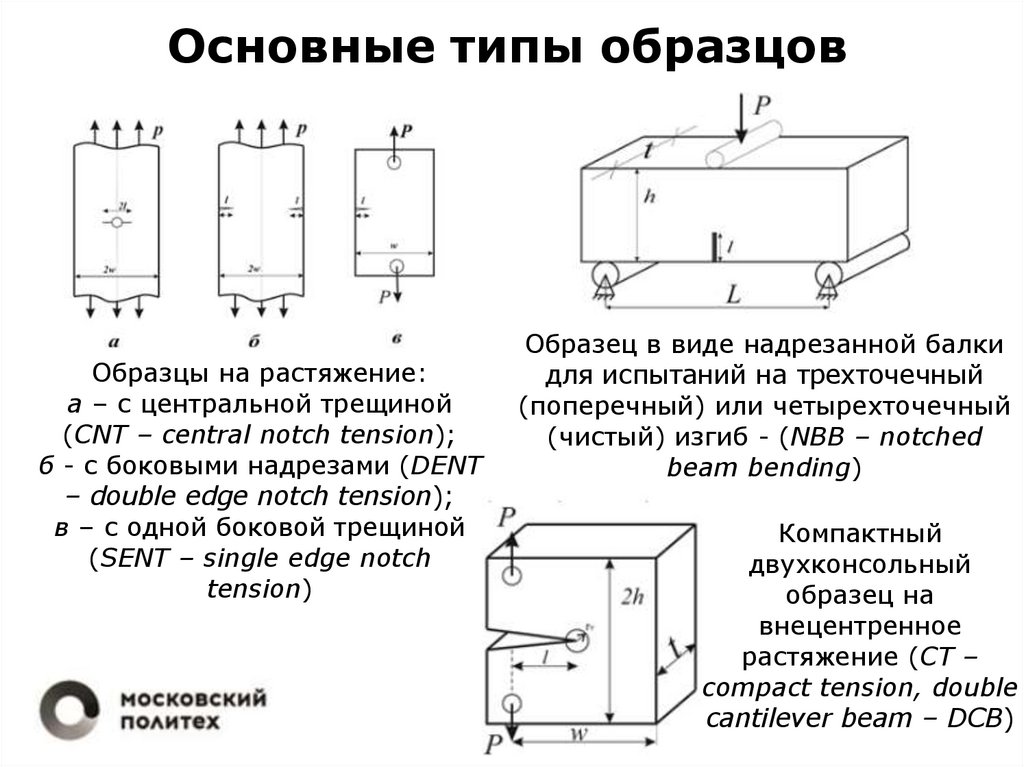
Основные типы образцов
Образцы на растяжение:
а – с центральной трещиной
(CNT – central notch tension);
б - с боковыми надрезами (DENT
– double edge notch tension);
в – с одной боковой трещиной
(SENT – single edge notch
tension)
Образец в виде надрезанной балки
для испытаний на трехточечный
(поперечный) или четырехточечный
(чистый) изгиб - (NBB – notched
beam bending)
Компактный
двухконсольный
образец на
внецентренное
растяжение (CT –
compact tension, double
cantilever beam – DCB)

7. Экспериментальное определение трещиностойкости. Численное определение К-тарировки

Схема компактного
двухконсольного образца на
внецентренное растяжение

8. Определение КИН через К-тарировку

два выражения для К-тарировки для надрезанных
балок, испытываемых на трехточечный изгиб:
и четырехточечный изгиб:

9. Определение критического коэффициента интенсивности напряжений при изгибе надрезанной балки и при растяжении плоских образцов с

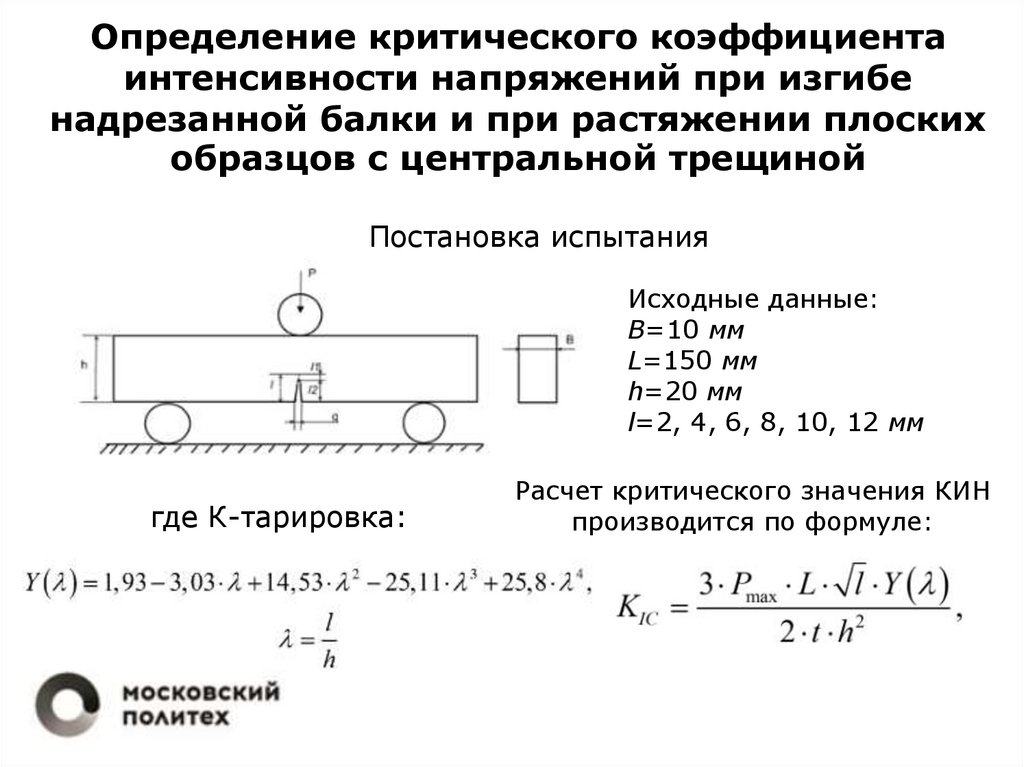
центральной трещиной
Постановка испытания
Исходные данные:
B=10 мм
L=150 мм
h=20 мм
l=2, 4, 6, 8, 10, 12 мм
где К-тарировка:
Расчет критического значения КИН
производится по формуле:

10. Требования к размерам образцов и к линейности диаграммы

Ограничения на размеры
В линейном случае поле напряжений около вершины
трещины определяется единственным параметром –
коэффициентом интенсивности напряжений:
где r – расстояние от вершины трещины. Если
предельный размер пластической зоны мал, то он
также определяется критическим КИН и пределом
текучести:

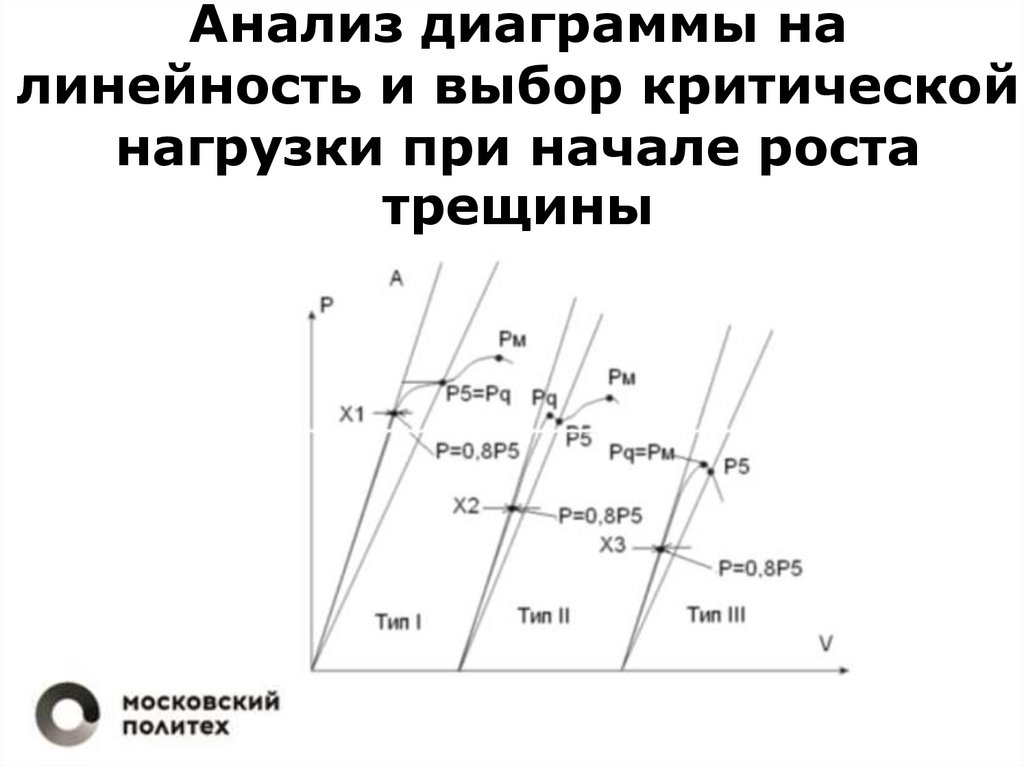
11. Анализ диаграммы на линейность и выбор критической нагрузки при начале роста трещины

12. Ограничения на линейность диаграммы

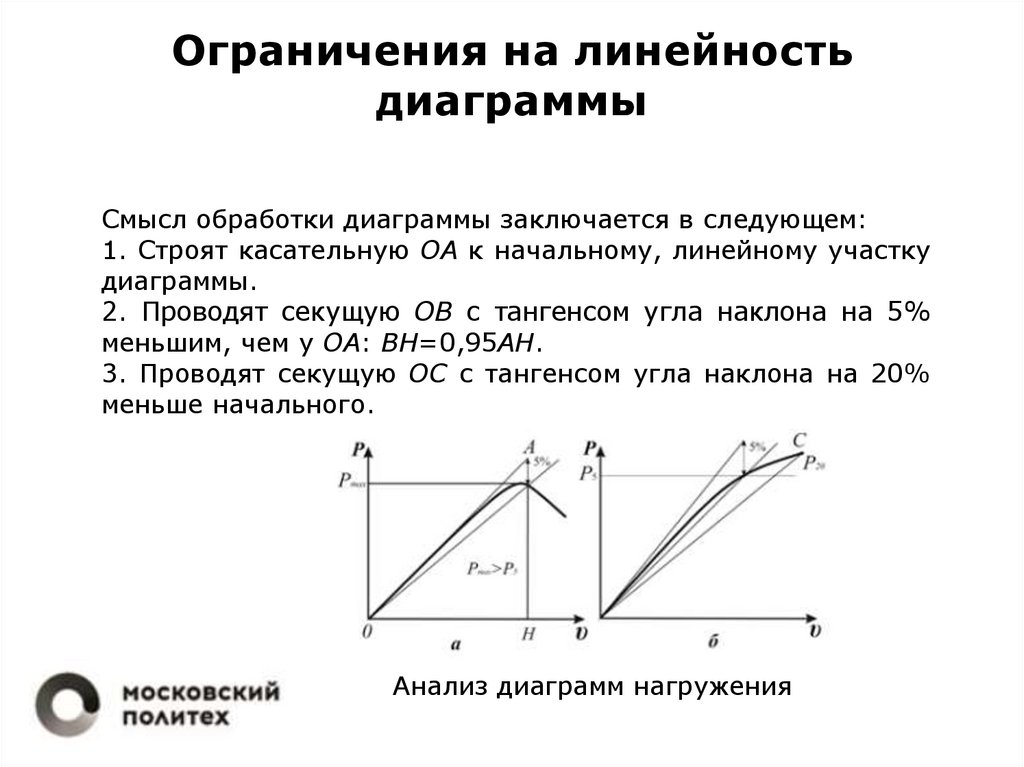
Смысл обработки диаграммы заключается в следующем:
1. Строят касательную ОА к начальному, линейному участку
диаграммы.
2. Проводят секущую ОВ с тангенсом угла наклона на 5%
меньшим, чем у ОА: ВН=0,95АН.
3. Проводят секущую ОС с тангенсом угла наклона на 20%
меньше начального.
Анализ диаграмм нагружения

13. Результаты работы

Проверка требований образца для выполнения
условий применимости линейной механики
разрушения:
при E=21000 кг/мм2

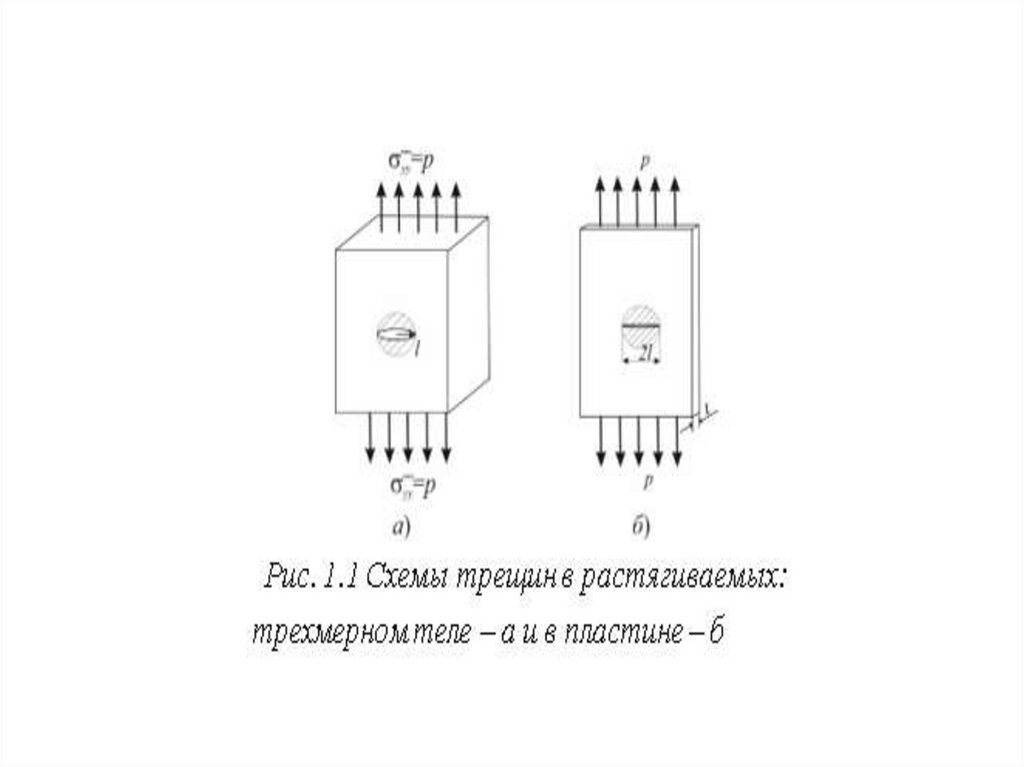
14. С3.2.2.Оценка допустимых: напряжений и длин трещин

Критическое равномерное
напряжение для тела с внутренней
(или для пластины со сквозной)
трещиной с начальной длиной 2l0
EGc
k1l0
c
Критическая длина
трещины 2l :
c
EGc
lc
k1 a2
:

15. Решение практических задач по анализу хрупкой прочности различных конструктивных элементов

Расчеты допустимых длин трещин через критический КИН
Непосредственное использование в расчетах энергетической
теории Гриффитса требует анализа напряженного состояния
конструкции в целом. В связи с этим английский инженер-механик
Ирвин предложил использовать в расчетах единственный
локальный
параметр
трещиностойкости
–
коэффициент
интенсивности
напряжений
(КИН),
представляющий
собой
коэффициент при сингулярном члене в выражении для напряжений
вблизи вершины трещины. Если значение КИН в конструкции
такое же, как в испытанном образце, то по условию хрупкого
разрушения конструкция и образец равноопасны.
Если в
конструкции достигается критическое значение КИН, определенное
в корректных испытаниях на образцах, то это означает, что
конструкция находится в критическом состоянии.

16. С3.2.3. Оценка КИН инженерным методом сечений и с помощью МКЭ

Коэффициент интенсивности напряжений, КИН (англ.
Stress Intensity factor) используется в линейной механике
разрушения для описания полей напряжений у вершины
трещины. Рост трещины начинается когда КИН достигает
критического значения K K
c
Три вида роста трещины

17. Приближенный метод сечений

Коэффициент интенсивности
напряжений для широкой пластины
с центральной трещиной:
l
yy
2K I a
K I yy l
2
КИН для широкой пластины с
наклонной трещиной:
K I sin l ;
yy
2
K II sin cos l
yy
Иллюстрация к методу сечений
для определения КИН

18. Теория Гриффитса. Зависимость критических напряжений от длины трещины

19.

20.

Рост трещины становится возможным,
когда при её подрастании высвобождение
(уменьшение) накопленной в теле упругой
энергии dU достаточно для образования
двух новых поверхностей трещины
площадью dS:

21.

Общая накопленная упругая энергия

22.

Изменение упругой энергии

23.

Основной результат, получаемый из
условия (1.1)

24.

Такой же, как (1.4), качественный результат
можно получить для пластины толщиной
t=1 со сквозной трещиной длиной 2l

25.

Для сквозной трещины в широкой
пластинке в условиях плоского
напряженного состояния это условие
принимает вид:
а для плоской деформации:

26. Связь удельной работы разрушения с критическим КИН

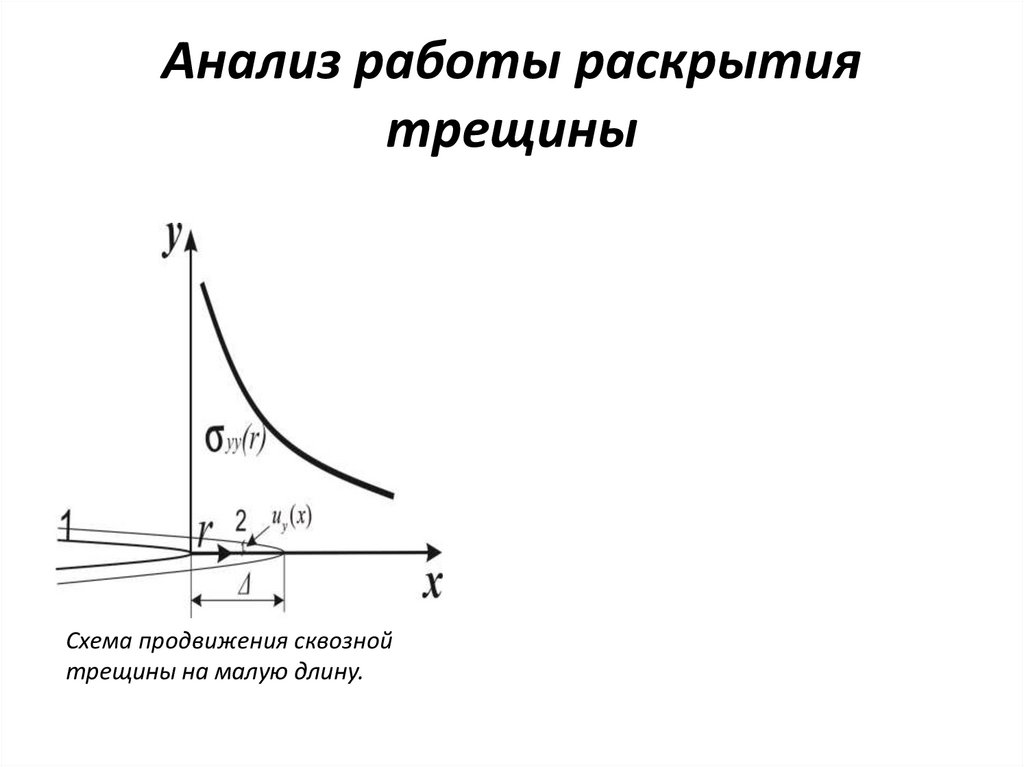
27. Анализ работы раскрытия трещины

Схема продвижения сквозной
трещины на малую длину.

28. Доказательство прямой связи скорости высвобождения энергии и коэффициента интенсивности напряжений

29. Вывод связи коэффициентов интенсивности напряжений со скоростями высвобождения энергии при других модах раскрытия трещины

30. Область применимости ЛМР

ЛМР имеет достаточно узкую область применения –
только для материалов с высоким пределом текучести
и с низкой трещиностойкостью, поэтому надо четко
сформулировать те ограничения, в рамках которых
ЛМР поставляет адекватные результаты.

31. Область применения ЛМР. Основные 5 моментов.

• 1. Достаточная «физическая» линейность
диаграммы деформирования
• 2. Ограниченность деформаций
• 3. Малый размер пластической зоны по
отношению к длине трещины.
• 4. Достаточная линейность диаграммы
нагружения
• 5. Достаточно выраженный момент начала
роста трещины

32. 3 ПУТИ перехода в область линейности

При невыполнении вышеописанных
требований необходимо:
1. Увеличить размеры образца
2. Ограничиться испытаниями при низких
температурах
3. Перейти к нелинейной механике
разрушения, к ее более универсальному
критерию.

33. Доказательство и численное сравнение эквивалентности энергетического (Гриффитса) и силового (Ирвина) критериев роста трещины

Прямая связь скорости высвобождения
энергии и коэффициента интенсивности
напряжений:
для плоской деформации:
EGI
K
;
2
(1 )
2
I
для плоского напряженного состояния:
K EGI .
2
I
Схема вычисления работы на
раскрытие трещины при её
подрастании
Эквивалентность силового и
энергетического критериев роста
трещины:
K Ic2 EGIc / (1 2 )
или
K Ic2 EGIc K I K Ic GI GIc

34. Критерий усреднения с учетом Т-напряжений

Критерий усреднения с учетом Тнапряжений

35. Критерий усреднения с учетом Т-напряжений

Одна из попыток уточнения подхода линейной механики
разрушения состоит в учете несингулярных членов в
степенном разложении выражения для напряжений около
вершины трещины. Эти несингулярные члены (не
обращающиеся в бесконечность в вершине трещины)
получили название «Т-напряжения».

36. Заключение

Предлагаем студентам просмотреть
дополнительные материалы, размещенные в
LMS Политеха (https://lms.mospolytech.ru)

37.

СПАСИБО ЗА ВНИМАНИЕ!