Похожие презентации:
Линейная механика разрушения
1.
МИНИСТЕРСТВО НАУКИ И ВЫСШЕГО ОБРАЗОВАНИЯ РОССИЙСКОЙ ФЕДЕРАЦИИМОСКОВСКИЙ ПОЛИТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ
Кафедра «Динамика, прочность машин и сопротивление материалов»
Дисциплина «Основы физики прочности и механики разрушения»
Тема 3. Линейная механика разрушения
Лекция 3.1. Теория Гриффитса-Ирвина. Коэффициент
интенсивности напряжений (КИН).
Лекция 3.2. Эквивалентность силового и
энергетического критериев разрушения.
Лектор:
д.т.н., профессор
Полилов А.Н.
Москва, 2020
2.
АннотацияИзучена
линейная
(сингулярная)
теория
упругости, энергетический критерий разрушения.
Рассмотрена связь силового и энергетического
критериев разрушения, энергетическое условие
Гриффитса-Ирвина для роста трещины, а также
оценки допустимых напряжений при известных
размерах дефектов.
3.
Разделы лекций 3.1, 3.2:3.1.1. Теория Гриффитса-Ирвина.
3.1.2.
Коэффициенты
напряжений (КИН).
интенсивности
3.2.
Эквивалентность
силового
энергетического критериев разрушения.
и
4.
План лекции 3.1:3.1.1. Теория Гриффитса-Ирвина
3.1.1.1. Энергетический критерий Гриффитса
3.1.1.2. Оценка допустимых: напряжений и длин трещин
3.1.1.3.
Экспериментальное
определение
удельной
разрушения
работы
3.1.2. Коэффициент интенсивности напряжений (КИН)
3.1.2.1. Модель трещины и асимптотика напряжений
3.1.2.2. Критерий Ирвина для роста трещины
3.1.2.3. Три моды роста трещины
3.1.2.4. Критерий роста наклонной трещины
3.1.2.5. Приближенный метод сечений
3.1.2.6.
Экспериментальное
определение
трещиностойкости.
Численное определение К-тарировки
План лекции 3.2
Эквивалентность силового и энергетического критериев
3.2.1. Анализ работы раскрытия трещины
3.2.2. Область применимости ЛМР
5.
3.1.1. Теория ГриффитсаИрвинаАлан Арнольд Гриффитс
(1893-1963) – A.A.Griffith
1. Механика разрушения
• Теоретическая
прочность,
концентрация
напряжений
2. Механика композитов
• Прочность тонких бездефектных волокон
• Стекло: пузырьки - давление, волокна –
эластика Эйлера, испытания петлей.
6.
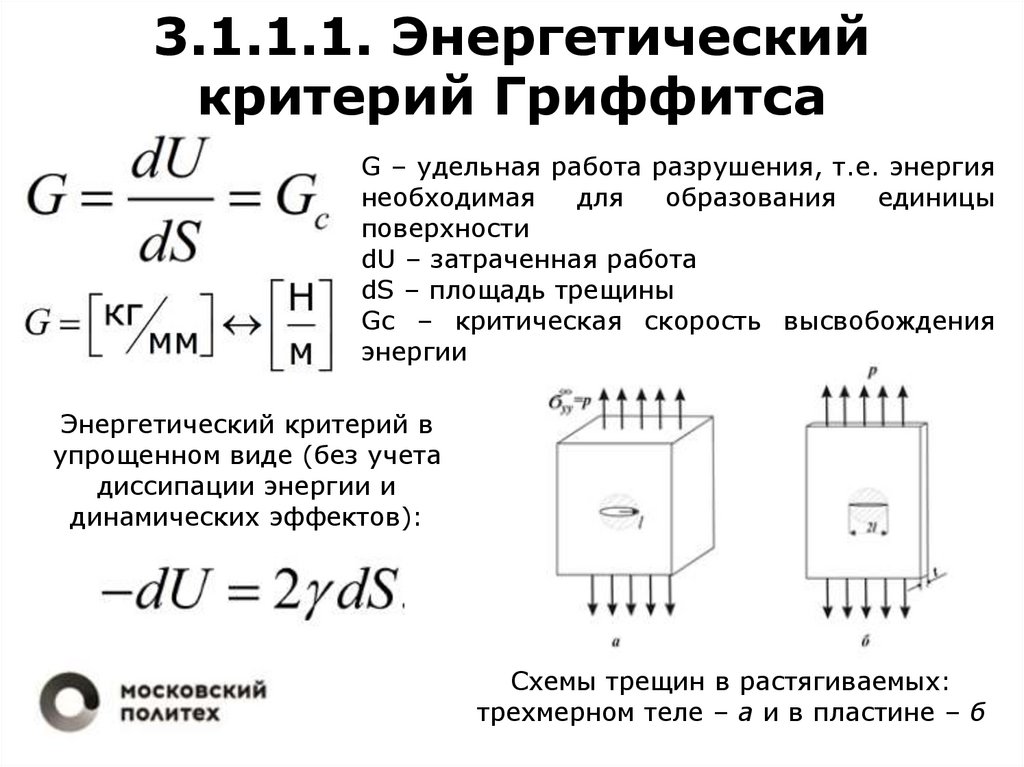
3.1.1.1. Энергетическийкритерий Гриффитса
G – удельная работа разрушения, т.е. энергия
необходимая
для
образования
единицы
поверхности
dU – затраченная работа
dS – площадь трещины
Gс – критическая скорость высвобождения
энергии
Энергетический критерий в
упрощенном виде (без учета
диссипации энергии и
динамических эффектов):
Схемы трещин в растягиваемых:
трехмерном теле – а и в пластине – б
7.
Общая накопленнаяупругая энергия:
U 2 (V k0l 3 ) / (2 E )
Качественный результат для
пластины толщиной t (=1) со
сквозной трещиной длиной
2l:
U (V k2tl ) / (2 E );
2
Изменение упругой
энергии:
dS 2 ldl
dU 3 2 k0l 2 dl / (2 E )
dU 2 dS
EGc
3k0
; k1
(1 2 )
k1l
4
2
dU 2tk2l dl / E; dS tdl;
dU / dS Gc EGc / (k2l ).
Для сквозной трещины в
широкой пластинке в
условиях плоского
напряженного состояния:
2 EGc / ( l )
Для плоской деформации:
2EGc / [(1 2 ) l ].
8.
3.1.1.2. Оценка допустимых:напряжений и длин трещин
Критическое равномерное
напряжение для тела с внутренней
(или для пластины со сквозной)
трещиной с начальной длиной 2l0
EGc
k1l0
c
Критическая длина
трещины 2l :
c
EGc
lc
k1 a2
:
9.
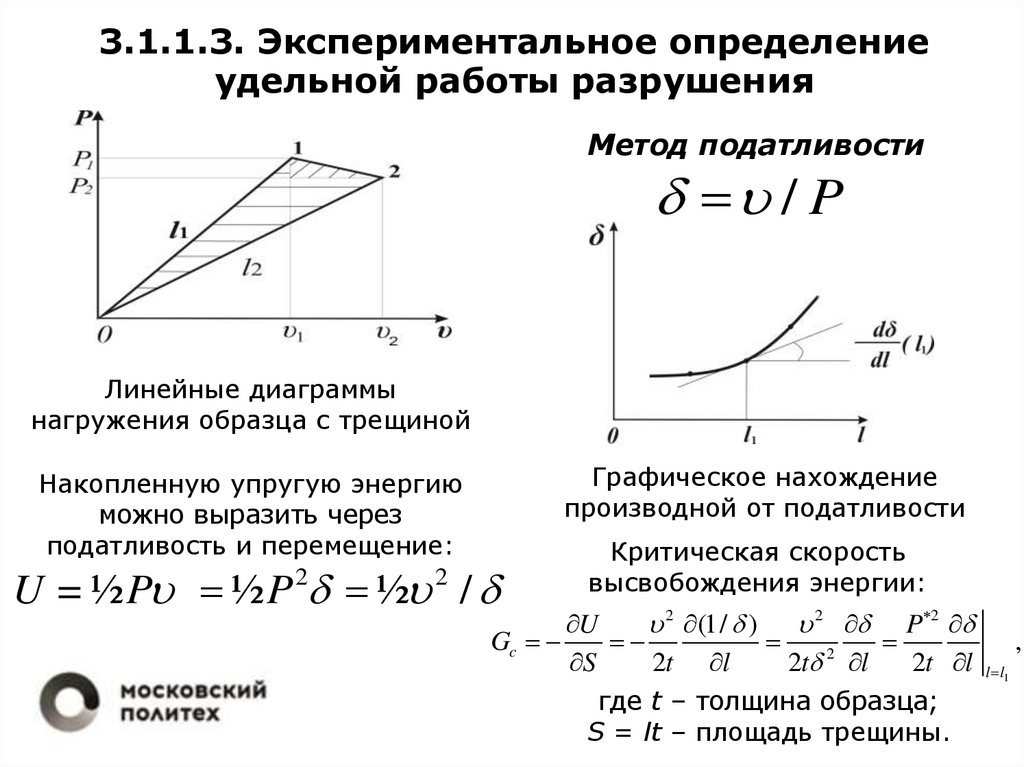
3.1.1.3. Экспериментальное определениеудельной работы разрушения
Метод податливости
/ P
Линейные диаграммы
нагружения образца с трещиной
Накопленную упругую энергию
можно выразить через
податливость и перемещение:
Графическое нахождение
производной от податливости
U = ½ P ½ P 2 ½ 2 /
Критическая скорость
высвобождения энергии:
U
2 (1/ ) 2 P 2
Gc
S
2t l
2t 2 l
2t l
где t – толщина образца;
S = lt – площадь трещины.
,
l l1
10.
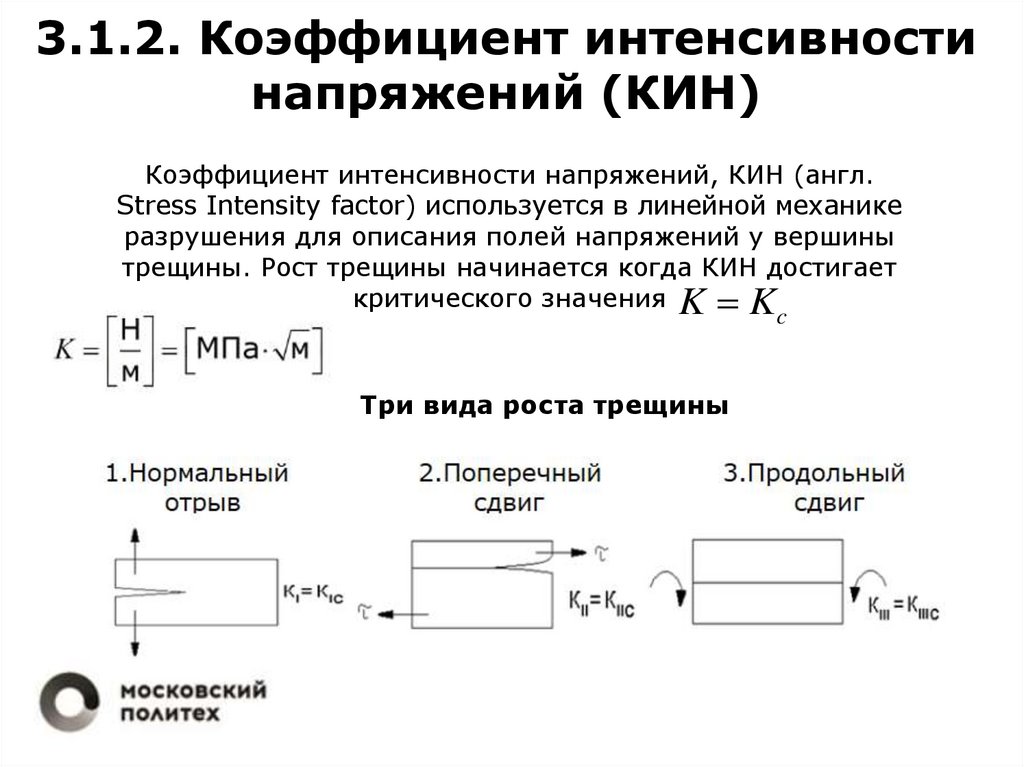
3.1.2. Коэффициент интенсивностинапряжений (КИН)
Коэффициент интенсивности напряжений, КИН (англ.
Stress Intensity factor) используется в линейной механике
разрушения для описания полей напряжений у вершины
трещины. Рост трещины начинается когда КИН достигает
критического значения K K
c
Три вида роста трещины
11.
2.2.1. Модель трещины и асимптотиканапряжений
F k l 2 z 2 - функция напряжений
yy xy 0 при x l;
u y = 0 при x l.
Производная от функции
напряжений:
dF
kz
dz
l2 z2
Напряжения вблизи вершины
трещины:
Модель трещины в виде
«математического» разреза
Коэффициентом интенсивности
напряжений (КИН):
dF
k (l +r )
k (1+r / l )
k l
yy ( x) Im
.
r / l 0
2
2
2
dz
2 r
(l r ) l
2r / l ( r / l )
yy
KI
3
yy ( x)
(1 O( 2 ))
4
2 r
yy
KI k l
КИН при одноосном
равномерном растяжении:
K I yy
l Y (l / w)
Y (l / w) К-тарировка.
12.
3.1.2.2. Критерий Ирвинадля роста трещины
Критерий Ирвина:
K I K Ic
Параметр Ирвина известен как «вязкость
разрушения» (трещиностойкость)
материала
13.
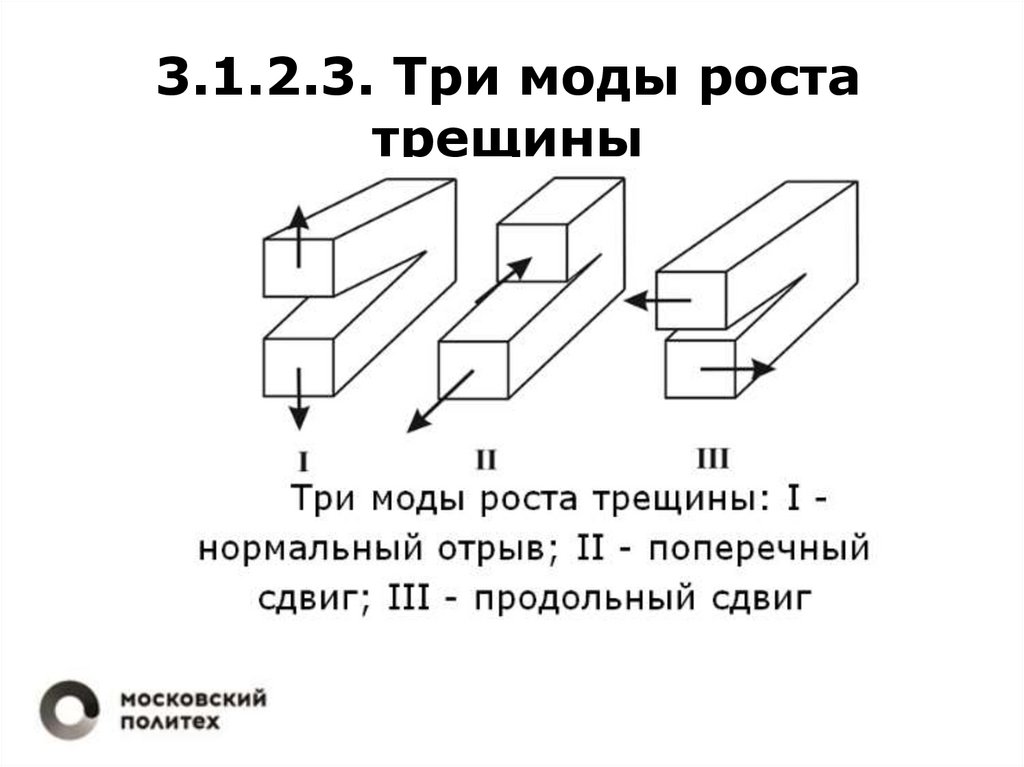
3.1.2.3. Три моды ростатрещины
14.
3.1.2.4. Критерий ростанаклонной трещины
Критерий суммирования
удельных, нормированных
энергий разрушения,
необходимых для роста
трещины:
GI GII
1
GIc GIIc
Схема растяжения пластины с
наклонной трещиной – а и
простейшие виды критерия
роста трещины при
комбинированной моде
перемещения берегов – б
15.
3.1.2.5. Приближенный методсечений
Коэффициент интенсивности
напряжений для широкой пластины
с центральной трещиной:
l
yy
2K I a
K I yy l
2
КИН для широкой пластины с
наклонной трещиной:
K I sin l ;
yy
2
K II sin cos l
yy
Иллюстрация к методу сечений
для определения КИН
16.
3.1.2.6. Экспериментальноеопределение трещиностойкости.
Численное определение К-тарировки
Схема компактного
двухконсольного образца на
внецентренное растяжение
17.
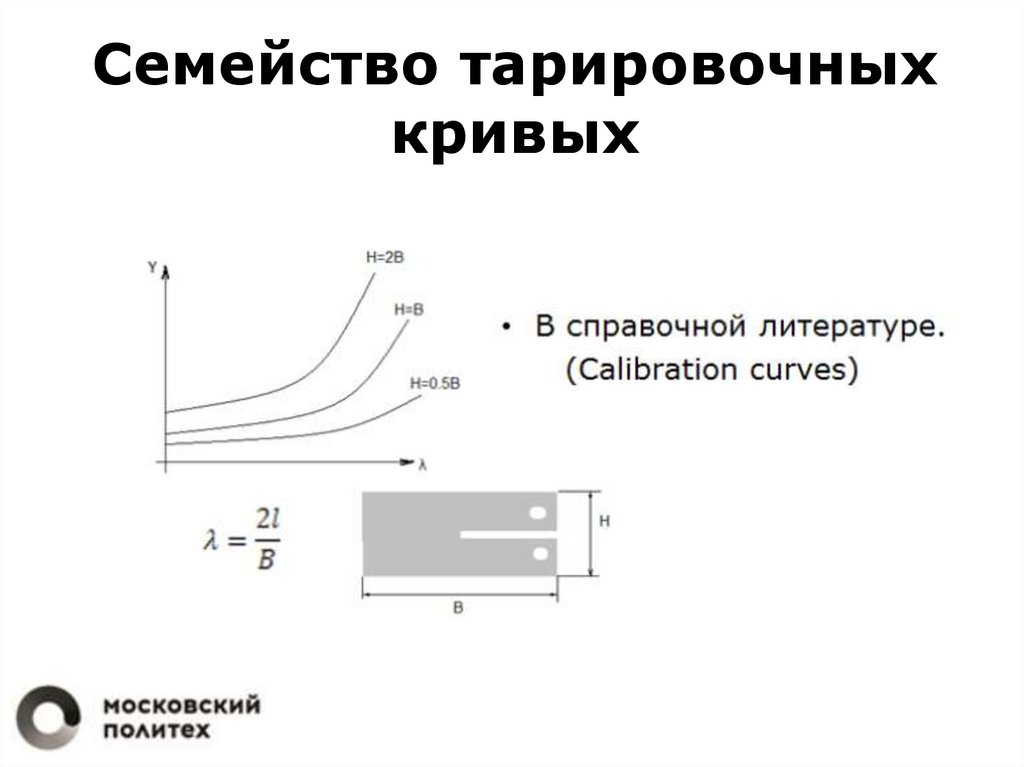
Семейство тарировочныхкривых
18.
Испытания на изгиб(с трещиной)
19.
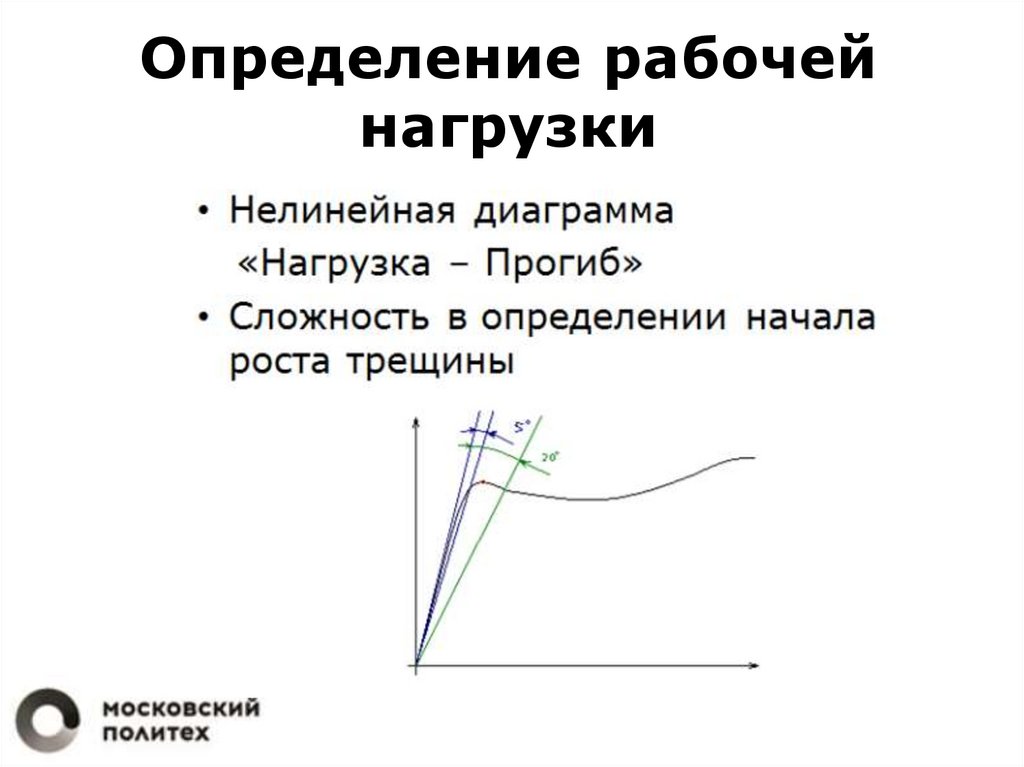
Определение рабочейнагрузки
20.
лекция 3.2.Эквивалентность силового и
энергетического критериев
Трещина получает возможность
распространяться тогда, когда:
1. Интенсивность освобождающей энергии G
достигает критического значения.
2. Коэффициент интенсивности К достигает
критического значения.
21.
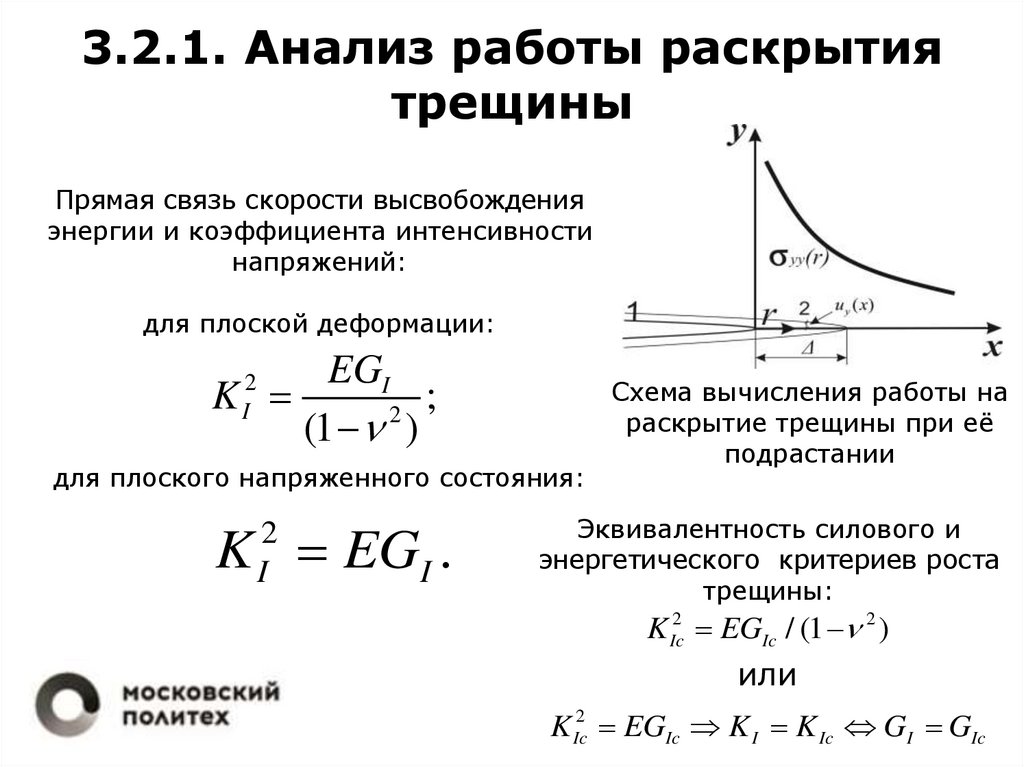
3.2.1. Анализ работы раскрытиятрещины
Прямая связь скорости высвобождения
энергии и коэффициента интенсивности
напряжений:
для плоской деформации:
EGI
K
;
2
(1 )
2
I
для плоского напряженного состояния:
K EGI .
2
I
Схема вычисления работы на
раскрытие трещины при её
подрастании
Эквивалентность силового и
энергетического критериев роста
трещины:
K Ic2 EGIc / (1 2 )
или
K Ic2 EGIc K I K Ic GI GIc
22.
3.2.2. Областиприменимости ЛМР
ЛМР имеет достаточно узкую область применения –
только для материалов с высоким пределом текучести
и с низкой трещиностойкостью, поэтому надо четко
сформулировать те ограничения, в рамках которых
ЛМР поставляет адекватные результаты.
23.
Ограниченность деформаций – геометрическая линейность, которая обеспечиваеткорректность постановки задач теории упругости на исходных, недеформированных
границах, в частности, на прямолинейных берегах трещины.
Малый размер
пластической зоны по отношению к длине трещины и к размерам образца, и поскольку
это обеспечивается специальными требованиями
rY
K / ,
2
I
2
Y
K I2
rY
2 Y2
l , t , ( w l ) 2,5K / .
2
Ic
2
Y
24.
Существуют широкие области наиболее опасных условийнагружения, когда именно линейная механика роста трещин даёт
надёжные оценки условий хрупкого разрушения. К таким
условиям нагружения относятся:
- низкие: климатические или криогенные температуры;
- многоосное напряженное состояние, затрудняющее
пластическое течение около вершины трещины;
- наличие химически активных сред (морская вода, сернистая
нефть, кислоты, щелочи);
- циклические нагрузки (классическая усталость в пределах
упругости);
- высокая скорость нагружения;
- облучение нейтронами или тяжелыми частицами
.
25.
ЗаключениеПредлагаем студентам просмотреть
дополнительные материалы, размещенные в
LMS Политеха (https://lms.mospolytech.ru)



















 Физика
Физика








