Прикладная механика. Часть II. Механика деформируемого твердого тела

1.

ПРИКЛАДНАЯ МЕХАНИКА. Часть II
Механика деформируемого твердого тела.
ЛИТЕРАТУРА
1.
Александров
А.В.,
Потапов
В.Д.,
Державин
Б.П.
Сопротивление
материалов. 7-е изд.— М.: Высшая школа, 2009. — 560 с.
2. Ильин В.Н. Грабарев С.П. Прикладная
механика. Часть 2. Основы
механики деформируемого твердого тела Учебное пособие. – М.: Академия
ГПС МЧС России, 2017 г.
Дополнительная
Сопротивление материалов:
3. Феодосьев В.И.
Учебник для студ-ов
высш.техн.учеб.зав. – 10-е изд., перераб. и доп. – М.: Изд-во МГТУ им. Н.Э.
Баумана, 2008. – 588 с.
4. Дарков А.В.
623 с.
Сопротивление материалов. – М. : Высшая школа, 2007. –
1

2. Тема 1 (8) Введение. Основные понятия МДТТ

1. Предварительные замечания
2. Понятия о деформациях
3. Основные задачи в сопротивлении
материалов
4. Расчетные схемы и классификация
несущих конструкций
5. Классификация внешних сил
6. Основные допущения, гипотезы СМ
2

3.

7. Метод сечений, внутренние силовые
факторы
8. Понятия о напряжениях
9. Классификация видов деформации
стержня
3

4. Предварительные замечания

Прикладная механика (ПМ) ч.2 –
основы механики деформируемого твердого тела
(МДТТ).
Изучаются два инженерных раздела МДТТ:
- сопротивление материалов (сопромат);
- строительная механика.
Предмет и методы сопротивления материалов и
строительной механики.
Сопротивление материалов - наука о прочности,
жесткости и устойчивости элементов
инженерных конструкций. Предмет изучения элементы конструкции (как правило, стержни). 4

5.

Строительная механика - наука о прочности,
жесткости и устойчивости инженерных
конструкций и сооружений. Предмет изучения
- конструкции и сооружения (как правило,
стержневые системы).
Другие разделы МДТТ (позволяющие решать
а) теория упругости;
задачи в более точной постановке с привлечением
более сложного математического аппарата):
б)
в)
г)
д)
е)
ж)
теория пластичности;
теория ползучести;
теория разрушения;
теория пластин и оболочек ;
теория колебаний механических систем;
теория устойчивости механических систем.
5

6.

Методы сопротивления материалов (сопромата) и
строительной механики - приближенные
инженерные, опирающиеся на законы и теоремы
механики сплошных сред, а также несложные
разделы математики.
Большой вклад в развитие науки внесли многие ученые
- из зарубежных
Г. Галилей, Р. Гук , Я. Бернулли, Л. Эйлер, Ш. Кулон,
О.Коши, А. Навье, С. Пуассон, Г. Ламе, Б. Клапейрон и
др.;
- из отечественных:
Д.И. Журавский, Н.А. Белелюбский, Ф.С. Ясинский,
Л.Д.Проскуряков, Б.Г.Галеркин, В.И.Смирнов, С.Л. Соболев,
А.И. Лурье, А.Н. Динник, Б.Н. Жемочкин, А.Н.Крылов,
В.3.Власов, А.А. Гвоздев, В.В. Болотин и многие и др.
6

7. Понятие о деформациях

Деформация тела - это изменение его объема, размеров
и формы под действием приложенных к нему сил или
температурных воздействий (- мера изменения
взаимного расположения точек твердого тела).
Различают деформации упругие и остаточные.
Деформация, которая исчезает после снятия нагрузки,
называется упругой.
Остаточная деформация - которая не исчезает после
снятия нагрузки.
Упругость - свойство тел деформироваться под
нагрузкой и восстанавливать свои первоначальные
геометрические параметры после снятия нагрузки.
7

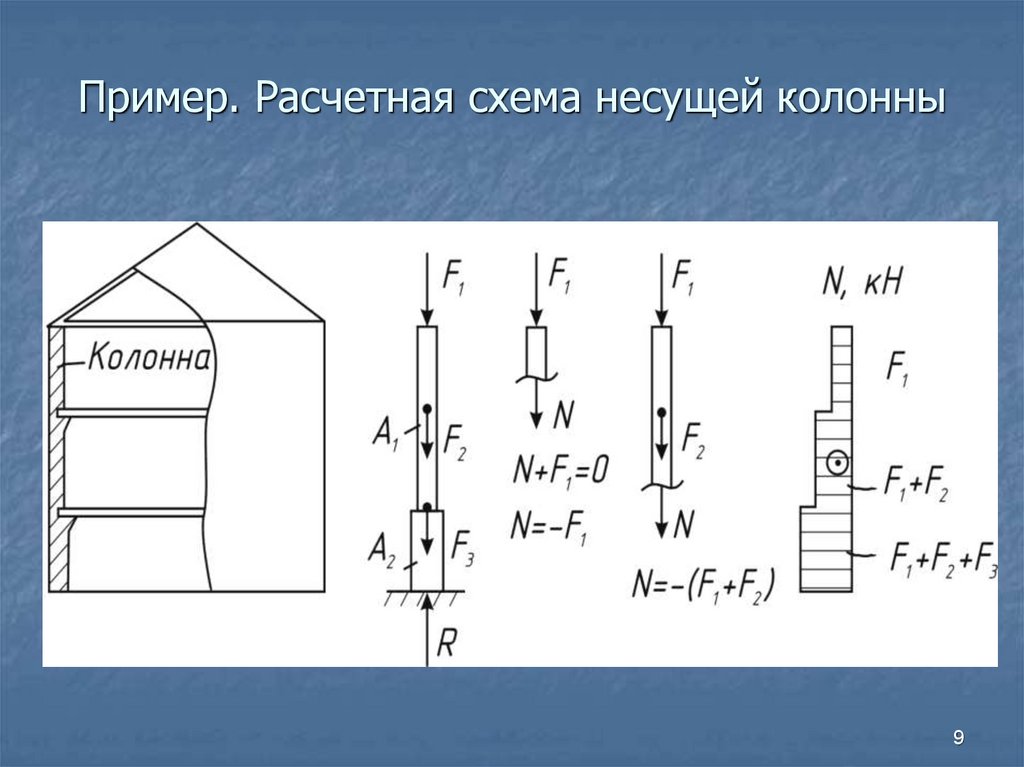
8. Понятие о расчетной схеме конструкций

Расчетная схема (РС) - это упрощенное
схематическое представление реального объекта, в
котором оставлены только главные, существенные
черты (второстепенные – отброшены).
8

9. Пример. Расчетная схема несущей колонны

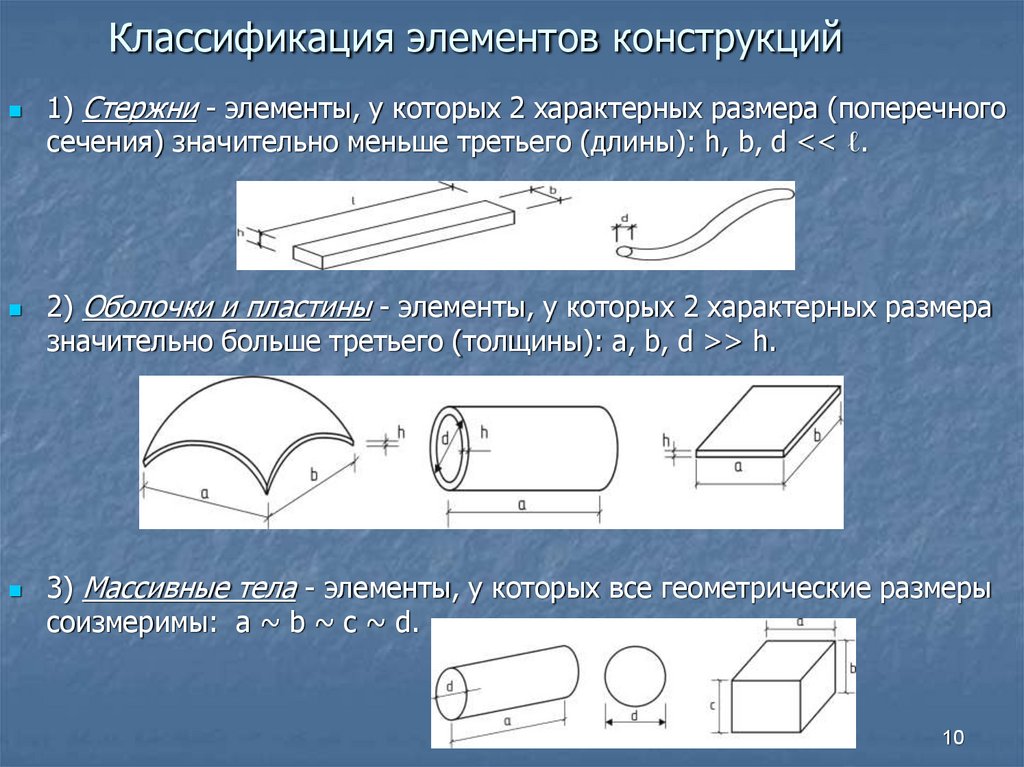
9

10. Классификация элементов конструкций

1) Стержни - элементы, у которых 2 характерных размера (поперечного
сечения) значительно меньше третьего (длины): h, b, d << ℓ.
2) Оболочки и пластины - элементы, у которых 2 характерных размера
значительно больше третьего (толщины): a, b, d >> h.
3) Массивные тела - элементы, у которых все геометрические размеры
соизмеримы: a ~ b ~ c ~ d.
10

11. Способы закрепления стержней и стержневых систем

V
А – шарнирно-неподвижная опора
H
V
V
V
В – шарнирно-подвижная опора
С - жесткая заделка
н,U - горизонтальное перемещение
V - вертикальное перемещение
φ - угол поворота
V
MA
H
11

12. Классификация конструкций

1. По геометрическим свойствам:
а) стержневые;
б) пластины и оболочки;
в) массивные тела.
2. По статическим свойствам:
а) статически определимые;
б) статически неопределимые.
3. По кинематическим свойствам:
а) геометрически неизменяемые;
б) геометрически изменяемые.
12

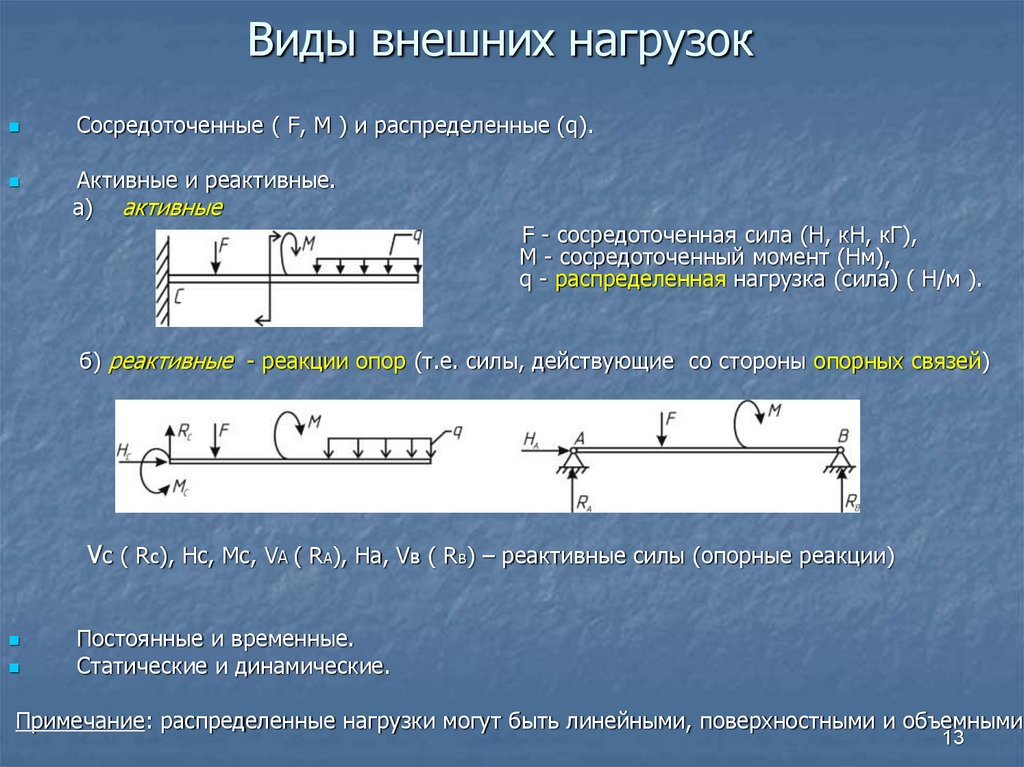
13. Виды внешних нагрузок

Сосредоточенные ( F, М ) и распределенные (q).
Активные и реактивные.
а) активные
F - сосредоточенная сила (Н, кН, кГ),
М - сосредоточенный момент (Нм),
q - распределенная нагрузка (сила) ( Н/м ).
б) реактивные - реакции опор (т.е. силы, действующие со стороны опорных связей)
Vc ( Rc), Hc, Mc, VA ( RA), Hа, Vв ( Rв) – реактивные силы (опорные реакции)
Постоянные и временные.
Статические и динамические.
Примечание: распределенные нагрузки могут быть линейными, поверхностными и объемными.
13

14. Гипотезы сопротивления материалов.

А. Общие гипотезы классической механики
а) гипотеза о сплошности материала, т.е.
материал полагается сплошным без учета атомной и
кристаллической структуры.
б) гипотеза об однородности, т.е. материал
считается одинаковым во всех точках тела,
однородным.
в) гипотеза об изотропности, т.е. материал по
всем направлениям имеет одинаковые свойства
(изотропный).
14

15.

г) гипотеза о малости деформаций и перемещений, т.е.
деформации и перемещения считаем малыми по сравнению с
начальными размерами тела.
v<<h
д) гипотеза о линейной упругости тела, т.е. деформация
пропорциональна нагрузке.
е) Справедлив принцип независимости действия сил
( принцип суперпозиции )
Результат воздействия нескольких внешн. факторов = ∑ результатов воздействия
каждого из них, прикладываемого в отдельности, и не зависит от
последовательности их приложения.
15

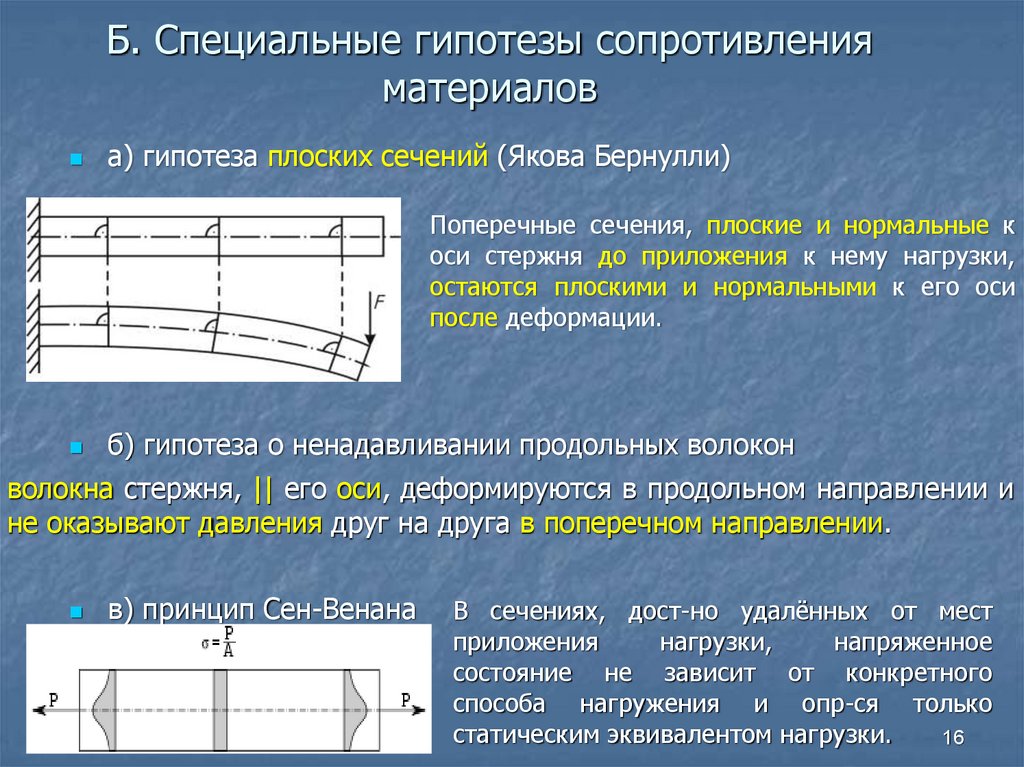
16. Б. Специальные гипотезы сопротивления материалов

а) гипотеза плоских сечений (Якова Бернулли)
Поперечные сечения, плоские и нормальные к
оси стержня до приложения к нему нагрузки,
остаются плоскими и нормальными к его оси
после деформации.
б) гипотеза о ненадавливании продольных волокон
волокна стержня, || его оси, деформируются в продольном направлении и
не оказывают давления друг на друга в поперечном направлении.
в) принцип Сен-Венана
В сечениях, дост-но удалённых от мест
приложения
нагрузки,
напряженное
состояние не зависит от конкретного
способа нагружения и опр-ся только
статическим эквивалентом нагрузки.
16

17.

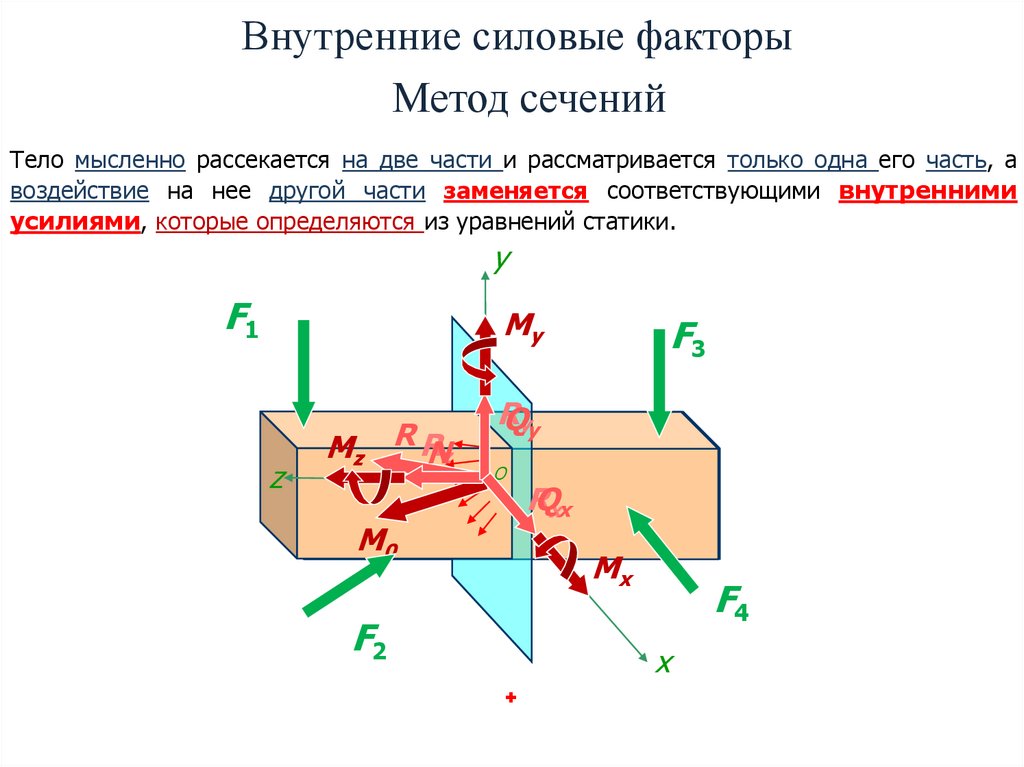
Внутренние силовые факторы
Метод сечений
Тело мысленно рассекается на две части и рассматривается только одна его часть, а
воздействие на нее другой части заменяется соответствующими внутренними
усилиями, которые определяются из уравнений статики.
y
F1
My
z
Mz R RNz
F3
RQyy
O
M0
RQxx
Mx
F2
F4
x
+

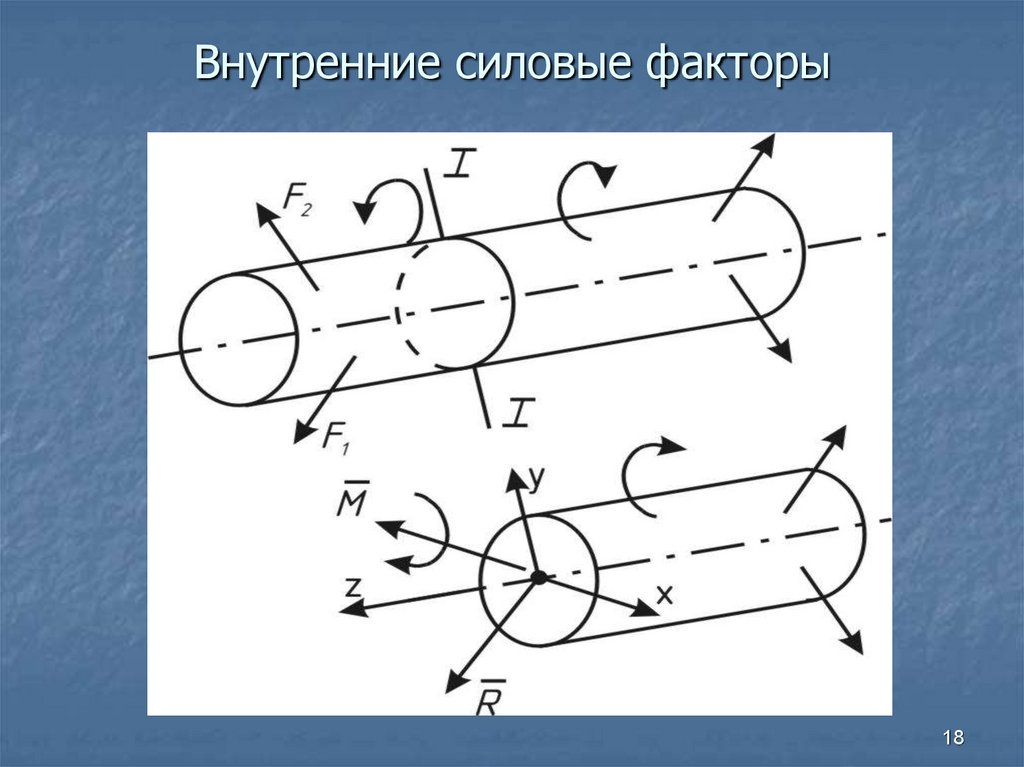
18. Внутренние силовые факторы

18

19.

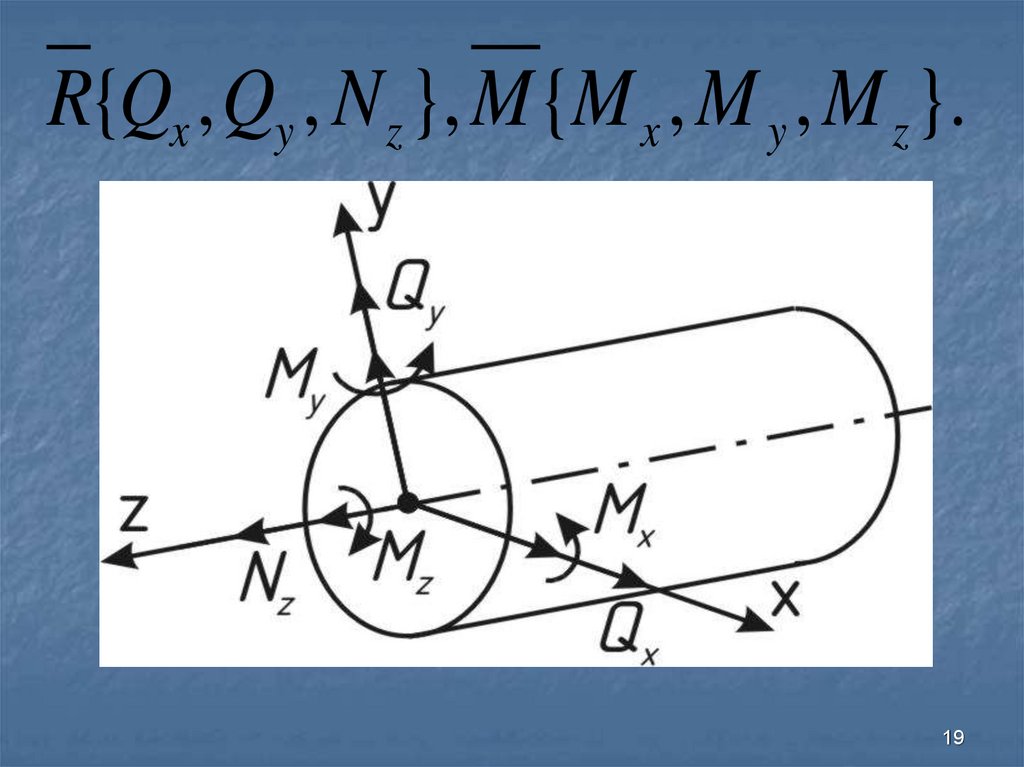
R{Qx , Qy , N z }, M {M x , M y , M z }.
19

20. Уравнения статики

Fx = 0
Fy = 0
Fz = 0
mx (F) = 0
my (F) = 0
mz (F) = 0
Qx = | Fx, внеш |;
Qy = | Fy ,внеш |;
Nz = | Fz ,внеш |;
Mx = | mx ,внеш |;
My = | my ,внеш |;
Mz = | mz ,внеш |;
20

21.

Метод сечений
21

22.

Понятие о напряжениях
Напряжение – мера интенсивности внутренних сил в точке твердого тела
Напряжение при изгибе - esfuerzo de flexion
Напряжение при кручении - esfuerzo de torsión, fatiga a la torsión
Или
Напряжение - это величина внутренней силы, приходящейся на
единицу площади (мысленно выделенной в теле).
А - площадь сечения;
А - элементарная площадь;
R - элементарная внутренняя сила;
p - полное напряжение, [H/м2];
- нормальное напряжение , [H/м2];
- касательное напряжение, [H/м2].
22

23.

23

24. Классификация видов деформации стержня

А. Простые виды деформации.
центральное растяжение и сжатие Nz 0
(Qx = Qy = Mz = My = Mx=0)
чистый изгиб Mx 0 или My 0
(Qx, Qy, Nz, Mx, Mz = 0)
сдвиг Qy 0 (Qx, Nz, Mx, My, Mz = 0) или Qx 0
кручение Mz 0 (Qx, Qy, Nz, Mx = 0)
Б. Сложные виды деформации.
косой изгиб: Мх 0, Му 0;
продольный изгиб: Nz 0, Мx 0;
внецентренное сжатие (или растяжение): Nz 0, Мx 0, Му 0;
изгиб с кручением: Мz 0, Мx 0, Му 0.
24